Calibration of the Discrete Element Method Parameters in Living Juvenile Manila Clam (Ruditapes philippinarum) and Seeding Verification
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Clam DEM Model
2.3. Measurement
2.3.1. The Static Friction Coefficient (μs)
2.3.2. The Restitution Coefficient (e)
2.3.3. The Static Repose Angle (θ)
2.4. DEM Simulation Calibration
2.4.1. Calibration of the Fixed Contact Parameters
2.4.2. Response Surface Simulation Test
2.5. Clam DEM Model Seeding Verification Test
2.6. Statistical Analysis
3. Results and Discussion
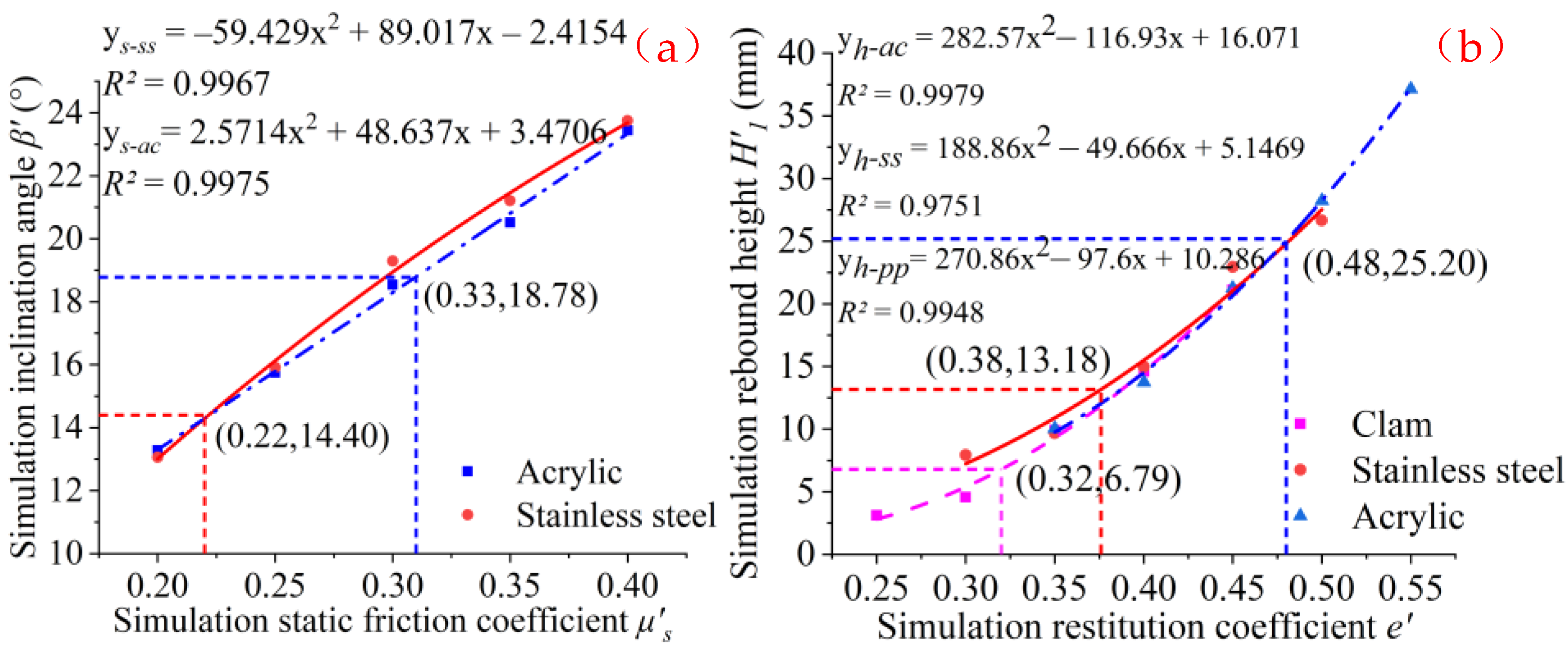
3.1. The Static Friction Coefficient (μs)
3.2. The Coefficient of Restitution (e)
3.3. Response Surface Simulation Test and ANOVA
3.4. Clam Seeding Verification Test
4. Conclusions
- (1)
- The clam simulation contact parameters of different contact materials (SS and AC) were determined by a DEM simulation calibration test. When SS was the contact material, the simulation contact parameters in the calibrated set included: μ′s-pw-ss = 0.22, e’pw-ss = 0.38, e’pp = 0.32, μ′r-pp-ss = 0.33, μ′s-pp-ss = 1.25, μ′r-pw-ss = 0.34. Similarly, with AC, μ′s-pw-ac =0.31, e’pw-ac = 0.48, e’pp = 0.32, μ′r-pp-ac = 0.20, μ′s-pp-ac = 1.12, μ′r-pw-ac = 0.17.
- (2)
- The accuracy of the simulation contact parameters (μ′s-pp, μ′r-pp, μ′s-pw) was simultaneously verified, and they were found to have a significant effect on the clam DEM model.
- (3)
- Through comparing the results of the clam realistic and simulated seeding tests, it was verified that the accuracy of the clam DEM model was high, and therefore it could be applied for clam seeding DEM simulation and equipment design in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, L.H.; Cai, S.L.; Chen, H.B.; Wu, J.N.; Liu, Z.Y.; Su, Y.C. Study of processing technology for leisure food of ready-to-eat Ruditapes philippinarum. J. Fish. Res. 2016, 38, 363–371. [Google Scholar]
- Yuan, H.; Shen, H.; Wang, L.B.; Shi, L.K. Ecological Culture Technology of Ruditapes Philippines Beach. Fish. Sci. Technol. Inf. 2014, 41, 54–56. [Google Scholar]
- Zeng, Z.W.; Ma, X.; Cao, X.L.; Li, Z.H.; Wang, X.C. Critical Review of Applications of Discrete Element Method in Agricultural Engineering. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
- Cundall, P.A.; Strack, O. A discrete numerical model for granular assemblies. Géotechnique 2008, 30, 331–336. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Li, Y.M.; Xu, L.Z.; Chen, J.; Zhao, Z.; Tang, Z. Dispersion and migration of agricultural particles in a variable-amplitude screen box based on the discrete element method. Comput. Electron. Agric. 2017, 142, 173–180. [Google Scholar] [CrossRef]
- Wang, Q.R.; Mao, H.P.; Li, Q.L. Modelling and simulation of the grain threshing process based on the discrete element method. Comput. Electron. Agric. 2020, 11, 178. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Chen, Y. Simulation of straw movement by discrete element modelling of straw-sweep-soil interaction. Biosyst. Eng. 2019, 180, 25–35. [Google Scholar] [CrossRef]
- Xie, H.F.; Gao, G.H.; Tian, B.X.; Li, B.W.; Zhang, S.; Huang, J. Optimization of Potato Soil Transportation Separation Mechanism Based on Discrete Element Method and TRIZ Theory. J. Phys. Conf. Ser. 2019, 1267. [Google Scholar] [CrossRef]
- Liu, W.Z.; HE, J.; Li, H.W.; Li, X.Q.; Zheng, K.; Wei, Z.C. Calibration of Simulation Parameters for Potato Minituber Based on EDEM. Trans. Chin. Soc. Agric. Mach. 2018, 49, 125–135. [Google Scholar]
- Grima, A.P.; Wypych, P.W. Investigation into calibration of discrete element model parameters for scale-up and validation of particle–structure interactions under impact conditions. Powder Technol. 2011, 212, 198–209. [Google Scholar] [CrossRef]
- Liu, F.Y.; Zhang, J.; Li, B.; Chen, J. Calibration of parameters of wheat required in discrete element method simulation based on repose angle of particle heap. Trans. Chin. Soc. Agric. Eng. 2016, 32, 247–253. [Google Scholar]
- Coetzee, C.J. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Shi, L.R.; Ma, Z.T.; Zhao, W.Y.; Yang, X.P.; Sun, B.G.; Zhang, J.P. Calibration of simulation parameters of flaxed seeds using discrete element method and verification of seed-metering test. Trans. Chin. Soc. Agric. Eng. 2019, 35, 25–33. [Google Scholar]
- González-Montellano, C.; Fuentes, J.M.; Ayuga-Téllez, E.; Ayuga, F. Determination of the mechanical properties of maize grains and olives required for use in DEM simulations. J. Food Eng. 2012, 111, 553–562. [Google Scholar] [CrossRef]
- Rackl, M.; Hanley, K.J. A methodical calibration procedure for discrete element models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Boikov, A.V.; Savelev, R.V.; Payor, V.A. DEM Calibration Approach: Design of experiment. J. Phys. Conf. Ser. 2018, 1015, 032017. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhou, W.X.; Ding, Z.J.; Li, X.X.; Zhang, C.G. Experimental determination of parameter effects on the coefficient of restitution of differently shaped maize in three-dimensions. Powder Technol. 2015, 284, 187–194. [Google Scholar] [CrossRef]
- Mousaviraad, M.; Tekeste, M.Z.; Rosentrater, K.A. Calibration and Validation of a Discrete Element Model of Corn Using Grain Flow Simulation in a Commercial Screw Grain Auger. Trans. ASABE 2017, 60, 1403–1415. [Google Scholar] [CrossRef] [Green Version]
- Pasha, M.; Hare, C.; Ghadiri, M.; Gunadi, A.; Piccione, P.M. Effect of particle shape on flow in discrete element method simulation of a rotary batch seed coater. Powder Technol. 2016, 296, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Coetzee, C. Calibration of the discrete element method: Strategies for spherical and non-spherical particles. Powder Technol. 2020, 364, 851–878. [Google Scholar] [CrossRef]
- Santos, K.G.; Campos, A.; Oliveira, O.S.; Ferreira, L.V.; Francisquetti, M.C.; Barrozo, M. DEM simulations of dynamic angle of repose of acerola residue: A parametric study using a response surface technique. In Proceedings of the XX Congresso Brasileiro de Engenharia Química, João Pessoa, Brazil, 7 December 2015. [Google Scholar]
- Zhao, Z.; Wu, Y.F.; Yin, J.J.; Tang, Z. Monitoring method of rice seeds mass in vibrating tray for vacuum-panel precision seeder. Comput. Electron. Agric. 2015, 114, 25–31. [Google Scholar]
- Zhang, S.; Tekeste, M.Z.; Li, Y.; Gaul, A.; Zhu, D.; Liao, J. Scaled-up rice grain modelling for DEM calibration and the validation of hopper flow. Biosyst. Eng. 2020, 194, 196–212. [Google Scholar] [CrossRef]
- Boac, J.M.; Ambrose, R.P.K.; Casada, M.E.; Maghirang, R.G.; Maier, D.E. Applications of Discrete Element Method in Modeling of Grain Postharvest Operations. Food Eng. Rev. 2014, 6, 128–149. [Google Scholar] [CrossRef] [Green Version]
- Ghodki, B.M.; Patel, M.; Namdeo, R.; Carpenter, G. Calibration of discrete element model parameters: Soybeans. Comput. Part. Mech. 2018, 6, 3–10. [Google Scholar] [CrossRef]
- Shi, L.R.; Sun, W.; Zhao, W.Y.; Yang, X.P.; Feng, B. Parameter determination and validation of discrete element model of seed potato mechanical seeding. Trans. Chin. Soc. Agric. Eng. 2018, 34, 35–42. [Google Scholar]
- Liao, Y.T.; Wang, Z.T.; Liao, Q.X.; Wan, X.Y.; Zhou, Y.; Liang, F. Calibration of Discrete Element Model Parameters of Forage Rape Stalk at Early Pod Stage. Trans. Chin. Soc. Agric. Mach. 2020, 51, 236–243. [Google Scholar]
- Wu, M.C.; Cong, J.L.; Yan, Q.; Zhu, T.; Peng, X.Y.; Wang, Y.S. Calibration and experiments for discrete element simulation parameters of peanut seed particles. Trans. Chin. Soc. Agric. Eng. 2020, 36, 30–38. [Google Scholar]
- Hao, J.J.; Long, S.F.; Li, H.; Jia, Y.L.; Ma, Z.K.; Zhao, J.G. Development of discrete element model and calibration of simulation parameters for mechanically-harvested yam. Trans. Chin. Soc. Agric. Eng. 2019, 35, 34–42. [Google Scholar]
- Mu, G. Research on Mechanical Properties Tests of Clam and Key Issues of Dredge Machinery. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Liu, W.B.; Zhang, H.B.; Li, X.C.; Zhang, G.C.; Zhang, Q.; Qu, S.G.; Gao, J.Y.; Fan, B.; Mu, G. Analysis of biomechanical properties of juvenile Manila clam for mechanization sowing. J. Dalian Ocean. Univ. 2020, 35, 455–461. [Google Scholar]
- Cabiscol, R.; Finke, J.H.; Kwade, A. Calibration and interpretation of DEM parameters for simulations of cylindrical tablets with multi-sphere approach. Powder Technol. 2018, 327, 232–245. [Google Scholar] [CrossRef]
- Ramírez-Gómez, Á.; Gallego, E.; Fuentes, J.M.; González-Montellano, C.; Ayuga, F. Values for particle-scale properties of biomass briquettes made from agroforestry residues. Particuology 2014, 12, 100–106. [Google Scholar] [CrossRef]
- González-Montellano, C.; Ramírez, Á.; Gallego, E.; Ayuga, F. Validation and experimental calibration of 3D discrete element models for the simulation of the discharge flow in silos. Chem. Eng. Sci. 2011, 66, 5116–5126. [Google Scholar] [CrossRef]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M. Discrete element modelling (DEM) input parameters: Understanding their impact on model predictions using statistical analysis. Comput. Part. Mech. 2015, 2, 283–299. [Google Scholar] [CrossRef] [Green Version]
- Yu, Q.; Liu, Y.; Chen, X.; Sun, K.; Lai, Q. Calibration and Experiment of Simulation Parameters for Panax notoginseng Seeds Based on DEM. Trans. Chin. Soc. Agric. Mach. 2020, 51, 123–132. [Google Scholar]
- Boikov, A.V.; Savelev, R.V.; Payor, V.A.; Vasileva, N.V. DEM calibration approach: Orthogonal experiment. J. Phys. Conf. Ser. 2019, 1210, 012025. [Google Scholar] [CrossRef]

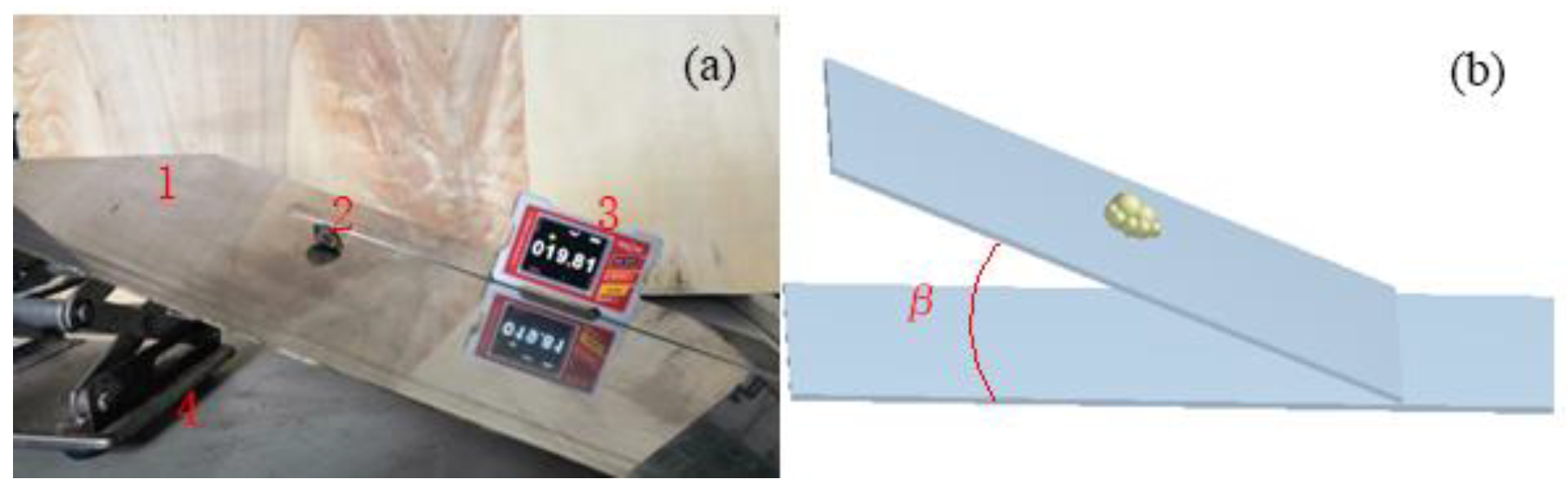




| Material Parameters | Symbol | Value |
|---|---|---|
| AC Poisson’s ratio | vac | 0.36 |
| AC shear modulus (Pa) | Gac | 2.30 × 107 |
| AC density (g mm−3) | ρac | 1.06 |
| SS Poisson’s ratio | vss | 0.30 |
| SS shear modulus (Pa) | Gss | 7.00 × 1010 |
| SS density (g mm−3) | ρss | 7.80 |
| Clam Poisson’s ratio | vcl | 0.33 [30] |
| Clam shear modulus (Pa) | Gcl | 5.56 × 107 [31] |
| Clam density (g mm−3) | ρcl | 1.58 |
| Approach | Parameters | Symbol | Value (°) | ||
|---|---|---|---|---|---|
| SS | AC | SS | AC | ||
| Direct measurement | Inclination angle β | βss | βac | 14.40 | 18.78 |
| Coefficient of static friction μs | μs-pw-ss | μs-pw-ac | 0.26 | 0.34 | |
| DEM simulation test | Inclination angle β’ | β’ss | β’ac | 14.97 | 19.12 |
| Coefficient of static friction μ′s | μ′s-pw-ss | μ′s-pw-ac | 0.22 | 0.31 | |
| Approach | Parameters | Symbol | Value (mm) | ||||
|---|---|---|---|---|---|---|---|
| SS | Clam | AC | SS | Clam | AC | ||
| Direct measurement | Rebound height H1 | H1-pw-ss | H1-pp | H1-pw-ac | 13.18 | 6.79 | 25.20 |
| coefficient of restitution e | epw-ss | epp | epw-ac | 0.30 | 0.21 | 0.41 | |
| DEM simulation test | Rebound height H’1 | H’1-pw-ss | H’1-pp | H’1-pw-ac | 12.96 | 6.93 | 25.63 |
| coefficient of restitution e | e’pw-ss | e’pp | e’pw-ac | 0.38 | 0.32 | 0.48 | |
| Levels | SS Factors | AC Factors | ||||
|---|---|---|---|---|---|---|
| μ′r-pp-ss | μ′s-pp-ss | μ′r-pw-ss | μ′r-pp-ac | μ′s-pp-ac | μ′r-pw-ac | |
| High (1) | 0.14 | 1.04 | 0.14 | 0.32 | 1.22 | 0.32 |
| Mid (0) | 0.18 | 1.08 | 0.18 | 0.34 | 1.24 | 0.34 |
| Low (−1) | 0.22 | 1.12 | 0.22 | 0.36 | 1.26 | 0.36 |
| Runs | Factors | Response | |||
|---|---|---|---|---|---|
| μ′r-pp | μ′s-pp | μ′r-pw | 𝜃’ss/(°) | 𝜃’ac/(°) | |
| 1 | −1 | −1 | 0 | 38.25 | 29.48 |
| 2 | 1 | −1 | 0 | 37.22 | 33.63 |
| 3 | −1 | 1 | 0 | 31.08 | 25.95 |
| 4 | 1 | 1 | 0 | 37.79 | 32.76 |
| 5 | −1 | 0 | 1 | 38.71 | 29.40 |
| 6 | 1 | 0 | 1 | 39.64 | 35.99 |
| 7 | −1 | 0 | 1 | 33.90 | 29.42 |
| 8 | 1 | 0 | 1 | 40.68 | 35.49 |
| 9 | 0 | −1 | 1 | 41.00 | 33.81 |
| 10 | 0 | 1 | 1 | 35.84 | 31.65 |
| 11 | 0 | −1 | 1 | 38.83 | 30.97 |
| 12 | 0 | 1 | 1 | 34.23 | 32.24 |
| 13 | 0 | 0 | 0 | 40.49 | 31.77 |
| 14 | 0 | 0 | 0 | 40.00 | 31.25 |
| 15 | 0 | 0 | 0 | 40.89 | 32.37 |
| 16 | 0 | 0 | 0 | 40.25 | 31.54 |
| 17 | 0 | 0 | 0 | 40.17 | 32.38 |
| Source | SS | AC | ||||||
|---|---|---|---|---|---|---|---|---|
| Sum of Squares | df | F Value | p Value | Sum of Squares | df | F Value | p Value | |
| Model | 129.92 | 9 | 45.13 | <0.0001 ** | 89.13 | 9 | 20.97 | <0.0003 ** |
| μ′r-pp | 22.41 | 1 | 70.07 | <0.0001 ** | 69.74 | 1 | 147.66 | <0.0001 ** |
| μ′s-pp | 33.46 | 1 | 104.6 | <0.0001 ** | 3.5 | 1 | 7.41 | 0.0297 * |
| μ′r-pw | 7.13 | 1 | 22.28 | 0.0022 ** | 0.93 | 1 | 1.97 | 0.203 |
| μ′r-ppμ′s-pp | 14.98 | 1 | 46.83 | 0.0002 ** | 1.77 | 1 | 3.75 | 0.0942 |
| μ′r-ppμ′r-pw | 8.56 | 1 | 26.75 | 0.0013 ** | 0.07 | 1 | 0.14 | 0.7164 |
| μ′s-ppμ′r-pw | 0.08 | 1 | 0.25 | 0.6357 | 2.94 | 1 | 6.23 | 0.0413 * |
| μ′r-pp2 | 13.02 | 1 | 40.72 | 0.0004 ** | 1.05 | 1 | 2.23 | 0.1793 |
| μ′s-pp2 | 26.66 | 1 | 83.35 | <0.0001 ** | 3.47 | 1 | 7.34 | 0.0302 * |
| μ′r-pw2 | 0.57 | 1 | 1.79 | 0.2228 | 6.19 | 1 | 13.11 | 0.0085 ** |
| Residual | 2.24 | 7 | 3.31 | 7 | ||||
| Lack of Fit | 1.76 | 3 | 4.94 | 0.0784 | 2.29 | 3 | 3.02 | 0.1569 |
| Pure Error | 0.48 | 4 | 1.01 | 4 | ||||
| Cor Total | 132.16 | 16 | 92.43 | 16 | ||||
| CV = 1.47% | CV = 2.16% | |||||||
| Rs2 = 0.9642 | Rs2 = 0.9831 | |||||||
| Adj−Rs2 = 0.9183 | Adj−Rs2 = 0.9613 | |||||||
| Adeq−Precision = 23.674 | Adeq−Precision = 18.636 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, G.; Li, X.; Zhang, H.; Zhang, Q.; Liu, W.; Mu, G. Calibration of the Discrete Element Method Parameters in Living Juvenile Manila Clam (Ruditapes philippinarum) and Seeding Verification. AgriEngineering 2021, 3, 894-906. https://doi.org/10.3390/agriengineering3040056
Li H, Zhang G, Li X, Zhang H, Zhang Q, Liu W, Mu G. Calibration of the Discrete Element Method Parameters in Living Juvenile Manila Clam (Ruditapes philippinarum) and Seeding Verification. AgriEngineering. 2021; 3(4):894-906. https://doi.org/10.3390/agriengineering3040056
Chicago/Turabian StyleLi, Hangqi, Guochen Zhang, Xiuchen Li, Hanbing Zhang, Qian Zhang, Wenbo Liu, and Gang Mu. 2021. "Calibration of the Discrete Element Method Parameters in Living Juvenile Manila Clam (Ruditapes philippinarum) and Seeding Verification" AgriEngineering 3, no. 4: 894-906. https://doi.org/10.3390/agriengineering3040056
APA StyleLi, H., Zhang, G., Li, X., Zhang, H., Zhang, Q., Liu, W., & Mu, G. (2021). Calibration of the Discrete Element Method Parameters in Living Juvenile Manila Clam (Ruditapes philippinarum) and Seeding Verification. AgriEngineering, 3(4), 894-906. https://doi.org/10.3390/agriengineering3040056





