Oil Palm Yield Estimation Based on Vegetation and Humidity Indices Generated from Satellite Images and Machine Learning Techniques
Abstract
:1. Introduction
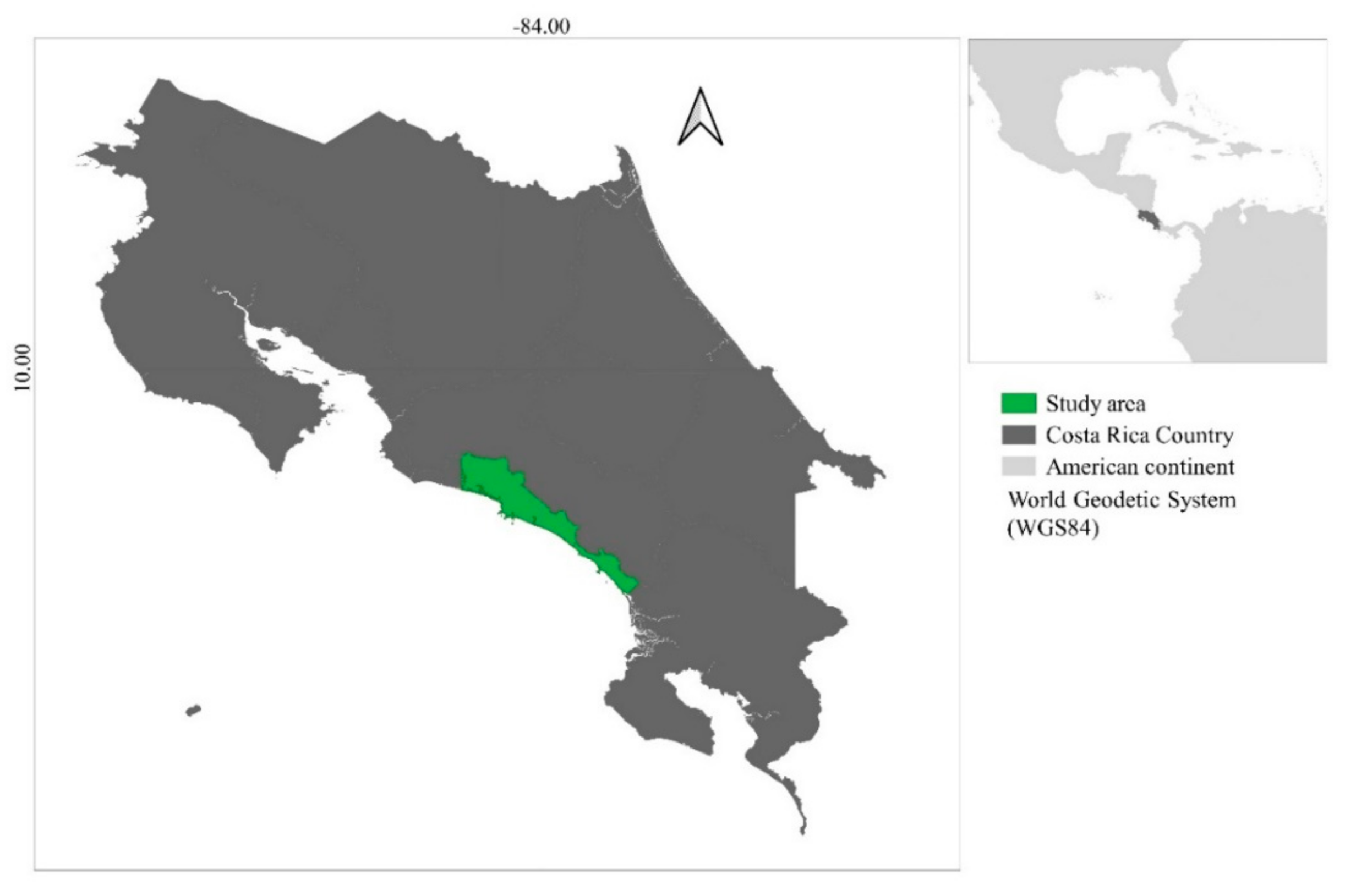
2. Materials and Methods
2.1. Variable Importance Random Forest Model
2.2. Variable Importance Neural Network Model
3. Results
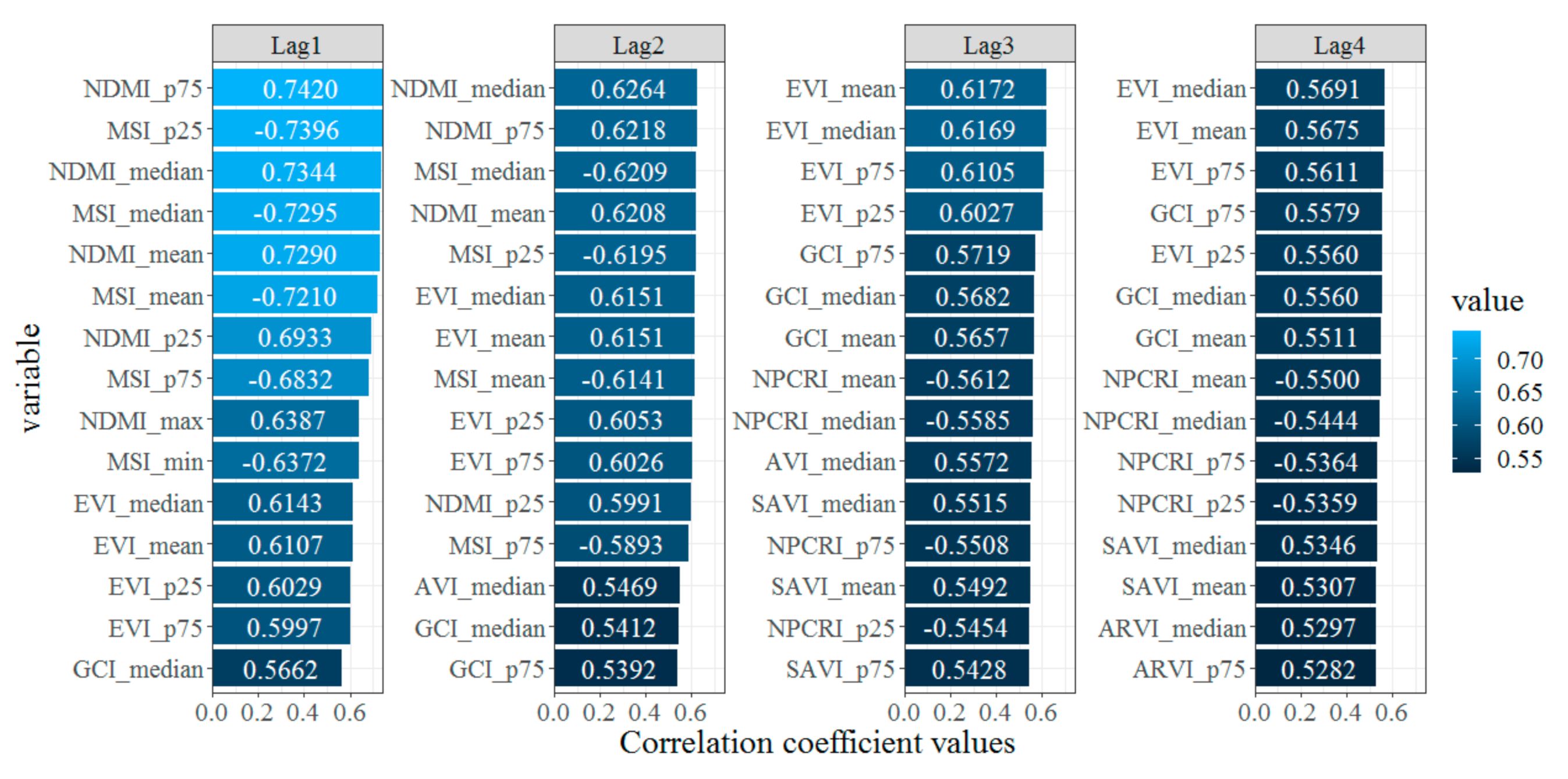
3.1. Correlations between Vegetation and Humidity Indices for Different Time Lags
3.2. Coefficients of Crop Production Prediction Models
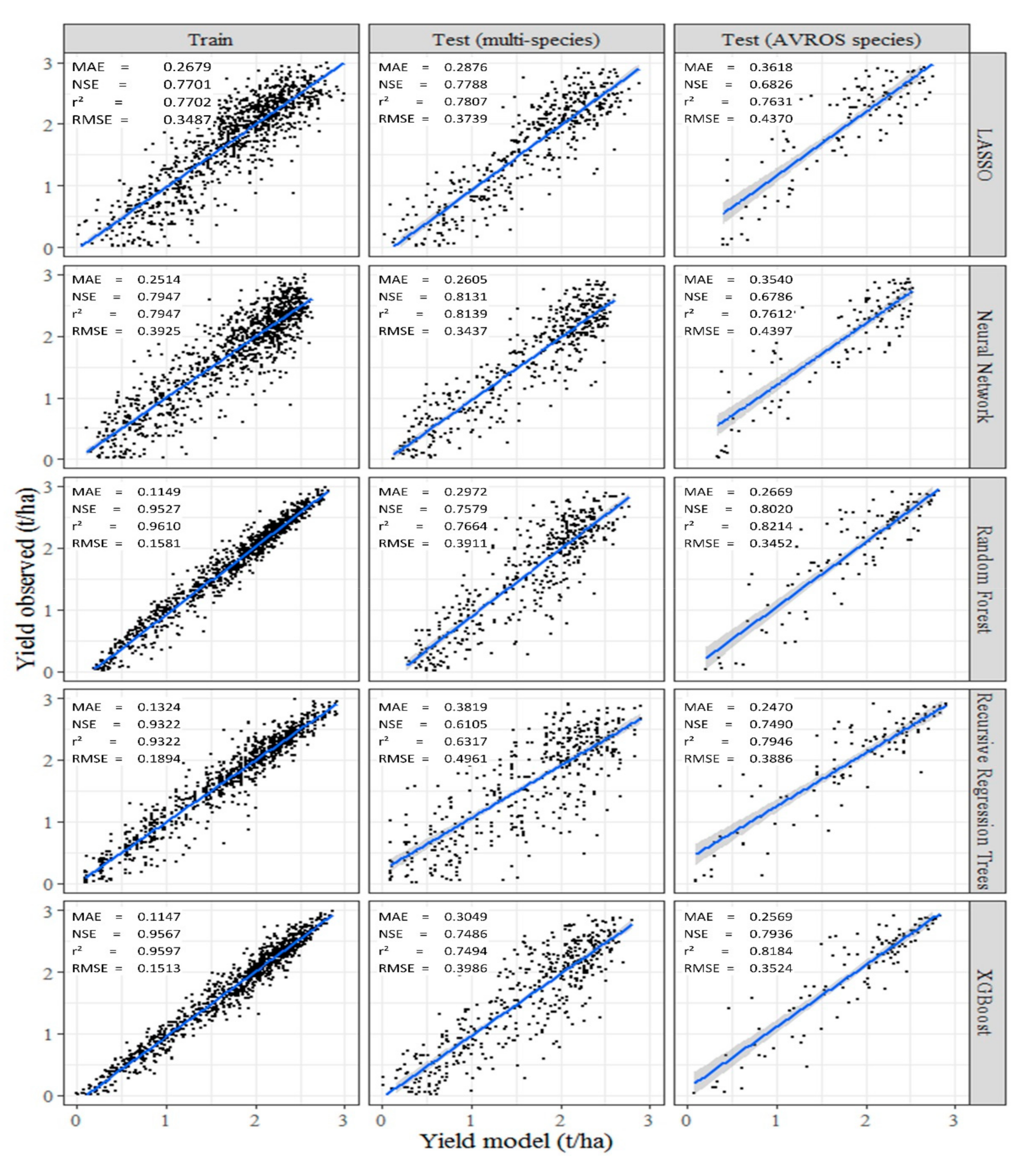
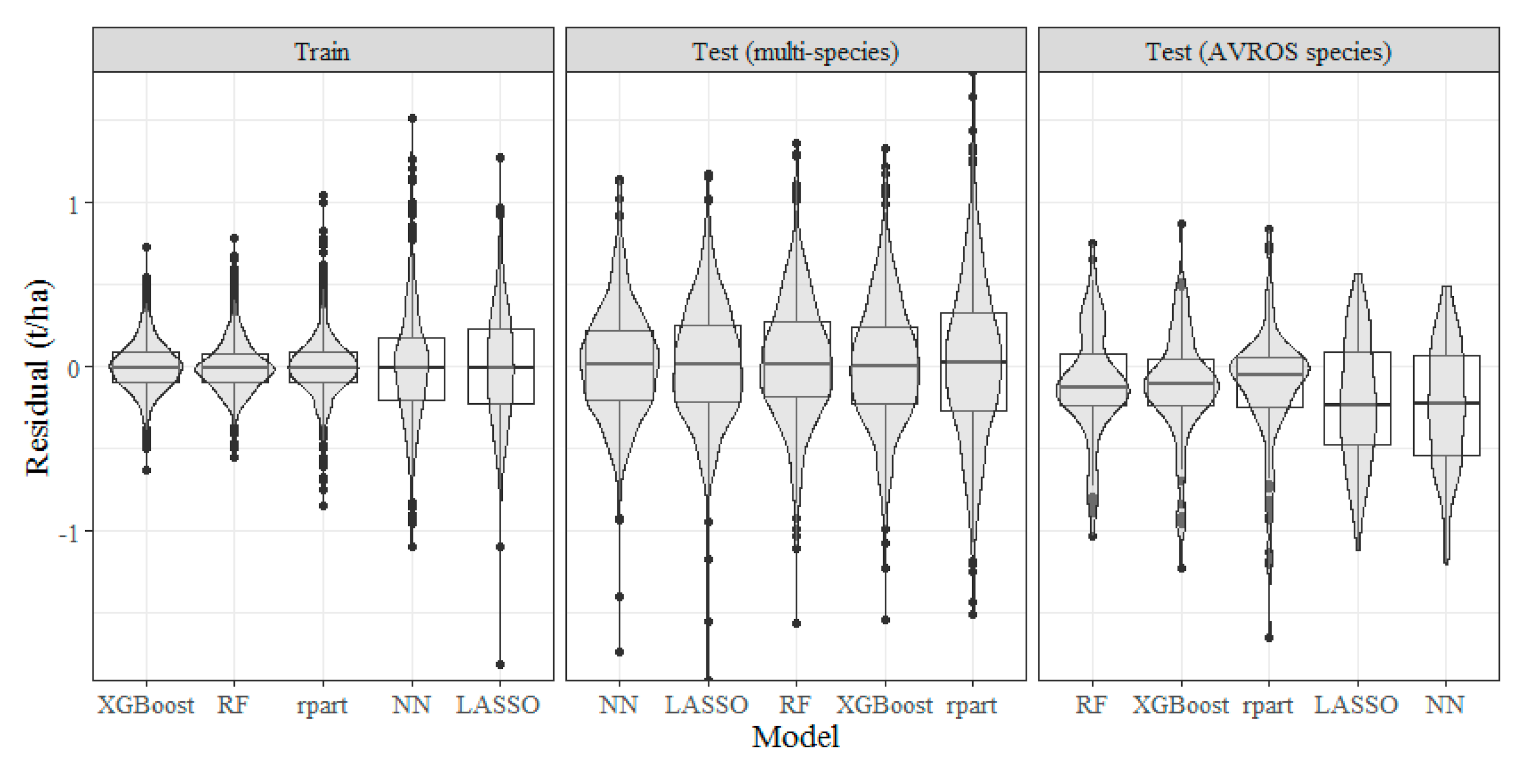
3.3. Calibration (Training) and Validation (Test) of Prediction Models for Crop Production
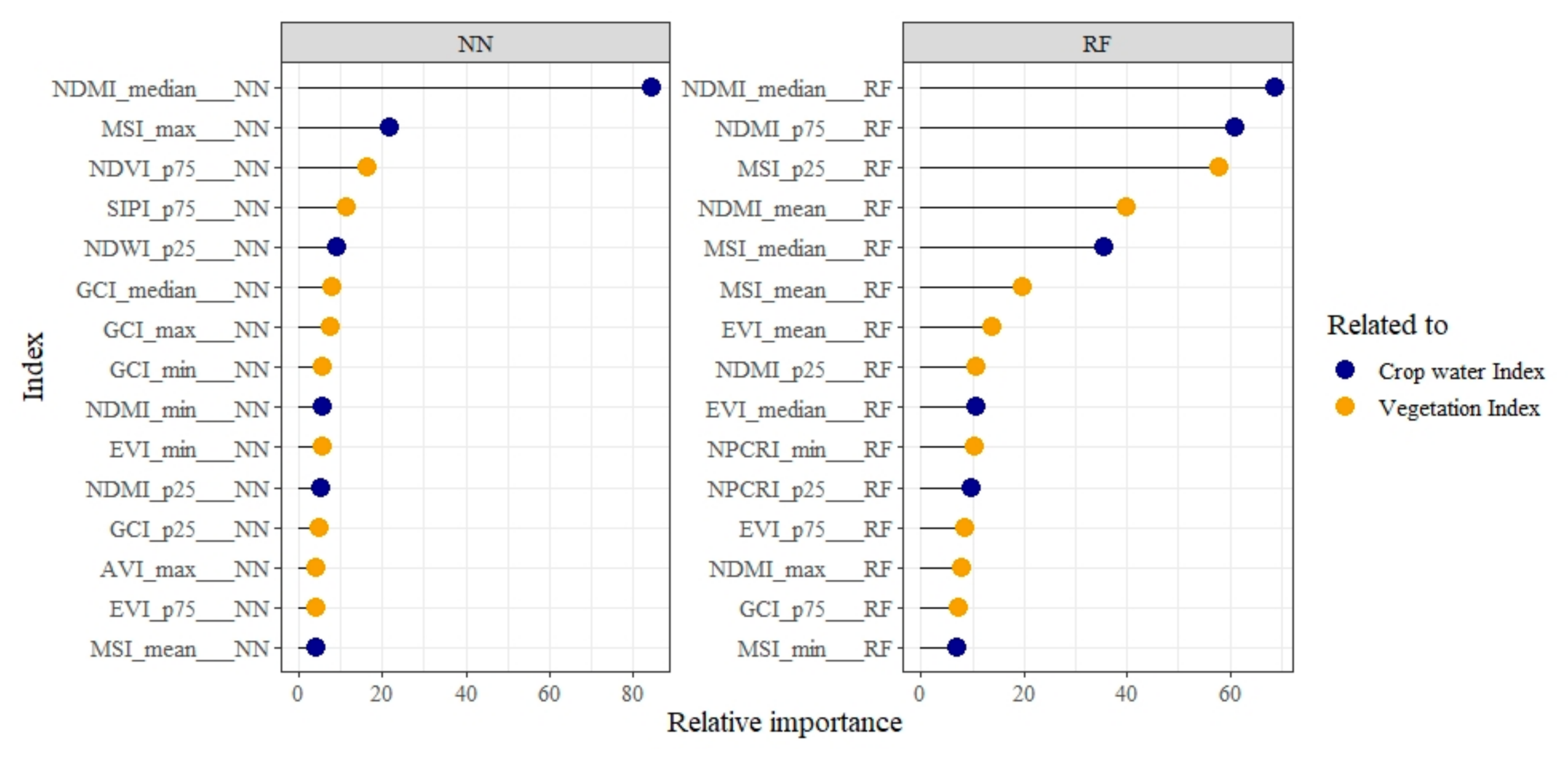
3.4. Importance of Vegetation Indices Variables in Crop Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Camacho, A.; Correa, C.V.; Arguello, H. An Analysis of Spectral Variability in Hyperspectral Imagery: A Case Study of Stressed Oil Palm Detection in Colombia. Int. J. Remote Sens. 2019, 40, 7603–7623. [Google Scholar] [CrossRef]
- Castellanos-Navarrete, A.; de Castro, F.; Pacheco, P. The Impact of Oil Palm on Rural Livelihoods and Tropical Forest Landscapes in Latin America. J. Rural Stud. 2021, 81, 294–304. [Google Scholar] [CrossRef]
- Da Silva Cabral de Moraes, J.R.; Souza Rolim, G.D.; Martorano, L.G.; de Oliveira Aparecido, L.E.; Padilha de Oliveira, M.D.S.; de Farias Neto, J.T. Agrometeorological Models to Forecast Açaí (Euterpe Oleracea Mart.) Yield in the Eastern Amazon. J. Sci. Food Agric. 2020, 100, 1558–1569. [Google Scholar] [CrossRef]
- Rodríguez, A.; Ruiz-Ramos, M.; Palosuo, T.; Carter, T.R.; Fronzek, S.; Lorite, I.J.; Ferrise, R.; Pirttioja, N.; Bindi, M.; Baranowski, P.; et al. Implications of Crop Model Ensemble Size and Composition for Estimates of Adaptation Effects and Agreement of Recommendations. Agric. For. Meteorol. 2019, 264, 351–362. [Google Scholar] [CrossRef] [PubMed]
- Akhter, R.; Sofi, S.A. Precision Agriculture Using IoT Data Analytics and Machine Learning. J. King Saud Univ.-Comput. Inf. Sci. 2021, in press. [Google Scholar] [CrossRef]
- Rodríguez, A.C.; D’Aronco, S.; Schindler, K.; Wegner, J.D. Mapping Oil Palm Density at Country Scale: An Active Learning Approach. Remote Sens. Environ. 2021, 261, 112479. [Google Scholar] [CrossRef]
- Morel, A.C.; Fisher, J.B.; Malhi, Y. Evaluating the Potential to Monitor Aboveground Biomass in Forest and Oil Palm in Sabah, Malaysia, for 2000–2008 with Landsat ETM+ and ALOS-PALSAR. Int. J. Remote Sens. 2012, 33, 3614–3639. [Google Scholar] [CrossRef]
- Ryu, J.-H.; Oh, D.; Cho, J. Simple Method for Extracting the Seasonal Signals of Photochemical Reflectance Index and Normalized Difference Vegetation Index Measured Using a Spectral Reflectance Sensor. J. Integr. Agric. 2021, 20, 1969–1986. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Klopfenstein, A.; Douridas, N.; Shearer, S. Integration of High Resolution Remotely Sensed Data and Machine Learning Techniques for Spatial Prediction of Soil Properties and Corn Yield. Comput. Electron. Agric. 2018, 153, 213–225. [Google Scholar] [CrossRef]
- Suharjito; Elwirehardja, G.N.; Prayoga, J.S. Oil Palm Fresh Fruit Bunch Ripeness Classification on Mobile Devices Using Deep Learning Approaches. Comput. Electron. Agric. 2021, 188, 106359. [Google Scholar] [CrossRef]
- Mamehgol Yousefi, D.B.; Mohd Rafie, A.S.; Abd Aziz, S.; Azrad, S.; Mazmira Mohd Masri, M.; Shahi, A.; Marzuki, O.F. Classification of Oil Palm Female Inflorescences Anthesis Stages Using Machine Learning Approaches. Inf. Process. Agric. 2020, 8, 537–549. [Google Scholar] [CrossRef]
- Zheng, J.; Fu, H.; Li, W.; Wu, W.; Yu, L.; Yuan, S.; Tao, W.Y.W.; Pang, T.K.; Kanniah, K.D. Growing Status Observation for Oil Palm Trees Using Unmanned Aerial Vehicle (UAV) Images. ISPRS J. Photogramm. Remote Sens. 2021, 173, 95–121. [Google Scholar] [CrossRef]
- Amirruddin, A.D.; Muharam, F.M.; Ismail, M.H.; Tan, N.P.; Ismail, M.F. Hyperspectral Spectroscopy and Imbalance Data Approaches for Classification of Oil Palm’s Macronutrients Observed from Frond 9 and 17. Comput. Electron. Agric. 2020, 178, 105768. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística y Censos [INEC]. VI Censo Nacional Agropecuario: Características de Las Fincas y de Las Personas Productoras, 1st ed.; Instituto Nacional de Estadística y Censos [INEC]: San José, Costa Rica, 2015; ISBN 978-9968-683-99-9. [Google Scholar]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Simmons, J.A.; Turner, I.L. Sub-Annual to Multi-Decadal Shoreline Variability from Publicly Available Satellite Imagery. Coast. Eng. 2019, 150, 160–174. [Google Scholar] [CrossRef]
- Aljahdali, M.O.; Munawar, S.; Khan, W.R. Monitoring Mangrove Forest Degradation and Regeneration: Landsat Time Series Analysis of Moisture and Vegetation Indices at Rabigh Lagoon, Red Sea. Forests 2021, 12, 52. [Google Scholar] [CrossRef]
- Dube, T.; Pandit, S.; Shoko, C.; Ramoelo, A.; Mazvimavi, D.; Dalu, T. Numerical Assessments of Leaf Area Index in Tropical Savanna Rangelands, South Africa Using Landsat 8 OLI Derived Metrics and In-Situ Measurements. Remote Sens. 2019, 11, 829. [Google Scholar] [CrossRef] [Green Version]
- Sykas, D. Spectral Indices with Multispectral Satellite Data. Available online: https://www.geo.university/pages/blog?p=spectral-indices-with-multispectral-satellite-data (accessed on 24 November 2021).
- Tan, C.; Zhou, X.; Zhang, P.; Wang, Z.; Wang, D.; Guo, W.; Yun, F. Predicting Grain Protein Content of Field-Grown Winter Wheat with Satellite Images and Partial Least Square Algorithm. PLoS ONE 2020, 15, e0228500. [Google Scholar] [CrossRef]
- Zakir, M. GIS and RS Based Spatio-Temporal Analysis of Soil Moisture/Water Content Variation in Southern Irrigated Part of Sindh, Pakistan. J. Remote Sens. GIS 2018, 7, 250. [Google Scholar] [CrossRef]
- Li, Z.; Sillanpää, M.J. Overview of LASSO-Related Penalized Regression Methods for Quantitative Trait Mapping and Genomic Selection. Theor. Appl. Genet. 2012, 125, 419–435. [Google Scholar] [CrossRef]
- Huo, J.; Shi, T.; Chang, J. Comparison of Random Forest and SVM for Electrical Short-Term Load Forecast with Different Data Sources. In Proceedings of the 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; IEEE: New York, NY, USA, 2017; pp. 1077–1080. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Nembrini, S. Prediction or Interpretability? Emerg. Themes Epidemiol. 2019, 16, 4. [Google Scholar] [CrossRef]
- Günther, F.; Fritsch, S. Neuralnet: Training of Neural Networks. R J. 2010, 2, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A Comparison of Random Forest and Its Gini Importance with Standard Chemometric Methods for the Feature Selection and Classification of Spectral Data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Da Costa, N.L.; de Lima, M.D.; Barbosa, R. Evaluation of Feature Selection Methods Based on Artificial Neural Network Weights. Expert Syst. Appl. 2021, 168, 114312. [Google Scholar] [CrossRef]
- Li, P.; Hua, P.; Gui, D.; Niu, J.; Pei, P.; Zhang, J.; Krebs, P. A Comparative Analysis of Artificial Neural Networks and Wavelet Hybrid Approaches to Long-Term Toxic Heavy Metal Prediction. Sci. Rep. 2020, 10, 13439. [Google Scholar] [CrossRef] [PubMed]
- Watt, M.S.; Leonardo, E.M.C.; Estarija, H.J.C.; Massam, P.; de Silva, D.; O’Neill, R.; Lane, D.; McDougal, R.; Buddenbaum, H.; Zarco-Tejada, P.J. Long-Term Effects of Water Stress on Hyperspectral Remote Sensing Indicators in Young Radiata Pine. For. Ecol. Manag. 2021, 502, 119707. [Google Scholar] [CrossRef]
- Sosa, L.; Justel, A.; Molina, Í. Detection of Crop Hail Damage with a Machine Learning Algorithm Using Time Series of Remote Sensing Data. Agronomy 2021, 11, 2078. [Google Scholar] [CrossRef]
- Busico, G.; Colombani, N.; Fronzi, D.; Pellegrini, M.; Tazioli, A.; Mastrocicco, M. Evaluating SWAT Model Performance, Considering Different Soils Data Input, to Quantify Actual and Future Runoff Susceptibility in a Highly Urbanized Basin. J. Environ. Manag. 2020, 266, 110625. [Google Scholar] [CrossRef]
- Diana, S.R.; Purnama, S.M.; Dharma, G.; Sutrisnanto, A.; Perwitasari, I.; Farida, F. Estimation the Amount of Oil Palm Production Using Artificial Neural Network and NDVI SPOT-6 Imagery. Int. J. Innov. Sci. Res. Technol. 2019, 4, 548–554. [Google Scholar]
- Hilal, Y.Y.; Ishak, W.; Yahya, A.; Asha’ari, Z.H. Development of Genetic Algorithm for Optimization of Yield Models in Oil Palm Production. Chil. J. Agric. Res. 2018, 78, 228–237. [Google Scholar] [CrossRef] [Green Version]
- Kartika, N.D.; Astika, I.W.; Santosa, E. Oil Palm Yield Forecasting Based on Weather Variables Using Artificial Neural Network. Indones. J. Electr. Eng. Comput. Sci. 2016, 3, 626–633. [Google Scholar] [CrossRef] [Green Version]
- Moldovan, D.; Anghel, I.; Cioara, T.; Salomie, I. Time Series Features Extraction Versus LSTM for Manufacturing Processes Performance Prediction. In Proceedings of the 2019 International Conference on Speech Technology and Human-Computer Dialogue (SpeD), Timisoara, Romania, 10–12 October 2019; IEEE: New York, NY, USA, 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Shareef, M.A.; Hasan, S.F. Characterization and Estimation of Dates Palm Trees in an Urban Area Using GIS-Based Least-Squares Model and Minimum Noise Fraction Images. J. Ecol. Eng. 2020, 21, 78–85. [Google Scholar] [CrossRef]
- Das, A.C.; Noguchi, R.; Ahamed, T. An Assessment of Drought Stress in Tea Estates Using Optical and Thermal Remote Sensing. Remote Sens. 2021, 13, 2730. [Google Scholar] [CrossRef]


| Bands | Wavelength (μm) | ||
|---|---|---|---|
| Landsat 5 | Landsat 7 | Landsat 8 | |
| 1 (BLUE) | 0.45–0.52 | 0.441–0.514 | |
| 2 (BLUE) | 0.442–0.5120 | ||
| 2 (GREEN) | 0.52–0.60 | 0.519–0.601 | |
| 3 (GREEN) | 0.533–0.590 | ||
| 3 (RED) | 0.63–0.69 | 0.631–0.692 | |
| 4 (RED) | 0.636–0.673 | ||
| 4 (NIR) | 0.76–0.90 | 0.772–0.898 | |
| 5 (NIR) | 0.851–0.879 | ||
| 5 (SWIR) | 1.55–1.75 | 1.547–1.749 | |
| 6 (SWIR) | 1.566–1.651 | ||
| Variable | Index | Equation | Source |
|---|---|---|---|
| Vegetation | ARVI | [17] | |
| Vegetation | AVI | [18] | |
| Vegetation | EVI | [19] | |
| Vegetation | GCI | [17] | |
| Vegetation | GNDVI | [19] | |
| Vegetation | NDVI | [19] | |
| Vegetation | NPCRI | [18] | |
| Vegetation | SAVI | [19] | |
| Vegetation | SIPI | [19] | |
| Water | MSI | [20] | |
| Water | NDMI | [20] | |
| Water | NDWI | [20] |
| Model | Parameters | Description | Source |
|---|---|---|---|
| LASSO | alpha | The elasticnet mixing parameter, with 0 ≤ α ≤ 1 | [21] |
| lambda | Regularization hyperparameter | ||
| RF | ntree | Number of trees to grow | [22] |
| mtry | Number of variables randomly sampled as candidates at each split | ||
| XGBoost | max.depth | Maximum depth of a tree | [23] |
| nrounds | The number of decision trees in the final model | ||
| nthread | Number of parallel threads used to run XGBoost | ||
| objective | Specify the learning task and the corresponding learning objective | ||
| RPART | minsplit | The minimum number of observations that must exist in a node in order for a split to be attempted. | [24] |
| minbucket | The minimum number of observations in any terminal node | ||
| cp | Complexity parameter | ||
| NN | threshold | A numeric value specifying the threshold for the partial derivatives of the error function as stopping criteria | [25] |
| stepmax | The maximum steps for the training of the neural network | ||
| algorithm | A string containing the algorithm type to calculate the neural network |
| Model | Variable/Value | NSE | RMSE | MAE | |
|---|---|---|---|---|---|
| LASSO | lambda = 0.0037 | 0.7701 | 0.3487 | 0.2679 | |
| Neural Network (NN) | stepmax = 1 × 106 | Algorithm did not converge | |||
| stepmax = 1 × 106 | Algorithm did not converge | ||||
| stepmax = 1 × 107 | 0.7947 | 0.3925 | 0.2514 | ||
| Random Forest (RF) | ntree = 5000 | 0.9519 | 0.1668 | 0.1282 | |
| ntree = 10,000 | 0.9527 | 0.1655 | 0.1266 | ||
| ntree = 15,000 | 0.9518 | 0.167 | 0.1279 | ||
| Recursive Partitioning and Regression Trees (RPART) | Minsplit = | 5 | 0.6652 | 0.4207 | 0.3217 |
| 10 | 0.6652 | 0.4207 | 0.3218 | ||
| 50 | 0.6652 | 0.4207 | 0.3218 | ||
| 100 | 0.6652 | 0.4207 | 0.3217 | ||
| 500 | 0.5495 | 0.488 | 0.3765 | ||
| 1000 | 0.4133 | 0.557 | 0.4364 | ||
| Complexity parameter (cp) = minsplit = 10 | 0.01 | 0.6652 | 0.4207 | 0.3218 | |
| 0.001 | 0.8875 | 0.2438 | 0.1876 | ||
| 0.0001 | 0.9322 | 0.1894 | 0.1324 | ||
| XGBoost | max.depth = 1 | 0.6777 | 0.4127 | 0.3180 | |
| max.depth = 2 | 0.8230 | 0.3059 | 0.2322 | ||
| max.depth = 3 | 0.9034 | 0.2259 | 0.1727 | ||
| max.depth = 4 | 0.9567 | 0.1512 | 0.1147 | ||
| max.depth = 5 | over fitting | ||||
| Method | Variables | Coefficient | Source |
|---|---|---|---|
| Artificial Neural Network | NDVI | r2 = 0.5100 | [32] |
| Genetic algorithm | Historical yield data, cropland information, climatic information, air pollutants | r2 = 0.9400 RMSE = 0.1500 t/ha | [33] |
| Artificial Neural Network | Climatic information | MAE = 0.5300 t/ha RMSE = 0.6800 t/ha | [34] |
| Long short-term memory (LSTM) | Historical yield data | MAPE = 2.7100% | [35] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watson-Hernández, F.; Gómez-Calderón, N.; da Silva, R.P. Oil Palm Yield Estimation Based on Vegetation and Humidity Indices Generated from Satellite Images and Machine Learning Techniques. AgriEngineering 2022, 4, 279-291. https://doi.org/10.3390/agriengineering4010019
Watson-Hernández F, Gómez-Calderón N, da Silva RP. Oil Palm Yield Estimation Based on Vegetation and Humidity Indices Generated from Satellite Images and Machine Learning Techniques. AgriEngineering. 2022; 4(1):279-291. https://doi.org/10.3390/agriengineering4010019
Chicago/Turabian StyleWatson-Hernández, Fernando, Natalia Gómez-Calderón, and Rouverson Pereira da Silva. 2022. "Oil Palm Yield Estimation Based on Vegetation and Humidity Indices Generated from Satellite Images and Machine Learning Techniques" AgriEngineering 4, no. 1: 279-291. https://doi.org/10.3390/agriengineering4010019
APA StyleWatson-Hernández, F., Gómez-Calderón, N., & da Silva, R. P. (2022). Oil Palm Yield Estimation Based on Vegetation and Humidity Indices Generated from Satellite Images and Machine Learning Techniques. AgriEngineering, 4(1), 279-291. https://doi.org/10.3390/agriengineering4010019








