For this work, a vehicle, aerodynamic and wind model have been coupled to reproduce the vehicle–driver system response when subject to crosswind at tunnel exit conditions. A high-sided lorry has been modeled for this purpose, together with an ad hoc numerical model of the wind. The test scenario runs in real-time on the VI-Grade GmbH (Darmstadt, DE) DiM400 dynamic driving simulator available at the DriSMi laboratory of Politecnico di Milano. The simulator used and its main characteristics will be reported in
Section 2.1. The simulator has been used to perform an experimental campaign with 28 different drivers. The aim was to gather experimental data in order to gain a deeper understanding of the general vehicle–driver system response in case of crosswind at tunnel exit when driving a high-sided lorry.
2.1. Dynamic Driving Simulator
The experimental campaign has been carried out using the state-of-the-art VI-Grade GmbH (Darmstadt, DE) DiM400 dynamic driving simulator. The simulator is installed at the DriSMi laboratory of Politecnico di Milano. A picture of the simulator is reported in
Figure 1.
The main characteristics of the simulator are that:
It is a cable-driven simulator. The degrees of freedom of longitudinal displacement, lateral displacement and yaw rotation are controlled by the 4 cables. The cables are devoted to reproducing low-frequency accelerations and motion with a bandwidth of up to 3 Hz;
The available workspace is 4 m × 4 m;
On top of the disk frame (controlled by the 4 cables), there is a hexalift system controlling the rotations and translations around the longitudinal, lateral, and vertical directions of the cockpit (bandwidth up to 30 Hz);
Eight shakers are mounted on the cockpit (bandwidth up to 200 Hz) to accurately reproduce vibrations.
To improve vibrations control, the simulator features a patented inertial compensation system (ICS) with moving masses;
The latency of the simulator is around 20 ms. Thanks to this low value, it is possible to provide the users with an enhanced level of immersion and realism.
Due to the dimension of its workspace, the DiM400 is one of the biggest driving simulators featuring a wrap-around 270 degrees conical fixed screen (a total of 5 Widescreen Ultra Extended Graphics Array projectors with 4K resolution are used).
The maximum accelerations reachable by the simulator are ±1.5 g for in-plane acceleration and ±2.5 g for vertical acceleration. Regarding the rotation angles, roll and pitch are limited to ±15, while the yaw is limited to ±62. This allows the simulator to perform 1:1 lane change simulations (no motion cueing algorithms need to be used).
An instrumented steering wheel and many biometric sensors (eye-tracker, EEG, ECG, Skin Potential Response, etc…) are available at the laboratory. They can be used to perform a wide variety of studies related to the human driver.
To reproduce the vehicle dynamics of the high-sided lorry on the simulator, the software VI-CarRealTime is used. To model the wind, an additional Simulink model has been created. For what regards the virtual graphics environment, VI-WorldSim has been used. The scenario designed for the tests is reported in
Figure 2. It has been created using Blender and Roadrunner.
2.3. Wind Model
Both a uniform and a turbulent wind model with a turbulence intensity of have been chosen to perform the tests. This particular value of turbulence intensity was chosen to ensure a maximum variability of ±5 km/h with respect to the mean wind speed.
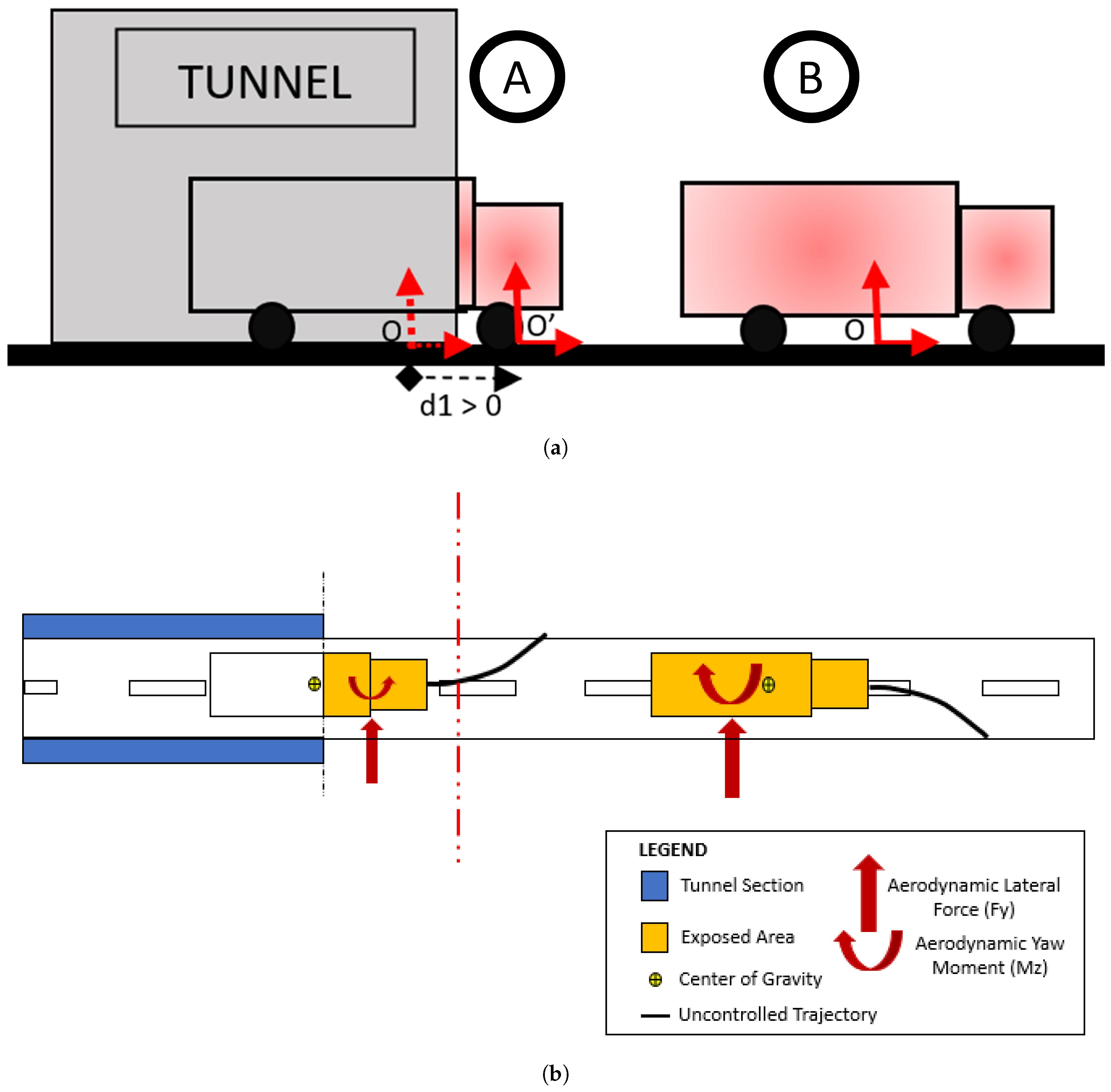
The aim of the study is to investigate the driver response at the tunnel exit. As the vehicle exits the tunnel, it is subject to aerodynamic forces varying with the relative position between the vehicle and the tunnel. Clearly, as the vehicle moves out of the tunnel, the exposed lateral surface of the vehicle to the wind increases. This phenomenon leads to a displacement of the point of application of aerodynamic forces and moments and to a magnitude of the aerodynamic forces and moments varying with the exposed lateral area of the high-sided lorry, as shown in
Figure 5a,b. The global effect on the aerodynamic forces and moments of both the exposed area and the center of pressure transition can be appreciated in
Figure 6.
Aside from a linear change in the aerodynamic forces and moments due to the change of the exposed lateral surface to the wind, the authors hypothesized a change in the point where the forces are acting on the vehicle (center of pressure) proportional to the change in the exposed area. This displacement of the center of pressure has a great influence on the yawing moment (generated mostly by the lateral aerodynamic force ) that the driver will experience when exiting/entering the tunnel.
Generally, for high-sided lorries this effect is even amplified due to their particular geometry. Indeed, due to their shape, the center of pressure usually lies behind the center of gravity (negative sign for the aerodynamic yawing coefficient
). This condition is met also for the truck used in this work, as can be seen in
Figure 3. The main term acting on the lorry is the aerodynamic yaw moment
that is a function only of the geometry of the vehicle. The position of the center of gravity with respect to the center of pressure changes the handling properties of the vehicle (easier or more difficult to control) and could increase or decrease the rollover risk (height of the center of gravity). However, the behavior of the driver is practically unaffected by the change in position of the center of gravity in terms of a sequence of actions, as will be shown subsequently in
Section 3.3.
When exiting the tunnel, the center of pressure will experience a transition passing from the front of the vehicle (ahead of the center of gravity) to its original position (behind the center of gravity). This leads to an overall yawing moment
that reverses in sign. This condition is schematized in
Figure 5a. Here it can be seen that while the lateral force
remains in the same direction, the yawing moments
experience a change in sign. The same is reported in a more quantitative way in
Figure 6. As can be expected, this poses a big challenge to the novice/non-expert driver that can be deceived by this sudden change in yawing moment
sign.
To model how the yawing moment
reported to the center of gravity of the vehicle (the pitching moment
has the same behavior) varies in the tunnel exit condition, Equation (
4) has been used. For the roll aerodynamic moment
it was simply necessary to scale its value according to the exposed area (the motion of the center of pressure had no effect in this case).
where
is the length of the truck reported in
Table 3,
L is the effective truck exposed length (
),
is the center of gravity
x position, and
is the varying application point of the forces (due to the exposed length—or equivalent area—of variation). To give the reader an idea of the displacement of the application point of the aerodynamic loads, its motion with respect to the system of reference used by Cheli et al. [
11,
12] to measure the aerodynamic coefficients was reported in
Figure 7. This system of reference was placed on the ground, at mid-wheelbase (and mid-track). To evaluate the aerodynamic moment at the center of gravity of the vehicle (Empty or Laden), it is necessary to add (or subtract) to the quantities reported in
Figure 7 the distance between the origin of the system of reference and the position of the center of gravity for the vehicle configuration chosen.
The modeling approach based on the effective exposed area (and linear shift of the center of pressure function on the exposed area) above described was used in many similar studies by authors like Charuvisit et al. [
5,
6], Rocchi et al. [
7] and Walczak [
27] to model the crosswind-vehicle interaction in presence of infrastructure elements. In particular, Charuvisit et al. [
5,
6] and Rocchi et al. [
7] adopted a discretized approach (the truck was divided into slices, each contributing to the total aerodynamic load acting on the vehicle), while Walczak [
27] adopted a continuous approach similar to the one proposed in this study. A validation of the proposed method was given by Quattromani et al. [
28]. These authors compared with success the above-mentioned discretized approach with numerical CFD results obtained for the case of a truck moving in the wake produced by a crosswind on a bridge pylon tower.
In Equation (
4),
is the aerodynamic yaw moment applied to the center of gravity, taking into account the translation of the forces application point due to the exposed area variation. In the case where the vehicle is completely inside the tunnel, of course, no aerodynamic forces are applied to the system except for the aerodynamic drag due to the vehicle speed itself (the wind is always coming orthogonal to the tunnel, never from a parallel direction).
For sake of completeness, it is reported in
Figure 8 a comparison between the lateral aerodynamic force
evaluated using the exposed area approach above described and a CFD case involving the same lorry used in this work running at 90 km/h with a 25 m/s crosswind at the tunnel exit. The simulated CFD case was taken by the previous work of Semeraro et al. [
21]. As can be seen, there is a good agreement between the two methods.
2.3.1. Scenario and Drivers
The virtual scenario used for the simulator tests has been created using Roadrunner. The scenario features a 2 km straight road with a total of 5 tunnels 75 m long. The tunnel size is ∼10 times the vehicle length. This measure has been designed to ensure that the vehicle reached a steady state condition inside the tunnel. Two vehicle configurations, Empty (without payload) and Laden (with a payload of ∼9600 kg), have been tested by each driver. For each vehicle configuration, two different vehicle speeds have been tested (65 km/h and 80 km/h). In the 5 different sections between the tunnels, different wind conditions (both in speed and direction) have been tested. They have been reported in
Table 4. The wind speed magnitudes have been selected keeping in mind the vehicle rollover thresholds of both the Empty and Laden vehicle configurations. As stated in
Section 2.3, both a turbulent or uniform crosswind could be imposed. During the experiment, the direction and sequence of wind speeds in the tests were selected randomly.
For what regards the 28 drivers, they were all volunteer university students (all males, with an average age of 23 years old). All the volunteers had a valid driving license (B license) for at least 4 years, but most of them had little to no experience in driving a truck. For this reason, before performing the experiment, each driver had a 10 min practice session on the dynamic driving simulator to get acquainted with the high-sided lorry (without crosswind).