RDE Calibration—Evaluating Fundamentals of Clustering Approaches to Support the Calibration Process
Abstract
:1. Introduction
- Increase the overall amount of data that is evaluated, thus making use of all available information;
- Increase the speed of measurement evaluations by handling large amounts of data, thus taking full advantage of virtually based test execution;
- Standardize the calibration process;
- Increase the quality of vehicle calibration by considering the effects of events that have little impact in a single test but may have a major impact in the daily use of the vehicle over the course of its useful life.
2. Materials and Methods
2.1. State of the Art
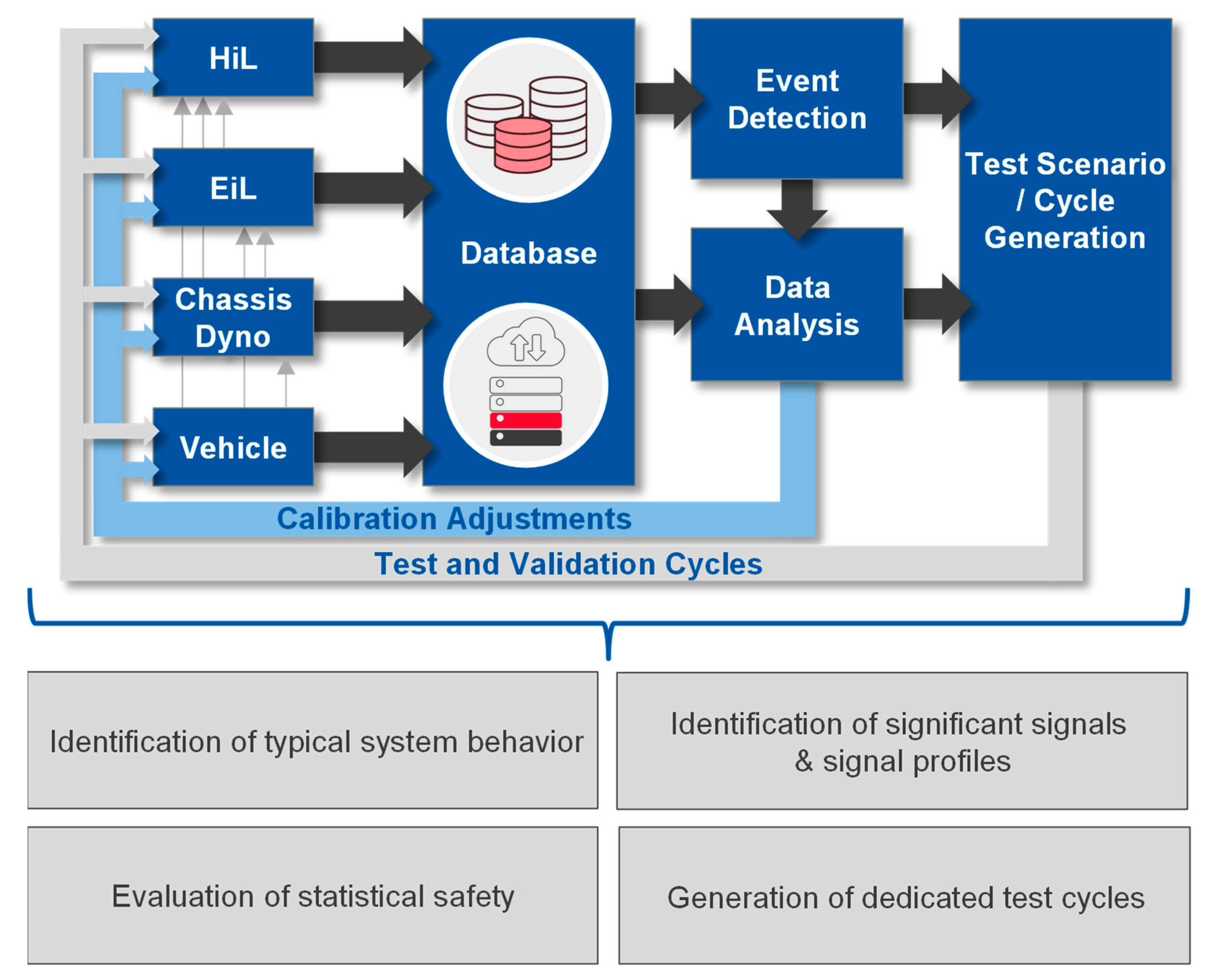
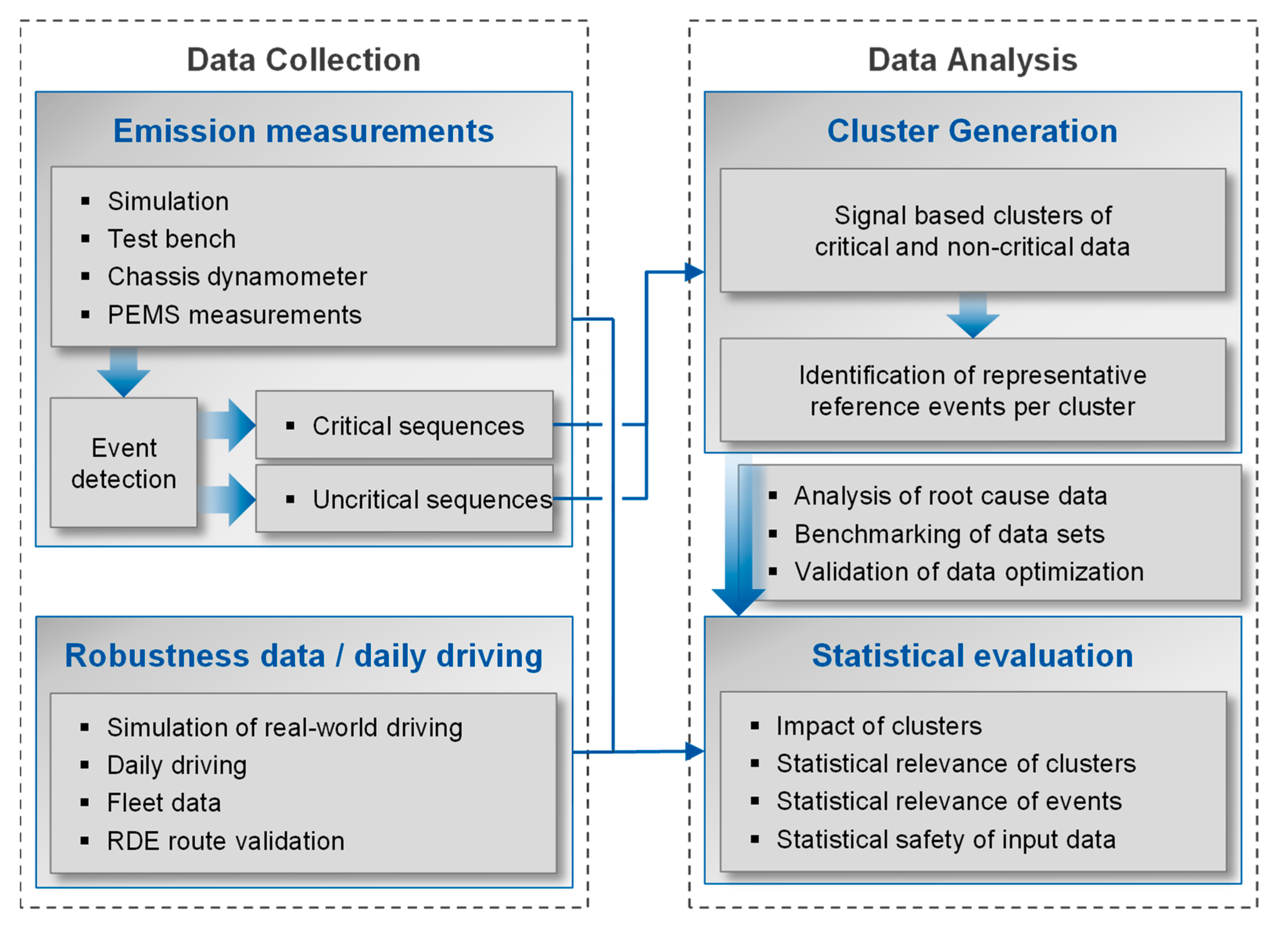
2.2. Context of the Proposed Methodology
3. Results
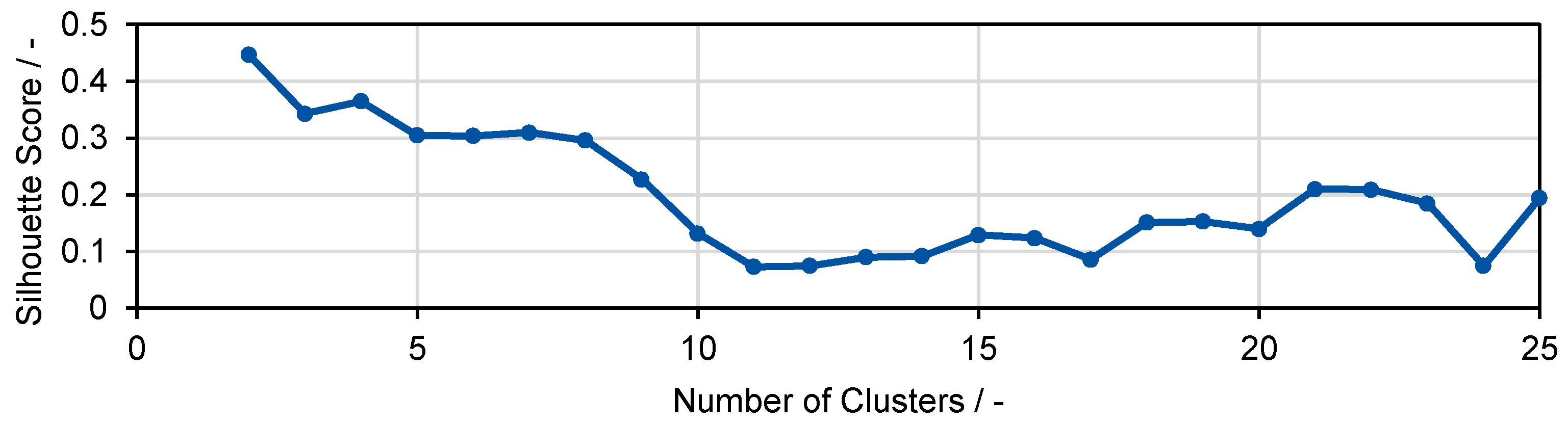
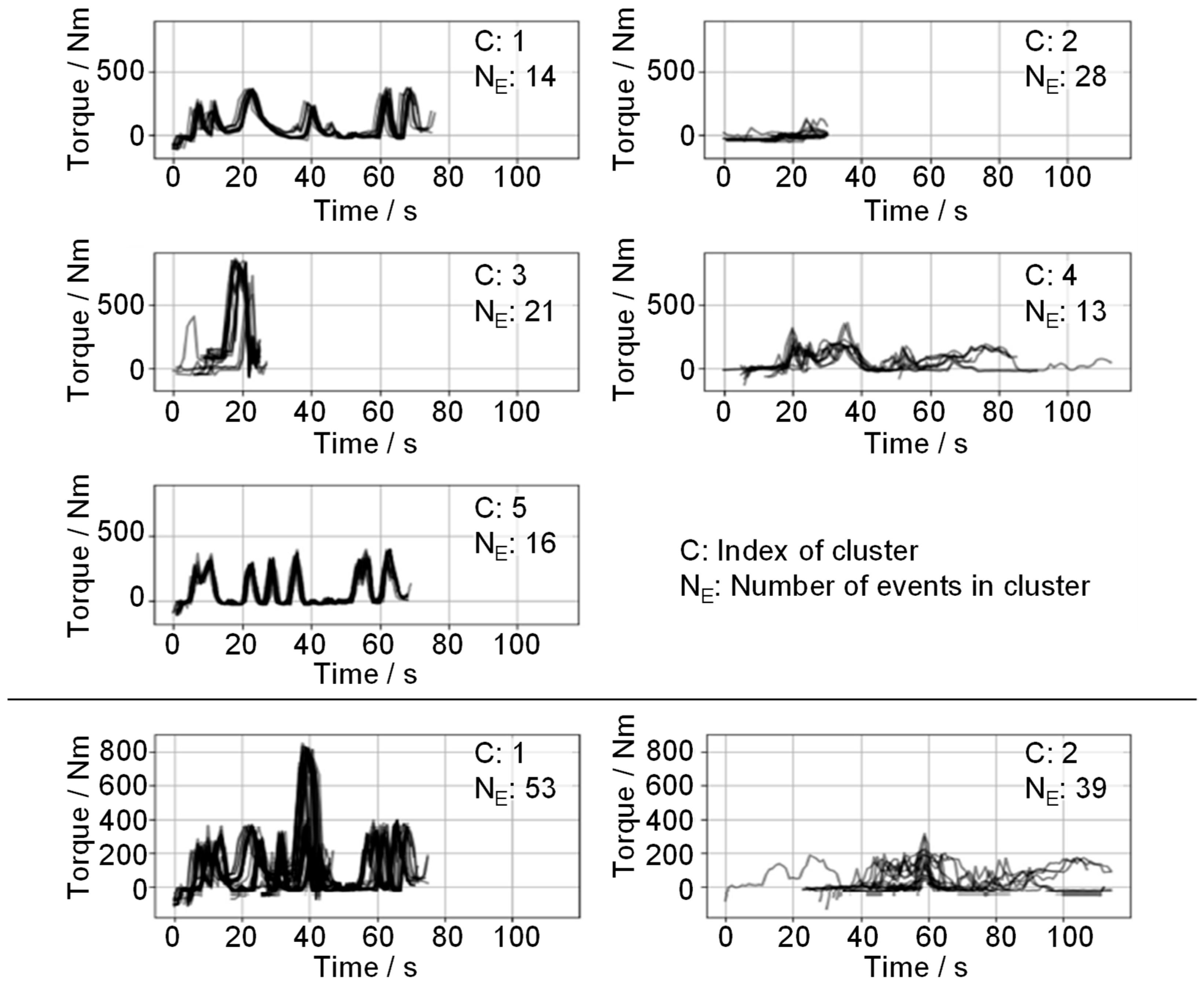
3.1. Hierarchical Clustering
3.2. Partitioning Cluster Methodologies
3.3. Density-Based Clustering
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commission. The European Green Deal: Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions. 2019. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex%3A52019DC0640 (accessed on 28 March 2023).
- Maurer, R.; Yadla, S.K.; Balazs, A.; Thewes, M.; Walter, V.; Uhlmann, T. Designing Zero Impact Emission Vehicle Concepts. In Experten-Forum Powertrain: Ladungswechsel und Emissionierung; Liebl, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-662-63523-0:75–116. [Google Scholar]
- Mulholland, E.; Miller, J.; Braun, C.; Jin, L.; Rodríguez, F. Quantifying the long-term air quality and health benefits from Euro 7/VII standards in Europe. Int. Counc. Clean Transp. 2021. [Google Scholar]
- Baumgarten, H.; Görgen, M.; Balazs, A.; Nijs, M. New Lambda = 1 Gasoline Powertrains New Technologies and Their Interaction with Connected and Autonomous Driving. In Proceedings of the 30th International AVL Conference Engine & Environment, Graz, Austria, 7–8 June 2018. [Google Scholar]
- Sterlepper, S.; Claßen, J.; Pischinger, S.; Görgen, M.; Cox, J.; Nijs, M.; Schraf, J. Relevance of Exhaust Aftertreatment System Degradation for EU7 Gasoline Engine Applications; SAE Technical Paper 2020-01-0382, 2020; SAE International 400 Commonwealth Drive: Warrendale, PA, USA, 21 April 2020. [Google Scholar] [CrossRef]
- European Commission. Commission Regulation (EU) 2017/1151. 2017. Available online: http://publications.europa.eu/resource/cellar/7d1c640d-62d8-11e7-b2f2-01aa75ed71a1.0006.02/DOC_1 (accessed on 28 March 2023).
- Europäischen Union. Verordnung (EU) 2019/631 des Europäischen Parlaments und des Rates; Europäischen Union: Maastricht, The Netherlands, 2019. [Google Scholar]
- European Commission. Proposal for a Regulation of the European Parliament and of the Council on Type-Approval of Motor Vehicles and Engines and of Systems, Components and Separate Technical Units Intended for Such Vehicles, with Respect to Their Emissions and Battery Durability (Euro 7) and Repealing Regulations (EC) No 715/2007 and (EC) No 595/2009. 2022, Volume 0365. Proposal. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A52022PC0586 (accessed on 28 March 2023).
- Boger, T.; Rose, D.; He, S.; Joshi, A. Developments for future EU7 regulations and the path to zero impact emissions—A catalyst substrate and filter supplier’s perspective. Transp. Eng. 2022, 10, 100129. [Google Scholar] [CrossRef]
- Claßen, J.; Krysmon, S.; Dorscheidt, F.; Sterlepper, S.; Pischinger, S. Real Driving Emission Calibration—Review of Current Validation Methods against the Background of Future Emission Legislation. Appl. Sci. 2021, 11, 5429. [Google Scholar] [CrossRef]
- Maurer, R.; Kossioris, T.; Hausberger, S.; Toenges-Schuller, N.; Sterlepper, S.; Günther, M.; Pischinger, S. How to define and achieve Zero-Impact emissions in road transport? Transp. Res. Part D Transp. Environ. 2023, 116, 103619. [Google Scholar] [CrossRef]
- Görgen, M.; Nijs, M.; Thewes, M.; Balazs, A.; Yadla, S.K.; Scharf, J.; Uhlmann, T.; Claßen, J.; Dorscheidt, F.; Krysmon, S.; et al. Holistic Hybrid RDE Calibration Methodology for EU7. Int. Mot. 2021, 189–215. [Google Scholar] [CrossRef]
- Maurer, R.; Kossioris, T.; Sterlepper, S.; Günther, M.; Pischinger, S. Achieving Zero-Impact Emissions with a Gasoline Passenger Car. Atmosphere 2023, 14, 313. [Google Scholar] [CrossRef]
- Dorscheidt, F.; Pischinger, S.; Claßen, J.; Sterlepper, S.; Krysmon, S.; Görgen, M.; Nijs, M.; Straszak, P.; Abdelkader, A.M. Development of a Novel Gasoline Particulate Filter Loading Method Using a Burner Bench. Energies 2021, 14, 4914. [Google Scholar] [CrossRef]
- Xia, F.; Dorscheidt, F.; Lücke, S.; Andert, J.; Gardini, P.; Scheel, T.; Walter, V.; Tharmakulasingam, J.K.R.; Böhmer, M.; Nijs, M. Experimental Proof-of-Concept of HiL Based Virtual Calibration for a Gasoline Engine with a Three-Way-Catalyst. 2019 JSAE/SAE Powertrains Fuels Lubr. 2019. [Google Scholar] [CrossRef]
- Picerno, M.; Lee, S.-Y.; Ehrly, M.; Schaub, J.; Andert, J. Virtual Powertrain Simulation: X-in-the-Loop Methods for Concept and Software Development. In Proceedings of the 21st Internationales Stuttgarter Symposium, Stuttgart, Germany, 30–31 March 2021; Bargende, M., Reuss, H.-C., Wagner, A., Eds.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021. ISBN 978-3-658-33465-9:531–545. [Google Scholar] [CrossRef]
- Krysmon, S.; Bonnaventure, R.; de Baroud, W.; Kluge, K. FEV’s modern X-in-the-Loop-Test Benches for Hybrid Powertrains. FEV Spectr. 2020, 71, 40–45. [Google Scholar]
- Nickel, D.; Behrendt, M.; Bause, K.; Albers, A. Connected testbeds—Early validation in a distributed development environment. In 18. Internationales Stuttgarter Symposium; Bargende, M., Reuss, H.-C., Wiedemann, J., Eds.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2018; pp. 1173–1185. ISBN 978-3-658-21193-6. [Google Scholar]
- Lee, S.-Y.; Andert, J.; Neumann, D.; Querel, C.; Scheel, T.; Aktas, S.; Miccio, M.; Schaub, J.; Koetter, M.; Ehrly, M. Hardware-in-the-Loop-Based Virtual Calibration Approach to Meet Real Driving Emissions Requirements; SAE Technical Paper 2018-01-0869, 2018, WCX World Congress Experience; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 10 April 2018. [Google Scholar] [CrossRef]
- Dorscheidt, F.; Düzgün, M.; Claßen, J.; Krysmon, S.; Pischinger, S.; Görgen, M.; Dönitz, C.; Nijs, M. Hardware-in-the-Loop Based Virtual Emission Calibration for a Gasoline Engine. SAE Tech. Pap. 2021. [Google Scholar] [CrossRef]
- Powertrain and Fluid Systems Conference and Exhibition. Emissions: Advanced catalyst and substrates, measurement and testing, and diesel gaseous emissions. In Proceedings of the Powertrain & Fluid Systems Conference & Exhibition, Pittsburgh, PA, USA, 27–30 October 2003; ISBN 0-7680-1319-4.
- Etzold, K.; Scheer, R.; Fahrbach, T.; Zhou, S.; Goldbeck, R.; Guse, D.; Frie, F.; Sauer, D.U.; De Doncker, R.W.; Andert, J. Hardware-in-the-Loop Testing of Electric Traction Drives with an Efficiency Optimized DC-DC Converter Control; SAE Technical Paper 2020-01-0462, WCX SAE World Congress Experience; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 21 April 2020. [Google Scholar] [CrossRef]
- Jiang, S.; Smith, M.H.; Kitchen, J.; Ogawa, A. Development of an Engine-in-the-loop Vehicle Simulation System in Engine Dynamometer Test Cell. SAE Tech. Pap. 2009. [Google Scholar] [CrossRef] [Green Version]
- Guse, D.; Claßen, J.; Kumagai, T.; Ueda, N.; Scharf, J.; Nijs, M.; Balazs, A.; Görgen, M. Powertrain development frontloading for RDE compliance—Part 2: Robust RDE compliant PN emissions calibration at Engine-in-the-Loop test bench. JSAE 2018. [Google Scholar]
- Heusch, C.; Guse, D.; Dorscheidt, F.; Claßen, J.; Fahrbach, T.; Pischinger, S.; Tegelkamp, S.; Görgen, M.; Nijs, M.; Scharf, J. Analysis of Drivability Influence on Tailpipe Emissions in Early Stages of a Vehicle Development Program by Means of Engine-in-the-Loop Test Benches; SAE Technical Paper 2020-01-0373, WCX SAE World Congress Experience; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 21 April 2020. [Google Scholar] [CrossRef]
- Heusch, C.; Pischinger, S.; Guse, D.; Trampert, S. Objektivierte Fahrbarkeitsuntersuchung am Powertrain-in-the-Loop-Prüfstand. Mtzextra 2021, 26, 24–29. [Google Scholar] [CrossRef]
- Wasserburger, A.; Didcock, N.; Hametner, C. Efficient real driving emissions calibration of automotive powertrains under operating uncertainties. Eng. Optim. 2021, 55, 140–157. [Google Scholar] [CrossRef]
- Maschmeyer, H. Systematische Bewertung Verbrennungsmotorischer Antriebssysteme Hinsichtlich Ihrer Realfahrtemissionen am Motorenprüfstand. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2017. [Google Scholar]
- Baumgarten, H.; Scharf, J.; Thewes, M.; Uhlmann, T.; Balazs, A.; Böhmer, M. Simulation-Based Development Methodology for Future Emission Legislation. In Proceedings of the 37th Internationales Wiener Motorensymposium, 28–29 April 2016. [Google Scholar]
- Böhmer, M. Simulation der Abgasemissionen von Hybridfahrzeugen für Reale Fahrbedingungen. Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 2017. [Google Scholar]
- Roberts, P.J.; Mumby, R.; Mason, A.; Redford-Knight, L.; Kaur, P. RDE Plus—The Development of a Road, Rig and Engine-in-the-Loop Test Methodology for Real Driving Emissions Compliance; SAE Technical Paper 2019-01-0756, WCX SAE World Congress Experience; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 9 April 2019. [Google Scholar] [CrossRef]
- Roberts, P.; Mason, A.; Whelan, S.; Tabata, K.; Kondo, Y.; Kumagai, T.; Mumby, R.; Bates, L. RDE Plus—A Road to Rig Development Methodology for Whole Vehicle RDE Compliance: Overview; SAE Technical Paper 2020-01-0376, WCX SAE World Congress Experience; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 21 April 2020. [Google Scholar]
- Donateo, T.; Giovinazzi, M. Building a cycle for Real Driving Emissions. Energy Procedia 2017, 126, 891–898. [Google Scholar] [CrossRef]
- Kondaru, M.K.; Telikepalli, K.P.; Thimmalapura, S.V.; Pandey, N.K. Generating a Real World Drive Cycle–A Statistical Approach; SAE Technical Paper 2018-01-0325, WCX World Congress Experience; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 10 April 2018. [Google Scholar] [CrossRef]
- Balau, A.E.; Kooijman, D.; Rodarte, I.V.; Ligterink, N. Stochastic Real-World Drive Cycle Generation Based on a Two Stage Markov Chain Approach. SAE Int. J. Mater. Manuf. 2015, 8, 390–397. [Google Scholar] [CrossRef]
- Ashtari, A.; Bibeau, E.; Shahidinejad, S. Using Large Driving Record Samples and a Stochastic Approach for Real-World Driving Cycle Construction: Winnipeg Driving Cycle. Transp. Sci. 2014, 48, 170–183. [Google Scholar] [CrossRef]
- Forster, D.; Inderka, R.B.; Gauterin, F. Data-Driven Identification of Characteristic Real-Driving Cycles Based on k-Means Clustering and Mixed-Integer Optimization. IEEE Trans. Veh. Technol. 2019, 69, 2398–2410. [Google Scholar] [CrossRef]
- Wasserburger, A.; Hametner, C. Automated Generation of Real Driving Emissions Compliant Drive Cycles Using Conditional Probability Modeling. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020; IEEE: Piscataway, NJ, USA. ISBN 978-1-7281-8959-8:1–6. [Google Scholar]
- Millo, F.; Piano, A.; Zanelli, A.; Boccardo, G.; Rimondi, M.; Fuso, R. Development of a Fully Physical Vehicle Model for Off-Line Powertrain Optimization: A Virtual Approach to Engine Calibration; SAE Technical Paper 2021-24-0004, 15th International Conference on Engines & Vehicles; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 12 September 2021. [Google Scholar] [CrossRef]
- Meli, M.; Pischinger, S.; Gärtner, J. Neural Network based ECU Software Function Representation and Optimization for Base Calibration of Internal Combustion Engines. In Proceedings of the 10. International Conference on Modeling and Diagnostics for Advanced Engine Systems, Sapporo, Japan, 5–8 July 2022. [Google Scholar]
- Meli, M.; Pischinger, S.; Kansagara, J.; Dönitz, C.; Liberda, N.; Nijs, M. Proof of Concept for Hardware-in-the-Loop Based Knock Detection Calibration; SAE Technical Paper 2021-01-0424, SAE WCX Digital Summit; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 13 April 2021. [Google Scholar] [CrossRef]
- Krysmon, S.; Dorscheidt, F.; Claßen, J.; Düzgün, M.; Pischinger, S. Real Driving Emissions—Conception of a Data-Driven Calibration Methodology for Hybrid Powertrains Combining Statistical Analysis and Virtual Calibration Platforms. Energies 2021, 14, 4747. [Google Scholar] [CrossRef]
- Claßen, J. Entwicklung statistisch relevanter Prüfszenarien zur Bewertung der Fahrzeug-Emissionsrobustheit unter realen Fahrbedingungen. Ph.D. Thesis, Universitätsbibliothek der RWTH, Aachen, Germany, 2022. [Google Scholar] [CrossRef]
- Claßen, J.; Pischinger, S.; Krysmon, S.; Sterlepper, S.; Dorscheidt, F.; Doucet, M.; Reuber, C.; Görgen, M.; Scharf, J.; Nijs, M.; et al. Statistically supported real driving emission calibration: Using cycle generation to provide vehicle-specific and statistically representative test scenarios for Euro 7. Int. J. Engine Res. 2020, 21, 1783–1799. [Google Scholar] [CrossRef]
- Claßen, J.; Sterlepper, S.; Dorscheidt, F.; Görgen, M.; Scharf, J.; Nijs, M.; Alt, N.; Balazs, A.; Böhmer, M.; Doucet, M.; et al. RDE cycle generation—A statistical approach to cut down testing effort and provide a secure base to approve RDE legislation compliance. Int. Mot. 2019, 76, 37–56. [Google Scholar] [CrossRef]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef] [Green Version]
- Serrà, J.; Arcos, J.L. An empirical evaluation of similarity measures for time series classification. Knowledge-Based Syst. 2014, 67, 305–314. [Google Scholar] [CrossRef] [Green Version]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2012. [Google Scholar] [CrossRef]
- Portnoff, M. Time-frequency representation of digital signals and systems based on short-time Fourier analysis. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 55–69. [Google Scholar] [CrossRef]
- Mateo, C.; Talavera, J.A. Short-Time Fourier Transform with the Window Size Fixed in the Frequency Domain (STFT-FD): Implementation. Softwarex 2018, 8, 5–8. [Google Scholar] [CrossRef]
- Abanda, A.; Mori, U.; Lozano, J.A. A review on distance based time series classification. Data Min. Knowl. Discov. 2018, 33, 378–412. [Google Scholar] [CrossRef] [Green Version]
- Batista, G.E.; Wang, X.; Keogh, E.J. A Complexity-Invariant Distance Measure for Time Series. In Proceedings of the 2011 SIAM International Conference on Data Mining, Mesa, AZ, USA, 28–30 April 2011; Liu, B., Liu, H., Clifton, C., Washio, T., Kamath, C., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2011; ISBN 978-0-89871-992-5:699–710. [Google Scholar]
- Petitjean, F.; Forestier, G.; Webb, G.I.; Nicholson, A.E.; Chen, Y.; Keogh, E. Faster and more accurate classification of time series by exploiting a novel dynamic time warping averaging algorithm. Knowl. Inf. Syst. 2015, 47, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Rani, S.; Sikka, G. Recent Techniques of Clustering of Time Series Data: A Survey. Int. J. Comput. Appl. 2012, 52, 1–9. [Google Scholar] [CrossRef]
- Goutte, C.; Toft, P.; Rostrup, E.; Nielsen, F.; Hansen, L.K. On Clustering fMRI Time Series. Neuroimage 1999, 9, 298–310. [Google Scholar] [CrossRef] [Green Version]
- Thorndike, R.L. Who belongs in the family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
- Jung, Y.; Park, H.; Du, D.-Z.; Drake, B.L. A Decision Criterion for the Optimal Number of Clusters in Hierarchical Clustering. J. Glob. Optim. 2003, 25, 91–111. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Wiedenbeck, M.; Züll, C. Klassifikation mit Clusteranalyse: Grundlegende Techniken hierarchischer und K-means-Verfahren. GESIS-How-10 2001. [Google Scholar]
- Na, S.; Xumin, L.; Yong, G. Research on k-means Clustering Algorithm: An Improved k-means Clustering Algorithm. In Proceedings of the 2010 Third International Symposium on Intelligent Information Technology and Security Informatics, Jian, China, 2–4 April 2010; IEEE: Piscataway, NJ, USA, 2011. ISBN 978-1-4244-6730-3:63–67. [Google Scholar]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Astels, S. hdbscan: Hierarchical density based clustering. J. Open Source Softw. 2017, 2, 205. [Google Scholar] [CrossRef]








| Emission Component | ||||||
| Number of events |
| Signal Number | Signal | Number of Clusters | Silhouette Score | Outliers |
|---|---|---|---|---|
| 1 | Engine speed | |||
| 2 | Vehicle speed | |||
| 3 | Downstream lambda sensor voltage (bank 1) | |||
| 4 | Downstream lambda sensor voltage (bank 2) | |||
| 5 | Bit fuel cut-off | |||
| 6 | Temperature of catalytic converter | |||
| 7 | Engine torque | |||
| 8 | Exhaust gas mass flow | |||
| 9 | Relative air charge |
| Emission Component | Signal | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| CO | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krysmon, S.; Claßen, J.; Pischinger, S.; Trendafilov, G.; Düzgün, M.; Dorscheidt, F. RDE Calibration—Evaluating Fundamentals of Clustering Approaches to Support the Calibration Process. Vehicles 2023, 5, 404-423. https://doi.org/10.3390/vehicles5020023
Krysmon S, Claßen J, Pischinger S, Trendafilov G, Düzgün M, Dorscheidt F. RDE Calibration—Evaluating Fundamentals of Clustering Approaches to Support the Calibration Process. Vehicles. 2023; 5(2):404-423. https://doi.org/10.3390/vehicles5020023
Chicago/Turabian StyleKrysmon, Sascha, Johannes Claßen, Stefan Pischinger, Georgi Trendafilov, Marc Düzgün, and Frank Dorscheidt. 2023. "RDE Calibration—Evaluating Fundamentals of Clustering Approaches to Support the Calibration Process" Vehicles 5, no. 2: 404-423. https://doi.org/10.3390/vehicles5020023
APA StyleKrysmon, S., Claßen, J., Pischinger, S., Trendafilov, G., Düzgün, M., & Dorscheidt, F. (2023). RDE Calibration—Evaluating Fundamentals of Clustering Approaches to Support the Calibration Process. Vehicles, 5(2), 404-423. https://doi.org/10.3390/vehicles5020023






