Influences on Vibration Load Testing Levels for BEV Automotive Battery Packs
Abstract
1. Introduction
Economic Considerations for Design in Automotive and Other Mobile Applications
2. Methods
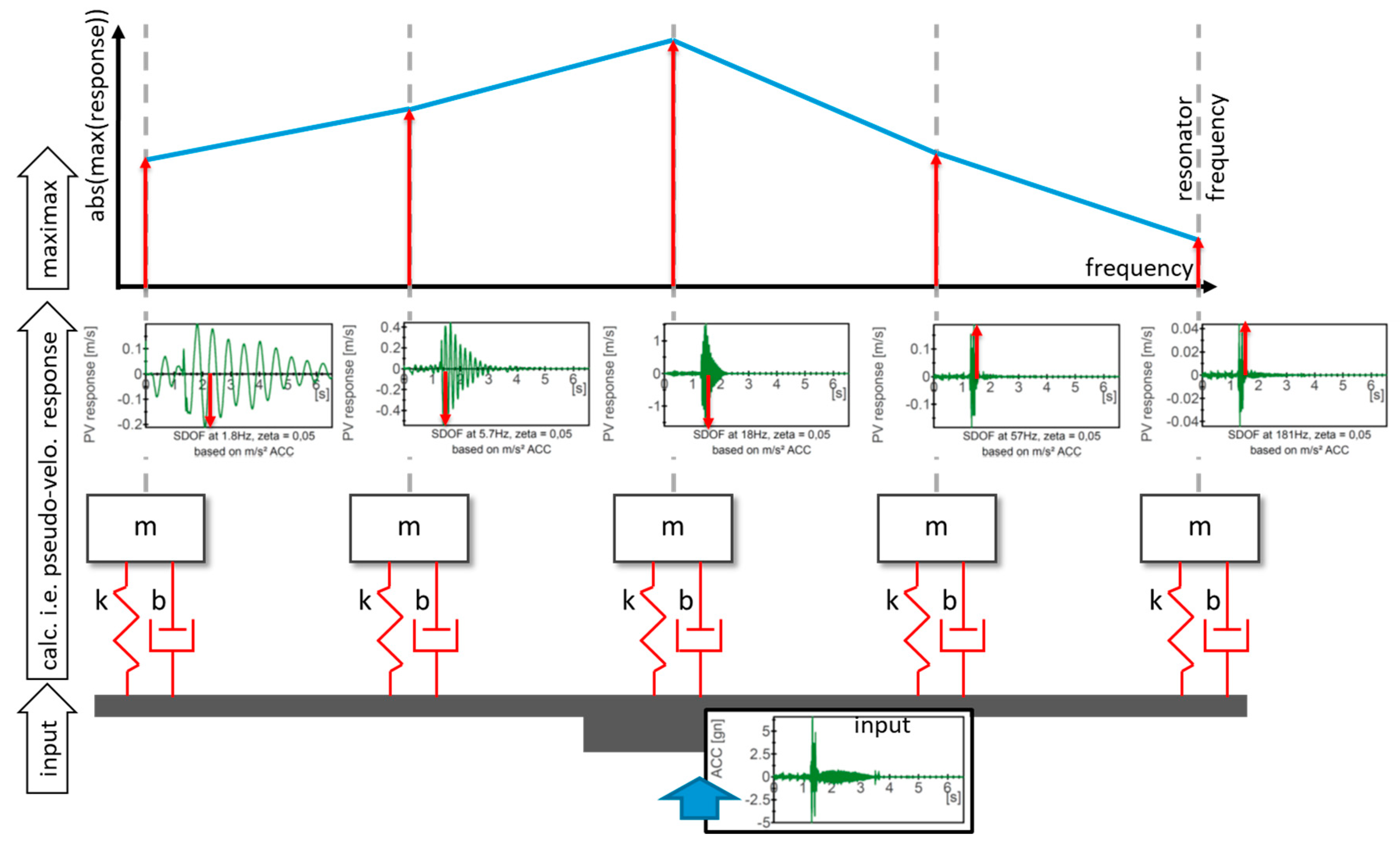
2.1. Movements in Time Domain
2.2. Comparison with Other Technical Solutions Regarding Mass and Stiffness
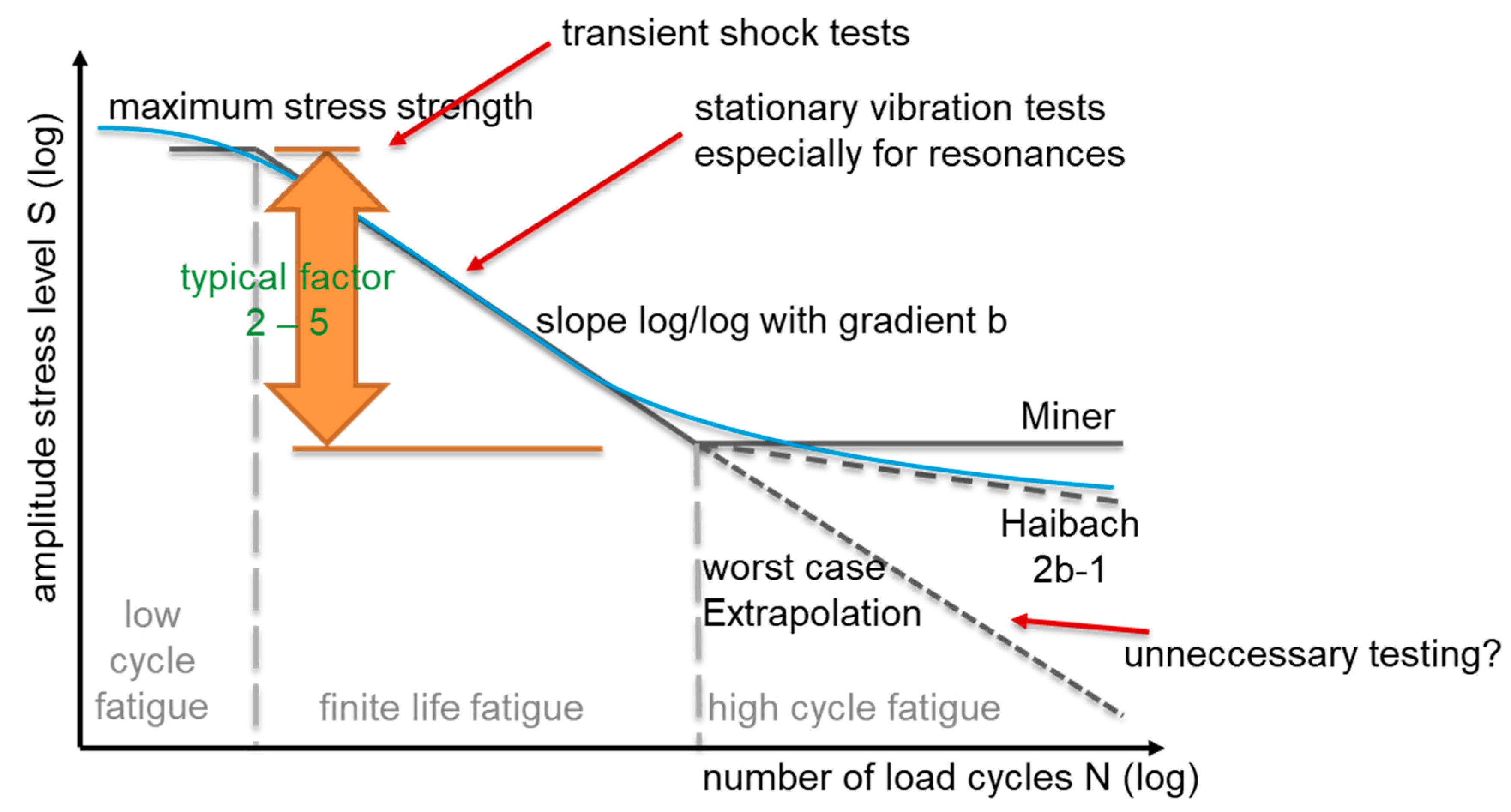
2.3. SRS for Boundary Considerations in SN Curve
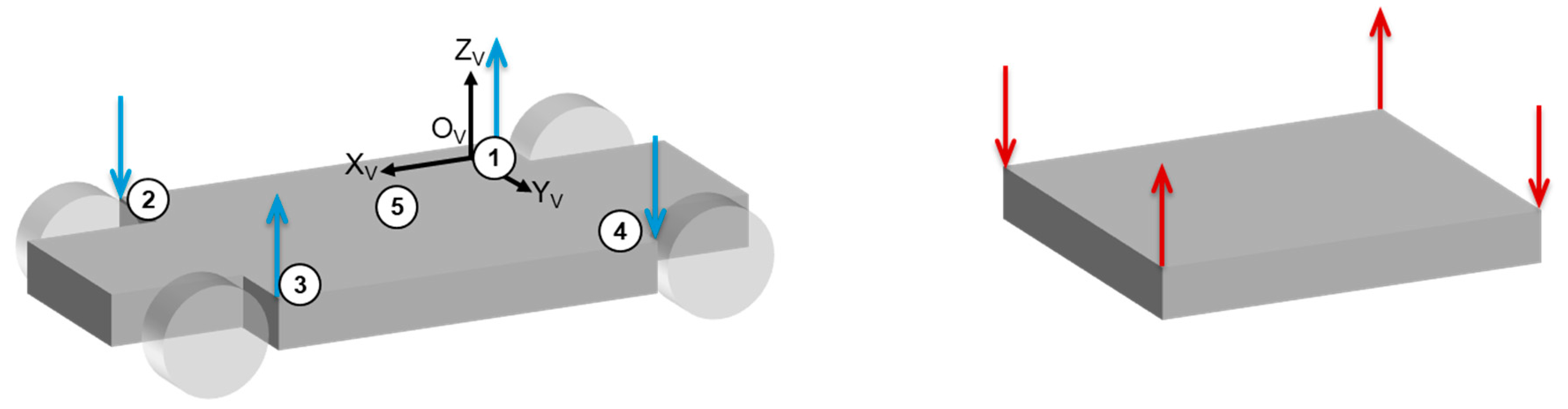
2.4. Measurement Data Set to Be Analyzed
2.5. Excitations from Vehicle–Ground Interaction
2.6. Vehicles of Preliminary Study
2.7. Measurement Equipment and Signal Quality
2.8. Normal Tolerance Limit on Power Spectral Density in Analysis Software
3. Results
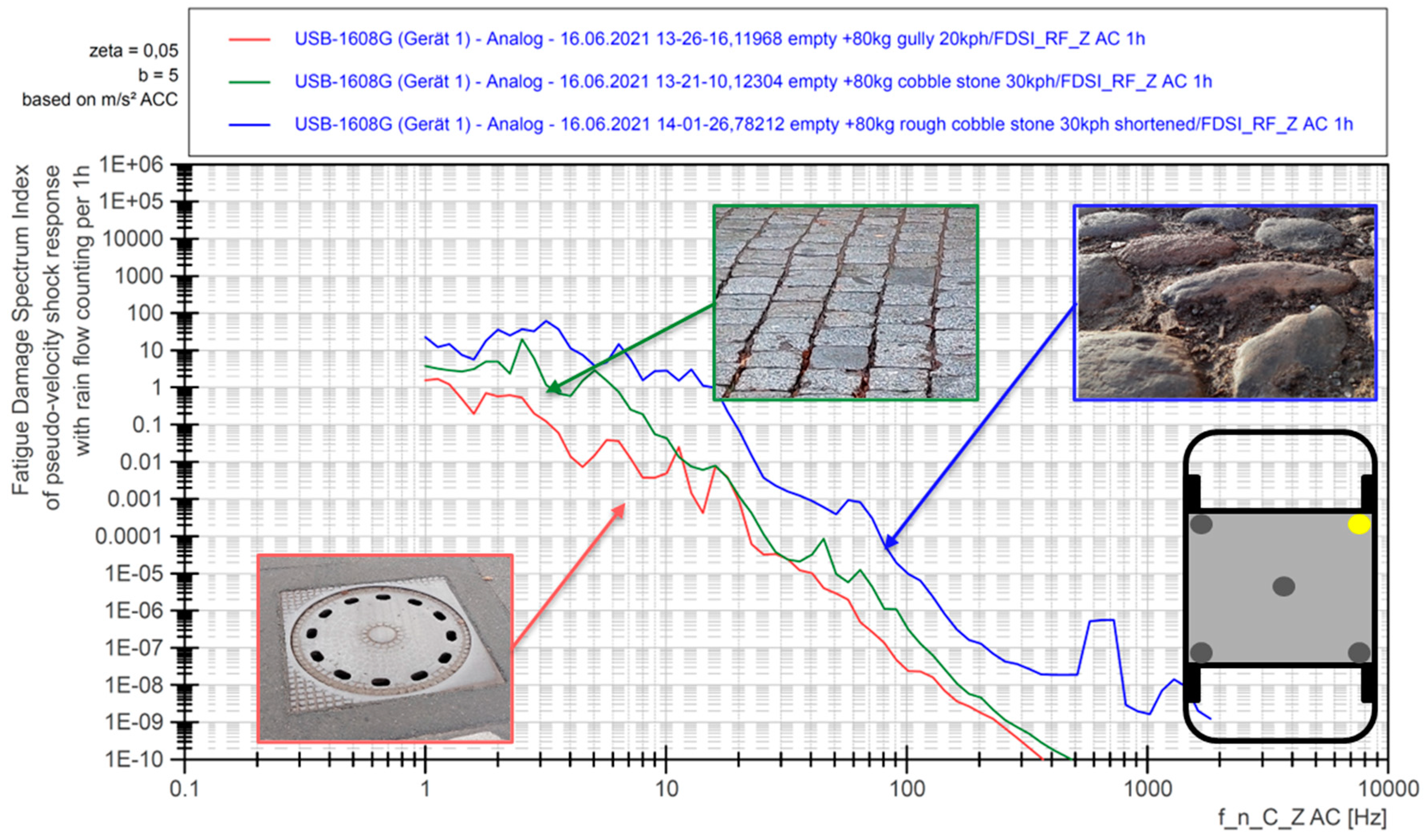
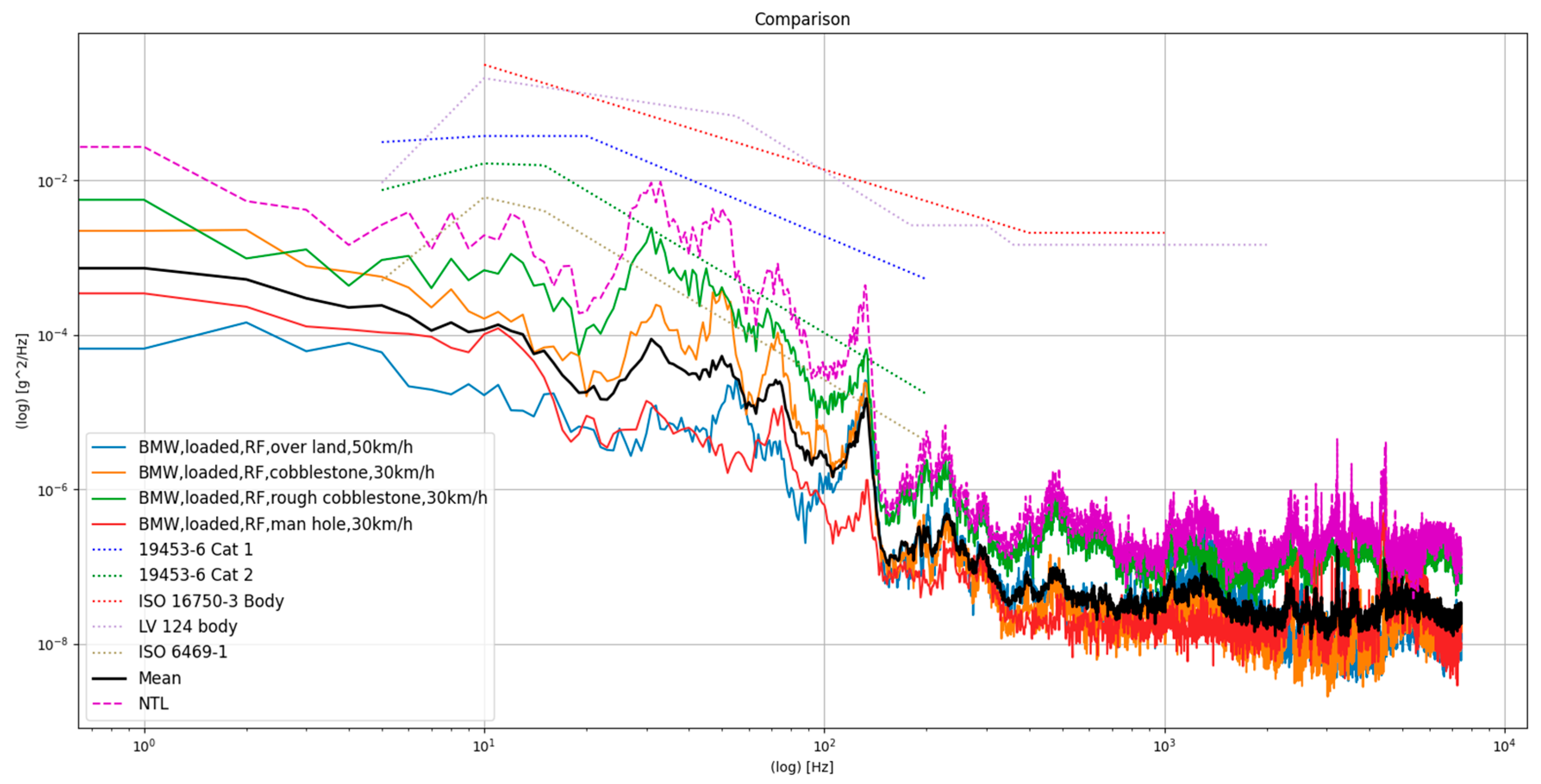
3.1. Power Spectral Density and Normal Tolerance Limits for Different Influence Factors
- Vehicle type (BMW i3, VW ID.3 and additional EVUM aCar commercial mini truck)
- Road surface (rough cobble stone, cobble stone, smooth tarmac)
- Mass loading of the vehicle (driver, extra load according to Table 2)
- Measurement points on the battery pack (4 in the corners, 1 in the center)
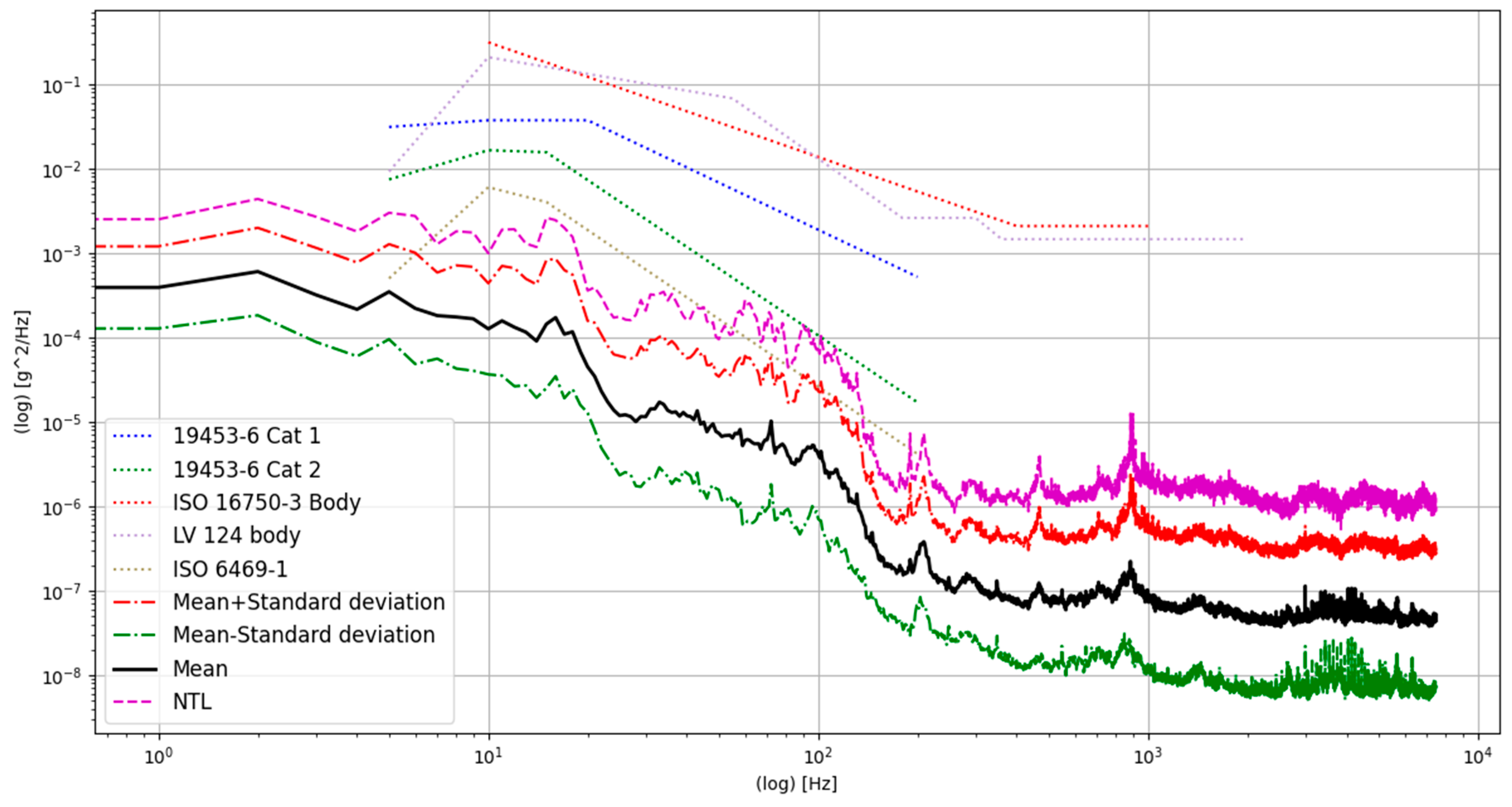
3.2. Power Spectral Density and Normal Tolerance Limits over All Measurements
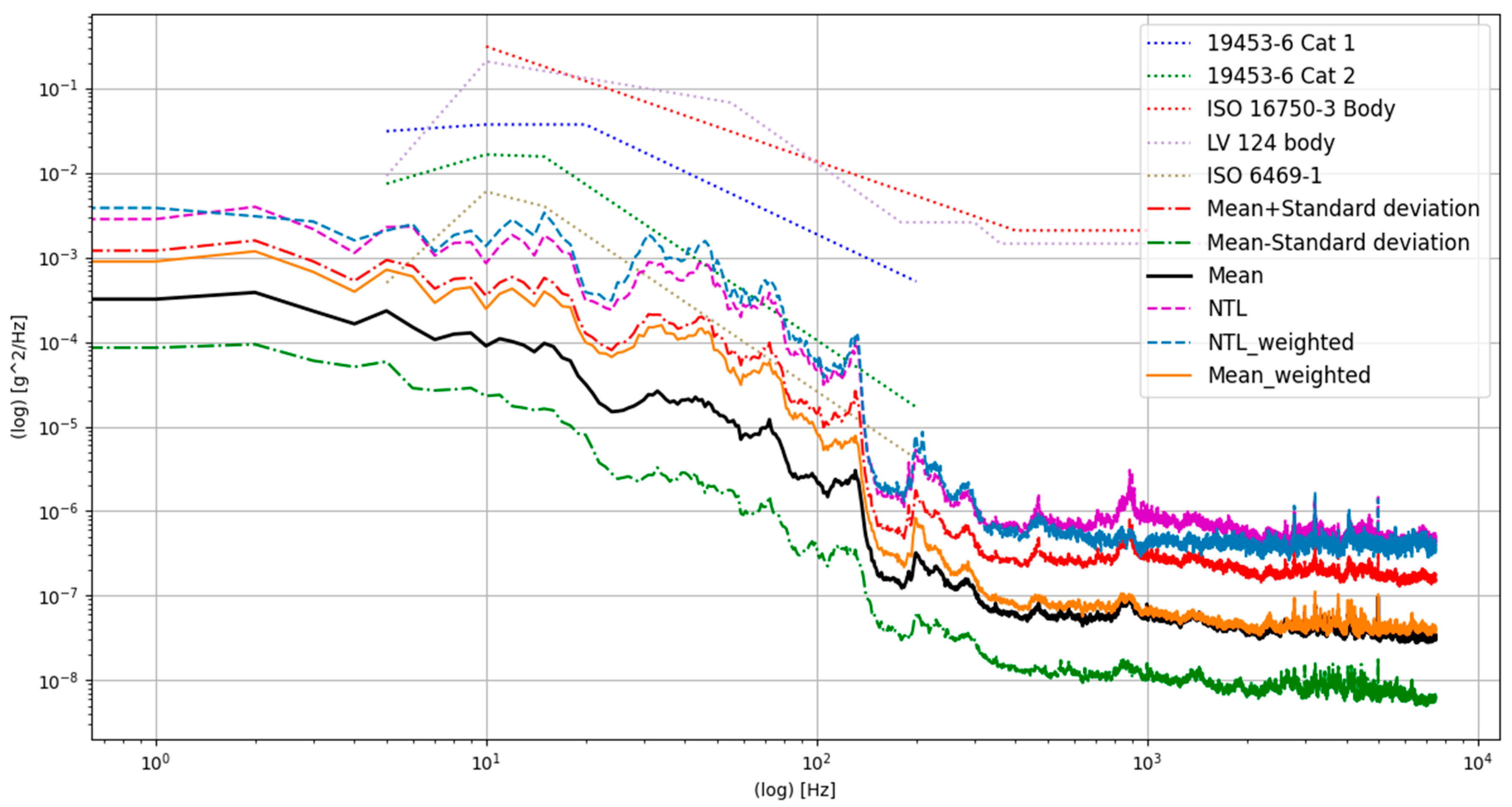
3.3. Comparison of NTL for BEVs and a Commercial Mini Truck
3.4. Assimilation of Combined Testing Profiles and Durations
3.5. Limitations of the Study
4. Conclusions
- The high-voltage battery packs of both standard automotive vehicles experience the highest loads at the corner points of the battery facing forward in the direction of driving.
- The loading of extra weight in the rear legroom of the standard automotive BEVs only has a minor influence on vibration levels and resonance frequencies of the pack [1].
- In contrast, the different driving road surfaces have a very strong influence on the measured accelerations. Due to low accelerations occurring on smooth tarmac, this influence can be neglected when testing the battery pack also under the rough road conditions used in this analysis because the levels remain far below infinite-life fatigue levels. The test profile created from the measured data with the given assumptions was then compared to applicable standards.
- Out of the standards considered in this comparison for life-time testing, only the profile of ISO19453-6 cat 2 seems to be suitable for a realistic, but in general conservative, fatigue life-time testing of the standard automotive battery packs. Using other standards, such as LV124-2 [24], ISO16750-3 [6] and ISO19453-6 [2] (category 1), may result in incorrect dimensioning of the structural parts and massive over-testing. Using ISO6469-1 [8] for life-time fatigue testing may result in significant under-testing. This standard is not designed for fatigue testing.
- Larger masses of bigger battery packs will also change the resulting excitation vibrations into the battery pack. It is assumed that larger masses reduce the vibration level in general and over a wide frequency range as can be seen by the difference of ISO19453-6 Cat 1 and Cat 2 [2] as well as the analysis of larger construction machinery battery packs.
- The combination of a very stiff suspension with high vibration power input to a small and lightweight battery pack such as in the commercial off-road mini truck clearly marks a worst case, increasing the calculated 95/50-NTL by at least one decade.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Plaumann, B. Towards Realistic Vibration Testing of Large Floor Batteries for Battery Electric Vehicles (BEV). Sound Vib. 2022, 56, 1–19. [Google Scholar] [CrossRef]
- ISO 19453-6; Road Vehicles—Environmental Conditions and Testing for Electrical and Electronic Equipment—Part 6. Traction Battery Packs and Systems. International Organization for Standardization: Geneva, Switzerland, 2020.
- Kutka, H.; Müller, C.; Fülöp, T.; Dörnhöfer, A. Multilevel fatigue analysis of RESS in BEV/HEV—Multilevel-Festigkeitsentwicklungen der HV-Speicher von BEV/HEV-Fahrzeugen. In Berichtsband zur 45. Tagung des DVM-Arbeitskreises Betriebsfestigkeit; Brune, M., Ed.; Deutscher Verband für Materialforschung und -Prüfung: Berlin, Germany, 2018; pp. 1–18. [Google Scholar]
- Hooper, J.M.; Marco, J. Characterising the in-vehicle vibration inputs to the high voltage battery of an electric vehicle. J. Power Sources 2014, 245, 510–519. [Google Scholar] [CrossRef]
- J2380_202112; Vibration Testing of Electric Vehicle Batteries. SAE International: Warrendale, PA, USA, 2021.
- ISO 16750-3; Road Vehicles—Environmental Conditions and Testing for Electrical and Electronic Equipment—Part 3: Mechanical Loads. International Organization for Standardization: Geneva, Switzerland, 2012.
- UN ECE Regulation No. 100; Agreement Concerning the Adoption of Uniform Technical Prescriptions for Wheeled Vehicles, Equipment and Parts Which Can Be Fitted and/or Be Used on Wheeled Vehicles and the Conditions for Reciprocal Recognition of Approvals Granted on the Basis of These Prescriptions: Addendum 99. UNECE: Geneva, Switzerland, 2013.
- ISO 6469-1; Electrically Propelled Road Vehicles—Safety Specifications—Part 1: Rechargeable Energy Storage System (RESS). International Organization for Standardization: Geneva, Switzerland, 2019.
- Kjell, G.; Lang, J.F. Comparing different vibration tests proposed for li-ion batteries with vibration measurement in an electric vehicle. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; IEEE: New York, NY, USA, 2013; pp. 1–11. [Google Scholar]
- Gao, W.; Li, X.; Ma, M.; Fu, Y.; Jiang, J.; Mi, C. Case Study of an Electric Vehicle Battery Thermal Runaway and Online Internal Short-Circuit Detection. IEEE Trans. Power Electron. 2020, 36, 2452–2455. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Giannelos, S.; Borozan, S.; Strbac, G. A Backwards Induction Framework for Quantifying the Option Value of Smart Charging of Electric Vehicles and the Risk of Stranded Assets under Uncertainty. Energies 2022, 15, 3334. [Google Scholar] [CrossRef]
- Borozan, S.; Giannelos, S.; Strbac, G. Strategic network expansion planning with electric vehicle smart charging concepts as investment options. Adv. Appl. Energy 2021, 5, 100077. [Google Scholar] [CrossRef]
- Schramm, D.; Hiller, M.; Bardini, R. Vehicle Dynamics: Modeling and Simulation; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- EN 1999-1-3; Eurocode 9: Design of Aluminium Structures—Part 1–3: Structures Susceptible to Fatigue. CEN: Brussels, Belgium, 2011.
- Gaberson, H.A.; Chalmers, R.H. Modal Velocity as a Criterion of Shock Severity. Shock. Vib. Bull. 1969, 40, 31–49. [Google Scholar]
- Gaberson, H.A. Shock Severity Estimation. Sound Vib. 2012, 46, 12–19. [Google Scholar]
- Ahlin, K. Comparison of test specifications and measured field data. Sound Vib. 2006, 40, 22–24. [Google Scholar]
- IEC 60721-2-9; Classification of Environmental Conditions—Part 2–9: Environmental Conditions Appearing in Nature—Measured Shock and Vibration Data—Storage, Transportation and In-Use. IEC: Geneva, Switzerland, 2015.
- ISO 18431-4; Mechanical Vibration and Shock—Signal Processing—Part 4: Shock-Response Spectrum Analysis. International Organization for Standardization: Geneva, Switzerland, 2007.
- Hooper, J.; Marco, J. Defining a Representative Vibration Durability Test for Electric Vehicle (EV) Rechargeable Energy Storage Systems (RESS). World Electr. Veh. J. 2016, 8, 327–338. [Google Scholar] [CrossRef]
- McNeill, S.I. Implementing the Fatigue Damage Spectrum and Fatigue Damage Equivalent Vibration Testing. In Proceedings of the 79th Shock and Vibration Symposium, Orlando, FL, USA, 26–30 October 2008. [Google Scholar]
- Kersch, K.; Wagner, A.; Kuttner, T.; Woschke, E. Improved Techniques for Uniaxial and Multiaxial Vibration Test Profile Definition. J. IEST 2020, 63, 53–62. [Google Scholar] [CrossRef]
- LV 124-2; Electric and Electronic Components in Motor Vehicles up to 3.5 t—General Requirements, Test Conditions and Tests Part 2: Environmental Requirements. Mercedes MBN: Stuttgart, Germany, 2013.
- MIL-STD-810; Environmental Engineering Considerations and Laboratory Tests. Department of Defence (DOD): Washington, DC, USA, 2014.
- Plaumann, B. Anforderungen an die Vibrationsprüfung von großen unterflurmontierten Batterien für batteriebetriebene Elektrofahrzeuge (BEV)—Requirements for vibration testing of large underfloor-mounted battery for Battery Electric Vehicles (BEV). In Proceedings of the Workshop Brennstoffzelle, Batterie, Elektrischer Antrieb—Anforderungen und Absicherung 2021, Ulm, Germany, 17–18 November 2021. [Google Scholar]
- Statista, Bundesamt für Strassen (Schweiz). Zustand der Straßen in der Schweiz nach Bereich im Jahr 2020. December 2021. Available online: https://de.statista.com/statistik/daten/studie/936023/umfrage/zustand-der-strassen-in-der-schweiz-nach-bereich/ (accessed on 1 December 2022).




| Properties | Category 1 | Category 2 | Category 3 |
|---|---|---|---|
| Weight | 10–30 kg | 200 kg | 400–700 kg |
| Placement | Different places in car | Tunnel area, rare seats, trunk | underfloor-mounted constructions |
| Application | Mild Hybrid Electric Vehicles (MHEVs) | Hybrid Electric Vehicles/Plugin Electric Vehicles (HEVs/PHEVs) | Battery Electric Vehicles (BEVs) |
| Vehicle | Compact BEV VW ID.3 | Compact BEV BMW i3 | EVUM aCar (Off-Road Mini Truck for Contrasting Design Requirements) |
|---|---|---|---|
| empty weight | 1810 kg | 1320 kg | 1460 kg |
| max gross weight | 2270 kg | 1670 kg | 2600 kg |
| added mass loading additional to driver etc. (80 kg) | 0 kg | 0 kg | 80 kg (permanent second passenger) |
| 87.5 kg | |||
| 200 kg | 162.5 kg | ||
| battery energy | 62 kWh | 33 kWh | 16.5 kWh |
| battery pack weight | 376 kg | 256 kg | ca. 225 kg |
| IEPE one-axial piezo accelerometer with charge amplifiers PCB M353B18 ± 500 gn at 10 mV/gn PCB-483C05 AC coupling with constant current for charge amplifiers |
| USB data acquisition system Meilhaus Redlab, rebranded Measurement Computing (MCC) 1608 G with 16 bit, 16 analog inputs at ±1 to 10 V, 250 kS/s common rate sampling rate per channel 15 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinzen, T.; Plaumann, B.; Kaatz, M. Influences on Vibration Load Testing Levels for BEV Automotive Battery Packs. Vehicles 2023, 5, 446-463. https://doi.org/10.3390/vehicles5020025
Heinzen T, Plaumann B, Kaatz M. Influences on Vibration Load Testing Levels for BEV Automotive Battery Packs. Vehicles. 2023; 5(2):446-463. https://doi.org/10.3390/vehicles5020025
Chicago/Turabian StyleHeinzen, Till, Benedikt Plaumann, and Marcus Kaatz. 2023. "Influences on Vibration Load Testing Levels for BEV Automotive Battery Packs" Vehicles 5, no. 2: 446-463. https://doi.org/10.3390/vehicles5020025
APA StyleHeinzen, T., Plaumann, B., & Kaatz, M. (2023). Influences on Vibration Load Testing Levels for BEV Automotive Battery Packs. Vehicles, 5(2), 446-463. https://doi.org/10.3390/vehicles5020025







