Parameter Identification and Dynamic Characteristic Research of a Fractional Viscoelastic Model for Sub-Frame Bushing
Abstract
:1. Introduction
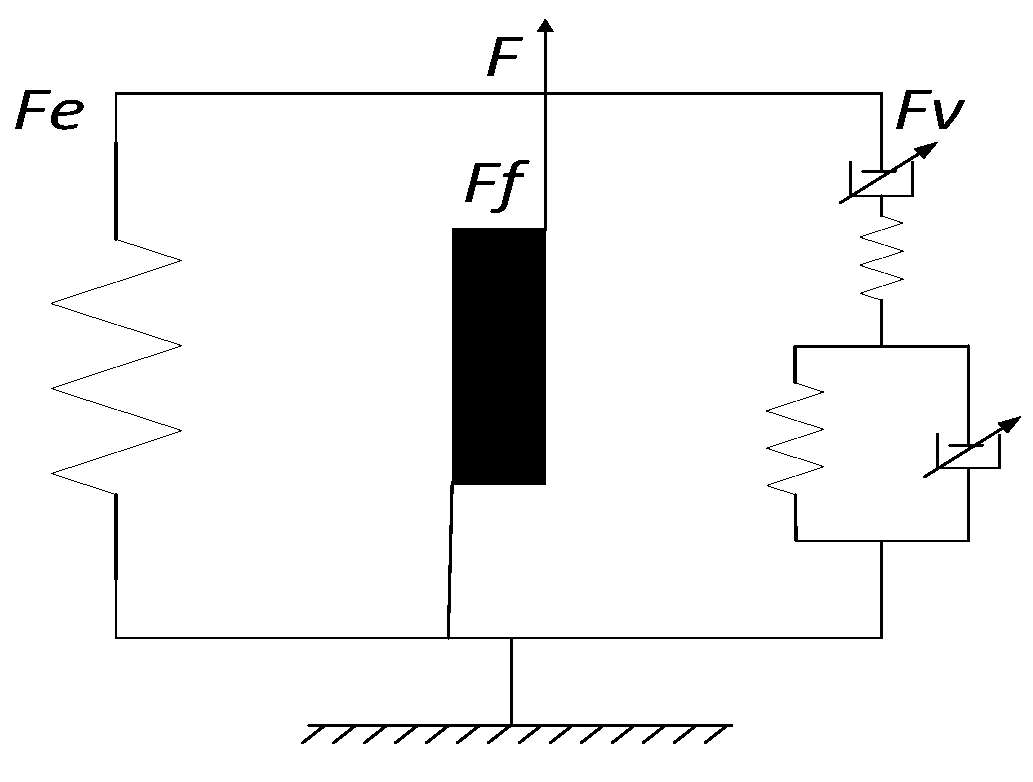
2. Establishment of the Rubber Bushing Dynamic Model
2.1. Elastic Element of the Rubber Bushing Model
2.2. Frictional Element of the Rubber Bushing Model
2.3. Viscoelastic Element of the Bushing Model
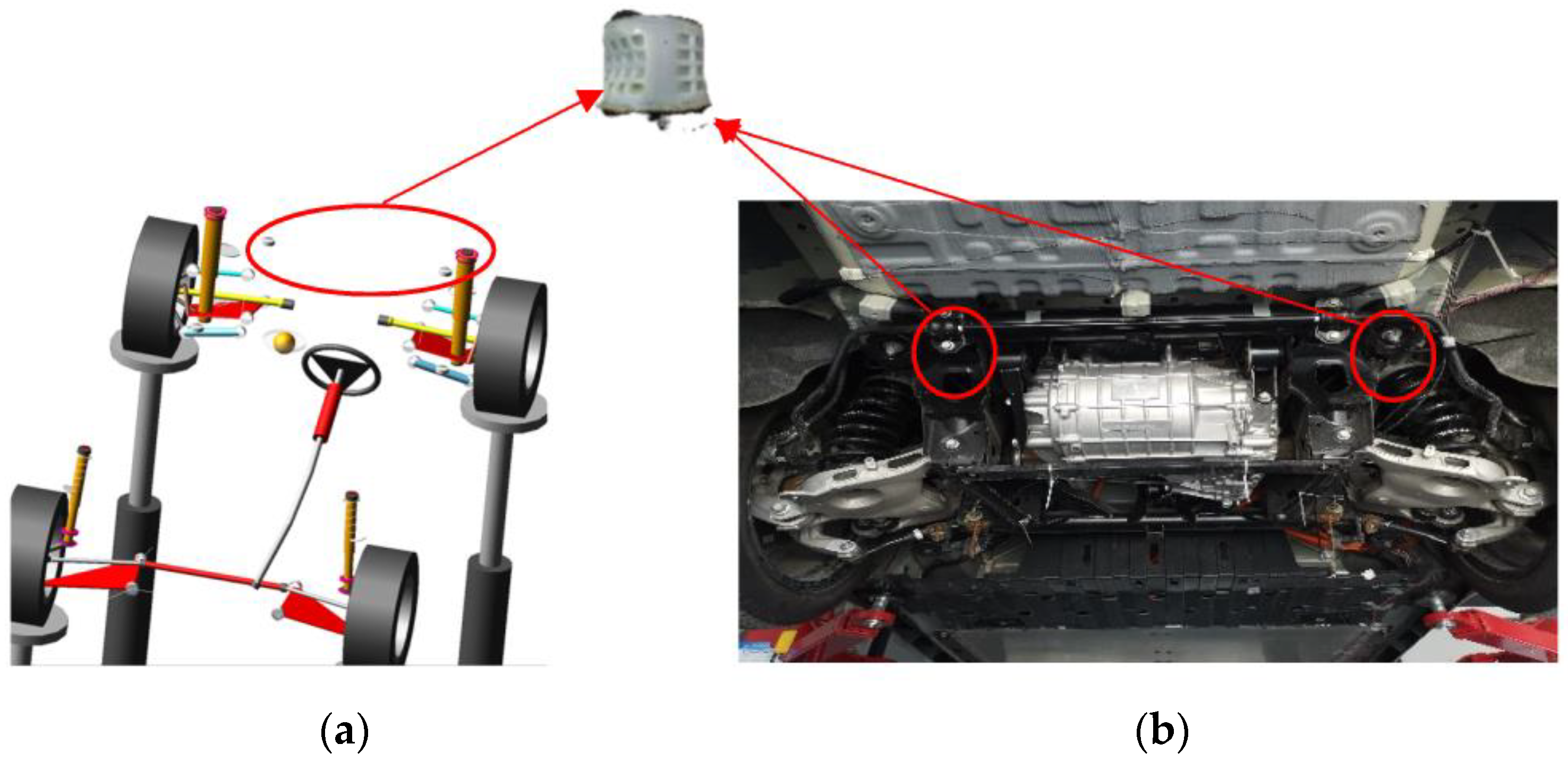
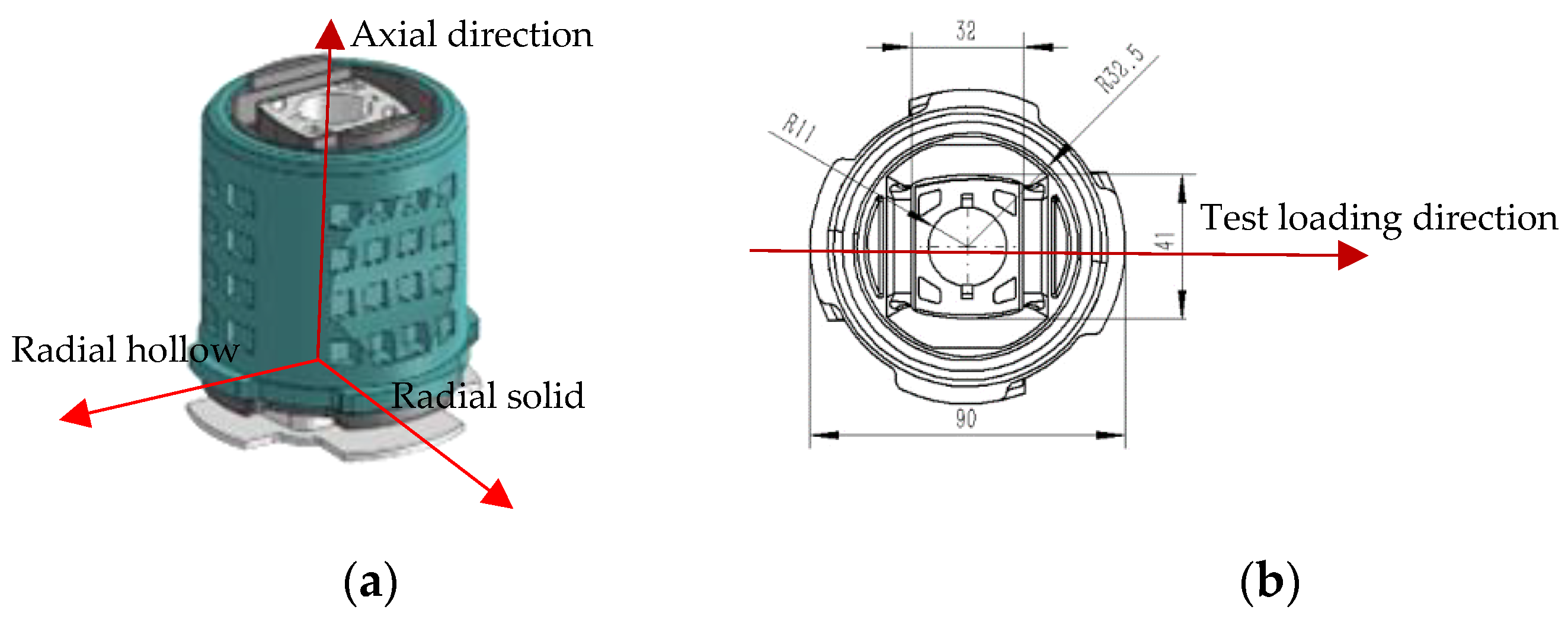
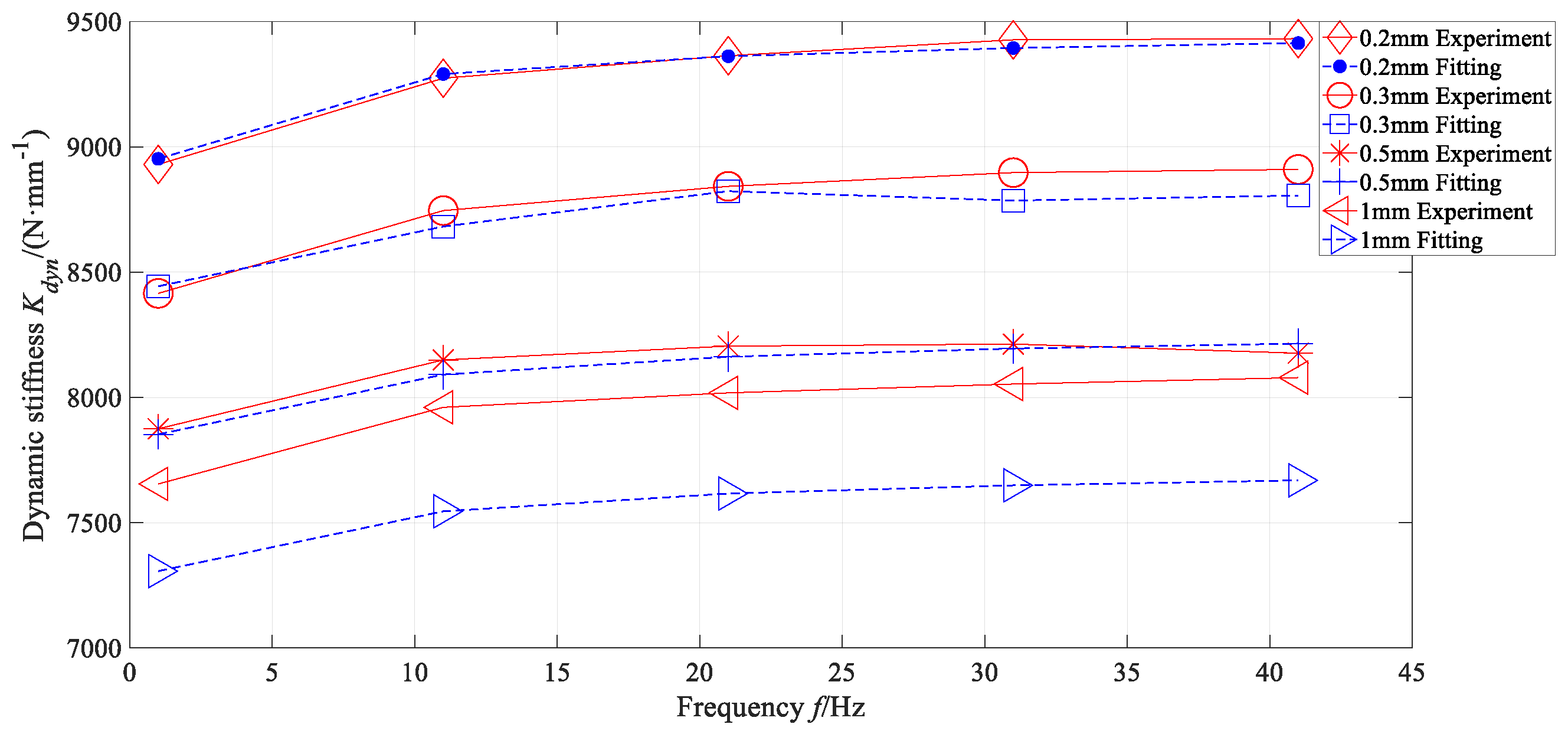
3. Rubber Bushing Tests
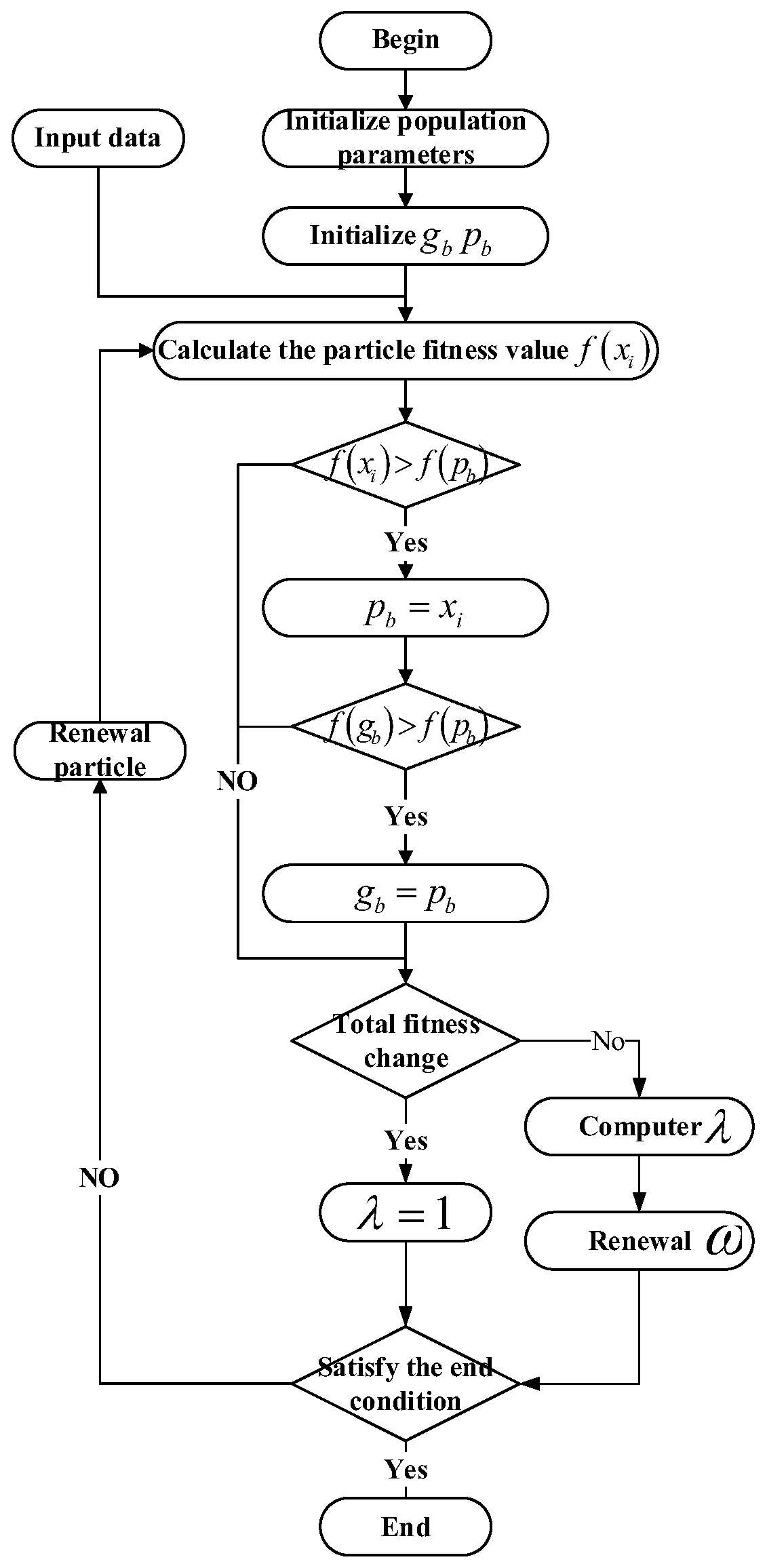
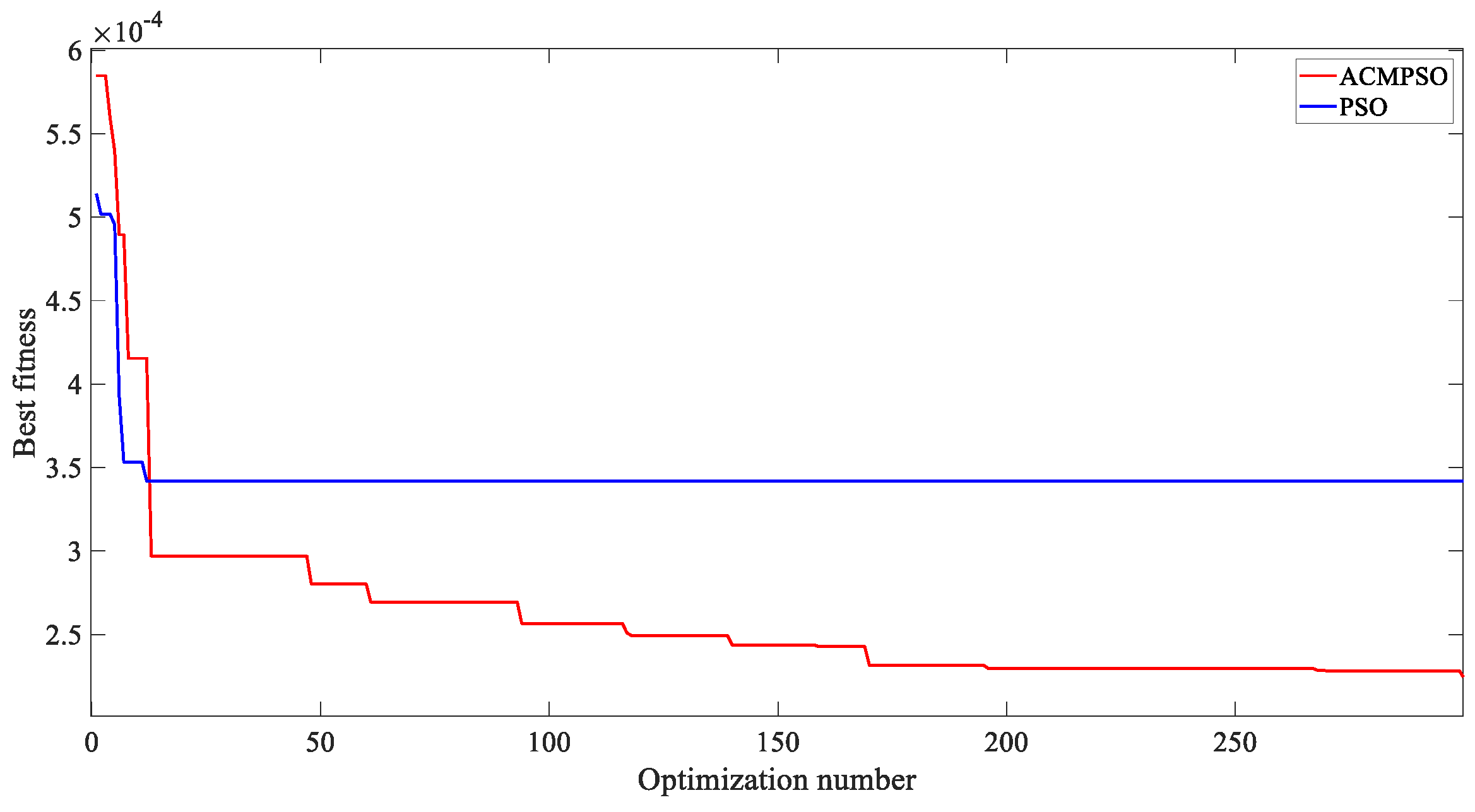
4. Parameter Identification of the Rubber Bushing Dynamic Model
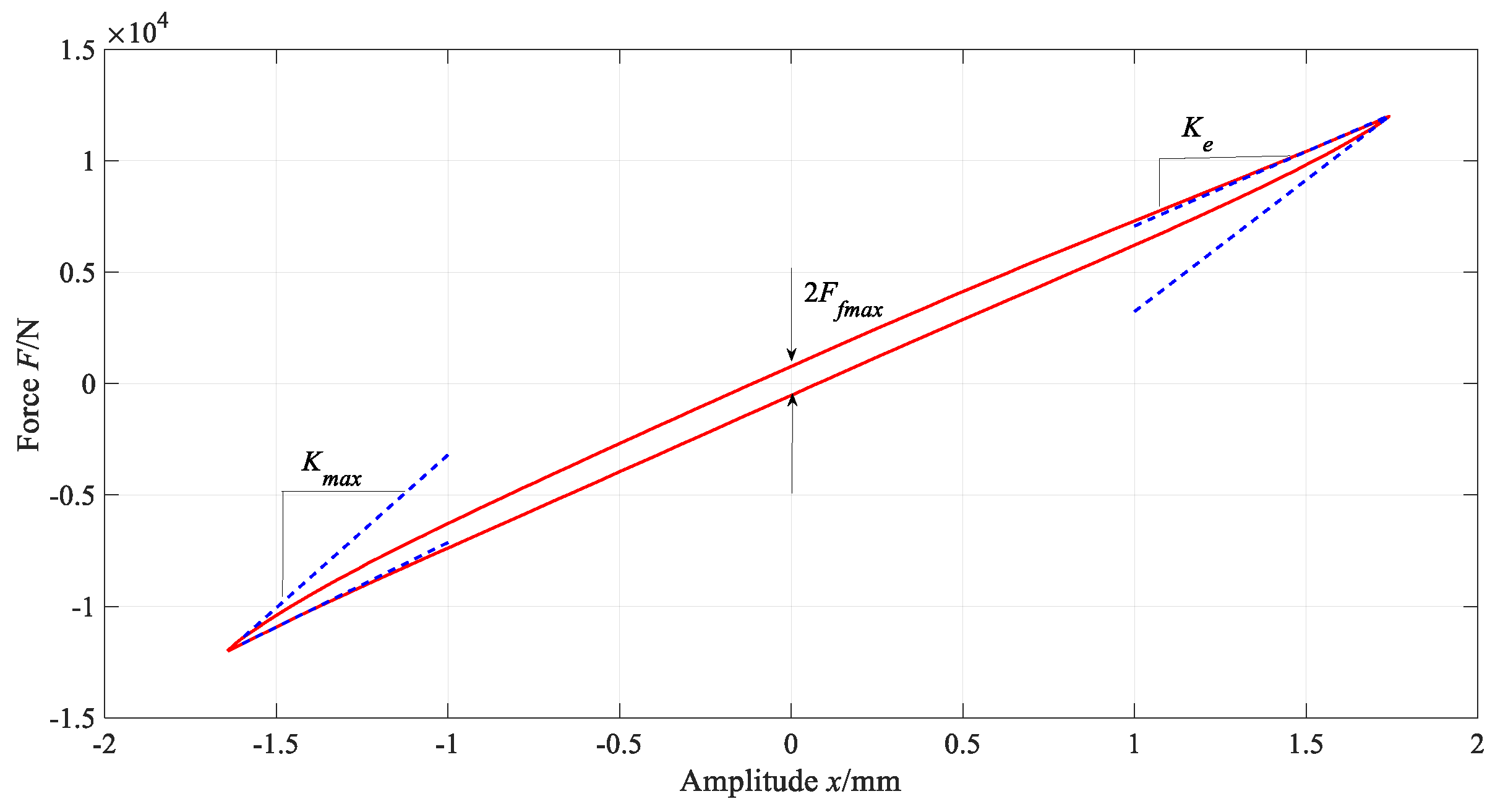
4.1. Identification of the Parameters of the Elastic and Friction Elements
4.2. Identification of the Parameters of the Viscoelastic Elements
5. Parameter Sensitivity Analysis of Viscoelastic Element of the Rubber Bushing Model
5.1. Choice of Parameter Sensitivity Analysis Method
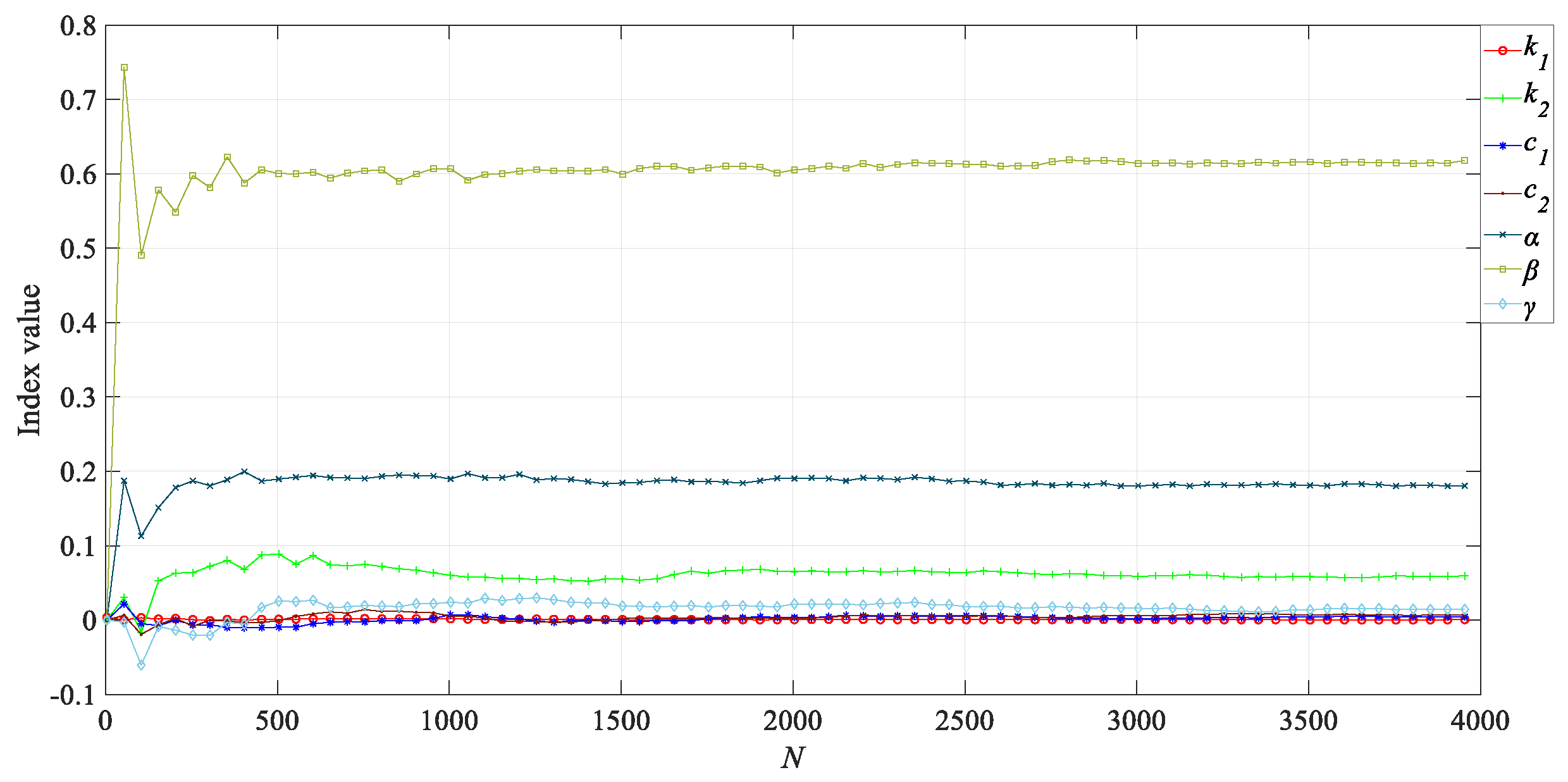
5.2. Sensitivity Analysis of Rubber Bushing Model Parameters Based on the Sobol Method
- Set parameter ranges: Define the ranges of the input parameters for the model.
- Set the number of sampling points: In this study, the number of sampling points N ranges from 4 to 4000, increasing by 50 at each step.
- Monte Carlo sampling: Use the Monte Carlo method to randomly sample the input parameters within their specified ranges.
- Form the sample matrices A and B: Based on the Monte Carlo sampling, form the sample matrices A and B, which represent the input parameter values.
- Calculate the model output: Use the sample matrices A and B to calculate the model output for each set of input parameter values.
- Compute the first-order and total sensitivity indices: Utilize the model output to calculate the first-order sensitivity indices and total sensitivity indices for each input parameter. These indices measure the contribution of each parameter to the output variance and the total effect of each parameter, respectively.
6. Conclusions
- The proposed combination of the Maxwell and Kelvin–Voigt models for the viscoelastic element in the rear sub-frame rubber bushing dynamic model significantly improves the fitting accuracy to the experimental data after parameter identification using an adaptive chaotic improved particle swarm optimization algorithm.
- The sensitivity analysis of the bushing model parameters reveals that recalibrating the , , and parameters further enhances the fitting accuracy of the model after re-identification.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Units |
| mm | |
References
- Yue, K.; Zhang, Y.; Xu, P. Comparison of Rubber Bushing Models for Loads Analysis; SAE Technical Paper 2021-01-0317; SAE: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Ambrósio, J.; Verissimo, P. Improved bushing models for general multibody systems and vehicle dynamics. Multibody Syst. Dyn. 2009, 22, 341–365. [Google Scholar] [CrossRef]
- Guo, R.; Guan, X. A Review of Studies on Rubber Sleeve Dynamic Models; China Society of Automotive Engineers. In Proceedings of 2010 China Society of Automotive Engineers Annual Congress, Shanghai, China, 10–11 June 2010; China Machine Press: Beijing, China, 2010; Volume 4. [Google Scholar]
- Sun, B. Experimental modeling study on dynamic characteristics of rubber spring in engineering vehicle suspension. China Mechanical. Eng. 2006, 17, 1313–1316. [Google Scholar] [CrossRef]
- Dzierzek, S. Experiment-Based Modeling of Cylindrical Rubber Bushings for the Simulation of Wheel; Suspension Dynamic Behavior; SAE Technical Paper 2000-01-0095; SAE: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Berg, M. A nonlinear rubber spring model for vehicle dynamics analysis. Veh. Syst. Dyn. 1998, 29, 723–728. [Google Scholar] [CrossRef]
- Zhao, Y.; Hou, Z. Two viscoelastic constitutive models of rubber materials based on fractional derivative. J. Tsinghua Univ. 2013, 53, 378383. [Google Scholar] [CrossRef]
- Metzler, R.; Nonnenmacher, T.F. Fractional relaxation processes and fractional rheological models for the description of a class of viscoelastic materials. Int. J. Plast. 2003, 19, 941–959. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–135. [Google Scholar] [CrossRef]
- Lin, S.; Gao, Q.; Li, Y.; Yang, X.; Zhao, X. A viscoelastic constitutive model considering wide temperature, wide frequency and wide dynamic displacement. J. Aerosp. Power 2007, 27, 431–438. [Google Scholar] [CrossRef]
- Liu, J.G.; Xu, M.Y. Higher order fractional constitutive equation of viscoelastic materials involving three different parameters and their relaxation and creep functions. Mech. Time Depend. Mater. 2006, 10, 263–279. [Google Scholar] [CrossRef]
- Gao, Q.; Feng, J.; Zheng, S.; Lin, Y. Study on high-order fractional derivative dynamic model of rubber sleeve. Automot. Eng. 2019, 41, 872–879. [Google Scholar] [CrossRef]
- Zou, K.; Ding, J. Research on parameter identification of robot dynamics. Mach. Tool. Hydraul. 2023, 10–13+18. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Saunders, D.W. Large elastic deformations of isotropic materials. Collect. Pap. R. S Rivin. 1997, 157–194. [Google Scholar]
- Rivlin, R.S. Large elastic deformations of isotropic materials. IV. Further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A 1948, 241, 379–397. [Google Scholar]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Ogden, R.W. Syntax of referencing. In Non-Linear Elastic Deformations; Ogden, R.W., Ed.; Dover Publication Inc.: Mineola, NY, USA, 1997; p. 221. [Google Scholar]
- Li, G.; Wu, L.; Zhang, S.; Liu, F. Frequency dependence prediction and parameter identification of rubber bushing. Sci. Rep. 2022, 12, 863. [Google Scholar] [CrossRef] [PubMed]
- Manias, S. Non-linear behavior of a rubber isolaror system using fractional derivatives. Veh. Syst. Dyn. 2002, 37, 217–236. [Google Scholar]
- Yang, T. Viscoelastic Theory and Application; Science Press: Beijing, China, 2004. (In Chinese) [Google Scholar]
- Zhang, G.; Zhang, J.; Guo, R.; Gao, Z.; Niu, Y. Dispatch Strategy of Cold-Hot-Electricity Trigeneration System Based on Adaptive Chaotic Particle Swarm Optimization Algorithm. Mod. Electr. Power 2020, 37, 551–558. [Google Scholar] [CrossRef]
- Vuillod, B.; Montemurro, M.; Panettieri, E.; Hallo, L. A comparison between Sobol’s indices and Shapley’s effect for global sensitivity analysis of systems with independent input variables. Reliab. Eng. Syst. Saf. 2023, 234, 109177. [Google Scholar] [CrossRef]





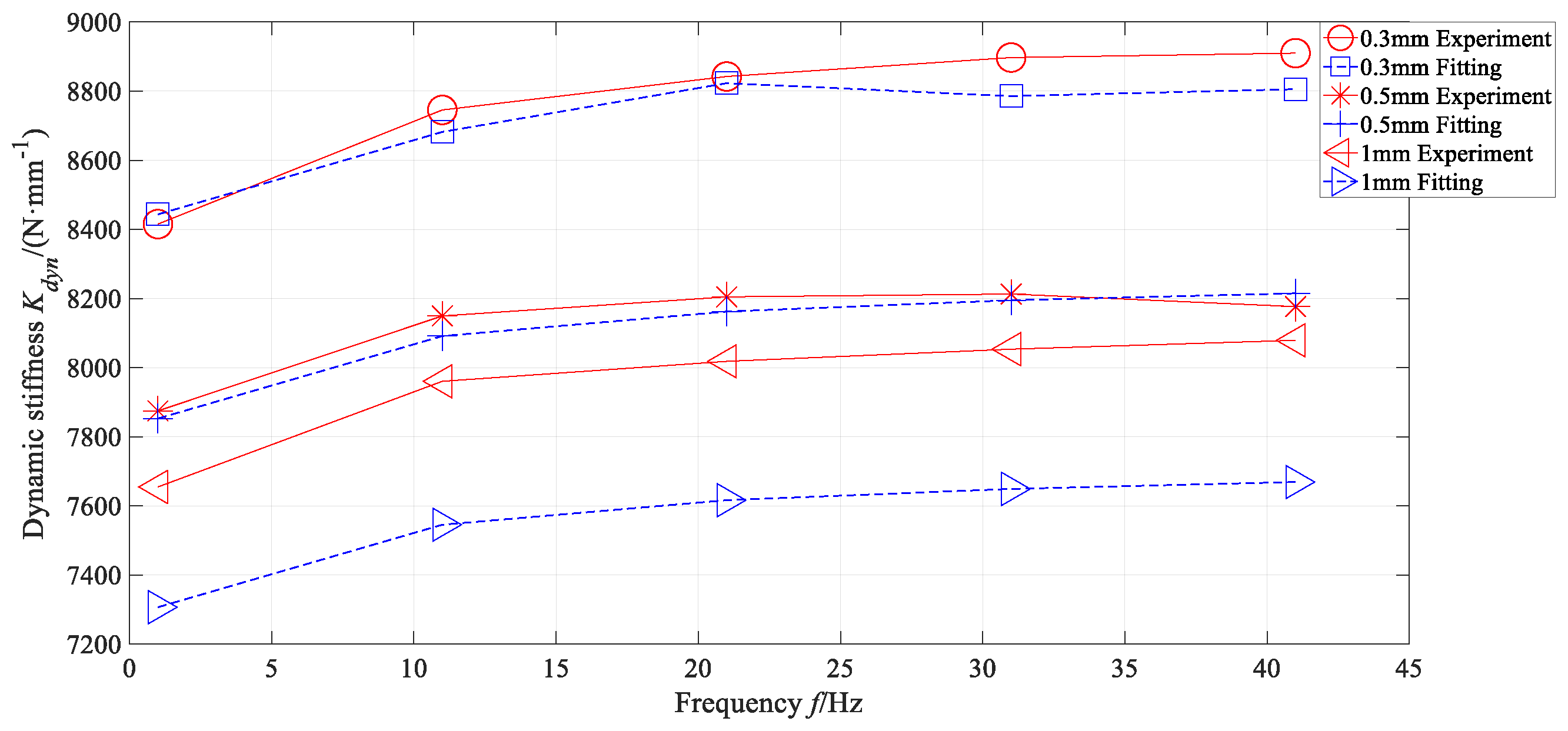
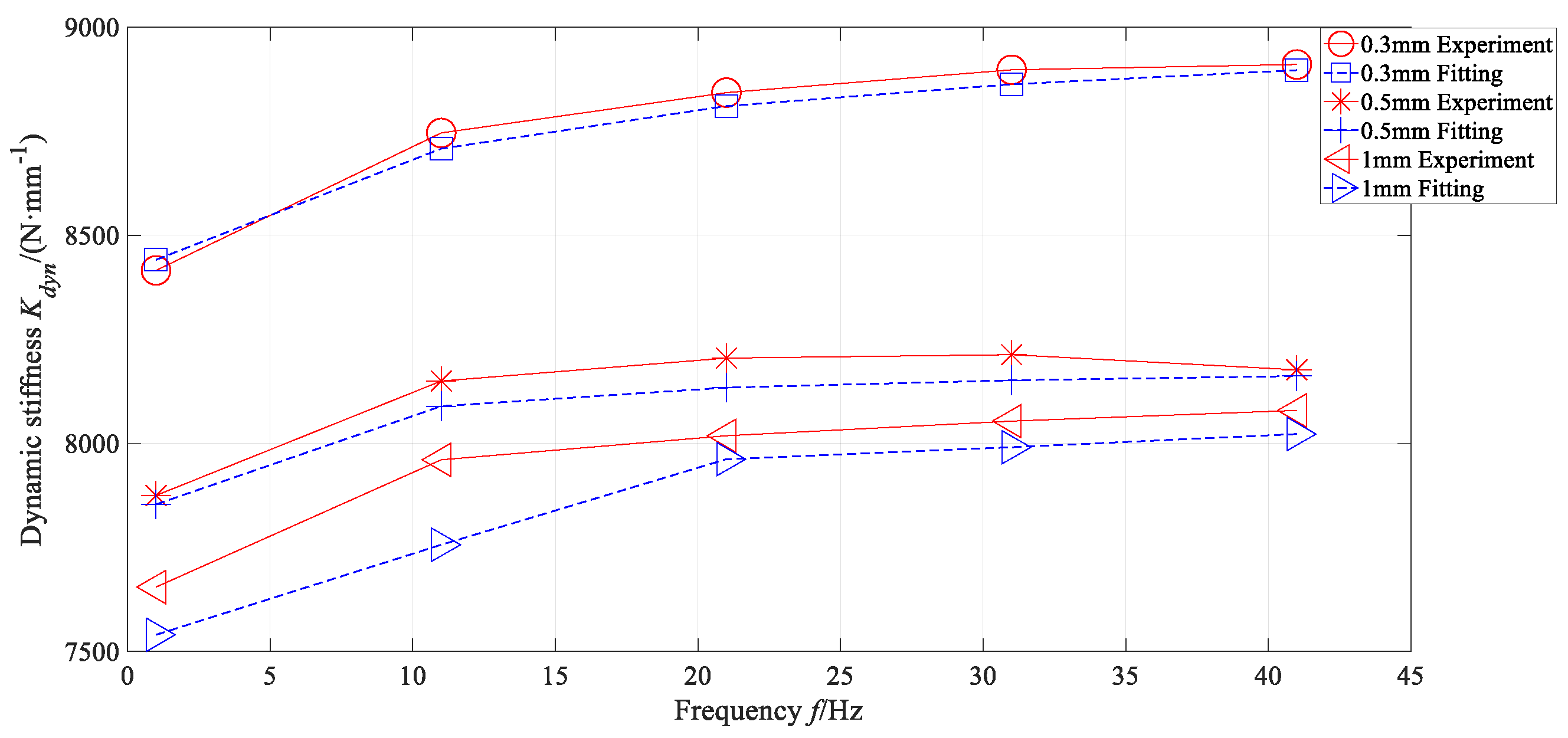
| Model Element | Parameter | Result |
|---|---|---|
| Elastic elements | /() | 6663.68 |
| 3 | ||
| 85.12 | ||
| −187.2 | ||
| 6782 | ||
| 136.2 | ||
| Friction elements | /() | 11,814.9 |
| / | 647.6625 | |
| /() | 0.1257 |
| Model Parameter | Identification Results |
|---|---|
| 1.2766 | |
| 243.8196 | |
| 49.2227 | |
| 15.2644 | |
| 0.8913 | |
| 0.9863 | |
| 0.937 |
| Model Parameter | Identification Results |
|---|---|
| [0, 10] | |
| [125, 400] | |
| [25, 75] | |
| [10, 20] | |
| [0.5, 1] | |
| [0.5, 1] | |
| [0.5, 1] |
| Model Parameter | First–Order Sobol’s Index | Total–Order Sobol’s Index |
|---|---|---|
| 0.0007 | 0.0005 | |
| 0.0593 | 0.1044 | |
| 0.0042 | 0.0145 | |
| 0.0066 | 0.0220 | |
| 0.1807 | 0.2670 | |
| 0.6180 | 0.7209 | |
| 0.0144 | 0.0388 |
| Amplitude (mm) | Error before Correction (%) | Error before Correction (%) |
|---|---|---|
| 0.3 | 4.07 | 2.43 |
| 0.5 | 4.42 | 4.38 |
| 1 | 28.82 | 7.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, L.; Zhou, F.; Cao, L.; Guo, S.; Huang, Z. Parameter Identification and Dynamic Characteristic Research of a Fractional Viscoelastic Model for Sub-Frame Bushing. Vehicles 2023, 5, 1196-1210. https://doi.org/10.3390/vehicles5030066
Chen B, Chen L, Zhou F, Cao L, Guo S, Huang Z. Parameter Identification and Dynamic Characteristic Research of a Fractional Viscoelastic Model for Sub-Frame Bushing. Vehicles. 2023; 5(3):1196-1210. https://doi.org/10.3390/vehicles5030066
Chicago/Turabian StyleChen, Bao, Lunyang Chen, Feng Zhou, Liang Cao, Shengxiang Guo, and Zehao Huang. 2023. "Parameter Identification and Dynamic Characteristic Research of a Fractional Viscoelastic Model for Sub-Frame Bushing" Vehicles 5, no. 3: 1196-1210. https://doi.org/10.3390/vehicles5030066
APA StyleChen, B., Chen, L., Zhou, F., Cao, L., Guo, S., & Huang, Z. (2023). Parameter Identification and Dynamic Characteristic Research of a Fractional Viscoelastic Model for Sub-Frame Bushing. Vehicles, 5(3), 1196-1210. https://doi.org/10.3390/vehicles5030066






