Modeling and Simulation of an Electric Rail System: Impacts on Vehicle Dynamics and Stability
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Simulation Design
- Vehicle type: 2 light vehicles (small electric SUV, city car) representative of vehicles on the French road network;
- Traffic speed: 50, 70, 90, 110 and 130 km/h;
- Asphalt skid resistance: SFC = 0.60;
- ERS skid resistance: SFC = 0.20, 0.30 and 0.50.
2.2. Ers System Modeling
2.3. Vehicle Modeling
2.4. Testing Maneuvers
2.4.1. Double-Lane Change Maneuver (Chicane)
2.4.2. Straight-Line Emergency Braking Maneuver
2.5. Parameters of Analysis
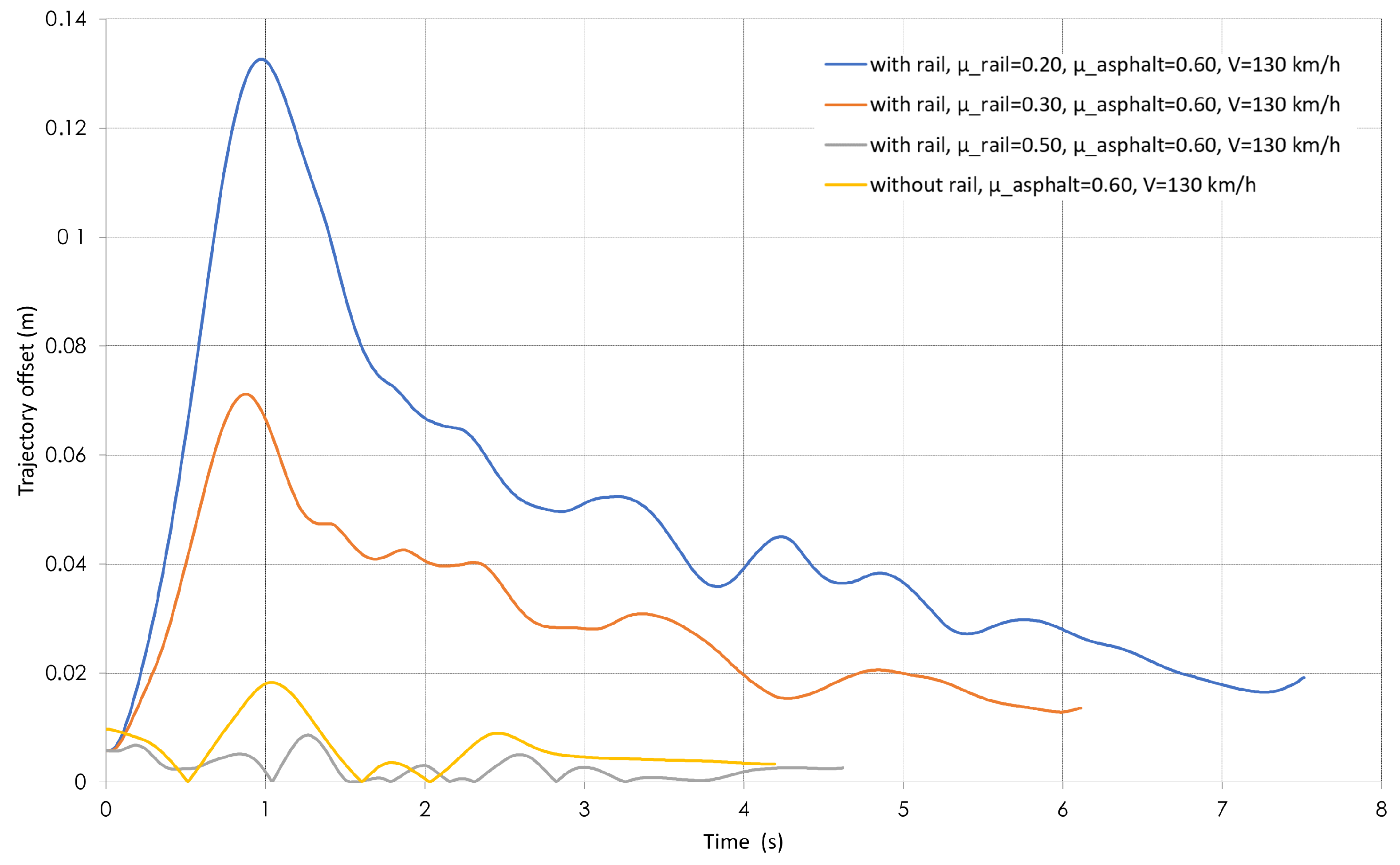
- Deviation between the target and actual trajectory, expressed in meters, is used to assess the risk of lane departure. It is calculated as the lateral distance between the vehicle’s center of gravity and the edge of the lane.
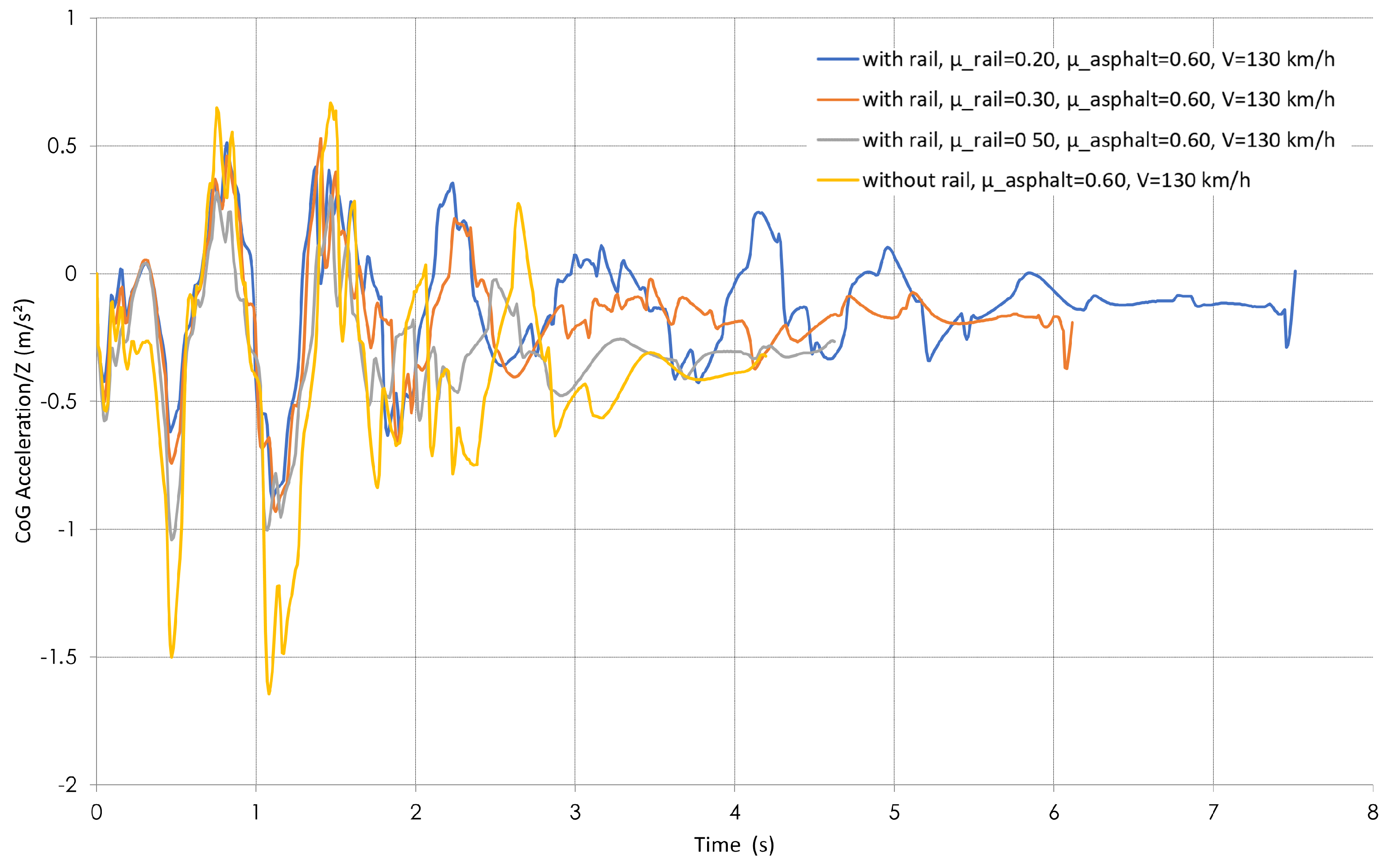
- Vertical acceleration, expressed in m/s2, causes vehicle oscillations, potentially leading to discomfort and loss of control. The human body can withstand up to 50 m/s2 before fainting, while in the transport sector, the usual comfort threshold is 4 m/s2 [25].
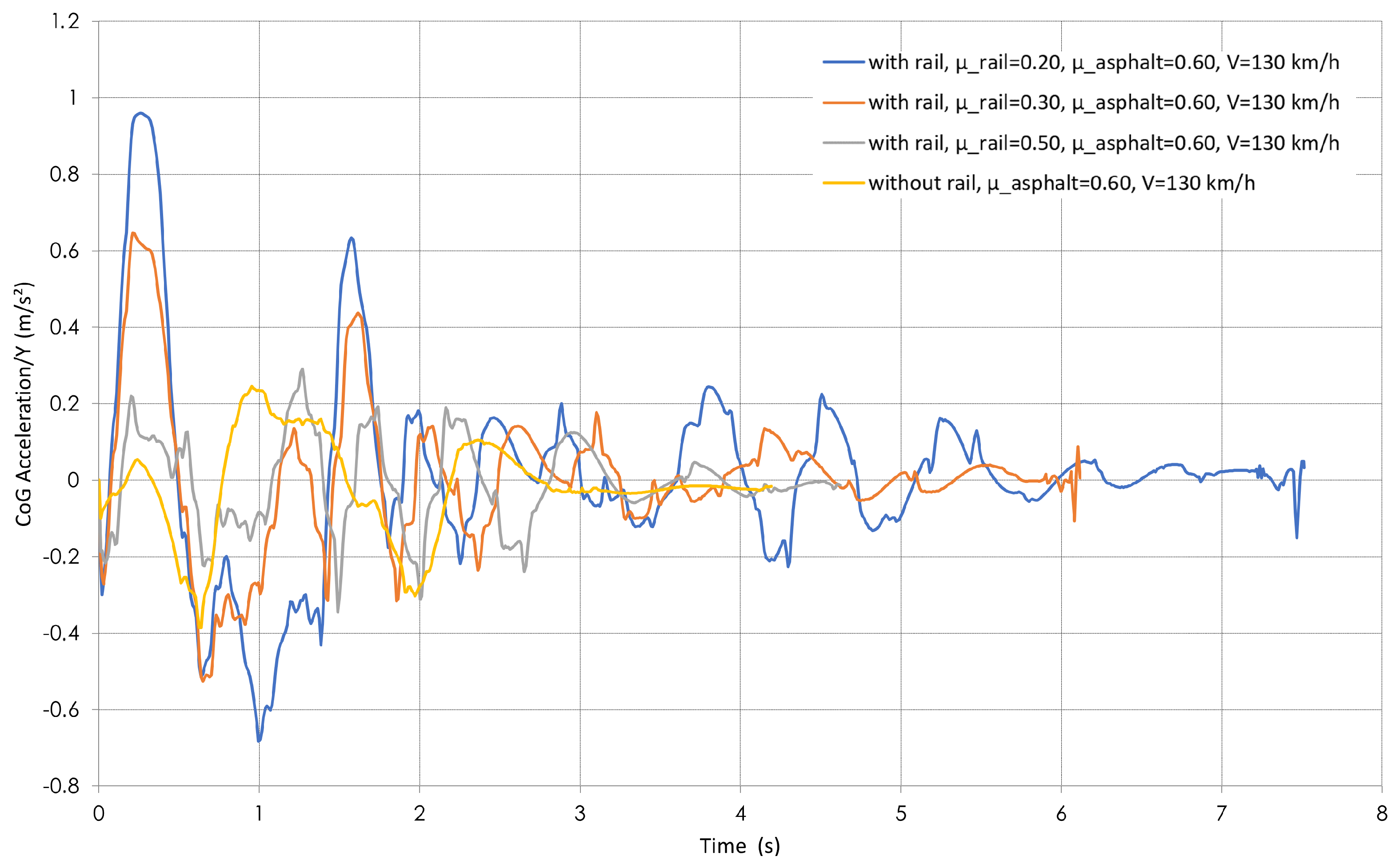
- Lateral acceleration, expressed in m/s2, influences passenger comfort. Values exceeding 5 m/s2 can cause discomfort to road users [25].
- Longitudinal acceleration, expressed in m/s2, affects passenger comfort and braking performance. A comfortable acceleration is around 3 m/s2, while emergency braking can reach 8–10 m/s2, causing significant discomfort [26].
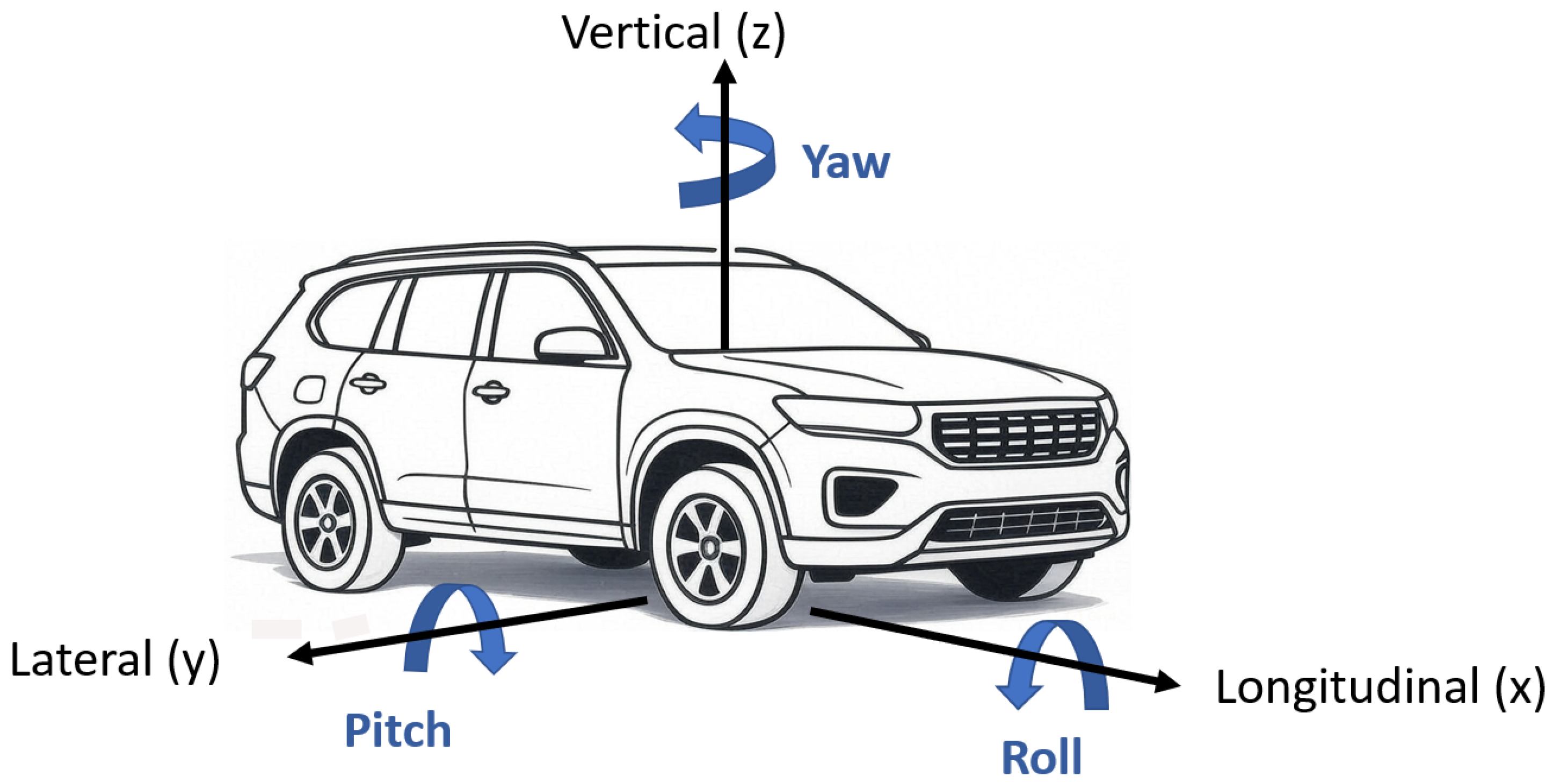
- Roll angle, expressed in degrees, describes the vehicle’s rotation around its longitudinal axis, influenced by road irregularities or centrifugal force during cornering. Roll is used to assess rollover risk. City cars typically exhibit roll angles of 2°–7°, with discomfort becoming noticeable around 7° and instability risks appearing beyond 10°–15°. However, rollover is unlikely due to their low center of gravity. SUVs, with a higher center of gravity, experience roll angles of 4°–10°, with discomfort felt at around 10° and instability risks above 15°–20°. Rollover becomes a concern at 25°–30°. Modern SUVs mitigate this risk with Electronic Stability Control (ESC) [27].
- Yaw angle, expressed in degrees, represents the vehicle’s horizontal rotation around its vertical axis. In heavy goods vehicles (HGVs), yaw is a key parameter for assessing jackknifing risk. City cars typically maintain yaw angles of 2°–5° in normal turns, with loss of control risks increasing above 10°–15°, especially in emergency maneuvers. SUVs, being taller and heavier, experience slightly higher yaw angles of 3°–7°, with instability risks rising beyond 12°–18°. Excessive yaw can lead to skidding or rollover, but ESC helps mitigate these risks [28].
- Pitch angle, expressed in degrees, describes the rotational movement around the vehicle’s transverse axis. This oscillating movement affects ride comfort. City cars typically experience pitch angles of 1°–4° during acceleration and braking, with discomfort noticeable around 5° and potential instability beyond 10°. SUVs, due to their higher center of gravity and softer suspension, exhibit greater pitch (2°–6°), with discomfort setting in above 6° and instability risks beyond 12°. Pitch is more pronounced in SUVs during heavy braking or acceleration, particularly in off-road conditions [29].
- Side slip angle, expressed in degrees, is the angle between the wheel direction and the actual trajectory of the vehicle. During cornering, this angle allows tire deformation to generate lateral forces (skid resistance). An increasing side slip angle indicates lateral instability.
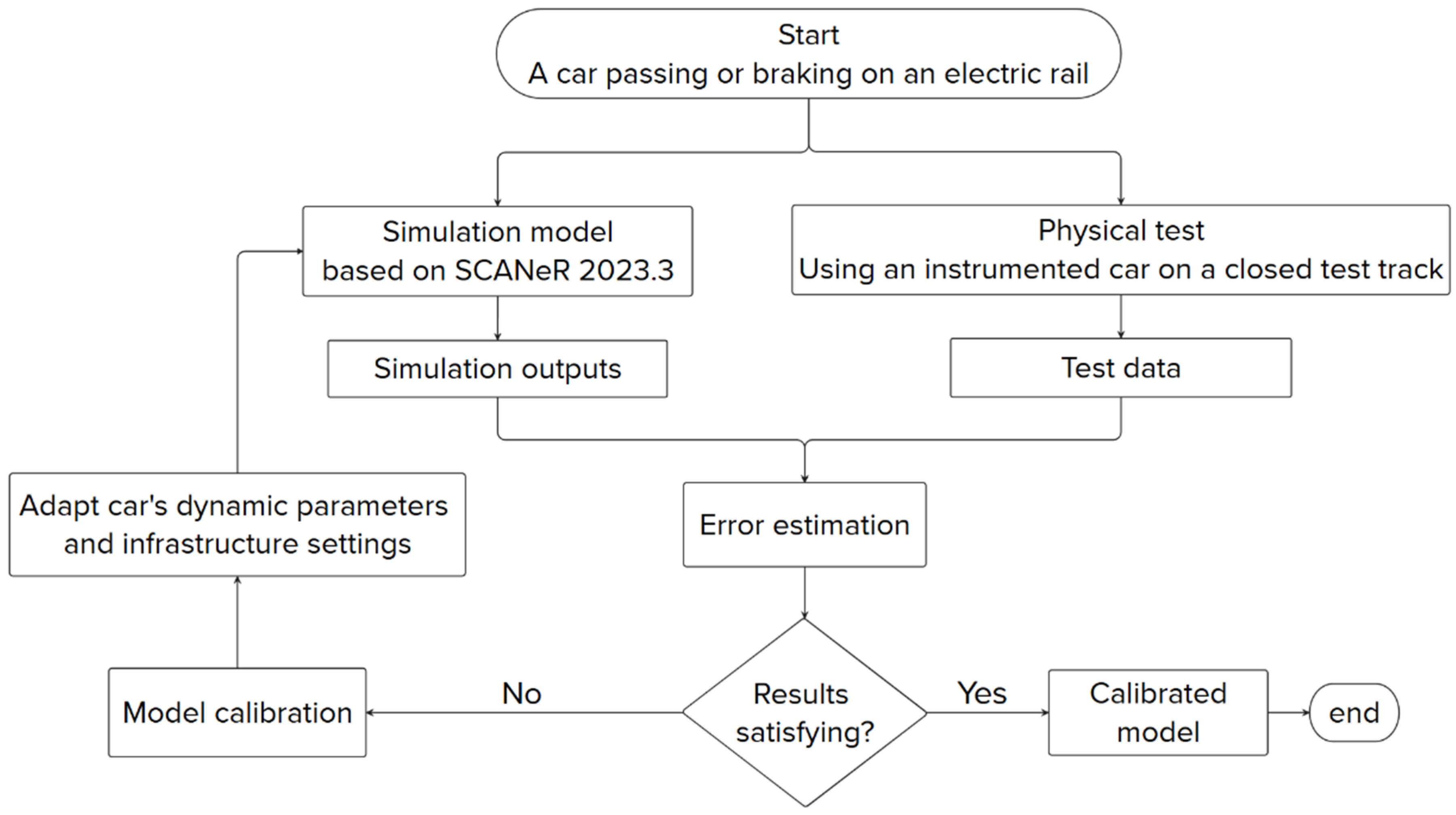
2.6. Model Calibration
3. Simulation Results—Double-Lane Change Maneuver
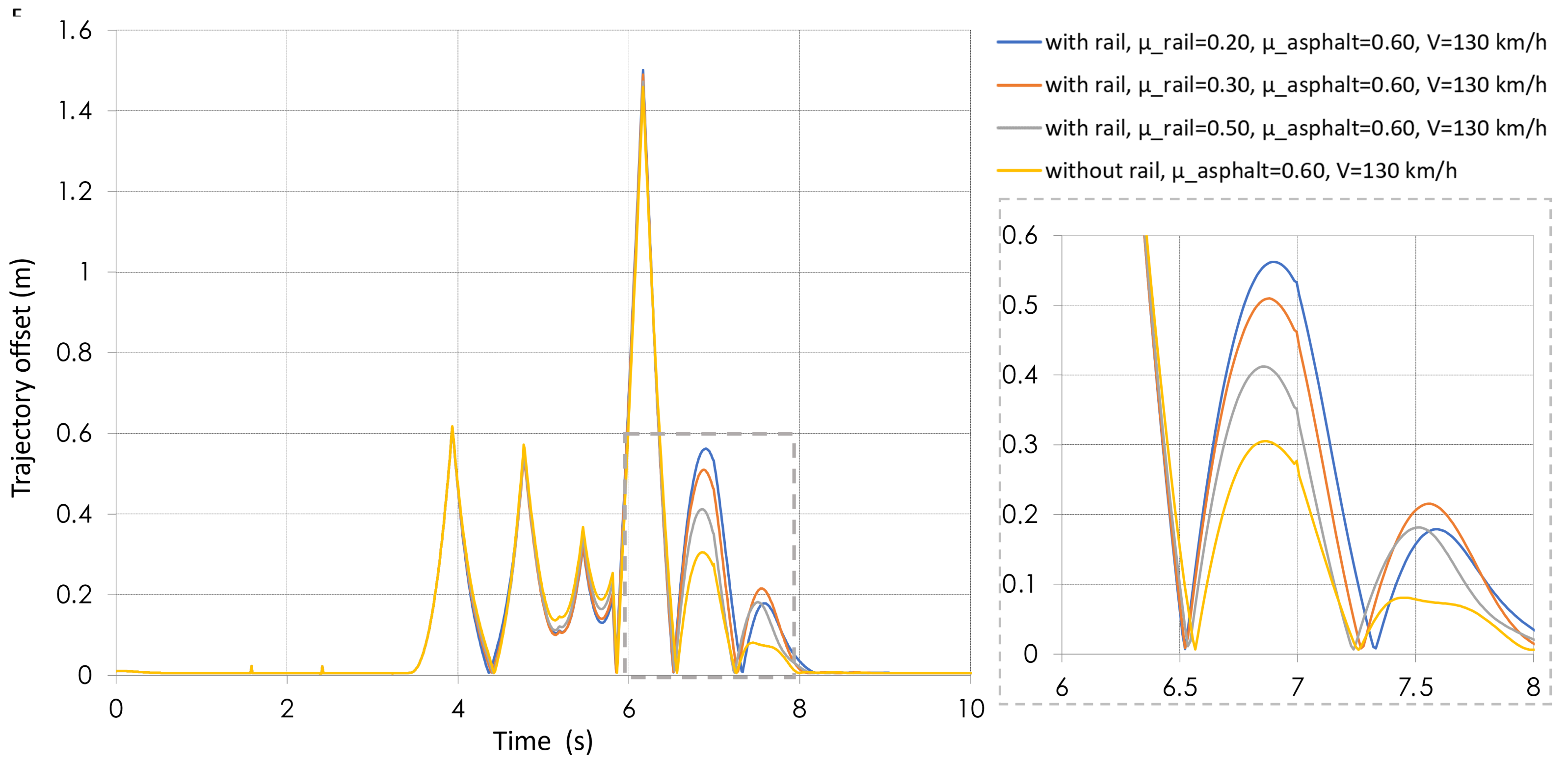
3.1. Trajectory Deviation
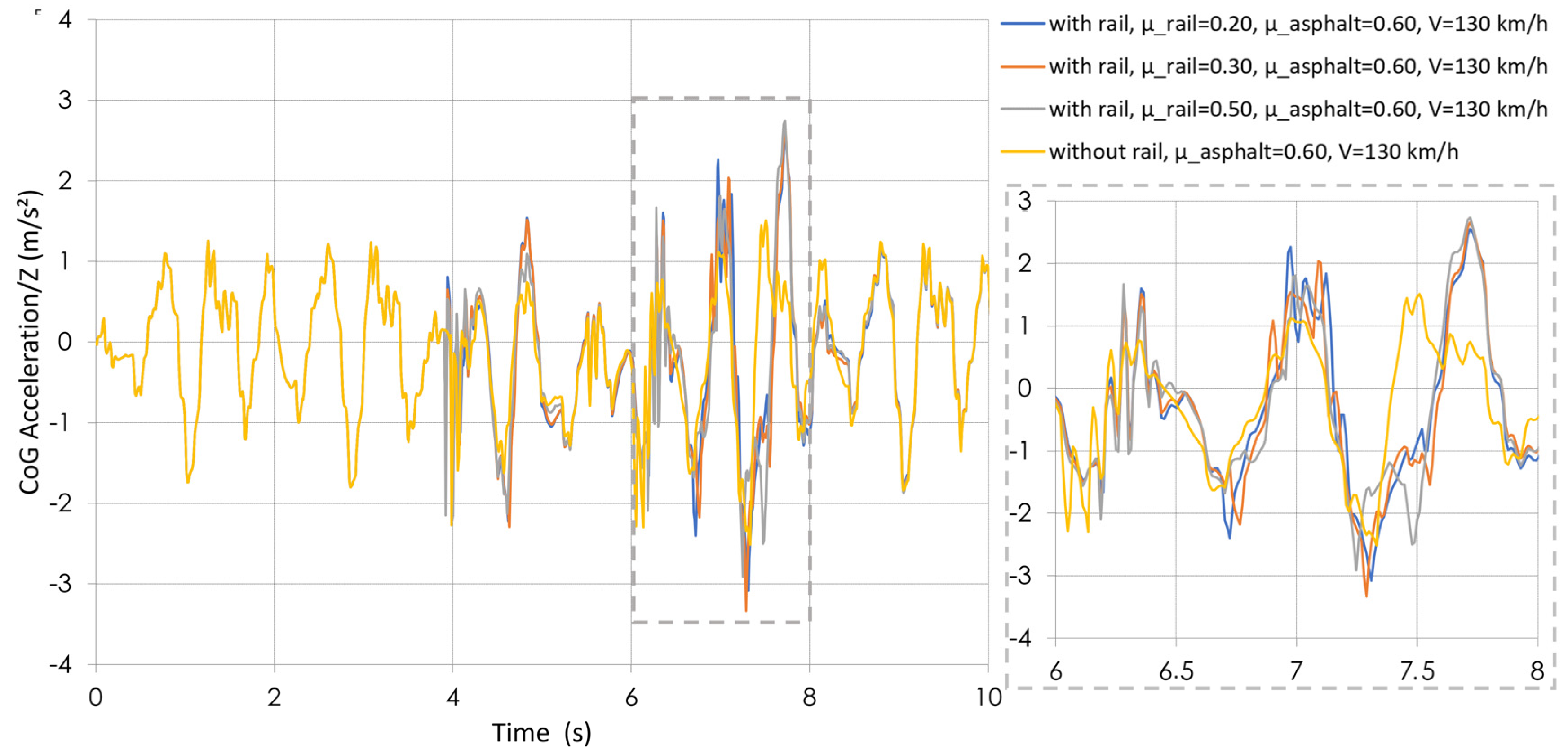
3.2. Vertical Acceleration
3.3. Lateral Acceleration
3.4. Longitudinal Acceleration
3.5. Roll Angle
3.6. Yaw Angle
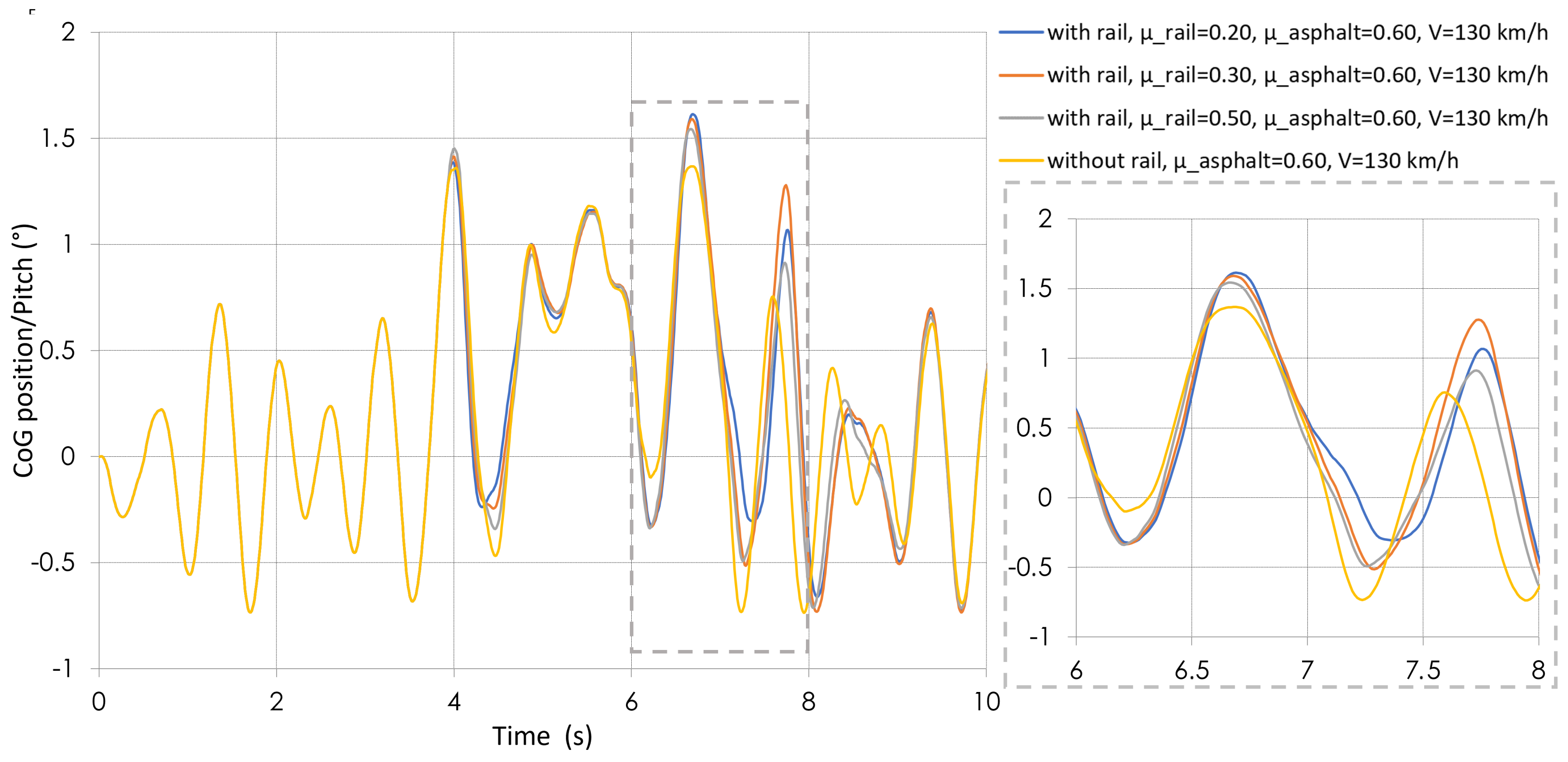
3.7. Pitch Angle
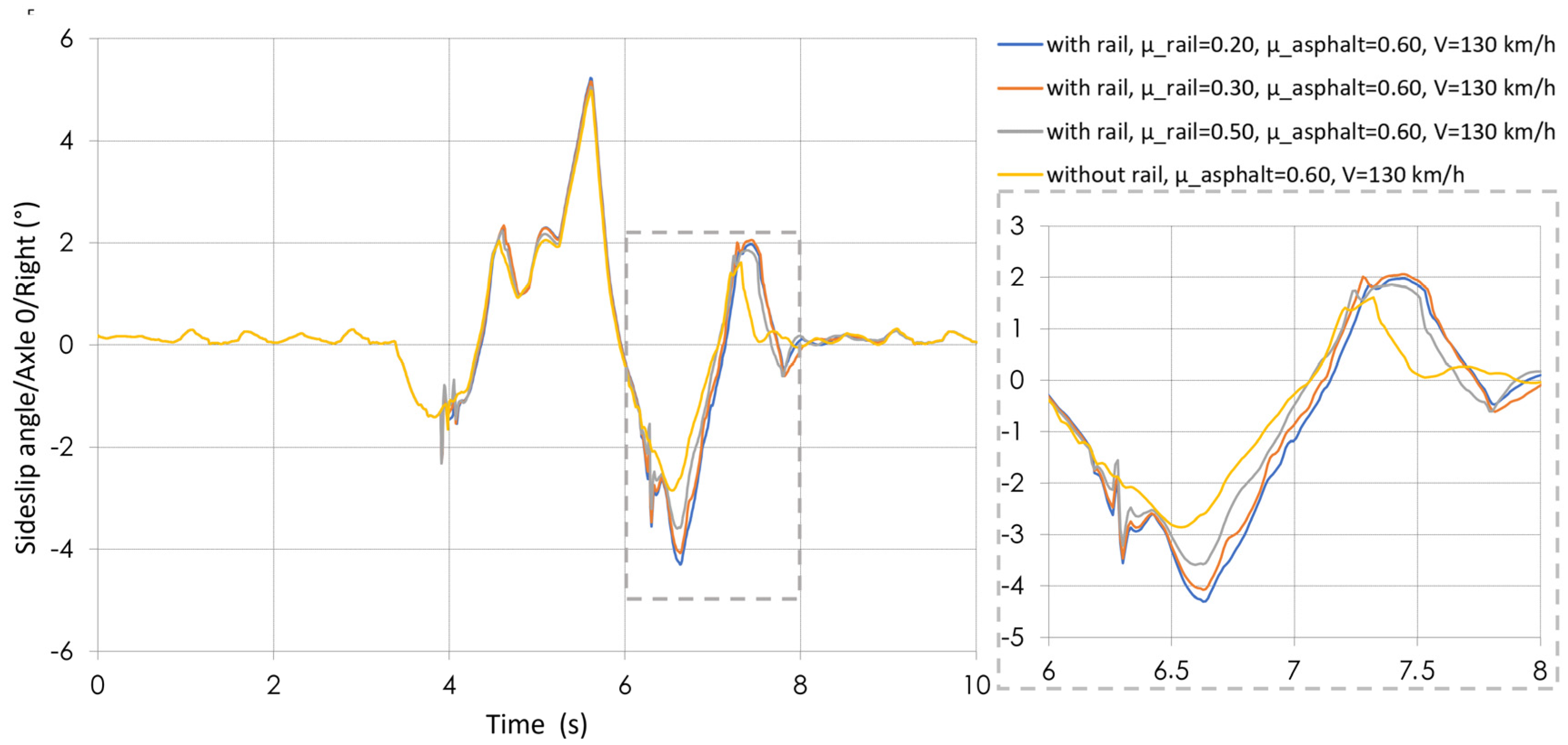
3.8. Side Slip Angle
4. Simulation Results-Emergency Braking
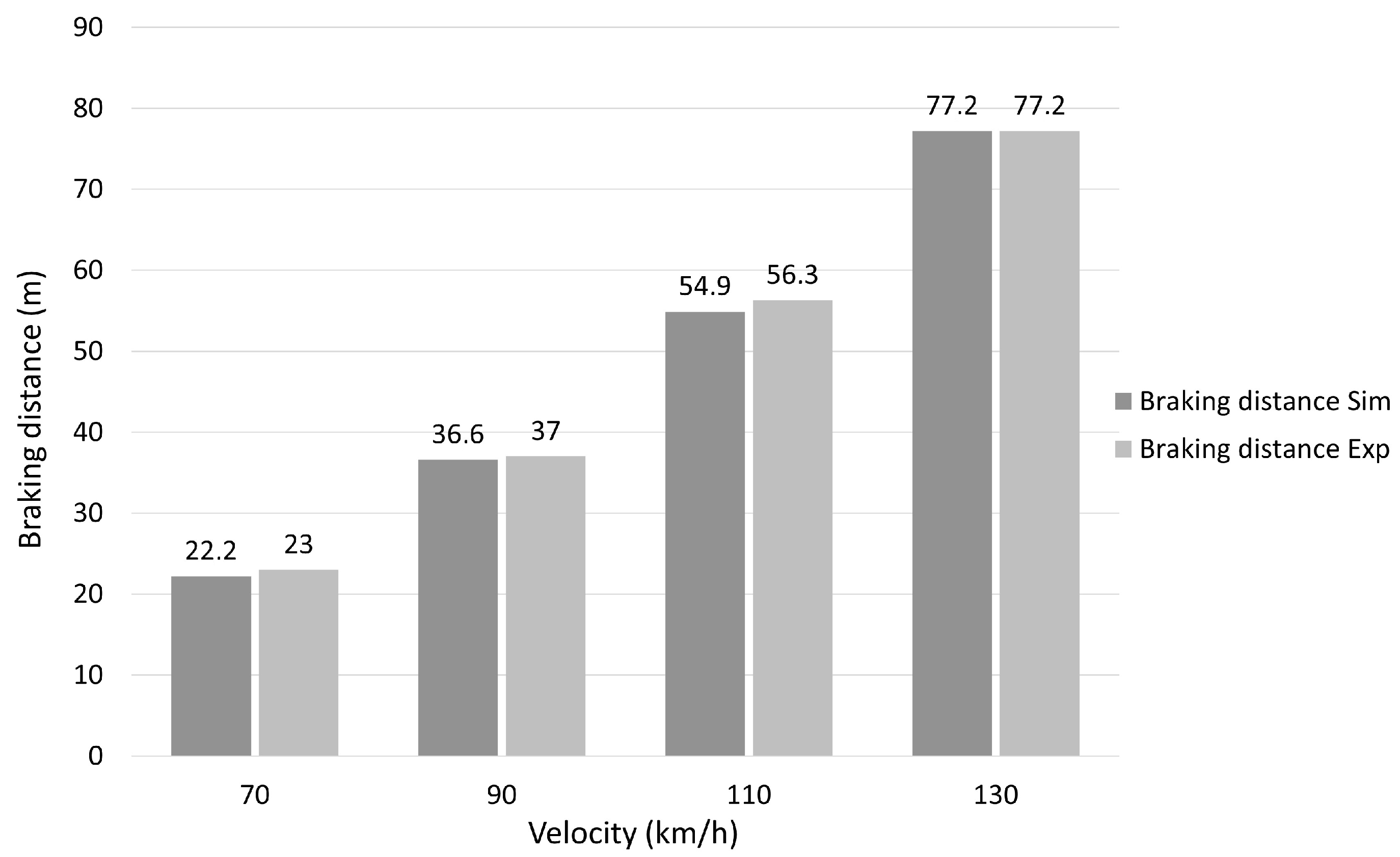
4.1. Braking Distance
4.2. Trajectory Deviation
4.3. Vertical Acceleration
4.4. Lateral Acceleration
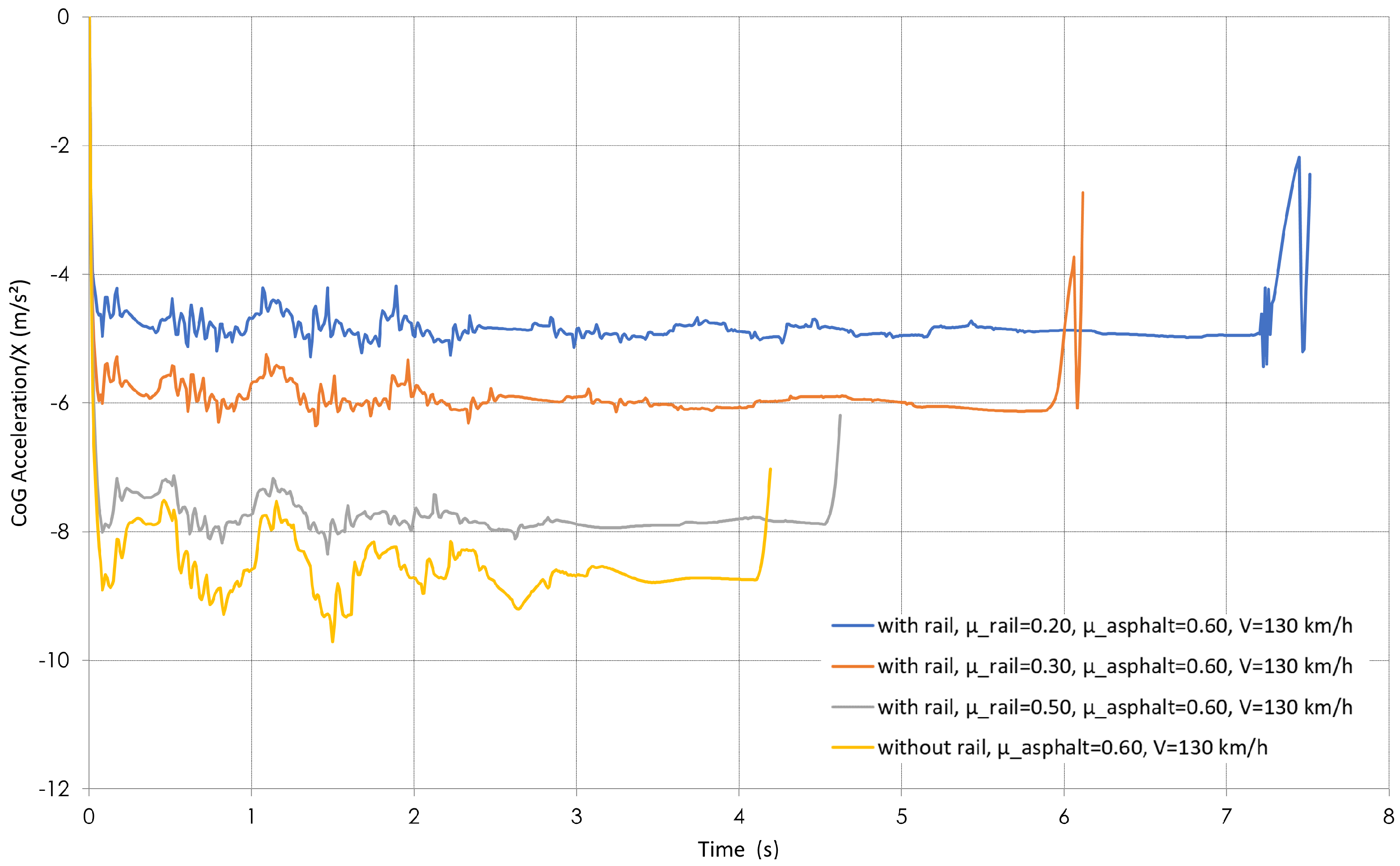
4.5. Longitudinal Acceleration
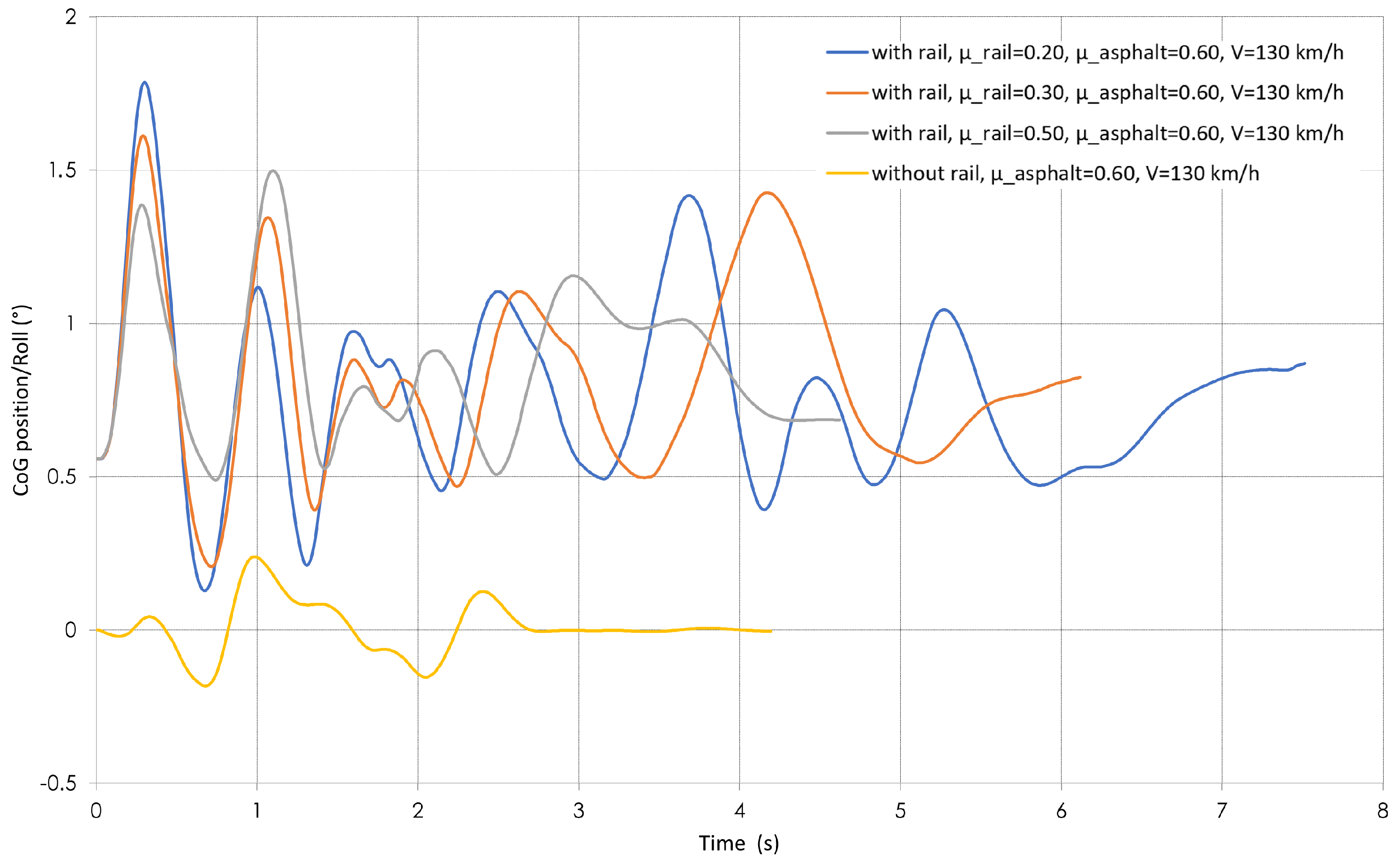
4.6. Roll Angle
4.7. Yaw Angle
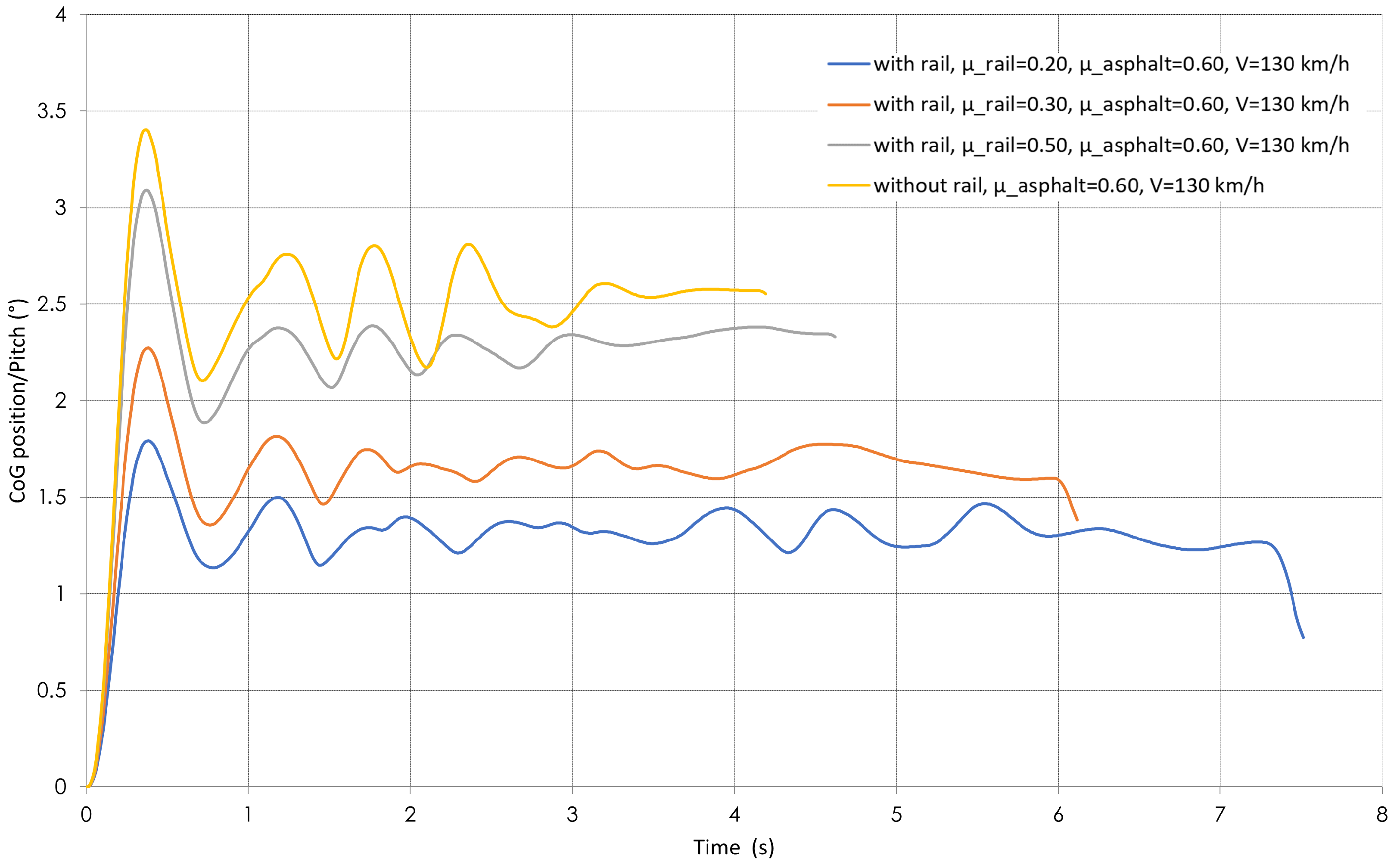
4.8. Pitch Angle
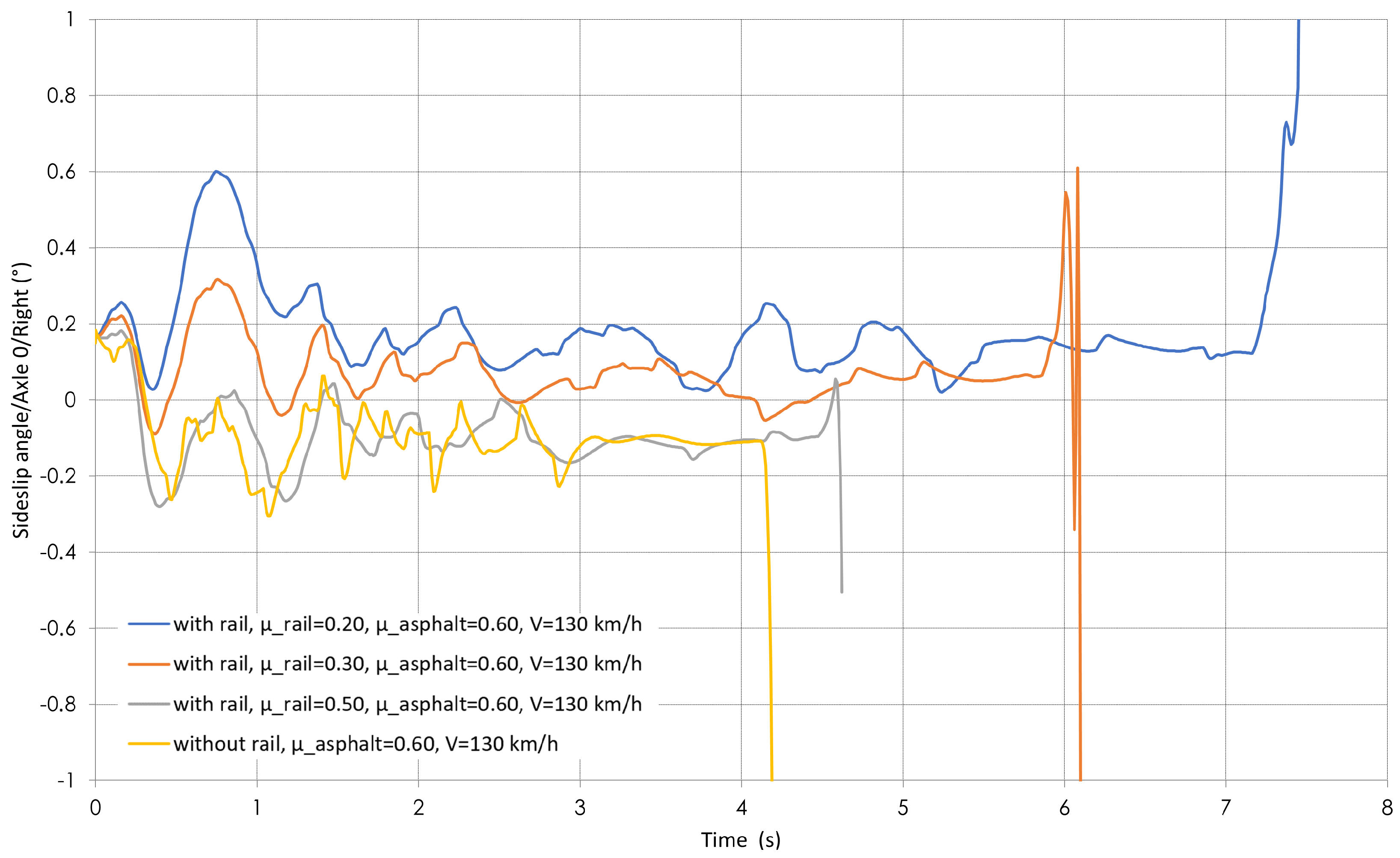
4.9. Side Slip Angle
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| ERS | Electric Road System |
| SFC | Sideforce Friction Coefficient |
| RRV | Road-Rail Vehicle |
| ABS | Anti-lock Braking System |
| IMU | Inertial Measurement Unit |
| SUV | Sports Utility Vehicle |
| SSD | Stopping Sight Distance |
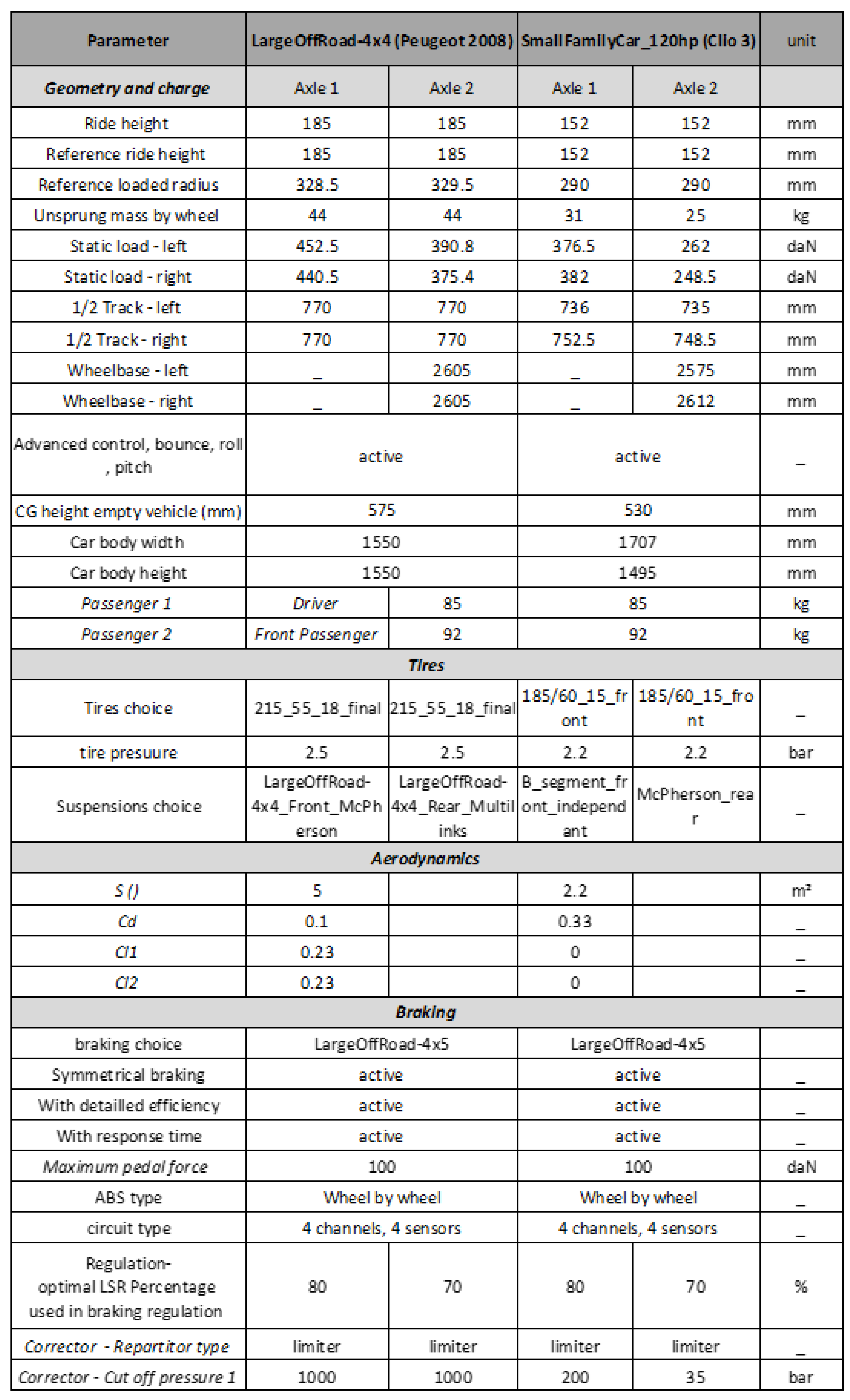
Appendix A. Modified Parameters of the Car Models in SCANeR 2023.3
References
- Yu, X.; LeBlanc, S.; Sandhu, N.; Wang, L.; Wang, M.; Zheng, M. Decarbonization potential of future sustainable propulsion—A review of road transportation. Energy Sci. Eng. 2024, 12, 438–455. [Google Scholar] [CrossRef]
- Lacire, S.; Hauet, J.-P. La Route éLectrique: Il Faut s’y préParer; Équilibre des Énergies: Paris, France, 2023. [Google Scholar]
- Des Routes éLectriques (ERS) Pour Contribuer à déCarboner le Transport Routier, Rapport du GT1: Intérêt des Solutions et Conditions de RéUssite; Ministère de la Transition Écologique: Paris, France, 2021.
- Bateman, D.; Leal, D.; Reeves, S.; Emre, M.; Stark, L.; Ognissanto, F.; Myers, R.; Lamb, M. Electric Road Systems: A Solution for the Future? 2018SP04EN; World Road Association: La Défense, France, 2018. [Google Scholar]
- Swedish, I.V. Slide-In Electric Road System-Inductive Project Report; Viktoria Swedish ICT: Gothenburg, Sweden, 2014. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Magel, E.; Tajaddini, A.; Trosino, M.; Kalousek, J. Traction, forces, wheel climb and damage in high-speed railway operations. Wear 2008, 265, 1446–1451. [Google Scholar] [CrossRef]
- Olofsson, U.; Sundvall, K. Influence of leaf, humidity and applied lubrication on friction in the wheel-rail contact: Pin-on-disc experiments. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2004, 218, 235–242. [Google Scholar] [CrossRef]
- Rong, K.-J.; Xiao, Y.-L.; Shen, M.-X.; Zhao, H.-P.; Wang, W.-J.; Xiong, G.-Y. Influence of ambient humidity on the adhesion and damage behavior of wheel–rail interface under hot weather condition. Wear 2021, 486, 204091. [Google Scholar] [CrossRef]
- Meymand, S.Z.; Keylin, A.; Ahmadian, M. A survey of wheel–rail contact models for rail vehicles. Veh. Syst. Dyn. 2016, 54, 386–428. [Google Scholar] [CrossRef]
- He, J.; Xiang, H.; Li, Y.; Han, B. Aerodynamic performance of traveling road vehicles on a single-level rail-cum-road bridge under crosswind and aerodynamic impact of traveling trains. Eng. Appl. Comput. Fluid Mech. 2022, 16, 335–358. [Google Scholar] [CrossRef]
- Gupta, A.; Pradhan, S.K.; Bajpai, L.; Jain, V. Numerical analysis of rubber tire/rail contact behavior in road cum rail vehicle under different inflation pressure values using finite element method. Mater. Today Proc. 2021, 47, 6628–6635. [Google Scholar] [CrossRef]
- Müller, S.; Blundell, M. The testing of pneumatic tyres for the interpretation of tyre behaviour for road/rail vehicles when operating on rails. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2023, 237, 3275–3284. [Google Scholar] [CrossRef]
- Chou, C.-P.; Lee, N. Skid resistance of manhole covers: Current situation in Taiwan. In Proceedings of the Eastern Asia Society for Transportation Studies Vol. 8, the 9th International Conference of Eastern Asia Society for Transportation Studies, Jeju, Republic of Korea, 20–23 June 2011; Eastern Asia Society for Transportation Studies: Kawana, Japan, 2011; p. 12. [Google Scholar]
- Huang, C. Evaluation of Skid Resistance of Pattern Design for Manhole Cover. Ph.D. Thesis, National Taiwan University, Taiwan, China, 2010. [Google Scholar]
- Chou, C.-P.; Huang, C.-K.; Chen, A.; Tsai, C.Y. Pattern design of manhole cover and its influence on skid resistance. Int. J. Pavement Res. Technol. 2013, 6, 351. [Google Scholar]
- Avsimulation Website. Available online: https://www.avsimulation.com/scaner-catalog/?lang=fr (accessed on 15 May 2024).
- Guo, C. Conception des Principes de Coopération Conducteur-véhicule Pour les Systèmes de Conduite Automatisée. Ph.D. Thesis, University of Valenciennes, Valenciennes, France, 2017. [Google Scholar]
- Guo, C.; Sentouh, C.; Popieul, J.-C.; Haué, J.-B.; Langlois, S.; Loeillet, J.-J.; Soualmi, B.; That, T.N. Cooperation between driver and automated driving system: Implementation and evaluation. Transp. Res. Part F Traffic Psychol. Behav. 2019, 61, 314–325. [Google Scholar] [CrossRef]
- Said, A.; Talj, R.; Francis, C.; Shraim, H. Local trajectory planning for autonomous vehicle with static and dynamic obstacles avoidance. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; IEEE: Piscatway, NJ, USA, 2021; pp. 410–416. [Google Scholar]
- Note du 30 Septembre 2015 Relative à L’uni Longitudinal des Couches de Roulement Neuves du Domaine Routier. Available online: https://www.legifrance.gouv.fr/circulaire/id/40089 (accessed on 15 May 2024).
- ISO. EN 13036-2008; Road and Airfield Surface Characteristics—Test Methods—Part 8: Determination of Transverse Unevenness Indices. European Committee for Standardization (CEN): Brussels, Belgium, 2008.
- Ahangarnejad, A.H.; Radmehr, A.; Ahmadian, M. A review of vehicle active safety control methods: From antilock brakes to semiautonomy. J. Vib. Control 2021, 27, 1683–1712. [Google Scholar] [CrossRef]
- ISO. ISO 3888-1:1999; Passenger Cars—Test Track for a Severe Lane-Change Manoeuvre. ISO: Geneva, Switzerland, 2001.
- ISO. 15622-2018; Intelligent Transport Systems—Adaptive Cruise Control Systems—Performance Requirements and Test Procedures. ISO: Geneva, Switzerland, 2018.
- ISO. ISO 2631:1997; Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration. ISO: Geneva, Switzerland, 1997. [Google Scholar]
- Boyd, P.L. NHTSA’s NCAP rollover resistance rating system. In Proceedings of the 19th International Technical Conference on the Enhanced Safety of Vehicles, Washington, DC, USA, 6 June 2005; pp. 1–10. [Google Scholar]
- Sivashankar, N.; Ulsoy, A.G. Yaw rate estimation for vehicle control applications. J. Dyn. Syst. Meas. Control. 1998, 120, 267–274. [Google Scholar] [CrossRef]
- Fujii, R.; Idehara, S. Analysis of Vehicle Longitudinal Dynamics during Acceleration and Braking Events. Int. J. Eng. Tech. Res. (IJETR) 2024, 14, 267–274. [Google Scholar]
- CEREMA (Centre d’Études et d’Expertise sur les Risques, l’Environnement, la Mobilité et l’Aménagement). Guide Technique de Conception des Routes; CEREMA: Paris, France, 2024. [Google Scholar]






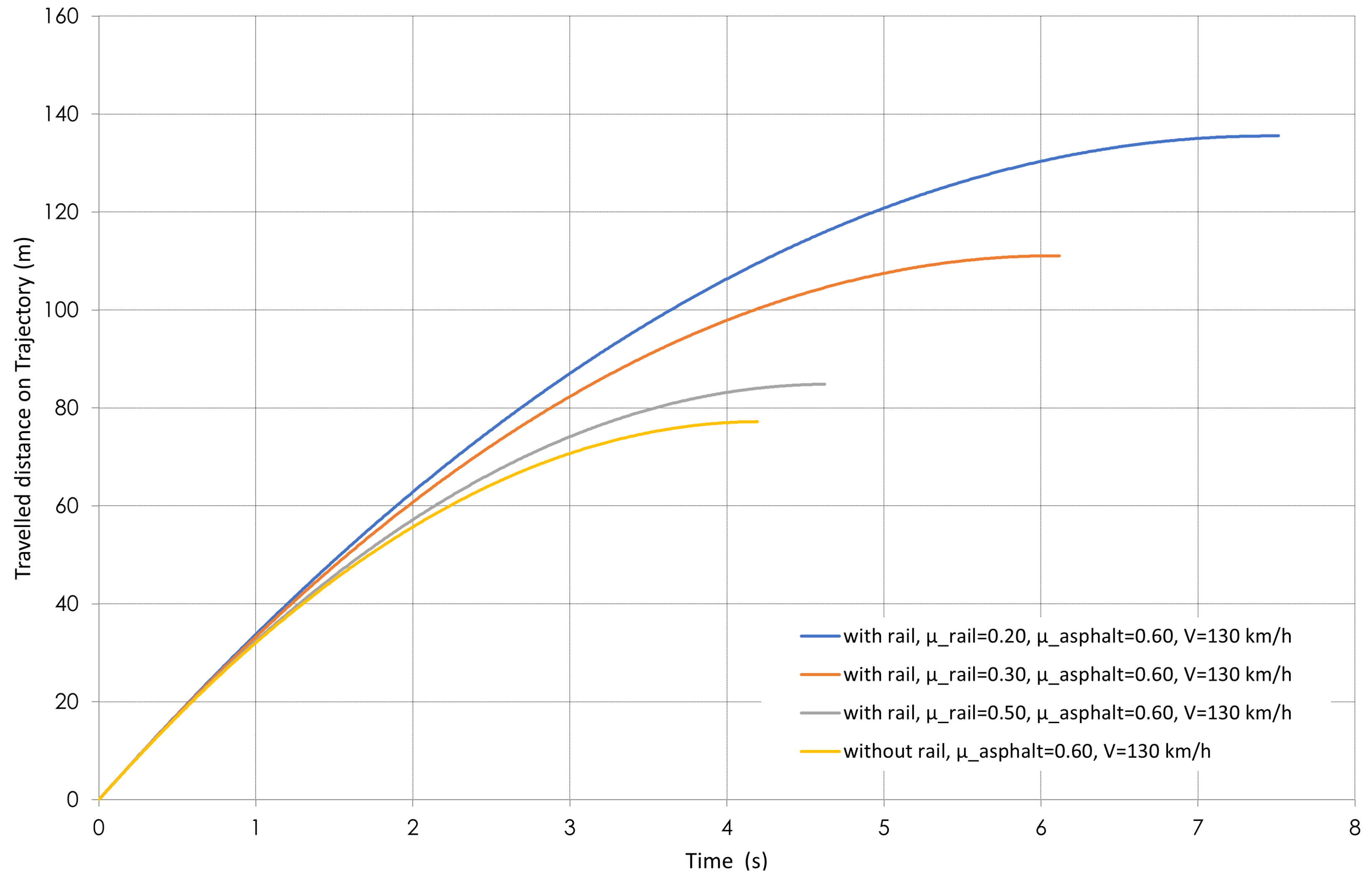

| Braking Distance (m) | ||||
|---|---|---|---|---|
| SCF | 70 km/h | 90 km/h | 110 km/h | 130 km/h |
| 0.2 | 39.3 | 64.8 | 96.8 | 135.6 |
| 0.3 | 23.4 | 52.9 | 79.2 | 111.1 |
| 0.5 | 24.4 | 40.3 | 60.4 | 84.9 |
| 0.6 | 22.2 | 36.6 | 54.9 | 77.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoman, M.; Cerezo, V. Modeling and Simulation of an Electric Rail System: Impacts on Vehicle Dynamics and Stability. Vehicles 2025, 7, 36. https://doi.org/10.3390/vehicles7020036
Shoman M, Cerezo V. Modeling and Simulation of an Electric Rail System: Impacts on Vehicle Dynamics and Stability. Vehicles. 2025; 7(2):36. https://doi.org/10.3390/vehicles7020036
Chicago/Turabian StyleShoman, Murad, and Veronique Cerezo. 2025. "Modeling and Simulation of an Electric Rail System: Impacts on Vehicle Dynamics and Stability" Vehicles 7, no. 2: 36. https://doi.org/10.3390/vehicles7020036
APA StyleShoman, M., & Cerezo, V. (2025). Modeling and Simulation of an Electric Rail System: Impacts on Vehicle Dynamics and Stability. Vehicles, 7(2), 36. https://doi.org/10.3390/vehicles7020036







