Nonclassical States for Non-Hermitian Hamiltonians with the Oscillator Spectrum

Abstract

In this paper, we show that the standard techniques that are utilized to study the classical-like properties of the pure states for Hermitian systems can be adjusted to investigate the classicality of pure states for non-Hermitian systems. The method is applied to the states of complex-valued potentials that are generated by Darboux transformations and can model both non-$PT$-symmetric and $PT$-symmetric oscillators exhibiting real spectra.

1. Introduction

In quantum mechanics one finds two important classes of states of the radiation field: Fock and coherent states. The former, introduced by Fock at the dawn of quantum theory, contain a precise number of photons and produce average fields equal to zero. With the exception of the vacuum, the Wigner distribution [1] exhibits negative values in some regions of the phase-space when it is evaluated with the Fock states. Thus, the properties of the quantum states of radiation fields that are occupied by a finite number of photons are far from the Maxwell theory. On the other hand, the coherent states were formally introduced in quantum optics by Glauber [2], although the first antecedents can be traced back to the Schrödinger papers on quantization, see, e.g., [3]. They produce average fields different from zero as well as nonnegative symmetrical Wigner distributions. While the coherent states are constructed as superpositions of Fock states, it is remarkable that their properties are very close to the Maxwell theory. This is because such states satisfy the notion of full coherence introduced by Glauber, while the Fock states (for $n\ne 0$) lack second (and higher) order coherence, and thus they are nonclassical. The set of nonclassical states includes also squeezed states [4], even and odd coherent states (also called Schrödinger cats) [5], binomial states [6,7], photon-added coherent states [8], etc. The difference between the classical and nonclassical properties of a given quantum state is strongly linked to the notion of entanglement [9], which is a fundamental concept required in the development of quantum computation and quantum information [10]. Noticeably, while investigating the quantum properties of a beam splitter, it has been found that the “entanglement of the output states is strongly related to the nonclassicality of the input fields” [11]. That is, the nonclassicality of an arbitrary (input) state can be tested by detecting entanglement in the output of a quantum beam splitter [11,12].

In the present work we study the nonclassical properties of the states of non-Hermitian Hamiltonians with real spectrum that are generated by Darboux transformations [13,14]. In general, the systems associated with non-Hermitian Hamiltonians are subject of investigation in many branches of contemporary physics [15]. The applications include the study of unstable (decaying) systems [16], light propagating in materials with a complex refractive index [17], $PT$-symmetric [18,19] and $PTC$-symmetric [20] interactions, multi-photon transition processes [21], diverse measurement techniques [22], and coherent states [3,23,24], among others. In the case of the Darboux deformed non-Hermitian systems, the eigenfunctions obey a series of oscillation theorems [25] that permit their study as if they were associated to Hermitian systems. Indeed, the representation space of such non-Hermitian systems can be equipped with a bi-orthogonal structure that provides complete sets of orthonormal states [13]. We shall focus on non-Hermitian oscillators since their bases of eigenfunctions can be used to construct optimized binomial states [26] and generalized coherent states [24], which in turn give rise to a wide diversity of pure states as particular cases. One of the main results reported in this paper is to show that the techniques used to study classical-like properties for Hermitian systems can be adjusted to investigate the classicality of the states of Darboux deformed non-Hermitian systems.

The outline of the paper is as follows: In Section 2 we revisit the main properties of the non-Hermitian oscillators we are interested in. The main differences between the conventional orthogonality and the bi-orthogonality are discussed in detail. In Section 3 we introduce the different bi-orthogonal superpositions of states that are to be analyzed, these include the optimized binomial states and diverse forms of generalized coherent states. Section 4 deals with the nonclassicality of the states defined in Section 3. Final comments are given in Section 5. We have added three appendices with relevant information that is used throughout the manuscript concerning operator algebras (Appendix A), and criteria of nonclassicality (Appendix B).

2. Non-Hermitian Oscillators

The solution to the eigenvalue problem of the dimensionless (mathematical) oscillator $H_{osc}=-\frac{d^2}{d{x}^2}+x^2$ is given by the discrete eigenvalues $E_n^{osc}=2n+1$ and normalized eigenfunctions

$${\phi }_n\left(x\right)=\frac{e^{-x^2/2}}{\sqrt{2^{n}n!\sqrt{\pi }}}{H}_n\left(x\right),n=0,1,\dots ,$$

(1)

where $H_n\left(x\right)$ stands for the Hermite polynomials [27]. Using the linearly independent solutions of the eigenvalue equation $H_{osc}u=-u$ and a set of real numbers $\{a,b,c,\lambda \}$ fulfilling $4ac-b^2=4{\lambda }^2$, it can be shown that

$$\alpha \left(x\right)=e^{x^2/2}{\left[\frac{a\pi }{4}{\mathrm{Erf}}^2\left(x\right)+\frac{b\sqrt{\pi }}{2}\mathrm{Erf}\left(x\right)+c\right]}^{1/2}$$

(2)

is a real-valued function which is free of zeros in $\mathbb{R}$, and defines the dimensionless potential

$$V_{\lambda }\left(x\right)=x^2-2-4\frac{d}{dx}\left[\frac{a\sqrt{\pi }\mathrm{Erf}\left(x\right)+b-i\frac{\lambda }{2}}{{\alpha }^2\left(x\right)}\right]$$

(3)

as a Darboux transformation of $V_{osc}\left(x\right)=x^2$ [13]. Here Erf$\left(x\right)$ defines the error function. If $\lambda \ne 0$, the Hamiltonian $H_{\lambda }=-\frac{d^2}{d{x}^2}+V_{\lambda }\left(x\right)$ is not self-adjoint since $V_{\lambda \ne 0}\left(x\right)$ is a complex-valued function. Nevertheless, it may be shown that the imaginary part of such potential is continuous in $\mathbb{R}$ and satisfies the condition of zero total area [25]:

$${\int }_{\mathbb{R}}\mathrm{Im}{V}_{\lambda }\left(x\right)dx=-{\left.\frac{2\lambda }{{\alpha }^2\left(x\right)}\right|}_{-\infty }^{+\infty }=0.$$

(4)

Equation (4) implies a balanced interplay between gain and loss of probability that does not depend on any other symmetry of either $\mathrm{Im}{V}_{\lambda }\left(x\right)$ or $\mathrm{Re}{V}_{\lambda }\left(x\right)$. For instance, besides fulfilling Equation (4), the profile of the real and imaginary parts of the oscillator depicted in Figure 1a is not particularly special (this has been obtained from Equation (3) with $a=5$, $b=8$, $c=5$ and $\lambda =3$). Looking for concrete symmetries we can take $b=0$ to get even and odd forms of $\mathrm{Im}{V}_{\lambda }\left(x\right)$ and $\mathrm{Re}{V}_{\lambda }\left(x\right)$, respectively. The result is a non-Hermitian oscillator which is invariant under $PT$-transformations [18]. This case is illustrated in Figure 1b for $a=c=\lambda =1$, and $b=0$. On the other hand, for $b=\pm 2\sqrt{ac}$, with a and c positive numbers, the parameter $\lambda$ is equal to zero and Equation (3) decouples into the pair of real-valued functions

$$V_{\lambda =0}^{\pm }(x;\gamma )=x^2-2-2\frac{d}{dx}\left(\frac{e^{-x^2}}{{\int }^x{e}^{-y^2}dy\pm \gamma }\right),\gamma =\sqrt{\frac{c}{a}},$$

(5)

where the condition $\gamma >\sqrt{\pi }/2$ must be satisfied to avoid singularities. Figure 1c shows $V_{\lambda =0}^{-}(x;\gamma )$ with $a=1$ and $c=0.88$. The concomitant $V_{\lambda =0}^{+}(x;\gamma )$ corresponds to the specular reflection of $V_{\lambda =0}^{-}(x;\gamma )$. The Hermitian oscillators of Equation (5) were first found by Abraham and Moses through the systematic use of the Gelfand-Levitan equation [28], and then recovered by Mielnik as an application of his generalized factorization method [29].

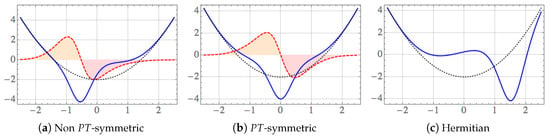
Figure 1. (Color online) the oscillators $V_{\lambda }\left(x\right)$ defined in Equation (3) can be categorized in three different classes: (a) Non $PT$-symmetric, (b) $PT$-symmetric, and (c) Hermitian. In (a) and (b) the imaginary part (dashed-red) satisfies the condition of zero total area, Equation (4). The zones of gain and loss of probability are shadowed in orange and red, respectively. In all the cases the curve in blue corresponds to the real part of $V_{\lambda }\left(x\right)$ and the dotted-black curve represents the shifted oscillator $V_{osc}\left(x\right)-2$, the latter is obtained from Equation (3) as a particular case.

Additionally, Equations (5) represent a family of systems that converge to the conventional oscillator in the limit $|\gamma |\to \infty$. Indeed, it may be verified that

$$\underset{|\gamma |\to \infty }{lim}{V}_{\lambda =0}(x;\gamma )\to x^2-2.$$

(6)

The oscillator $V_{osc}\left(x\right)-2$ is thus a member of the family of complex-valued potentials $V_{\lambda }\left(x\right)$ introduced in Equation (3). This is depicted in the plots of Figure 1 as a reference.

• Fundamental solutions. Another remarkable profile of the complex-valued oscillators of Equation (3) is that the functions

  $${\psi }_{n+1}\left(x\right)=\left[\frac{d}{dx}-\frac{{\alpha }^{\prime }\left(x\right)}{\alpha \left(x\right)}+i\frac{\lambda }{{\alpha }^2\left(x\right)}\right]{\phi }_n\left(x\right),n=0,1,\dots ,$$

  (7)

  are normalizable solutions of the related eigenvalue equation $H_{\lambda }{\psi }_{n+1}\left(x\right)=E_{n+1}{\psi }_{n+1}\left(x\right)$ for $E_{n+1}=2n+1$. The additional normalizable function

  $${\psi }_0\left(x\right)=\frac{1}{\alpha \left(x\right)}exp\left[iarctan\left(\frac{a\sqrt{\pi }\mathrm{Erf}\left(x\right)+b}{2\lambda }\right)\right]$$

  (8)

  also solves the eigenvalue equation defined by $H_{\lambda }$, but it is not derivable from the set ${\phi }_n\left(x\right)$ and belongs to the energy $E_0=-1$. The spectrum of the potential $V_{\lambda }\left(x\right)$ is therefore composed of the equidistant energies $E_n=2n-1$, $n\ge 0$.
• Bi-orthogonality. While the functions ${\psi }_n\left(x\right)$ are normalizable, they form a peculiar set since ${\psi }_0\left(x\right)$ is orthogonal to all the ${\psi }_{n+1}\left(x\right)$ while the latter are not mutually orthogonal. As a result, in contrast with the Hermitian case, the norm of any superposition of states ${\psi }_{n+1}\left(x\right)$ depends not only on the modulus of the related coefficients but also on the phase shift between them. For instance, the norm of

  $$\mathsf{\Psi }\left(x\right)=\frac{\theta }{||{\psi }_{n+1}||}{\psi }_{n+1}\left(x\right)+\frac{\mu }{||{\psi }_{m+1}||}{\psi }_{m+1}\left(x\right),\theta ,\mu \in \mathbb{C},$$

  (9)

  satisfies

  $${||\mathsf{\Psi }||}^2={|\theta |}^2+{|\mu |}^2+2|\theta \mu |{\xi }_{n+1,m+1}cos(\delta +{\gamma }_{n+1,m+1}),\delta =\arg \left({\theta }^{*}\mu \right),$$

  (10)

  where $z^{*}$ is the complex-conjugate of $z\in \mathbb{C}$. The numbers ${\xi }_{n+1,m+1}$ and ${\gamma }_{n+1,m+1}$ are, respectively, the modulus and argument of the product between ${\psi }_{n+1}\left(x\right)$ and ${\psi }_{m+1}\left(x\right)$. Thus, depending on the phase-shift $\delta$, the non-orthogonality of the set ${\psi }_{n+1}\left(x\right)$ produces the oscillations of $||\mathsf{\Psi }||$. The complexity of such a dependence increases with the number of elements in the superposition.
  One can face the above difficulties by introducing a bi-orthogonal system (see relevant information in Reference [24]), formed by the eigenfunctions ${\psi }_n\left(x\right)$ of $H_{\lambda }$ and those of its Hermitian-conjugate $H_{\lambda }^{†}\equiv {\overline{H}}_{\lambda }$, written as ${\overline{\psi }}_m\left(x\right)$. The main point is that the bi-product $\left({\overline{\psi }}_m,{\psi }_n\right)={\int }_{\mathbb{R}}{\overline{\psi }}_m^{*}\left(x\right){\psi }_n\left(x\right)dx$ is equal to zero if $n\ne m$, and serves to define the bi-norm $||{\psi }_n{||}_B=||{\overline{\psi }}_n{||}_B$ if $n=m$.
  Therefore, besides the conventional normalization ${\psi }_n\left(x\right)/||{\psi }_n||$, we have at hand the bi-normalization ${\psi }_n\left(x\right)/||{\psi }_n{||}_B$, with $||{\psi }_{n+1}{||}_B=\sqrt{2(n+1)}$ for $n\ge 0$. The bi-norm $||{\psi }_0{||}_B$ of the ground state depends on the set $\{a,b,c,\lambda \}$ [24]. The real and imaginary parts of ${\psi }_n\left(x\right)$, as well as the probability density $|{\psi }_n{\left(x\right)|}^2$, behave qualitatively equal in both normalizations but their bi-normalized values are usually larger than those obtained with the conventional normalization. Such a difference is reduced as n increases. This property is illustrated in Figure 2 for the first three eigenfunctions ${\psi }_n\left(x\right)$, and the corresponding probability densities $|{\psi }_n{\left(x\right)|}^2$, of the complex-valued oscillator depicted in Figure 1a.
  

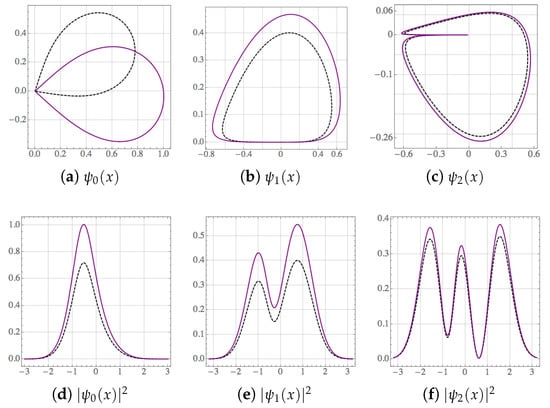  Figure 2. (Color online) bi-normalization (continuous-purple) against conventional normalization (dotted-black) for the first three eigenfunctions ${\psi }_n\left(x\right)$—upper row—and probability densities $|{\psi }_n{\left(x\right)|}^2$—lower row—of the complex-valued oscillator of Equation (3) shown in Figure 1a. The eigenfunctions are depicted in the Argand–Wessel representation with $\mathrm{Re}{\psi }_n\left(x\right)$ and $\mathrm{Im}{\psi }_n\left(x\right)$ in the horizontal and vertical axes, respectively. They have been constructed from Equations (7) and (8) with $a=5$, $b=8$, $c=5$ and $\lambda =3$.
  The bi-orthogonal approach avoids the interference produced by the non-orthogonality. For instance, if the states in Equation (9) are substituted by their bi-normalized versions, we obtain the bi-orthogonal superposition

  $${\mathsf{\Psi }}_B\left(x\right)=\frac{\theta }{\sqrt{2(n+1)}}{\psi }_{n+1}\left(x\right)+\frac{\mu }{\sqrt{2(m+1)}}{\psi }_{m+1}\left(x\right).$$

  (11)
  The bi-norm of the latter state does not depend on the phase-shift

  $${||\mathsf{\Psi }||}_B^2={\int }_{\mathbb{R}}{\overline{\mathsf{\Psi }}}_B^{*}\left(x\right){\mathsf{\Psi }}_B\left(x\right)dx={|\theta |}^2+{|\mu |}^2,$$

  (12)

  so that ${\mathsf{\Psi }}_B\left(x\right)$ is uniquely bi-normalized to 1 by the constant ${(|\theta |}^2+{|\mu |}^2{)}^{-1}$. An additional property of the bi-orthogonal superpositions is that the values of their real and imaginary parts, as well as the values of the corresponding probability densities, are shorter than those obtained from the conventional approach. We show this property in Figure 3 for the superpositions of Equations (9) and (11) with $n=0$, $m=1$, $|\theta |=|\mu |=1/\sqrt{2}$, and three different values of the phase-shift $\delta$. Formally, one may say that $\mathsf{\Psi }\left(x\right)$ and ${\mathsf{\Psi }}_B\left(x\right)$ represent two different superpositions of the states ${\psi }_{n+1}\left(x\right)$ and ${\psi }_{m+1}\left(x\right)$. In the sequel we shall take full advantage of the mathematical simplifications offered by the bi-orthogonal approach.
  

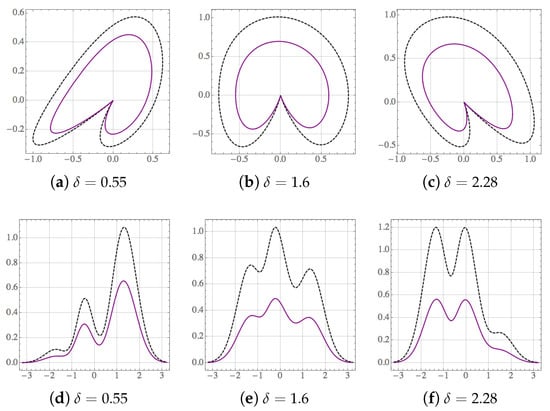  Figure 3. (Color online) the upper row shows the Argand–Wessel diagrams of the superpositions $\mathsf{\Psi }\left(x\right)$ and ${\mathsf{\Psi }}_B\left(x\right)$, Equations (9) and (11), respectively, for $n=0$, $m=1$, $|\theta |=|\mu |=1/\sqrt{2}$, and the indicated values of the phase-shift $\delta$. The corresponding probability densities are shown in the lower row. The code of colors and plot-style is the same as in Figure 2.
• Operator algebras. It can be shown that there exist at least two different algebras of operators associated with the eigenstates of the complex-valued oscillator $V_{\lambda }\left(x\right)$ [30]. They are generated by two different pairs of ladder operators (see Appendix A for details). The first pair, $\mathcal{A}$ and ${\mathcal{A}}^{+}$, together with the Hamiltonian $H_{\lambda }$, satisfy the quadratic polynomial (Heisenberg) algebra

  $$[\mathcal{A},{\mathcal{A}}^{+}]=2\left(3H_{\lambda }+1\right)\left(H_{\lambda }+1\right),[H_{\lambda },\mathcal{A}]=-2\mathcal{A},[H_{\lambda },{\mathcal{A}}^{+}]=2{\mathcal{A}}^{+}.$$

  (13)
  The second pair of ladder operators, denoted by ${\mathcal{C}}_w$ and ${\mathcal{C}}_w^{+}$, together with the Hamiltonian $H_{\lambda }$, and an additional operator $I_w$, satisfy the distorted (Heisenberg) algebra

  $$[{\mathcal{C}}_w,{\mathcal{C}}_w^{+}]=I_w,[H_{\lambda },{\mathcal{C}}_w]=-2{\mathcal{C}}_w,[H_{\lambda },{\mathcal{C}}_w^{+}]=2{\mathcal{C}}_w^{+},$$

  (14)

  where w is a non-negative parameter that defines the ‘distortion’ suffered by the oscillator algebra when one substitutes the operators ${\mathcal{C}}_w$, ${\mathcal{C}}_w^{+}$, and $H_{\lambda }$ for the conventional boson operators, $\widehat{a}$, ${\widehat{a}}^{†}$, and $\widehat{n}$, respectively. The algebras of Equations (13) and (14) will serve to the analysis of classicality of the states associated with the complex-valued oscillators of Equation (3).

3. Bi-Orthogonal Superpositions

We shall study the properties of diverse superpositions of states ${\psi }_n\left(x\right)$ by using

(i)

Bi-normalization to obtain regular probability densities.

(ii)

Bi-orthogonality to avoid the interference associated with non-orthogonality.

The space of states of $H_{\lambda }$, denoted ${\mathcal{H}}_{\lambda }$, consists of all the bi-orthogonal superpositions

$$\varphi \left(x\right)=\sum _{k=0}^{\infty }{c}_k{\psi }_k\left(x\right),c_k=\left({\overline{\psi }}_k,\varphi \right)\in \mathbb{C},$$

(15)

such that

$${||\varphi ||}_B^2=(\overline{\varphi },\varphi )=\sum _{k=0}^{\infty }{|c_k|}^2<\infty .$$

(16)

In turn, ${\overline{\mathcal{H}}}_{\lambda }$ denotes the space spanned by the states ${\overline{\psi }}_n\left(x\right)$. The series decomposition of $\overline{\varphi }\left(x\right)$, which is concomitant to $\varphi \left(x\right)$ in Equation (16), is obtained from Equation (15) by changing ${\psi }_k\left(x\right)\to {\overline{\psi }}_k\left(x\right)$. To simplify the notation, hereafter we use no label to denote the bi-orthogonal properties of the system $\{{\overline{\psi }}_n\left(x\right),{\psi }_m\left(x\right)\}$.

The approach we are going to use identifies a threefold partnership between $H_{\lambda }$, ${\overline{H}}_{\lambda }$, and the conventional oscillator $H_{osc}$, where the eigenvalues play a main role. That is, the triad $\{{\overline{H}}_{\lambda },H_{osc},H_{\lambda }\}$ represents a system for which the energies $E_{n+1}=E_n^{osc}=2n+1$ are threefold degenerate while the energy $E_0=-1$ is only twofold degenerate. In this sense, our model is a generalization of the supersymmetric approach [31] since $H_{\lambda }$ and ${\overline{H}}_{\lambda }$ are treated as two different faces of the same system, which can be studied in much the same way as in the Hermitian approaches [24].

We are interested in two different classes of superpositions. The optimized superpositions are such that their nonclassicality can be manipulated by tuning the number of elements as well as the state of lowest energy in the sum. The generalized coherent states are constructed in terms of the algebras underlying the complex-valued oscillators of Equation (3) and form an over-complete set in ${\mathcal{H}}_{\lambda }$. Next, we analyze these classes in detail.

3.1. Optimized Binomial States

Let us consider a superposition of $N+1$ adjacent states

$${\varphi }_b\left(x\right)=\sum _{k=0}^N{c}_k^b{\psi }_{k+r}\left(x\right),$$

(17)

where the non-negative integer $r\ge 0$ determines the state ${\psi }_r\left(x\right)$ of the lowest energy that is included in the packet, and the coefficients $c_k^b$ give rise to the binomial distribution

$$|c_k^b{|}^2=\left(\begin{array}{c}N\\ k\end{array}\right)p^k{(1-p)}^{N-k},0\le p\le 1,k\le N.$$

(18)

That is, Equation (17) is bi-normalized and includes only the eigenstates belonging to the energies $E_r,E_{r+1},\dots ,E_{r+N}$. Equation (18) means that the probability of finding the system in the state ${\psi }_{k+r}\left(x\right)$ is weighted by the probability p of having success k times in n trials. The superpositions of Equation (17) are called “optimized binomial” states [26] since (for $r=0$) they converge to the conventional binomial superposition at the oscillator limit.

To investigate the properties of ${\varphi }_b\left(x\right)$ let us take $p\approx 0$. The modulus $|c_0^b|$ of the first coefficient in the expansion is close to 1 and the other coefficients are almost zero. Then, the state ${\psi }_r\left(r\right)$ is very influential in the behavior of the entire packet since it is weighted by $c_0^b$ in the superposition. The situation changes if $p\approx 1$ since in this case the modulus $|c_N^b|$ of the last coefficient in the sum is close to 1, while the moduli of the other coefficients are almost zero. In such case, ${\psi }_{N+r}\left(x\right)$ is the state of major influence in the packet.

Another important feature of the optimized binomial states is that their mean energy ${\mathcal{E}}_b$ depends on the number r which labels the lowest of the involved energies

$${\mathcal{E}}_b={⟨H_{\lambda }⟩}_b=2(Np+r)-1.$$

(19)

Considering $0\le p\le 1$, we have

$$2r-1\le {\mathcal{E}}_b\le 2(N+r)-1.$$

(20)

That is, ${\mathcal{E}}_b$ is bounded from below by r, and from above by N and r. Fixing ${\mathcal{E}}_b$ and r in Equation (19) we can write

$$Np=\frac{1}{2}\left({\mathcal{E}}_b+1-2r\right).$$

(21)

Then, from Equation (18) we arrive at the Poisson distribution:

$$\underset{N\to +\infty }{lim}{|c_k^b|}^2=\frac{e^{-\frac{{\mathcal{E}}_b+1-2r}{2}}}{k!}{\left(\frac{{\mathcal{E}}_b+1-2r}{2}\right)}^k.$$

(22)

In this form, as a limit version of the optimized binomial state ${\varphi }_b\left(x\right)$, we introduce the optimized Poisson state

$${\varphi }_P\left(x\right)=e^{-\frac{{|z|}^2}{2}}\sum _{k=0}^{\infty }\frac{z^k}{\sqrt{k!}}{\psi }_{k+r}\left(x\right),{|z|}^2=\frac{{\mathcal{E}}_b+1-2r}{2}.$$

(23)

In the quantum oscillator limit of Equation (6), the superposition of Equation (23) acquires the form

$${\varphi }_P^{osc}\left(x\right)={\left.\underset{|\gamma |\to +\infty }{lim}{\varphi }_P\left(x\right)\right|}_{\lambda =0}=\sum _{k=0}^{+\infty }{c}_k^P{\phi }_{k+r}\left(x\right),c_k^P=e^{-\frac{{|z|}^2}{2}}\frac{z^k}{\sqrt{k!}},$$

(24)

which coincides with the conventional coherent state for $r=0$, see Equation (A25) of Appendix B.

3.2. Generalized Coherent States

The ground state ${\psi }_0\left(x\right)$ is annihilated by both pairs of ladder operators $\mathcal{A}$, ${\mathcal{A}}^{+}$, and ${\mathcal{C}}_w$, ${\mathcal{C}}_w^{+}$, see Appendix A. In any case we can construct coherent states as eigenstates of the respective annihilator operator. We write

$${\varphi }^{\left(\gamma \right)}\left(x\right)=\sum _{k=0}^{+\infty }{c}_k^{\left(\gamma \right)}{\psi }_{k+1}\left(x\right),\gamma =\mathcal{N},w,{\mathcal{N}}_d,w_d.$$

(25)

The super-index $\gamma$ stands for natural ($\mathcal{N}$), distorted (w), natural displaced (${\mathcal{N}}_d$), and distorted displaced ($w_d$). Such nomenclature refers to the form in which the coefficients $c_k^{\left(\gamma \right)}$ have been selected, as it is explained below. For simplicity, we use Dirac notation.

If the superposition of Equation (25) is an eigenvector of the natural annihilation operator $\mathcal{A}$ with complex eigenvalue z, then it is a natural coherent state [24]. We write (A factor $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ of the complex eigenvalue reported in [24] has been absorbed in z.)

$$|z⟩=|{\varphi }^{\left(\mathcal{N}\right)}⟩,c_k^{\left(\mathcal{N}\right)}=\frac{1}{\sqrt{{}_0{F}_2{(1,2,|z|}^2)}}\frac{z^k}{k!\sqrt{(k+1)!}}.$$

(26)

Notice that also the ground state $|{\psi }_0⟩$ is eigenvector of $\mathcal{A}$, but its complex eigenvalue is equal to zero. Moreover, as $|z=0⟩=|{\psi }_1⟩$, we see that the eigenvalue $z=0$ is twice degenerate. The straightforward calculation shows that the vectors $|{\psi }_0⟩$ and $|z⟩$ minimize the uncertainty relation (A9). In this sense $|{\psi }_0⟩$ and $|z⟩$ represent two different types of minimal uncertainty states.

Similarly, the distorted coherent states [24] are defined as eigenvectors of the distorted annihilation operator ${\mathcal{C}}_w$ with complex eigenvalue z. In this case we write

$$|z,w⟩=|{\varphi }^{\left(w\right)}⟩,c_k^{\left(w\right)}=\frac{1}{\sqrt{{}_1{F}_1{(1,w,|z|}^2)}}\frac{z^k}{\sqrt{{\left(w\right)}_k}},$$

(27)

with ${\left(w\right)}_k=w(w-1)\cdots (w-k+1)$ being the Pochhammer symbol [27]. The eigenvalue $z=0$ is also twice degenerate because $|{\psi }_0⟩$ and $|z=0,w⟩=|{\psi }_1⟩$ are annihilated by ${\mathcal{C}}_w$. As $|{\psi }_0⟩$ and $|z,w⟩$ minimize the uncertainty relation of Equation (A16), they represent two different types of minimal uncertainty states.

Another interesting superposition, Equation (25), is obtained by demanding that the vector $|{\varphi }^{\left(\gamma \right)}⟩$ be the displaced version of a fiducial state. The states $|{\psi }_0⟩$ and $|{\psi }_1⟩$ are invariant under the action of the operator exponentiations $e^{-z^{*}\mathcal{A}}$ and $e^{-z^{*}{\mathcal{C}}_w}$, because they are annihilated by both operators $\mathcal{A}$ and ${\mathcal{C}}_w$. The latter means that $|{\psi }_0⟩$ and $|{\psi }_1⟩$ can be used as fiducial states. Considering the operators

$$D\left(z\right)=e^{z{\mathcal{A}}^{+}}{e}^{-z^{*}\mathcal{A}},D_w\left(z\right)=e^{z{\mathcal{C}}_w^{+}}{e}^{-z^{*}{\mathcal{C}}_w},$$

(28)

which one has the ‘displaced’ states $|{\varphi }^{\left({\mathcal{N}}_d\right)}⟩=D\left(z\right)|{\psi }_1⟩$ and $|{\varphi }^{\left(w_d\right)}⟩=D_w\left(z\right)|{\psi }_1⟩$. Remark that the ground state $|{\psi }_0⟩$ is invariant under the action of $D\left(z\right)$ and $D_w\left(z\right)$, so it is also a displaced state.

In the rest of this work we shall omit the description of the states $|{\varphi }^{\left({\mathcal{N}}_d\right)}⟩$ since their properties are qualitatively similar to those of the (distorted) displaced coherent states:

$$|{\psi }_0{⟩,|z,w⟩}_d=|{\varphi }^{\left(w_d\right)}⟩,c_k^{\left(w_d\right)}=\frac{1}{\sqrt{{}_1{F}_1{(w,1,|z|}^2)}}\frac{z^k\sqrt{{\left(w\right)}_k}}{k!}.$$

(29)

In contrast to the previous superpositions, the states ${|z,w⟩}_d$ do not minimize the uncertainty relation of Equation (A16) for arbitrary values of z, but only for $z=0$. The latter means that $|{\psi }_0⟩$ and $|{\psi }_1⟩$ are the only displaced coherent states of minimal uncertainty.

4. Nonclassical States for Non-Hermitian Oscillators

The P-representation introduced by Glauber [32] and Sudarshan [33] defines a limit for the classical description of radiation fields. If the P-function is not accurately interpretable as a probability distribution then the field “will have no classical analog” [2]. This notion of nonclassicality applies immediately to the Fock states $|n⟩$ for $n\ne 0$ because their P-functions are as singular as the derivatives of the delta function ${\delta }^{\left(2\right)}\left(z\right)=\delta \left(\mathrm{Re}\left(z\right)\right)\delta \left(\mathrm{Im}\left(z\right)\right)$, and are negative in some regions of the complex z-plane. The latter means that the light beams represented by any of the Fock states $|n\ne 0⟩$ cannot be described in terms of the electrodynamics introduced by Maxwell. In turn, the Glauber states [2], usually denoted $|\alpha ⟩$, are classical because their P-function is precisely ${\delta }^{\left(2\right)}(z-\alpha )$. The vacuum $|0⟩$ is also classical as it is a coherent state with complex eigenvalue equal to zero. In general, the states for which the quadrature variances obey the inequalities

$${\left(\mathsf{\Delta }\widehat{x}\right)}^2\ge \frac{1}{2},{\left(\mathsf{\Delta }\widehat{p}\right)}^2\ge \frac{1}{2},$$

(30)

which admit a non-negative P-function [2]. Here, ${\left(\mathsf{\Delta }A\right)}^2=⟨A^2⟩-{⟨A⟩}^2$ stands for the variance of the operator A. If either of Equations (30) is not satisfied, the P-function is ill-defined and the state is called “squeezed” [4,34,35]. In these cases it is better to represent the state using the Wigner distribution [1], which is regular and always exists. Nonclassical states have Wigner functions which either are negative in some regions of the phase-space or are squeezed in one of the variables of the phase-space.

In modern days, the nonclassicality of a state can be tested by another excellent method, which follows from the use of the quantum beam splitter. It creates entangled states at its output ports while at least one of its inputs are fed with a nonclassical state. The device is used frequently both in theory and experiment, since it not only tests the nonclassicality of the state, but also quantifies the degree of nonclassicality in an efficient way [11,12]. There are some well-known nonclassical states in the literature, which include squeezed states [4], even and odd coherent states (also called Schrödinger cats) [5], binomial states [6,7], photon-added coherent states [8], etc. Apart from the nonclassical states that arise from the harmonic oscillator, there exist many other such states emerging from different generalizations of coherent states; see, for instance [36]. Other interesting nonclassical states have also been shown to originate from some mathematical frameworks, in particular, from the noncommutative systems reported in [37,38,39]. The striking feature of such systems is that they give rise to well-defined nonclassical states although the corresponding models are non-Hermitian.

Quite recently it has been shown that the appropriate generalizations of the oscillator algebra permit the construction of nonlinear coherent states that satisfy a closure relation which is expressed uniquely in terms of the Meijer G-function [40]. This property automatically defines the delta distribution as the corresponding P-representation. However, in the same work, it is also shown that does not exist a classical analog for such states since they lack second-order coherence and exhibit antibunching. Thus, although their P-representation is a delta function, the nonlinear coherent states studied in [40] are not classical since they are not fully coherent in the sense established by Glauber [2]. Similar results have been obtained for the para-Bose oscillator [41,42]. The algebras of Equations (13) and (14) that we have used to construct the coherent states of Section 3.2 satisfy the requirements established in [40]. Considering also that the bi-orthogonality permits to operate the non-Hermitian oscillators as in the conventional Hermitian case, it may be shown that the corresponding P-representation is proportional to the delta distribution. Nevertheless, the latter means the existence of a classical analog only if the states of Section 3.2 are fully coherent.

Instead of investigating whether our coherent states lack second (or higher) order coherence, we shall use some of the techniques described in Appendix B to study their classicalness. Namely, we are going to study the corresponding variances, Mandel parameter, Wigner distribution and purity.

4.1. Nonclassical Optimized Binomial States

Let us investigate the properties of the distorted quadratures of Equation (A15) in terms of the optimized binomial states of Equations (17) and (18). The variances ${\left(\mathsf{\Delta }{X}_w\right)}^2$ and ${\left(\mathsf{\Delta }{P}_w\right)}^2$ may be expressed in the form of Equation (A17) of Appendix B:

$${\left(\mathsf{\Delta }{X}_w\right)}^2=\frac{1}{4}|{⟨I_w⟩}_b|+U_1,{\left(\mathsf{\Delta }{P}_w\right)}^2=\frac{1}{4}|{⟨I_w⟩}_b|-U_2,$$

(31)

where we have used Equation (A16) and ${⟨I_w⟩}_b\equiv ⟨{\overline{\varphi }}_b|I_w|{\varphi }_b⟩=1+(w-1)\left({\delta }_{r,1}{c}_0^2+{\delta }_{r,0}{c}_1^2\right)-{\delta }_{r,0}{c}_0^2$. The straightforward calculation gives $U_1=\frac{1}{2}\left(M_1+M_2\right)-M_3^2$ and $U_2=\frac{1}{2}\left(M_1-M_2\right)$, with

$$\begin{array}{c}{M}_1=\sum _{k=0}^{N-2}{\Omega }_{k,r}^{\left(1\right)}{c}_{k+2}{c}_k\sqrt{(k+r+w-1)(k+r+w)},\hfill \end{array}$$

(32)

$$\begin{array}{c}{M}_2=\sum _{k=0}^N(k+r+w-2){\Omega }_{k,r}^{\left(2\right)}{c}_k^2,M_3=\sum _{k=0}^{N-1}{\Omega }_{k,r}^{\left(1\right)}{c}_{k+1}{c}_k\sqrt{(k+r+w-1)}.\hfill \end{array}$$

(33)

In the above expressions ${\Omega }_{k,r}^{\left(1\right)}=1-{\delta }_{k,r}{\delta }_{r,0}$, and ${\Omega }_{k,r}^{\left(2\right)}={\Omega }_{k,r}^{\left(1\right)}-{\delta }_{k,1}{\delta }_{r,0}-{\delta }_{k,0}{\delta }_{r,1}$. Hereafter we make ${\theta }_k=0$ in $c_k=|c_k^b|e^{i{\theta }_k}$.

It may be shown that there is always a subset of the mean energies of Equations (19) and (20) for which ${\left(\mathsf{\Delta }{X}_w\right)}^2<\frac{1}{4}{⟨I_w⟩}_b$. Thus, it is always possible to find a mean energy ${\mathcal{E}}_b$ producing the squeezing of the distorted quadrature $X_w$. The latter is illustrated in Figure 4 for $r=2$, $N=10$ and two different values of w. In turn, the squeezing of $P_w$ occurs for $r=0$ only, and it is not as strong as the one suffered by $X_w$ since ${\left(\mathsf{\Delta }{P}_w\right)}^2$ is just slightly larger than $\frac{1}{4}{⟨I_w⟩}_b$. In general, the optimized binomial states of Equation (17) are of minimal uncertainty (i.e., they are classical states) only at the lowest mean energy for either (i) $r=0$ and any value of w, or (ii) $r=2$ and $w=0$.

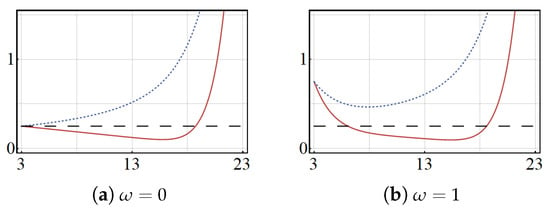
Figure 4. (Color online) the variances of Equation (31) and expectation value $\frac{1}{4}{⟨I_w⟩}_b$ of the optimized binomial states of Equation (17). The functions ${\left(\mathsf{\Delta }{X}_w\right)}^2$ and ${\left(\mathsf{\Delta }{P}_w\right)}^2$ are depicted in solid-red and dotted-blue, respectively; the expectation value is in dashed-black. We have used $N=10$, $r=2$, and the indicated values of $\omega$. The horizontal axis refers to the allowed mean energy ${\mathcal{E}}_b$ introduced in Equations (19) and (20).

In the quantum oscillator limit of Equation (6) one has

$${\varphi }_b^{osc}\left(x\right)={\left.\underset{|\gamma |\to \infty }{lim}{\varphi }_b\left(x\right)\right|}_{\lambda =0}=\sum _{k=0}^N|c_k^b|e^{i{\theta }_k}{\phi }_{k+r}\left(x\right).$$

(34)

Clearly, we recover the conventional binomial state for $r=0$. This state is squeezed in the quadrature $\widehat{x}$, for $N=10$ and $p=0.5$, as shown in the Wigner distribution of Figure 5a. If $r\ge 1$, besides the squeezing of $\widehat{x}$, the Wigner distribution exhibits negative values in different zones of the phase-space, see Figure 5b,c. The latter results confirm that the optimized binomial states of Equation (34) are stronger nonclassical than the conventional ones.

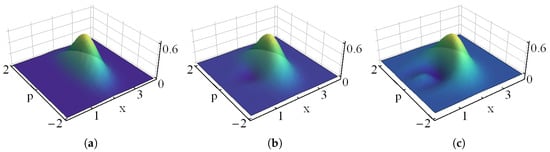
Figure 5. Wigner distribution of the optimized binomial states of Equation (34). The panel is constructed with (a) $p=0.5$, $r=0$, (b) $p=0.4$, $r=1$, and (c) $p=0.3$, $r=2$. In all cases $N=10$ and ${\mathcal{E}}_b=9$.

To get more insights about the optimized binomial states of Equation (34) we have depicted the related Mandel parameter Q, as a function of p, in Figure 6. For $p=1$ the superposition of Equation (17) is reduced to the state ${\phi }_{N+r}\left(x\right)$, so that all the curves shown in Figure 6 converge to $-1$ as $p\to 1$. In turn, for $r\ne 0$, all the curves take the value $-1$ at $p=0$ since only the Fock state ${\phi }_{r\ne 0}\left(x\right)$ is included in the sum. Thus, for $r\ne 0$ and any p, the Mandel parameter Q in this case is always negative. Then, the optimized binomial states of Equation (34) are sub-Poissonian for $r\ne 0$, and thus do not admit any classical description.

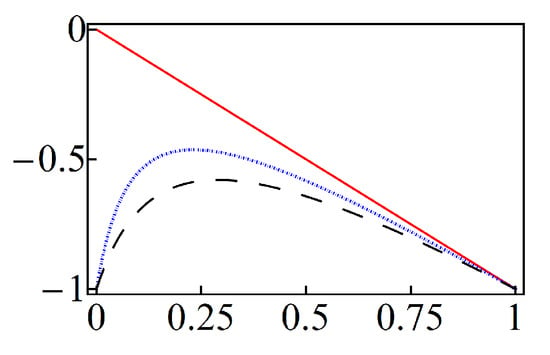
Figure 6. (Color online) Mandel parameter Q of the optimized binomial states of Equation (34) in terms of the probability p. The curves correspond to $N=10$ with $r=0$ (red-solid), $r=1$ (blue-dotted) and $r=2$ (black-dashed).

Let us apply also the beam-splitter technique (see Appendix B) to the states we are dealing with. We may study the purity (linear entropy) $S_L$ in terms of either the transmission coefficient T of the beam-splitter or the probability p that defines the superposition of Equation (34). In the former case it is convenient to fix N and ${\mathcal{E}}_b$ to parameterize the purity with r and p. Then one finds that the purity is equal to zero for $T=0$ and $T=1$, see Figure 7. However, it is important to remark that such results give no special information since they correspond to complete reflectance (i.e., the beam-splitter is indeed a perfect mirror) and complete transparency (no beam-splitter), so the output is, respectively, the vacuum and the state which was injected in input. In general, for other values of T, the purity reaches its maximum at $T=\sqrt{0.5}$, i.e., when the testing beam-splitter is $50/50$.

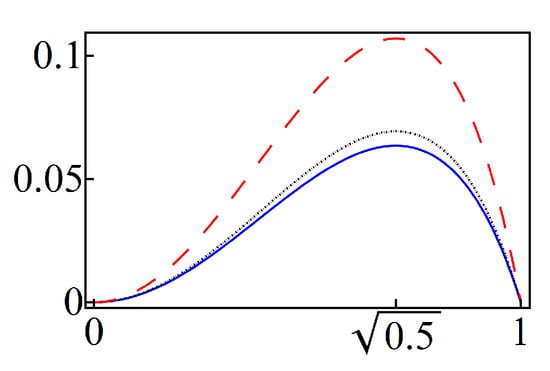
Figure 7. (Color online) purity $S_L$ of the optimized binomial states of Equation (34) in terms of the transmission coefficient T of a testing beam-splitter. In all cases $N=10$ and ${\mathcal{E}}_b=9$. The curves correspond to $p=0.5$, $r=0$ (solid-blue), $p=0.4$, $r=1$ (dotted-black), and $p=0.3$, $r=2$ (dashed-red).

To analyze $S_L$ in terms of the probability p we must fix N and T. Then, with exception of the purity for $r=0$, we find $S_L>0$ for any value of p (see Figure 8). The latter confirms, once again, that the optimized binomial states ${\varphi }_b\left(x\right)$ are nonclassical. Concerning the case $r=0$, the purity is equal to zero at $p=0$ only. Thus, the superposition of Equation (34) only includes the vacuum state ${\phi }_0\left(x\right)$, which is clearly classical.

Figure 8. (Color online) purity $S_L$ of the optimized binomial states of Equation (34) in terms of the probability p with $N=10$. We have used a $50/50$ beam-splitter ($T=\sqrt{0.5}$) for $r=0$ (solid-blue), $r=1$ (dotted-black) and $r=2$ (dashed-red). Compare with Figure 7.

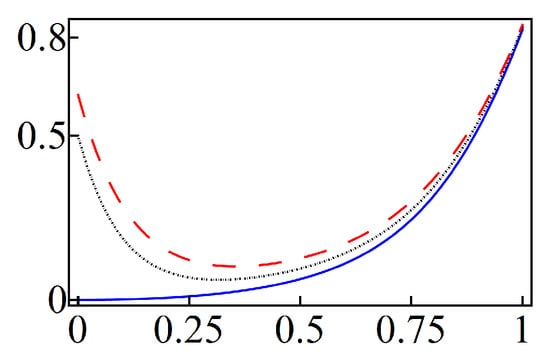
Nonclassical Optimized Poisson States

It may be shown that the optimized Poisson states of Equation (23) are minimum uncertainty states for concrete values of the parameters like either $r=1,\omega =1$, or $r=2,\omega =0$. In any case, they become states of minimum uncertainty as $|z|\to \infty$. For other values of the parameters either ${\left(\mathsf{\Delta }{X}_w\right)}^2$ or ${\left(\mathsf{\Delta }{P}_w\right)}^2$ is squeezed, see Figure 9.

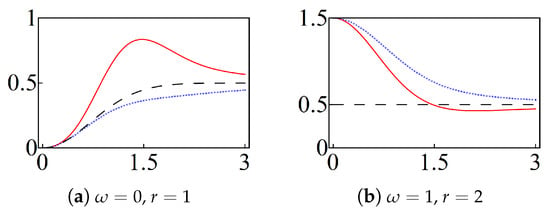
Figure 9. (Color online) the variances ${\left(\mathsf{\Delta }{X}_w\right)}^2$ and ${\left(\mathsf{\Delta }{P}_w\right)}^2$, in solid-red and dotted-blue, respectively, of the optimized Poisson states of Equation (23) for the indicated values of $\omega$ and r. The minimum uncertainty (dashed-black) is included as a reference.

In the quantum oscillator limit of Equation (6), the superposition of Equation (23) acquires the form of Equation (24). As indicated above, for $r=0$ this state is reduced to the conventional coherent state, so that the Mandel parameter is equal to zero, as expected. For other values of r, the optimized Poisson states of Equation (24) are sub-Poissonian. In fact, in Figure 10 we see that the Mandel parameter becomes zero as $|z|\to \infty$, and it is equal to $-1$ for $r\ne 0$ at $z=0$ (i.e., at the lowest mean energy ${\mathcal{E}}_b=2r-1$). In other words, for $r\ne 0$ and finite values of z, the optimized Poisson states ${\varphi }_P^{osc}\left(x\right)$ are nonclassical.

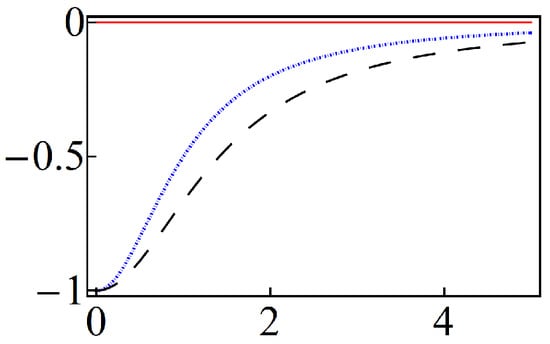
Figure 10. (Color online) Mandel parameter Q of the optimized Poisson states of Equation (24) as a function of $|z|$. The curves correspond to $r=0$ (solid-red), $r=1$ (dotted-blue) and $r=2$ (dashed-black).

For completeness, we show the Wigner function of ${\varphi }_P^{osc}\left(x\right)$ in Figure 11. Clearly, for $r=0$ one has a conventional (classical) coherent state. Other values of r give rise to both, the squeezing of $\widehat{x}$ and the negativity of the Wigner function in some regions of the phase-space.

• Photon added coherent states. Equation (24) resembles the structure of the photon-added coherent states for the conventional harmonic oscillator [8], written in Dirac notation as

  $$|{\alpha }^{\left(pa\right)}⟩=\sum _{k=0}^{+\infty }{c}_k^{\left(pa\right)}|{\phi }_{k+r}⟩,c_k^{\left(pa\right)}={\left[\frac{(k+r)!}{{}_1{F}_1{(r+1,1,|\alpha |}^2)r!}\right]}^{1/2}\frac{{\alpha }^k}{k!},\alpha \in \mathbb{C}.$$

  (35)

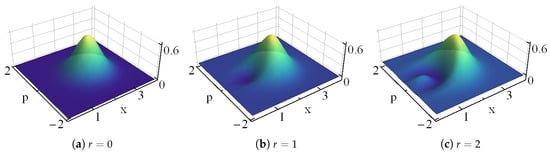
Figure 11. Wigner distribution of the optimized Poisson states of Equation (24). The panel is constructed with $|z|=\sqrt{5}$ (a), $|z|=2$ (b), $|z|=\sqrt{3}$ (c), and the indicated values of r; in all cases ${\mathcal{E}}_b=9$.

In both cases the superpositions are infinite and start with the eigenstate $|{\phi }_r⟩$. The main difference lies on the coefficients, for if we make $z=\alpha$, then

$$c_k^{\left(pa\right)}={\left[\frac{{(k+1)}_r}{{}_1{F}_1{(r+1,1,|\alpha |}^2)r!}\right]}^{1/2}{e}^{\frac{{|\alpha |}^2}{2}}{c}_k^P,$$

(36)

If $r=0$ we see that, up to the normalization constant $e^{-{|\alpha |}^2/2}$, the coefficients are the same. For other values of r the superpositions of Equations (24) and (35) are different in general.

Let us compare $|{\alpha }^{\left(pa\right)}⟩$ with $|{\varphi }_P^{osc}⟩$ in order to identify which one is stronger nonclassical. Using the beam-splitter technique, we find that the nonclassicality of these states depends on different parameters. For instance, in Figure 12a we have fixed the value of the mean energy as ${\mathcal{E}}_b=9$ and, after adjusting the parameters z, $\alpha$, and r, the purities $S_L\left({\varphi }_P^{osc}\right)$ and $S_L\left({\alpha }^{\left(pa\right)}\right)$ have been depicted in terms of the transmission coefficient T. As a global property, we see that the purity is maximum at $T=\sqrt{0.5}$ in all the cases. Besides, we can appreciate that $S_L\left({\varphi }_P^{osc}\right)<S_L\left({\alpha }^{\left(pa\right)}\right)$. Thus, for the parameters used in the figure the state $|{\alpha }^{\left(pa\right)}⟩$ is stronger nonclassical than $|{\varphi }_P^{osc}⟩$. The situation changes if we fix T, and adjust the other parameters to plot the purity $S_L$ in terms of $|z|$. Then $S_L\left({\varphi }_P^{osc}\right)>S_L\left({\alpha }^{\left(pa\right)}\right)$ holds for small values of $|z|$ and $|\alpha |$, and $S_L\left({\varphi }_P^{osc}\right)<S_L\left({\alpha }^{\left(pa\right)}\right)$ is valid for large values of such parameters. The latter is illustrated in Figure 12b for $T=\sqrt{0.5}$ and $|z|=|\alpha |$.

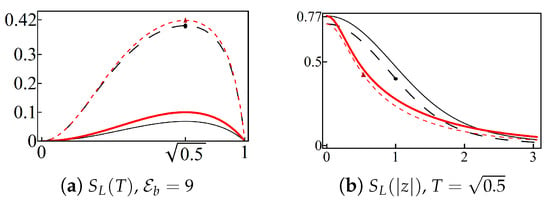
Figure 12. (Color online) the purities of the photon-added coherent state, Equation (24), and the Poisson state, Equation (35), are, respectively, depicted in red and black. In (a) the mean energy is fixed, ${\mathcal{E}}_b=9$, and the purities are plotted in terms of the transmission coefficient T with $r=2$ (thick-solid for Equation (24) and solid for Equation (35)) and $r=4$ (shot-dashed for Equation (24) and long-dashed for Equation (35)). In (b) the transmission coefficient is fixed, $T=\sqrt{0.5}$, and the purities are shown in terms of z with $r=4$ (shot-dashed for Equation (24) and long-dashed for Equation (35)) and $r=6$ (thick-solid for Equation (24) and solid for Equation (35)). For comparison, in both figures the disk and triangle mark the purity evaluated at the same parameters.

4.2. Nonclassical Natural Coherent States

By construction, the natural coherent states $\{|{\psi }_0⟩,|z⟩\}$ minimize the uncertainty relation of Equation (A9) of Appendix A to investigate their properties in the oscillator limit of Equation (6), we first calculate the purity $S_L$ using Equation (A23) of Appendix B with $r=1$, $c_k=c_k^{\left(\mathcal{N}\right)}$, and $N\to +\infty$ in the Fock basis $|{\phi }_k⟩$. The result is depicted in Figure 13a. As we can see, this function is always different from zero and decreases as $|z|\to \infty$ for any value of the transmission coefficient T. That is, the states $|z^{osc}⟩$ are nonclassical. The latter is confirmed by noticing that the Mandel parameter Q is always negative, as it is shown in Figure 13b.

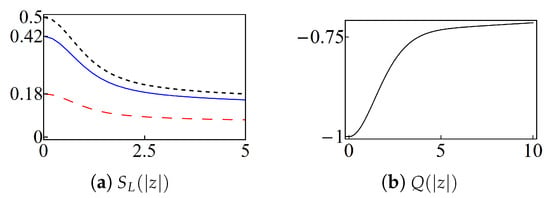
Figure 13. (Color online) (a) purity of the natural coherent state $|z^{osc}⟩$ in terms of $|z|$ for different values of the transmission coefficient: $T=\sqrt{0.1}$ (dashed-red), $T=\sqrt{0.3}$ (solid-blue) and $T=\sqrt{0.5}$ (dotted-black). (b) The corresponding Mandel parameter in terms of z.

On the other hand, the variances of the physical quadratures $\widehat{x}$ and $\widehat{p}$ can be expressed in the form of Equation (A17) of Appendix B, with $A=\widehat{x}$, $B=\widehat{p}$, and

$$\begin{array}{c}{U}_1=1+{\left[\mathrm{Re}\left(z\right)\right]}^{2}f\left(z\right),U_2=1+{\left[\mathrm{Im}\left(z\right)\right]}^{2}f\left(z\right),\\ {\displaystyle f\left(z\right)=\frac{{}_0{F}_2{(2,3;|z|}^2)}{{}_0{F}_2{(1,2;|z|}^2)}-2{\left[\frac{{}_0{F}_2{(2,2;|z|}^2)}{{}_0{F}_2{(1,2;|z|}^2)}\right]}^2.}\end{array}$$

(37)

In Figure 14, we show the regions of the complex z-plane where the squeezing of either $\widehat{x}$ (grey zones) or $\widehat{p}$ (mesh, dashed blue zones) occurs. Notice that the squeezing is maximum at the phase values $\varphi =0,\pi$, and $\varphi =\frac{\pi }{2},\frac{3\pi }{2}$, respectively. The white zones are the regions of no-squeezing, they overrun four distinguishable areas defined along the phase values $\varphi =\frac{k\pi }{4}$, $k=1,3,5,7$, and a circle of radius $|z|\approx 5$ that is centered at the origin. Comparing the Figure 13 and Figure 14, we see that the purity and the Mandel parameter give information that is complementary to that obtained from the variances of the quadratures. Namely, $S_L$ and Q indicate strong nonclassicality for the states $|z^{osc}⟩$ that satisfy the condition $|z|\lesssim 5$, where no squeezing is expected for neither $\widehat{x}$ nor $\widehat{p}$.

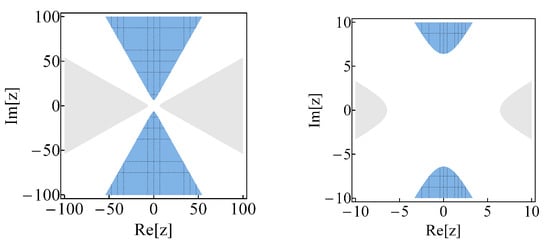
Figure 14. (Color online) regions of the complex plane where squeezing occurs. The grey (mesh, dashed blue) zones correspond to the values of $z\in \mathbb{C}$ for which $\widehat{x}$ ($\widehat{p}$) is squeezed. In turn, the grey and blue zones are centered at $\varphi =0,\pi$ and $\varphi =\frac{\pi }{2},\frac{3\pi }{2}$, respectively.

In Figure 15 we show the density plots of the Wigner function of $|z^{osc}⟩$ for different values of z. In particular, for $z=0$ the natural coherent state $|z^{osc}⟩$ is nonclassical because it coincides with the first excited state of the oscillator $|{\phi }_1⟩$, as shown in Figure 15a. If $|z|>5$ and $\varphi =0$ the quadrature $\widehat{x}$ is squeezed; this is illustrated in Figure 15b with $z=30$. In turn, for $z=i30$ one has the opposite result, $\widehat{p}$ is squeezed; see Figure 15c.

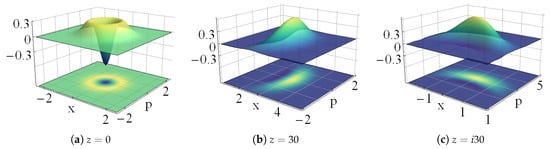
Figure 15. Wigner distribution of the natural coherent sates $|z^{osc}⟩$ for the indicated values of z.

Even and Odd Natural Coherent States

We can use the natural coherent states of Equation (26) to construct additional nonclassical states. Following [5] we introduce the vectors

$$|z_{\pm }⟩={\left[1\pm \frac{{}_0{F}_2{(1,2,-|z|}^2)}{{}_0{F}_2{(1,2,|z|}^2)}\right]}^{-1/2}\left(\frac{|z⟩\pm |-z⟩}{\sqrt{2}}\right),$$

(38)

and call them “even” and “odd” natural cat states, respectively. The related Mandel parameter Q is always negative, see Figure 16a, so that $|z_{\pm }⟩$ are nonclassical. The variances of the natural quadratures of Equation (A8) can be expressed in the form of Equation (A17) of Appendix B, with $A=X_{\mathcal{N}}$, $B=P_{\mathcal{N}}$, and

$$\begin{array}{c}{U}_1^{(\pm )}=2\left[{\displaystyle \frac{{\left[\mathrm{Re}\left(z\right)\right]}^2{}_0{F}_2{(1,2;|z|}^2)\mp {\left[\mathrm{Im}\left(z\right)\right]}^2{}_0{F}_2{(1,2;-|z|}^2)}{{}_0{F}_2{(1,2;|z|}^2)\pm {}_0{F}_2{(1,2;-|z|}^2)}}\right],\\ U_2^{(\pm )}=-2\left[{\displaystyle \frac{{\left[\mathrm{Im}\left(z\right)\right]}^2{}_0{F}_2{(1,2;|z|}^2)\mp {\left[\mathrm{Re}\left(z\right)\right]}^2{}_0{F}_2{(1,2;-|z|}^2)}{{}_0{F}_2{(1,2;|z|}^2)\pm {}_0{F}_2{(1,2;-|z|}^2)}}\right].\end{array}$$

(39)

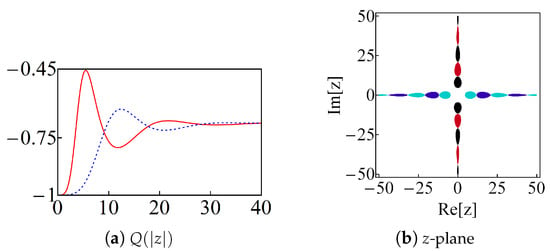
Figure 16. (Color online) (a) the Mandel parameter Q of the even (solid-red) and odd (dahsed-blue) natural cat states of Equation (38) as a function of $|z|$. (b) Regions of the complex z-plane for which squeezing occurs. The red (even) and black (odd) regions correspond to the values of $z\in \mathbb{C}$ for which $P_{\mathcal{N}}$ is squeezed. Blue (even) and green (odd) regions correspond to the squeezing of $X_{\mathcal{N}}$.

In this case the quadratures are squeezed in very localized regions that are distributed along the real and imaginary axes of the complex z-plane. This is illustrated in Figure 16b, where we can appreciate a ‘discretization’ of the eigenvalue z as follows. The quadrature $X_{\mathcal{N}}$ is maximally squeezed along the real axis, in intervals $|z_k^{\left(j\right)}|\pm {\mathcal{\ell }}_k^{\left(j\right)}$ that are defined by the points $|z_k^{\left(j\right)}|$, $k=1,2,\dots$, with ${\mathcal{\ell }}_k^{\left(j\right)}>0$, and j denoting either even (e) or odd (o). For odd natural cats we make $j=o$, with $|z_1^{\left(o\right)}|$ defining the green zones that are closest to the origin in Figure 16b. For the even natural cats we write $j=e$, with $|z_1^{\left(e\right)}|$ defining the blue zones that are closest to the origin in the same figure. The intersection of the above intervals is empty, and they are such that the points $|z_k^{\left(j\right)}|$ interlace. That is $|z_k^{\left(o\right)}|<|z_k^{\left(e\right)}|<|z_{k+1}^{\left(o\right)}|<|z_{k+1}^{\left(e\right)}|<\cdots$. The phases constraining the green and blue zones are defined in intervals ${\varphi }_k^{\left(j\right)}\pm d_k^{\left(j\right)}$, with $d_k^{\left(j\right)}>0$, that are shorter as k increases. A similar description holds for the squeezing of $P_{\mathcal{N}}$ along the imaginary axis.

In the oscillator limit of Equation (6), the natural cat states $|z_{\pm }^{osc}⟩$ preserve their nonclassicality. In Figure 17 the Wigner function becomes negative in diverse zones of the complex z-plane. Such regions are less evident for $|z|\to \infty$.

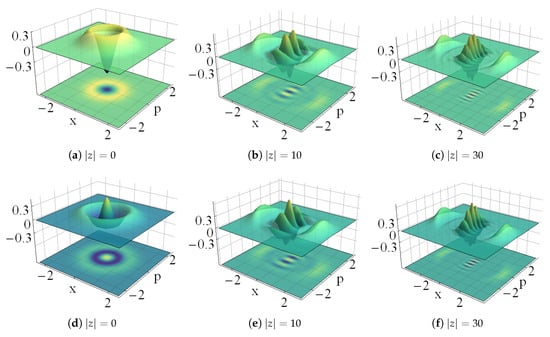
Figure 17. Wigner distributions of the even (upper row) and odd (lower row) natural cat states $|z_{\pm }^{osc}⟩$ for $z=|z|e^{i\theta }$, with $\theta =0$ and the indicated values of $|z|$.

4.3. Nonclassical Distorted Coherent States

By construction, the distorted coherent states $\{|{\psi }_0⟩,|z,w⟩\}$ are minimal uncertainty states with respect to the uncertainty relation of Equation (A16). In the oscillator limit, the Mandel parameter Q depends on the parameter of distortion. In Figure 18a, we see that the states $|z^{osc},w⟩$ are sub-Poissonian for any value of $|z|$ whenever $w=1$. For arbitrary values of $w>1$, they are nonclassical only in the interval $(0,|z_w|)$. Here the value of $|z_w|$ is defined by w: it is larger if the value of w is increased.

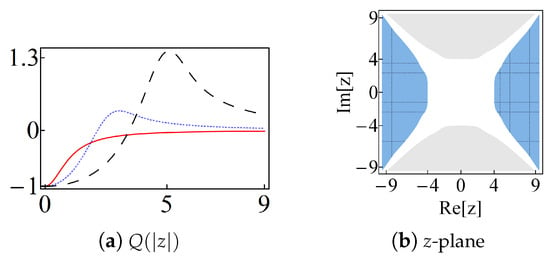
Figure 18. (Color online) the Mandel parameter Q of the distorted coherent state $|z^{osc},w⟩$ is shown in (a) as a function of $|z|$ for $w=1$ (solid-red), $w=5$ (dotted-blue), and $w=20$ (dashed-black). In (b) we show the regions of squeezing in the complex z-plane for $w=20$. The code of colors is the same as in Figure 14b.

The variances of the physical quadratures $\widehat{x}$ and $\widehat{p}$ can be expressed in the form given by Equation (A17) of Appendix B, with $A=\widehat{x}$, $B=\widehat{p}$, and

$$\begin{array}{c}\hfill U_1=\frac{\mathrm{Re}\left(z^2\right)f_2{(|z|}^2,\omega )+{}_1{F}_1\left({2,\omega ,|z|}^2\right)}{{}_1{F}_1{(1,\omega ;|z|}^2)}-2{\left[\frac{\mathrm{Re}\left(z\right)f_1(z,\omega )}{{}_1{F}_1{(1,\omega ;|z|}^2)}\right]}^2,\\ \hfill U_2=\frac{\mathrm{Re}\left(z^2\right)f_2{(|z|}^2,\omega )-{}_1{F}_1\left({2,\omega ,|z|}^2\right)}{{}_1{F}_1{(1,\omega ;|z|}^2)}+2{\left[\frac{\mathrm{Im}\left(z\right)f_1(z,\omega )}{{}_1{F}_1{(1,\omega ;|z|}^2)}\right]}^2,\end{array}$$

(40)

where

$$\begin{array}{c}\hfill f_1(z,\omega )=\sum _{n=0}^{+\infty }{|z|}^{2n}\sqrt{\frac{n+2}{{\left(\omega \right)}_n{\left(\omega \right)}_{n+1}}},f_2{(|z|}^2,\omega )=\sum _{n=0}^{+\infty }{|z|}^{2n}\sqrt{\frac{(n+2)(n+3)}{{\left(\omega \right)}_n{\left(\omega \right)}_{n+2}}}.\end{array}$$

(41)

For $w\approx 1$, the quadratures $\widehat{x}$ and $\widehat{p}$ are squeezed along the real and imaginary axes, respectively. However, for larger values of w, they are squeezed along the imaginary and real axes. Thus, for $w>>1$ the squeezing is rotated by $\frac{\pi }{2}$, as shown in Figure 18b.

Even and Odd Distorted Coherent States

For the even and odd distorted cats

$$|z_{\pm },w⟩={\left[1\pm \frac{{}_1{F}_1{(1,w,-|z|}^2)}{{}_1{F}_1{(1,w,|z|}^2)}\right]}^{-1/2}\left(\frac{|z,w⟩\pm |-z,w⟩}{\sqrt{2}}\right),$$

(42)

the variances of the distorted quadratures of Equation (A15) can be expressed in the form given by Equation (A17) of Appendix B, with $A=X_w$, $B=P_w$, and

$$\begin{array}{c}{U}_1^{(\pm )}=2\left[{\displaystyle \frac{{\left[\mathrm{Re}\left(z\right)\right]}^2{}_1{F}_1{(1,w;|z|}^2)\mp {\left[\mathrm{Im}\left(z\right)\right]}^2{}_1{F}_1{(1,w;-|z|}^2)}{{}_1{F}_1{(1,w;|z|}^2)\pm {}_1{F}_1{(1,w;-|z|}^2)}}\right],\\ U_2^{(\pm )}=-2\left[{\displaystyle \frac{{\left[\mathrm{Im}\left(z\right)\right]}^2{}_1{F}_1{(1,w;|z|}^2)\mp {\left[\mathrm{Re}\left(z\right)\right]}^2{}_1{F}_1{(1,w;-|z|}^2)}{{}_1{F}_1{(1,w;|z|}^2)\pm {}_1{F}_1{(1,w;-|z|}^2)}}\right].\end{array}$$

(43)

In Figure 19, we show the regions of the complex z-plane where $X_w$ and $P_w$ are squeezed for the even distorted cat $|z_{+},w⟩$ with the indicated value of w. Depending on the phase $\varphi$, the squeezing is present in zones defined by the interval $0<|z|\lesssim 7$ and aligned with either the real or the imaginary axes. Such zones are of maximum width at $|z|\approx 3.5$ and are slenderer as either $|z|\to 0$ or $|z|\to \infty$.

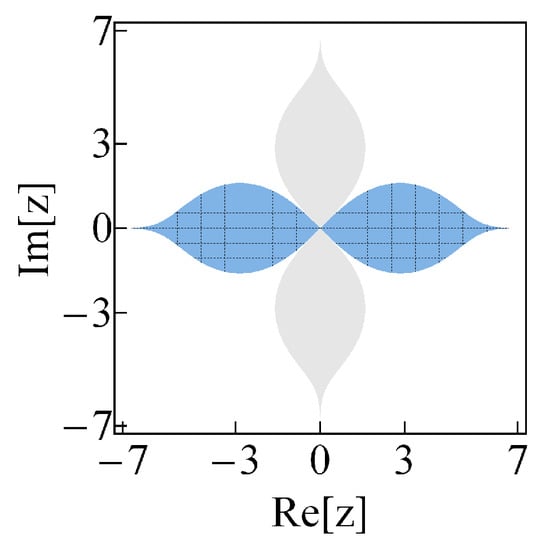
Figure 19. (Color online) regions of squeezing in the complex z-plane for the even distorted cat $|z_{+},w⟩$ with $w=20$. The grey (mesh, dashed blue) zones correspond to the values of $z\in \mathbb{C}$ for which $X_w\left(P_w\right)$ is squeezed. The white zones indicate the values of z for which both variances are bigger than the average uncertainty.

In the oscillator limit of Equation (6), the variances of $\widehat{x}$ and $\widehat{p}$ are calculated using Equation (A17) of Appendix B, with

$$\begin{array}{c}\hfill U_1^{(\pm )}=\frac{\mathrm{Re}\left(z^2\right)\left[f_2{(|z|}^2,w)\pm f_2{(-|z|}^2,w)\right]+\left[{}_1{F}_1\left({2,\omega ;|z|}^2\right)\pm {}_1{F}_1\left(2,\omega ;-{|z|}^2\right)\right]}{{}_1{F}_1{(1,\omega ;|z|}^2)\pm {}_1{F}_1{(1,\omega ;-|z|}^2)},\\ \hfill U_2^{(\pm )}=\frac{\mathrm{Re}\left(z^2\right)\left[f_2{(|z|}^2,w)\pm f_2{(-|z|}^2,w)\right]-\left[{}_1{F}_1\left({2,\omega ;|z|}^2\right)\pm {}_1{F}_1\left(2,\omega ;-{|z|}^2\right)\right]}{{}_1{F}_1{(1,\omega ;|z|}^2)\pm {}_1{F}_1{(1,\omega ;-|z|}^2)},\end{array}$$

(44)

and $f_2{(|z|}^2,w)$ given in Equation (41). The quadratures $\widehat{x}$ and $\widehat{p}$ are squeezed in narrow zones of the complex z-plane that are defined along the real and imaginary axis, respectively. As in the previous cases, there is no squeezing for small values of $|z|$. Moreover, the squeezing regions are slenderer as $|z|\to \infty$. To illustrate the phenomenon, in Figure 20 we show the behavior of the U-functions that define the variances ${\left(\mathsf{\Delta }\widehat{x}\right)}^2$ and ${\left(\mathsf{\Delta }\widehat{p}\right)}^2$ of the even distorted cat $|z_{+}^{osc},w⟩$. As $U_1^{(+)}$ is positive definite along the real axis, see Figure 20c, the quadrature $\widehat{p}$ is squeezed in the intervals of the real axis where the function $U_2^{(+)}$ is non-negative. The latter can be identified in Figure 20a. Similarly, from Figure 20c we see that $U_2^{(+)}$ is negative along the imaginary axis. Then, $\widehat{x}$ is squeezed in the intervals of the imaginary axis for which $U_1^{(+)}$ is negative, see Figure 20b.

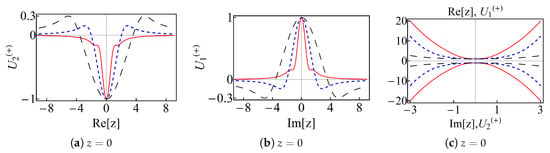
Figure 20. (Color online) the parameters $U_1^{(+)}$ and $U_2^{(+)}$ defining the variances of the physical quadratures $\widehat{x}$ and $\widehat{p}$ for the even distorted cat state $|z_{+}^{osc},w⟩$. In (a) we show the behavior of $U_2^{(+)}$ along the real axis of the complex z-plane. In (b) it is shown $U_1^{(+)}$ along the imaginary axis. The graphic (c) shows $U_1^{(+)}$ and $U_2^{(+)}$ along the imaginary and the real axis, respectively. In all the graphics $w=1$ is in solid-red, $w=5$ in dotted-blue, and $w=20$ in dashed-black curves.

In Figure 21 and Figure 22 we show the density plot of the Wigner distribution of the even and odd cat states of Equation (42), respectively. In both cases we have used $|z_{\pm }^{osc},w⟩$ for $w=1$, $w=5$, and different values of z. The Wigner distribution is negative in different regions of the complex z-plane, and it exhibits oscillations as $|z|$ increases. The distortion parameter w is used to control such oscillations by reducing their number as w increases.

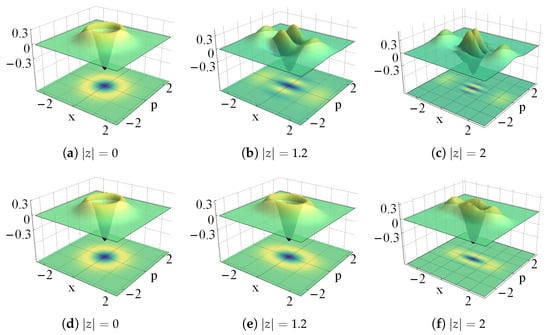
Figure 21. Wigner distribution of the distorted even cat states $|z_{+}^{osc},w⟩$ for $w=1$ (upper row), $w=5$ (lower row). Here $z=|z|e^{i\varphi }$, with $\varphi =0$, and the indicated values of $|z|$.

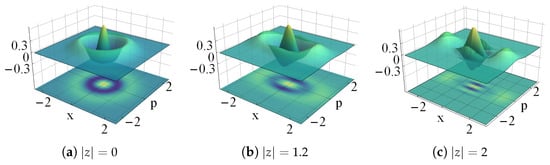
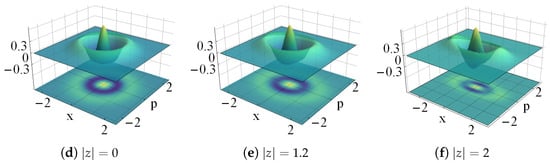
Figure 22. Wigner distribution of the distorted odd cat states $|z_{-}^{osc},w⟩$ for $w=1$ (upper row), $w=5$ (lower row). Here $z=|z|e^{i\varphi }$, with $\varphi =0$, and the indicated values of $|z|$.

On the other hand, the straightforward calculation shows that neither $X_w$ nor $P_w$ are squeezed for the odd distorted cats $|z_{-},w⟩$. The same holds for the physical quadratures $\widehat{x}$ and $\widehat{p}$, evaluated in the oscillator limit state $|z_{-}^{osc},w⟩$.

4.4. Nonclassical Displaced Coherent States

Let us analyze the properties of the displaced coherent states $|{\psi }_0⟩$ and ${|z,w⟩}_d$ introduced in Equation (29). In the oscillator limit, the variances of the physical quadratures $\widehat{x}$ and $\widehat{p}$ are derived from Equation (A17) of Appendix B, with

$$\begin{array}{c}\hfill U_1=\frac{\mathrm{Re}\left(z^2\right)h_2{(|z|}^2,\omega )+{}_2{F}_2\left({2,\omega ;1,1;|z|}^2\right)}{{}_1{F}_1{(1,\omega ;|z|}^2)}-2{\left[\frac{\mathrm{Re}\left(z\right)h_1(z,\omega )}{{}_1{F}_1{(1,\omega ;|z|}^2)}\right]}^2,\\ \hfill U_2=\frac{\mathrm{Re}\left(z^2\right)h_2{(|z|}^2,\omega )-{}_2{F}_2\left({2,\omega ;1,1;|z|}^2\right)}{{}_1{F}_1{(1,\omega ;|z|}^2)}+2{\left[\frac{\mathrm{Im}\left(z\right)h_1(z,\omega )}{{}_1{F}_1{(1,\omega ;|z|}^2)}\right]}^2,\end{array}$$

(45)

and

$$\begin{array}{cc}\hfill & h_1(z,\omega )=\sum _{n=0}^{+\infty }\frac{{|z|}^{2n}}{n!}\frac{\sqrt{{\left(\omega \right)}_n{\left(\omega \right)}_{n+1}(n+2)}}{(n+1)!},\hfill \\ \hfill & h_2{(|z|}^2,\omega )=\sum _{n=0}^{+\infty }\frac{{|z|}^{2n}}{n!}\frac{\sqrt{{\left(\omega \right)}_n{\left(\omega \right)}_{n+2}(n+2)(n+3)}}{(n+2)!}.\hfill \end{array}$$

(46)

The squeezing of $\widehat{x}$ and $\widehat{p}$ for $|z^{osc}{,w⟩}_d$ is quite similar to that obtained for the distorted coherent states of the previous section.

On the other hand, for the even and odd displaced coherent states

$$|z_{\pm }{,w⟩}_d={\left[1\pm \frac{{}_1{F}_1{(w,1,-|z|}^2)}{{}_1{F}_1{(w,1,|z|}^2)}\right]}^{-1/2}\left({|z,w⟩}_d\pm {|-z,w⟩}_d\right),$$

(47)

where the variances of the distorted quadratures of Equation (A15) are calculated from Equation (A17) of Appendix B, with

$$\begin{array}{c}\hfill U_1^{(\pm )}=\frac{\mathrm{Re}\left(z^2\right)\left[h_2{(|z|}^2,w)\pm h_2{(-|z|}^2,w)\right]+\left[{}_2{F}_2\left({2,\omega ;1,1;|z|}^2\right)\pm {}_2{F}_2\left(2,\omega ;1,1;-{|z|}^2\right)\right]}{{}_1{F}_1{(1,\omega ;|z|}^2)\pm {}_1{F}_1{(1,\omega ;-|z|}^2)},\\ \hfill U_2^{(\pm )}=\frac{\mathrm{Re}\left(z^2\right)\left[h_2{(|z|}^2,w)\pm h_2{(-|z|}^2,w)\right]-\left[{}_2{F}_2\left({2,\omega ;1,1;|z|}^2\right)\pm {}_2{F}_2\left(2,\omega ;1,1;-{|z|}^2\right)\right]}{{}_1{F}_1{(1,\omega ;|z|}^2)\pm {}_1{F}_1{(1,\omega ;-|z|}^2)},\end{array}$$

and $h_2{(|z|}^2,w)$ given in Equation (46). From Figure 23 we see that, along the real axis, the function $U_1^{(+)}$ is positive definite for any w while $U_2^{(+)}$ is non-negative for $w=1$ only. Similarly, along the imaginary axis, $U_2^{(+)}$ is always negative but only for $w=1$ the function $U_1^{(+)}$ is negative. The conclusion is that only for $w=1$ we obtain the squeezing of either $X_w$ or $P_w$. Remarkably, for this value of the parameter of distortion, the distorted and the displaced coherent states coincide.

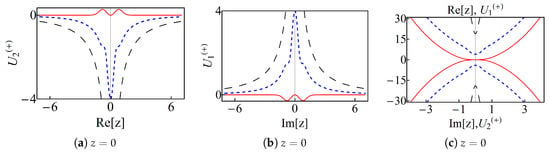
Figure 23. (Color online) the parameters $U_1^{(+)}$ and $U_2^{(+)}$ defining the variances of the distorted quadratures $X_w$ and $P_w$ according to Equation (A17) of Appendix B for the even displaced cat state $|z_{+}{,w⟩}_d$. In (a) we show the behavior of $U_2^{(+)}$ along the real axis of the complex z-plane. In (b) it is shown $U_1^{(+)}$ along the imaginary axis. The graphic (c) shows $U_1^{(+)}$ and $U_2^{(+)}$ along the imaginary and the real axis, respectively. In all the graphics $w=1$ is in solid-red, $w=5$ in dotted-blue, and $w=20$ in dashed-black curves.

5. Conclusions

We have studied the nonclassical properties of some pure states of the non-Hermitian Hamiltonians with real spectrum that are generated by Darboux (supersymmetric) transformations. Our interest has been focused on non-Hermitian oscillators since their eigenfunctions form bi-orthogonal bases of states in a straightforward form [24]. Depending on the parameters that define the Darboux transformation, these oscillators may be either parity-time-symmetric or non-parity-time-symmetric [13]. The pure states studied in this work are constructed as superpositions of the related bi-orthogonal basis, they include the so-called optimized Binomial and optimized Poisson states [26,30], together with the even and odd versions of the generalized coherent states that are associated with the dynamical algebras of the non-Hermitian oscillators [24,30].

One of the main results reported in this paper is to show that the techniques used to study classical-like properties for Hermitian systems can be adjusted to investigate the classicality of the states of non-Hermitian systems. The latter is relevant considering that, although the non-Hermitian systems are widely used in contemporary physics [16,17,18,19,20,21,22], the classicality of the related quantum states is rarely studied. The main difficulty is that non-Hermiticity of a given operator implies that the orthonormal properties of the related eigenfunctions are not granted a priori. Since most of the approaches implemented to analyze classicality assume orthonormality of states, it is not clear how to translate such methods to the non-Hermitian case in general. Such a difficulty can be overpassed by considering a bi-orthogonal basis for the space of states of the non-Hermitian system, just as we have shown throughout this work. It is expected that our approach can be applied in the study of resonances [16] (where the non-Hermiticity of the Hamiltonian defining the interaction of a scatterer with a projectile leads to the temporal trapping of the later by the former) and in the propagation of light in materials with complex refractive index [17] (where the imaginary part of the refractive index may model absorption or amplification of electromagnetic signals).

Concerning the non-Hermitian oscillators we have shown that the corresponding bi-orthogonal bases converge to the Fock basis in the appropriate limit (i.e., after canceling the imaginary part of the potential and properly selecting the parameters), so that the bi-orthogonal superpositions of such states are reduced to pure states of the conventional harmonic oscillator. In particular, we have found that the generalized coherent states of the non-Hermitian oscillators are not minimum uncertainty states for the physical position and momentum quadratures in the oscillator limit. Nevertheless, they exhibit some interesting nonclassical behavior. For instance, depending on the module and complex-phase of the coherence parameter $\alpha$, the physical quadratures can be squeezed for the class of generalized coherent states that we have called “natural” (see Section 3.2). The squeezing is clearly exhibited in the corresponding Wigner distribution and revealed by the Mandel parameter for which it is shown that the photon number distribution is sub-Poissonian. The other class of generalized coherent states, called “distorted”, have similar quadrature squeezing properties. However, the Mandel parameter reveals a different behavior since the photon distribution becomes sub-Poissonian for some values of $|\alpha |$, but it converges to a Poissonian distribution at the limit $|\alpha |\to \infty$. The latter implies a nonclassical-to-classical transition for the distorted coherent states (see [8] for the results on the matter for photon-added coherent states). Such a transition can be also manipulated with the parameter w that defines the related dynamical algebra.

Our method can be extended to construct and study intelligent states associated with the dynamical algebras of the non-Hermitian oscillators. The model involves finite difference equations, which deserve special treatment. Work in this direction is in progress.