ANNs Predicting Noisy Signals in Electronic Circuits: A Model Predicting the Signal Trend in Amplification Systems
Abstract
:1. Introduction
- ‘Material and Methods’ section explaining the adder Op. Amp. circuital model, the simulation planning including different noises as examples, and the data processing workflow implanting ANN data processing;
- ‘Results’ section including time domain and frequency domain results of the circuital Adder-model, and ANN predictions of output signals;
- ‘Discussion’ section discussing advantages, perspectives disadvantages, limitations, and use criteria of the proposed approach in embedded and automated systems enabling corrective actions;
- ‘Conclusions’ section summarizing results and enhancing perspectives.
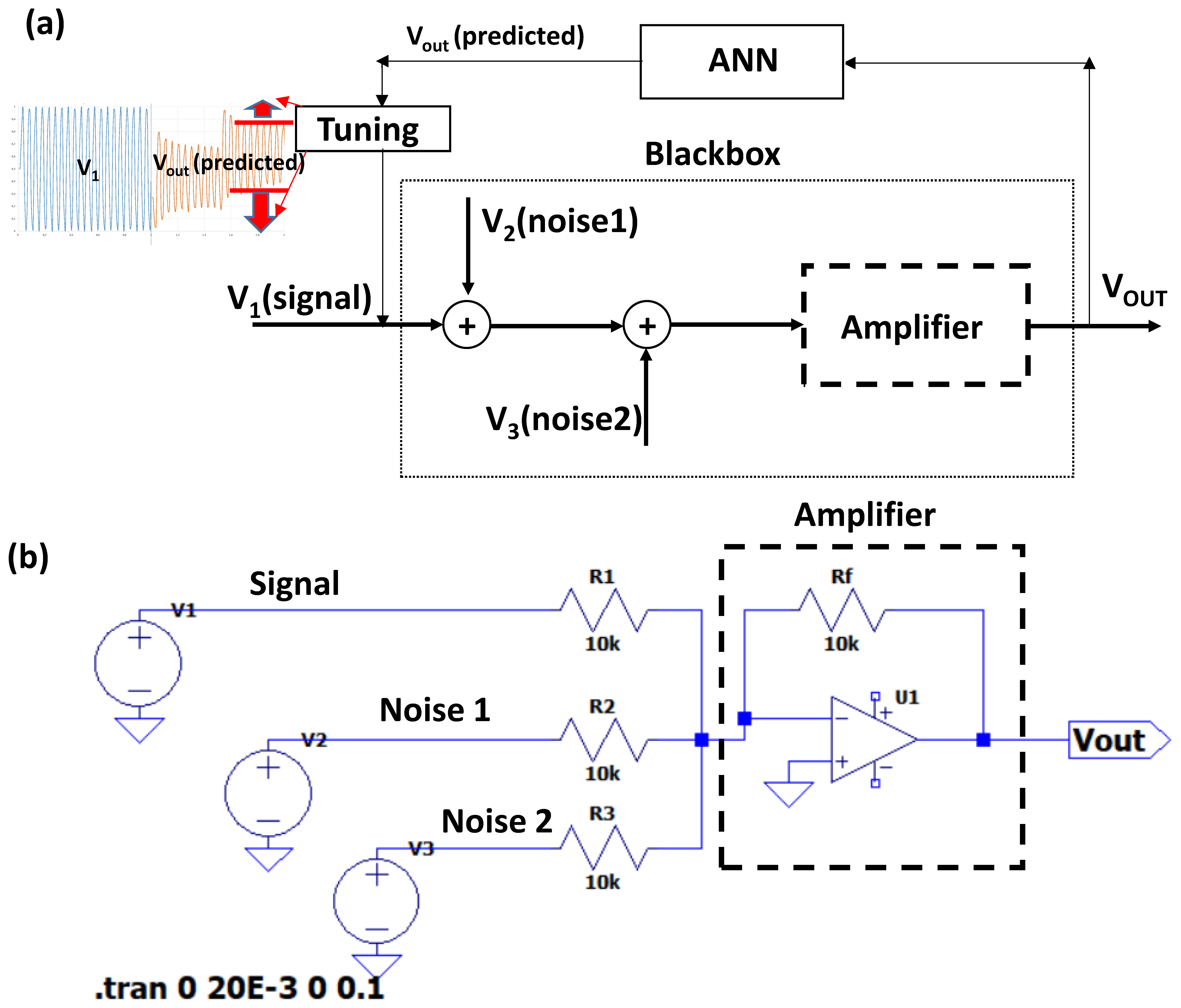
2. Materials and Methods
- Input signal (V1): pure sinusoidal signal with f of 1 kHz, Voffset = 1 Volts, and Vamp = 2 Volts;
- Noise (a): sinusoidal pulse signal with f of 1 kHz, Td = 10−2 s, ϑ = 500 s−1, φ = 45 deg., and Vamp = 2 Volts;
- Noise (b): sinusoidal pulse signal with f of 1 kHz, Td = 0 s, ϑ = 500 s−1, φ = 45 deg., and Vamp = 2 Volts;
- Noise (c): sinusoidal pulse signal with f of 4 kHz, Td = 0.002 s, ϑ = 0 s−1, φ = 0 deg., and Vamp = 2.4 Volts;
- Noise (d): sinusoidal pulse signal with f of 4 kHz, Td = 0.008 s, ϑ = 500 s−1, φ = 45 deg., and Vamp = 2 Volts;
- Noise (e): sinusoidal pulse signal with f of 3.3 kHz, Td = 0.003 s, ϑ = 0 s−1, φ = 0 deg., and Vamp = 2.4 Volts;
- Noise (f): sinusoidal pulse signal with f of 1 kHz, Td = 0.008 s, ϑ = 500 s−1, φ = 45 deg., and Vamp = 2 Volts;
- Noise (g): sinusoidal pulse signal with f of 8 kHz, Td = 0.002 s, ϑ = 0 s−1, φ = 0 deg., and Vamp = 2.4 Volts;
- Noise (h): sinusoidal pulse signal with f of 8 kHz, Td = 0.008 s, ϑ = 500 s−1, φ = 45 deg., and Vamp = 2 Volts.
- Data pre-processing: data importing in local repository, data manipulation, and data filtering;
- Data processing: ANN training and ANN testing models;
- Data output: data visualization, algorithm performance scoring, and data exporting.

- -
- ‘File Reader’: importing the .txt values of the simulations (outputs of the LTspice tool);
- -
- ‘RowID’: generating time attributes (time steps as new column);
- -
- ‘String Manipulation’ and ‘String to Number’: setting of the time column to integer attribute type;
- -
- ‘Column Filter’: selecting of only the time steps and Vout columns;
- -
- ‘Normalize’: normalizing the Vout signal;
- -
- ‘Partitioning’: partitioning of the dataset into training and testing dataset;
- -
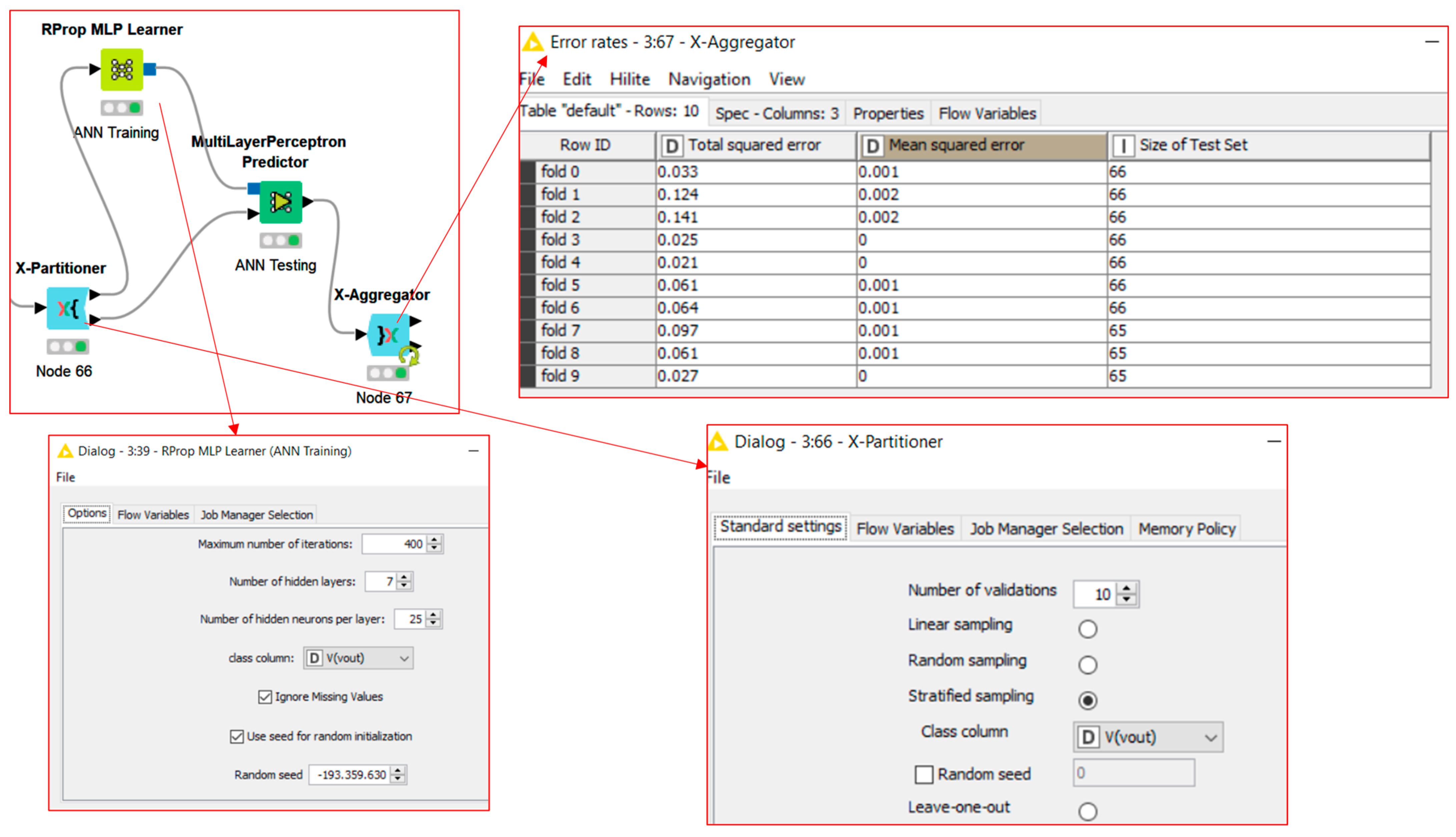
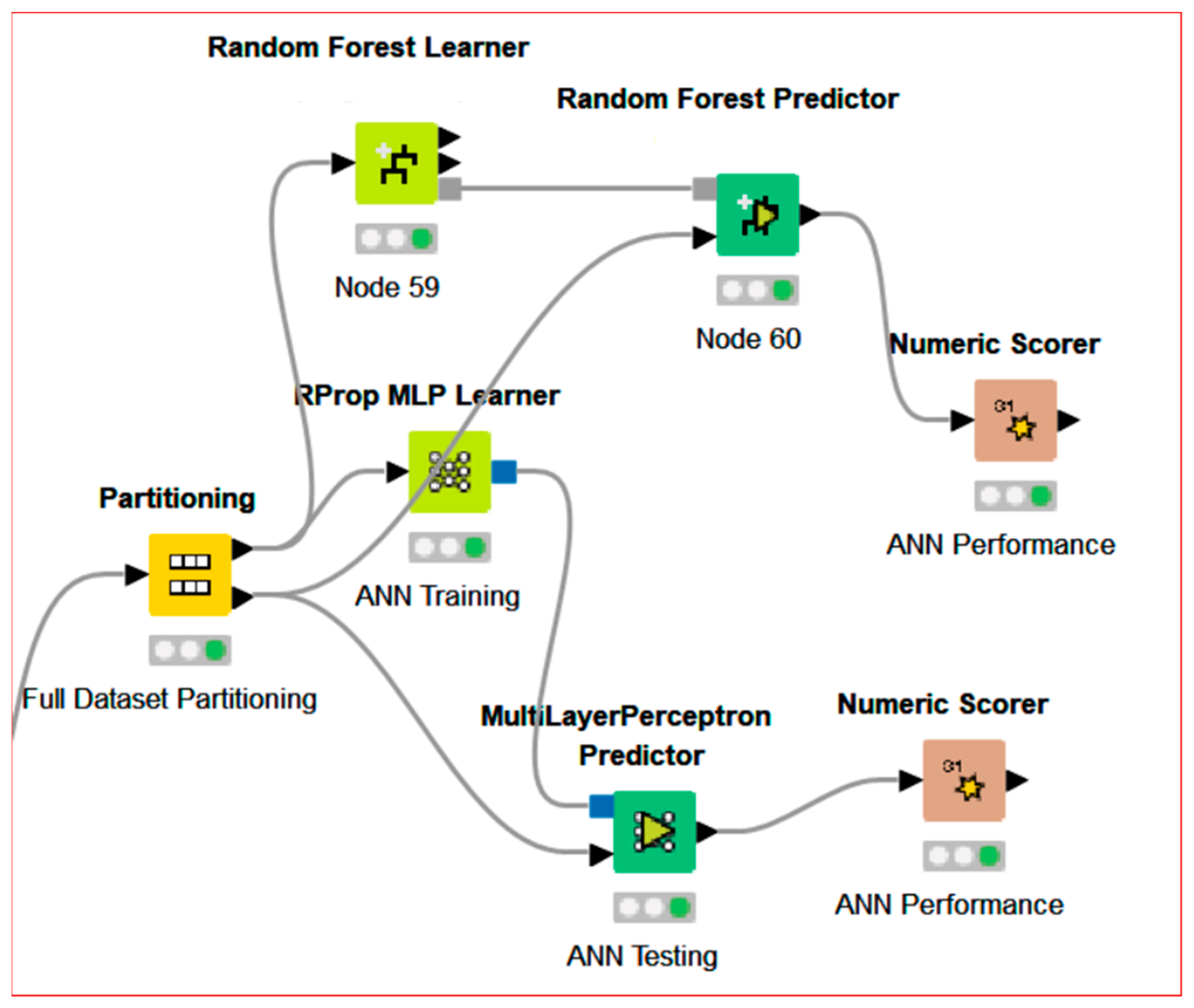
- ‘Rprop MLP Learner’: ANN training model based on Multilayer Perceptron (MLP) with adaptive RPROP algorithm [31];
- -
- ‘Multilayer Perceptron Predictor’: testing the ANN-MLP model;
- -
- ‘Column Appender’: appending different Vout signals of the simulations listed in Table 1;
- -
- ‘Numeric Scorer’: evaluating ANN performance (R2, mean absolute error, mean squared error, root mean squared error, mean signed difference, mean absolute percentage error, adjusted R2);
- -
- ‘Line Plot’: plotting of the prediction results;
- -
- ‘Excel Writer’: exporting prediction results in excel file format to be plotted by other dashboards or data visualization plugins.
3. Results
- KNIME simulation predicting the noisy predicted Vout signals.
3.1. LTspice Results
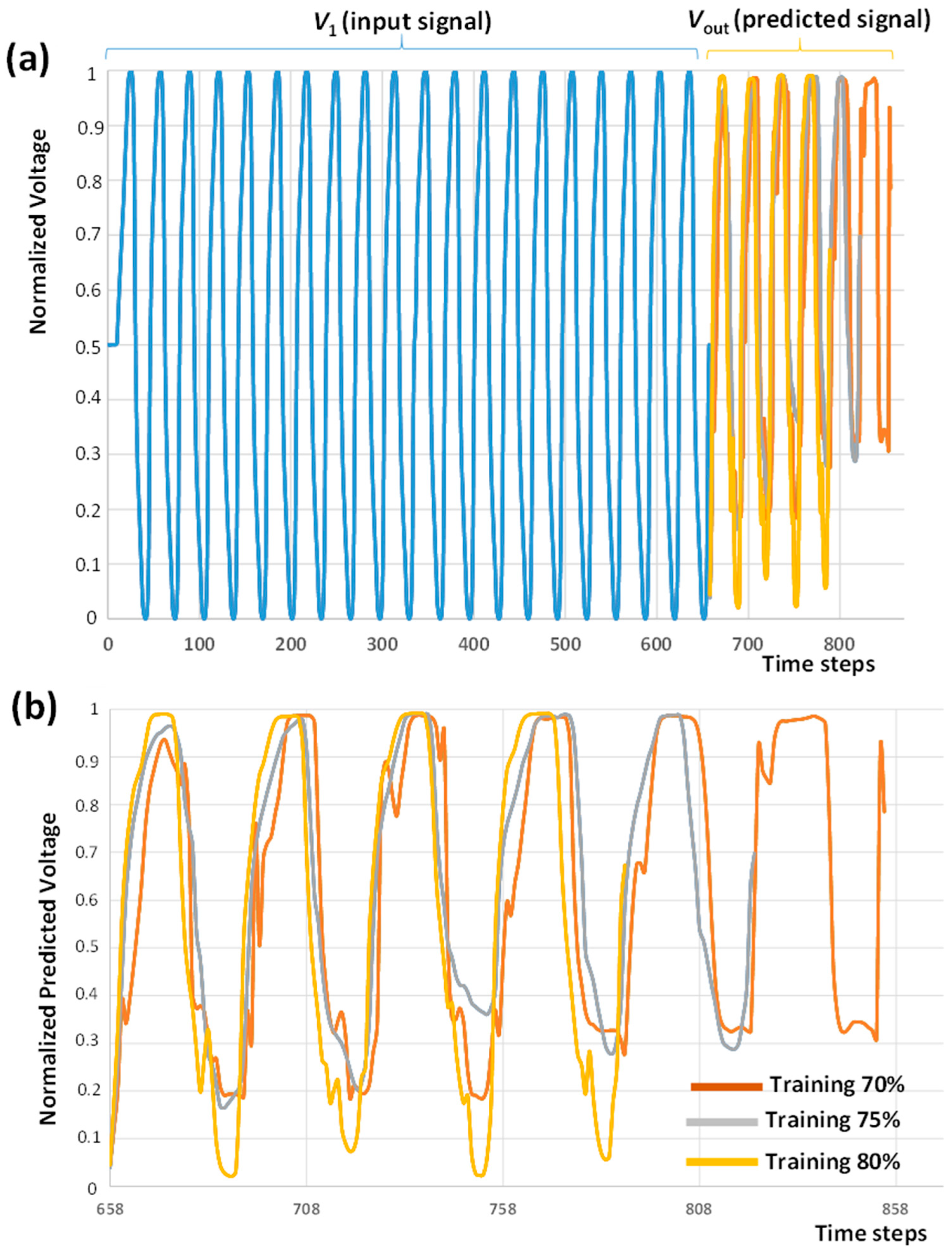
3.2. ANN Predicted Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
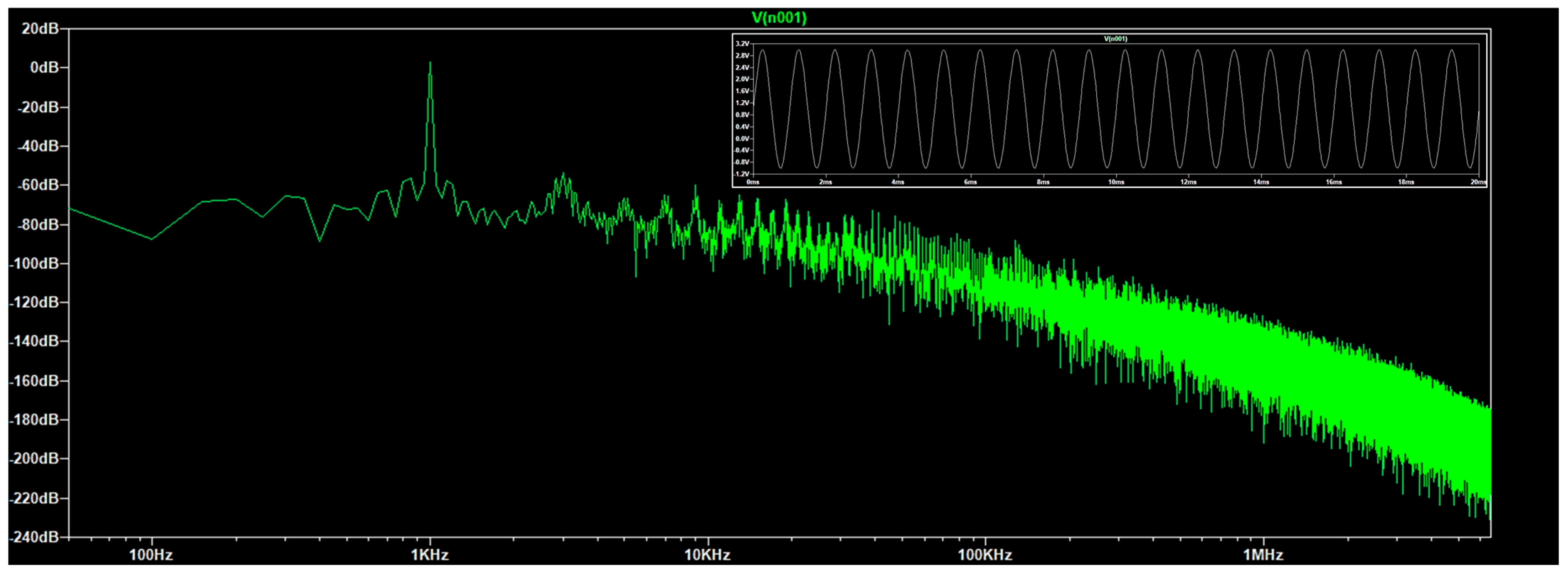
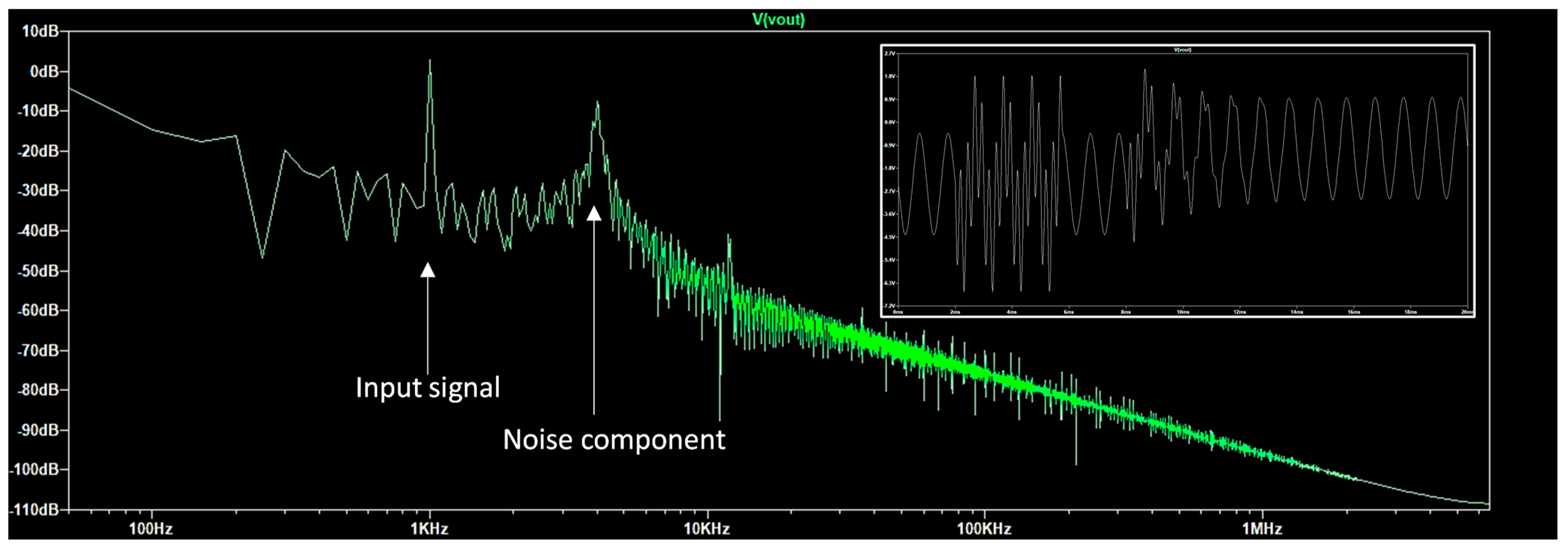
Appendix B. ANN Algorithm Architecture and Performance Aspects
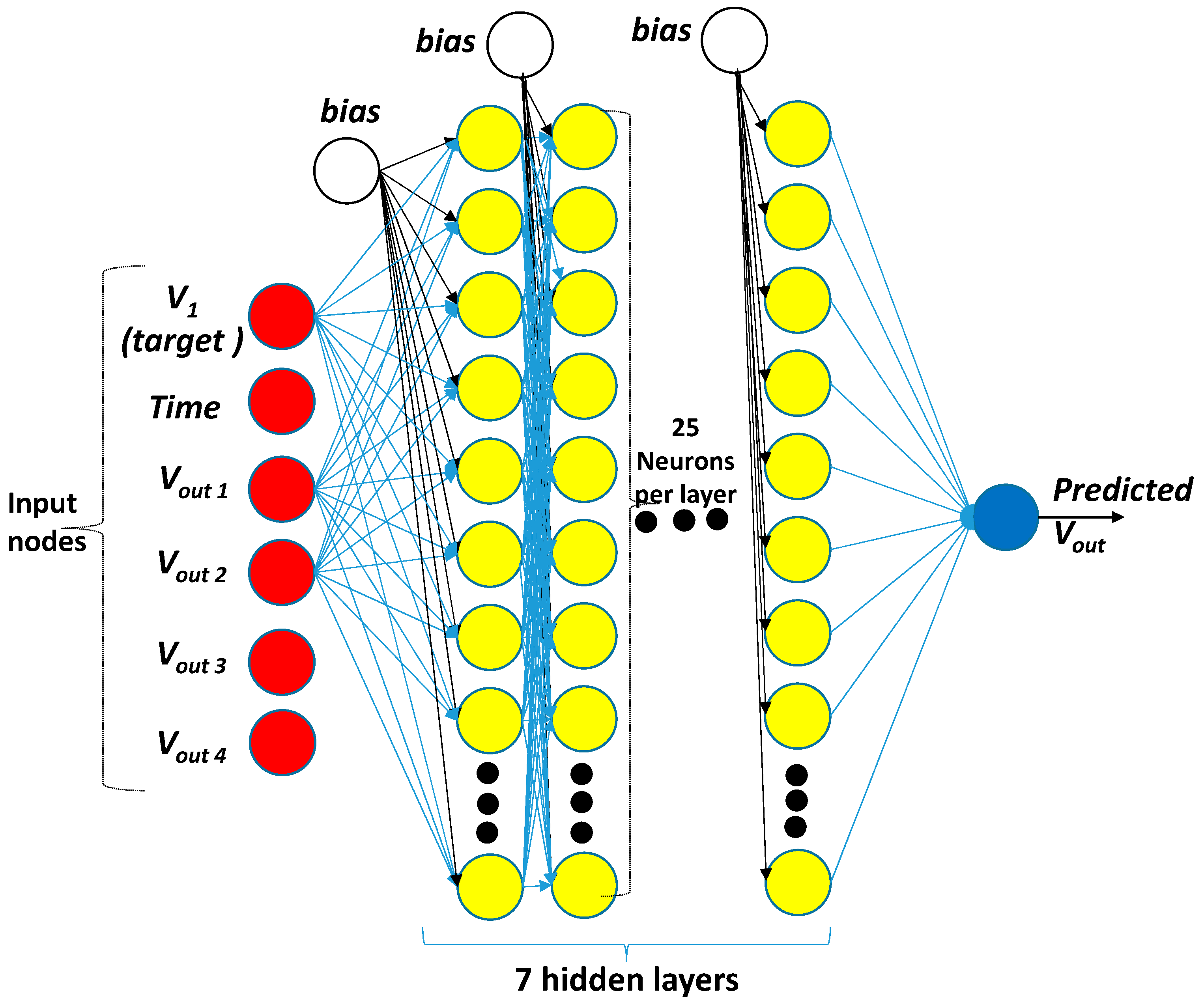
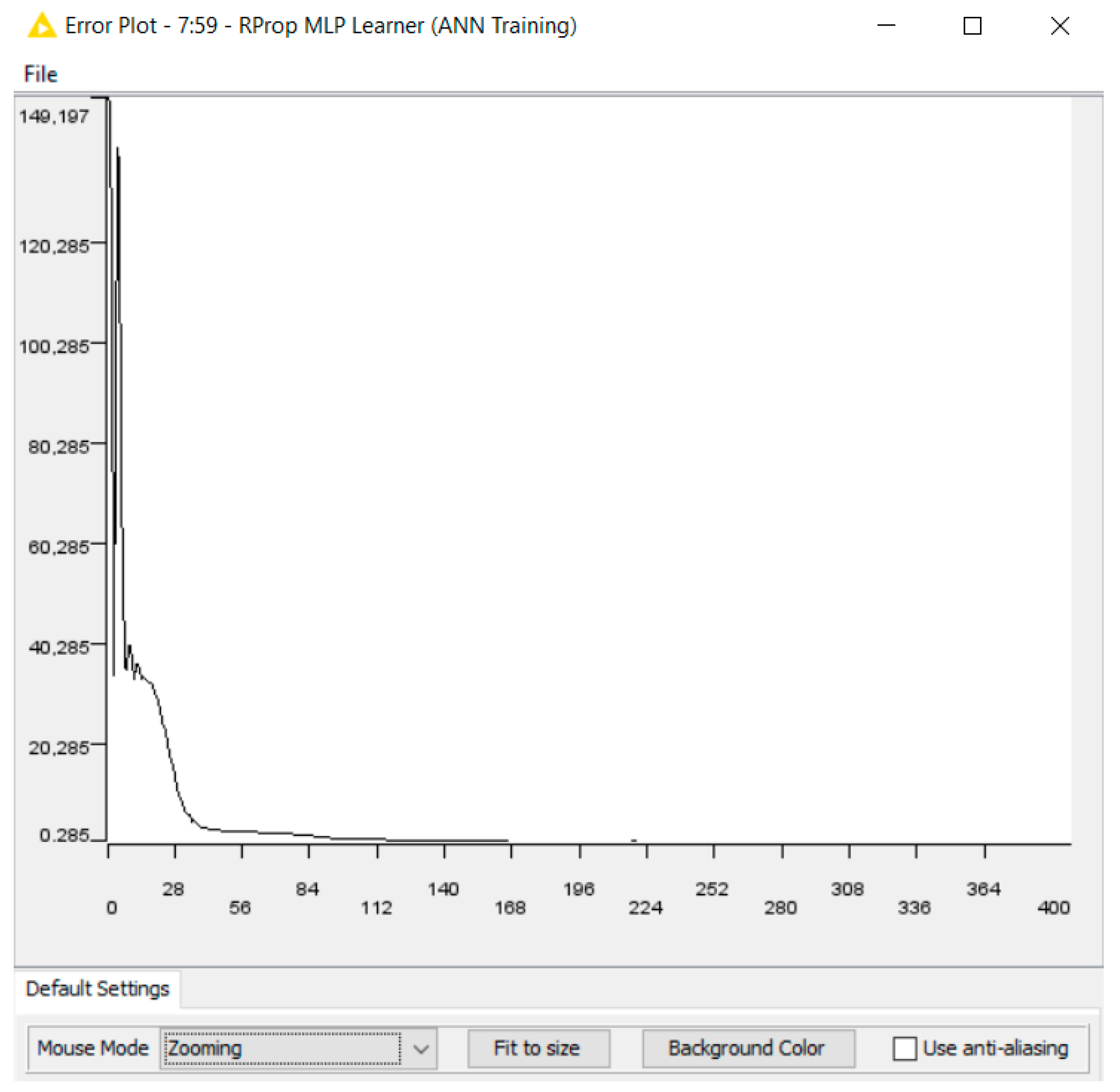
References
- Zhao, H.; Chen, Z.; Shu, X.; Shen, J.; Liu, Y.; Zhang, Y. Multi-Step Ahead Voltage Prediction and Voltage Fault Diagnosis Based on Gated Recurrent Unit Neural Network and Incremental Training. Energy 2023, 266, 126496. [Google Scholar] [CrossRef]
- Mokhtar, M.; Robu, V.; Flynn, D.; Higgins, C.; Whyte, J.; Loughran, C.; Fulton, F. Prediction of Voltage Distribution Using Deep Learning and Identified Key Smart Meter Locations. Energy AI 2021, 6, 100103. [Google Scholar] [CrossRef]
- Alsouda, Y.; Pllana, S.; Kurti, A. A Machine Learning Driven IoT Solution for Noise Classification in Smart Cities. arXiv 2018, arXiv:1809.00238. [Google Scholar]
- Alsouda, Y.; Pllana, S.; Kurti, A. IoT-Based Urban Noise Identification Using Machine Learning: Performance of SVM, KNN, Bagging, and Random Forest. In Proceedings of the International Conference on Omni-Layer Intelligent Systems, Crete, Greece, 5–7 May 2019; ACM: New York, NY, USA, 2019. [Google Scholar]
- Rahman, M.S.; Ghosh, T.; Aurna, N.F.; Kaiser, M.S.; Anannya, M.; Hosen, A.S.M.S. Machine Learning and Internet of Things in Industry 4.0: A Review. Measur. Sens. 2023, 28, 100822. [Google Scholar] [CrossRef]
- Lo Brano, V.; Ciulla, G.; Di Falco, M. Artificial Neural Networks to Predict the Power Output of a PV Panel. Int. J. Photoenergy 2014, 2014, 193083. [Google Scholar] [CrossRef]
- Shingare, S.S.; Khampariya, P.; Bakre, S.M. Efficient Fault Detection and Location in Extra High Voltage Networks: An Artificial Neural Network (ANN)-Based Approach. Int. J. Intell. Syst. Appl. Eng. 2023, 11, 1051–1060. [Google Scholar]
- Ogar, V.N.; Hussain, S.; Gamage, K.A.A. The Use of Artificial Neural Network for Low Latency of Fault Detection and Localisation in Transmission Line. Heliyon 2023, 9, e13376. [Google Scholar] [CrossRef]
- Rosa, J.P.S.; Guerra, D.J.D.; Horta, N.C.G.; Martins, R.M.F.; Lourenço, N.C.C. Using Artificial Neural Networks for Analog Integrated Circuit Design Automation; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Massaro, A. Electronics in Advanced Research Industries: Industry 4.0 to Industry 5.0 Advances; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Massaro, A. Intelligent Materials and Nanomaterials Improving Physical Properties and Control Oriented on Electronic Implementations. Electronics 2023, 12, 3772. [Google Scholar] [CrossRef]
- Arabi, A.; Ayad, M.; Bourouba, N.; Benziane, M.; Griche, I.; Ghoneim, S.S.M.; Ali, E.; Elsisi, M.; Ghaly, R.N.R. An Efficient Method for Faults Diagnosis in Analog Circuits Based on Machine Learning Classifiers. Alex. Eng. J. 2023, 77, 109–125. [Google Scholar] [CrossRef]
- Sobanski, P.; Kaminski, M. Application of Artificial Neural Networks for Transistor Open-circuit Fault Diagnosis in Three-phase Rectifiers. IET Power Electron. 2019, 12, 2189–2200. [Google Scholar] [CrossRef]
- Zhao, T.; Wei, J.; Lan, B.; Peng, Q.; Wan, J. A Unified Black-box Macro Model for Analog Circuit Based on Artificial Neural Network. Int. J. Circuit Theory Appl. 2023, 51, 4455–4464. [Google Scholar] [CrossRef]
- Yarikkaya, S.; Vardar, K. Neural Network Based Predictive Current Controllers for Three Phase Inverter. IEEE Access 2023, 11, 27155–27167. [Google Scholar] [CrossRef]
- Vargas, F.; Borba, D.; Benfica, J.D.; Syed, R.T. Artificial Neural Network Accelerator for Classification of In-Field Conducted Noise in Integrated Circuits’ DC Power Lines. In Proceedings of the 2023 IEEE 29th International Symposium on On-Line Testing and Robust System Design (IOLTS), Crete, Greece, 3–5 July 2023; pp. 1–6. [Google Scholar]
- Ferdous, H.; Jahan, S.; Tabassum, F.; Islam, M.I. The performance analysis of digital filters and ANN in DE-noising of speech and biomedical signal. Int. J. Image Graph. Signal Process. 2023, 1, 63–78. [Google Scholar] [CrossRef]
- Dieste-Velasco, M.I.; Diez-Mediavilla, M.; Alonso-Tristán, C. Regression and ANN Models for Electronic Circuit Design. Complexity 2018, 2018, 7379512. [Google Scholar] [CrossRef]
- Mina, R.; Jabbour, C.; Sakr, G.E. A Review of Machine Learning Techniques in Analog Integrated Circuit Design Automation. Electronics 2022, 11, 435. [Google Scholar] [CrossRef]
- Kouhalvandi, L.; Guerrieri, S.D. Modeling of HEMT Devices through Neural Networks: Headway for Future Remedies. In Proceedings of the 2023 10th International Conference on Electrical and Electronics Engineering (ICEEE), Istanbul, Turkiye, 8–10 May 2023; pp. 261–267. [Google Scholar]
- Gao, Z.; Yan, S.; Zhang, J.; Mascarenhas, M.; Nejabati, R.; Ji, Y.; Simeonidou, D. ANN-Based Multi-Channel QoT-Prediction over a 563.4-Km Field-Trial Testbed. J. Lightwave Technol. 2020, 38, 2646–2655. [Google Scholar] [CrossRef]
- Marinković, Z.; Crupi, G.; Caddemi, A.; Marković, V.; Schreurs, D.M.M.-P. A Review on the Artificial Neural Network Applications for Small-signal Modeling of Microwave FETs. Int. J. Numer. Model. 2020, 33, e2668. [Google Scholar] [CrossRef]
- Marinković, Z.; Pronić-Rančić, O.; Marković, V. Small-Signal and Noise Modeling of Class of HEMTs Using Knowledge-Based Artificial Neural Networks. Int. J. RF Microw. Comput-Aid. Eng. 2013, 23, 34–39. [Google Scholar] [CrossRef]
- Zur, R.M.; Jiang, Y.; Pesce, L.L.; Drukker, K. Noise Injection for Training Artificial Neural Networks: A Comparison with Weight Decay and Early Stopping. Med. Phys. 2009, 36, 4810–4818. [Google Scholar] [CrossRef]
- Lee, C.-I.; Lin, Y.-T.; Lin, W.-C. Improved Artificial Neural Network RF Noise Model for MOSFETs Operating in Avalanche Region. Electron. Lett. 2016, 52, 232–234. [Google Scholar] [CrossRef]
- Amaral, A.; Gusmão, A.; Vieira, R.; Martins, R.; Horta, N.; Lourenço, N. An ANN-Based Approach to the Modelling and Simulation of Analogue Circuits. In Proceedings of the 2023 19th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Funchal, Portugal, 3–5 July 2023; pp. 1–4. [Google Scholar]
- Litovski, V. 5.4 Low-Noise Amplifiers. In Lecture Notes in Electrical Engineering; Springer Nature: Singapore, 2024; pp. 91–141. [Google Scholar]
- Cornell University. An Active Noise Canceler to Eliminate the 60 Hz Noise Found in Electrical Signals Due to AC Power-Line Contamination. Available online: https://people.ece.cornell.edu/land/courses/ece4760/FinalProjects/s2008/rmo25_kdw24/rmo25_kdw24/index.html#references (accessed on 13 April 2024).
- LTspice. Available online: https://www.analog.com/en/resources/design-tools-and-calculators/ltspice-simulator.html (accessed on 13 April 2024).
- KNIME. Available online: https://www.knime.com/ (accessed on 13 April 2024).
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm. In Proceedings of the IEEE International Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 586–591. [Google Scholar]
- Ding, J.; Peres, Y.; Ranade, G.; Zhai, A. When Multiplicative Noise Stymies Control. Ann. Appl. Probab. 2019, 29, 1963–1992. [Google Scholar] [CrossRef]
- Monjur, M.M.R.; Heacock, J.; Calzadillas, J.; Mahmud, M.D.S.; Roth, J.; Mankodiya, K.; Sazonov, E.; Yu, Q. Hardware Security in Sensor and Its Networks. Front. Sens. 2022, 3, 850056. [Google Scholar] [CrossRef]
- Monjur, M.R.; Sunkavilli, S.; Yu, Q. ADobf: Obfuscated Detection Method against Analog Trojans on I2C Master-Slave Interface. In Proceedings of the 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 9–12 August 2020; pp. 1064–1067. [Google Scholar]
- Monjur, M.; Calzadillas, J.; Yu, Q. Hardware Security Risks and Threat Analyses in Advanced Manufacturing Industry. ACM Trans. Des. Automat. Electron. Syst. 2023, 28, 1–22. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, C.; Li, Z.; Ding, K.; Wang, C. Knowledge-Driven Digital Twin Manufacturing Cell towards Intelligent Manufacturing. Int. J. Prod. Res. 2020, 58, 1034–1051. [Google Scholar] [CrossRef]
- Abdoune, F.; Cardin, O.; Nouiri, M.; Castagna, P. Real-Time Field Synchronization Mechanism for Digital Twin Manufacturing Systems. IFAC 2023, 56, 5649–5654. [Google Scholar] [CrossRef]
- Soori, M.; Arezoo, B.; Dastres, R. Digital Twin for Smart Manufacturing, A Review. Sustain. Manuf. Serv. Econ. 2023, 2, 100017. [Google Scholar] [CrossRef]
- Massaro, A. Advanced Electronic and Optoelectronic Sensors, Applications, Modelling and Industry 5.0 Perspectives. Appl. Sci. 2023, 13, 4582. [Google Scholar] [CrossRef]
- Subramaniam, S.R.; Georgakis, A. A Simple Filter Circuit for Denoising Biomechanical Impact Signals. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 6938–6941. [Google Scholar]
- Yu, F.-M.; Lee, K.-C.; Jwo, K.-W.; Chang, R.-S.; Lin, J.-Y. Low Distortion of Noise Filter Realization with 6.34 V/Μs Fast Slew Rate and 120 mVp-p Output Noise Signal. Sensors 2021, 21, 1008. [Google Scholar] [CrossRef]
- Lyu, P.; Zhang, H.; Yu, W.; Liu, C. A Novel Model-Independent Data Augmentation Method for Fault Diagnosis in Smart Manufacturing. Procedia CIRP 2022, 107, 949–954. [Google Scholar] [CrossRef]
- Massaro, A. Multi-Level Decision Support System in Production and Safety Management. Knowledge 2022, 2, 682–701. [Google Scholar] [CrossRef]
- Lovisolo, L.; Tcheou, M.P.; da Silva, E.A.B.; Rodrigues, M.A.M.; Diniz, P.S.R. Modeling of Electric Disturbance Signals Using Damped Sinusoids via Atomic Decompositions and Its Applications. EURASIP J. Adv. Signal Process. 2007, 029507. [Google Scholar] [CrossRef]
- Cordero, R.; Estrabis, T.; Gentil, G.; Caramalac, M.; Suemitsu, W.; Onofre, J.; Brito, M.; dos Santos, J. Tracking and Rejection of Biased Sinusoidal Signals Using Generalized Predictive Controller. Energies 2022, 15, 5664. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Chen, C.-I.; Fu, W.-C.; Lee, Y.-D.; Cheng, C.-C.; Chen, Y.-F. A Hybrid Approach for Low-Voltage AC Series Arc Fault Detection. Energies 2023, 16, 1256. [Google Scholar] [CrossRef]
- Monedero, I.; Leon, C.; Ropero, J.; Garcia, A.; Elena, J.M.; Montano, J.C. Classification of Electrical Disturbances in Real Time Using Neural Networks. IEEE Trans. Power Deliv. 2007, 22, 1288–1296. [Google Scholar] [CrossRef]




| Simulation | V2 (Noise 1 of Figure 1b) | V3 (Noise 2 of Figure 1b) |
|---|---|---|
| Simulation 1 | Noise (a) | Noise (b) |
| Simulation 2 | Noise (c) | Noise (d) |
| Simulation 3 | Noise (e) | Noise (f) |
| Simulation 4 | Noise (g) | Noise (h) |
| Parameter | ANN-MLP | RF |
|---|---|---|
| R2 | 0.96 | 0.96 |
| Mean Absolute Error (MAE) | 0.02 | 0.031 |
| Mean Squared Error (MSE) | 0.001 | 0.002 |
| Root Mean Squared Error (RMSE) | 0.034 | 0.039 |
| Mean Signed Difference (MSD) | 0.021 | 0.014 |
| Mean Absolute Percentage Error | 0.054 | 0.062 |
| ANN Prediction Aspects | Advantages | Disadvantages |
|---|---|---|
| ANN training model | Possibility to construct the training model by considering the historical output data of the circuits without knowing the noisy profile (black box behavior). | A good training requires a dataset including all the potential noises which could influence the output signal (a long time is required to store information about the impact of probable noises). |
| Predictive Maintenance | The prediction of a strong noisy signal trend could enable predictive maintenance processes avoiding machine breakage. | Difficulty to distinguish dangerous noisy signals to enable the predictive maintenance procedures. |
| Machine tuning | The signal trend prediction allows for the automation of the input signal setting, thus anticipating corrective actions. A feedback system controlled by an AI engine could optimize the parameter setting generating a new input signal correcting control errors [10]. | A correct machine tuning is performed when probable noises are considered. New typologies of disturbs or noises not included as historical Vout could provide wrong predictions and, consequently, wrong tuning or parameter setting. |
| Multiplicative noises | The ANN prediction is adaptable also when unwanted random signals are multiplied into machine control inputs [32]. | The error prediction increases with the complexity of noises as for multiplicative noises. |
| Intentional manumission | The prediction of possible noisy trend is important also to find possible hardware analog Trojans [33,34,35]. | Difficulty to distinguish the hardware attacks to noises and disturbs intrinsic of machinery. |
| Digital Twin (DT) | The proposed approach is suitable to developing DT models [36,37,38] simulating the behavior of whole production lines in manufacturing industries. | DT models could be approximate and not match with the real behavior of the production processes. |
| Technological Limits | Technology Description | Technological Perspectives |
|---|---|---|
| Real time prediction | The time delay of the data processing defines a quasi-real data processing. Strong delays are possible for big data processing. | Some advanced technologies such as edge computing or quantum computing [39] could be adopted for a real time data processing computing massive datasets. |
| Knowledge of the noise spectra | Generally, the noises knowledge is missing: both time domain profile and frequency spectrum are unknown. Some useful information is possible to obtain for noises characterized by a carrier which is visible in the whole spectrum of the output signal (see Appendix A). | Machine learning supervised algorithms could be applied to also predict the behavior of the output signal in the frequency domain by applying denoising filtering approaches [40,41]. |
| Dataset availability | The data availability are fundamental for data processing of machine learning supervised algorithms requiring a large number of cleaned data to optimize the training model. | Some methodologies such as augmented data [42] could be adopted to increase the dataset. |
| Automated Controlling Systems (ACS) | The big data processing requires a high computational cost generating delays or interrupts before to execute the decision-making automatic systems less effective. | A specific calculus engine could be used to increase the efficiency of the automated controlling systems. |
| Testing dataset | The testing dataset (last values of Vout signals) could be not influenced by noises and, consecutively, the prediction could be partially wrong. | Other techniques for the extraction of the testing model (such as linear sampling or random sampling) could include with a greater probability the noisy behavior. |
| Training dataset | The training dataset should include a variety of probable noises. | The historical dataset could be selected by eliminating redundancies and longtime of regular signal (pre-filtering approach of the training dataset). |
| Classification of the single noise | When many noises influence the output signal, it is very difficult to classify each noise signal. | Due to the difficulty to classify and filter the single noise, it is possible in advance to tune or adjust the profile of the whole signal output. |
| Function of the Model (Sequential Steps) | Use Criteria | Possible Corrective Actions |
|---|---|---|
| Definition of the time intervals to detect and store data outputs. | Cleaning of the dataset (filtering of wrong data or missing values). |
| Definition of the accuracy of the sampling (sampling time step definition). | Decrease in the sampling time to store also highly variable noises. |
| Frequency analysis matching with the time domain one to find possible noises characterized by carriers: the trend of the output predicted signals are compared with the FFT spectra to extract information about possible carries thus supporting noise classification. | Application of narrow filters to suppress undesired carriers. |
| Creation of the ANN training model by considering different voltage output. | Use of augmented data to increase the efficiency of the training model. |
| Selection of the testing dataset possibly including the noise effects. | Change in the testing dataset dimension to include possible noises. |
| Analysis and interpretation of the predicted output signals. | Possible corrective actions are defined by considering priorities and multi-level Decision Support Systems (DSSs) [43]. |
| Tuning of the input signals matching with ANN data prediction interpretation by acting on the input signal (regulation of the input signal or adding of further control signal). | Use of denoising filters according with the predicted output trend and with the FFT responses (suppression of undesired carriers). Modification of the input signal combining other input signals able to correct the minimum and the maximum amplitude of the output signal. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massaro, A. ANNs Predicting Noisy Signals in Electronic Circuits: A Model Predicting the Signal Trend in Amplification Systems. AI 2024, 5, 533-549. https://doi.org/10.3390/ai5020027
Massaro A. ANNs Predicting Noisy Signals in Electronic Circuits: A Model Predicting the Signal Trend in Amplification Systems. AI. 2024; 5(2):533-549. https://doi.org/10.3390/ai5020027
Chicago/Turabian StyleMassaro, Alessandro. 2024. "ANNs Predicting Noisy Signals in Electronic Circuits: A Model Predicting the Signal Trend in Amplification Systems" AI 5, no. 2: 533-549. https://doi.org/10.3390/ai5020027
APA StyleMassaro, A. (2024). ANNs Predicting Noisy Signals in Electronic Circuits: A Model Predicting the Signal Trend in Amplification Systems. AI, 5(2), 533-549. https://doi.org/10.3390/ai5020027






