Interactive Agent-Based Simulation for Experimentation: A Case Study with Cooperative Game Theory

Abstract

Incorporating human behavior is a current challenge for agent-based modeling and simulation (ABMS). Human behavior includes many different aspects depending on the scenario considered. The scenario context of this paper is strategic coalition formation, which is traditionally modeled using cooperative game theory, but we use ABMS instead; as such, it needs to be validated. One approach to validation is to compare the recorded behavior of humans to what was observed in our simulation. We suggest that using an interactive simulation is a good approach to collecting the necessary human behavior data because the humans would be playing in precisely the same context as the computerized agents. However, such a validation approach may be suspectable to extraneous effects. In this paper, we conducted a correlation research experiment that included an investigation into whether game theory experience, an extraneous variable, affects human behavior in our interactive simulation; our results indicate that it did not make a significant difference. However, in only 42 percent of the trials did the human participants’ behavior result in an outcome predicted by the underlying theory used in our model, i.e., cooperative game theory. This paper also provides a detailed case study for creating an interactive simulation for experimentation.

1. Introduction

The nature of humans as autonomous interacting agents who change their behavior by adapting and learning in their environment makes their study difficult. A human system, resulting from human behavior, is a complex adaptive system (CAS) [1,2]. As such, studying a CAS needs methods and techniques which is appropriate for solving CAS problems. The method used will depend on the human behavior being considered. One form of human behavior is human decision-making. In this paper, we are interested in studying human decisions concerning strategic coalition formation. Different modeling methods exist to study this form of human behavior in a CAS context, for example, agent-based modeling [3] and game theory [4].

Strategic coalitions form when there exist benefits from doing so to the individuals involved. Cooperative game theory (CGT) is the standard method used to study strategic coalitional formation [5]. An alternative approach to modeling multiple interacting humans is ABMS [6]. However, it is not necessarily clear how human behavior should be incorporated in ABMS. An et al. [7] have advocated that modeling human decisions is an important challenge for agent-based modeling and simulation (ABMS). Additionally, Cheng et al. [8] regard modeling human behavior as a current challenge for modeling and simulation (M&S). This paper represents an attempt to aid in solving these challenges.

ABMS models the micro-level behavior of heterogenous agents interacting in an environment to gain insights into emergent macro-level outcomes [2,9]. Since it involves multiple interacting decision-making agents, there is a potential for ABMS to be used in the context of strategic coalition formation; the ABMSCORE algorithm was developed for this purpose [3,10]. The interactive agent-based simulation presented in this paper uses the ABMSCORE algorithm, as well as replacing one of the computerized agents with a real human, in order to investigate the macro-level outcome of the simulation.

To study human strategic decisions, we use the interactive agent-based simulation model of strategic coalition formation that incorporates cooperative game theory and actual human subjects in one modeling framework. As we mentioned, our interactive simulation replaces a computerized agent with a human player; the reason for doing this is that authors wished to compare the outcomes generated by the ABMSCORE algorithm to actual human behavior. Previous research has shown that the ABMSCORE algorithm compares favorably to the game-theoretical results [10], but there was a desire to compare its outcomes to those generated by actual human behavior [11]. In the research presented in this paper, we have an interest in gaining insight into the macro-level outcome of the interactive simulation and what potential extraneous variables may impact those outcomes. This paper also provides details, using the Overview, Design concepts, Details (ODD) protocol [12], of the interactive simulation used in the research.

The scenario used in our interactive simulation experiment is a type of game called the glove game (or shoe game). It has previously been used in human subject experiments [13,14]. Glove games, a type of cooperative game-theoretic game, are a simple form of a market economy involving non-transferrable utility [15,16]. In a glove game, each player is endowed with a different number of right-hand and left-hand gloves and tries to form coalitions of players in order to increase their payoff; only pairs of gloves have value in our scenario, and both left-hand and right-hand gloves are generic so that any left-hand glove can be matched with any right-hand glove. The details of the glove game will be provided in the background section.

Glove games were coded into the ABMSCORE algorithm and adapted to create an interactive simulation model for use during our trials. During each trial, the human subject would play in multiple different glove games with up to seven players. The human player takes the role of one of the players, with the remaining being controlled by computerized agents (using the ABMSCORE algorithm). In other words, in each simulation, there is only one human, and all other players are computerized agents. Each round of the game involves the players proposing new coalitions to the other players. The outcome of a given game is a coalition structure. Coalition structure is the partition of players into disjoint coalitions [17].

In our interactive simulation, the human is playing the exact same role as one of the computerized agents. As both human and computerized agents are playing the game in the same (computerized) context, we hope to limit extraneous variable effects when comparing the macro-level outcomes. However, it is possible that using an interactive simulation, in itself, generates extraneous variables that affect the macro-level outcomes both positively and negatively. In this paper, we consider several factors that could affect the accuracy of modeling human behavior within the ABMSCORE modeling approach.

An obvious requirement in modeling human decisions is that the computerized agents’ decisions are consistent with that of the humans they are representing. First, before studying the macro-level behavior, we need to be sure that the computerized agents in the model behave consistently as a human subject would in the proposed simulation framework at the micro-level. In other words, do the computerized agents represent human subjects accurately so that the interpretation of the final simulation outcome is credible. In our previous research, we have shown that the ABMSCORE algorithm conforms to human decisions in the context of strategic group formation; in Collins et al. [18], we checked the consistency of behavior at the micro-level: whether computerized agents make the same decisions as humans to join a coalition or not and make the same coalition suggestion or not. The results showed that our algorithm could replicate human behavior at the micro-level. However, participants who had experience in game theory tended to be more consistent. While our ABMSCORE algorithm can replicate human decisions at the micro-level, we are interested to see whether our algorithm was consistent at the macro-level. The macro-level outcome, which is considered in this research, is the coalition structure. As such, the final coalition in which a human is a member at the end of the game is of interest to us. This coalition is compared to the ideal coalition, as determined by cooperative game theory, which we call the core coalition. Core coalitions are defined and discussed later in the paper. In this research, we use the same data set as we used in the Collins et al. [18].

Explicitly, we want to evaluate the human’s final coalition to see if it is a core coalition (macro-level). As with our previous study, we also expect that having/not having game theory experience could affect the human’s final coalition. As such, game theory experience would be considered an extraneous variable.

Extraneous variables are variables that affect the outcomes of an experiment that were not explicitly accounted for in a given experimental design. For example, in a team situation, unaccounted-for social dynamics might affect an individual’s decision-making. It is not clear what extraneous variables might affect an individual’s decision-making in the context of an interactive simulation, but we attempt to discover some. This research hopes to help future researchers in modeling human strategic decisions, by ABMS, in a more effective and robust manner.

The next section gives some background into the use of humans in experiments involving game theory or agent-based modeling to investigate human behavior. A detailed description of our interactive agent-based model is provided in the third section using the ODD protocol. This is followed by a discussion on our methodology. The final sections discuss the implications of our results, identify limitations, and reach conclusions.

2. Background

Since our experiment uses an interactive hybrid simulation of ABMS and cooperative game theory, a brief overview of existing research that uses these modeling approaches in human subject experimentation is given below. Our focus is on research into human behavior.

2.1. Cooperative Game Theory

Traditionally, strategic group formation is modeled using cooperative game theory. Cooperative game theory (1) focuses on games involving more than two players, and (2) focuses on coalition formation and how the payoffs will be distributed amongst the coalition members [19]. Many solution mechanisms have been proposed in cooperative game theory; the main two are the core [20] and the Shapley value [21]. The Shapley value requires the underlying game to be super-additive; to avoid this limitation, we use core. In its essence, the core of a cooperative game represents the coalition structure of the players, where no subgroup of players has an incentive to form a new coalition. A coalition structure is a covering set of disjoint coalitions over the players, i.e., each player belongs to one, and only one, coalition. If that coalition only contains the player, it is called a singleton coalition. If a coalition contains all players, it is called the grand coalition. A particular game might have multiple coalition structures in its core, one or none. To give a deeper understanding of the core concept, we will give some examples when we introduce the glove game.

There exists a small number of papers that experimentally studied human behavior in strategic group formation in the context of cooperative game theory and the core. In this limited number of papers, the application of human subject experiments is also scarce. In all cooperative game theory papers that we found, which used human subject experimentation, the purpose was to capture different factors that can affect coalition formation outcome in different contexts. For instance, Murnighan and Roth [13] conducted an experiment to understand the effect of communication or information availability between players in shoe games; Bolton et al. [22] considered the role of different types of communication configuration; Murnighan and Roth [14] considered the effect of communication ability and group size in the context of shoe games; Neslin and Greenhalgh [23] looked at the impact of power, conflict, and influence in negotiation between players; Montero et al. [24] evaluated the effects of power in the voting environment; Beimborn [25] looked at financial information transparency between firms, and Berl et al. Berl, McKelvey [26] examined core validity with regard to human plays. None of these papers used an interactive simulation approach.

2.2. Agent-Based Modeling

Agent-based modeling is a method focused on creating models of interacting autonomous agents in a virtual environment [6]. An agent-based simulation is the dynamic implementation of an agent-based model. Collectively, these parts are known as Agent-Based Modeling and Simulation. Modelers can give instructions to hundreds or thousands of “agents”, all operating autonomously within an agent-based simulation [27]; as such, ABMS is a bottom-up modeling approach [9].

A vital aspect of an agent-based model is that agents are not aggregated but autonomous, adaptive, and can be heterogeneous [28]. ABMS is, thus, appropriate to model situations that are analogous to these aspects. The most obvious example of autonomous, adaptive, and heterogeneous agents are humans and, as such, it has been repeatedly advocated that ABMS is an appropriate method for modeling human systems in a variety of different fields; such as economics [29], social sciences [6], or engineering [30].

ABMS provides a useful insight into a system by observing the macro-level emergent behavior that results from (micro-level) agent interactions. Beyond its inability to model human behavior [8], there are other concerns. For example, it focuses on individualist behavior as opposed to external behavior generated by a group [3]; to incorporate this external behavior, a modeler could aggregate the agents into groups, but aggregating agents into group decision-makers would effectively wipe out individual agents’ interactions and, potentially, the emergent behavior they generate. Collins and Frydenlund [3] proposed a solution to this problem by introducing strategic group formation in ABMS with the incorporation of game theory techniques, which allows agents to decide which groups they will join (adapt), thus retaining their individualism. This approach is part of the hybrid modeling method that we use in the experiment.

Within agent-based modeling, human subject experimentation has been used to understand human behavior in multiple contexts like emergency evacuation [31], resource allocation system [32], commodity market [33], knowledge management [34], etc. In most cases, researchers aimed to study two phenomena: (1) the effect of human behaviors for development or change in the system of study and (2) the effect of the system of study circumstances on human behavior. ABMS and human subject experiments were used in tandem to compensate for each other’s weakness in modeling human behavior. Based on the experiment presented in this paper, we focused on papers that use ABMS to support an experiment.

ABMS can provide results that support experimental findings and/or play a complementary role in situations where human subject experimentation does not work. For instance, Zhao et al. [35] studied the strategic behavior of agents in a resource allocation system to reach a balance of resource allocation and reduce instability; a computer-aided human subject experiment was run with both humans as normal agents and artificial agents who were mimicking human participants behavior; the human subject experiment results and underlying mechanism was confirmed with the application of ABMs. Liang et al. [36] studied the principle of increasing entropy in an isolated social system using a human subject experiment, but also ABMS was used to go beyond limitations in the human subject experiment to expand the findings. Song et al. [37] studied risk-return relation for investors in a market under market efficiency and closeness; first, they conducted multiple computer-aided human subject experiments to understand human thoughts about the relationship between risk and return, then they created an ABMS of the human subject experiment scenario to compare results with the human subject experiment and explore the underlying mechanism in the human subject experiment. Liang et al. [32] conducted a computer-aided human subject experiment to study the role of contrarian behavior in a resource allocation system; due to limitations with the experimental approach, they decided to use an agent-based model based on the resource allocation system to make the result of study more robust.

In the research studies discussed, human subject experimentation and ABMS were mainly conducted separately. The research methodologies were improved by incorporating both human subject experimentation and ABMS. The aim of these combined methodologies was to address the weaknesses of each method individually and overcome these weaknesses with the other method’s strengths. Thus, there exists a benefit of applying ABMS and human subject experimentation simultaneously to address research questions because the two approaches both help support and validate each other’s findings. Hence, the use of an interactive simulation in our study.

2.3. Game Theory and Agent-Based Modeling

Hybrid simulation modeling has gained popularity in recent years [38] due to its ability to overcome the weakness of one methodology by augmenting it with another. Hybrid simulations are simulations that have modules built using two or more different modeling paradigms, usually using discrete event simulation (DES), systems dynamics, and agent-based modeling [38]. The hybrid modeling approach used in our experiment enriches agent-based modeling by incorporating game theory concepts within it, specifically, a heuristic algorithm for strategic group formation. The hybrid model algorithm used in this paper was first developed by Collins and Frydenlund [3] and improved upon by Vernon-Bido and Collins [10]. This algorithm is known as the ABMSCORE algorithm.

There are few enriched hybrid simulations using game theory within the extant literature. Beyond our approach, Hill et al. [39] create a hybrid simulation model using a search game combined with agent-based modeling to simulate the searching for U-boats in the Second World War. Bonnevay et al. [40] used agent-based modeling to simulate cooperative game theory, whereas our hybrid approach incorporates cooperative game theory into agent-based modeling. Finally, Janovsky and DeLoach [41] created a heuristic for finding the core in a multi-agent environment; this has similarities to our hybrid approach but is focused purely on algorithm development as opposed to its application. Future practical application of the ABMSCORE algorithm is the main driver behind the research presented in this paper. Other researchers have used Monte Carlo simulation to validate their cooperative game theory results; see [42,43,44] for applications to swarms and dynamic networks.

Our focus on strategic group formation, as the phenomenon of our modeling interest, is driven by our belief that ABMS needs to account for coalition formation if it is going to be used to model large numbers of humans interacting. The ABMSCORE algorithm’s applicability is demonstrated through examples of modeling farming cooperatives [45] and group formation in minority games [46]. The experiment presented in this paper is the first time that a hybrid model has been used in a human subject experiment.

Game Theory and Agent-Based Modeling in Human Subject Experimentation

We conducted a literature review of papers that use human subject experimentation, game theory, and ABMS within one methodology framework. In most papers, the research was to study human behavior. In all cases, human subject experiments were conducted based on the game theory framework to (1) generate results and rules which can be used as an input to an agent-based model or (2) using the human subject experiment’s output to help validate the results from the agent-based simulation. However, it is questionable whether many of these studies actually used ABMS since their models did not contain key tenets of it: autonomy, heterogeneity, and the ability to adapt [28]. We focus the remainder of our discussion on papers that, we believe, implement ABMS as opposed to just computational game theory models; we accept that there is some subjective judgment in this process because there is no agreed-upon definition of ABMS, nor is one likely to be agreed upon in the near future [47].

In the situation where human subject experiments were conducted based on the game theory framework to generate results and rules which can be used as an input to an agent-based model, Takko [48] conducted a human subject experiment using a cooperative game to study risk perception and rationality behind human decisions, The results from the experiment were used as input rules to construct an agent-based model which can replicate human behavior. Coen [49] conducted an experiment based on the social dilemma to define rules representing how people make decisions in a competitive environment. He then incorporated the rules generated from the human subject experiment into an ABMS to discover what decisions were effective. In an incentive situation, Dal Forno and Merlone [50] used the social dilemma to run a human subject experiment to capture human behavior, where grounded theory was used to reveal the rules from the experiment; these rules were then used as an input to the ABMS to check the accuracy of results from grounded theory. Pansini et al. [51] did a human subject experiment based on the prisoners’ dilemma to study how mutual profitability can be gained in a society with uneven distribution of wealth between citizens while the ABMS was used to validate the result.

There exist situations that use the human subject experiment as a validation tool to the results outputted from ABMS. For instance, Li, Yang [52] studied cooperation and competition behavior at the same time by incorporating Janus game rules into an agent-based simulation; then, to see how the model works, a human subject experiment was conducted. In the context of market exchange, Sohn [53] studied human decisions by considering the coordination game model in ABMS; then, a human subject experiment was conducted to validate the results. Bhattacharya, Takko [54] Conducted a human experiment through online game alongside with an ABMS to get insight into the rationality behind human decision-making in the context of group formation; by comparing ABMS output to the human behavior they understood that the agent-based model act more efficiently toward human behavior under special circumstances.

In this section, we have discussed research that used agent-based models and/or human subject experiments with the application of game theory interchangeably to address research problems. Since our hybrid interactive simulation was used within our experiment, as opposed to separately validate it, it is unclear whether our experiment belongs to either type of investigation discussed above. None of the papers discussed used a hybrid modeling approach.

2.4. Glove Game

The glove game is a simple market economy game with two commodities: left-hand gloves and right-hand gloves. This game was chosen because it is a game that involves coalition formation that is easy for the experiment participants to understand or, at least, less complicated than other cooperative games. An easily understood game was essential as the participants needed to learn the game in a relatively short span of time. The glove game involves players forming coalitions with other players to form pairs of gloves, which are sold for a profit. Each player starts with a different initial endowment of left-hand gloves and right-hand gloves. A coalition is a group of players that pools their gloves. All the left-hand gloves are identical to the right-hand gloves; however, only pairs of gloves are worth anything. The players in any given coalition combine their gloves to form the maximum number of pairs and share the generated revenue equally. For simplicity, a pair of gloves is assumed to be worth one dollar, and our computerized agent had risk-neutral utility.

It was assumed that revenue generated by a coalition is distributed evenly amongst its players. This assumption makes our version of the glove game a non-transferable utility game (or no side payments), specifically, a hedonic game [17,55]. Thus, the payoff for player ‘a’ in coalition ‘S’ is:

$$U\left(a,S\right)=\raisebox{1ex}{$min\left({{\displaystyle \sum }}_{b\in S}L\left(b\right),{{\displaystyle \sum }}_{b\in S}R\left(b\right)\right)$}\!\left/ \!\raisebox{-1ex}{$\left|S\right|$}\right.$$

(1)

where L(.) is the number of left-hand gloves of a player, and R(.) is the number of right-hand gloves.

To help the reader understand the glove game, a simple example is now provided in Figure 1.

Consider a game with three players: A, B, and C in Figure 1. As illustrated in Figure 1a, ‘A’ has one left-hand glove and two right-hand gloves, represented as <1, 2>. ‘B’ has <5, 0> and ‘C’ has <0, 5>.

As shown in Figure 1c, a stable coalition structure for our game is {A}{BC}. It is stable because there does not exist a subset of players that could obtain a higher overall payoff through forming a new coalition (if a subset of players could obtain higher payoffs, it is said that the coalition structure is dominated [55]). The set of all stable coalition structures is called the core set. The core set is, thus, the set of all coalition structures that are not dominated, and no player has an incentive to leave its current coalition. In our example, the game only has one member of the core: {A}{BC}. The version of the core described here is a slight departure from the usual definition (which involves imputations [56]), and strictly speaking, we are defining the core partition of a hedonic game [17,55]. However, the two concepts are equivalent [57].

As it is depicted in Figure 1b, note that player ‘A’ would obtain a higher payoff in this game if they were in coalition {AB}. However, player ‘B’ has an incentive to deviate and join coalition {BC}; thus, the coalition structure {AB}{C} is not stable. In this paper, we focus on stability as this is the usual focus of game theory. For more examples of glove games, refer to Collins et al. [18] research paper.

The next section provides the details of the interactive agent-based simulation used in our experiment.

3. Agent-Based Model and Simulation

During our experiment trials, the human player interacts with the computerized agents through a specially designed computer program, which we have been referring to as the interactive agent-based simulation. All interactions of human players with the simulation are captured in each game. These interactions effectively reflect the human participant’s decisions throughout the experiment. This section describes the underlying model of the simulation. The model’s description follows the ODD (Overview, Design concepts, Details) protocol for describing agent-based models [58], as updated by Grimm et al. [12]. The model was built in the NetLogo agent-based modeling environment [27,59].

3.1. ODD Description of the Model Used in the Experiment to Study Human Decision-Making of Coalition Formation

3.1.1. Purpose and Patterns

The model’s purpose is to collect information on human decision-making in the context of coalition formation games. The model uses an interactive approach, and a single human is involved in each experimental trial. All other agents are controlled by the ABMSCORE algorithm [10]. The glove game, a standard cooperative game, is used as the model’s scenario.

3.1.2. Entities, State Variables, and Scales

The model abstracts the glove game into computerized form. The glove game is a standard game from cooperative game theory. The players are trying to sell pairs of gloves, and they can form coalitions with other players to form more glove pairs by pooling their gloves. Each player has a fixed endowment of gloves to create pairs. The coalitions that form are the output of interest from the game. The players are the agents in the model; the players are, collectively, the human player and the computerized agents.

Agents: players

Environment: A abstract social setting where players are able to communicate with each other about forming coalitions.

Variables: The player variables are coalition membership, left-hand gloves, right-hand gloves.

Coalition Membership: This variable indicates the current coalition that a player is a member. Each coalition is assigned an index number; even a coalition of only one player, known as a singleton coalition, is assigned an index number.

Left-hand Gloves: This variable represents a player’s endowment of left-hand gloves, which are fixed throughout the game.

Right-hand Gloves: This variable represents a player’s endowment of right-hand gloves, which are fixed throughout the game.

Gloves are used to work out the value of a coalition. All other variables are calculated from these variables.

• Scales

A round of the game represents an arbitrary time scale.

3.1.3. Process Overview and Scheduling

During each round, the players have an opportunity to suggest coalitions to the other players, and, if acceptable, new coalitions are formed and the old ones updated. This process is repeated for several rounds. The human player proposes first, followed by the computerized agents. The computerized players’ proposed coalitions are generated by the ABMSCORE algorithm [10]. The consistency of computerized agent decisions and human decisions on whether computerized agents make the same decisions as humans to join a coalition or not and make the same coalition suggestion or not was discussed in Collins et al. [18], and the results indicated that our heuristic algorithm was consistent with that of human decisions and the consistency was higher in the group of humans with game theory experience. The main loop is shown in a flow diagram in Figure 2. As the diagram indicates, both the human player and the computerized agents, via the ABMSCORE algorithm, have an opportunity to suggest coalitions to the other players. Further details of the algorithm are discussed in the sub-model section below.

3.1.4. Design Concepts

• Basic principles

The simulation model is a computerized abstraction of the glove game; the glove game is a cooperative game [16] that has been used in human-subject experimentation [13]. In the game, all computerized agents are utility maximizers, which is a common assumption in game theory where utility is called payoff. As such, the computerized agents’ decisions are driven by a desire to increase their payoff. The game has complete information.

• Emergence

There are two emergent phenomena that are hoped to be observed from the simulation run. The first is that human players play like the computerized agents; that is, their decisions are consistent with what the computerized agents would do in a similar situation (micro-level), which was shown to be consistent in Collins et al. [18]. The second emergent behavior is that the final coalition, of which a human is a member (macro-level outcome), is a core coalition. The focus of this paper is on the second emergent phenomenon.

• Adaptation

The way that the players adapt their situation is to join coalitions. They can only be a member of one coalition at a time and can only join a coalition that is suggested to them. Both the human player and the ABMSCORE algorithm can suggest coalitions. It is important to note that a new suggested coalition will only form if all its potential members agree to form the coalition. This means that if a new coalition includes a player, that player has veto power over its formation. The computerized agents will only join a new coalition if the payoff they would receive is higher than their current payoff, i.e., the payoff they would receive from their current coalition.

Since players can leave a coalition, other members of their old coalition will find themselves in a new coalition (a coalition with one player less); as a result of this, a player’s payoff might go down because their coalition has fewer glove pairs due to another player’s departure. Players are unable to stop another player from leaving a coalition; they only control their own membership destiny. Note that in Hart and Kurz [16] version of the glove game, it was assumed the coalition collapsed after a player left, resulting in all the remaining players being in their singleton coalitions; this is an assumption that is not followed in our model.

• Objectives

All the computerized agents’ objective is to be a member of a coalition that maximizes their payoff. In the glove game, the payoff of a given agent ‘a’ in coalition ‘S’ is in Equation (1).

The human player is also instructed that the computerized agents trying to maximize their utility; however, whether they choose to try and do that or not; is completely their choice. It is possible that human players follow other objectives, e.g., complete the experiment as quickly as possible.

• Learning

This model does not include learning.

• Prediction

This model does not include prediction modeling.

• Sensing

The computerized agents do not sense each other in spatial terms. Through a graphical user interface (GUI), the human player has complete knowledge of the game situation, i.e., the current coalitions and the glove endowments of each player. The graphical representation that the human player sees is shown in Figure 3.

In the GUI, each player is represented by a static circle and alphabetic figure like A–G. Each player’s glove endowment is shown immediately below the player’s circle; for example, Figure 3 shows player F has two left-hand gloves (red) and a right-hand glove (blue), whereas player B only has four left-hand gloves. The current coalitions are represented in the GUI as colors of the players; for example, Figure 3 shows that players A and F are in a coalition, so are players C and G; all other players are in a singleton coalition. The human player is always player A.

• Interaction

There is no direct interaction between players; however, their decisions can affect each other’s payoff. When a player decides to leave or joins a coalition, then there might be a change in the coalition’s value; this change in value affects the payoff of its members. The value of a coalition is the number of glove pairs that can be made from all its members’ gloves, whereas its member’s payoff is its value divided by the coalition size.

To understand this indirect interaction, consider players C and G in the example game shown in Figure 3. While these two players are in a coalition together, they can create three pairs of gloves and get a payoff of 1.5 each. However, if player C leaves the coalition, player G would get a payoff of zero. Thus, player C’s actions indirectly affect player G’s utility.

Strategic coalition formation requires multiple decision-makers to interact. By simulating the other decision-makers and only using a single human in the simulation, the effects of complicated interpersonal dynamics can be avoided, thus increasing the internal validity of our experiment [60]. However, removing the inter-personal relationships does limit the external validity of our experiment.

• Stochasticity

The only stochastic elements of the model are the coalition suggestions made by the ABMSCORE algorithm. Six different suggested coalitions are made by the algorithm during each step of a model run. The six suggested coalitions each represent a different type of coalition formation [10]. For example, one approach could be to suggest the combining of two randomly chosen coalitions to create a new larger coalition. The six different coalition approaches are briefly discussed in the sub-model section.

The inclusion of an actual human’s decisions within the model creates uncertainty; however, this behavior is not necessarily stochastic for a given individual. The human player’s decision-making type is stochastic with regard to its distribution, i.e., different people will use different processes to make their decisions.

• Collectives

Coalitions are a form of collective. The model focus is on the formation of coalitions in the glove game. In the model, the coalitions are not represented as agents but as a numerical variable of each player; if two players share the same number, they are in the same coalition.

• Observation

There are a variety of observations that are recorded after the human player makes a decision in a given trial. These include the current coalition structure, the suggested coalition, and the human player’s current payoff. It was also recorded whether or not the final coalition structure was a core partition and whether or not the human player’s final coalition is a core coalition; if the human player’s coalition was in a core partition, it is called a core coalition. Finally, all human player’s decisions at the individual level (micro-level) are compared to what the computerized agents would do, and a Boolean value recorded to see whether their behavior is consistent with the computerized agent. This consistency has been discussed in [18].

3.1.5. Initialization

All players do not start in a coalition. We call the coalition of a player on their own the singleton coalitions. The glove game considered determines the number of players and their initial glove endowments. Note that a player’s glove endowments are fixed and do not change during the game.

3.1.6. Input Data

As Grimm et al. [12] specify in their ODD description, input data refers to data that is input during a simulation run instead of its initialization. As such, there is no input data for our model.

3.1.7. Sub-Models

There are two sub-models worthy of discussion. The first is the Graphical User Interface (GUI) used by the human player. The second is the ABMSCORE algorithm.

• Graphical User Interface

The purpose of the GUI is to provide the human player with an overview of the game situation as well as suggest coalitions or respond to suggested coalitions. The GUI allows the human player to see the endowment of other players and the current game situation, as discussed in the sensing section above. Figure 3 shows a screenshot of the GUI.

The GUI allows the human player to suggest coalitions on their turn; this is achieved by clicking on other players’ circles they wish to form a coalition. These circles turn into squares if selected. Once the human player is happy with their selection, they simply press “happy with the selection”. If they do not wish to make a selection, then simply selecting no player and pressing “happy with the selection” will move the game onto the computerized agents’ turns. Once the human player is happy with the coalition structure presented, they simply press “Finish” to end the game.

• Algorithm Steps

There is one human player in the model, and all other players are controlled by the ABMSCORE algorithm. The purpose of the algorithm is to simulate the computerized agents’ behavior of joining and suggesting coalitions. The version of the algorithm used in the model was the advanced version developed by Vernon-Bido and Collins [10]. There are three parts used within the algorithm: coalition suggestion, coalition evaluation, and coalition updating. These three parts control changes to the coalition structure, which is the main output of the model. The coalition involves six types of suggestions: joint coalition, exit coalition, create a pair coalition, defect coalition, split coalition, and return to an individual coalition. All three parts of the algorithm are explained in detail in Vernon-Bido and Collins [10].

4. Methodology

The purpose of the experiment is to investigate whether the algorithm was consistent with human behavior and whether game theory experience affects human behavior in an interactive simulation with regard to strategic group formation at the macro-level. To this end, a wide variety of participants were recruited to undertake trials in an interactive simulation of some glove games. Only one human was used per trial to avoid the complexities that emerge from human interaction. Since strategic group formation requires multiple decision-makers, the other players were controlled by the ABMSCORE algorithm [10].

4.1. Experimental Method

There is no one universal way to conduct human subject experiments, and different academic fields have different approaches based on their underlying foundations and requirements [61]. Since M&S is a multidisciplinary field [62], it is not clear what approach to human subject research standards should be followed. This paper intends to advance agent-based modeling, as opposed to economics or sociology and, as such, we do not wish to enter the debate of which human subject experimental approach is “correct”; as such, we opt for a weaker experimental method called correlation research as defined by Jhangiani et al. [60].

The consequence of opting to define our research approach by this weaker experimental method is that our research findings can only be considered indicators of the phenomena as opposed to conclusive findings. The reason for producing non-conclusive findings is due to the limitations of the correlation research approach, e.g., no conditions or controls [60].

Though we do not conduct a human subject experiment, we will refer to our investigation as “the experiment”, though, strictly, speaking is not a scientific experiment in the psychological sense. It should be noted that many of the “experiments” described in the background section would also be considered correlation research; these include the experimental design of previous experiments using the glove game [13,14].

Correlational Research

Correlation research is a weaker form of research, compared to human subject experimentation, because of two main reasons: (1) it does not contain procedures to help ensure causation direction is known, and (2) the potential impact of extraneous variables is not controlled. Correlation research purely looks at whether two things are related and ignores the context [60]. The two variables under consideration in our research are game theory experience and the ability of the human players to find a stable coalition (i.e., core coalition).

There are several reasons for using correlated research; two are mentioned here. Firstly, when the independent variable (i.e., game theory experience) cannot be manipulated. Secondly, when the experimenters believe there is no correlation between the variables. More discussions on experimental design are given in the limitation section.

4.2. Prototype

Before that main experiment was conducted, a prototype experiment was completed. The approach of this prototype is discussed in Saolyleh et al. [63]. The prototype’s key finding was that even though the glove games used are simplistic cooperative games, their mechanism can be confusing to novices. There were two major changes based on this finding. Firstly, each trial is conducted with an instructor to explain the process as opposed to a completely web-based interface. Secondly, the participants undertook more training example games before they completed the main trial games.

4.3. Recruitment Approach

A convenience sampling approach was used for human participant recruitment [60]. The participants were invited to the experiment from a variety of demographics, including the Old Dominion University community, without bias by e-mail/social media and word-of-mouth communication, a wide range of individuals participated in the study.

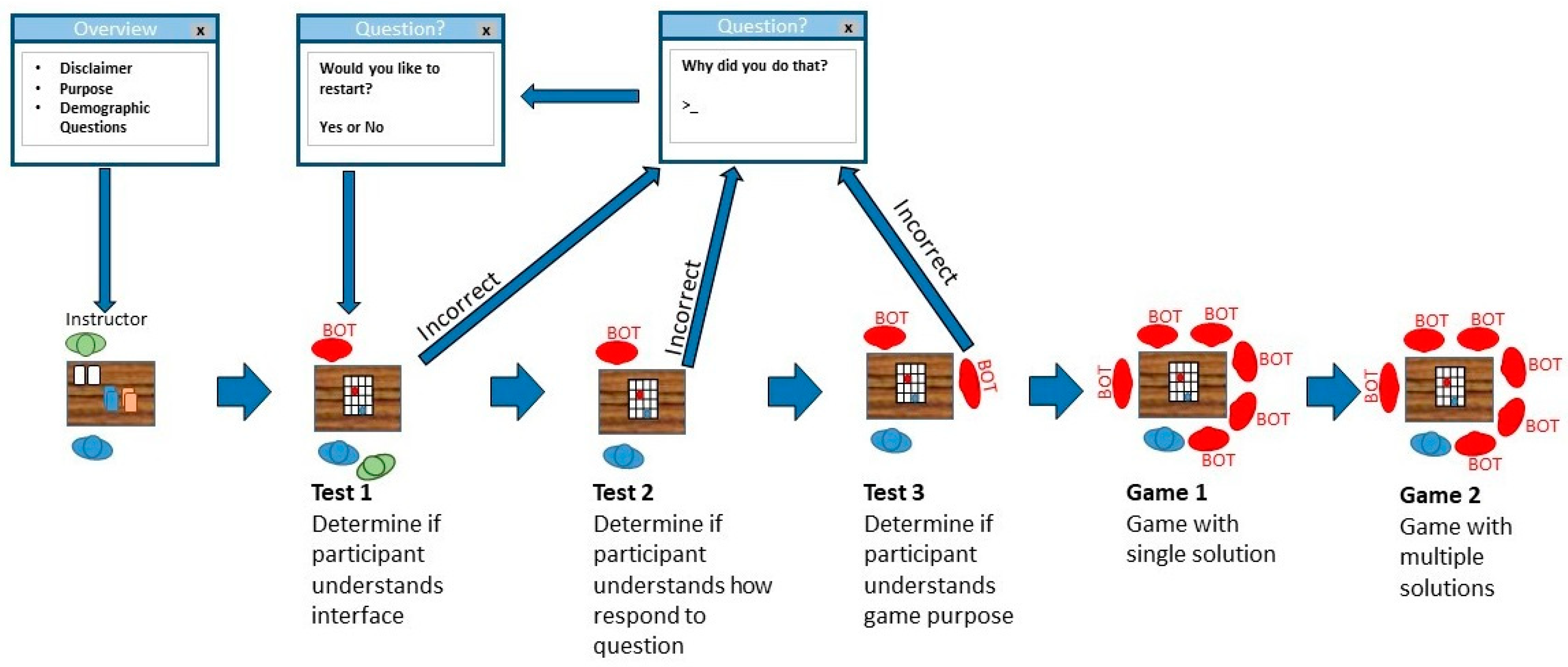
4.4. Experimental Protocol

The experimental protocol is split into three phases: (1) initial overview, (2) pre-testing phase, and (3) trial phase. An overview of the experimental protocol is provided in Figure 4. The purpose of the first phase is to collect demographic information about the participants and explain the glove game. The purpose of the second phase determines if the participants understand the glove game and GUI interface. The final phase’s purpose is to collect data about the resultant coalition structures generated by the participants’ decisions.

Throughout each trial, the participant will play seven games, namely: two verbally presented training games with visuals to aid participant understanding, three computerized training games using the GUI, and two computerized trial games using the GUI. The games increase in complexity as the trial progresses.

Initially, the participants are shown a disclaimer about the experiment and their ability to quit at any time. This included a description of the purpose of the experiment. They were then asked to fill out a questionnaire, the details of which are given in the data collection section below. The decision to ask the participants to fill out the questionnaire first was deliberate; this is discussed in the discussion section. The final part of this phase is for the instructor/facilitator to provide a scripted overview of the glove game, which includes two verbally presented games.

The participants are then shown the GUI—Figure 3—and are asked to complete three test games on it, and they were informed that they are only playing against computerized agents. Finding the solution of all three test games is relatively simple as the games only involve two or three players. If the players make unexpected decisions and coalition selections, they are asked why and given a chance to repeat the test games.

If a human participant is able to pass this initial comprehension pre-test, they then proceed to the two actual trial games. The participants play the two games presented in the glove game, known as the single-core trial game and multiple-core trial game, representatively. Each game is multi-staged, so multiple decisions were collected per participant per game. We did the data analysis for these two actual trial games.

4.5. Data Collection

There are two sets of data collected per trial: demographic information and simulation output data. The demographic information was collected using a questionnaire. Demographic information collected included age, sex, education, board game, video game, and game theory experience. The participants were asked to characterize their experience in the following discrete scale:

• What is your expertise in game theory? “None”, “Low”, “Medium”, “High”, “Never heard of it”, “Prefer not to answer”.

Though participants’ demographic information was collected, no directly identifiable information was collected to ensure the Internal Review Board (IRB) approval of our experiment. All game outcomes were collected through computer simulation. This was easy to do because the participants were interacting with games through the GUI. All the trial data can be found at https://www.comses.net/codebases/3039b5b4-9a52-4195-a444-0a3a87ef229d/releases/2.5.0/ (accessed on 24 September 2021).

5. Results

As mentioned earlier, we only conducted the data analysis for results from the last two trial games after the human subject had completed the five training games. For each of the last two games, a total of 31 trials were conducted from a wide range of individuals in terms of game theory experience, age, education level, and gender (in total, 62 trials). Figure 5 shows an in-person trial where the participant is being trained in the mechanics of the glove game using specially designed playing cards.

The results that are presented in this section are focused on the analysis of simulation macro-level outcomes. Specifically, game theory experience impacts on the human’s behavior at the simulation macro-level outcomes. There are two types of results discussed in this section: descriptive statistics and game theory experience impact of the simulation outcome.

The descriptive statistics give an overview of the population by demographics, as well as some high-level statistics on performance. The analysis of the game theory experience and the impact on the final simulation outcomes is conducted using various inferential statistical tests; the analysis indicates that the game theory experience has not made a significant difference both positively and negatively on the simulation macro-level outcomes.

5.1. Descriptive Statistics

The 31 participants had a wide range of demographic characteristics in age (all adults), gender, and education level. Discussion on the demographic information collected can be found in Collins and Etemadidavan [11]. Considering the game theory experience questions, assumed extraneous variable in this paper, the number that answered “Medium” or “High” are called “experienced in game theory”. The rest are considered as “not experienced in game theory”.

Table 1. The population of the study: experienced vs. not experienced in game theory.

Category	Population
Experienced in game theory	8
Not experienced in game theory	23

shows the spread of the participants divided into “experienced” or “not experienced” in game theory.

Considering the two trial games, one of these trial games had a single-core partition solution, and the other had four possible coalition structure solutions. This research’s key question is whether the simulation outcome of the trial games were core partitions and game theory experience, affected the probability of it being a core partition. However, due to the nuances of the experiment, a weaker outcome for comparison was considered. This outcome was whether the human player final coalition is a member of a core partition; this is called a “core coalition”.

The weaker outcome is required because our interest was in the human subject’s behavior and not the computerized agent’s behavior. Since the human participant cannot control what coalitions will form outside their own coalition, it seems inappropriate to judge their performance based on all coalitions in a coalition structure. Thus, the focus is on core coalitions, where the human player does have some control. There is only one possible coalition that contains the human player in the single-core trial game and is in a core partition. There are four such coalitions in the multiple-core trial game, a unique one for each of the four core partitions.

Regarding the first research interest to see whether the human’s final coalition is the same as a core coalition, which is suggested by cooperative game theory, we compared these two coalitions, and we ended up that in 42% of the time, the human’s final coalition was the same as core coalition which is depicted in

Table 2. Human final coalition compared to the expected core coalition.

Category	Percentage
The human’s final coalition is a member of the core	42%
The human’s final coalition is not a member of the core	58%

.

We have conducted further analysis and compared payoffs received by the human at the end of the game to the expected core payoff based on the cooperative game theory solution concept. As it is shown in

Table 3. Human final payoff compared to the expected core payoff.

Category	Percentage
The human’s final payoff is core payoff or higher	60%
The human’s final payoff is less than the core payoff	40%

, the payoff which humans received at the end of the trial was at least as good as the core payoffs about 60% of the time.

By considering findings from Table 2 and Table 3, we can conclude that although only 42% of the time humans find core coalition, 60% of the time, their received payoffs were equal or even greater than the expected core payoff. This could imply that humans, in the majority of cases, behaved to maximize their payoffs, as they were trained, regardless of paying attention that the final coalition is a stable coalition or not.

In the next section, the second assumption regarding extraneous variables known as game theory experience in this research will be discussed.

5.2. Game Theory Experiences Impact

This section focuses on the impact of the human game theory experience on the simulation outcomes, specifically, the coalition structures of the two trial games. Additionally, we should note that we examined the impact of demographic information that was collected, viewing them as extraneous variables, on the simulation outcomes, and it seems there is no significant difference between the variety of demographics in the population on the simulation outcome; the detail can be found in Collins and Etemadidavan [11].

To understand the impact of game theory experience on the outcome of the trials, several different hypotheses were constructed. Two of the hypotheses are focused solely on payoff; the rationale for this is that the core is not the only solution mechanism available, and the players might focus on maximizing their payoff; hence it seems prudent to explicitly focus some hypotheses directly on the payoff obtained. There were three main hypothesis questions that were asked about each characteristic:

• Does the experience affect the outcome of being a core coalition?
• Does the experience affect the final payoff of the human player?
• Do those with the experience receive, on average, a higher payoff than those that do not?

The first two questions were tested using the Chi-squared test for independence [64]. Since the payoff structure is different for the two games, the third question must be split by game. The third was tested using a standard t-test.

For the purpose of the statistical analysis,

Table 4. A contingency table shows the impact of board game experience on whether human participants’ final coalition was a core coalition.

	Core Coalition Membership	Otherwise
Game theory experience	7	9
No experience	19	27

is shown as a contingency table that was constructed to determine whether a participant’s game theory experience had an impact on their final coalition, specifically, whether they ended up in the core coalition or not. A Chi-Squared test of independence was conducted on this table, resulting in a p-value of 0.86; from this result, we cannot conclude that game theory experience makes a difference whether a participant’s final coalition is a core coalition. Note again that being in a core coalition is different from the final payoff of a participant.

The null hypothesis for

Table 5. A contingency table shows the impact of game theory experience on whether human participants’ final payoff was a core payoff.

	Core Payoff or Greater	Less Than Core Payoff
Game theory experience	11	5
No experience	26	20

is defined as “There is no difference on the payoff which a human with/without game theory experience receives at the end of each game”.

Although the result from Table 5 is not significant, p-value = 0.39, and the null hypothesis cannot be rejected; it can be seen that the rate of humans with game theory experience which received less than core payoff (5 out of 11) is lower than human without game theory experience (20 out of 26).

For the third step, Pearson’ Correlation coefficient tests for games with single and multiple cores have been conducted, and the result has been shown in

Table 6. Test for a relation between player’s game theory experience and final payoff in each trial game (with single and multiple cores). The T-test brackets show the means with experience and without.

Experience Characteristics	Game	Final Payoff
		Correlation	p-Value	T-Test of Sample Means	p-Value
Game Theory Experience	Single	0.08	0.69	(1.69, 1.65)	0.32
Game Theory Experience	Multiple	0.04	0.82	(1.53, 1.51)	0.43

.

Alternative Hypothesis: 

There exists a difference between different experienced group average final payoffs.

Based on Table 6, there is no relation between a player’s payoff and game theory experience because the p-value is greater than 0.05.

While our interactive simulation model was consistent with the human decisions in the micro-level [18] (i.e., whether computerized agents make the same decisions as humans to join a coalition or not and make the same coalition suggestion or not), this was not the case at the macro-level with the expected coalition only being reached 42% of the time. Additionally, we had hypothesized that someone with experiences in game theory would affect a human player’s performance in the simulation macro-level outcome; however, our correlation research indicates they did not make a significant difference on human performance. We should mention that we also conducted all statistical analysis for both board game experience and video game experience, other two experiences which we were collected through the questionnaires; the results have shown that these two experiences also do not make a significant difference in human decisions based on the human’s final coalition.

Given the statistical findings and these collaborating points, we now believe that game theory experience, as well as demographic information, such as age, education level, and gender [11], do not make a significant difference to the simulation’s outcome, at least in the case of the glove game. However, these conclusions should be considered weak due to the limitations of our experimental and statistical approach, which are discussed further in the next section.

The next stage for the research is to consider other human characteristics and to understand, more deeply, why the humans’ behaved as they did in the experimental trials. This might be achieved through a more robust experimental design.

5.3. Implications of the Findings

The implications of these findings are two-fold. Firstly, game theory and gaming experience do not seem to matter with regard to interactive simulation experimentation. This means that future studies might not need to consider it when constructing future interactive simulation experiment designs, simplifying the experimental design. Of course, our result is not definitive but given the wealth of possible extraneous variables, a researcher that conducts human subject experiments faces having some justification for not considering one of them is useful. Secondly, the human participants are not driven by the same motivation as the computerized agents, i.e., a desire to find a stable coalition structure. This is not surprising because game theory is a normative method and not necessarily descriptive [65].

6. Limitations and Discussion

There are several limitations with the methodology used to conduct our research, and improvements could be made in future research. In this section, we discuss some of those limitations, including their consequences on conclusions from our findings and potential alternatives for future research. The discussion includes limitations on the methodology, the experimental protocol, and statistical tests.

6.1. Methodology

The research uses a correlation research approach as opposed to a human subject experiment. A human subject experiment would have been more ideal for our investigation due to its internal validity. Validity, in this sense, is meant experimental validity [60] as opposed to M&S validity [66]. Internal validity is how well the design of an experiment allows for conclusions to be made about its outcomes. Tenets of internal validity include directionality, i.e., knowing that A causes B as opposed to B causing A, and random assignment of participants to control and treatment conditions, which is used to limit the impact of confounding variables, i.e., uncontrolled variables that affect the context of the experiment. Correlation research has neither of these tenets, so our findings provide evidence that game theory experience does not matter as opposed to conclusive evidence in the experimental sense. As mentioned previously, most similar research studies, especially those using simulation, would not satisfy the criteria for a human subject experiment.

6.2. Experiment Protocol

There are several potential confounding variables that result from our experiment protocol, which, again, limit the conclusiveness of our results. In this section, we discuss three of them: carryover effect, participant use, and game construction.

6.2.1. Carryover Effect

There are several potential carryover effects that result from our experiment protocol; we discuss three here: training effect, game ordering, and questionnaire question ordering. Carryover effects are when an event earlier in the trial could affect the outcome of a later participant decision.

The first carryover effect discussed is training. Obviously, training the human participants to play glove games influences their decisions in the trial games. From our prototype, we realized the need for training in playing the glove game due to the complexity of cooperative game theory to novices [63]. The issue is whether the training led them to make certain decisions or goals, which they would have made differently in other training was conducted. This issue could have been investigated if we had used different training games for different groups of participants and compared the outcomes to see the training’s effect.

The second carryover effect we discuss is the ordering of the games. The single-core game was always played first, followed by the multiple-core game. It is possible that the “practice effect” affected the results of the second game, i.e., the players had more practice in playing the glove game by the time they got to the second trial game, so they performed better at it. However, the outcomes of games were not directly compared in our analysis, and, as such, we do not conclude any practice effect. This game ordering effect could be tested by switching the order of the trial games using a simultaneous within-subject design.

The final carryover effect we discuss relates to asking the participants to answer the questionnaire first, before the games. This decision was made because we felt that the participant’s perceived performance in the games they just played would affect their answers to the questions given if the questionnaire was given last. For example, if a participant believed they performed badly in the games, then they might be tempted to downplay their gaming experience. The downside of conducting the questionnaire first is the potential impact from the experimenter’s expectancy; that is, the experiment’s facilitator might expect someone with lots of gaming experience to do well, so, subconsciously, provide them will more help. Since the facilitator was not involved in the two trial games (as they are computer-based), this bias was avoided.

6.2.2. Participants

As previously mentioned, we used convivence sampling as our approach to obtain participants. This obviously biases our sample to friends and acquittance we knew. Additionally, volunteers tend not to be representative of the general population due to having, on average, higher IQ, and higher social class than the general population [67]. This issue is generally accepted within an experiment’s tolerance of uncertainty.

6.2.3. Glove Game

Ideally, we would have liked our results to be applicable to all strategic coalition formation situations; however, it is feasible that our results are only applicable to glove games as glove games could, in themselves, be an extraneous variable. We could have used randomized hedonic games, using the approach outlined in [68,69]; however, again, such a new experimental approach would have required hundreds of participants. As such, our conclusions are limited to glove games.

6.3. Statistical Tests

6.3.1. Sample Size

The sample size of our study is another limitation because we only had 31 participants. This limited size caused poor p-values to be observed from our statistical tests, and, as a result, our findings are not conclusive. Having a larger sample size could help improve our conclusion.

6.3.2. Causality

Since we used a correlated research approach, we would not have known the causality of results if correlations had been found. For example, do people play games because they are good at them, or does playing games make you a better game player? From personal experience, we speculate that it is both, and there is a cyclic relationship, but this is very hard to detect.

6.3.3. Power Analysis

Power analysis is an important aspect of modern statistical analysis. Conducting post hoc analysis on our dataset using the G* power tool [70], we discovered that a large effect size is required for the acceptable power of our tests. This is unsurprising given the relatively small sample size. We believe our results still hold though a large effect size does imply that we are assuming that there is a large distributional difference between our null hypothesis and any alternative hypothesis.

7. Conclusions

The results from a correlation research experiment into the macro-level outcomes of a simulation and the effects of game theory experience on humans’ strategic behavior in an interactive simulation are presented in this paper. The scenario under consideration is the glove game, which is a form of hedonic game from cooperative game theory. Due to limitations in our approach, our results are not conclusive, but they do indicate that game theory experience does not make a significant difference in the human participants’ final coalition, at least in the context of the glove games considered.

Humans are heterogeneous, and, as a result, their decision-making processes are different. This heterogeneity makes them ideal for being stimulated by ABMS. However, there is a need to validate any modeling of human behavior. Comparing the behavior of humans to what would be expected in a simulation is one approach to this validation. We suggest that an interactive simulation is a good approach to collecting the data on human behavior because the humans are playing in the exact same context as the computerized agents. However, accurately incorporating human behavior into ABMS not only requires a deep understanding of what human behavior is but also what extraneous variables affect this behavior. The correlated research outlined in this paper represents an attempt to determine if game theory experience is one such extraneous variable in the context of glove games.

Beyond the correlated research, this paper also provides a case study for creating an interactive simulation in experimentation. This paper provides a detailed explanation, using the ODD protocol, of the model used in the experiment to drive the glove game simulation, and it also provides a detailed overview of a method to conduct an interactive simulation experiment of strategic coalition formation that only involves a single human in each trial. The other players were controlled by the ABMSCORE algorithm. It is hoped that this method, used in the case study, will be helpful to other researchers who wish to conduct similar research. Regarding the human training approach, all the participants played “correctly” in the first five test games of the trials, which shows our training approach was effective. These test games only had up to three players. However, the trial participants only found the core coalition in 42% of cases of the more complex trial games of seven players; we believe it is due to the complexity of the cooperative game theory, which can be difficult for novices to understand.