Virtual Modelling Framework-Based Inverse Study for the Mechanical Metamaterials with Material Nonlinearity
Abstract
:1. Introduction
2. Theoretical Formulation of the Virtual Model
2.1. Finite Element Method
2.2. Extended Support Vector Regression
3. Numerical Investigations
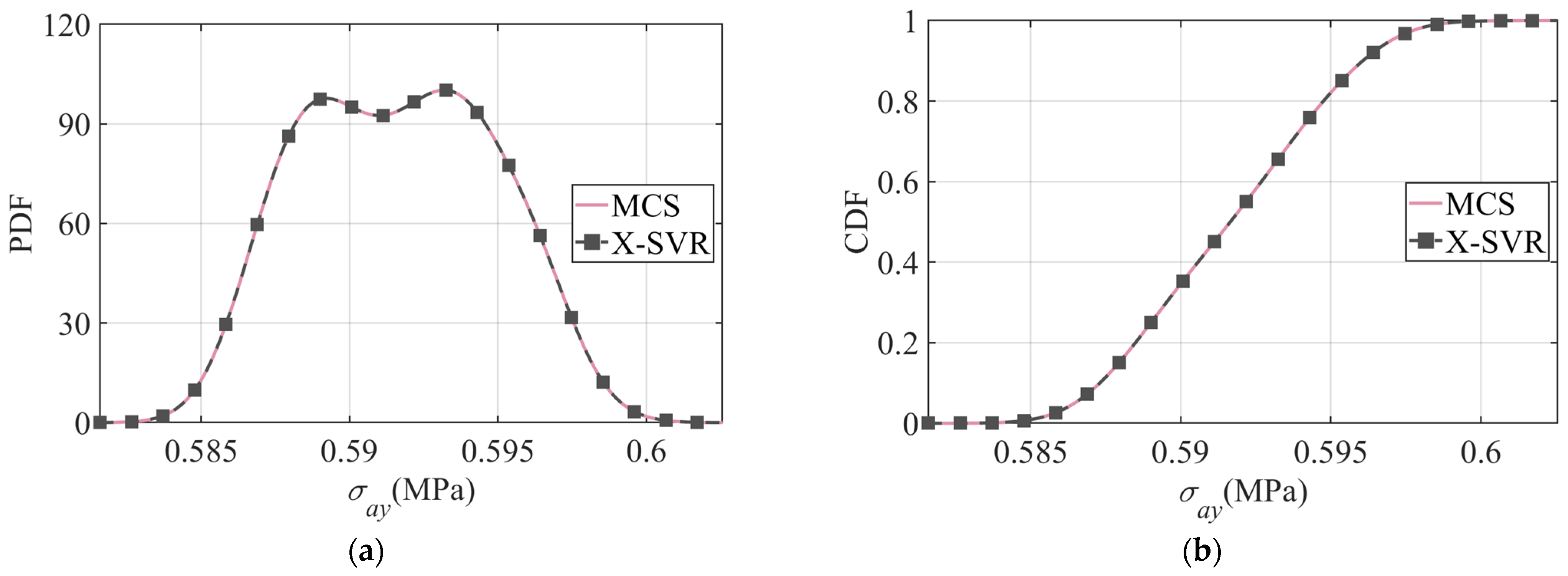
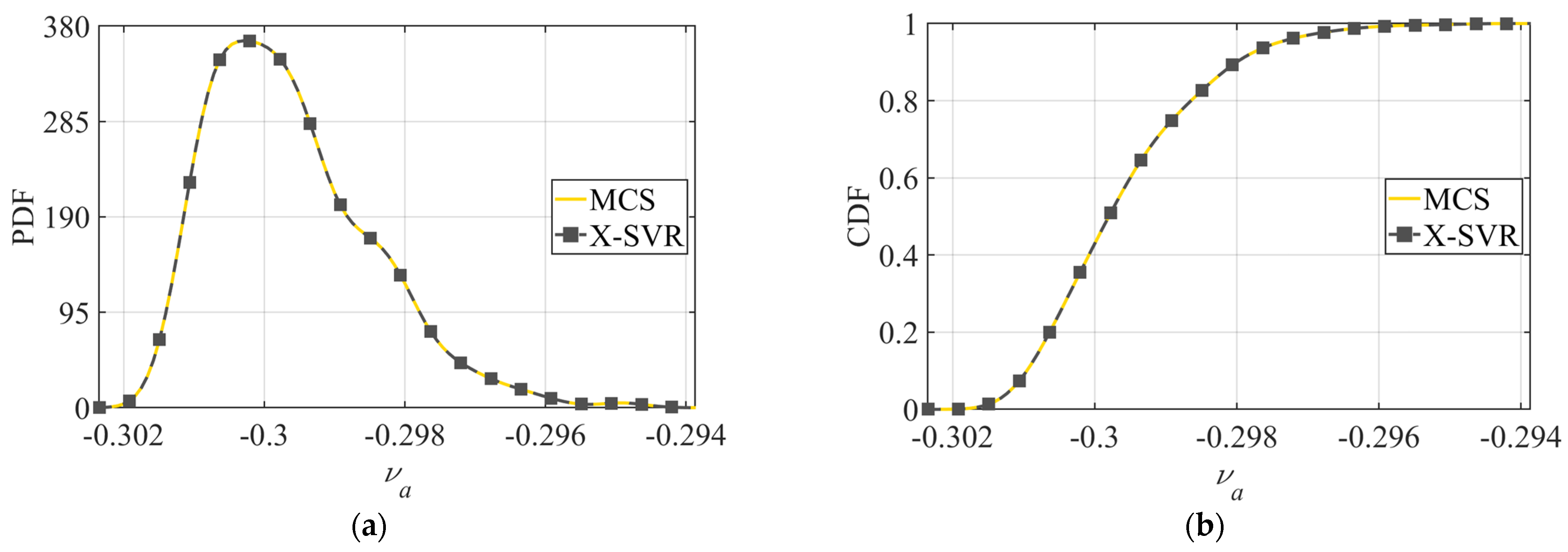
3.1. Uncertainty Analysis
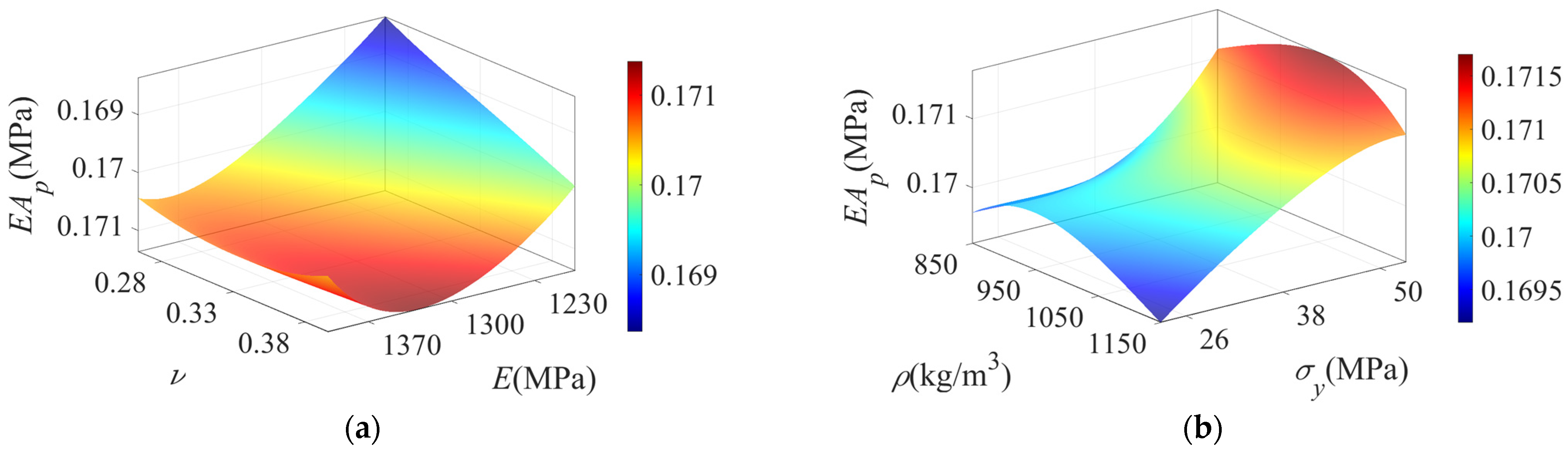
3.2. Sensitivity Analysis
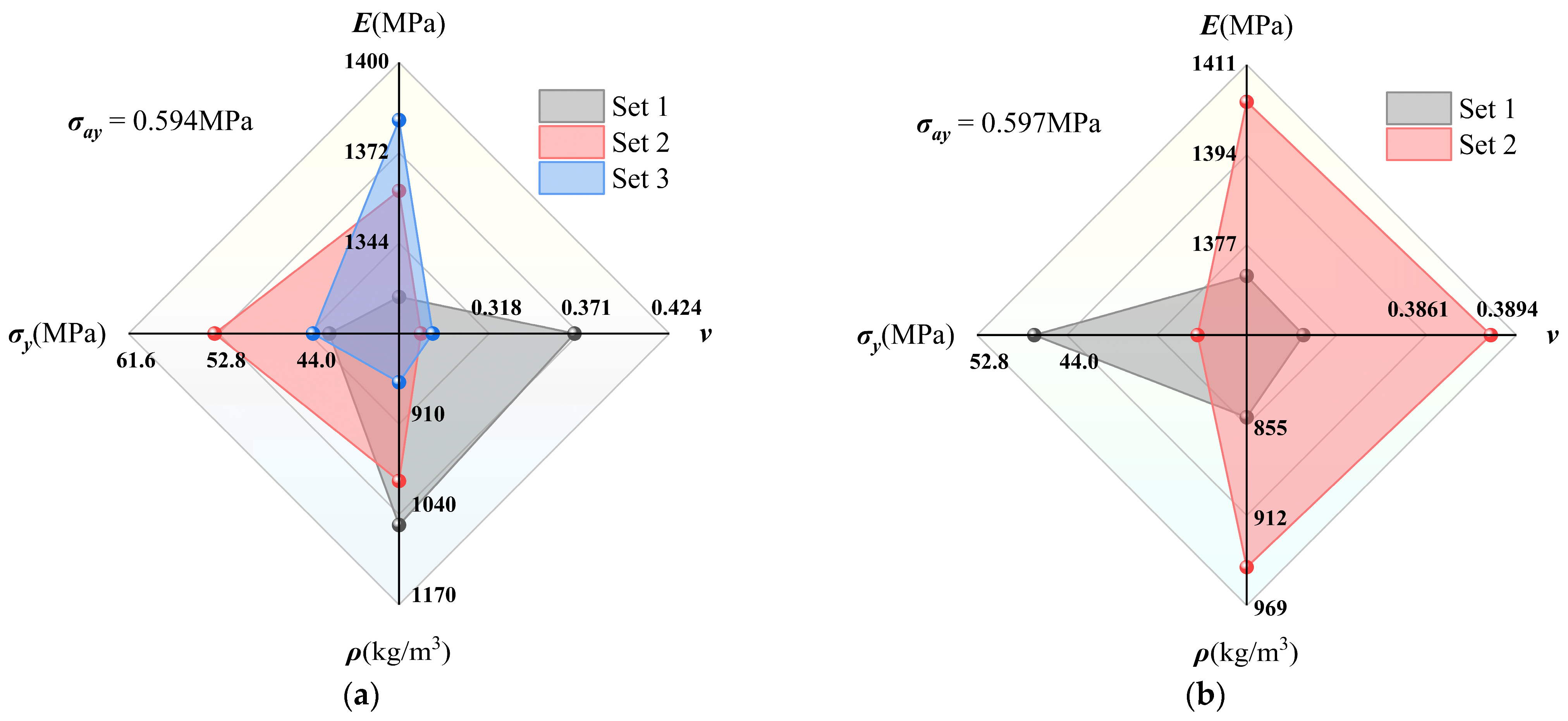
3.3. Inverse Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hwang, D.; Lee, C.; Yang, X.; Pérez-González, J.M.; Finnegan, J.; Lee, B.; Markvicka, E.J.; Long, R.; Bartlett, M.D. Metamaterial adhesives for programmable adhesion through reverse crack propagation. Nat. Mater. 2023, 22, 1030–1038. [Google Scholar] [CrossRef]
- Fisher, T. International Journal of Mechanical Sciences High-velocity impact response of 3D-printed composite mechanical metamaterials. Int. J. Mech. Sci. 2025, 286, 109905. [Google Scholar] [CrossRef]
- Sinha, P.; Mukhopadhyay, T. Programmable multi-physical mechanics of mechanical metamaterials. Mater. Sci. Eng. R Rep. 2023, 155, 100745. [Google Scholar] [CrossRef]
- El Helou, C.; Buskohl, P.R.; Tabor, C.E.; Harne, R.L. Digital logic gates in soft, conductive mechanical metamaterials. Nat. Commun. 2021, 12, 1633. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Ferracin, S.; Raney, J.R. Programmable responsive metamaterials for mechanical computing and robotics. Nat. Comput. Sci. 2024, 4, 567–573. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Wei, Z.; Wang, K.; Chen, Y.; Zhu, R.; Huang, G.; Hu, G. Engineering zero modes in transformable mechanical metamaterials. Nat. Commun. 2023, 14, 1266. [Google Scholar] [CrossRef]
- Li, S.; Zhao, D.; Niu, H.; Zhu, X.; Zang, J. Observation of elastic topological states in soft materials. Nat. Commun. 2018, 9, 1370. [Google Scholar] [CrossRef]
- Tzarouchis, D.C.; Edwards, B.; Engheta, N. Programmable wave-based analog computing machine: A metastructure that designs metastructures. Nat. Commun. 2025, 16, 908. [Google Scholar] [CrossRef]
- Kaya, K.; Iseri, E.; van der Wijngaart, W. Soft metamaterial with programmable ferromagnetism. Microsyst. Nanoeng. 2022, 8, 127. [Google Scholar] [CrossRef]
- Hu, X.; Tan, T.; Wang, B.; Yan, Z. A reprogrammable mechanical metamaterial with origami functional-group transformation and ring reconfiguration. Nat. Commun. 2023, 14, 6709. [Google Scholar] [CrossRef]
- Chen, T.; Pauly, M.; Reis, P.M. A reprogrammable mechanical metamaterial with stable memory. Nature 2021, 589, 386–390. [Google Scholar] [CrossRef] [PubMed]
- Jiao, P.; Mueller, J.; Raney, J.R.; Zheng, X.; Alavi, A.H. Mechanical metamaterials and beyond. Nat. Commun. 2023, 14, 6004. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Harursampath, D.; Dhawan, S.; Sahni, M.; Saxena, S.; Mallick, R. Physics-informed neural network for solving a one-dimensional solid mechanics problem. Modelling 2024, 5, 1532–1549. [Google Scholar] [CrossRef]
- Chen, R.; Jin, X.; Laima, S.; Huang, Y.; Li, H. Intelligent modeling of nonlinear dynamical systems by machine learning. Int. J. Non-Linear Mech. 2022, 142, 103984. [Google Scholar] [CrossRef]
- Tian, Y.; Feng, Y.; Ruan, D.; Luo, Z.; Yang, C.; Wu, D.; Gao, W. Full-field experiment-aided virtual modelling framework for inverse-based stochastic prediction of structures with elastoplasticity. Comput. Methods Appl. Mech. Eng. 2024, 431, 117284. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, Y.; Wu, D.; Chen, X.; Gao, W. Virtual modelling integrated phase field method for dynamic fracture analysis. Int. J. Mech. Sci. 2023, 252, 108372. [Google Scholar] [CrossRef]
- Mei, T.; Meng, Z.; Zhao, K.; Chen, C.Q. A mechanical metamaterial with reprogrammable logical functions. Nat. Commun. 2021, 12, 7234. [Google Scholar] [CrossRef]
- Chen, L.; Lian, H.; Xu, Y.; Li, S.; Liu, Z.; Atroshchenko, E.; Kerfriden, P. Generalized isogeometric boundary element method for uncertainty analysis of time-harmonic wave propagation in infinite domains. Appl. Math. Model. 2023, 114, 360–378. [Google Scholar] [CrossRef]
- Ha, C.S.; Yao, D.; Xu, Z.; Liu, C.; Liu, H.; Elkins, D.; Kile, M.; Deshpande, V.; Kong, Z.; Bauchy, M.; et al. Rapid inverse design of metamaterials based on prescribed mechanical behavior through machine learning. Nat. Commun. 2023, 14, 5765. [Google Scholar] [CrossRef]
- Bostanabad, R.; Chan, Y.C.; Wang, L.; Zhu, P.; Chen, W. Globally approximate Gaussian processes for big data with application to data-driven metamaterials design. J. Mech. Des. 2019, 141, 111402. [Google Scholar] [CrossRef]
- Chan, Y.C.; Ahmed, F.; Wang, L.; Chen, W. METASET: Exploring shape and property spaces for data-driven metamaterials design. J. Mech. Des. 2021, 143, 031707. [Google Scholar] [CrossRef]
- Liu, G.; Chen, G.; Cui, F. Nonlinear dynamic analysis of ring truss antenna equivalent to the cylindrical shell with thermal excitation. Eur. J. Mech. A/Solids 2021, 85, 104109. [Google Scholar] [CrossRef]
- Varanis, M.; Silva, A.L.; Balthazar, J.M.; Pederiva, R. A Tutorial Review on Time-Frequency Analysis of Non-Stationary Vibration Signals with Nonlinear Dynamics Applications. Braz. J. Phys. 2021, 51, 859–877. [Google Scholar] [CrossRef]
- Dash, R.C.; Maiti, D.K.; Singh, B.N. Nonlinear dynamic analysis of galloping based piezoelectric energy harvester employing finite element method. Mech. Adv. Mater. Struct. 2022, 29, 4964–4971. [Google Scholar] [CrossRef]
- Liu, X.; Yu, X.; Tong, J.; Wang, X.; Wang, X. Mixed uncertainty analysis for dynamic reliability of mechanical structures considering residual strength. Reliab. Eng. Syst. Saf. 2021, 209, 107472. [Google Scholar] [CrossRef]
- Wu, R.M.; Yu, C.Q.; Wang, L.Q.; Tong, J.Z. Shear elastic buckling of corrugated steel plate shear walls with stiffeners considering torsional rigidity. Thin-Walled Struct. 2025, 206, 112646. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Tong, J.; Lincoln, R.; Zhang, L.; Liu, Y.; Evans, K.E.; Groh, R.M.J. Data-driven design of well-behaved nonlinear structures: A case study on the von Mises truss. Int. J. Solids Struct. 2025, 309, 113146. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Yan, Y.; Tong, J.; Lincoln, R.; Zhang, L.; Liu, Y. Exploiting reprogrammable nonlinear structural springs for enhancing the manoeuvrability of a vibro-impact capsule robot. J. Sound Vib. 2025, 595, 118775. [Google Scholar] [CrossRef]
- Hüllermeier, E.; Waegeman, W. Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 2021, 110, 457–506. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Q.; Wu, D.; Chen, X.; Gao, W. Nonlinear dynamic stability analysis of clamped and simply supported organic solar cells via the third-order shear deformation plate theory. Eng. Struct. 2022, 252, 113616. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Q.; Feng, Y.; Gao, W. Nonlinear dynamic analysis of geometrically imperfect multi-direction functionally graded graphene platelet reinforced composite plates with magneto-electro-elastic sheets subjected to blast load. Appl. Math. Model. 2025, 142, 115957. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Q.; Feng, Y.; Luo, Z.; Ruan, D.; Gao, W. Nonlinear dynamic analysis of the graphene platelets reinforced porous plate with magneto-electro-elastic sheets subjected to impact load. Nonlinear Dyn. 2024, 112, 1661–1690. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Q.; Feng, Y.; Yu, Y.; Wu, D.; Chen, X.; Gao, W. Nonlinear dynamic analysis of the functionally graded graphene platelets reinforced porous plate under moving mass. Thin-Walled Struct. 2023, 183, 110363. [Google Scholar] [CrossRef]
- Pilozzi, L.; Farrelly, F.A.; Marcucci, G.; Conti, C. Machine learning inverse problem for topological photonics. Commun. Phys. 2018, 1, 57. [Google Scholar] [CrossRef]
- Filippi, M.; Magliacano, D.; Petrolo, M.; Carrera, E. Wave Propagation in Prestressed Structures with Geometric Nonlinearities Through Carrera Unified Formulation. AIAA J. 2025, 63, 292–308. [Google Scholar] [CrossRef]
- Alomarah, A.; Masood, S.H.; Sbarski, I.; Faisal, B.; Gao, Z.; Ruan, D. Compressive properties of 3D printed auxetic structures: Experimental and numerical studies. Virtual Phys. Prototyp. 2020, 15, 1–21. [Google Scholar] [CrossRef]
- Phung-Van, P.; Hung, P.T.; Tangaramvong, S.; Nguyen-Xuan, H.; Thai, C.H. A novel Chebyshev-based both meshfree method and shear deformation theory for functionally graded triply periodic minimal surface flat plates. Comput. Struct. 2025, 309, 107660. [Google Scholar] [CrossRef]
- Su, R.; Boonlertnirun, P.; Tangaramvong, S.; Song, C. Isosurface-based marching cube algorithm for smooth geometric topology optimization within adaptive octree SBFE approach. Eng. Anal. Bound. Elem. 2024, 168, 105920. [Google Scholar] [CrossRef]
- Yang, J.; Ni, Z.; Fan, Y.; Hang, Z.; Liu, H.; Feng, C. Machine learning aided uncertainty analysis on nonlinear vibration of cracked FG-GNPRC dielectric beam. Structures 2023, 58, 105456. [Google Scholar] [CrossRef]
- Truong, V.H.; Tangaramvong, S.; Pham, H.A.; Nguyen, M.C.; Su, R. An efficient archive-based parameter-free multi-objective Rao-DE algorithm for bi-objective optimization of truss structures. Comput. Struct. 2025, 308, 107647. [Google Scholar] [CrossRef]
- Zhou, K.; Enos, R.; Zhang, D.; Tang, J. Uncertainty analysis of curing-induced dimensional variability of composite structures utilizing physics-guided Gaussian process meta-modeling. Compos. Struct. 2022, 280, 114816. [Google Scholar] [CrossRef]
- Truong, V.H.; Pham, H.A.; Tangaramvong, S. An efficient method for nonlinear inelastic truss optimization based on improved k-nearest neighbor comparison and Rao algorithm. Structures 2025, 71, 108158. [Google Scholar] [CrossRef]
- Su, R.; Zhang, X.; Tangaramvong, S.; Song, C. Adaptive scaled boundary finite element method for two/three-dimensional structural topology optimization based on dynamic responses. Comput. Methods Appl. Mech. Eng. 2024, 425, 116966. [Google Scholar] [CrossRef]
- Ma, Q.; Rejab, M.R.M.; Siregar, J.P.; Guan, Z. A review of the recent trends on core structures and impact response of sandwich panels. J. Compos. Mater. 2021, 55, 2513–2555. [Google Scholar] [CrossRef]
- Ma, Q.; Rejab, M.R.M.; Song, Y.; Zhang, X.; Hanon, M.M.; Abdullah, M.H.; Kumar, A.P. Effect of infill pattern of polylactide acid (PLA) 3D-printed integral sandwich panels under ballistic impact loading. Mater. Today Commun. 2024, 38, 107626. [Google Scholar] [CrossRef]







| X-SVR | Neural Network | Gaussian Processes | Numerical Results | ||
|---|---|---|---|---|---|
| Case 1 | Results | 0.592507 | 0.593272 | 0.592305 | 0.592516 |
| RE (%) | 0.0015 | 0.1276 | 0.0356 | ||
| Case 2 | Results | 0.590369 | 0.590586 | 0.590562 | 0.590247 |
| RE (%) | 0.0207 | 0.0574 | 0.0533 | ||
| Case 3 | Results | 0.594512 | 0.594243 | 0.594135 | 0.594518 |
| RE (%) | 0.0010 | 0.0462 | 0.0645 |
| Variational Material Properties | Distribution Type | Mean | Standard Deviation | Interval |
|---|---|---|---|---|
| Uniform | 1300 | 6.5 | [1267.5, 1332.5] | |
| Normal | 0.33 | 0.0264 | [0.23, 0.43] | |
| Normal | 1000 | 60 | [810, 1190] | |
| Lognormal | 3.6376 | 0.1819 | [20, 70] |
| Indicator | EA | ||
|---|---|---|---|
| 0.9875 | 0.9990 | 0.9779 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Feng, Y.; Gao, W. Virtual Modelling Framework-Based Inverse Study for the Mechanical Metamaterials with Material Nonlinearity. Modelling 2025, 6, 24. https://doi.org/10.3390/modelling6010024
Tian Y, Feng Y, Gao W. Virtual Modelling Framework-Based Inverse Study for the Mechanical Metamaterials with Material Nonlinearity. Modelling. 2025; 6(1):24. https://doi.org/10.3390/modelling6010024
Chicago/Turabian StyleTian, Yuhang, Yuan Feng, and Wei Gao. 2025. "Virtual Modelling Framework-Based Inverse Study for the Mechanical Metamaterials with Material Nonlinearity" Modelling 6, no. 1: 24. https://doi.org/10.3390/modelling6010024
APA StyleTian, Y., Feng, Y., & Gao, W. (2025). Virtual Modelling Framework-Based Inverse Study for the Mechanical Metamaterials with Material Nonlinearity. Modelling, 6(1), 24. https://doi.org/10.3390/modelling6010024







