Abstract
The rise of telehealth in smart cities has introduced both opportunities and challenges, particularly in securing sensitive patient data and ensuring reliable authentication. This paper presents a chaos-based dynamic authentication scheme designed to address these challenges. Utilizing the inherent unpredictability and sensitivity of chaotic systems, the proposed method ensures robust protection against various attacks, including replay, brute-force, man-in-the-middle, collision, and parameter prediction. The scheme operates through a dynamic challenge–response mechanism using chaotic maps, which generate highly unpredictable authentication parameters. Simulations demonstrate the system’s strong resilience, minimal collision rate, and adaptability to diverse telehealth devices. By safeguarding sensitive telehealth data and promoting secure access control, this research provides a foundational framework for implementing secure authentication systems in smart cities. Future directions include real-world deployment and integration with advanced technologies like blockchain to further enhance security and scalability.
1. Introduction
Telehealth has revolutionized modern healthcare by enabling remote, efficient, and accessible medical services, an essential advancement in the era of smart cities. The integration of advanced technologies such as the Internet of Things (IoT) [1], 5G connectivity [2], and artificial intelligence (AI) [3] has accelerated the adoption of telehealth, providing real-time monitoring, automated diagnosis, and remote consultations. As cities continue to develop smart infrastructures, governments and healthcare institutions are increasingly prioritizing telehealth solutions to enhance public health services, reduce hospital congestion, and improve healthcare accessibility [4,5]. However, the widespread use of interconnected telehealth platforms raises significant security concerns that must be addressed to protect sensitive patient data [6].
Telehealth systems process large volumes of sensitive medical data, including Electronic Health Records (EHRs), medical images, real-time physiological readings, and personal health information (PHI). Ensuring the confidentiality, integrity, and availability of these data is critical for maintaining trust and the reliability of healthcare services [7]. However, securing telehealth infrastructures poses several challenges. First, these systems operate in diverse environments with varying security levels, often relying on public networks, which increases their exposure to unauthorized access and cyber threats [8]. Additionally, Adhering to legal frameworks like the Health Insurance Portability and Accountability Act (HIPAA) [9] and the General Data Protection Regulation (GDPR) [10] necessitates implementing stringent data protection measures. HIPAA mandates safeguarding Protected Health Information (PHI), encompassing any data that can identify a patient, such as names, addresses, and medical records. Similarly, GDPR enforces strict guidelines on processing personal data, including health-related information, to uphold individual privacy rights. Compliance with these regulations requires robust encryption and strict access controls to ensure the confidentiality and integrity of sensitive information.
Traditional authentication methods, such as passwords, multi-factor authentication (MFA), and biometric verification, face significant limitations in telehealth environments. Passwords and PINs are vulnerable to phishing, brute-force, and dictionary attacks, while MFA adds complexity, particularly for elderly patients or individuals with limited digital literacy [11,12]. Furthermore, biometric authentication methods, including fingerprint and facial recognition [13], require specialized hardware that may not be available on all devices and are susceptible to spoofing and replay attacks. These limitations highlight the need for a more adaptive and resilient authentication framework that can address the evolving security threats in telehealth.
To address security and data management challenges in telehealth, a centralized architecture is often employed, where multiple entities—including patients, physicians, telehealth platforms, and medical databases—interact through a secure central hub. This structure facilitates controlled data access, and enhances system reliability by integrating authentication and encryption protocols. A conceptual representation of this centralized telehealth model is illustrated in Figure 1, where the central hub acts as a secure intermediary, ensuring efficient communication and data exchange among all participating entities.
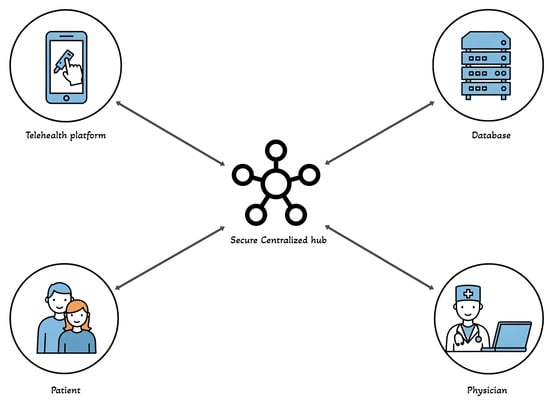
Figure 1.
Centralized telehealth model where key entities—patients, physicians, telehealth platforms, and databases—interact through a secure hub, ensuring efficient data management and controlled access.
To further enhance security, this paper introduces a chaos-based authentication method tailored to telehealth environments. Unlike conventional authentication mechanisms that rely on static credentials, chaotic systems exploit randomness and exhibit sensitivity to initial conditions, and non-linearity to generate dynamic authentication parameters that are highly resistant to attacks. This approach ensures that authentication credentials continuously evolve, providing robust protection against replay attacks, where attackers attempt to reuse captured credentials, man-in-the-middle attacks, where communication is intercepted and altered. At the core of this method lies a carefully designed 1D chaotic equation, which exhibits high sensitivity to initial conditions and parameter variations. This property makes it computationally infeasible for adversaries to predict or reconstruct authentication parameters. Potential applications of this method in telehealth scenarios include securing patient data transmission in telecare medicine information systems (TMIS) and enhancing authentication protocols for remote healthcare services. This paper is structured as follows:
2. Background and Related Work
2.1. Telehealth and Smart Cities
The integration of telehealth services into smart city infrastructures has revolutionized healthcare delivery, enabling real-time monitoring and remote consultations [14]. This advancement uses Internet of Things (IoT) devices and wireless communication technologies to provide efficient and accessible healthcare services to urban populations [15]. However, the widespread adoption of telehealth in smart cities introduces significant security and privacy challenges that must be addressed to ensure the safety and confidentiality of patient information [16,17].
2.2. Authentication in Telehealth
Authentication is a critical component in telehealth systems, ensuring that only authorized users and devices can access sensitive medical data [18,19,20]. Traditional authentication methods, such as passwords and PINs, have proven inadequate due to vulnerabilities like phishing and brute-force attacks [21,22,23]. To address these weaknesses, biometric authentication has been explored as an alternative. Recent advancements in biometric authentication aim to mitigate traditional vulnerabilities. For instance, the adoption of advanced biometric schemes, including those utilizing the Social Internet of Things (SIoT), has been proposed to enhance security in e-healthcare applications [24]. While these solutions offer improved resistance to spoofing attacks, their implementation must account for factors such as user acceptance, processing overhead, and potential privacy concerns to ensure they do not impede the accessibility and efficiency of telehealth services [25,26,27].
To enhance security, multi-factor authentication (MFA) has been proposed, combining multiple factors such as something the user knows (e.g., password), something the user has (e.g., smart card), and something the user is (e.g., biometric trait) [28,29]. Studies indicate that integrating MFA into telemedicine significantly reduces security risks related to unauthorized access to patient data [20]. However, balancing security with user convenience and system efficiency remains a challenge, as complex authentication mechanisms can hinder accessibility [30,31].
Recent advancements in telehealth authentication have explored the integration of blockchain technology to enhance security and decentralization. For instance, a blockchain-based user authentication scheme incorporating access control and physical unclonable functions (PUF) has been proposed to ensure secure data sharing across healthcare providers and device identification [32]. Additionally, the implementation of federated authentication systems, which allow multiple healthcare providers to share authentication credentials securely, has been recognized as a means to streamline access while maintaining data integrity [33]. Adherence to international standards, such as ISO 27799 [34], which provides guidelines for information security management in health using ISO/IEC 27002, and the NIST Cybersecurity Framework [35], which offers a structured approach to managing and mitigating cybersecurity risks , is crucial in ensuring that telehealth systems meet global security benchmarks. Additionally, the ethical considerations of biometric authentication in telehealth remain a critical challenge [36]. The use of biometric identifiers, such as facial recognition and fingerprints, raises concerns regarding privacy, consent management, and potential biases in authentication models. A recent analysis of biometric privacy frameworks highlights the necessity for strict data governance, informed consent policies, and enhanced encryption techniques to ensure compliance with global healthcare security regulations. Addressing these ethical and legal considerations is crucial for the responsible deployment of biometric technologies in telehealth environments, ensuring both security and patient trust in authentication mechanisms.
2.3. Chaos-Based Security in Telehealth
Chaotic maps, known for their ergodicity, sensitivity to initial conditions, and nonlinearity, have been widely utilized to enhance security mechanisms in telehealth systems. Their inherent unpredictability makes them suitable for developing encryption algorithms that protect sensitive medical data against various security threats [37]. In medical image encryption, chaos-based methods have demonstrated significant potential. For instance, Javan et al. [38] proposed an encryption technique leveraging the multi-mode synchronization of hyper-chaotic systems, while Kiran et al. [39] introduced a SCAN- and chaotic map-based model for securing e-healthcare images.
For secure telemedicine communication, Ettiyan and Geetha [40] developed a hybrid encryption scheme integrating DNA-based encryption and chaotic systems for lightweight wearable medical devices. Additionally, Michel et al. [41] proposed a multi-user communication scheme based on binary phase shift keying (BPSK) and the two-dimensional Hénon map within a direct sequence spread spectrum (DS/SS) framework to ensure biosignal privacy.
Chaos-based encryption techniques have also been applied to physiological signal protection. In the domain of ECG signal encryption, Cárdenas-Valdez et al. [42] presented a chaotic-based system for enhancing data integrity during telemedicine transmission. Similarly, Rajasree et al. [43] employed Hénon and Baker maps for ECG signal encryption, while Murillo et al. [44] introduced a double chaotic layer encryption algorithm for clinical signals in telemedicine. For EEG signals, Shahzadi et al. [45] utilized optical chaos for secure remote monitoring, and Lin et al. [46] developed a chaos-based encryption approach specifically tailored for EEG data.
Beyond encryption, chaos-based authentication schemes have been proposed to strengthen telehealth security. Kamble et al. [47] demonstrated the effectiveness of conformal Chebyshev chaotic maps in constructing authentication protocols for telemedicine services. Meanwhile, Li et al. [48] introduced a dynamic identity-based authentication scheme leveraging chaotic maps to ensure anonymity and resistance against impersonation attacks.
These studies collectively highlight the potential of chaos-based security approaches in addressing critical challenges in telehealth, offering robust solutions for encryption, secure communication, and authentication in medical data transmission.
2.4. Motivation for the Proposed Approach
While existing authentication methods have their merits, they often fall short in addressing the unique security challenges and hardware limitations of many of these chaotic systems [49]. The dynamic and distributed nature of telehealth devices, coupled with the sensitivity of patient data, necessitates a more robust and adaptable authentication mechanism. This work proposes a chaos-based authentication method aiming to overcome the limitations of traditional approaches by taking advantage of the inherent properties of chaotic systems while utilizing a hardware-friendly new 1D-map.
3. Proposed 1D Chaotic Map: The Asymmetric Cubic Logistic Map (ACLM)
The proposed map, termed the Asymmetric Cubic Logistic Map (ACLM), is defined by the following recurrence relation:
where r and s are control parameters. The first term corresponds to the classical logistic map, while the second term introduces an asymmetric cubic modification. The additional term influences the map’s behavior by shifting the nonlinearity, effectively breaking the symmetry of the classical logistic function.
The primary motivation for introducing this modification is to enhance the map’s chaotic properties and increase the complexity of the resulting dynamics, making it more suitable for authentication and cryptographic applications.
3.1. Bifurcation Diagram Analysis
A fundamental way to understand the dynamic behavior of a chaotic map is through its bifurcation diagram, which illustrates the long-term steady-state behavior of as a function of the parameter values. Figure 2 presents the bifurcation diagrams of the ACLM for different values of r while varying s. The results indicate that the classical period-doubling route to chaos is visible for moderate values of r. As s increases, the bifurcation structure shifts, leading to earlier transitions into chaotic behavior. For larger values of s, the diagram exhibits more fragmented bands, indicating a richer chaotic structure than the standard logistic map. The breaking of symmetry in the diagram is evident, reinforcing the impact of the cubic term on the system dynamics.
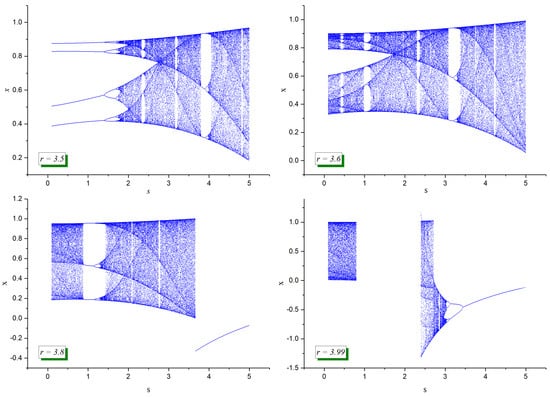
Figure 2.
Bifurcation diagrams of the ACLM for different values of r and s.
3.2. Lyapunov Exponent Analysis
To quantify chaos, the Lyapunov exponent (LE) is computed, which measures the sensitivity of trajectories to initial conditions. The Lyapunov exponent is defined as follows:
Figure 3a shows the Lyapunov exponent as a function of the parameter s and . The results confirm that the Lyapunov exponent remains positive over a wide range of s, indicating strong chaotic behavior. Higher values of s tend to increase the LE, which implies an enhanced level of unpredictability in the map.
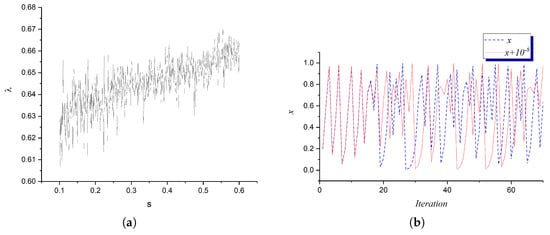
Figure 3.
(a) Lyapunov exponent as a function of s and (b) sensitivity to initial conditions in the ACLM.
3.3. Sensitivity to Initial Conditions
A defining characteristic of chaotic maps is their extreme sensitivity to initial conditions, meaning that two trajectories starting from slightly different initial values diverge exponentially over time. Figure 3b illustrates this property by comparing two trajectories initialized with a minute difference of . The results indicate that the two sequences remain close for a short period before deviating significantly, highlighting the unpredictable nature of the ACLM.
3.4. Phase Space Representation
The phase space plots of the ACLM, shown in Figure 4, depict the relationship between and for different parameter values. As r increases, the shape of the attractor deforms, reflecting the impact of s in shifting the symmetry. The maps exhibit dense chaotic regions, confirming their suitability for cryptographic applications. While certain parameter values result in periodic orbits, others generate fully chaotic structures.
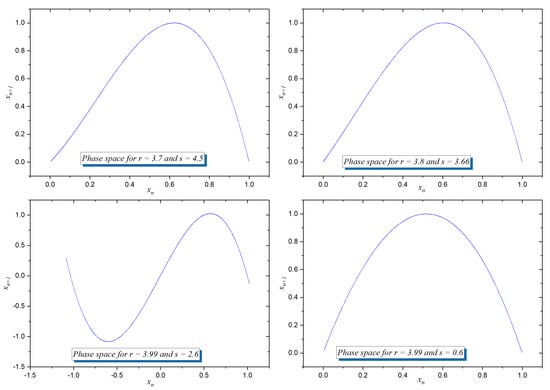
Figure 4.
Phase space plots for different values of r and s.
3.5. Implications for Authentication Applications
The ACLM exhibits strong chaotic properties, as evidenced by its bifurcation diagram, positive Lyapunov exponents, phase space complexity, and sensitivity to initial conditions. These characteristics make it well suited for authentication mechanisms, where unpredictability and complexity are crucial. The asymmetric nature of the map adds an additional layer of security, making it resistant to conventional cryptanalysis techniques that rely on symmetric chaotic systems. Furthermore, the parameter-dependent shift in nonlinearity enables the flexible tuning of its chaotic properties, allowing for adaptable security configurations in authentication frameworks.
4. Proposed Challenge–Response Authentication Scheme
Challenge–response authentication (CRA) is a widely used security mechanism where an entity (the verifier) sends a challenge to another entity (the prover), who must compute and return a valid response to prove authenticity. This approach ensures that authentication occurs without exposing sensitive credentials, thereby enhancing security [50].
Traditional CRA mechanisms rely on cryptographic techniques such as hash-based and public-key cryptography-based authentication. However, these methods can be vulnerable to replay attacks, man-in-the-middle (MITM) attacks, and brute-force attempts [51]. To address these security challenges, this work exploits the proposed ACLM map, harnessing its sensitivity to initial conditions and deterministic randomness to design a challenge–response authentication scheme that strengthens security, mitigates common attack vectors, and enables efficient authentication in resource-constrained telehealth applications.
The proposed authentication scheme consists of four main phases. In the enrollment phase, the telehealth device (TD) and the user’s authorized device (UD) securely synchronize their shared chaotic parameters, which are stored locally to prevent interception. The challenge generation phase follows, where the TD computes a unique chaotic challenge value based on a predefined number of iterations and appends a timestamp to ensure freshness and protect against replay attacks. Next, during the response generation phase, the UD utilizes the received challenge and shared chaotic parameters to generate an authentication response through additional iterations of the chaotic map. Finally, in the verification phase, the TD replicates the response computation to validate the received response, granting access if the values are within the acceptable tolerance and the challenge remains within its validity period. This structured process ensures secure, efficient, and attack-resistant authentication in telehealth environments.
4.1. Enrollment Phase
Figure 5 depicts the enrollment phase where both the Telehealth Device (TD) and the User’s Authorized Device (UD) securely synchronize their shared chaotic parameters, {r, s, }. These parameters are stored locally on both devices and are never transmitted over the network to prevent interception. This phase ensures that both devices share identical configurations, enabling consistent chaotic behavior during subsequent phases.
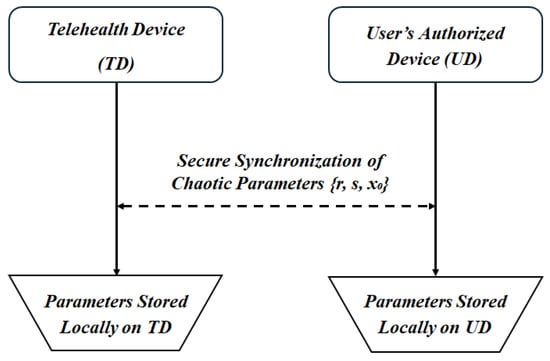
Figure 5.
Enrollment phase of the proposed system where system parameters are synchronized and stored.
4.2. Challenge Generation
The TD initiates the authentication process by generating a unique challenge based on the proposed ACLM chaotic map, as illustrated in Figure 6. Using the shared initial value , the TD performs N iterations of the chaotic map defined by Equation (1) to compute a chaotic value . For example, iterations might yield . To ensure temporal uniqueness, the TD incorporates a timestamp T into the challenge.
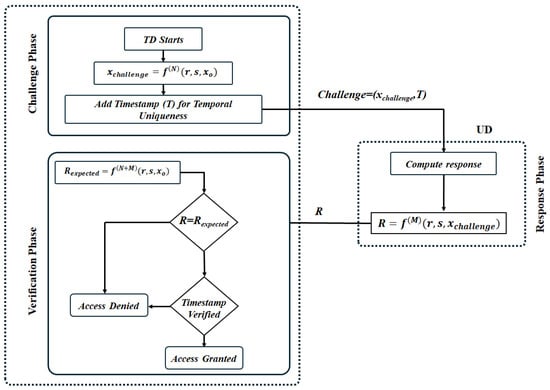
Figure 6.
Overview of the authentication process. The figure illustrates the following three phases: (1) challenge generation, where the TD computes a unique chaotic challenge with a timestamp; (2) response generation, where the UD computes a response using the received challenge; and (3) verification phase, where the TD validates the response and determines the authentication outcome.
The generated challenge is represented as follows:
where T is the timestamp, and is the chaotic output after N iterations. The timestamp helps in preventing replay attacks and ensures the challenge remains valid within a predefined time window.
4.3. Response Generation
Upon receiving the challenge from the TD, the UD computes a response to prove its authenticity, as shown in the response phase of Figure 6. The UD uses the shared chaotic parameters and performs M iterations of the chaotic map starting from . The response is calculated as follows:
where denotes M iterations of the chaotic map. This response is sent back to the TD for verification.
4.4. Verification Phase
The TD verifies the authenticity of the UD by replicating the response generation process. Using the received challenge , the TD performs the same M iterations of the chaotic map to compute the expected response , as follows:
As depicted in the verification phase of Figure 6, the TD compares the received response with . If the two values match within a predefined tolerance, authentication is deemed successful as follows:
Conversely, if the two values do not match, access is denied as follows:
Additionally, the TD verifies that the challenge has not expired by checking the validity of the timestamp T using the threshold . If T falls outside the acceptable range, the TD rejects the response and terminates the authentication process, ensuring protection against replay attacks and stale challenges.
To illustrate the scheme, consider the following example. During the challenge generation phase, the TD computes after 10 iterations of the chaotic map. The UD then calculates a response by performing five additional iterations. The TD verifies the response by replicating the same five iterations, confirming that . Since , authentication is successful.
4.5. Security Advantages
The proposed scheme offers the following advantages: 1. Unpredictability: The chaotic map’s sensitivity to initial conditions ensures responses are highly unpredictable. 2. Replay attack resistance: Each challenge is unique due to its dependence on the chaotic map and timestamp, preventing the reuse of previous responses. 3. No secret exposure: The shared parameters and chaotic map remain securely stored in the devices and are never transmitted. 4. Efficiency: The chaotic map computations are lightweight and suitable for resource-constrained devices like telehealth systems.
This combination of chaos-based dynamics and robust authentication mechanisms makes the scheme highly suitable for secure access control in telehealth applications.
5. Simulation Results and Analysis
To evaluate the security and robustness of the proposed chaotic-based dynamic authentication scheme, several attack scenarios were simulated, including replay, brute-force, man-in-the-middle (MITM), collision, and parameter prediction attacks. The following subsections provide detailed analysis, supported by graphical visualizations, and summarize the results in a consolidated table.
5.1. Noise Tolerance Analysis
Chaotic-based authentication systems are inherently sensitive to initial conditions, which can lead to inefficiencies by preventing authenticated users from gaining access due to even minimal perturbations. This sensitivity poses a fundamental challenge, as noise in real-world communication channels can disrupt authentication. To mitigate this issue, we leverage the transient phase of the proposed chaotic map. During this phase, trajectories that start from slightly different initial conditions remain nearly similar before diverging in later iterations. By carefully selecting N, M, or other control parameters within this transient region, authentication stability can be preserved while maintaining the system’s security guarantees. This approach allows the system to settle before extracting the authentication response, reducing the effects of initial condition sensitivity and enhancing reliability.
To evaluate the robustness of the proposed authentication scheme against noise perturbations, we conducted a False Rejection Rate (FRR) analysis under varying noise levels. The system’s sensitivity to small perturbations was tested by modifying different parameters, including the challenge–response iterations , the chaotic map parameter r, the asymmetry parameter s, and the response matching threshold .
Authentication in the system is performed by iterating the chaotic function in (1) for N steps to generate the challenge and applying an additional M iterations to compute the response using (4). The computed response is verified by ensuring that the expected and received values are within an acceptable error threshold .
The False Rejection Rate (FRR) is defined as follows:
We tested noise levels in the range and ran 1000 trials per configuration. For each trial, the authentication process was executed with the same parameter settings, and the system determined whether the authentication was successful or resulted in a false rejection. The FRR was then computed as the proportion of failed authentications over the total trials, ensuring a statistically meaningful analysis.
The transient phase played a crucial role in mitigating the effects of noise by allowing slight perturbations to remain within tolerable bounds before chaotic divergence set in. However, increasing N and M had a pronounced effect on FRR, as shown in Figure 7a. While larger values of N and M enhance security by making authentication responses more unpredictable, they also make the system more susceptible to noise. This effect is particularly evident when , where FRR reaches 100%, even at , indicating that excessive iterations amplify sensitivity to small perturbations.
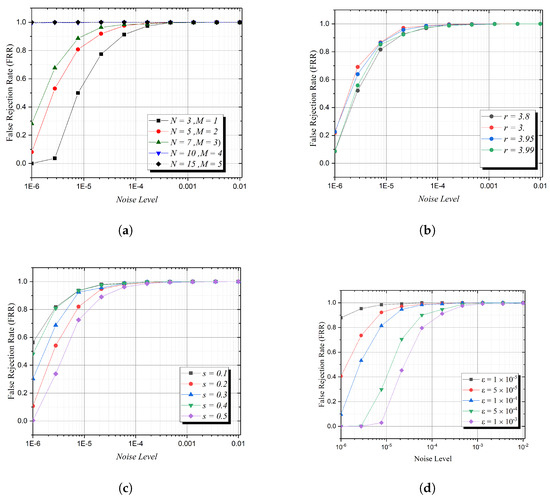
Figure 7.
Impact of different parameters on noise tolerance in authentication. (a) Effect of on FRR, (b) effect of r on FRR, (c) effect of s on FRR, (d) effect of threshold on FRR.
The influence of the chaotic parameter r on FRR, illustrated in Figure 7b, highlights that higher values of r (closer to ) significantly increase instability. As r approaches its upper bound, the chaotic system becomes more sensitive to initial condition variations, leading to a higher probability of authentication failures when noise is introduced.
Similarly, the asymmetry parameter s exhibits a direct correlation with FRR, as depicted in Figure 7c. Larger values of s increase nonlinearity, which enhances security but at the cost of reduced noise tolerance. Authentication stability is compromised as s grows, making it essential to find an optimal balance that maintains security while minimizing the unnecessary rejection of valid users.
The selection of the response matching threshold is another critical factor in ensuring noise resilience, as demonstrated in Figure 7d. A low imposes a strict matching criterion, increasing the likelihood of false rejections, while a high improves tolerance but may reduce security. Our experiments show that setting provides an effective compromise, significantly reducing FRR while maintaining authentication robustness.
These results emphasize that a carefully tuned configuration of and is necessary to achieve a balance between security and reliability. The transient phase approach successfully mitigates sensitivity issues, demonstrating that moderate values of , lower s, and an adaptive threshold can effectively enhance authentication performance in noisy environments.
5.2. Replay Attack
Replay attacks occur when an adversary intercepts a valid challenge–response pair and reuses it to gain unauthorized access. The effectiveness of such attacks depends on factors such as the time window in which responses remain valid, network conditions, and the attacker’s ability to capture and resend authentication data. If the response remains valid for too long, an attacker may successfully replay a previously captured response within that timeframe, bypassing authentication.
In its current state, the proposed authentication scheme employs timestamps to limit the validity of each challenge–response pair. When a challenge is issued, the Telehealth Device (TD) includes a timestamp T, and the User Device (UD) must respond before the response expires. Authentication is considered valid only if the following holds:
where is the expiration threshold for authentication responses. However, research suggests that replay attacks may still be feasible within a short period, particularly in environments where authentication traffic can be intercepted with minimal delay.
The chaotic nature of the authentication system provides additional security by making it computationally infeasible for an attacker to regenerate valid responses. Even if a valid response is captured, an adversary cannot accurately compute the next valid response without knowing the shared chaotic parameters and the iteration count M. However, without additional safeguards, a recorded response could be replayed within the authentication window, presenting a security risk.
To mitigate this vulnerability, enhancements can be introduced to further limit the feasibility of replay attacks. A one-time challenge-use policy should be enforced, ensuring that once a challenge has been successfully used, it is marked and cannot be reused within the system. This can be represented as follows:
where represents the set of previously used challenges. Another effective measure is the introduction of nonce-based validation, where a unique nonce N is incorporated into each session, ensuring that even if an attacker intercepts a response, it cannot be reused in subsequent authentication attempts. This modification alters the response computation as follows:
To further strengthen the authentication mechanism, HMAC authentication can be implemented. This approach ensures message integrity and prevents response reuse by incorporating a cryptographic key K into the authentication response. The new authentication equation is expressed as follows:
Since the key K is never transmitted, an attacker cannot forge or replay a valid response, even if they possess previously intercepted challenge–response pairs.
While the existing authentication scheme provides a robust foundation using chaotic maps, additional security measures such as one-time-use challenges, nonce-based validation, and cryptographic authentication further enhance its resilience against replay attacks. By integrating these modifications, the risk of successful replay attacks is significantly reduced, while maintaining system efficiency and usability.
5.3. Brute-Force Attack
Brute-force attacks involve an adversary randomly guessing responses to a given challenge in an attempt to match the correct response. The proposed chaotic-based authentication scheme is inherently resistant to such attacks due to the unpredictability, nonlinearity, and extreme sensitivity of the response to variations in the chaotic map parameters and the iteration count M. Without precise knowledge of these parameters, an attacker can only rely on random guessing, making brute-force attacks infeasible.
In our experimental setup, a challenge is issued, and a valid response is generated using the Asymmetric Cubic Logistic Map (ACLM) with predefined parameters. The attacker then attempts to guess the response through random sampling over attempts. To evaluate the system’s resistance to such attacks, we measure the probability of successfully guessing the correct response within a given tolerance , where authentication is granted if the following holds:
Figure 8a presents the probability of a brute-force attempt succeeding as a function of the tolerance . As expected, reducing the tolerance significantly decreases the probability of an attacker correctly guessing the response. For , the success rate is approximately , but as is reduced to , the probability of success drops to nearly zero, emphasizing the effectiveness of the chaotic authentication scheme in resisting brute-force attacks.
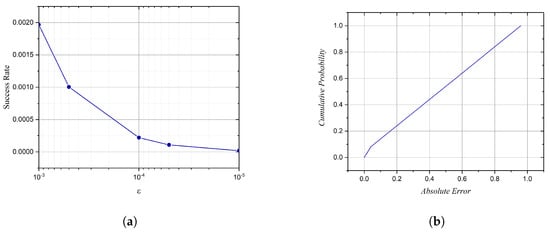
Figure 8.
Visualization of brute-force attack resilience. (a) The probability of success in guessing the correct response decreases significantly with stricter tolerance. (b) The CDF confirms that brute−force guesses follow a uniform error distribution, reinforcing the unpredictability of the chaotic authentication system.
The sensitivity to initial conditions in the ACLM further strengthens security. Even minor deviations in initial values or parameters lead to drastically different responses, ensuring that two nearly identical challenge inputs will produce highly divergent outputs. This property, combined with the secret iteration count M, makes response prediction virtually impossible, even with exhaustive search methods. Additionally, the system exhibits ergodicity, meaning that the response space is uniformly distributed, preventing an attacker from inferring statistical patterns.
Figure 8b further illustrates the robustness of the system through the Cumulative Distribution Function (CDF) of the absolute error between guessed responses and the true response. The CDF represents the probability that a guessed response deviates from the correct value by at most a given error threshold. A linear increase in the CDF suggests that the guessing distribution is entirely uniform, with no regions of higher probability density. This confirms that brute-force attempts result in uniformly random errors, reinforcing the notion that an adversary cannot exploit any predictable structure in the response space.
The results demonstrate that, without knowledge of the exact chaotic parameters and iteration count, an attacker is left with a purely random guessing strategy. Given the low probability of success at small tolerance values, the system effectively nullifies brute-force attacks, ensuring secure authentication.
5.4. Collision Attack
Collision attacks occur when multiple challenges produce identical responses, potentially compromising security. In a secure authentication scheme, each challenge must yield a unique response to ensure the integrity of the system. The chaotic map used in the proposed authentication method is designed to minimize such collisions, making use of its inherent sensitivity to initial conditions and parameter variations.
In the simulated attack, 100 random challenges were generated, and their corresponding responses were computed using the chaotic map. The results, visualized in Figure 9, show that no two challenges produced identical responses, demonstrating the system’s resilience against collision attacks. Blue dots represent unique responses for each challenge, and any collisions, if present, would have been marked in red for clear identification. The absence of red markers affirms the robustness of the chaotic map in preventing collisions and ensuring a secure response distribution.
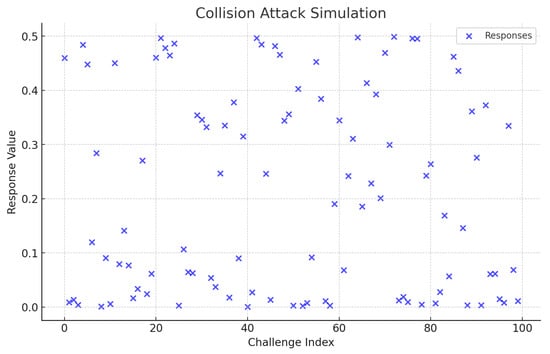
Figure 9.
Collision attack simulation. Blue dots represent unique responses for each challenge. The absence of red markers indicates no collisions, showcasing the chaotic map’s resilience against collision attacks.
The chaotic map’s ability to generate highly sensitive and unique responses for even slight variations in input ensures that collision attacks are effectively mitigated. This property is critical for maintaining the security and reliability of the authentication system, especially in environments handling large volumes of sensitive data.
5.5. Parameter Prediction Attack
In this simulation, an adversary attempts to infer the chaotic parameters r and s of the Asymmetric Cubic Logistic Map (ACLM) to reconstruct the response for a given challenge. The attack assumes that the number of iterations used to compute the response, N and M, is known to the adversary. The optimization process employs the Particle Swarm Optimization (PSO) algorithm, where the adversary uses the challenge value alone to estimate the underlying chaotic parameters.
For each attempt, a random challenge is generated using the ACLM (1). The adversary, lacking knowledge of the true values of r and s, attempts to optimize these parameters using PSO. The objective is to minimize the error between the actual authentication response and the response generated with the estimated parameters as follows:
where the estimated response is obtained by applying M additional iterations of the chaotic map as follows:
The results of the attack are illustrated in Figure 10. Each valid response, computed using the true chaotic parameters, is shown as a blue dot, while the corresponding response generated using the optimized parameters is represented by a red dot. Dotted gray lines connect the two responses for each challenge, emphasizing the deviation between the actual and predicted responses.
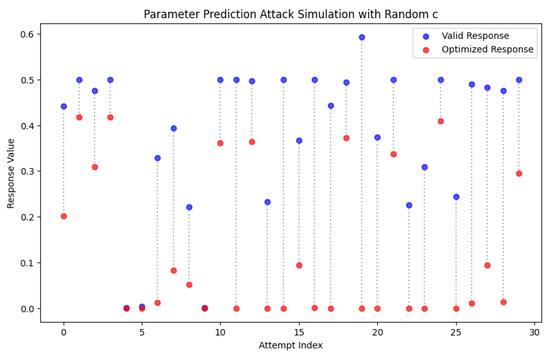
Figure 10.
Parameter prediction attack simulation with PSO. Blue stars represent valid responses, red stars represent responses based on optimized parameters, and gray dotted lines highlight the deviations. The results demonstrate the chaotic map’s robustness against parameter prediction attacks.
The results confirm that the chaotic system’s extreme sensitivity to initial conditions and high nonlinearity introduce significant deviations between the valid and guessed responses, making parameter estimation highly unreliable. Even with sophisticated optimization techniques such as PSO, the adversary fails to accurately reconstruct the authentication response. This outcome underscores the resilience of the ACLM-based authentication system against parameter prediction attacks, ensuring that an attacker cannot derive the necessary chaotic parameters to replicate valid responses.
5.6. Performance Estimation in Telehealth Processors
To provide insight into the computational efficiency of the proposed chaos-based authentication scheme, we estimate its execution time and energy consumption using hardware platforms commonly employed in telehealth applications. Among the most widely used processors in embedded medical devices are ARM Cortex-M4 (Arm Ltd., Cambridge, UK) and Texas Instruments MSP430 (Texas Instruments Inc., Dallas, TX, USA) [52,53], both known for their ability to balance processing power with energy efficiency. ARM Cortex-M4 [54] is a 32-bit processor designed with a 3-stage pipeline, DSP instructions, and an optional Floating Point Unit (FPU), making it well suited for real-time signal processing. In contrast, the MSP430 [55] is a 16-bit ultra-low-power microcontroller optimized for wearable health monitoring systems, featuring multiple low-power modes and fast wake-up capabilities to extend battery life in portable devices.
Since direct hardware testing is not conducted in this study, an estimation approach is used to approximate execution time and energy consumption based on known processor characteristics. The MATLAB (Version 9.14, MathWorks, Natick, MA, USA) [56] implementation of the authentication scheme is rewritten in C to align with embedded system constraints, ensuring compatibility with ARM Cortex-M4 and MSP430 architectures. The total number of CPU cycles required for authentication is then analyzed based on each processor’s instruction set. Given that each microcontroller executes operations at different speeds, execution time is estimated using the following formula:
where f represents the processor’s clock speed (in Hz). To estimate energy consumption, we use a standard power model where the total estimated energy E required per authentication cycle is calculated as follows:
where P is the estimated power consumption of the processor (in watts). The estimated execution time and energy consumption for the full authentication process are presented in Table 1. The column labeled “Estimated Algorithm Execution Cycles” refers to the total number of processor cycles required to execute the entire authentication scheme, including challenge generation, response computation, and verification. This metric is specific to the algorithm and is not to be confused with the general cycle characteristics of the processors themselves.

Table 1.
Estimated computational overhead and energy consumption for chaos-based authentication.
The estimated execution time and estimated energy consumption suggest that the proposed authentication scheme is highly efficient and suitable for low-power telehealth devices. On the ARM Cortex-M4, the scheme completes authentication in an estimated 50 µs, consuming approximately an estimated 2.5 µJ of energy, demonstrating its capability to operate in real-time applications with minimal energy requirements. On the TI MSP430, authentication completes in an estimated 1.25 ms, with an estimated energy consumption of 6.25 µJ, making it a viable choice for wearable medical devices that require energy efficiency. These estimates suggest that the proposed authentication scheme provides a lightweight and computationally efficient alternative to traditional authentication mechanisms, with significantly lower estimated execution time and estimated energy demands.
Since these results are based on estimations, future research will focus on validating these estimated metrics through direct hardware implementation and empirical testing to further optimize real-world performance.
6. Practical Considerations and Deployment Strategies
Although the proposed chaos-based authentication scheme demonstrates strong security properties and computational efficiency, certain practical considerations must be taken into account when transitioning from theoretical feasibility to real-world implementation. One such factor is the adaptability of the system across different hardware architectures. The authentication process relies on precise numerical computations, where floating-point arithmetic variations between different processing units (e.g., 16-bit, 32-bit, or 64-bit architectures) can introduce slight deviations in chaotic trajectory calculations. These discrepancies arise due to differences in bit representation and rounding behavior, potentially leading to authentication failures even for valid users. To mitigate this, the implementation ensures that both the Token Device (TD) and the User Device (UD) operate under the same numerical precision standard. The fixed-point arithmetic method can also be utilized in constrained embedded environments to eliminate floating-point inconsistencies. Furthermore, adaptive precision synchronization protocols can be introduced to dynamically adjust precision tolerance thresholds, reducing the likelihood of false rejections caused by hardware-level differences. Another consideration is authentication stability across different system configurations, particularly in noisy environments. The system’s sensitivity to initial conditions, while a key security feature, also requires careful parameter selection to balance unpredictability with robustness. The noise tolerance analysis conducted in this study demonstrates that the scheme remains resilient under reasonable noise levels when using optimized values of N and M. However, at extreme values of these parameters, authentication performance can be affected due to increased response divergence. To address this, adaptive error thresholds were introduced, allowing controlled deviations in authentication responses to accommodate small perturbations while maintaining security integrity. By addressing these practical considerations and implementing the outlined mitigation strategies, the proposed authentication scheme can maintain its efficiency, security, and adaptability across a wide range of telehealth applications, reinforcing its viability for real-world deployment.
7. Conclusions
This paper introduced a chaotic-based dynamic authentication scheme tailored for secure telehealth applications in smart cities. Through simulations and analysis, the scheme demonstrated robust protection against various attack scenarios, including replay, brute-force, collision, and parameter prediction attacks. The inherent properties of chaotic maps, such as unpredictability and sensitivity to initial conditions, were instrumental in achieving high levels of security. The results validate the practicality and effectiveness of the proposed approach, providing a reliable framework for safeguarding sensitive telehealth data. While the proposed chaotic authentication scheme has demonstrated strong security properties through simulations, real-world implementation and testing remain essential next steps. Future work will involve collaboration with healthcare and IT security professionals to refine the proposed authentication model and address real-world deployment challenges. In addition to that, integrating blockchain-based authentication mechanisms could enhance the security and scalability of the proposed scheme, enabling decentralized identity management in telehealth environments. Additionally, conducting a user experience (UX) study would provide valuable insights into the usability and adaptability of the authentication process in real-world clinical settings.
Author Contributions
Conceptualization, R.A.E.; Methodology, M.N.; Software, R.A.E.; Validation, R.A.E.; Writing—original draft, R.A.E.; Writing—review and editing, M.N.; Project administration, R.A.E.; Funding acquisition, R.A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by Institutional Fund Projects under grant no. (IFPIP:1116-144-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Graham, C.M.; Jones, N. Impact of IoT on geriatric telehealth. Work. Older People 2020, 24, 231–243. [Google Scholar] [CrossRef]
- Georgiou, K.E.; Georgiou, E.; Satava, R.M. 5G use in healthcare: The future is present. JSLS J. Soc. Laparosc. Robot. Surg. 2021, 25, e2021.00064. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Woo, S.; Ferrell, A. Artificial intelligence assisted telehealth for nursing: A scoping review. J. Telemed. Telecare 2025, 31, 140–149. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, M.B.; Rajagopal, S.; Prieto-Simón, B.; Pogue, B.W. Recent advances in smart wearable sensors for continuous human health monitoring. Talanta 2024, 272, 125817. [Google Scholar] [CrossRef]
- Morita, P.P.; Sahu, K.S.; Oetomo, A. Health monitoring using smart home technologies: Scoping review. JMIR MHealth UHealth 2023, 11, e37347. [Google Scholar] [CrossRef]
- Mohammadzadeh, Z.; Saeidnia, H.R.; Lotfata, A.; Hassanzadeh, M.; Ghiasi, N. Smart city healthcare delivery innovations: A systematic review of essential technologies and indicators for developing nations. BMC Health Serv. Res. 2023, 23, 1180. [Google Scholar] [CrossRef]
- Kruse, C.S.; Frederick, B.; Jacobson, T.; Monticone, D.K. Cybersecurity in healthcare: A systematic review of modern threats and trends. Technol. Health Care 2017, 25, 1–10. [Google Scholar] [CrossRef]
- Cui, L.; Xie, G.; Qu, Y.; Gao, L.; Yang, Y. Security and privacy in smart cities: Challenges and opportunities. IEEE Access 2018, 6, 46134–46145. [Google Scholar] [CrossRef]
- Health Insurance Portability and Accountability Act of 1996. 1996. Available online: https://www.govinfo.gov/app/details/PLAW-104publ191 (accessed on 8 February 2025).
- Regulation (EU) 2016/679 of the European Parliament and of the Council of 27 April 2016 on the Protection of Natural Persons with Regard to the Processing of Personal Data and on the Free Movement of Such Data, and Repealing Directive 95/46/EC (General Data Protection Regulation). 2016. Available online: https://eur-lex.europa.eu/eli/reg/2016/679/oj (accessed on 8 February 2025).
- Sharma, M.K.; Nene, M.J. Two-factor authentication using biometric based quantum operations. Secur. Priv. 2020, 3, e102. [Google Scholar] [CrossRef]
- Karuppiah, M.; Saravanan, R. Cryptanalysis and an improvement of new remote mutual authentication scheme using smart cards. J. Discret. Math. Sci. Cryptogr. 2015, 18, 623–649. [Google Scholar] [CrossRef]
- Lien, C.W.; Vhaduri, S. Challenges and opportunities of biometric user authentication in the age of iot: A survey. ACM Comput. Surv. 2023, 56, 1–37. [Google Scholar] [CrossRef]
- Atkinson, J.; Hastie, R.; Walker, S.; Lindquist, A.; Tong, S. Telehealth in antenatal care: Recent insights and advances. BMC Med. 2023, 21, 332. [Google Scholar] [CrossRef] [PubMed]
- Poongodi, M.; Sharma, A.; Hamdi, M.; Maode, M.; Chilamkurti, N. Smart healthcare in smart cities: Wireless patient monitoring system using IoT. J. Supercomput. 2021, 77, 12230–12255. [Google Scholar] [CrossRef]
- Sookhak, M.; Tang, H.; He, Y.; Yu, F.R. Security and privacy of smart cities: A survey, research issues and challenges. IEEE Commun. Surv. Tutor. 2018, 21, 1718–1743. [Google Scholar] [CrossRef]
- Ismagilova, E.; Hughes, L.; Rana, N.P.; Dwivedi, Y.K. Security, privacy and risks within smart cities: Literature review and development of a smart city interaction framework. Inf. Syst. Front. 2022, 24, 393–414. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, J. A secure three-factor-based authentication with key agreement protocol for e-Health clouds. J. Supercomput. 2021, 77, 3359–3380. [Google Scholar] [CrossRef]
- Sodhro, A.H.; Awad, A.I.; van de Beek, J.; Nikolakopoulos, G. Intelligent authentication of 5G healthcare devices: A survey. Internet Things 2022, 20, 100610. [Google Scholar] [CrossRef]
- Suleski, T.; Ahmed, M.; Yang, W.; Wang, E. A review of multi-factor authentication in the Internet of Healthcare Things. Digit. Health 2023, 9, 20552076231177144. [Google Scholar] [CrossRef]
- Mishra, D.; Mukhopadhyay, S. Cryptanalysis of Wu and Xu’s authentication scheme for Telecare Medicine Information Systems. arXiv 2013, arXiv:1309.5255. [Google Scholar]
- Wang, X.; Yan, Z.; Zhang, R.; Zhang, P. Attacks and defenses in user authentication systems: A survey. J. Netw. Comput. Appl. 2021, 188, 103080. [Google Scholar] [CrossRef]
- Zukarnain, Z.A.; Muneer, A.; Ab Aziz, M.K. Authentication securing methods for mobile identity: Issues, solutions and challenges. Symmetry 2022, 14, 821. [Google Scholar] [CrossRef]
- Arpitha, T.; Chouhan, D.; Shreyas, J. Anonymous and robust biometric authentication scheme for secure social IoT healthcare applications. J. Eng. Appl. Sci. 2024, 71, 8. [Google Scholar] [CrossRef]
- Matyáš, V.; Říha, Z. Biometric authentication—Security and usability. In Advanced Communications and Multimedia Security, Proceedings of the IFIP TC6/TC11 Sixth Joint Working Conference on Communications and Multimedia Security, Portorož, Slovenia, 26–27 September 2002; Springer: Boston, MA, USA, 2002; pp. 227–239. [Google Scholar]
- Abdullahi, S.M.; Sun, S.; Wang, B.; Wei, N.; Wang, H. Biometric template attacks and recent protection mechanisms: A survey. Inf. Fusion 2024, 103, 102144. [Google Scholar] [CrossRef]
- Sharma, S.; Saini, A.; Chaudhury, S. A survey on biometric cryptosystems and their applications. Comput. Secur. 2023, 134, 103458. [Google Scholar] [CrossRef]
- Wang, D.; He, D.; Wang, P.; Chu, C.H. Anonymous two-factor authentication in distributed systems: Certain goals are beyond attainment. IEEE Trans. Dependable Secur. Comput. 2014, 12, 428–442. [Google Scholar] [CrossRef]
- Khajehzadeh, L.; Barati, H.; Barati, A. L2AI: Lightweight three-factor authentication and authorization in IOMT blockchain-based environment. arXiv 2024, arXiv:2407.12187. [Google Scholar]
- Baseer, S.; Charumathi, K. Multi-Factor Authentication: A User Experience Study. 2024. Available online: https://ssrn.com/abstract=4840295 (accessed on 14 March 2025).
- Ogbanufe, O.M.; Baham, C. Using multi-factor authentication for online account security: Examining the influence of anticipated regret. Inf. Syst. Front. 2023, 25, 897–916. [Google Scholar] [CrossRef]
- Shi, S.; Luo, M.; Wen, Y.; Wang, L.; He, D. A Blockchain-Based User Authentication Scheme with Access Control for Telehealth Systems. Secur. Commun. Netw. 2022, 2022, 6735003. [Google Scholar] [CrossRef]
- Goswami, S.A.; Dave, S.; Patel, K.C. Healthcare Informatics Security Issues and Solutions Using Federated Learning. In Federated Learning for Smart Communication Using IoT Application; Chapman and Hall/CRC: Boca Raton, FL, USA, 2024; pp. 124–154. [Google Scholar]
- ISO 27799:2016; Health Informatics—Information Security Management in Health Using ISO/IEC 27002. ISO: Geneva, Switzerland, 2016. Available online: https://www.iso.org/standard/62777.html (accessed on 14 March 2025).
- NIST CSWP 29; The NIST Cybersecurity Framework (CSF) 2.0. National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024. [CrossRef]
- Kluge, E.H.W. Ethical and legal challenges for health telematics in a global world: Telehealth and the technological imperative. In The Ethical Challenges of Emerging Medical Technologies; Routledge: Oxfordshire, UK, 2020; pp. 223–227. [Google Scholar]
- Elmanfaloty, R.A.; Alnajim, A.M.; Abou-Bakr, E. A finite precision implementation of an image encryption scheme based on DNA encoding and binarized chaotic cores. IEEE Access 2021, 9, 136905–136916. [Google Scholar] [CrossRef]
- Javan, A.A.K.; Jafari, M.; Shoeibi, A.; Zare, A.; Khodatars, M.; Ghassemi, N.; Alizadehsani, R.; Gorriz, J.M. Medical images encryption based on adaptive-robust multi-mode synchronization of Chen hyper-chaotic systems. Sensors 2021, 21, 3925. [Google Scholar] [CrossRef]
- Kiran, M.; Gururaj, H.; Almeshari, M.; Alzamil, Y.; Ravi, V.; Sudeesh, K. Efficient SCAN and Chaotic Map Encryption System for Securing E-Healthcare. Sensors 2023, 24, 47. [Google Scholar] [CrossRef]
- Ettiyan, R.; Geetha, V. A hybrid logistic DNA-based encryption system for securing the Internet of Things patient monitoring systems. Healthc. Anal. 2023, 3, 100149. [Google Scholar] [CrossRef]
- Michel-Macarty, J.A.; Murillo-Escobar, M.A.; López-Gutiérrez, R.M.; Cruz-Hernández, C.; Cardoza-Avendaño, L. Multiuser communication scheme based on binary phase-shift keying and chaos for telemedicine. AEU-Int. J. Electron. Commun. 2018, 96, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Cárdenas-Valdez, J.R.; Ramírez-Villalobos, R.; Ramirez-Ubieta, C.; Inzunza-Gonzalez, E. Enhancing Security of Telemedicine Data: A Multi-Scroll Chaotic System for ECG Signal Encryption and RF Transmission. Entropy 2024, 26, 787. [Google Scholar] [CrossRef] [PubMed]
- Rajasree, G.; Kumar, M.S. Secure transmission and monitoring of ECG signals based on chaotic mapping algorithms. Autom. časopis Autom. Mjer. Elektron. Računarstvo Komun. 2024, 65, 957–972. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cardoza-Avendaño, L.; López-Gutiérrez, R.M.; Cruz-Hernández, C. A double chaotic layer encryption algorithm for clinical signals in telemedicine. J. Med. Syst. 2017, 41, 59. [Google Scholar] [CrossRef]
- Shahzadi, R.; Anwar, S.M.; Qamar, F.; Ali, M.; Rodrigues, J.J.; Alnowami, M. Secure EEG signal transmission for remote health monitoring using optical chaos. IEEE Access 2019, 7, 57769–57778. [Google Scholar] [CrossRef]
- Lin, C.F.; Shih, S.H.; Zhu, J.D. Chaos-based encryption system for encrypting electroencephalogram signals. J. Med. Syst. 2014, 38, 49. [Google Scholar] [CrossRef]
- Kamble, A.; Gaikwad, V.; Tembhurne, J. A provably lightweight mutually authentication and key establishment protocol using extended chaotic map for telecare medicine information system. Int. J. Inf. Technol. 2023, 15, 3211–3227. [Google Scholar] [CrossRef]
- Li, C.T.; Lee, C.C.; Weng, C.Y.; Chen, S.J. A secure dynamic identity and chaotic maps based user authentication and key agreement scheme for e-healthcare systems. J. Med. Syst. 2016, 40, 233. [Google Scholar] [CrossRef]
- Rizk, M.R.M.; Nasser, A.M.A.; El-Badawy, E.S.A.; Abou-Bakr, E. A new approach for obtaining all logic gates using Chua’s Circuit: Advantages and disadvantages. In Proceedings of the 2012 International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 3–5 July 2012; pp. 730–733. [Google Scholar] [CrossRef]
- Kushwaha, P.; Sonkar, H.; Altaf, F.; Maity, S. A brief survey of challenge–response authentication mechanisms. In ICT Analysis and Applications, Proceedings of ICT4SD 2020, Goa, India, 23–24 July 2020; Springer: Singapore, 2021; Volume 2, pp. 573–581. [Google Scholar]
- Idriss, T.A.; Idriss, H.A.; Bayoumi, M.A. A Lightweight PUF-Based Authentication Protocol Using Secret Pattern Recognition for Constrained IoT Devices. IEEE Access 2021, 9, 80546–80558. [Google Scholar] [CrossRef]
- Osama, M.; Ateya, A.A.; Sayed, M.S.; Hammad, M.; Pławiak, P.; Abd El-Latif, A.A.; Elsayed, R.A. Internet of medical things and healthcare 4.0: Trends, requirements, challenges, and research directions. Sensors 2023, 23, 7435. [Google Scholar] [CrossRef] [PubMed]
- Nivetha, B.; Kumar, E.S.M. Iot based nicu baby healthcare monitoring system. Mater. Today Proc. 2020, 33, 4837–4841. [Google Scholar] [CrossRef]
- Arm Ltd. Arm Cortex-M4 Processor Datasheet. 2018. Available online: https://developer.arm.com/documentation/102832/latest/ (accessed on 14 March 2025).
- Texas Instruments. MSP430G2x53, MSP430G2x13 Mixed Signal Microcontroller Datasheet. 2013. Available online: https://www.ti.com/lit/ds/symlink/msp430g2553.pdf (accessed on 14 March 2025).
- The MathWorks, Inc. MATLAB R2023a, version 9.14; The MathWorks, Inc.: Natick, MA, USA, 2023; Available online: https://www.mathworks.com (accessed on 14 March 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).