A Review of Finite Element Studies on Laser-Based Acoustic Applications in Solid Media
Abstract
:1. Introduction
2. Guided Ultrasonic Waves in Solid Media
2.1. Laser Ultrasonic Guided Waves
2.2. Laser Ultrasonic Guided Waves for Solid Material Characterization
2.3. Transducer-Generated Ultrasonic Guided Waves
3. Guided Ultrasonic Waves in Defect Identification
3.1. Laser Ultrasonic Guided Waves
3.2. Transducer-Generated Ultrasonic Guided Waves
4. Laser Ultrasonic Guided Waves in Biomedical Diagnostics
4.1. Laser Ultrasonic Guided Waves in Human Skin
4.2. Laser Ultrasonic Guided Waves in Dental Applications
5. FEM and Laser-Based Acoustics in Engineering Applications
6. Advances, Challenges, and Future Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Ciarlet, P.; Lunéville, E. The Finite Element Method: From Theory to Practice; Wiley: Hoboken, NJ, USA, 2023; pp. 1–376. [Google Scholar]
- Xu, C.; Li, W. Fundamentals of Ultrasonic Testing; CRC Press: Boca Raton, FL, USA, 2024; pp. 1–445. [Google Scholar]
- Farrar, C.R.; Dervilis, N.; Worden, K. The Past, Present and Future of Structural Health Monitoring: An Overview of Three Ages. Strain 2025, 61, e12495. [Google Scholar] [CrossRef]
- Patel, A.D.; Chopra, R.; Avram, M.; Sakamoto, F.H.; Kilmer, S.; Anderson, R.R.; Ibrahimi, O.A. Updates on Lasers in Dermatology. Dermatol. Clin. 2024, 42, 33–44. [Google Scholar] [CrossRef] [PubMed]
- Hassani, S.; Dackermann, U. A Systematic Review of Advanced Sensor Technologies for Non-Destructive Testing and Structural Health Monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Ding, L.; Wan, H.; Lu, Q.; Chen, Z.; Jia, K.; Ge, J.; Yan, X.; Xu, X.; Ma, G.; Chen, X.; et al. Using Deep Learning to Identify the Depth of Metal Surface Defects with Narrowband SAW Signals. Opt. Laser Technol. 2023, 157, 108758. [Google Scholar] [CrossRef]
- Zhang, J.; Wan, H.; Sun, F.; Chen, X.; Jia, K.; Fan, L.; Cheng, L.; Xu, X.; Yan, X.; Yuan, P.; et al. Laser ultrasonic inspection of surface and subsurface defects in materials based on deep learning. Nondestruct. Test. Eval. 2024, 1–20. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bedford, A.; Drumheller, D.S. Introduction to Elastic Wave Propagation; Springer: Cham, Switzerland, 2023; pp. 1–378. [Google Scholar]
- Scruby, C.B.; Drain, L.E. Laser Ultrasonics: Techniques and Applications; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Zarei, A.; Pilla, S. Laser Ultrasonics for Nondestructive Testing of Composite Materials and Structures: A Review. Ultrasonics 2024, 136, 107163. [Google Scholar] [CrossRef]
- Spytek, J.; Ambrozinski, L.; Pelivanov, I. Non-Contact Detection of Ultrasound with Light—Review of Recent Progress. Photoacoustics 2023, 29, 100440. [Google Scholar] [CrossRef]
- Davis, S.J.; Edwards, C.; Taylor, G.S.; Palmer, S.B. Laser-Generated Ultrasound: Its Properties, Mechanism, and Multifarious Applications. J. Phys. D Appl. Phys. 1993, 26, 329–348. [Google Scholar] [CrossRef]
- Xu, B.; Shen, Z.; Wang, J.; Ni, X.; Guan, J.; Lu, J. Thermoelastic Finite Element Modeling of Laser Generation Ultrasound. J. Appl. Phys. 2006, 99, 033508. [Google Scholar] [CrossRef]
- Lee, J.H.; Burger, C.P. Finite Element Modeling of Laser-Generated Lamb Waves. Comput. Struct. 1995, 54, 499–514. [Google Scholar] [CrossRef]
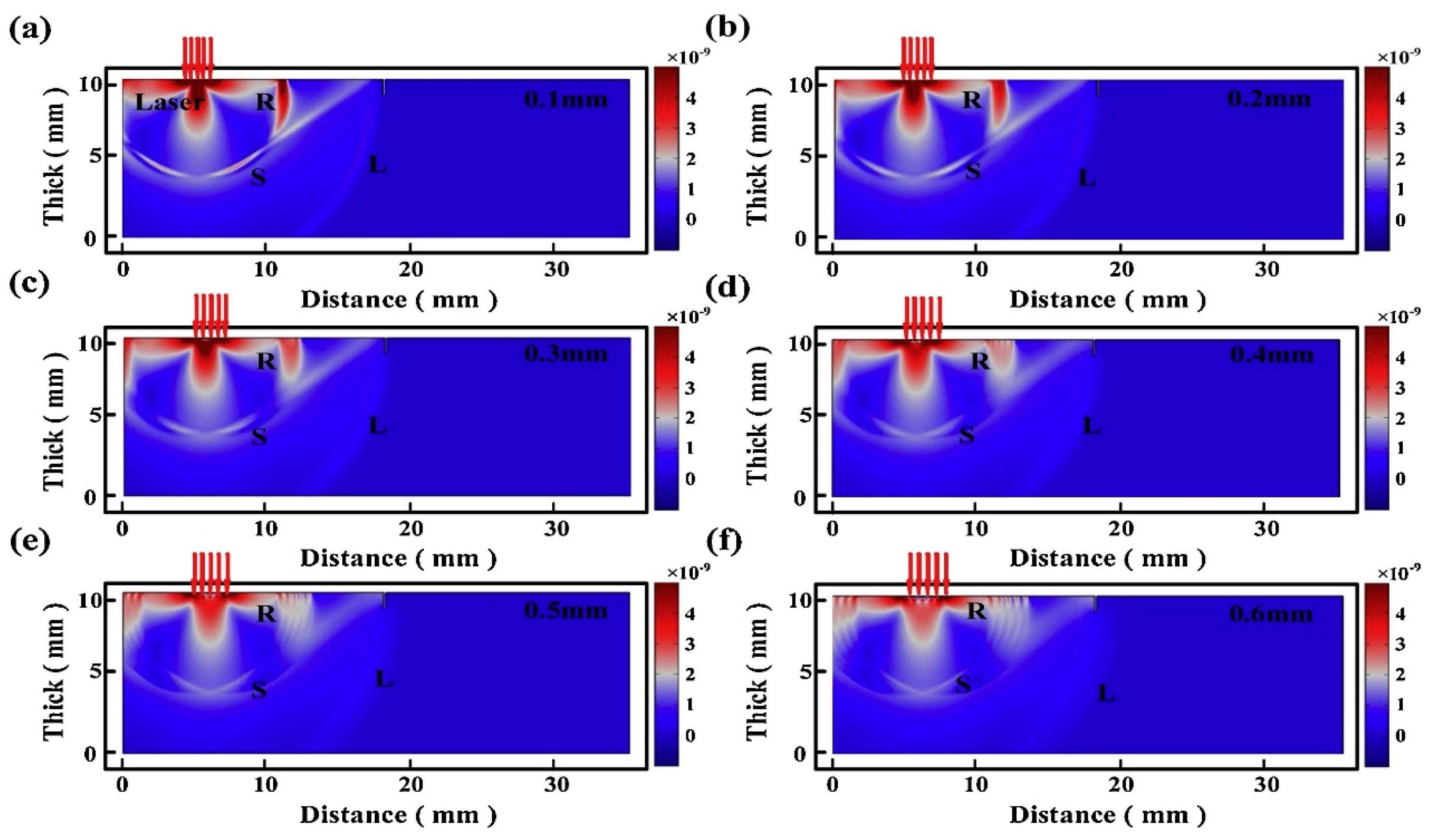
- Xu, B.; Shen, Z.; Ni, X.; Lu, J.; Wang, Y. Finite Element Model of Laser-Generated Surface Acoustic Waves in Coating-Substrate System. J. Appl. Phys. 2004, 95, 2109–2115. [Google Scholar]
- Shen, Z.; Xu, B.; Ni, X.; Lu, J. Numerical Simulation of Laser-Generated Ultrasonic Waves in Layered Plates. J. Phys. D Appl. Phys. 2004, 37, 2364–2370. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Z.; Ni, X.; Xu, B.; Guan, J.; Lu, J. Numerical Simulation of Laser-Generated Surface Acoustic Waves in the Transparent Coating on a Substrate by the Finite Element Method. Opt. Laser Technol. 2007, 39, 21–28. [Google Scholar]
- Wang, J.; Shen, Z.; Xu, B.; Ni, X.; Guan, J.; Lu, J. Numerical Simulation of Laser-Generated Ultrasound in Non-Metallic Material by the Finite Element Method. Opt. Laser Technol. 2007, 39, 806–813. [Google Scholar] [CrossRef]
- Zhao, Y.; Shen, Z.; Lu, J.; Ni, X. Simulation on Laser-Induced Surface Acoustic Wave on Isotropic Cylinders by Finite Element Method. Opt. Laser Technol. 2007, 39, 774–777. [Google Scholar]
- Xu, B.; Feng, J.; Xu, G.; Wang, J.; Sun, H.; Cao, G. Laser-Generated Thermoelastic Acoustic Sources and Lamb Waves in Anisotropic Plates. Appl. Phys. A 2008, 91, 173–179. [Google Scholar]
- Xu, B.; Wang, F.; Feng, J.; Wang, J.; Sun, H.; Luo, Y. Laser-Generated Thermoelastic Acoustic Sources and Acoustic Waves in Anisotropic Plate. Sci. China Ser. E-Tech. Sci. 2009, 52, 566–574. [Google Scholar]
- Tang, S.-W.; Yang, C.-H. A Comparison of Laser Ultrasound Measurements and Finite-Element Simulations for the Dispersion Behavior of Antisymmetric Flexural Modes Propagating along Wedge Tips with Coatings. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2674–2682. [Google Scholar] [CrossRef]
- Cerniglia, D.; Pantano, A.; Mineo, C. Influence of Laser Beam Profile on the Generation of Ultrasonic Waves. Appl. Phys. A 2011, 105, 959–967. [Google Scholar]
- Feng, W.; Yang, D.; Zhu, X.; Guo, Y.; Liao, W. Simulation of Laser-Generated Longitudinal and Shear Ultrasonic Waves in a Diamond Anvil Cell by the Finite Element Method. J. Appl. Phys. 2012, 111, 013107. [Google Scholar]
- Dixon, S.; Harrison, T.; Fan, Y.; Petcher, P.A. Thermoelastic Laser Generated Ultrasound Using a Ring Source. J. Phys. D Appl. Phys. 2012, 45, 175103. [Google Scholar] [CrossRef]
- Soltani, P.; Akbareian, N. Finite Element Simulation of Laser Generated Ultrasound Waves in Aluminum Plates. Lat. Am. J. Solids Struct. 2014, 11, 1761–1776. [Google Scholar] [CrossRef]
- Dimitriou, V.; Kaselouris, E.; Orphanos, Y.; Bakarezos, M.; Vainos, N.; Tatarakis, M.; Papadogiannis, N.A. Three Dimensional Transient Behavior of Thin Films Surface under Pulsed Laser Excitation. Appl. Phys. Lett. 2013, 103, 114104. [Google Scholar]
- Dimitriou, V.; Kaselouris, E.; Orphanos, Y.; Bakarezos, M.; Vainos, N.; Nikolos, I.K.; Tatarakis, M.; Papadogiannis, N.A. The Thermo-Mechanical Behavior of Thin Metal Films under Nanosecond Laser Pulse Excitation Above the Thermoelastic Regime. Appl. Phys. A 2015, 118, 739–748. [Google Scholar] [CrossRef]
- Kaselouris, E.; Nikolos, I.K.; Orphanos, Y.; Bakarezos, E.; Papadogiannis, N.A.; Tatarakis, M.; Dimitriou, V. Elastoplastic study of nanosecond-pulsed laser interaction with metallic films using 3D multiphysics fem modeling. Int. J. Damage Mech. 2016, 25, 42–55. [Google Scholar]
- Abdullaev, A.; Muminov, B.; Rakhymzhanov, A.; Mynbayev, N.; Utegulov, Z.N. Examination of Nanosecond Laser Melting Thresholds in Refractory Metals by Shear Wave Acoustics. AIP Adv. 2017, 7, 075203. [Google Scholar]
- Guan, Y.-J.; Sun, H.-X.; Yuan, S.-Q.; Ge, Y.; Xia, J.-P. Propagation Characteristics of Laser-Generated Surface Acoustic Waves in Composite Plate with Gradient Changes of Near-Surface Viscous Moduli. Acta Phys. Sin. 2016, 65, 224201. [Google Scholar] [CrossRef]
- Grabec, T.; Veres, I.A.; Ryzy, M. Surface Acoustic Wave Attenuation in Polycrystals: Numerical Modeling Using a Statistical Digital Twin of an Actual Sample. Ultrasonics 2022, 119, 106585. [Google Scholar] [CrossRef]
- Liang, X.; Lin, B.; Liu, Z.; Ma, X. Study on Dispersion and Attenuation of Laser-Induced Surface Acoustic Wave by Grinding Surface Roughness. Appl. Acoust. 2022, 199, 109028. [Google Scholar]
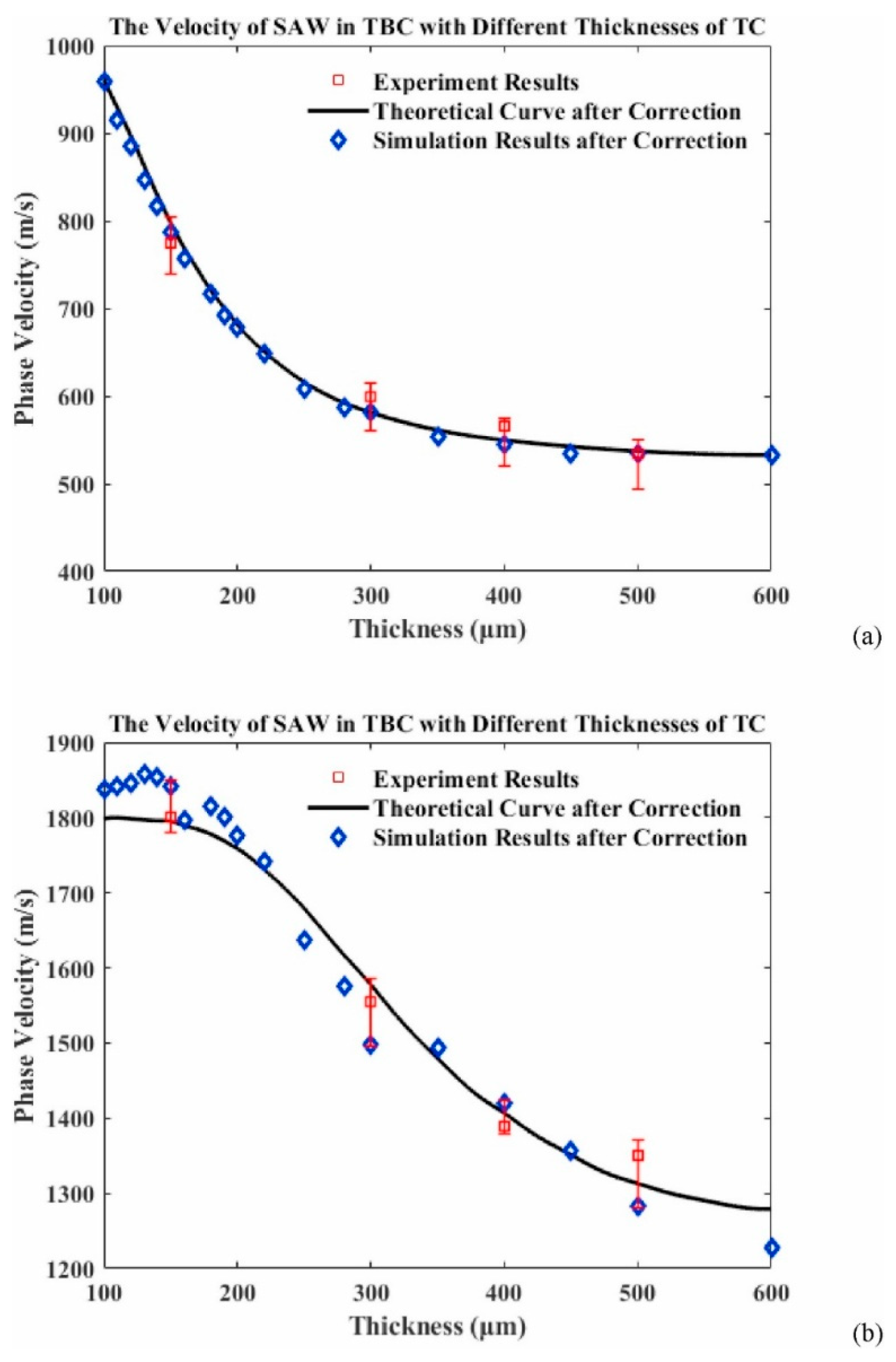
- Huang, Y.; Li, B.; Chen, L.; Zhang, Z.; Qin, F. Influence of Top-Coat Thickness of Thermal Barrier Coating on Time–Frequency Domain and Dispersion Characteristics of Laser-Induced Surface Acoustic Wave. Appl. Acoust. 2023, 203, 109230. [Google Scholar]
- Papadaki, H.; Kaselouris, E.; Bakarezos, M.; Tatarakis, M.; Papadogiannis, N.A.; Dimitriou, V. A Computational Study of Solid Si Target Dynamics under ns Pulsed Laser Irradiation from Elastic to Melting Regime. Computation 2023, 11, 240. [Google Scholar] [CrossRef]
- Giannetti, C.; Revaz, B.; Banfi, F. Thermomechanical Behavior of Surface Acoustic Waves in Ordered Arrays of Nanodisks Studied by Near-Infrared Pump-Probe Diffraction Experiments. Phys. Rev. B 2007, 76, 125413. [Google Scholar] [CrossRef]
- Nakamura, A.; Shimojima, T.; Ishizaka, K. Finite-Element Simulation of Photoinduced Strain Dynamics in Silicon Thin Plates. Struct. Dyn. 2021, 8, 024103. [Google Scholar] [PubMed]
- Kosma, K.; Kaleris, K.; Kaselouris, E.; Kaniolakis-Kaloudis, E.; Petrakis, S.; Orphanos, Y.; Gagaoudakis, E.; Binas, V.; Bakarezos, E.; Tatarakis, M.; et al. Pump-Probe Reflectivity Studies of Ultrashort Laser-Induced Acousto-Mechanical Strains in ZnO Films. Appl. Phys. A 2023, 129, 597. [Google Scholar] [CrossRef]
- Kaleris, K.; Kaniolakis-Kaloudis, E.; Kaselouris, E.; Kosma, K.; Gagaoudakis, E.; Binas, V.; Petrakis, S.; Dimitriou, V.; Bakarezos, M.; Tatarakis, M.; et al. Efficient Ultrafast Photoacoustic Transduction on Tantalum Thin Films. Appl. Phys. A 2023, 129, 527. [Google Scholar]
- Wang, Z.; Min, J.; Hu, J.; Wang, Z.; Chen, X.; Tang, Z.; Liu, S. Femtosecond Laser-Acoustic Modeling and Simulation for AlCu Nanofilm Nondestructive Testing. Front. Mech. Eng. 2024, 19, 33. [Google Scholar] [CrossRef]
- Xu, B.; Shen, Z.; Ni, X.; Wang, J.; Guan, J.; Lu, J. Determination of Elastic Properties of a Film-Substrate System by Using the Neural Networks. Appl. Phys. Lett. 2004, 85, 6161–6163. [Google Scholar]
- Yuan, L.; Shi, Y.; Shen, Z.; Ni, X. Laser-Induced Ultrasonic Waves in Steels with Gradient Changes of Elastic Property. Opt. Laser Technol. 2008, 40, 325–329. [Google Scholar]
- Dong, L.; Li, J.; Ni, C.; Shen, Z.; Ni, X. Evaluation of Residual Stresses Using Laser-Generated SAWs on Surface of Laser-Welding Plates. Int. J. Thermophys. 2013, 34, 1066–1079. [Google Scholar]
- Sherman, B.; Liou, H.-C.; Balogun, O. Thin Film Interface Stresses Produced by High Amplitude Laser Generated Surface Acoustic Waves. J. Appl. Phys. 2015, 118, 135303. [Google Scholar]
- Knapp, M.; Lomonosov, A.M.; Warkentin, P. Accurate Characterization of SiO2 Thin Films Using Surface Acoustic Waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 736–743. [Google Scholar] [CrossRef]
- Zhan, Y.; Lin, Z.-Y.; Liu, C.-S. Experiment and Finite Element Simulation for Laser Ultrasonic Measurement of the Elastic Constants of Metal Materials. J. Northeast. Univ. 2018, 39, 1363–1368. [Google Scholar]
- Ye, C.; Ume, I.C.; Zhou, Y.; Reddy, V.V.B. Inspection of the Residual Stress on Welds Using Laser Ultrasonic Supported with Finite Element Analysis. Manuf. Rev. 2019, 6, 3. [Google Scholar]
- Zhang, L.; Xiao, X.; Qi, H.; Liu, Z.; Zhang, J.; Chen, L. Finite Element Simulation and Experimental Study of Laser-Generated Surface Acoustic Waves on Determining Mechanical Properties of Thin Film. J. Appl. Phys. 2022, 132, 245106. [Google Scholar]
- Qian, C.; Kou, X.; Pei, C.; Chen, Z. Topcoat Thickness Measurement of Thermal Barrier Coating Using Grating Laser Acoustic Spectrum Method. Ceram. Int. 2022, 48, 3676–3684. [Google Scholar]
- Meng, J.; Hou, W.; Li, X.; Song, C.; Zhang, J. Laser Ultrasonic Inspection for Mechanical Properties of Materials at High Temperature. J. Appl. Phys. 2023, 134, 053101. [Google Scholar]
- Burger, R.; Hallum, G.E.; Auer, R.; Schweiger, D.; Redka, D.; Domke, M.; Grosse, C.U.; Huber, H.P.; Wu, D. Velocimetry of GHz Elastic Surface Waves in Quartz and Fused Silica Based on Full-Field Imaging of Pump–Probe Reflectometry. Photoacoustics 2024, 38, 100627. [Google Scholar]
- Morvan, B.; Wilkie-Chancellier, N.; Duflo, H.; Tinel, A.; Duclos, J. Lamb Wave Reflection at the Free Edge of a Plate. J. Acoust. Soc. Am. 2003, 113, 1417–1425. [Google Scholar]
- Dutton, B.; Boonsang, S.; Dewhurst, R.J. A New Magnetic Configuration for a Small In-Plane Electromagnetic Acoustic Transducer Applied to Laser-Ultrasound Measurements: Modelling and Validation. Sens. Actuators A 2006, 125, 249–259. [Google Scholar] [CrossRef]
- Fromme, P.; Pizzolato, M.; Robyr, J.-L.; Masserey, B. Lamb Wave Propagation in Monocrystalline Silicon Wafers. J. Acoust. Soc. Am. 2018, 143, 287–295. [Google Scholar] [CrossRef]
- Weser, R.; Darinskii, A.N.; Weihnacht, M.; Schmidt, H. Experimental and Numerical Investigations of Mechanical Displacements in Surface Acoustic Wave Bounded Beams. Ultrasonics 2020, 106, 106077. [Google Scholar] [CrossRef] [PubMed]
- Park, S.-J.; Joo, Y.-S.; Kim, H.-W.; Kim, S.-K. Selective Generation of Lamb Wave Modes in a Finite-Width Plate by Angle-Beam Excitation Method. Sensors 2020, 20, 3868. [Google Scholar] [CrossRef]
- Mohammadgholiha, M.; Zonzini, F.; Moll, J.; De Marchi, L. Directional Multifrequency Guided Waves Communications Using Discrete Frequency-Steerable Acoustic Transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 70, 494–505. [Google Scholar]
- Jiang, C.; Li, W.; Ng, C.-T.; Deng, M. Numerical and Experimental Investigations on Quasistatic Pulse Generation of Ultrasonic Guided Waves in Fiber Reinforced Composite Pipes. J. Sound Vib. 2024, 574, 118238. [Google Scholar]
- Bouzzit, A.; Martinez, L.; Arciniegas, A.; Hebaz, S.-E.; Wilkie-Chancellier, N. Study of Rayleigh Waves Interaction with a Spherical Ball in Contact with a Plane Surface for the Development of a New NDT Method for Ball Bearings. Ultrasonics 2024, 136, 107156. [Google Scholar] [PubMed]
- Xie, L.; Lian, Y.; Du, F.; Wang, Y.; Lu, Z. Optical Methods of Laser Ultrasonic Testing Technology in Industrial and Engineering Applications: A Review. Optics Laser Technol. 2024, 176, 110876. [Google Scholar]
- Xu, X.; Ran, B.; Jiang, N.; Xu, L.; Huan, P.; Zhang, X.; Li, Z. A Systematic Review of Ultrasonic Techniques for Defects Detection in Construction and Building Materials. Measurement 2024, 226, 114181. [Google Scholar]
- Cerniglia, D.; Pantano, A. Experimental and Numerical Method for Nondestructive Ultrasonic Defect Detection. In Nondestructive Testing: Methods, Analyses and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2011; pp. 63–94. [Google Scholar]
- Sato, H.; Ogiso, H.; Yamanaka, K. Finite Element Method Analysis of Evaluation of Surface Micro Cracks Using Laser Ultrasound Generated by Phase Velocity Scanning Method. Jpn. J. Appl. Phys. 2003, 42, 3184–3188. [Google Scholar]
- Yamanaka, K.; Nagata, Y.; Koda, T. Selective Excitation of Single-Mode Acoustic Waves by Phase Velocity Scanning of a Laser Beam. Appl. Phys. Lett. 1991, 58, 1591–1593. [Google Scholar]
- Jeong, H. Finite Element Analysis of Laser-Generated Ultrasound for Characterizing Surface-Breaking Cracks. J. Mech. Sci. Technol. 2005, 19, 1116–1122. [Google Scholar]
- Guan, J.; Shen, Z.; Ni, X.; Wang, J.; Lu, J.; Xu, B. Numerical Simulation of the Reflected Acoustic Wave Components in the Near Field of Surface Defects. J. Phys. D Appl. Phys. 2006, 39, 1237–1243. [Google Scholar]
- Shi, Y.; Shen, Z.; Ni, X.; Lu, J.; Guan, J. Finite Element Modeling of Acoustic Field Induced by Laser Line Source Near Surface Defect. Opt. Express 2007, 15, 5512–5520. [Google Scholar] [PubMed]
- Fomitchov, P.A.; Kromine, A.K.; Sohn, Y.; Krishnaswamy, S.; Achenbach, J.D. Ultrasonic Imaging of Small Surface-Breaking Defects Using Scanning Laser Source Technique. Rev. Prog. Quant. Nondestruct. Eval. 2002, 21A, 356–362. [Google Scholar]
- Jian, X.; Fan, Y.; Edwards, R.S.; Dixon, S. Surface-Breaking Crack Gauging with the Use of Laser Generated Rayleigh Waves. J. Appl. Phys. 2006, 100, 064907. [Google Scholar]
- Jian, X.; Baillie, I.; Dixon, S. Steel Billet Inspection Using Laser-EMAT System. J. Phys. D Appl. Phys. 2007, 40, 1501–1506. [Google Scholar]
- Wang, J.-S.; Xu, X.-D.; Liu, X.-J.; Xu, G.-C. Low Pass Effect of Surface Defect Metal Based on Laser Ultrasonic. Acta Phys. Sin. 2008, 57, 7765–7769. [Google Scholar]
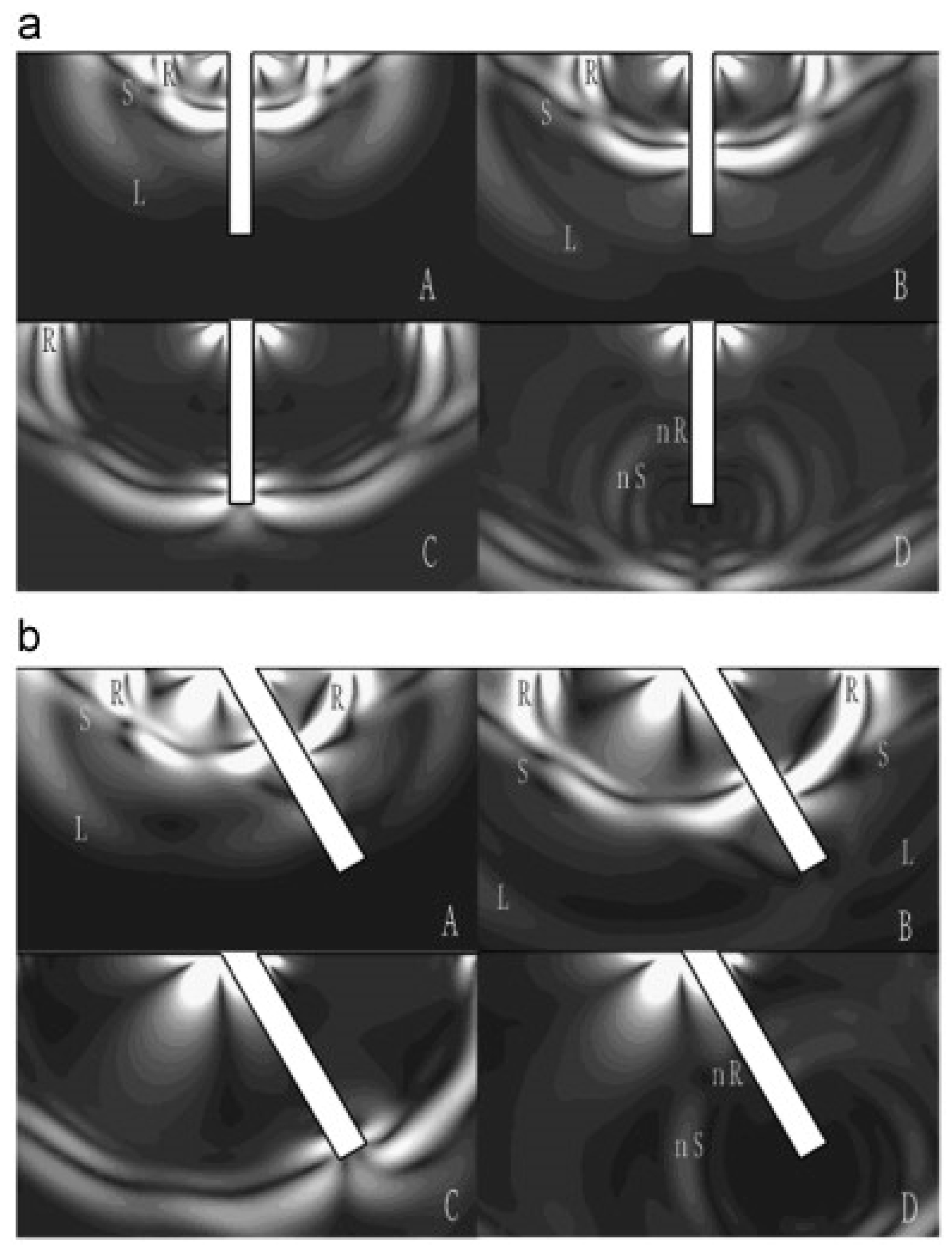
- Ni, C.; Shi, Y.; Shen, Z.; Lu, J.; Ni, X. An Analysis of Angled Surface-Breaking Crack Detection by Dual-Laser Source Generated Ultrasound. NDT&E Int. 2010, 43, 470–475. [Google Scholar]
- Ni, C.; Shi, Y.; Shen, Z.; Lu, J. Study of Dual-Laser-Generated Surface Acoustic Waves Interacting with Multiangled Surface Breaking Cracks by Finite Element Method. Jpn. J. Appl. Phys. 2010, 49, 046603. [Google Scholar]
- Dai, Y.; Xu, B.; Luo, Y.; Li, H.; Xu, G. Finite Element Modeling of the Interaction of Laser-Generated Ultrasound with a Surface-Breaking Notch in an Elastic Plate. Opt. Laser Technol. 2010, 42, 693–697. [Google Scholar]
- Guan, J. Numerical Study on Depth Gauging of Surface Breaking Defects Using Laser-Generated Surface Acoustic Waves. Jpn. J. Appl. Phys. 2011, 50, 032703. [Google Scholar]
- Dong, L.; Ni, C.; Shen, Z.; Ni, X. Numerical Simulation of Evaluation of Surface Breaking Cracks by Array-Lasers Generated Narrow-Band SAW. Acoust. Phys. 2011, 57, 730–736. [Google Scholar] [CrossRef]
- Pei, C.; Fukuchi, T.; Zhu, H.; Koyama, K.; Demachi, K.; Uesaka, M. A Study of Internal Defect Testing With the Laser-EMAT Ultrasonic Method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2702–2708. [Google Scholar] [PubMed]
- Burrows, S.E.; Dutton, B.; Dixon, S. Laser Generation of Lamb Waves for Defect Detection: Experimental Methods and Finite Element Modeling. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 82–89. [Google Scholar]
- Zeng, W.; Wang, H.-T.; Tian, G.-Y.; Hu, G.-X.; Wen, W. Research on the Oscillation Effect of Near-Surface Metal Defect Based on Laser-Generated Acoustic Surface Wave. Acta Phys. Sin. 2015, 64, 134302. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, K.; Zhou, J.; Sun, G.; Wang, J. Application of Laser Ultrasonic Technique for Non-Contact Detection of Structural Surface-Breaking Cracks. Opt. Laser Technol. 2015, 73, 173–178. [Google Scholar] [CrossRef]
- Ni, C.; Dong, L.; Shen, Z.; Ni, X.; Shi, D. Numerical Simulation Study of Defect Detections by Using Laser Array Generated Giant Acoustic Waves. Int. J. Thermophys. 2015, 36, 1236–1243. [Google Scholar] [CrossRef]
- Ni, C.; Dong, L.; Li, J.; Shen, Z.; Ni, X.; Shi, D. Study of Laser-Array-Source-Generated Narrow-Band Acoustic Waves Interacting with Surface-Breaking Cracks Using Finite Element Method. Int. J. Thermophys. 2015, 36, 1266–1273. [Google Scholar] [CrossRef]
- Chen, M.-I.; Tesng, S.-P.; Lo, P.-Y.; Yang, C.-H. Characterization of Wedge Waves Propagating Along Wedge Tips with Defects. Ultrasonics 2018, 82, 289–297. [Google Scholar] [CrossRef]
- Sun, G.; Zhao, L.; Dong, M.; Lou, X.; Zhu, L. Non-Contact Characterization of Debonding in Lead-Alloy Steel Bonding Structure with Laser Ultrasound. Optik 2018, 164, 734–744. [Google Scholar] [CrossRef]
- Orphanos, Y.; Kosma, K.; Kaselouris, E.; Vainos, N.; Dimitriou, V.; Bakarezos, M.; Tatarakis, M.; Papadogiannis, N.A. Integrated nanosecond laser full-field imaging for femtosecond laser-generated surface acoustic waves in metal film-glass substrate multilayer materials. Appl. Phys. A 2019, 125, 269. [Google Scholar] [CrossRef]
- Kaselouris, E.; Skarvelakis, E.; Nikolos, I.K.; Stavroulakis, G.E.; Orphanos, Y.; Bakarezos, E.; Papadogiannis, N.A.; Tatarakis, M.; Dimitriou, V. Simulation of the transient behavior of matter with characteristic geometrical variations & defects irradiated by nanosecond laser pulses using FEA. Key Eng. Mater. 2016, 665, 157–160. [Google Scholar]
- Hao, S.; Xiaorong, G.; Lin, L.; Hongna, Z.; Yunjie, Z. Finite Element Simulation and Experiment on Interaction of Surface Waves Excited by Laser Point or Line Source with Rail Defects. Laser Optoelectron. Prog. 2019, 56, 08201. [Google Scholar]
- Jiang, Y.; Chen, S.; Wang, K.; Zhang, X.; Liu, H.; Li, Y. Quantitative Detection of Rail Head Internal Hole Defects Based on Laser Ultrasonic Bulk Wave and Optimized Variational Mode Decomposition Algorithm. Measurement 2023, 218, 113185. [Google Scholar] [CrossRef]
- Zeng, W.; Yao, Y. Numerical Simulation of Laser-Generated Ultrasonic Waves for Detection of Surface Defects on a Cylinder Pipe. Optik 2020, 212, 164650. [Google Scholar] [CrossRef]
- Zeng, W.; Yao, Y.; Qi, S.; Liu, L. Finite Element Simulation of Laser-Generated Surface Acoustic Wave for Identification of Subsurface Defects. Optik 2020, 207, 163812. [Google Scholar]
- Zeng, W.; Zou, X.; Yao, F. Finite Element Simulation of Phased Array Laser-Generated Surface Acoustic Wave for Identification of Surface Defects. Optik 2020, 224, 165733. [Google Scholar] [CrossRef]
- Kou, X.; Pei, C.; Chen, Z. Fully Noncontact Inspection of Closed Surface Crack with Nonlinear Laser Ultrasonic Testing Method. Ultrasonics 2021, 114, 106426. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, X.; Qin, X.; Hua, L.; Xu, M. Laser Ultrasonic Inspection of a Wire + Arc Additive Manufactured (WAAM) Sample with Artificial Defects. Ultrasonics 2021, 110, 106273. [Google Scholar]
- Zeng, Y.; Wang, X.; Qin, X.; Hua, L.; Liu, G.; Guan, S. Laser Ultrasonic Inspection of Defects in Wire Arc Additive Manufactured Samples with Different Surface Profiles. Measurement 2022, 188, 110597. [Google Scholar]
- Lin, J.; Wang, C.; Wang, W.; Chen, J.; Sun, A.; Ju, B.-F. Quantitative Evaluation of Subsurface Cracks with Laser-Generated Surface Wave Based on Back Propagation Neural Network. Appl. Phys. A 2022, 128, 581. [Google Scholar] [CrossRef]
- Hosten, B.; Bacon, C.; Biateau, C. Finite Element Modeling of the Temperature Rise Due to the Propagation of Ultrasonic Waves in Viscoelastic Materials and Experimental Validation. J. Acoust. Soc. Am. 2008, 124, 3491–3496. [Google Scholar] [PubMed]
- Thring, C.B.; Fan, Y.; Edwards, R.S. Focused Rayleigh Wave EMAT for Characterization of Surface-Breaking Defects. NDTE Int. 2016, 81, 20–27. [Google Scholar]
- Sato, H.; Ogiso, H.; Yamashita, Y.; Funada, Y. Laser Ultrasonic Technique to Non-Destructively Detect Cracks on a Ni-Based Self-Fluxing Alloy Fabricated Using Directed Energy Deposition (DED). Mater. Trans. 2020, 61, 1994–2001. [Google Scholar]
- Peyton, C.; Dixon, S.; Dutton, B.; Vesga, W.; Edwards, R.S. Reflection Behavior of SH0 from Small Defects in Thin Sheets, with Application to EMAT Inspection of Titanium. Nondestruct. Test. Eval. 2024, 39, 2330–2353. [Google Scholar]
- L’Etang, A.; Huang, Z. FE Simulation of Laser Generated Surface Acoustic Wave Propagation in Skin. Ultrasonics 2006, 44, e1243–e1247. [Google Scholar]
- Li, X.; Wang, C.; Xiang, H.; Zhang, G. Finite Element Simulation of Ultrasonic Guided Waves Generated by a Pulsed Laser in Human Skin. Instrum. Sci. Technol. 2006, 34, 711–725. [Google Scholar]
- Li, C.; Li, S.; Guan, G.; Wei, C.; Huang, Z.; Wang, R.K. A Comparison of Laser Ultrasound Measurements and Finite Element Simulations for Evaluating the Elastic Properties of Tissue Mimicking Phantoms. Opt. Laser Technol. 2012, 44, 866–871. [Google Scholar]
- Humphries, A.; Lister, T.S.; Wright, P.A.; Hughes, M.P. Finite Element Analysis of Thermal and Acoustic Processes During Laser Tattoo Removal. Lasers Surg. Med. 2013, 45, 108–115. [Google Scholar]
- Chen, K.; Fu, X.; Dorantes-Gonzalez, D.J.; Lu, Z.; Li, T.; Li, Y.; Wu, S.; Hu, X. Simulation Study of Melanoma Detection in Human Skin Tissues by Laser-Generated Surface Acoustic Waves. J. Biomed. Opt. 2014, 19, 077007. [Google Scholar]
- An, R.; Luo, X.; Shen, Z. Numerical and Experimental Investigation of the Influence of Tumor Size on Laser-Induced Ultrasonics in Soft Tissue. Laser Phys. 2014, 24, 045604. [Google Scholar]
- Li, T.; Fu, X.; Chen, K.; Dorantes-Gonzalez, D.J.; Li, Y.; Wu, S.; Hu, X. Simulation Study and Guidelines to Generate Laser-Induced Surface Acoustic Waves for Human Skin Feature Detection. Opt. Laser Technol. 2015, 75, 16–23. [Google Scholar]
- Zeng, W.; Wang, F.; Miao, L.; You, F.; Yao, F. Laser Ultrasonic Melanoma Detection in Human Skin Tissues via Pearson Correlation Coefficient. Optik 2020, 222, 165478. [Google Scholar]
- Zeng, W.; Liao, Y.; Chen, Y.; Diao, Q.; Fu, Z.; Yao, F. Research on Classification and Recognition of Skin Tumors by Laser Ultrasound Using Support Vector Machine Based on Particle Swarm Optimization. Opt. Laser Technol. 2023, 158, 108810. [Google Scholar]
- Sun, K.; Yuan, L.; Shen, Z.; Zhu, Q.; Lu, J.; Ni, X. Experimental and Numerical Studies for Nondestructive Evaluation of Human Enamel Using Laser Ultrasonic Technique. Appl. Opt. 2013, 52, 6896–6905. [Google Scholar] [PubMed]
- Sun, K.; Yuan, L.; Shen, Z.; Xu, Z.; Zhu, Q.G.; Ni, X.; Lu, J. Scanning Laser-Line Source Technique for Nondestructive Evaluation of Cracks in Human Teeth. Appl. Opt. 2014, 53, 2366–2374. [Google Scholar]
- Yuan, L.; Sun, K.; Shen, Z.; Ni, X.; Lu, J. Theoretical Study of the Effect of Enamel Para meters on Laser-Induced Surface Acoustic Waves in Human Incisor. Int. J. Thermophys. 2015, 36, 1057–1065. [Google Scholar]
- Sun, K.; Yuan, L.; Shen, Z.; Zhu, Q. Nondestructive Evaluation of Demineralized Enamel in a Human Incisor and Molar Using Laser Ultrasonics. Appl. Opt. 2018, 57, 1231–1240. [Google Scholar]
- Hériveaux, Y.; Audoin, B.; Biateau, C.; Nguyen, V.-H.; Haïat, G. Ultrasonic Propagation in a Dental Implant. Ultrasound Med. Biol. 2020, 46, 1464–1473. [Google Scholar]
- Buehrle, R.D.; Fleming, G.A.; Pappa, R.S.; Grosveld, F.W. Finite Element Model Development for Aircraft Fuselage Structures. S.V. Sound Vibr. 2001, 35, 32–38. [Google Scholar]
- Van der Auweraer, H.; Steinbichler, H.; Vanlanduit, S.; Haberstok, C.; Freymann, R.; Storer, D.; Linet, V. Application of Stroboscopic and Pulsed-Laser Electronic Speckle Pattern Interferometry (ESPI) to Modal Analysis Problems. Meas. Sci. Technol. 2002, 13, 451–463. [Google Scholar]
- Yang, J.; Ume, I.C. Thermomechanical Reliability Study of Flip-Chip Solder Bumps: Using Laser Ultrasound Technique and Finite Element Method. IEEE Trans. Adv. Packag. 2009, 32, 729–739. [Google Scholar]
- Yamaguchi, M.; Liu, J.; Ye, D.; Lu, T.-M. Coherent Acoustic Vibrations in Silicon Submicron Spiral Arrays. J. Appl. Phys. 2009, 106, 033517. [Google Scholar]
- Huang, Y.-H.; Ma, C.-C. Finite Element and Experimental Results of Transverse Vibration for GT-Cut and SC-Cut Quartz Plates with Fixed and Free Boundary Conditions and Multiple Methods of Excitation. Smart Mater. Struct. 2009, 18, 085017. [Google Scholar]
- Huang, Y.-H.; Ma, C.-C. Experimental Measurements and Finite Element Analysis of the Coupled Vibrational Characteristics of Piezoelectric Shells. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 785–798. [Google Scholar]
- Klepka, A.; Pieczonka, L.; Staszewski, W.J.; Aymerich, F. Impact Damage Detection in Laminated Composites by Non-Linear Vibro-Acoustic Wave Modulations. Compos. Part B 2014, 65, 99–108. [Google Scholar]
- Eriksson, T.J.R.; Ramadas, S.N.; Dixon, S.M. Experimental and Simulation Characterisation of Flexural Vibration Modes in Unimorph Ultrasound Transducers. Ultrasonics 2016, 65, 242–248. [Google Scholar]
- Galos, J.; Khatibi, A.A.; Mouritz, A.P. Vibration and Acoustic Properties of Composites with Embedded Lithium-Ion Polymer Batteries. Compos. Struct. 2019, 220, 677–686. [Google Scholar]
- Silva, A.C.S.; Sebastian, C.M.; Lambros, J.; Patterson, E.A. High Temperature Modal Analysis of a Non-Uniformly Heated Rectangular Plate: Experiments and Simulations. J. Sound Vib. 2019, 443, 397–410. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaselouris, E.; Dimitriou, V. A Review of Finite Element Studies on Laser-Based Acoustic Applications in Solid Media. Modelling 2025, 6, 26. https://doi.org/10.3390/modelling6020026
Kaselouris E, Dimitriou V. A Review of Finite Element Studies on Laser-Based Acoustic Applications in Solid Media. Modelling. 2025; 6(2):26. https://doi.org/10.3390/modelling6020026
Chicago/Turabian StyleKaselouris, Evaggelos, and Vasilis Dimitriou. 2025. "A Review of Finite Element Studies on Laser-Based Acoustic Applications in Solid Media" Modelling 6, no. 2: 26. https://doi.org/10.3390/modelling6020026
APA StyleKaselouris, E., & Dimitriou, V. (2025). A Review of Finite Element Studies on Laser-Based Acoustic Applications in Solid Media. Modelling, 6(2), 26. https://doi.org/10.3390/modelling6020026







