LMI-Based State Feedback Control Structure for Resolving Grid Connectivity Issues in DFIG-Based WT Systems
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. Significance of Study
1.4. Contributions
- Based on the Lyapunov approach, voltage stabilization criteria in terms of an LMI are determined. Effective steadiness is achieved using the proposed control structure under balanced and unbalanced grid conditions, resulting in a substantial improvement in the performance of the DFIG control system.
- The proposed method requires neither component decomposition nor a chain of cascaded current loops. Moreover, it does not request any information regarding bounds on disturbances. It only involves some basic modifications in the DFIG controls to achieve the control target. Hence, this control design is feasible and suitable for WPPs.
- The proposed method guarantees robust system behavior unaffected by parametric uncertainties and exterior disturbances over the complete response.
- In the event of unsuccessful fault-ride through operations, the proposed structure would establish a quick and smooth grid connection since it tracks grid voltage conditions directly. Moreover, the proposed structure would not cause any malfunctions since the stator voltage is directly regulated to match the grid voltage.
- The proposed control scheme effectively controls stator voltages of the DFIG to reliably follow unbalanced grid voltage, frequency, and voltage phase, avoiding the impacts of inrush current to both the DFIG and the grid at the time of connection.
1.5. Paper Structure
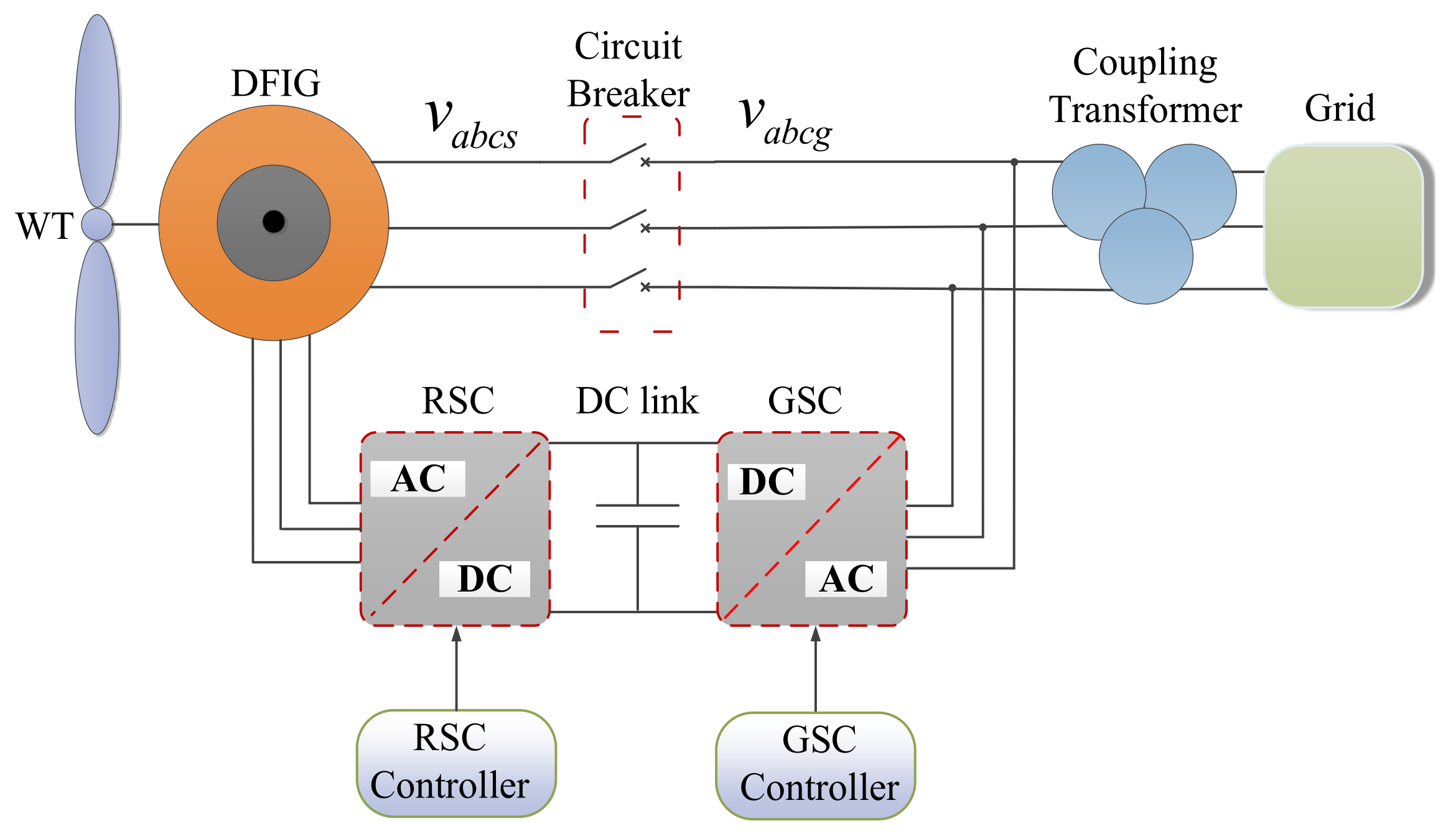
2. Overview of System Structure
3. Modeling of a DFIG
4. State-Space Representation of DFIG Voltage Dynamics for Grid Connection
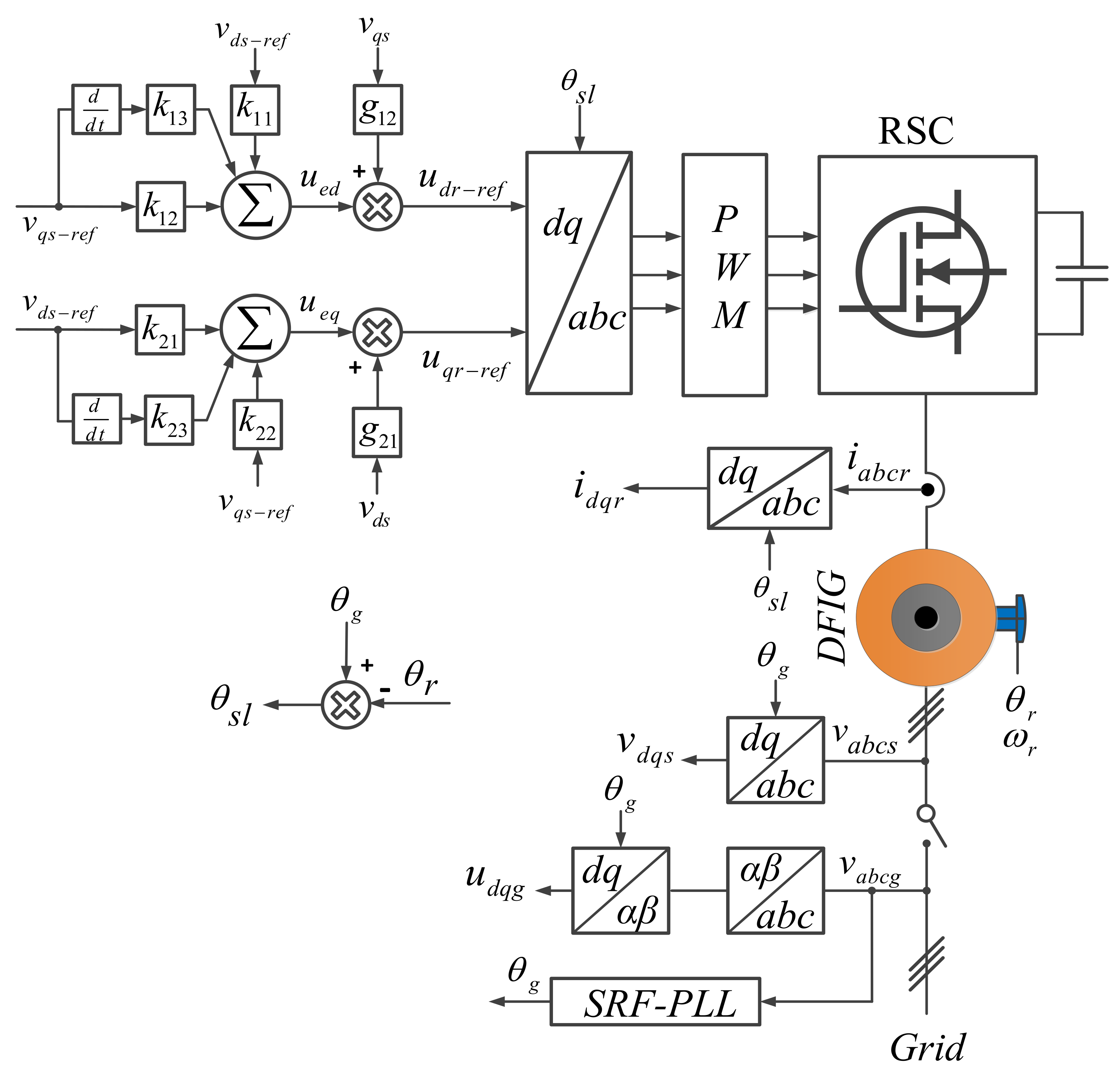
5. System Stabilization Control via LMI-Based State Feedback
6. Closed-System Stability Analysis
- V is continuously differentiable
- V is positive-definite function
- The time derivative of V is negative definitewhich was already established in Equation (44). It ensures the non-singularity of the control system (32) and the closed-system stability is guaranteed. □
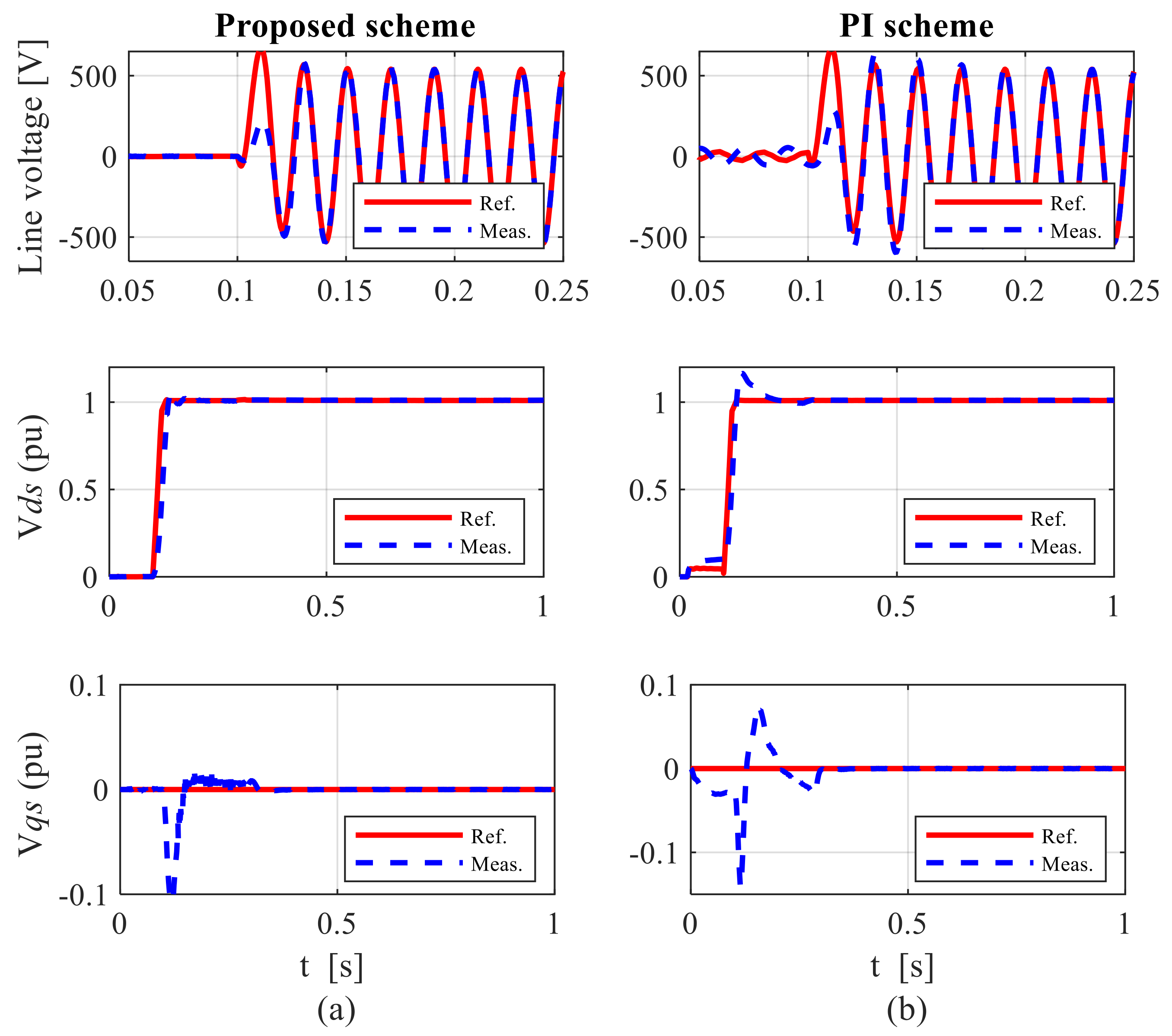
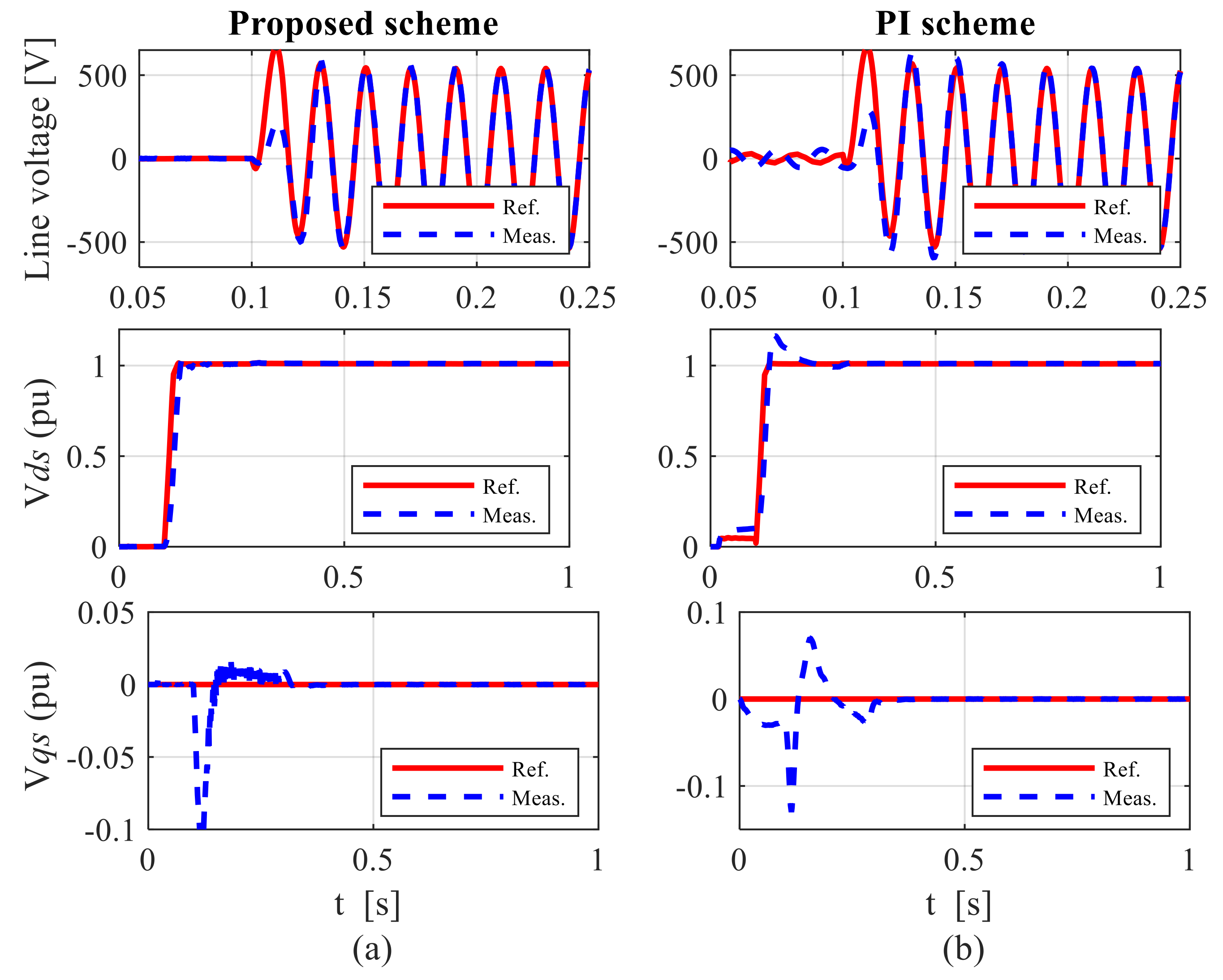
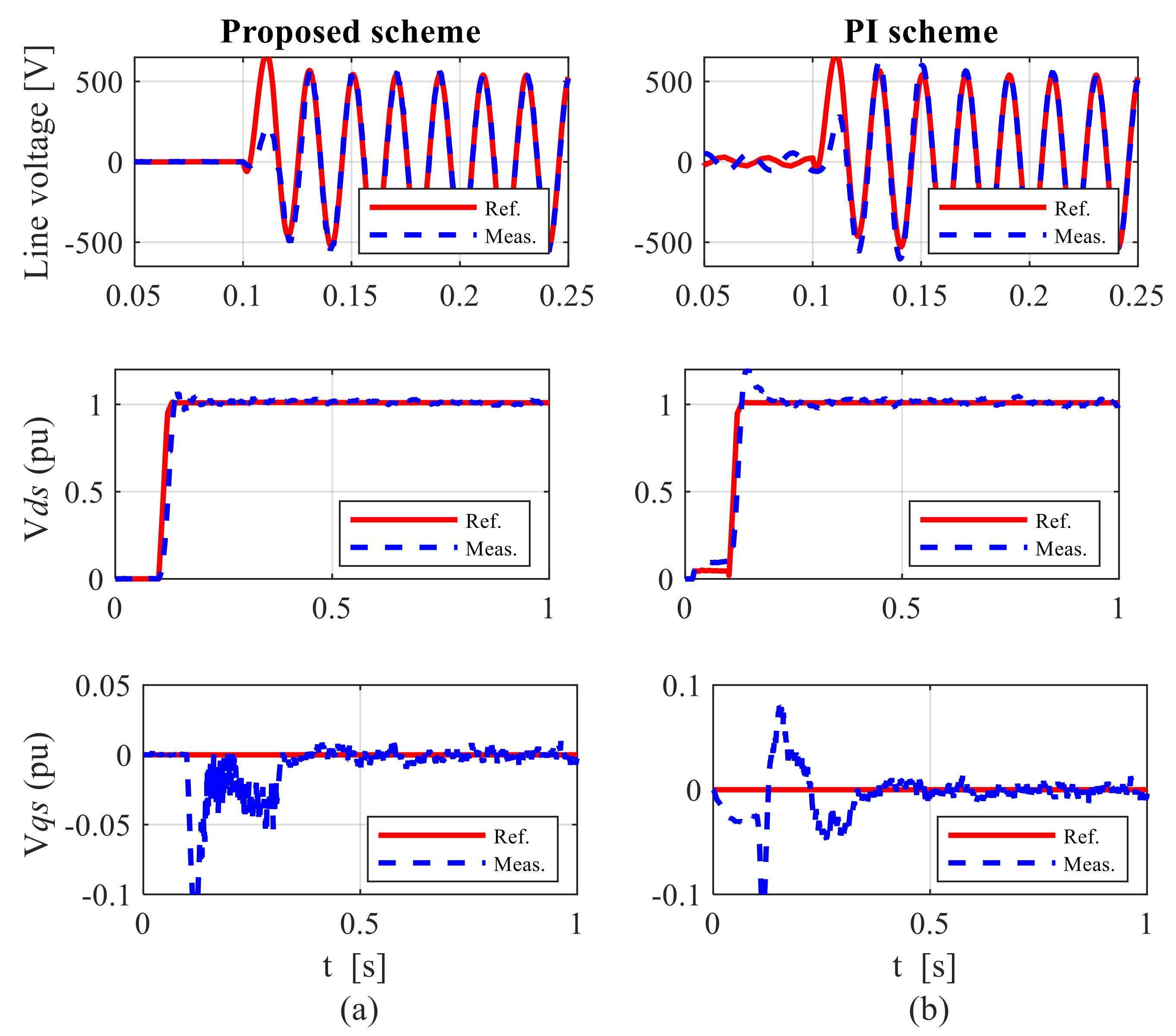
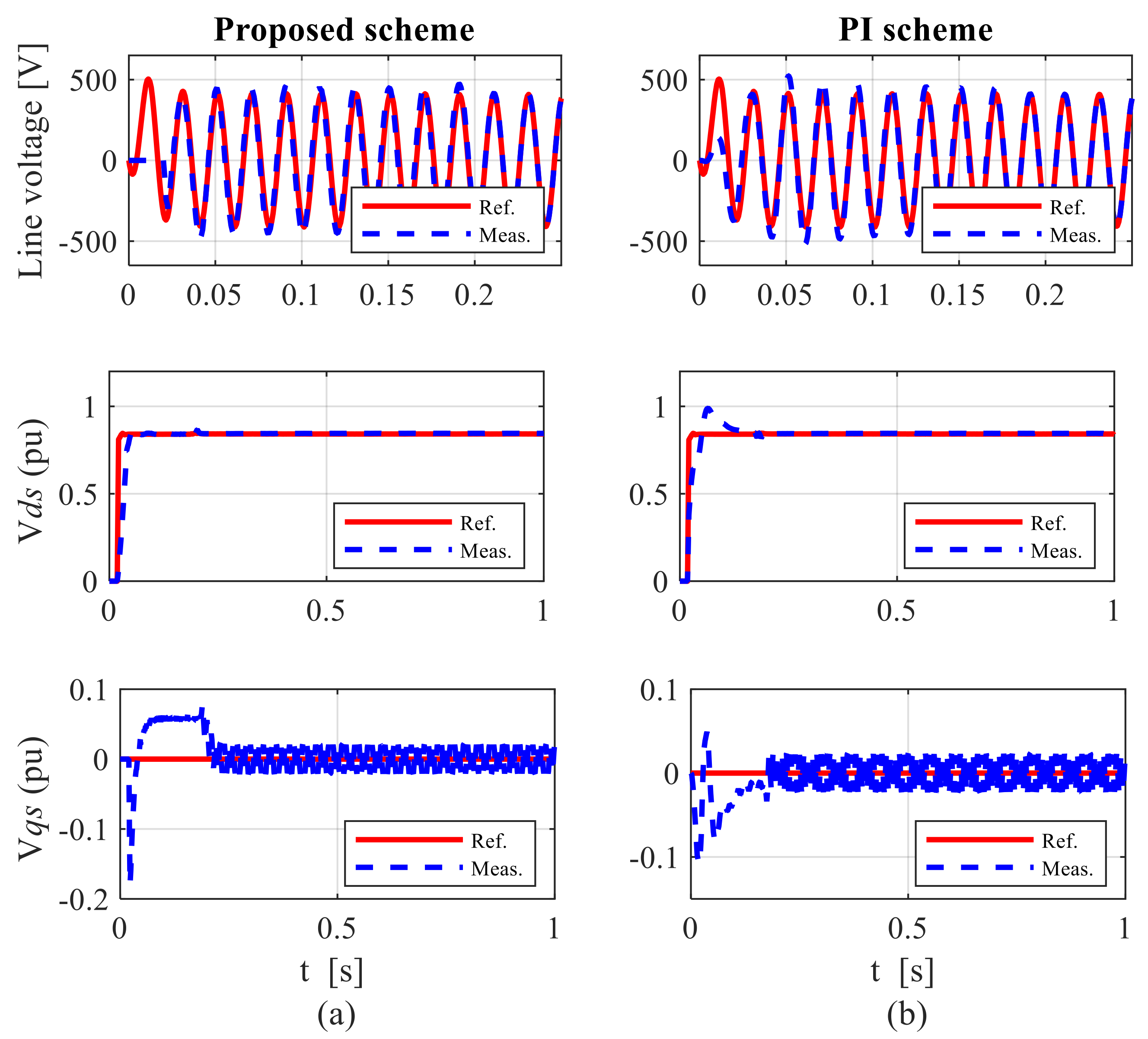
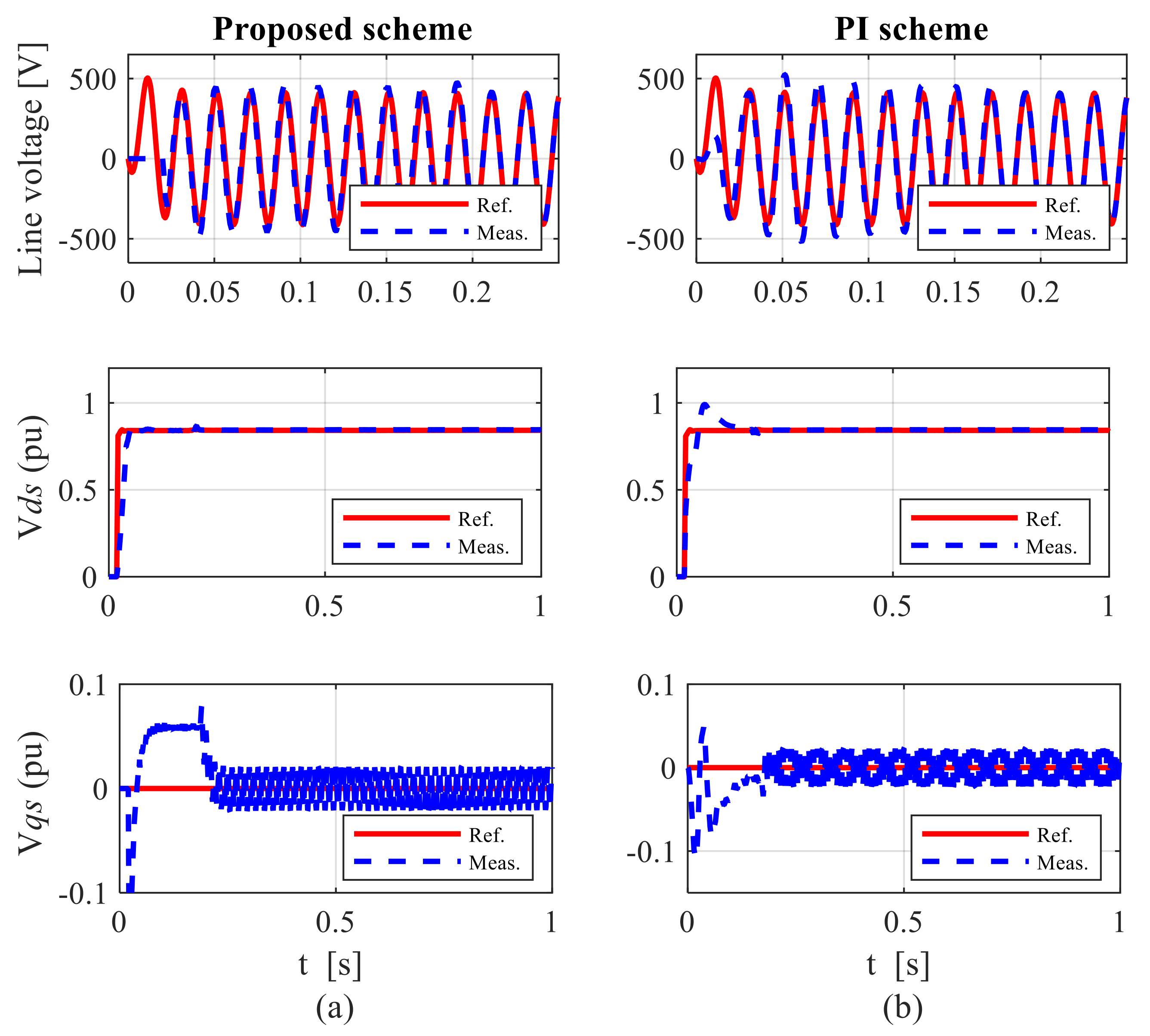
7. Results and Discussion
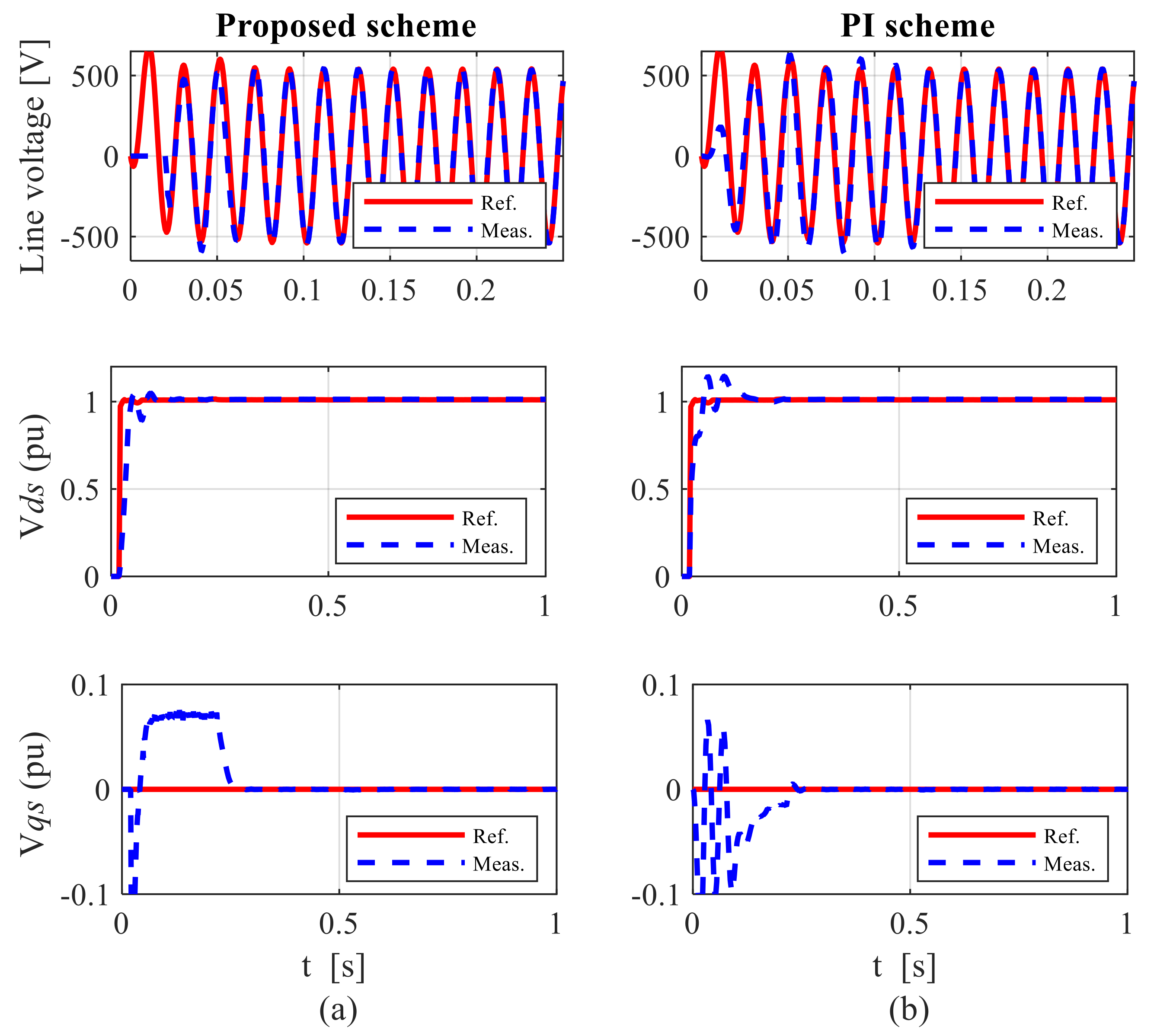
7.1. Control Performance under Balanced Grid Conditions
- Case 1: Performance during sub-synchronous speed operation;
- Case 2: Performance during super-synchronous speed operation;
- Case 3: Performance under various parametric uncertainties during sub-synchronous speed operation;
- Case 4: Performance under external disturbance during sub-synchronous speed operation.
7.1.1. Case 1: Performance during Sub-Synchronous Speed Operation
7.1.2. Case 2: Performance during Super-Synchronous Speed Operation
7.1.3. Case 3: Performance under Various Parametric Uncertainties during Sub-Synchronous Speed Operation
- Scenario 1: Increase the Lm of the generator to 200% of its rated value;
- Scenario 2: Increase the Rr of the generator to 150% of its rated value;
- Scenario 3: Decrease the Rr of the generator to 50% of its rated value.
7.1.4. Case 4: Performance under External Disturbance during Super-Synchronous Speed Operation
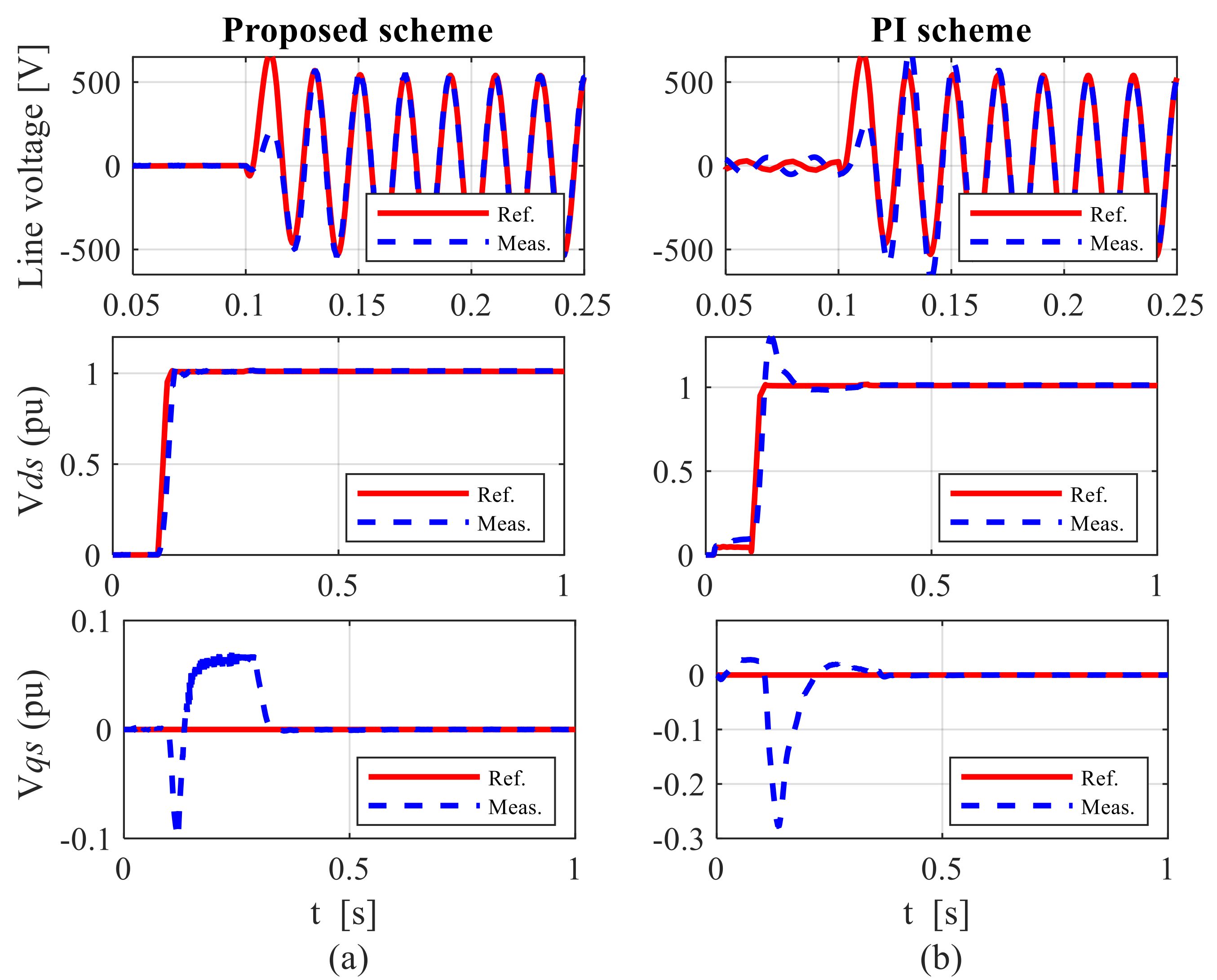
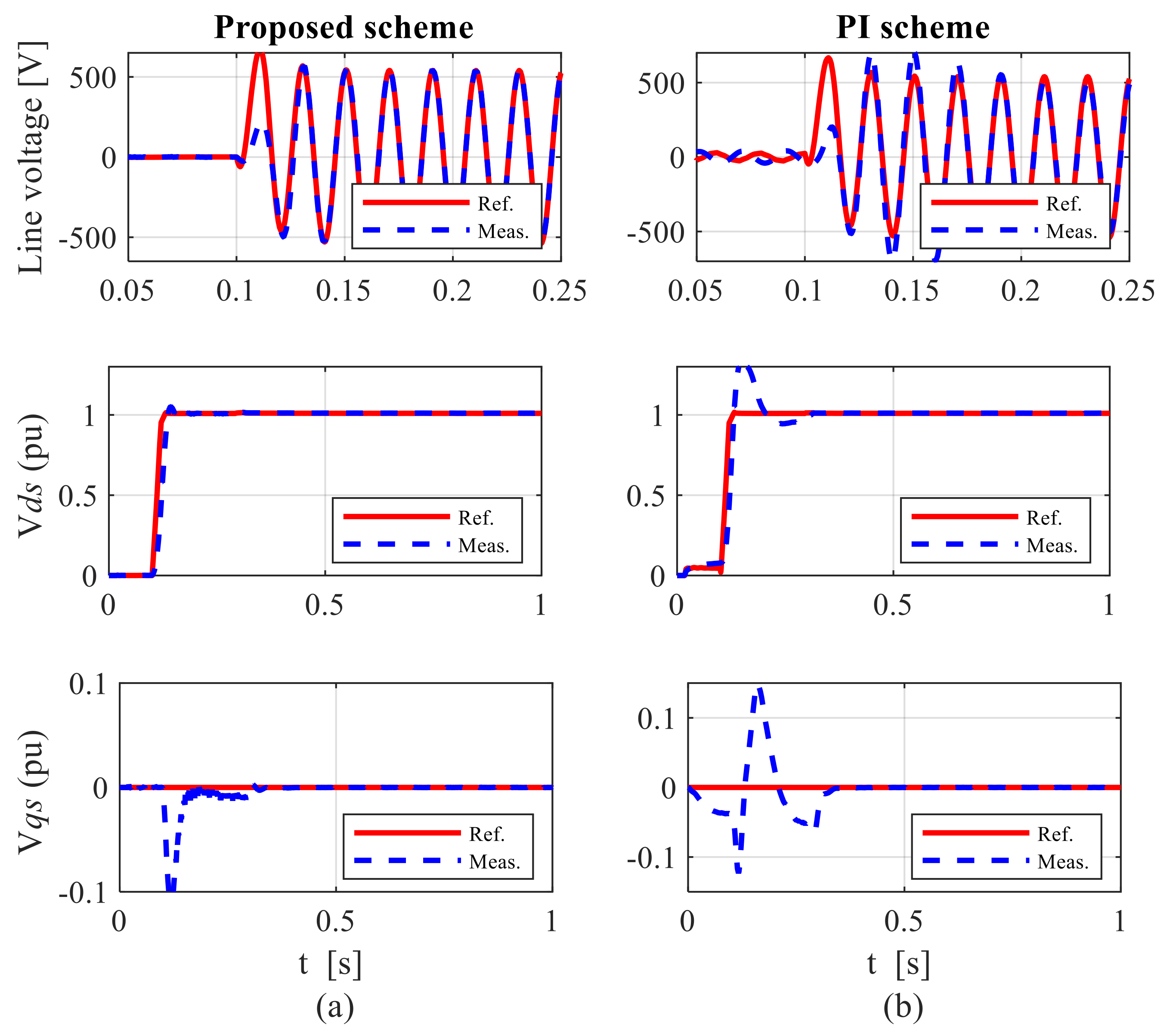
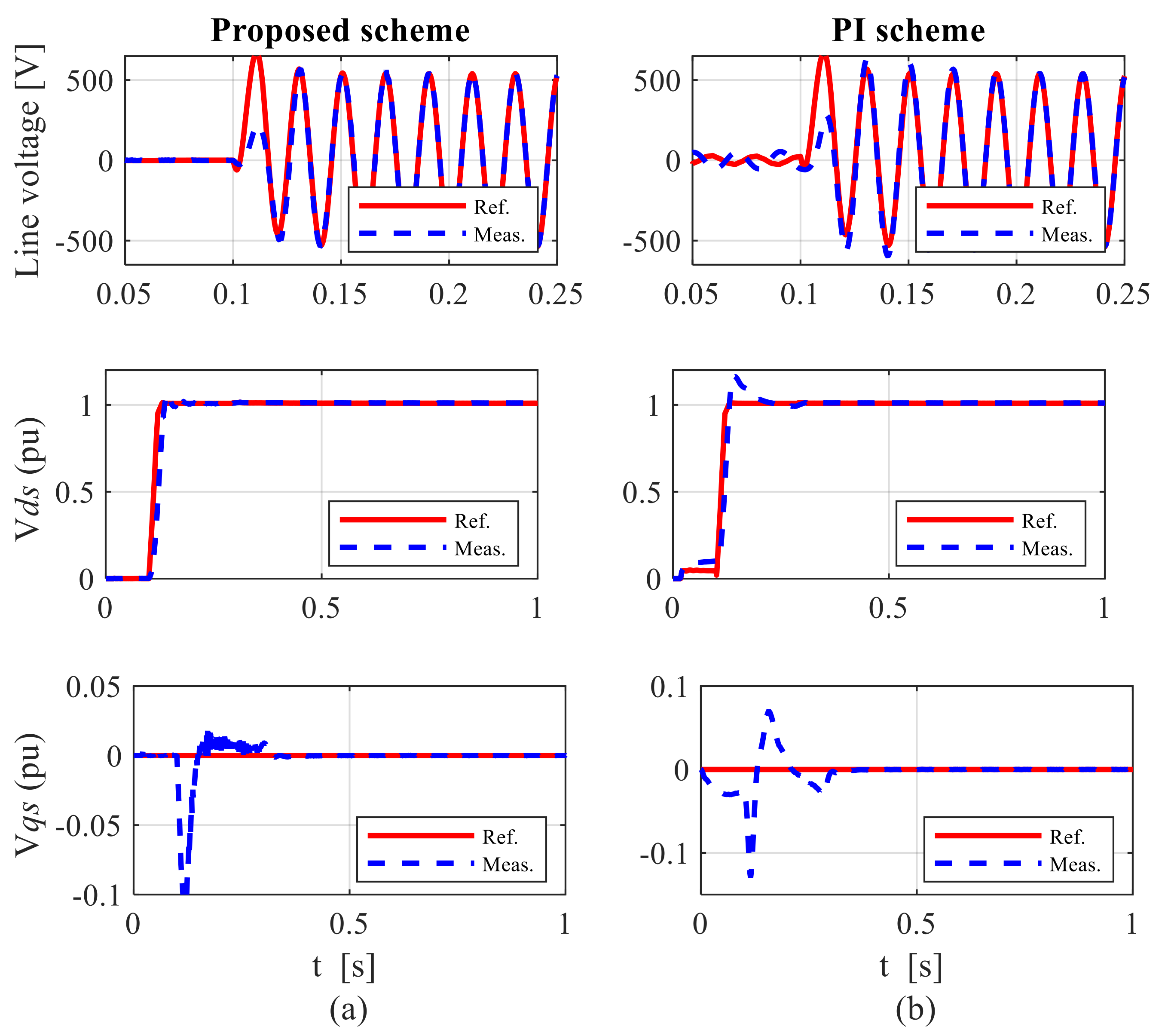
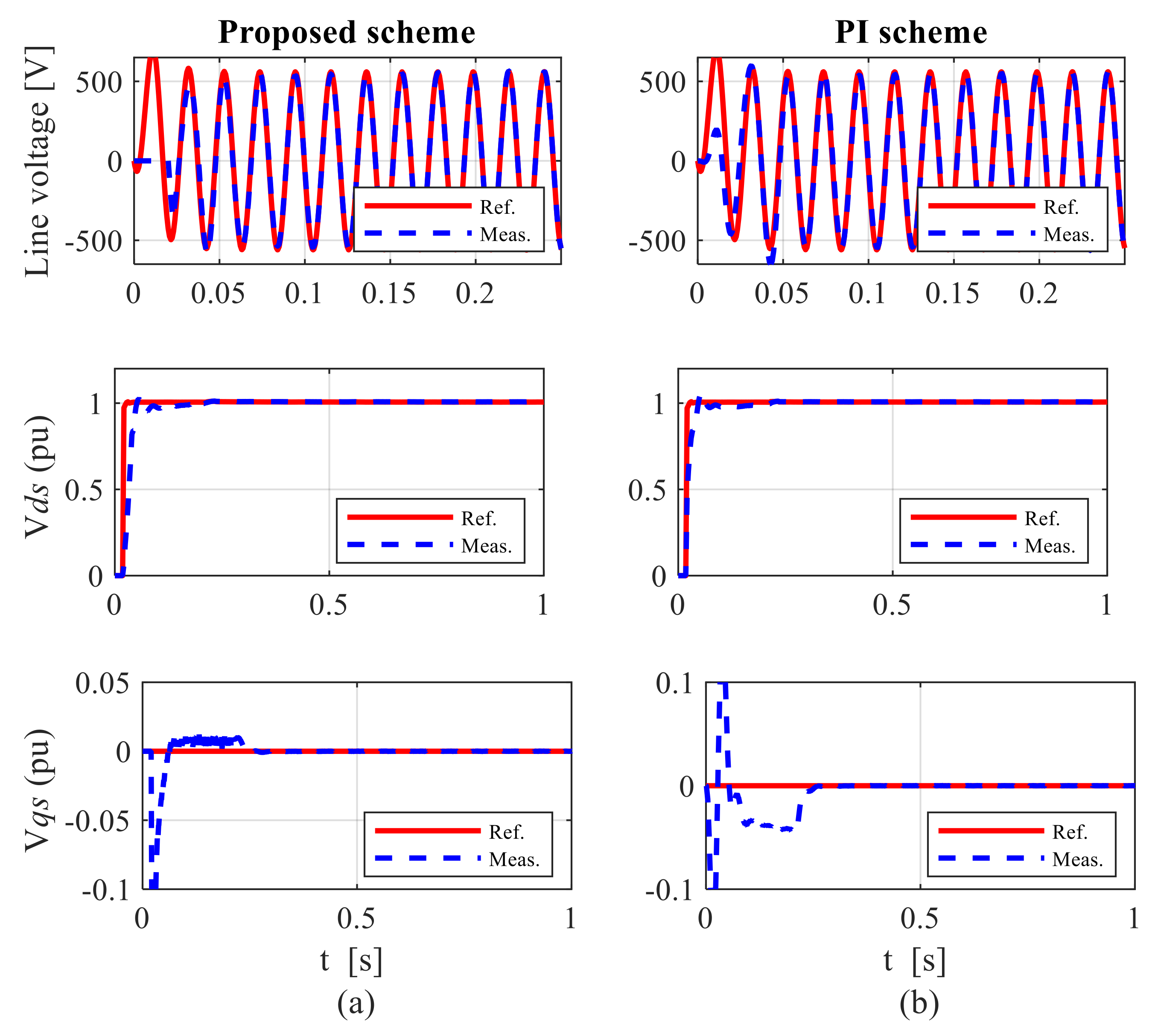
7.2. Control Performance under Unbalanced Grid Conditions
- Case 1: Performance during sub-synchronous speed operation;
- Case 2: Performance during super-synchronous speed operation;
- Case 3: Performance under various parametric uncertainties during super-synchronous speed operation;
- Case 4: Performance under variation in phase angle during super-synchronous speed operation;
- Case 5: Performance under variations in grid voltage frequency during sub-synchronous speed operation.
7.2.1. Case 1: Performance during Sub-Synchronous Speed Operation
7.2.2. Case 2: Performance during Super-Synchronous Speed Operation
7.2.3. Case 3: Performance under Various Parametric Uncertainties during Super-Synchronous Speed Operation
7.2.4. Case 4: Performance under Variation in Phase Angle during Super-Synchronous Speed Operation
7.2.5. Case 5: Performance under Variations in Grid Voltage Frequency during Sub-Synchronous Speed Operation
- Scenario 1: Grid frequency is at 48 Hz, and all phase voltages are set to their nominal values;
- Scenario 2: Grid frequency is at 52 Hz, and all phase voltages are set to their nominal values.
8. Conclusions
- Simulation studies showed that the proposed control structure offered fast and precise tracking of the grid voltage under various grid conditions, thus indicating its suitability in wind power applications.
- The proposed control structure accounted well for the rapid onset of the grid voltage at the stator terminals of the DFIG under diverse grid conditions, with negligible effects on the DFIG and the grid.
- The simple implementation of the proposed control structure makes it feasible and practical for wind energy integration.
- The proposed control structure is independent of machine parameter variations and directly injects the desired voltage vector into the power converter.
- It rapidly synchronizes the DFIG to the power grid, even in the presence of parametric uncertainties and exterior disturbances.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value | Unit |
|---|---|---|
| Turbine rated mechanical power | 1.5 | MW |
| Rated wind speed | 12 | m/s |
| Air density | 1.225 | kg/m3 |
| Optimal tip–speed ratio | 8.1 | - |
| Maximum power coefficient | 0.48 | - |
| Parameter | Value | Unit |
|---|---|---|
| Rated generator power | 1.6 | MW |
| Pole-pair number | 2 | Nos. |
| Stator winding resistance | 2.65 | mΩ |
| Rotor winding resistance | 2.63 | mΩ |
| Stator leakage inductance | 0.1687 | mH |
| Rotor leakage inductance | 0.1337 | mH |
| Magnetizing inductance | 5.4749 | mH |
| Inertia constant | 3 | s |
| Friction factor | 0.01 | - |
| Parameter | Value | Unit |
|---|---|---|
| Rated grid line-to-line voltage | 690 | V(rms) |
| Rated frequency | 50 | Hz |
| DC-link voltage reference | 1150 | V |
| DC-link capacitance | 20 | mF |
| Grid-side filter resistance | 1.8 | mΩ |
| Grid-side filter inductance | 0.5 | mH |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| k11 | 0.2929 | k12 | 5.6342 |
| k21 | –5.6342 | k22 | 0.2929 |
| k13 | 0.9762 | k23 | –0.9762 |
| g12 | –5.6327 | g21 | 5.6327 |
| PI Gains | kp | ki |
|---|---|---|
| Current controllers | 0.02123 | 9.938 × 10−3 |
| Voltage controllers | 0.1146 | 144 |
Appendix B. Tuning Procedure of PI Controllers
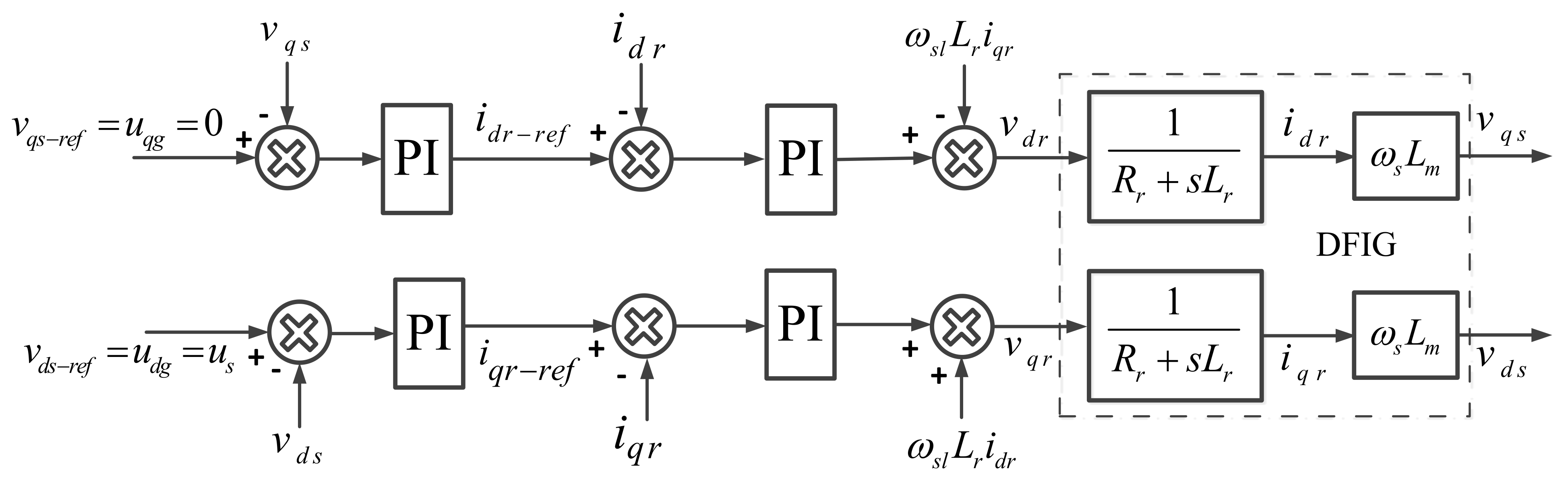
Appendix B.1. Inner-Current PI Controller Design

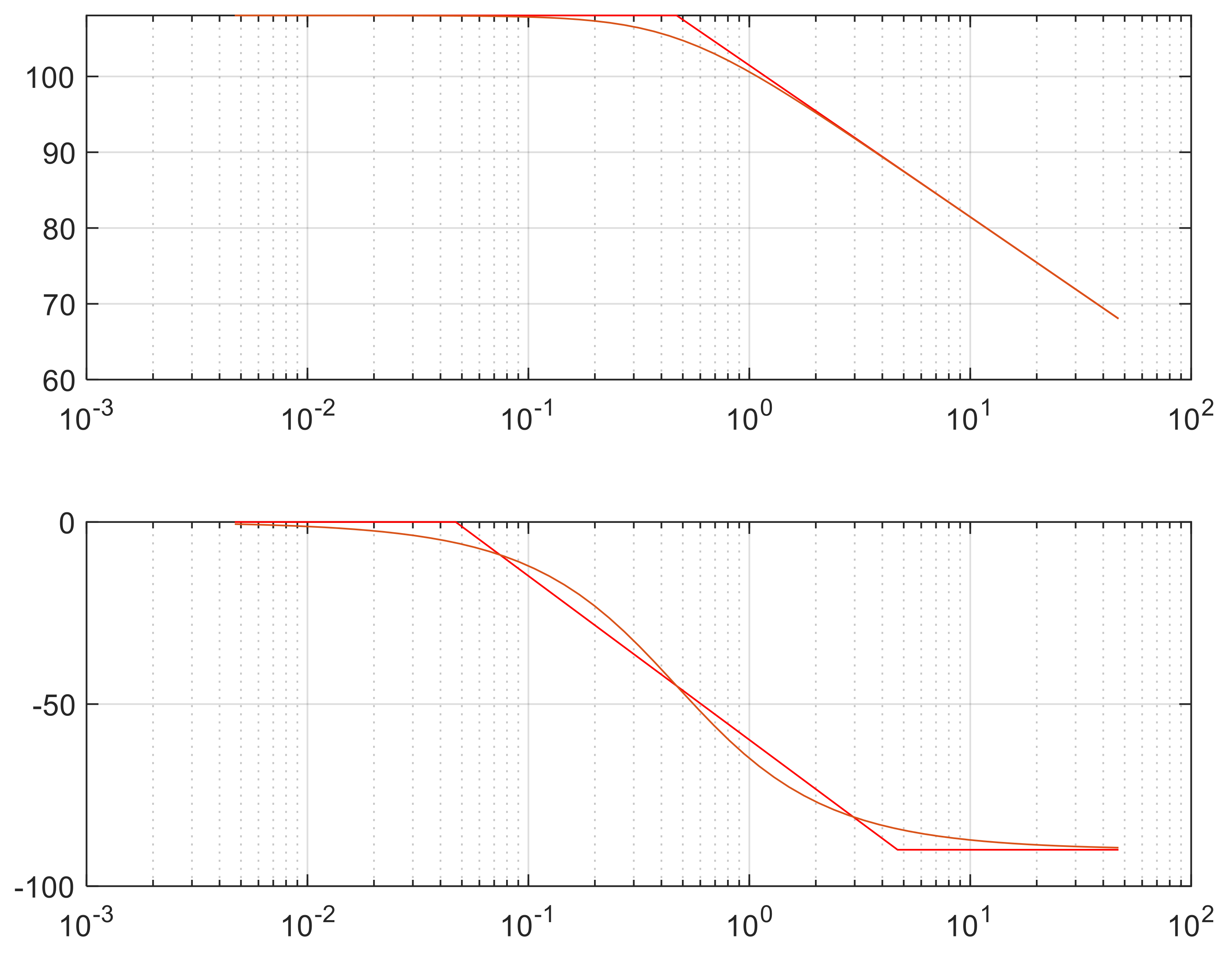

Appendix B.2. Outer-Voltage PI Controller Design

References
- Ali, M.A.S.; Mehmood, K.K.; Kim, C.-H. Full operational regimes for SPMSG-based WECS using generation of active current references. Int. J. Electr. Power Energy Syst. 2019, 112, 428–441. [Google Scholar] [CrossRef]
- Shen, Y.W.; Ke, D.-P.; Sun, Y.-Z.; Kirchen, D.S.; Qiao, W.; Deng, X.-T. Advanced auxiliary control of an energy storage device for transient voltage support of a doubly fed induc-tion generator. IEEE Trans. Sustain. Energy 2016, 7, 63–76. [Google Scholar] [CrossRef]
- Chen, J.; Lin, T.; Wen, C.; Song, Y. Design of a unified power controller for variable-speed fixed-pitch wind energy conversion system. IEEE Trans. Ind. Electron. 2016, 63, 4899–4908. [Google Scholar] [CrossRef]
- Ali, M.A.S.; Mehmood, K.K.; Baloch, S.; Kim, C.-H. Modified rotor-side converter control design for improving the LVRT capability of a DFIG-based WECS. Electr. Power Syst. Res. 2020, 186, 106403. [Google Scholar] [CrossRef]
- Ali, M.A.S.; Mehmood, K.K.; Kim, C.-H. Power System Stability Improvement through the Coordination of TCPS-based Damping Controller and Power System Stabilizer. Adv. Electr. Comput. Eng. 2017, 17, 27–36. [Google Scholar] [CrossRef]
- Ali, M.A.S.; Mehmood, K.K.; Park, J.K.; Kim, C.-H. Battery Energy Storage System-Based Stabilizers for Power System Oscillations Damping. J. Korean Inst. Illum. Electr. Install. Eng. 2016, 10, 75–84. [Google Scholar] [CrossRef]
- Chen, S.Z.; Cheung, N.C.; Wong, K.C.; Wu, J. Grid Synchronization of Doubly-fed Induction Generator Using Integral Variable Structure Control. IEEE Trans. Energy Convers. 2009, 24, 875–883. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G.; Alghamdi, A.S.; Eltamaly, A.M.; Al-Saud, M.S.; Praveen, P.R.; Sayed, K.; Bindu, G.R.; Tlili, I. Design of State Feedback Current Controller for Fast Synchronization of DFIG in Wind Power Generation Systems. Energies 2019, 12, 2427. [Google Scholar] [CrossRef] [Green Version]
- Jaalam, N.; Rahim, N.; Bakar, A.; Tan, C.; Haidar, A. A comprehensive review of synchronization methods for grid-connected converters of renewable energy source. Renew. Sustain. Energy Rev. 2016, 59, 1471–1481. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.A.S.; Mehmood, K.K.; Kim, J.S.; Kim, C.-H. ESD-based Crowbar for Mitigating DC-link Variations in a DFIG-based WECS. In Proceedings of the International Conference on Power Systems Transients, Perpignan, France, 16–20 June 2019; pp. 1–6. [Google Scholar]
- Ali, M.A.S.; Mehmood, K.K.; Baloch, S.; Kim, C.-H. Wind-Speed Estimation and Sensorless Control for SPMSG-Based WECS Using LMI-Based SMC. IEEE Access 2020, 8, 26524–26535. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Xu, D.; Chen, W.; Zhu, N. Advanced Control of Doubly Fed Induction Generator for Wind Power Systems; Wiley-IEEE Press: Piscataway, NJ, USA, 2018. [Google Scholar]
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; Wiley-IEEE Press: Piscataway, NJ, USA, 2011. [Google Scholar]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems; Wiley-IEEE Press: Piscataway, NJ, USA, 2011. [Google Scholar]
- Ali, M.A.S. Utilizing Active Rotor-Current References for Smooth Grid Connection of a DFIG-Based Wind-Power System. Adv. Electr. Comput. Eng. 2020, 20, 91–98. [Google Scholar] [CrossRef]
- Wong, K.C.; Ho, S.L.; Cheng, K.W.E. Direct Voltage Control for Grid Synchronization of Doubly-fed Induction Generators. Electr. Power Compon. Syst. 2008, 36, 960–976. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G. Synchronization of DFIG in wind power generation. Renew. Energy 2012, 44, 193–198. [Google Scholar]
- Ghasemi, A.; Refan, M.H.; Amiri, P. Enhancing the performance of grid synchronization in DFIG-based wind turbine under unbalanced grid conditions. Electr. Eng. 2020, 102, 1175–1194. [Google Scholar] [CrossRef]
- Khan, A.; Hu, X.M.; Khan, M.A.; Barendse, P. Doubly fed induction generator open stator synchronized control during un-balanced grid voltage condition. Energies 2020, 13, 3155. [Google Scholar] [CrossRef]
- Dida, A.; Merahi, F.; Mekhilef, S. New grid synchronization and power control scheme of doubly-fed induction generator based wind turbine system using fuzzy logic control. Comput. Electr. Eng. 2020, 84, 106647. [Google Scholar] [CrossRef]
- Muttaqi, K.M.; Hagh, M.T. A synchronization control technique for soft connection of doubly-fed induction generator based wind turbines to the power grid. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Perez, M.A.; Espinoza, J.R.; Moran, L.A.; Torres, M.A.; Araya, E.A. A Robust Phase-Locked Loop Algorithm to Synchronize Static-Power Converters with Polluted AC Systems. IEEE Trans. Ind. Electron. 2008, 55, 2185–2192. [Google Scholar] [CrossRef]
- Dash, P.; Jena, R.; Panda, G.; Routray, A. An extended complex Kalman filter for frequency measurement of distorted signals. IEEE Trans. Instrum. Meas. 2000, 49, 746–753. [Google Scholar] [CrossRef] [Green Version]
- McGrath, B.; Holmes, D.G.; Galloway, J.J.H.G. Power Converter Line Synchronization Using a Discrete Fourier Transform (DFT) Based on a Variable Sample Rate. IEEE Trans. Power Electron. 2005, 20, 877–884. [Google Scholar] [CrossRef]
- Yazdani, D.; Bakhshai, A.; Joos, G.; Mojiri, M. A Real-Time Extraction of Harmonic and Reactive Current in a Nonlinear Load for Grid-Connected Converters. IEEE Trans. Ind. Electron. 2009, 56, 2185–2189. [Google Scholar] [CrossRef]
- Yin, G.; Guo, L.; Li, X. An Amplitude Adaptive Notch Filter for Grid Signal Processing. IEEE Trans. Power Electron. 2013, 28, 2638–2641. [Google Scholar] [CrossRef]
- Wang, Y.F.; Li, Y.W. Analysis and Digital Implementation of Cascaded Delayed-Signal-Cancellation PLL. IEEE Trans. Power Electron. 2010, 26, 1067–1080. [Google Scholar] [CrossRef]
- Nascimento, P.S.B.; De-Souza, H.E.P.; Neves, F.A.S.; Limongi, L.R. FPGA implementation of the generalized delay signal cancelation–phase locked loop method for detecting harmonic sequence components in three-phase signals. IEEE Trans. Ind. Electron. 2013, 60, 645–658. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D. Design-Oriented Study of Advanced Synchronous Reference Frame Phase-Locked Loops. IEEE Trans. Power Electron. 2012, 28, 765–778. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D.; Guerrero, J. Advantages and Challenges of a Type-3 PLL. IEEE Trans. Power Electron. 2013, 28, 4985–4997. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Espin, F.; Figueres, E.; Garcera, G. An Adaptive Synchronous-Reference-Frame Phase-Locked Loop for Power Quality Improvement in a Polluted Utility Grid. IEEE Trans. Ind. Electron. 2012, 59, 2718–2731. [Google Scholar] [CrossRef] [Green Version]
- Reyes, M.; Rodriguez, P.; Vazquez, S.; Luna, A.; Teodorescu, R.; Carrasco, J.M. Enhanced Decoupled Double Synchronous Reference Frame Current Controller for Unbalanced Grid-Voltage Conditions. IEEE Trans. Power Electron. 2012, 27, 3934–3943. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Mojiri, M.; Safaee, A.; Walseth, J.A.; Khajehoddin, S.A.; Jain, P.; Bakhshai, A. A New Phase-Locked Loop System for Three-Phase Applications. IEEE Trans. Power Electron. 2013, 28, 1208–1218. [Google Scholar] [CrossRef]
- Liccardo, F.; Marino, P.; Raimondo, G. Robust and Fast Three-Phase PLL Tracking System. IEEE Trans. Ind. Electron. 2010, 58, 221–231. [Google Scholar] [CrossRef]
- Escobar, G.; Martinez-Montejano, M.F.; Valdez, A.A.; Martinez, P.R.; Hernandez-Gomez, M. Fixed-Reference-Frame Phase-Locked Loop for Grid Synchronization under Unbalanced Operation. IEEE Trans. Ind. Electron. 2010, 58, 1943–1951. [Google Scholar] [CrossRef]
- Carugati, I.; Donato, P.G.; Maestri, S.; Carrica, D.; Benedetti, M. Frequency Adaptive PLL for Polluted Single-Phase Grids. IEEE Trans. Power Electron. 2012, 27, 2396–2404. [Google Scholar] [CrossRef]
- Rodriguez, P.; Alvaro, L.; Raúl, S.M.-A.; Ion, E.-O.; Remus, T.; Frede, B. A stationary reference frame grid synchronization system for three-phase grid-connected power convert-ers under adverse grid conditions. IEEE Trans. Power Electron. 2012, 27, 99–1128. [Google Scholar] [CrossRef]
- Rodríguez, P.; Luna, A.; Candela, I.; Mujal, R.; Teodorescu, R.; Blaabjerg, F. Multiresonant Frequency-Locked Loop for Grid Synchronization of Power Converters under Distorted Grid Conditions. IEEE Trans. Ind. Electron. 2010, 58, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Mellouli, M.; Mahmoud, M.; Slama, J.B.H.; Al-Haddad, K. A third-order MAF based QT1-PLL that is robust against harmon-ically distorted grid voltage with frequency deviations. IEEE Trans. Energy Convers. 2021, 36, 1600–1613. [Google Scholar] [CrossRef]
- Kanjiya, P.; Khadkikar, V.; El Moursi, M. A Novel Type-1 Frequency-Locked Loop for Fast Detection of Frequency and Phase with Improved Stability Margins. IEEE Trans. Power Electron. 2015, 31, 2550–2561. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C.; Abusorrah, A.M.; Al-Turki, Y. A Study on Three-Phase FLLs. IEEE Trans. Power Electron. 2019, 34, 213–224. [Google Scholar] [CrossRef] [Green Version]




| Cases | Proposed | PI | ||||||
|---|---|---|---|---|---|---|---|---|
| ISE | ITSE | IAE | ITAE | ISE | ITSE | IAE | ITAE | |
| C_1 | 0.004932 | 0.000959 | 0.01104 | 0.001354 | 0.00654 | 0.001025 | 0.02122 | 0.002305 |
| C_2 | 0.005091 | 0.000862 | 0.01475 | 0.002226 | 0.007169 | 0.0009543 | 0.02581 | 0.003019 |
| C_3, S_1 | 0.004975 | 0.0009604 | 0.01139 | 0.001435 | 0.008199 | 0.0009346 | 0.02815 | 0.003782 |
| C_3, S_2 | 0.004935 | 0.0009269 | 0.01113 | 0.001375 | 0.005646 | 0.001023 | 0.02123 | 0.002308 |
| C_3, S_3 | 0.004931 | 0.0009514 | 0.01092 | 0.001329 | 0.005644 | 0.001026 | 0.02129 | 0.002319 |
| C_4 | 0.005165 | 0.001015 | 0.01456 | 0.002185 | 0.005664 | 0.0009101 | 0.02271 | 0.002686 |
| Cases | Proposed | PI | ||||||
|---|---|---|---|---|---|---|---|---|
| ISE | ITSE | IAE | ITAE | ISE | ITSE | IAE | ITAE | |
| C_1 | 0.005256 | 0.0002445 | 0.01048 | 0.001462 | 0.005584 | 0.0003418 | 0.02231 | 0.001466 |
| C_2 | 0.01121 | 0.0004142 | 0.04112 | 0.003704 | 0.01146 | 0.0004645 | 0.04143 | 0.003786 |
| C_3, S_1 | 0.007371 | 0.0002198 | 0.02771 | 0.001985 | 0.008003 | 0.0002264 | 0.02818 | 0.002314 |
| C_3, S_2 | 0.005746 | 0.0002321 | 0.02337 | 0.001563 | 0.008368 | 0.0003693 | 0.0295 | 0.002457 |
| C_3, S_3 | 0.00575 | 0.0002209 | 0.02342 | 0.001567 | 0.00838 | 0.0003697 | 0.02954 | 0.002466 |
| C_4 | 0.00794 | 0.000277 | 0.02255 | 0.001158 | 0.01189 | 0.0002023 | 0.02311 | 0.00118 |
| C_5, S_1 | 0.009207 | 0.0001123 | 0.01909 | 0.0001095 | 0.01151 | 0.0001792 | 0.0219 | 0.0005891 |
| C_5, S_2 | 0.006344 | 0.000379 | 0.01965 | 0.0008119 | 0.01052 | 0.0006346 | 0.01971 | 0.001121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.A.S. LMI-Based State Feedback Control Structure for Resolving Grid Connectivity Issues in DFIG-Based WT Systems. Eng 2021, 2, 562-591. https://doi.org/10.3390/eng2040036
Ali MAS. LMI-Based State Feedback Control Structure for Resolving Grid Connectivity Issues in DFIG-Based WT Systems. Eng. 2021; 2(4):562-591. https://doi.org/10.3390/eng2040036
Chicago/Turabian StyleAli, Muhammad Arif Sharafat. 2021. "LMI-Based State Feedback Control Structure for Resolving Grid Connectivity Issues in DFIG-Based WT Systems" Eng 2, no. 4: 562-591. https://doi.org/10.3390/eng2040036
APA StyleAli, M. A. S. (2021). LMI-Based State Feedback Control Structure for Resolving Grid Connectivity Issues in DFIG-Based WT Systems. Eng, 2(4), 562-591. https://doi.org/10.3390/eng2040036






