Evolutionary Priority-Based Dynamic Programming for the Adaptive Integration of Intermittent Distributed Energy Resources in Low-Inertia Power Systems

Abstract

The variability and uncertainty caused by the increased penetrations of renewable energy sources must be properly considered in day-ahead unit commitment, optimal power flow, and even real-time economic dispatch problems. Besides achieving minimum cost, modern generation schedules must satisfy a larger set of different complex constraints. These account for the generation constraints in the presence of renewable generation, network constraints affected by the distributed energy resources, bilateral contracts enclosing independent capacity provision, ancillary power auctions, net-metering and feed-in-tariff prosumers, and corrective security actions in sudden load variations or outage circumstances. In this work, a new method is presented to appropriately enhance the integration of distributed energy resources in low-inertia power grids. Based on optimal unit commitment schedules derived from priority-based dynamic programming, the potential of increasing the renewable capacity was examined, performing simulations for different scenarios. To ameliorate the expensive requirement of computational complexity, this approach aimed at eliminating the increased exploration-exploitation efforts. On the contrary, its promising solution relies on the evolutionary commitment of the next optimum configuration based on priority-list schemes to accommodate the intermittent generation progressively. This is achieved via the collection of mappings that transform many-valued clausal forms into satisfiability equivalent Boolean expressions.

1. Introduction

Intelligent scheduling of power systems for the seamless integration of intermittent generation, weather-dependent devices, responsive appliances, and plug-in electric vehicles constitutes a crucial solution in delivering future low-carbon energy [1]. The time mismatches between energy supply and demand form one of the biggest challenges in global energy planning and are probably the major obstacles to the integration of renewable energy sources. The volatility caused by increased penetrations of renewable energy must be properly considered in day-ahead unit commitment (UC), in order to cope with operational issues such as insufficient ramping capabilities of thermal generating units, inadequate spinning reserves, transmission congestion, and involuntary load interruptions [2,3]. Hence, power decision makers need to devise adequate and effective flexibility plans for their power systems so as to guarantee power balance and ensure feasible and economical operation over different time horizons and under different generational, environmental, and technical constraints [4]. These constraints are typically captured by means of UC models used to determine both the commitment status and power dispatch of different generating units. However, the repeating procedure concerns a huge number of combinations and is infeasible to be enumerated completely, even for medium-scale systems and short-term scheduling periods (hours, days, or a week) [5].

The UC problem has commonly been interpreted as a mixed-integer, multi-variate, non-convex, and non-linear optimization problem, with a large number of complex constraints. Divided into mathematical, heuristic, meta-heuristic, and hybrid, the various approaches broadly aimed at converging high-quality solutions with optimum exploration-exploitation trade-offs. Mathematical optimization constitutes a more flexible approach, allowing the constraints to easily be added. Priority-list forms the simplest method and relies on the order of increasing operating cost to commit and de-commit the generation units. The main advantage regards the rapid access to the optimal solution while satisfying the system-wide constraints, whereas the unit-specific constraints deteriorate the priority, leading to sub-optimal solutions [6]. Lagrange relaxation belongs to the dual optimization techniques, providing probably the simplest modification of model characteristics of large-scale power systems. It is capable of handling the unit-specific constraints separately and system-wide constraints by making use of respective Lagrange multipliers. The comparative lower bound is iteratively obtained by the imposed relaxed problem posing a sensitivity relating to the identical cost-coefficients treatment. Consequently, this mechanism can only recommend near optimal solutions [7]. Branch and bound divide the original problem into numerous sub-problems considering the upper and lower limits to exclude the infeasible solutions through branching and delimiting. Therefore, the real optimum combination may be discarded during the process, resulting in a regional solution [8]. The state-of-the-art mathematical approach refers to the mixed-integer linear programming method, which typically converts the complex nonlinear restriction problem into an easily solved sequence linear programming sub-problem. The formulation in terms of linear equation and inequality constraints cannot guarantee optimality and execution times are drastically increased with increasing generating units [9].

Mathematical approaches constitute exact methods towards convergence and their inherent transitions depend on the gradient information about the objective. In their effort to extend the exploration space and converge to a global optimum solution, many heuristic alternatives have taken place. These approaches are commonly viewed as population-based mechanisms and, according to the process they imitate, are classified as swarm-inspired, evolution-inspired, and physics-inspired [10]. The main advantages lie in the flexibility they offer in allowing practical operating constraints to be integrated and the moderate computational memory and running time [11,12]. On the contrary, heuristic approaches are very specific and problem-dependent, making decisions based on pre-calculated priority rules. To employ more rigorous methods and generate problem-independent solutions, meta-heuristic approaches have been proposed. This way, higher-level techniques can be applied at the expense of large computational efforts’ requirement. In contrast to deterministic mathematical, both heuristic and meta-heuristic methods involve randomness and use the stochastic approach in moving from one solution to another. Thus, neither the magnitude of their sub-optimality nor their overall problem dimensionality can be estimated [13].

To overcome the aforementioned drawbacks and avoid unacceptable solutions in terms of both convergence time and sub-optimal costs, many researchers have turned to hybrid techniques. Utilizing the merits of mathematical and heuristic methods, the proposed solutions are facing the continuous problem of finding the absolute trade-off between exploration and exploitation [14]. Specifically, to avoid local solutions that lead to premature convergence and increase the solving accuracy at reasonable computational efforts, during the searching process they also exploit the stochastic transition of the heuristic approach to progressively discover an optimal generation output based on reward/penalty signals [15]. To solve the large-scale, nonlinear, mixed-integer UC problem, de-commitment heuristics of generating units and reserve repair procedures were proposed [16]. To this end, some representative hybrid methods are those that combine binary components to dictate whether a state will take 0 or 1 value, by making use of an exact method to handle the system-wide constraints and search mechanism to handle the non-continuous, unit-specific constraints. Such paradigms include the binary whale optimization algorithm, binary artificial sheep algorithm, binary particle swarm optimization, binary gravitational search algorithm, binary bat algorithm, binary dragonfly algorithm, and binary grey wolf algorithm [17].

Based on the presented description, there has not yet been an analytical method that can reach a guaranteed global solution without any requirements for parameters’ tuning to fit the model characteristics of the assessed power system. Exhaustive enumeration still constitutes the only way to achieve a global optimum solution at the expense of dimensionality burden. Identifying its ability to overcome the difficulty of non-convexity and non-linearity of large-scale systems, we proposed a radically different approach to ensure optimality in the least possible iterations and through a tractable procedure. Our purpose is to offer a simple method that (1) can easily be developed without expert knowledge around programming; (2) can automatically be adjusted on each power system layout without the need of additional parameters setting; (3) can exploit heuristic only as a pre-process task, providing traceable transitions until the convergence; and (4) can alleviate the dependence of the overall problem dimensionality on the number of participating generators.

The proposed solution relies on the framework of Boolean mapping (BM) [18]: It constitutes a collection of mappings that transform many-valued clausal forms into satisfiability equivalent Boolean expressions, to analyse their complexity and evaluate them empirically on a set of benchmarks. This is an artificial intelligence tool that consists of modelling hard combinatorial problems as instances of the propositional satisfiability problem. The tool can be engaged with higher-level techniques to drive optimization via consecutive encoding/decoding, preserving the observability, resilience, and reliability in solutions. In this work, these advances were exploited to design a BM object based on enhanced priority lists. Mapping towards a convex optimization problem, we made use of modified neural networks to achieve the global optimum solution. Apparently, this paradigm offers the opportunity of discovering optima of unprecedented quality, as it ameliorates the reliance on assumptions, the functional form of which might be far from the reality.

Note that, although there is a large amount of literature about BM, most research works concentrate on optimizing integer variables and most implementations are restricted in communication networks. Besides, there has not yet been a BM formulation that can address a combinatorial optimization problem such as that of UC. We provide strong experimental evidence regarding the efficacy and the superiority of our novel approach by considering a real-world scenario of a power system consisting of 10 thermal generating units and a 24-h residual power demand. In this context, we employed our proposed approach to achieve a system-wise UC schedule that ensures the global minimum production cost, satisfying the underlying technical and operational constraints. Following, we assess our solution to large-scale power systems consisting of up to 100 generating units and compare the obtained results with benchmark alternative methods.

The contribution of this work is three fold: (1) exact observations can be reached through enhanced priority mechanisms and artificial neural networks; (2) an effective means of eliminating the need of stochastic search methods to provide a solution based on optimal exploration-exploitation trade-offs; and (3) a solution that is intrinsically designed to converge in the least possible number of function evaluations, decoupling the computational complexity from the number of participating generating units.

The rest of the paper is organized as follows. In the following Section, we define the UC problem along with the main constraints that must be always satisfied. Section 3 describes the BM framework, as well as the modified neural network model that it uses for inference purposes. In Section 4, we perform an extensive experimental evaluation. We consider optimal UC in a real-world power network and we employ our approach to achieve a configuration that reliably minimizes the associated production cost. We saw that our approach completely outperformed the existing alternatives by a large margin, thus providing an extremely beneficial tool to system administrators. Finally, the conclusions are drawn in Section 5.

2. Unit Commitment Problem Formulation

The decision process of the UC problem possesses a non-convex, multi-variate, mixed-integer, and extremely non-linear objective. It can be formulated so as to minimize operational costs subject to both coupling and unit-specific constraints. The UC model treats the generation features and residual load as input data, to obtain the commitment status and generation dispatch of the available generating units at the output. In this regard, it provides the ability to save a lot of money on an annual basis by making use of exact mathematical and/or (meta)heuristic mechanisms [19].

2.1. Objective Function

In most approaches, the total production cost of a power system consisting of N thermal units is mainly represented by the cost of fuel and start-up cost during a specified period T. Mathematically, the objective is formulated as follows:

$$f\left(U_i^t,P_i^t\right)={\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{i=1}^N\left[F_i\left(P_i^t\right)+\left(1-U_i^{t-1}\right)S{U}_i\right]U_i^t$$

(1)

where $U_i^t$ determines the on–off states of generating units, while the thermal generation cost is expressed as $F_i\left(P_i^t\right)$. It depends on the production level $P_i^t$ of each unit i and the fuel cost coefficients a_i, b_i, and c_i derived from the convolution of the specific fuel cost and heat rate curve according to Equation (2) [20]. In our formulation, the respective start-up cost $S{U}_i$ is treated as a warmth-independent parameter, receiving a constant value for each unit at a given time interval t [21].

$$F_i\left(P_i^t\right)=a_i+b_i·P_i^t+c_i·{\left(P_i^t\right)}^2$$

(2)

2.2. Constraints

The considered constraints that must be satisfied throughout the optimization process can be classified as unit-specific, plant-wide, and system-wide. The system-wide constraints refer to the system power balance and spinning reserve, while the unit-specific restrictions concern the power boundaries, ramping capabilities, minimum state-change times, and status restrictions pertaining to each individual participating generator. The plant-wide constraint includes a limitation that impacts the available actions within a whole plant and is known as crew constraint [22].

(1)

c₁: System power balance. The equality constraint that forces the total committed production to meet the residual, net load demand $P_{netD}^t$ at each time-interval. While the distributed energy resources (DERs) hold the priority in production, the residual load is expressed as the total demand minus the aggregated power output from DERs.

$${\displaystyle \sum }_{i=1}^N{U}_i^t·P_i^t=P_{netD}^t$$

(3)

(2)

c₂: Spinning reserve. The inequality constraint to ensure that the power margins are satisfied based on the maximum ramping capacity ($P_{i,max-cap}^t$) of each unit, taking into account the ramp rate limits.

$${\displaystyle \sum }_{i=1}^N{U}_i^t·P_{i,\max -cap}^t\ge P_{netD}^t+S{R}^t$$

(4)

(3)

c₃: Generator capacity limits. The minimum and maximum rated powers that allow the generating units to operate only within their boundaries.

$$U_i^t·P_{i,\min }^t\le P_i^t\le U_i^t·P_{i,\max }^t$$

(5)

(4)

c₄: Minimum up (MU_i) and down (MD_i) times. The minimum required duration before a generator can change its status. The t_u and t_d represent the time a unit has started-up or shut-down, respectively.

$$\Delta U_i=1 if {\displaystyle \sum }_{t=td}^{t-1}\left(1-U_i^t\right)\ge M{D}_i$$

(6)

$$\Delta U_i=-1 if {\displaystyle \sum }_{t=tu}^{t-1}{U}_i^t\ge M{U}_i$$

(7)

(5)

c₅: Ramp up/down capability. The rate of change of power output between adjacent hours is restricted by ramp-up (RU_i) and ramp-down (RD_i) capability regarding each generation unit [4].

$$\Delta P_i\le R{U}_i, if \Delta P_i>0$$

(8)

$$\Delta P_i\ge -R{D}_i, if \Delta P_i<0$$

(9)

(6)

c₆: Unit status restrictions. Must run, must out, and run at fixed MW output constitute the three states of exceptional generating units j.

$$\forall t\in 𝒯\{\begin{array}{l}{U}_j^t=1, \mathit{if} j^{\mathit{th}} \mathit{unit} \mathit{must} \mathit{run}\\ U_j^t=0, \mathit{if} j^{\mathit{th}} \mathit{unit} \mathit{must} \mathit{out}\\ P_j^t=\{\begin{array}{l}0, \mathit{if} U_j^t=0\\ c_j, \mathit{if} U_j^t=1\end{array}, \mathit{if} j^{\mathit{th}} \mathit{at} \mathit{fixed} \mathit{output}\end{array}$$

(10)

(7)

c₇: Plant crew constraints (Cr). The plant-wide constraint that pertains to the number of units that can simultaneously start up (or shut down) based on the number of available operators [23].

$${\displaystyle \sum }_{i=1}^N{U}_i^t\left(1-U_i^{t-1}\right)+U_i^{t-1}\left(1-U_i^t\right)\le c_r$$

(11)

2.3. Solution Methodology

Denoting $\left(U_i^t,P_i^t\right)$ by x, the problem of finding the global minimizer $x_{*}$ of the scalar objective function $f\left(x\right)$ over some bounded domain, typically $\mathrm{X}\subset {ℝ}^D$, subject to a set of $K=7$ constraints $c_1, \dots , c_K$, can be defined as:

$$x_{*}=\underset{x\in X}{\mathrm{argmin}}f\left(x\right) s.t. c_1\left(x\right)\le 0,\dots ,c_7\left(x\right)\le 0$$

(12)

This forms a NP hard combinatorial and non-convex optimization task. In the presence of discontinuous binary and dynamic continuous constraints, the global optimum solution can only be obtained via complete enumeration. The huge number of all possible combinations is estimated as ${\left(2^N-1\right)}^T$, making severe capacity limitations to generate them, even for day-ahead schedules and medium-scale power systems. Therefore, the elapsed time needed to recommend the final solution through dynamic programming is greater than the assessed optimization horizon [24].

Recognizing the ability to overcome non-convexity and non-linearity, we aimed at developing an algorithm able to converge to a solution after global exploration but without the need to include the stochastic approach in moving from one solution to another. Instead, we were looking for an analytical mechanism capable of ensuring the minimum cost at the least possible number of trials (function evaluations), providing flexibility with respect to problem diversity and enabling automatic procedures without the need of any parameters setting to respond. This involves mapping to a different domain in a way that reduces dimensionality and guarantees optimality.

Initially, we considered that x represents the binary on/off status taking the value 0 when a generator is off and 1 when the respective unit is on-line such that $x\in \left\{0,1\right\}$. By making use of Boolean expressions, we mapped the problem of the feasible binary combinations $x:X\to ℝ$ to a decimal, integer domain, which read as $\tilde{x}:X\to {\mathbb{N}}^{+}$. This way, we achieved a dimensionality reduction in the order of N, since the required vector to indicate a Nx1 binary combination was then converted to be expressed via an integer value. Based on this framework, a CxT matrix could be built to represent all possible combinations C during the time frame T. In order to develop an automated procedure able to move towards the minimum cost, we considered the sum of the T inputs. Each value was taken individually from the T (Cx1) vectors.

At this point, we can say that the problem (1) was transformed to:

$$f\left(\tilde{x}\right)={\displaystyle \sum }_{t=1}^T{\tilde{x}}_t$$

(13)

To guarantee optimality, we had to ensure that the lowest values of $\tilde{x}$ corresponded to those combinations that undoubtedly gave the least-cost binary combination. Hence, before proceeding with the transformation, we created an optimal rearrangement of the generating units based on enhanced priority lists. Then, the ordinally valued states $\overrightarrow{x}$ followed a descending ranking order to ensure that the most economical combinations resulted in smaller decimal expressions and vice versa.

To tackle the problem of non-linearity, the optimal power contribution $P_{*}$ of the committed units was addressed at the final stage of our proposed approach via non-linear programming with equality and inequality constraints. This way, we preserved that the economic dispatch (ED) solution did not appear as a sub-problem to UC once the constraints were met. A simplified diagram of the proposed solution is depicted in Figure 1, while the constraints’ treatment at each stage is explained at the following section.

3. Mathematical Framework and Clarifications

In this section, we provide the step-by-step procedure followed by our developed algorithm in a mathematical fashion. The process was divided into four main stages and each stage dealt with different constraints so that by the end of the task they were all met confidently. In brief, the construction of enhanced priority-list schemes preceded the Boolean mapping process. The descending order took into account the must-run units and, once the appropriate priority was given to the generating units, all feasible combinations were generated considering the satisfaction of load balance and spinning reserve. Then, the problem was transformed into the convex minimum-sum problem of (13) with the aid of Boolean coding.

A further stage took place, employing a mechanism able to iteratively select the next minimum candidate $\tilde{x}$. During this process, Boolean decoding was applied for every recommendation and the satisfaction of state constraints, including MU, MD, and Cr, was checked. If qualified, non-linear programming was performed, certifying whether the imposed ramping capabilities satisfied both the system-wide constraints and optimal power contribution was obtained at the minimum cost. Once observing the first feasible combination of the objective (13), the model stopped being updated and the algorithm made the final recommendation ${\overrightarrow{x}}_{*}$, providing the algorithm’s best estimate and completing the proposed optimization loop. Figure 2 demonstrates the comprehensive flow diagram of our paradigm.

3.1. Enhanced Priority List Schemes’ Formulation

The concept of committing thermal generation units by priority until the residual load demand satisfaction is not new. Priority list schemes based on the incremental generation cost present principal advantages over their mathematical alternatives. In this work, instead of extracting the order based on conventional priority-based approaches, which rely on single-factor reordering, we proposed an enhanced priority list that could be obtained based on a novel model. Apart from the incremental cost of each individual generator, this model also accounted for the maximum power ratings, the minimum up times, and start-up costs as follows:

$$F_i^{\left(1\right)}=\frac{d\left(F\left(P_i\right)\right)}{d{P}_i}|\begin{array}{c}i\ne j \\ P_i=\frac{P_{i,min}+P_{i,max}}{2}\end{array}$$

(14)

$$F_i^{\left(2\right)}=P_{i,max}$$

(15)

$$F_i^{\left(3\right)}=M{U}_i$$

(16)

$$F_i^{\left(4\right)}=S{U}_i$$

(17)

This technique constitutes a pre-process task, which means that it takes place only at the beginning of the optimization. Our enhanced approach introduced the fundamental assumption that the new configuration was determined with the descending order of the developed list, considering the available units (or excluding the must-run units j). The optimal priority was given based on the normalization function of Equation (18).

$$F_i^{*}=\frac{F_i^{\left(1\right)}}{min\left(F_i^{\left(1\right)}\right)}+\frac{1}{\left(\frac{F_i^{\left(2\right)}}{min\left(F_i^{\left(2\right)}\right)}\right)}+\frac{1}{\left(\frac{F_i^{\left(3\right)}}{min\left(F_i^{\left(3\right)}\right)}\right)}+\frac{1}{\left(\frac{F_i^{\left(4\right)}}{min\left(F_i^{\left(4\right)}\right)}\right)}$$

(18)

Considering the contribution of must-run generators, a binary generator was used to produce the feasible combinations, relying on the rearrangement so that $\overrightarrow{x}=R\left(F_i^{*}\right)$. Equation (19) dictates a typical example distinguishing the must-run units ($j=2$) with bold values.

$$\overrightarrow{x}={\left[\begin{array}{ccccc}\begin{array}{cc}0& 0\end{array}& & 0& \mathbf{1}& \mathbf{1}\\ \begin{array}{cc}0& 0\end{array}& \cdots & 1& \mathbf{1}& \mathbf{1}\\ ⋮& & & ⋮& \\ \begin{array}{cc}0& 1\end{array}& & 1& \mathbf{1}& \mathbf{1}\\ ⋮& \ddots & & ⋮& \\ \begin{array}{cc}1& 1\end{array}& \cdots & 1& \mathbf{1}& \mathbf{1}\end{array}\right]}_{CxN}$$

(19)

3.2. Boolean Mapping: Encoding/Decoding

BM provides numerous applications in computer-aided design. The uselessness of this technique in practice stems from the size of the Boolean functions that can be addressed by the transformation [25]. However, it operates as an inexpensive surrogate to guide the transformation algorithm towards convex objectives that can be explicitly handled. The basis of our implementation was an efficient algorithm that maps large binary vectors (or matrices) into integers (or integer vectors). For encoding purposes, it involved base-q expansion functions, defined as follows:

$$\tilde{x}={\displaystyle \sum }_{i=0}^{N-1}{\overrightarrow{x}}_{N-i}·q^i$$

(20)

In our case, the binary representation referred to base-2 system ($q=2$). This way, the set $D_N=\left\{{\overrightarrow{x}}_N,{\overrightarrow{x}}_{N-1},\dots ,{\overrightarrow{x}}_1\right\},$ which showed a possible combination $C^t$ at t, could be represented by ${\tilde{x}}^t$. Likewise, the set of natural numbers expressing the feasible combinations n during the assessed time frame T was determined by T (nx1) vectors.

Lemma (Boolean satisfiability problem): For any $\overrightarrow{x}$, the value $f\left(\overrightarrow{x}\right)$ is a lower bound on the optimal objective function value $f\left({\tilde{x}}_{*}\right)$ of the original problem.

Property (Clause bounding interpretation): The optimal solution $f\left(\tilde{x}\right)$ constitutes a lower bound on the value $f\left({\tilde{x}}_{*}\right)$ of a feasible solution such that:

$$f\left({\tilde{x}}_{*}\right)=\underset{\tilde{x}}{\max }f\left(\tilde{x}\right)$$

(21)

The reversible Boolean transformation (decoding process) retrieves the binary status ${\overrightarrow{x}}_i$ from the positive integer value $\tilde{x}$ based on q-base deduction functions such as Equations (22) and (23).

$$d_i=\lceil \frac{\tilde{x}}{q^{N-i}}\rceil$$

(22)

$${\overrightarrow{x}}_i=\{\begin{array}{c}\tilde{x}-q·d_{i-1}, if i=N\\ d_{i+1}-q·d_i, elsewhere\end{array}$$

(23)

3.3. Conceptual Convex Optimization

So far, we have mapped the highly non-linear and non-convex combinatorial problem to a convex integer minimization task. As a result, the requested minimizer ${\tilde{x}}_{*}$ can now read as:

$${\tilde{x}}_{*}=\underset{\tilde{x}\in X}{\mathrm{argmin}}f\left(\tilde{x}\right)$$

(24)

subject to the constraints $c_4$ and $c_7$. The minimization problem could be explicitly solved even with linear regression techniques. To develop an algorithm capable of moving towards the most promising regions, that is, the next minimum valued $\tilde{x}$, we chose to evolve non-linear regression mechanisms. For example, we made use of feed-forward neural networks, modified to deal with integers with the help of an appropriate activation function [26]. The developed model exploited a neural network with one hidden layer employed as follows:

$$h=\varphi \left({\displaystyle \sum }_{n=1}^{N_p}{w}_n{\tilde{x}}_n+\beta \right)$$

(25)

$$y={\displaystyle \sum }_{t=1}^T\left(w_t{h}_t+{\beta }_y\right)$$

(26)

The $\varphi (.)$ is the selected activation function, β represents the bias operator, $N_P$ is the population size, and h expresses the output of the hidden layer. For such a Τ-dimensional optimization problem, the pattern solution is demonstrated by a 1xT array, as defined below:

$$\tilde{x}=\left[\begin{array}{ccccc}{\tilde{x}}^1& {\tilde{x}}^2& {\tilde{x}}^3& \cdots & {\tilde{x}}^T\end{array}\right]$$

(27)

The temporal optimal solution y at each iteration t is assumed as target data, and the scope is to effectively reduce the error between this target outcome and the progressively obtained pattern solutions. Thus, between the consecutive iterations k and k + 1, the pattern population matrix (Equation (28)), weight matrix (Equation (29)), and respective cost function (Equation (30)),

$$X\left(k\right)=\left[\begin{array}{ccc}\begin{array}{cc}{\tilde{x}}_1^1& {\tilde{x}}_1^2\end{array}& \cdots & {\tilde{x}}_1^T\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{\tilde{x}}_{N_P}^1& {\tilde{x}}_{N_P}^2\end{array}& \cdots & {\tilde{x}}_{N_P}^T\end{array}\right]$$

(28)

$$W\left(k\right)=\left[\begin{array}{ccc}{w}_1^1& \cdots & w_1^{N_P}\\ ⋮& \ddots & ⋮\\ w_{N_P}^1& \cdots & w_{N_P}^{N_P}\end{array}\right]$$

(29)

$$C\left(k\right)={\displaystyle \sum }_{t=1}^T{y}_t$$

(30)

are updated as follows:

$${\widehat{x}}_t\left(k+1\right)={\displaystyle \sum }_{n=1}^{N_P}{w}_{nt}\left(k\right)·{\widehat{x}}_n\left(t\right)$$

(31)

$${\widehat{x}}_n\left(k+1\right)={\widehat{x}}_n\left(k\right)+{\widehat{x}}_t\left(k+1\right)$$

(32)

$${\widehat{w}}_n\left(k+1\right)={\widehat{w}}_n\left(k\right)+q·\left[{\widehat{w}}_t\left(k\right)-{\widehat{w}}_n\left(k\right)\right]$$

(33)

$$\beta \left(k+1\right)=1-\frac{k}{k_{max}}$$

(34)

where n and t refer to predictors and target, respectively. Our initial target was determined as the minimum cost value, which corresponds to the input expressed by the first row of $X$ ($X_1=[\begin{array}{cccc}{\tilde{x}}_1^1& {\tilde{x}}_1^2& \dots & {\tilde{x}}_1^T\end{array}]$). The selected activation function combines a membership function that enables or disables the node output given the set of inputs and a sigmoid activation function. This way, we ensured that each selected input ${\tilde{x}}_n\in {\tilde{X}}_T$ such that:

$$g_t\left({\tilde{x}}_n\right)=\{\begin{array}{c}1 if {\tilde{x}}_n\in {\tilde{X}}_t\\ 0 if {\tilde{x}}_n\notin {\tilde{X}}_t\end{array}$$

(35)

$$\varphi (.)=g\left({\tilde{x}}_n\right)·\sigma (.)$$

(36)

3.4. Economic Dispatch Solution

The problem of finding the optimal power contribution (or global minimizer to Equation (2), $P_{*}$), given the optimum achieved binary schedule ${\overrightarrow{x}}_{*}$, was conducted as a non-linear programming problem subject to the coupling constraints $c_1$ and $c_2$, the boundary limits of $c_3$, and ramping restrictions of $c_5$.

A solver to this must guide the optimization towards the minimum cost $F\left(P_{*}\right)$ of a problem specified as:

$$P_{*}=\underset{P\in X}{\mathrm{argmin}}F\left({\overrightarrow{x}}_{*},P\right) s.t.\{\begin{array}{c}{\overrightarrow{x}}_{*}·P=P_{netD}\\ {\overrightarrow{x}}_{*}·P_{max-cap}\ge P_{netD}+SR\\ {\overrightarrow{x}}_{*}·P_{min}\le P\le {\overrightarrow{x}}_{*}·P_{max}\\ \Delta P-\begin{array}{c}RU\le 0\\ RD\ge 0\end{array}\end{array}$$

(37)

4. Experimental Evaluation

Inspired from the previously described state-of-the-art advances, in this section we perform a thorough assessment of our paradigm for addressing the UC challenge, adopting common experimental setups. Our vision was (1) to ameliorate the need of manually specifying any parameter’s settings to initialize or guide optimization; (2) to allow discovering quality solutions to the UC problem at the minimum possible number of function evaluations; and (3) to retain the burden of dimensionality at reasonably low levels. For this purpose, we first provided the validation of our approach based on a 10-unit system, certifying its performance towards global exploration. Then, we compared our solution in terms of cost and computational complexity with benchmark alternatives in larger-scale power systems.

4.1. Method Validation

In this study, we considered a power system consisting of 10 generating units, the properties of which are summarized in

Table 1. Characteristics of the thermal generating units.

Unit i	a ($/MW2h)	b ($/MWh)	c ($/h)	SU ($)	Pmin (MW)	Pmax (MW)	MU (h)	MD (h)	RU (MW/h)	RD (MW/h)
1	0.00048	16.19	1000	4500	225	682.5	8	8	405	405
2	0.00031	17.26	970	5000	225	682.5	8	8	405	405
3	0.00200	16.60	700	550	30	195	5	5	54	54
4	0.00211	16.50	680	560	30	195	5	5	54	54
5	0.00398	19.70	450	900	37.5	243	6	6	67.5	67.5
6	0.00712	22.26	370	170	30	120	3	3	54	54
7	0.00079	27.74	480	260	37.5	127.5	3	3	67.5	67.5
8	0.00413	25.92	660	30	15	82.5	1	1	27	27
9	0.00222	27.27	665	30	15	82.5	1	1	27	27
10	0.00173	27.79	670	30	15	82.5	1	1	27	27

. The input variable of power net-load demand was defined over a daily horizon of 24 hourly intervals, as depicted in

Table 2. Net load demand (MW) for 24 h.

Hour	Load	Hour	Load	Hour	Load
1	700	9	1300	17	1000
2	750	10	1400	18	1100
3	800	11	1450	19	1200
4	850	12	1500	20	1400
5	950	13	1400	21	1300
6	1000	14	1300	22	1100
7	1150	15	1200	23	900
8	1200	16	1050	24	800

, while the spinning reserve required was rated at 50 MW $\forall t\in T$, which constituted a standard practice in low-inertia power grids [27].

Formulating the generation ranking based on the proposed enhanced priority-list technique (Equation (18)), the rearrangement of the generators is listed in

Table 3. Enhanced priority-list scheme formulation.

Unit	1	2	3	4	5	6	7	8	9	10
Priority list	1	2	4	3	5	6	7	8	9	10
Boolean Configuration	10	9	8	7	6	5	3	4	2	1

. In the same table, a further row illustrates the new configuration needed to model the UC problem as a BM task, whereby the prioritized units represent low-valued decimals, which, in turn, lead to low-cost solutions.

Based on this configuration, all feasible combinations C, in terms of system adequacy (power output and spinning reserve), were generated and the Boolean mapping procedure was performed to produce a convex CxT-dimensional object. A segmented representative of this example is demonstrated below (

Table 4. Convex object obtained from Boolean encoding.

t	2	4	6	8	10	12	14	16	18	20
C1	3	3	3	3	7	7	3	3	3	7
C2	5	7	7	7	11	11	7	7	7	11
C3	6	11	11	11	15	15	11	11	11	15
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
C40	55	74	93	119	159	167	125	87	93	159
C41	57	75	94	121	163	171	126	89	94	163
C42	58	77	95	122	167	175	127	90	95	167
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
C114	155	186	234	285	382	447	343	215	234	382
C115	157	187	235	286	383	451	347	217	235	383
C116	158	189	237	287	387	455	349	218	237	387
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
C799	1023	-	-	-	-	-	-	-	-	-

).

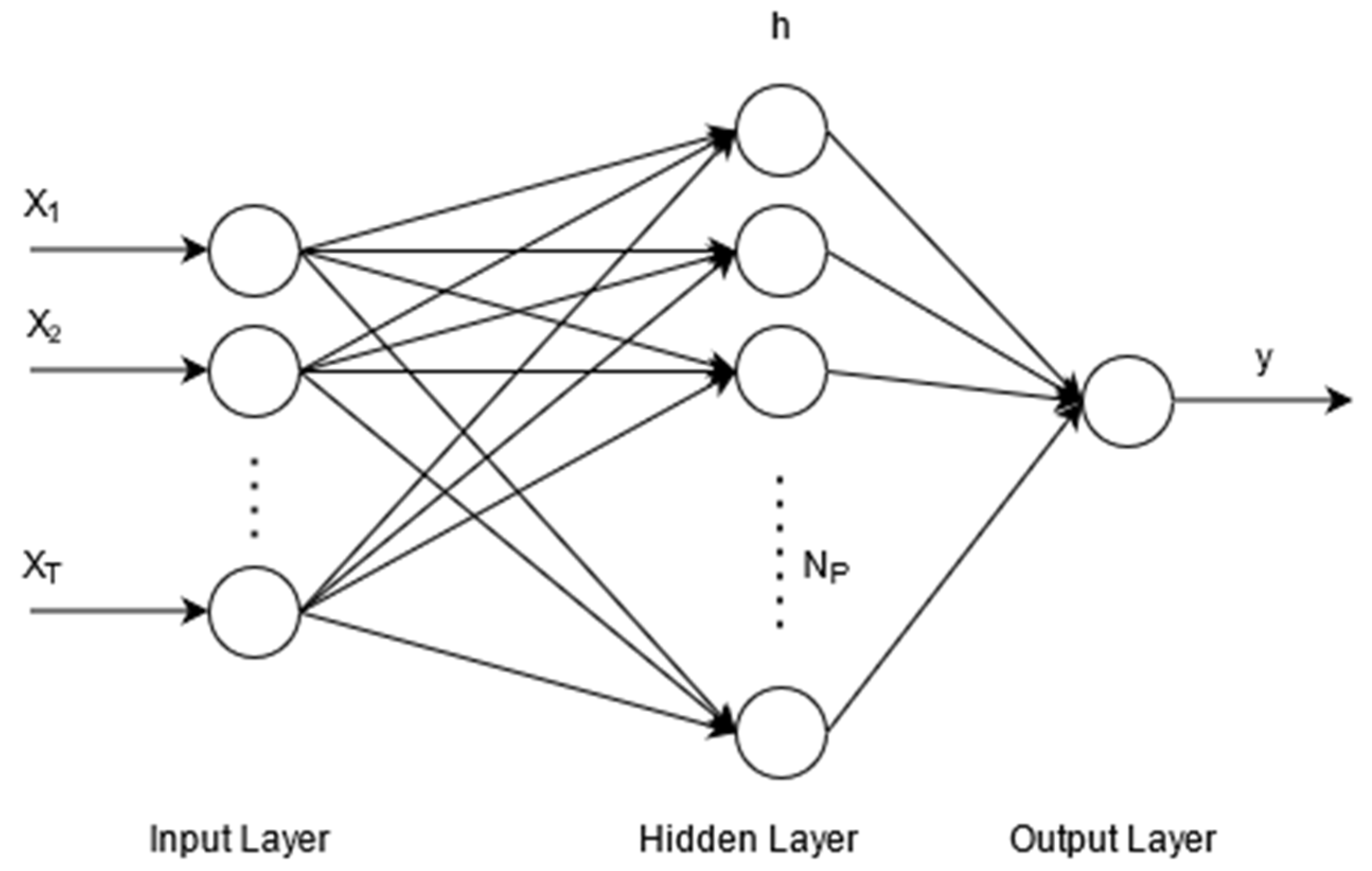
In this form, the modified neural network can receive the values with the aid of T independent inputs and effectively guide the optimization towards the minimum cost, as determined in Equation (30). The developed feed-forward neural is presented in Figure 3, while a plausible implementation can be observed in Figure 4.

According to the performed simulations, a global optimum solution was achieved, offering a UC schedule at a minimum total production cost of $504,803.7. This was certified by the exhaustive enumeration method, which converged to the same result. The minimum cost function obtained at the output of the modified neural equalled to 476, and the respective UC schedule and economic dispatch are offered in

Table 5. Global optimum UC of the proposed BM solution (* indicates the priority ordered units, while bold numbers show the must-run units).

Rank (i *)	1–8	9–13	14–19	20	21–24
1	1	1	1	1	1
2	1	1	1	1	1
4	0	1	0	0	0
3	0	0	0	0	0
5	0	0	0	0	0
6	0	0	0	0	0
7	0	0	0	0	0
8	0	0	0	1	0
9	0	0	0	1	0
10	0	0	0	0	0

and Figure 5, respectively. By making use of BM, the algorithm undoubtedly succeeded in suggesting the optimum scheduling. The minimum number of committed generating units was achieved throughout the time horizon, and the most economic dispatch was reached, satisfying the unit-specific, plant-wide, and system-wise constraints. The complete enumeration obtained exactly the solution via dynamic programming, at the expense of extremely time-consuming convergence intervals. Finally,

Table 6. Comparative results pertaining the 10-unit system.

Method	Number of Function Evaluations	Elapsed Time (sec)	Minimum TPC Achieved
Proposed BM	8901	1063.2	504,803.7
Exhaustive Enumeration	1.7259 × 1072	131,400	504,803.7

TPC = Total production cost ($).

includes the comparisons between the proposed BM and exhaustive enumeration approach.

4.2. Comparative Assessment

In our realization of the BM pipeline, the exact form of the total production cost was retrieved by means of a neural network and non-linear regression model. The postulated model was presented with weighted observations $\left\{\widehat{x},y\right\}$ fed back to the model during the optimization process, enabling efficient prediction of how the dependent variable y would change when the values of the independent/optimizable variables $\tilde{x}$ were modified. In this Section, a thorough experimental assessment of the proposed approach was performed, adopting a common setup, described, for instance, in [17]. Our purpose was to assess the BM computational complexity in large-scale power systems, which is of utmost importance in real-world settings where scheduling decisions may need to be made within limited time-windows.

The comparative assessment regards the power system characteristics of 10 generators presented previously and the replicated equivalents of 20, 40, 80, and 100 units with identical features. All simulations were performed on a computer with Intel-Core i7-4510U CPU @2.6 GHz, 64-bit operating system (Windows 10), and 6 GB of memory. The program was written in MATLAB (MATLAB R2018, MathWorks). To render our experimental setup more realistically, the additional constraint of spinning reserve requirement was set to 5% of the total load, which is a standard practice adopted by system operators [28].

Further, to obtain some comparative results, we compared our solution with some benchmark alternatives under the same experimental scenarios. Specifically, we considered: (1) the heuristic Genetic algorithm (GA) [29], particle swarm optimization (PSO) [30], and simulated annealing (SA) [31]; (2) the mathematical Lagrange relaxation (LR) [32], mixed-integer non-linear programming (MINLP) [33], and priority list (PL) [34]; and (3) the hybrid binary whale optimization algorithm (BWOA) [17], binary successive civilized swarm optimization (BSCSO) [35], and binary gray wolf optimization (BGWO) [30]. The obtained results are provided in

Table 7. Cost ($) comparisons under different case studies.

Method	10 Units	20 Units	40 Units	80 Units	100 Units
GA	563,977	1,126,243	2,252,909	4,507,692	5,626,361
PSO	563,954	1,125,279	2,248,163	4,495,032	5,619,284
SA	565,828	1,126,254	2,250,012	4,498,076	5,617,876
LR	566,107	1,128,362	2,258,503	4,526,022	5,657,277
MINLP	567,022	1,138,513	2,257,248	4,526,022	5,646,219
PL	563,977	1,124,369	2,246,508	4,489,322	5,605,678
BWOA	563,936	1,123,560	2,223,926	4,478,412	5,599,281
BSCSO	553,423	-	2,183,232	-	5,510,962
BGWO	563,937	1,123,297	2,244,701	4,483,381	5,604,146
BM	504,804	1,009,607	2,019,215	4,038,430	5,048,037

.

As we observed, our proposed approach based on BM yielded the best optimal solution, which decreased the minimum achieved TPC by a whopping $598K in the case of a 100-unit system. This is an unprecedented improvement over the current alternatives. In addition, it offers strong empirical evidence that the proposed Boolean mapping paradigm brings significant merit and benefits to the design of successful UC models. Within the three categories, PSO, PL, and BSCSO seem advantageous over their respective heuristic, mathematical, and hybrid competitors. The mathematical PL prevailed over PSO in medium- to large-scale systems (greater than 20 generating units), whereas the hybrid alternatives offered lower-cost solutions in each case study.

The second key aspect that characterized the optimization process refers to the number of attempts (function evaluations) performed by the algorithm to converge to a minimum solution. In Figure 6, the number of function evaluations (NFE) with respect to the number of participating units pertaining to the best approach within each category are illustrated and compared with those required by the proposed BM.

As can be seen, the BM mechanism provided a linear relationship between the required evaluations while the considered methods showed an exponential increase with respect to the participating generating units. This stems from the fact that the Boolean mapping led to 2D decimal matrices, which were further treated as T = 24 independent inputs by the neural network. This resulted in the dimensional decoupling from the number of available units N, and the system complexity depended exclusively on the time intervals of the optimization horizon (T). Moreover, the postulated decimal configuration of the feasible combinations was addressed in the absence of any stochastic search mechanism, eliminating the need for a required exploration-exploitation process, which constitutes an intensive task to reach the optimum trade-off. In terms of NFE per unit rates, PL constituted the next best-fit solution following by PSO. However, both methods provided quite higher values in terms of TPC. Relating to the next optimum solution offered by BSCSO, this showed higher NFE per unit rates, which increased with increasing generators in the system.

5. Conclusions

In this work, a novel approach for addressing the UC problem based on Boolean mapping paradigm was proposed. The main motivational forces behind our work were (1) an effective means of eliminating the need of stochastic search methods to provide a solution based on optimal exploration-exploitation trade-off and (2) a solution that is intrinsically designed to converge in the least possible number of function evaluations, decoupling the computational complexity from the number of participating generating units.

Our proposed method relies on enhanced priority-list schemes and an effective coding/decoding algorithm for enabling Boolean inference of the decimal form of the underlying cost function, as well as the utilization of a state-of-the-art scheme for selecting the next function evaluation, namely, a feed-forward neural network. Following a four-stage procedure, the imposed constraints were sequentially satisfied, decoupling the binary complicated constraints by the discontinuous dynamical restrictions. A thorough experimental evaluation of our approach was provided under standard scenarios and compared with benchmark alternatives. As observed, the proposed solution outperformed its alternatives in terms of both the ultimate system’s total production costs and the number of required function evaluations. These findings strongly collaborate our theoretical claims that Boolean mapping can adequately overcome the non-convexity problem that aggravates the UC task.

As for future directions for research, we indicate the inclusion of stochastic (or fuzzy) formulations to represent the renewable generation uncertainty in the objective. More extended works may also involve multi-bus formulations introducing the real power network constraints and the participation of storage. By increasing the formulation complexity our novel approach might allow for even higher optimization performance.