Non-Linear Investigation of a Functionally Graded Pipe ^†

Abstract

A pipe subjected to an evenly distributed internal pressure is investigated in this theoretical paper. The pipe has a thin wall that is built-up by a functionally graded engineering material. The circumferential stresses and strains in the pipe wall are investigated. In essence, the current investigation is non-linear since the wall behaves as a non-linear elastic body with non-linearly distributed properties through the wall thickness. The different stages of the work of the wall are investigated and the corresponding parameters of stressed and strained state are derived. The dependence of the pressure on the material and geometrical parameters are studied.

1. Introduction

Pipes are used as important components of various engines, machines, aids, and facilities in numerous applications in different areas of modern technologies [1,2,3]. Pipes can also be used as structural members in construction engineering. Most frequently, pipes contain liquids under pressure [4,5,6,7]. Therefore, the investigation of the behaviour of pipes subjected to internal pressure represents a problem that has strong relations with the design of pipe systems.

The functionally graded materials represent highly interesting and rapidly developing types of engineering materials, which can be opened up to a variety of possibilities [8,9,10,11]. In mechanical engineering, for instance, the share of these materials uninterruptedly grows and contributes significantly to the quality and the competitive power of products.

This paper analyzes a pipe made of a functionally graded structural material. The pipe is under a uniform internal pressure. The purpose of the analysis is to determine the parameters of the stressed and strained state of the pipe wall. The latter behaves as a non-linear elastic body. In addition, the pipe material properties are distributed non-linearly through the wall thickness. Based upon the performed analysis, some recommendations for increasing the pressure are formulated.

2. Pipe Non-Linear Investigation

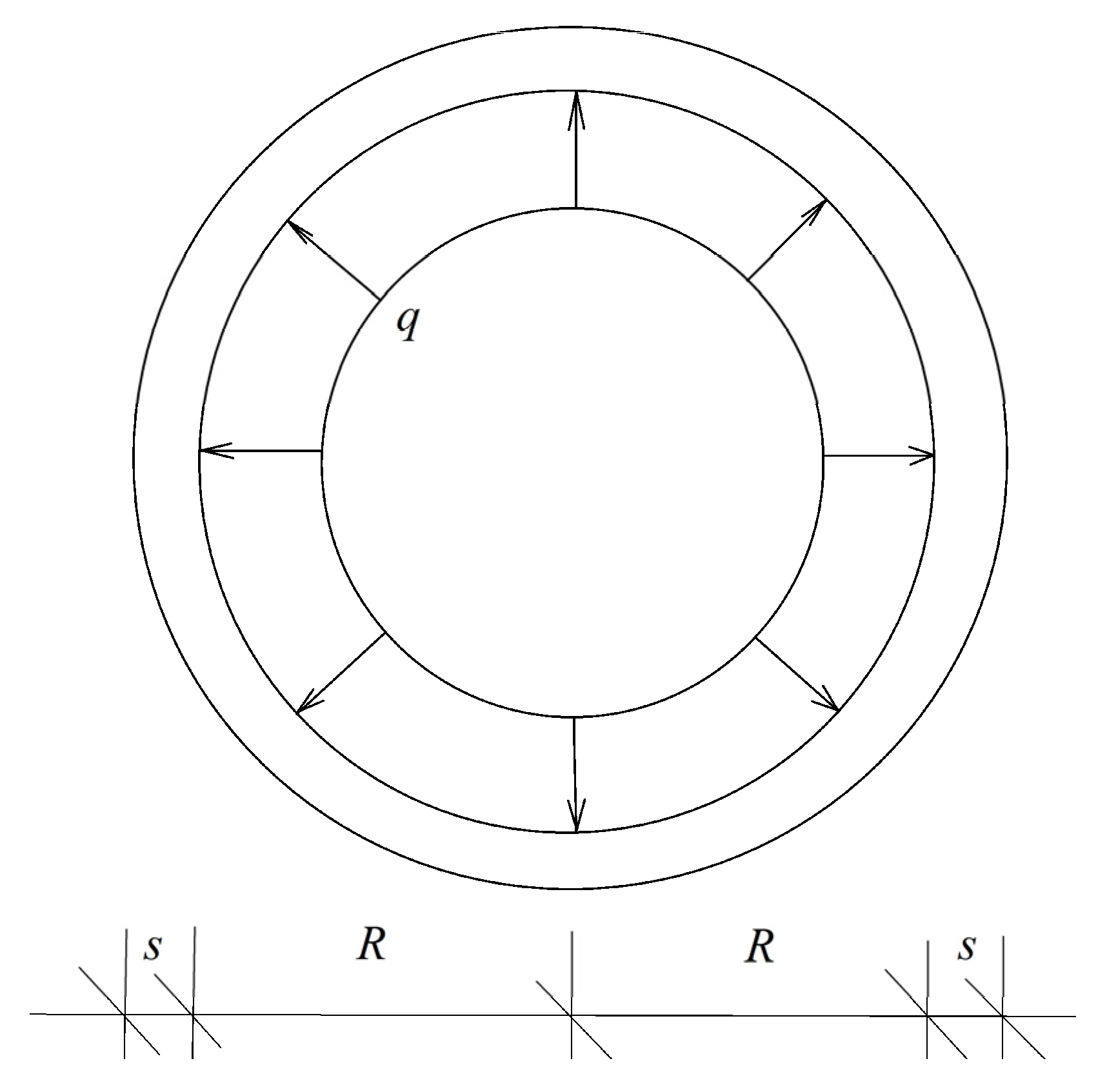
Figure 1 represents the cross-section of a pipe with radius, $R$. The thickness of the pipe wall is $s$ where $s<<R$, i.e., the wall is thin. The pipe is subjected to a uniform internal pressure, $q$. Since the wall is thin, the pipe essentially is under pure tension in circumferential direction.

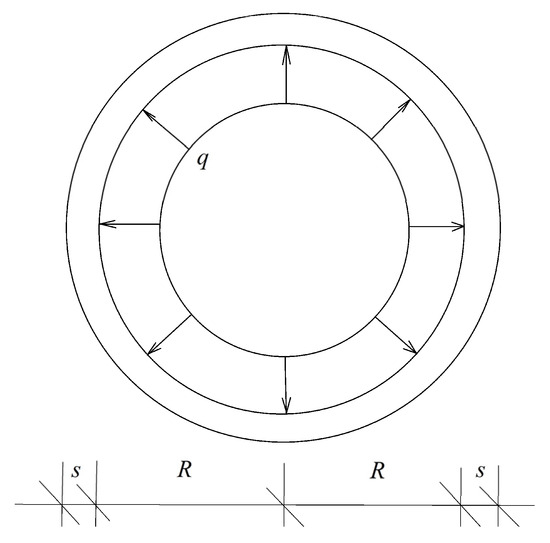
Figure 1. Pipe under internal pressure.

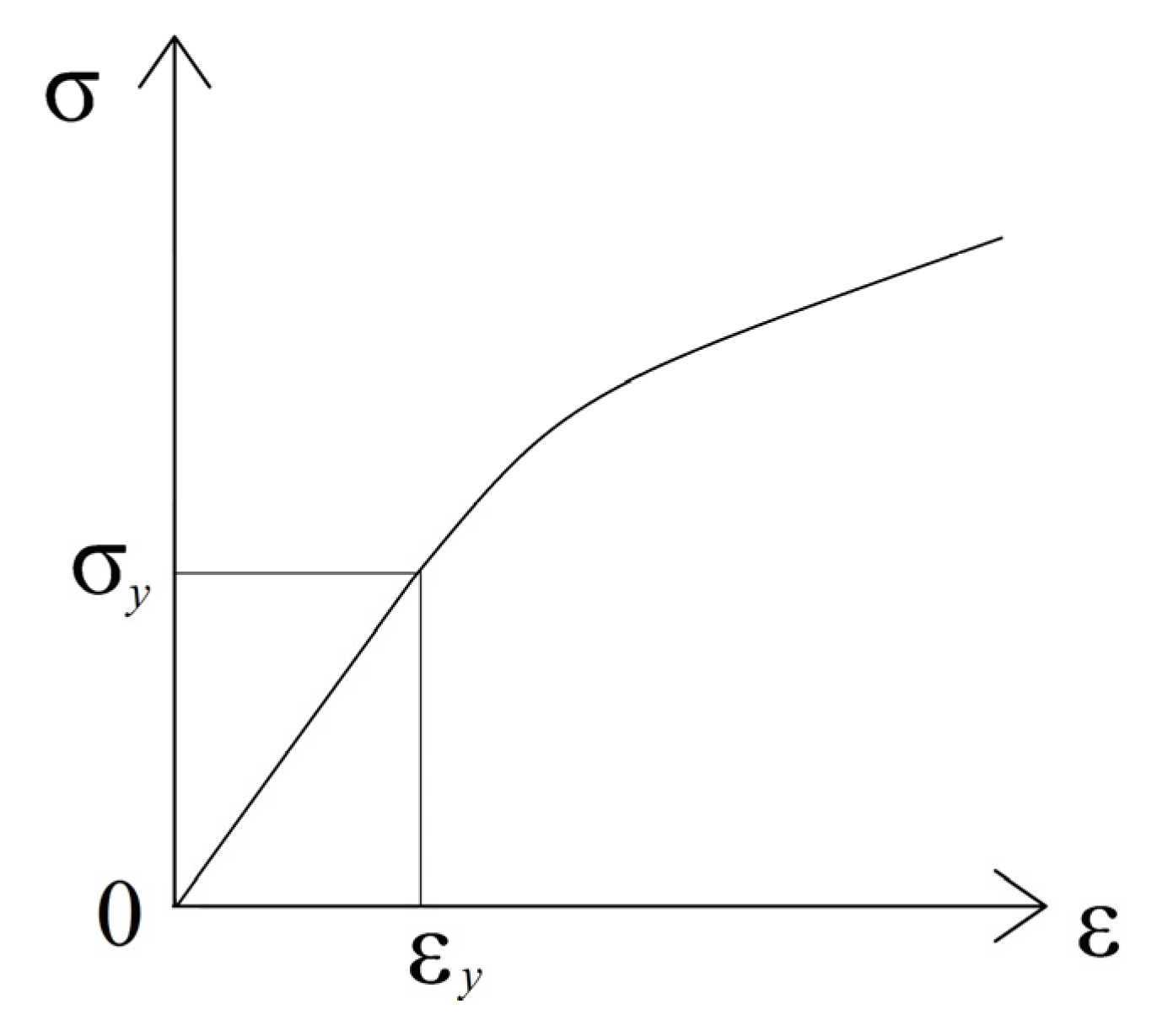
Formula (1) expresses a non-linear stress–strain relation that is applied as a constitutive law for the pipe wall [12].

$$\epsilon =\left\{\begin{array}{c}{\displaystyle \frac{\sigma }{E}},\hspace{0.33em}\sigma \le {\sigma }_y\\ {\displaystyle \frac{{\sigma }_y}{E}}\left[{\displaystyle \frac{1}{n}}{\left({\displaystyle \frac{\sigma }{{\sigma }_y}}\right)}^n-{\displaystyle \frac{1}{n}}+1\right],\hspace{0.33em}\sigma >{\sigma }_y\end{array}\right.,$$

(1)

where $\epsilon$ and $\sigma$ are the circumferential strain and stress in the pipe wall, $E$ is the modulus of elasticity, ${\sigma }_y$ is the yield stress, $n$ is a parameter.

The stress–strain diagram that corresponds to (1) is shown in Figure 2.

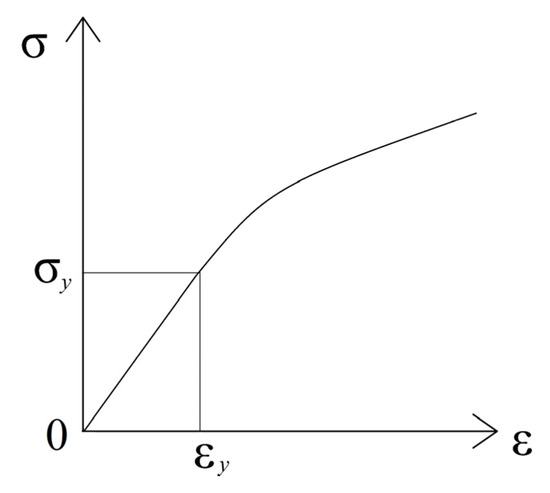
Figure 2. Stress–strain diagram.

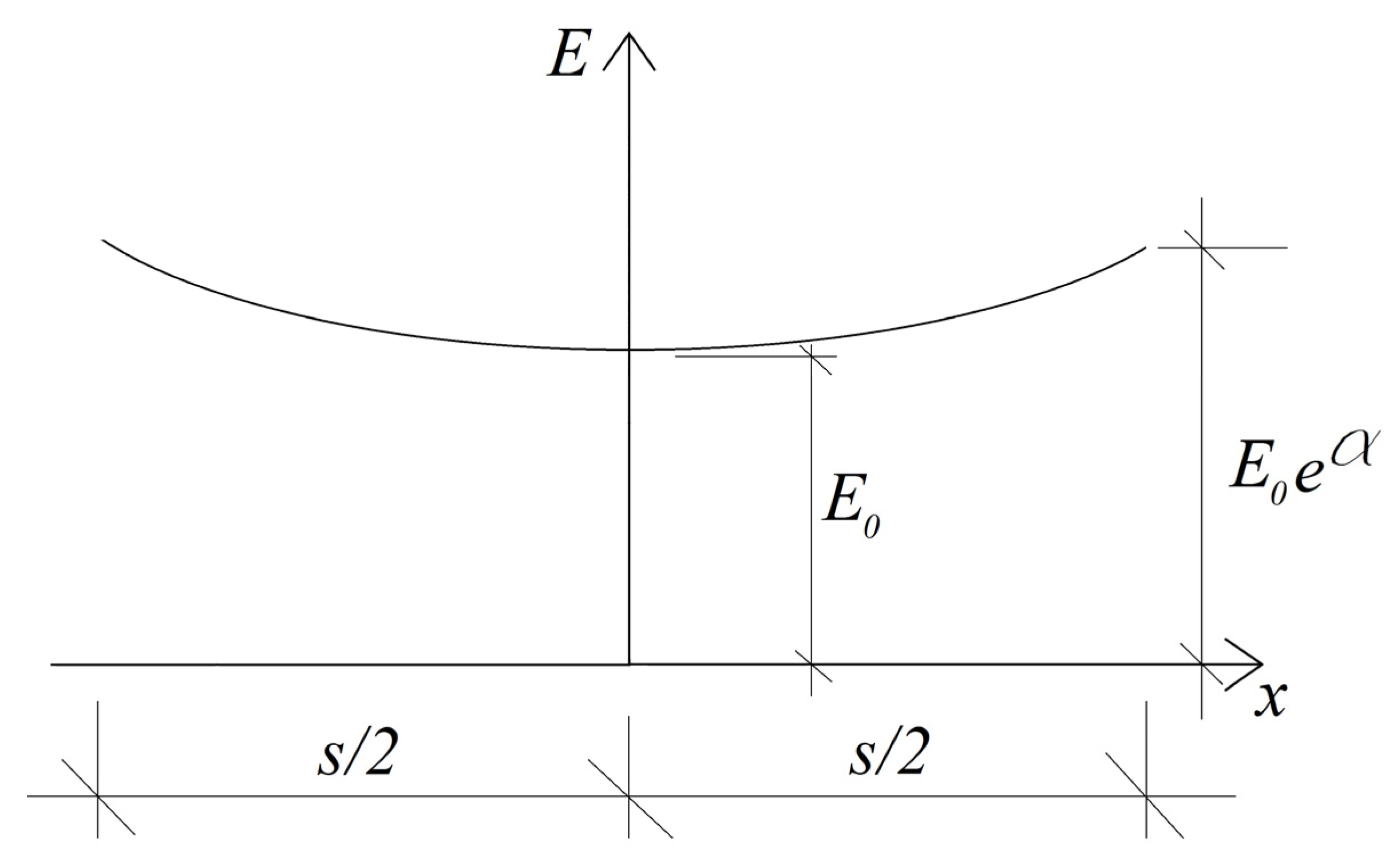
The pipe wall is functionally graded along its thickness. Thus, $E$ and $n$ vary smoothly along the pipe wall thickness according to exponential laws, which are a common choice for functionally graded products. Here, an important peculiarity is that this variation is symmetric with respect to the pipe middle surface, i.e.,

$$E=E_0{e}^{\alpha {\displaystyle \frac{\left|x\right|}{\frac{s}{2}}}},$$

(2)

$$n=n_0{e}^{\beta {\displaystyle \frac{\left|x\right|}{\frac{s}{2}}}},$$

(3)

where

$$-{\displaystyle \frac{s}{2}}\le x\le {\displaystyle \frac{s}{2}}.$$

(4)

The quantities $\alpha$ and $\beta$ are parameters, $E_0$ and $n_0$ are the values on $E$ and $n$ in the middle surface. Figure 3 illustrates how $E$ varies along the wall thickness (variation of $n$ is identical).

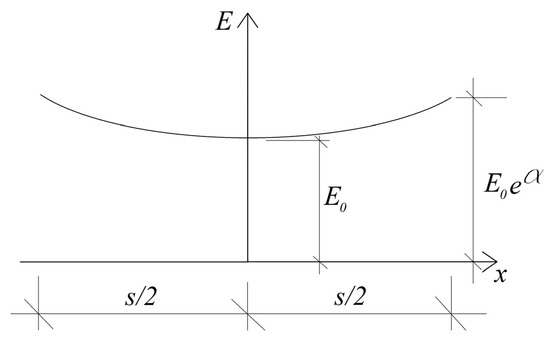
Figure 3. Schema of variation of $E$ along the wall thickness.

The circumferential force, $N$, in the pipe wall is

$$N=qR.$$

(5)

From the equilibrium, one has

$$N=2{\displaystyle \underset{0}{\overset{\frac{s}{2}}{\int }}\sigma dx},$$

(6)

where $\sigma$ is

$$\sigma =\left\{\begin{array}{c}E\epsilon ,\hspace{0.33em}\epsilon \le {\epsilon }_y\\ {\sigma }_y{\left[n\left({\displaystyle \frac{E\epsilon }{{\sigma }_y}}+{\displaystyle \frac{1}{n}}-1\right)\right]}^{{\displaystyle \frac{1}{n}}},\hspace{0.33em}\epsilon >{\epsilon }_y\end{array}\right..$$

(7)

Here, relations (7) are found from (1), $E$ and $n$ are given by (2) and (3), respectively. One determines $\epsilon$ from (6) by the MatLab 6.5. According to the stage of work of the pipe wall along the thickness, three cases are possible when using Equation (6).

In the first stage, the entire pipe wall behaves as a linear-elastic body. Thus, the stress is

$$\sigma =E\epsilon .$$

(8)

Therefore,

$$N=2{\displaystyle \underset{0}{\overset{\frac{s}{2}}{\int }}E\epsilon dx}.$$

(9)

In the second stage, the parts near the pipe wall surfaces will be in a non-linear elastic state, while the core of the pipe wall still will be in linear-elastic state. Hence,

$$N=2{\displaystyle \underset{0}{\overset{\frac{s}{2}-p}{\int }}{\sigma }_{el}dx}+2{\displaystyle \underset{\frac{s}{2}-p}{\overset{\frac{s}{2}}{\int }}{\sigma }_{elpl}dx} ,$$

(10)

where

$$0<p<{\displaystyle \frac{s}{2}},$$

(11)

$${\sigma }_{el}=E\epsilon ,$$

(12)

for

$$\epsilon \le {\epsilon }_y$$

(13)

and

$${\sigma }_{elpl}={\sigma }_y{\left[n\left({\displaystyle \frac{E\epsilon }{{\sigma }_y}}+{\displaystyle \frac{1}{n}}-1\right)\right]}^{{\displaystyle \frac{1}{n}}}$$

(14)

for

$$\epsilon >{\epsilon }_y.$$

(15)

In (10), the parameter, $p$, is the size of the part that is in non-linear elastic state.

In the third stage, the entire pipe wall behaves as a non-linear elastic body. Therefore,

$$N=2{\displaystyle \underset{0}{\overset{\frac{s}{2}}{\int }}{\sigma }_{elpl}dx}.$$

(16)

Note that at

$$p={\displaystyle \frac{s}{2}},$$

(17)

Formula (10) converts into (16).

The strain is determined from (9), (10), or (16) for the different stages of the pipe wall behaviour. One applies this strain for obtaining of $\sigma$ via the corresponding dependency in (7).

One can prove the validity of the above-described analysis of functionally graded pipe on base of the following reasoning. Note that at

$$\alpha =0$$

(18)

and

$$\beta =0.$$

(19)

Formulas (2) and (3) convert into

$$E=E_0$$

(20)

and

$$n=n_0 .$$

(21)

In addition, at

$${\sigma }_y\to \infty ,$$

(22)

relation (1) converts into

$$\sigma =E\epsilon .$$

(23)

This indicates that by inserting of (18)–(23) in (9), (10), and (16), one has to obtain the strain in the wall of a homogeneous linear-elastic pipe. Indeed, after inserting of (18)–(22) in (9), (10), and (16), one has

$$\epsilon ={\displaystyle \frac{qR}{Es}},$$

(24)

which is the known solution of the strain for a homogeneous linear-elastic pipe [13].

One can apply the analysis of the stresses and strains developed here for obtaining useful information about the influence of the parameters of the functionally graded wall on the pressure in the pipe.

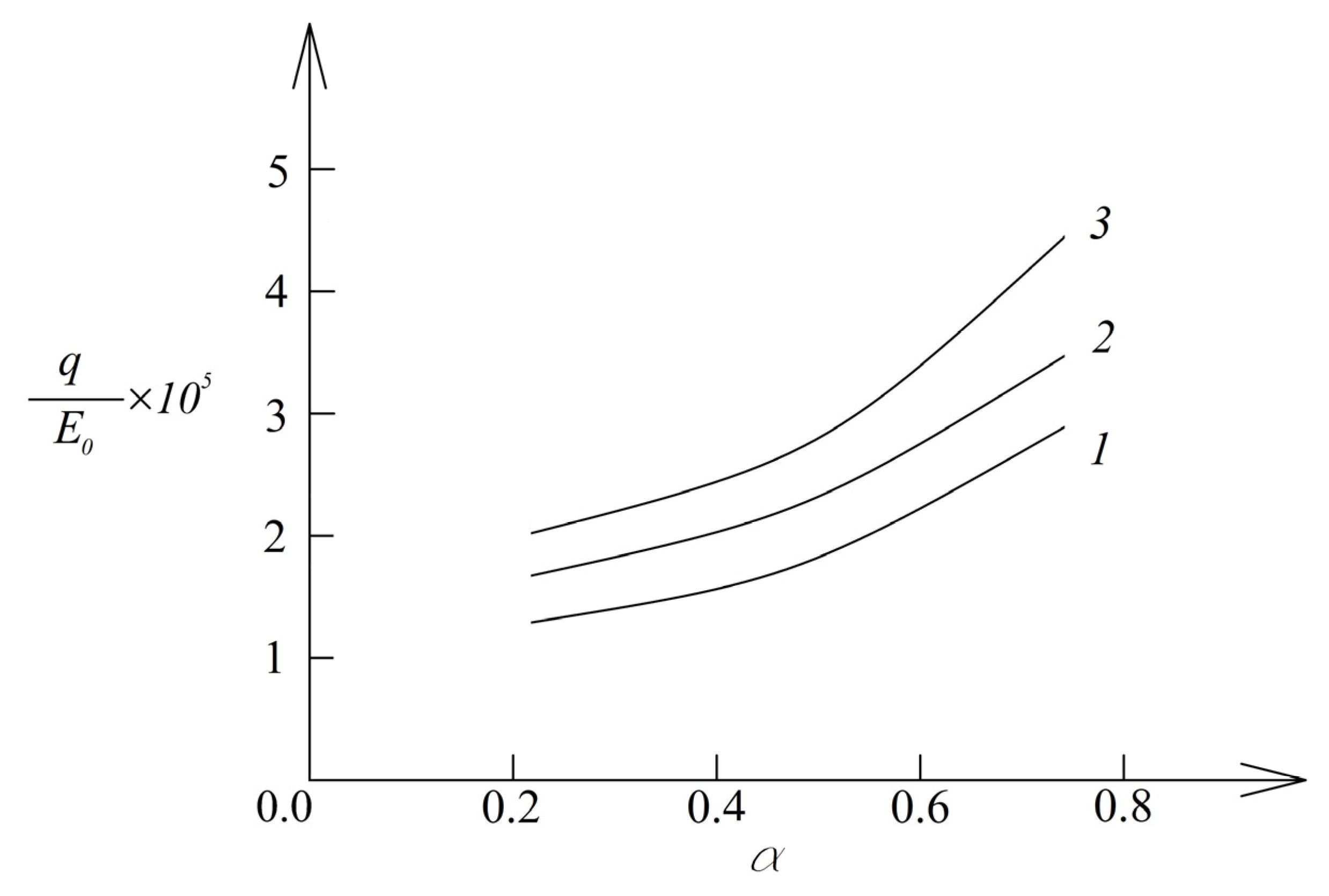
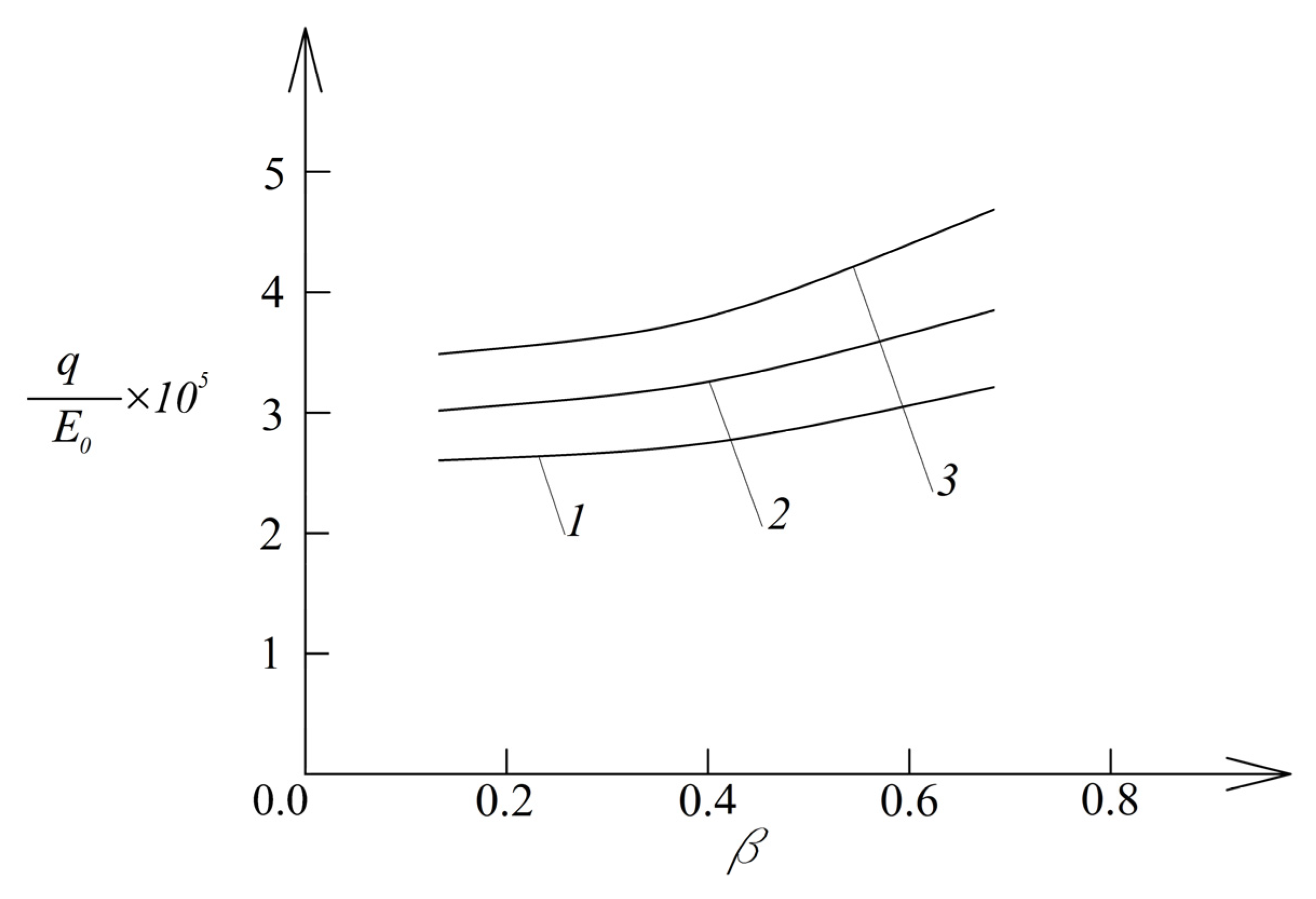
For instance, the analysis generates the dependence of the normalized pressure, $q/E_0$, on the parameter, $\alpha$, and $s/R$ ratio at $p=s/4$ and $n=3$ that is illustrated in Figure 4.

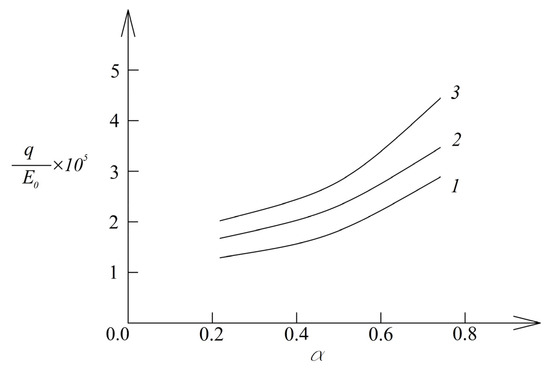
Figure 4. Diagrams of the dependence of normalized pressure on the parameter $\alpha$ (1—for $s/R=0.02$, 2—for $s/R=0.004$, and 3—for $s/R=0.006$).

The dependence of the normalized pressure, $q/E_0$, on the parameter, $\beta$, and ${\sigma }_y/E_0$ ratio is also studied (this dependence is shown in Figure 5).

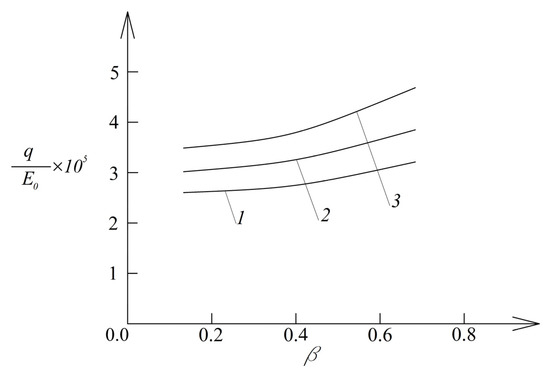
Figure 5. Diagrams of the dependence of normalized pressure on the parameter $\beta$ (1—for ${\sigma }_y/E_0=0.0003$, 2—for ${\sigma }_y/E_0=0.0005$, and 3—for ${\sigma }_y/E_0=0.0007$).

3. Conclusions

An investigation of a thin pipe under a uniform internal pressure is reported. There are two basic points in this investigation. The first one is that the pipe wall is functionally graded through the thickness. The second one is that the pipe behaves as a non-linear elastic body. It is known that one of the important practical questions in the engineering design of pipes is how the internal pressure can be increased without compromising the normal exploitation of the pipe. For functionally graded pipes, in particular, the investigation that is reported here gives the following answers to the above question. First, the pressure can be increased by using functionally graded materials (for the pipe wall) which have higher values of parameters, $\alpha$ and $\beta$, and higher ${\sigma }_y/E_0$ ratio. Increasing the $s/R$ ratio is also a way of rising of the pressure in the pipe. The study limitation is that it holds only thin wall pipes.