Short Term Load Forecasting for Electric Power Utilities: A Generalized Regression Approach Using Polynomials and Cross-Terms †
Abstract
:1. Introduction
- GLRM-PCT serves as a benchmark STLF model for electric utilities in Pakistan;
- Use of synthetic weather stations for STLF models in electric utilities of Pakistan;
- High-resolution interpretability, unlike previously developed black-box models;
- Incorporates a diverse combination of both quantitative and qualitative variables;
- The proposed model also takes advantage of the recency effects;
- Evaluation using five different performance metrics for a broader readership.
2. Methodology
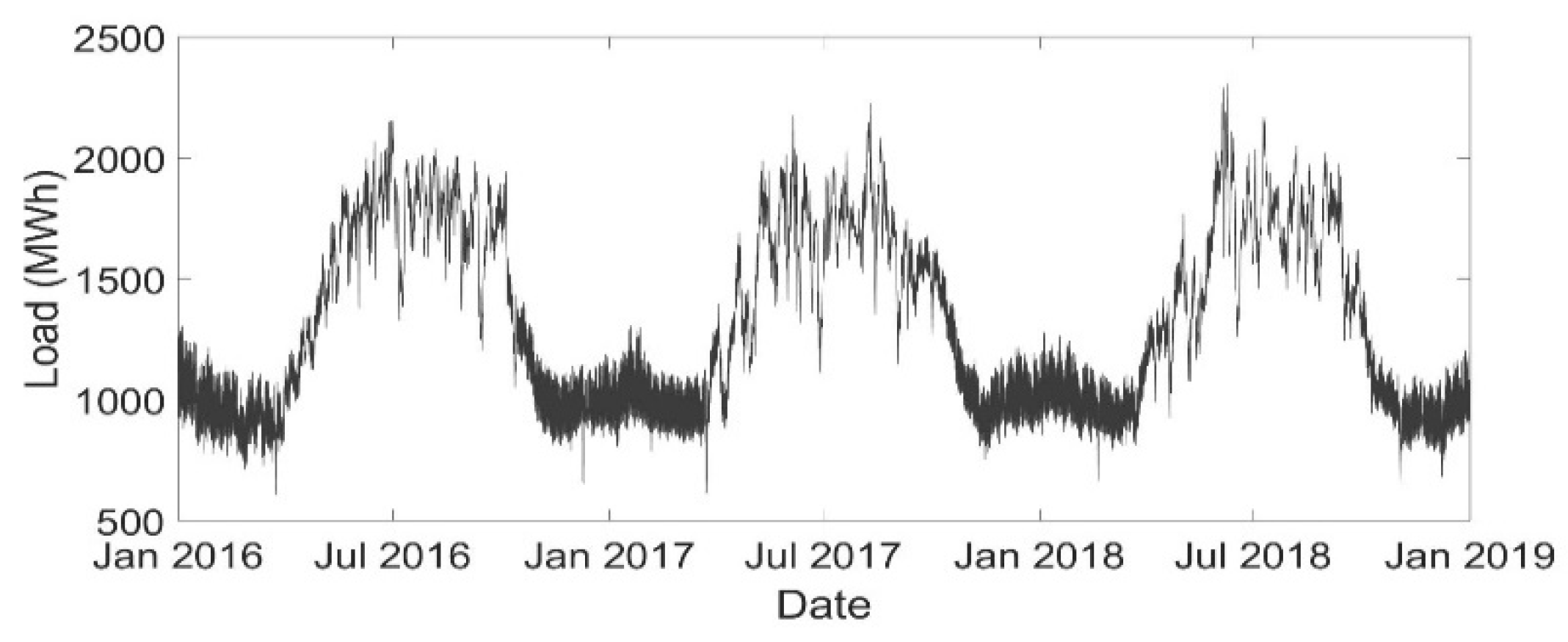
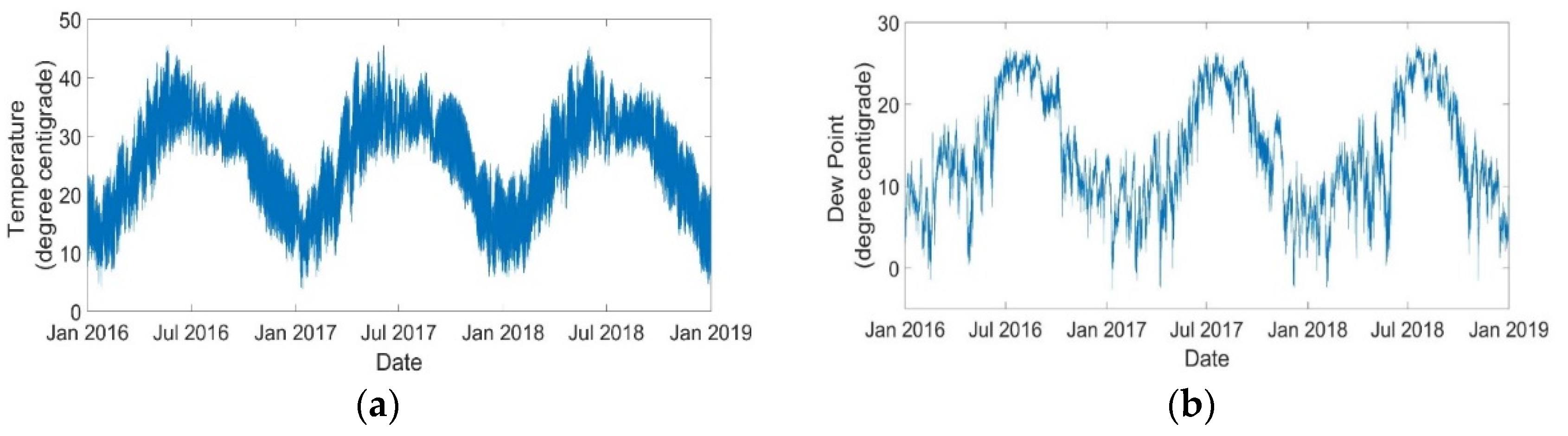
2.1. Data Collection and Model Development
2.1.1. Target Variable; Load
2.1.2. Demand Determinants
3. Forecasting Techniques
3.1. Multiple Linear Regression
3.2. Multiple Linear Regression with Polynomials and Cross Terms
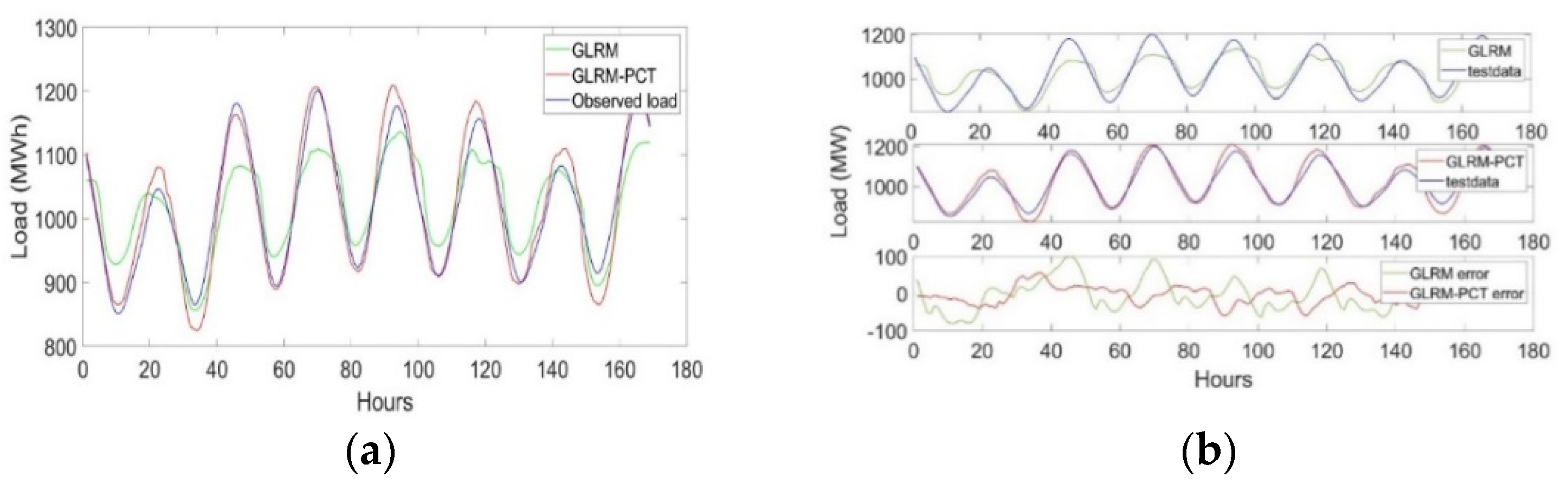
4. Results and Discussion
5. Conclusions
Conflicts of Interest
References
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Mir, A.A.; Alghassab, M.; Ullah, K.; Khan, Z.A.; Lu, Y.; Imran, M. A Review of Electricity Demand Forecasting in Low and Middle Income Countries: The Demand Determinants and Horizons. Sustainability 2020, 12, 5931. [Google Scholar] [CrossRef]
- Hu, R.; Wen, S.; Zeng, Z.; Huang, T. A short-term power load forecasting model based on the generalized regression neural network with decreasing step fruit fly optimization algorithm. Neurocomputing 2017, 221, 24–31. [Google Scholar] [CrossRef]
- Abbas, F.; Feng, D.; Habib, S.; Rahman, U.; Rasool, A.; Yan, Z. Short Term Residential Load Forecasting: An Improved Optimal Nonlinear Auto Regressive (NARX) Method with Exponential Weight Decay Function. Electronics 2018, 7, 432. [Google Scholar] [CrossRef] [Green Version]
- Copernicus. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels (accessed on 14 July 2020).
| Forecasting Techniques | Performance Metrics | |||||||
|---|---|---|---|---|---|---|---|---|
| MAE (MW) | MAPE (%) | RMSE (MW) | R-Squared | Adjusted r-Squared | ||||
| Train | Test | Train | Test | Train | Test | |||
| GLRM | 43.349 | 45.815 | 3.338 | 3.544 | 59.351 | 61.47 | 0.972 | 0.972 |
| GLRM-PCT | 35.349 | 36.883 | 2.668 | 2.83 | 50.62 | 51.108 | 0.981 | 0.981 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mir, A.A.; Ullah, K.; Khan, Z.A.; Bashir, F.; Khan, T.U.R.; Altamimi, A. Short Term Load Forecasting for Electric Power Utilities: A Generalized Regression Approach Using Polynomials and Cross-Terms. Eng. Proc. 2021, 12, 21. https://doi.org/10.3390/engproc2021012021
Mir AA, Ullah K, Khan ZA, Bashir F, Khan TUR, Altamimi A. Short Term Load Forecasting for Electric Power Utilities: A Generalized Regression Approach Using Polynomials and Cross-Terms. Engineering Proceedings. 2021; 12(1):21. https://doi.org/10.3390/engproc2021012021
Chicago/Turabian StyleMir, Aneeque Ahmed, Kafait Ullah, Zafar A. Khan, Furrukh Bashir, Tauseef Ur Rehman Khan, and Abdullah Altamimi. 2021. "Short Term Load Forecasting for Electric Power Utilities: A Generalized Regression Approach Using Polynomials and Cross-Terms" Engineering Proceedings 12, no. 1: 21. https://doi.org/10.3390/engproc2021012021
APA StyleMir, A. A., Ullah, K., Khan, Z. A., Bashir, F., Khan, T. U. R., & Altamimi, A. (2021). Short Term Load Forecasting for Electric Power Utilities: A Generalized Regression Approach Using Polynomials and Cross-Terms. Engineering Proceedings, 12(1), 21. https://doi.org/10.3390/engproc2021012021








