Output Feedback Control of Two-Time-Scale Permanent-Magnet DC Motor Using High-Gain Observers ^†

Abstract

In this paper, we propose a methodology for implementing an output feedback control (OFC) strategy for a two-time-scale nonlinear system. A permanent-magnet DC motor model is utilized. We estimated the states using a high-gain observer for a two-time-scale nonlinear system. The results demonstrate the robustness and efficacy of the suggested OFC technique. Furthermore, the output feedback control approach exhibits robustness to parametric uncertainties, thereby making it feasible for practical implementation in a two-time-scale nonlinear system.

1. Introduction

Small parameters such as capacitances and time constants are the cause of the development of singular perturbation theory. These parameters are usually ignored in dynamic models to simplify the models; however, this over-simplification comes at a cost. Singular perturbation theory ensures that this over-simplified model remains useful for analysis and control design [1]. Multiple-time-scale systems are common in science and engineering as many scientific and engineering processes exhibit multiple-time-scale behavior [2]. In a two-time-scale system, some states evolve slowly with time, while other states evolve at a faster rate with time. The state model of a system depends on a small perturbation parameter ε, which is either the system’s parameter or injected artificially to produce a two-time-scale system. Setting ε = 0 brings an abrupt change in the dynamic behavior of a system and produces a reduced-order system [3].

The measurement of all the variables of interest in a dynamic system is not feasible due to cost-related considerations or technical limitations. These constraints necessitate the use of output feedback control (OFC) in place of full-state feedback control (SFC). The most widely used solution to the problem, when states are required but not measured, is to use an observer for state estimation. The Luenberger observer and Kalman filter are commonly used for the state estimation of linear systems. For nonlinear systems, linear observers are applied after linearizing the system about the equilibrium point. However, this technique is local and only works when the states are evolved in the vicinity of the point of linearization. For global results, nonlinear observers are used for nonlinear systems.

The theory of multiple-time-scale behavior has been developed and analyzed widely; however, the nonlinear state estimation of multiple-time-scale systems is still an open area of research. There are limited results on nonlinear observer design for nonlinear singularly perturbed systems. However, these nonlinear state estimation techniques are not appropriate in terms of observer gains when used for multiple-time-scale systems.

With the advancements in nonlinear control theory, special attention has been given to nonlinear observers. High-gain observers (HGOs), being robust to parametric and modeling uncertainties, have gained more attention in nonlinear control systems [4]. Through the utility of the separation principle, controls and observers can be designed separately, and the results under SFC are similar to those of OFC given that the so-called high-gain parameter approaches zero. In recent years, extensive research has been conducted on the design, analysis and implementation of high-gain observers for nonlinear systems; however, there is a lack of research and literature available on the topic of robust observer design, for both slow and fast states simultaneously, using HGO.

In this article, we addressed the problem of state estimation via HGO for a class of standard two-time-scale systems. We propose an HGO-based OFC technique for a two-time-scale model of a permanent-magnet direct current (PMDC) motor. We show that the proposed HGO follows the separation principle, i.e., as the value of the high-gain parameter is reduced sufficiently, the response of OFC approaches that of SFC.

2. Output Feedback Control Design

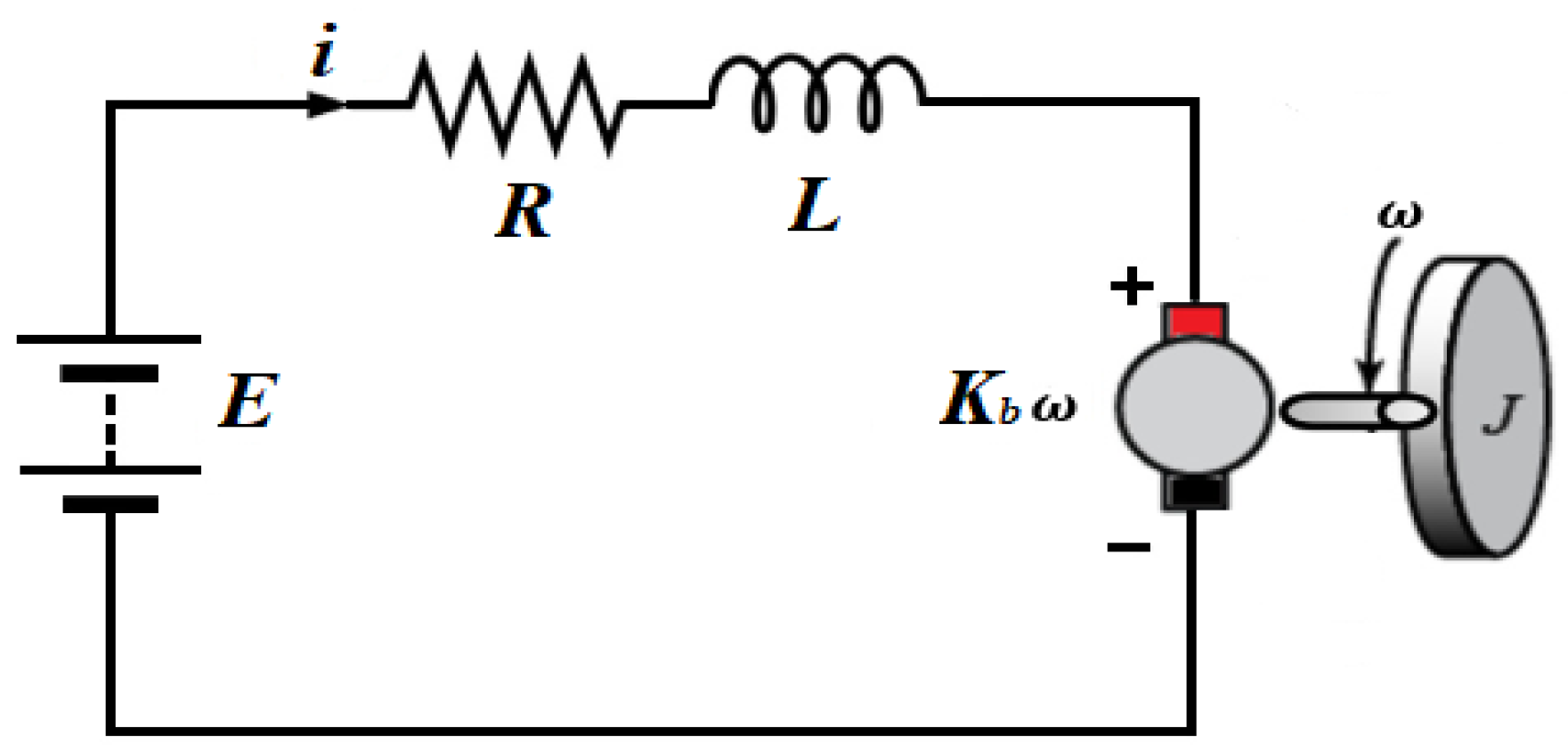
Permanent-magnet motors are widely used in a large number of electrical and mechanical applications. Figure 1 shows the equivalent circuit of a PMDC motor. The dynamic model of a PMDC motor at no load is represented by the following state equations [3]:

$$J\frac{d\omega }{dt}=k_{t}i,$$

(1)

$$L\frac{di}{dt}=-k_b\omega -Ri+E,$$

(2)

where $\omega$ represents the angular speed, $i$ denotes the armature circuit current, $L$ represents the armature inductance, $J$ represents the rotor moment, $R$ is the armature circuit resistance, $k_b$ is the back emf constant and $k_t$ is the torque constant. The input of the system is input voltage $E$, whereas the angular speed is the output of the system, defined as $\omega$. Singular perturbation theory states that the perturbation parameter $\epsilon$ should be dimensionless. Thus, defining the dimensionless parameters as ${\omega }_r=\omega / \mathsf{\Theta }$ and $i_r=iR/k_b\mathsf{\Theta }$ and $E_r=E/k_b\mathsf{\Theta }$, systems (1) and (2) take the following form:

$${\mathcal{T}}_m\frac{d{\omega }_r}{dt}=i_r,$$

(3)

$${\mathcal{T}}_e\frac{d{i}_r}{dt}=-{\omega }_r-i_r+E_r,$$

(4)

where ${\mathcal{T}}_m=JR/k_t{k}_b$ and ${\mathcal{T}}_e=L/R$ are mechanical and electrical time constants, respectively. Since ${\mathcal{T}}_m\gg {\mathcal{T}}_e$, defining a dimensionless time variable $t_r=t/{\mathcal{T}}_m$, the systems (3) and (4) takes the following form:

$$\frac{d{\omega }_r}{d{t}_r}=i_r,$$

(5)

$$\epsilon \frac{d{i}_r}{d{t}_r}=-{\omega }_r-i_r+E_r,$$

(6)

where the dimensionless perturbation parameter $\epsilon$ is defined as:

$$\epsilon =\frac{{\tau }_e}{{\tau }_m}=\frac{L{k}_t{k}_b}{J{R}^2},$$

(7)

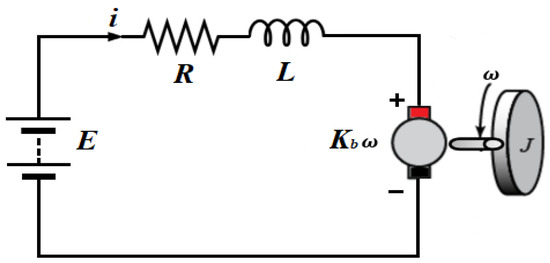
Figure 1. Equivalent Circuit of permanent-magnet DC Motor.

Setting $\epsilon =0$ in (6),

$$i_r=-{\omega }_r+E_r=h\left(x\right),$$

(8)

and with a change in coordinates $y=i_r-h\left(x\right)=i_r+{\omega }_r-E_r$, and taking the input voltage $E_r=-k_1{\omega }_r-k_2{i}_r$, the boundary-layer model

$$\frac{dy}{d\tau }=-\left(1+k_2\right)y,$$

(9)

is globally exponentially stable for $k_1=1$ and $k_2>-1$, and the HGOs for the slow and fast variables are taken as:

$$\frac{d{\widehat{\omega }}_r}{d{t}_r}={\widehat{i}}_r+\frac{{\alpha }_1}{\epsilon }\left({\omega }_r-{\widehat{\omega }}_r\right),$$

(10)

$$\epsilon \frac{d\widehat{y}}{d{t}_r}=-\left(1+k_2\right)\widehat{y}+\frac{{\beta }_1}{\overline{\epsilon }}\left({\omega }_r-{\widehat{\omega }}_r\right),$$

(11)

with the globally bounded control law

$$E_r=-k_1{\widehat{\omega }}_r-k_2{\widehat{i}}_r,$$

(12)

whereas the control input can be globally bounded by saturating it outside the region of interest and ${\widehat{i}}_r=\widehat{y}-{\widehat{\omega }}_r-E_r$.

3. Simulation Results

This section presents the simulation results of the OFC designed for the PMDC motor model. To investigate the efficacy of the designed HGOs on the PMDC model, it is simulated in MATLAB. The parameters utilized are: $J=1.8\times {10}^{-4}{ \mathrm{kgm}}^2$, $k_t=0.057 \mathrm{Nm}/\mathrm{A}$, $k_b=0.057 \mathrm{Vs}/\mathrm{rad}$, $L=0.9 \mathrm{mH}$, $R=10 \mathsf{\Omega }$, ${\omega }_r\left(0\right)=0.1$, $i_r\left(0\right)=0.5$ and ${\widehat{\omega }}_r\left(0\right)={\widehat{i}}_r\left(0\right)=0$. The controller parameters $k_1=k_2=1$ and the observer parameters are taken as ${\alpha }_1={\beta }_1=2$, whereas the high-gain parameters are chosen such that $\overline{\epsilon }=\epsilon =0.1$. The control input is constrained within the range of 0 to 10. Within a 20% range, the parameters deviate from their nominal values.

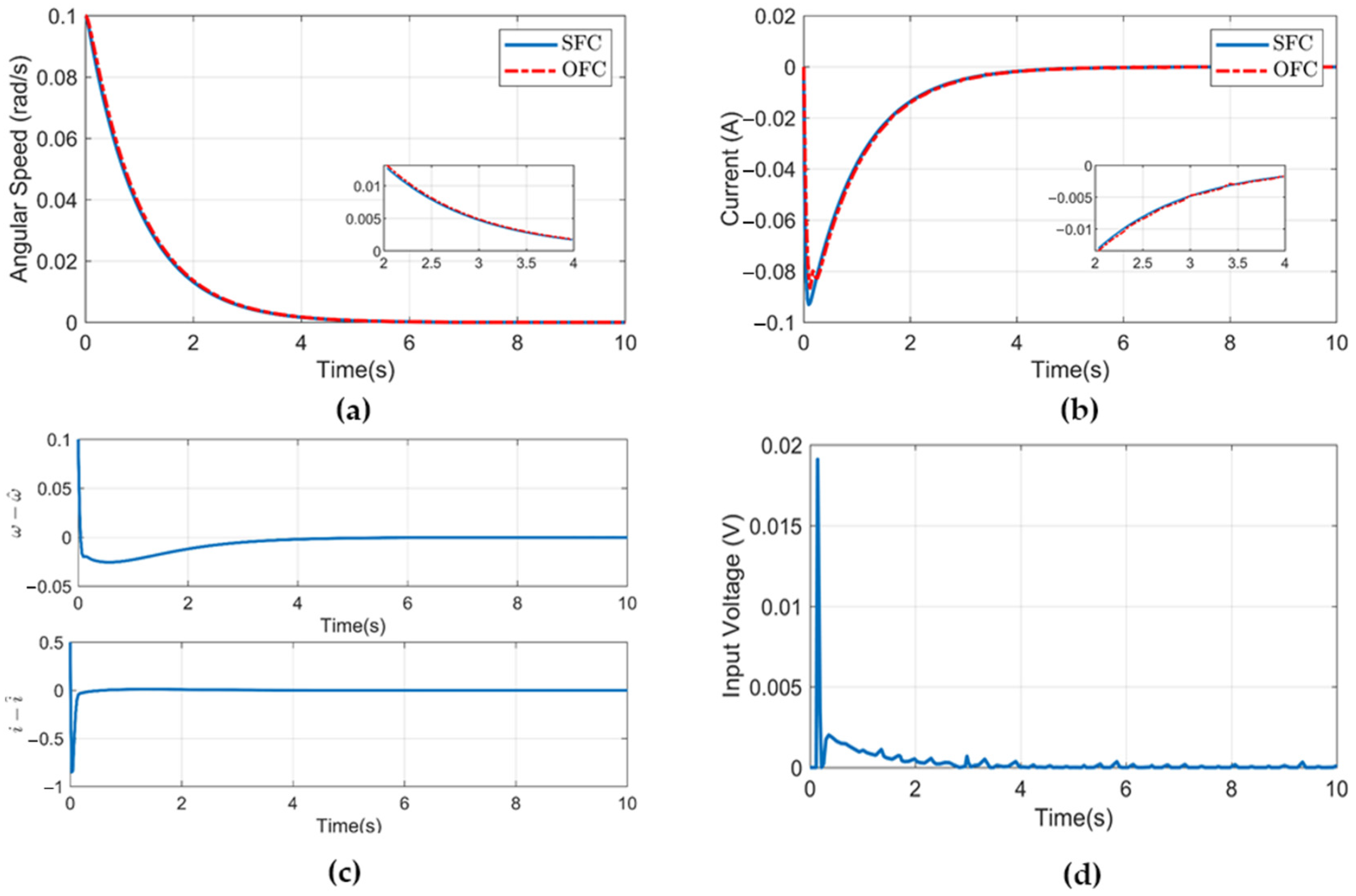
Figure 2a shows a comparison of the angular speed under SFC and OFC. The slow state $\omega$ shows a slow transient in the response. The response of the fast state is shown in Figure 2b. The current exhibits a fast transient initially due to the two-time-scale system. The response under SFC approaches the response under OFC for angular velocity and current. Thus, the state estimation using the high-gain observer shows the robustness of the observer. Figure 2c shows the estimation error of the angular velocity and current. The input voltage response under OFC is presented in Figure 2d.

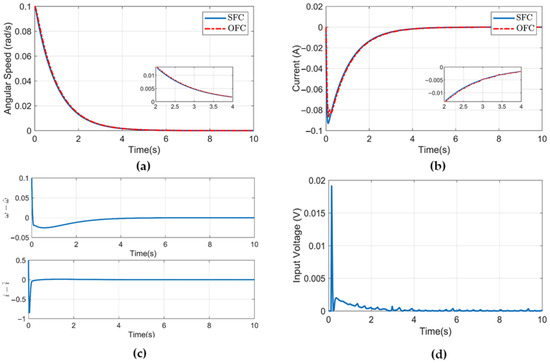
Figure 2. (a) Angular speed of the PMDC under SFC and OFC. (b) Armature current under SFC and OFC. (c) Estimation error of the estimated states with measured states. (d) Input voltage under OFC.

Figure 2 shows that the estimation error of the fast state converges more rapidly compared to the slow state. Hence, as the estimation error becomes zero quickly, the slow state estimation is guaranteed to converge in finite time. The input voltage depicts a peak due to the fast convergence of the fast state. However, this could be reduced by restricting the input signal inside the region of interest and making the input globally bounded.

4. Conclusions

In this article, an OFC is designed for a two-time-scale nonlinear system. The proposed OFC is demonstrated on a PMDC motor example to provide empirical evidence regarding the effectiveness and robustness of the observer. The results demonstrate that the response under OFC not only matches that under state feedback control, but also shows immunity to parametric uncertainties, which makes it practically implementable for two-time-scale nonlinear systems.