Bootstrap Selector for the Smoothing Parameter of Beran’s Estimator ^†

Abstract

This work proposes a resampling technique to approximate the smoothing parameter of Beran’s estimator. It is based on resampling by the smoothed bootstrap and minimising the bootstrap approximation of the mean integrated squared error to find the bootstrap bandwidth. The behaviour of this method has been tested by simulation on several models. Bootstrap confidence intervals are also addressed in this research and their performance is analysed in the simulation study.

1. Introduction

Let ${\left\{(X_i,Z_i,{\delta }_i)\right\}}_{i=1}^n$ be a simple random sample of $(X,Z,\delta )$ with X being the covariate, $Z=min\{T,C\}$ the observed variable and $\delta =I_{T\le C}$ the uncensoring indicator. Usually, T is the time until the occurrence of an event and C is the censoring time. The generalised product-limit estimator of the conditional survival function proposed in [1] is given by

$$\begin{array}{ccc}{\widehat{S}}_h^B\left(t\right|x)& =& {\displaystyle \prod _{i=1}^n\left(1-{\displaystyle \frac{I_{\{Z_i\le t,{\delta }_i=1\}}{w}_{n,i}\left(x\right)}{1-{\sum }_{j=1}^n{I}_{\{Z_j<Z_i\}}{w}_{n,j}\left(x\right)}}\right)}\hfill \end{array}$$

(1)

where

$$w_{n,i}\left(x\right)={\displaystyle \frac{K\left((x-X_i)/h\right)}{{\sum }_{j=1}^{n}K\left((x-X_j)/h\right)}}$$

with $i=1,\dots ,n$ and $h=h_n$ is the bandwidth for the covariable. This estimator depends on a smoothing parameter which is, in practice, unknown. Therefore, finding a method for automatic selection of this bandwidth is truly interesting and very helpful in the analysis of real data subject to censoring. Bootstrap confidence intervals of $S\left(t\right|x)$ are also proposed.

2. Bandwidth Selector

Let $r{I}_h\subset \mathbb{R}$ be an appropriate pilot bandwidth. The bootstrap resampling algorithm consists of generating $U_i\sim U(0,1)$ and $V_i\sim K$ and obtaining

$$X_i^{*}=X_{\left[n{U}_i\right]+1}+r{V}_i,$$

$$Z_i^{*}=Z_{\left[n{U}_i\right]+1},$$

$${\delta }_i^{*}={\delta }_{\left[n{U}_i\right]+1},$$

for each $i=1,\cdots ,n$. The bootstrap sample is formed as ${\left\{(X_i^{*},Z_i^{*},{\delta }_i^{*})\right\}}_{i=1}^n$.

The optimal smoothing parameter is the bandwidth that minimizes the mean integrated squared error given by:

$$MIS{E}_x\left(h\right)=E\left(\int {\left({\widehat{S}}_h\left(t\right|x)-S\left(t\right|x)\right)}^{2}dt\right).$$

Then, the bootstrap bandwidth is obtained by minimizing the Monte Carlo approximation of the bootstrap MISE defined as follows

$$\begin{array}{ccc}MIS{E}_x^{*}\left(h\right)& \simeq & {\displaystyle {\displaystyle \frac{1}{B}}\sum _{j=1}^B\left(\int {\left({\widehat{S}}_h^{*\left(j\right)}\left(t\right|x)-{\widehat{S}}_r\left(t\right|x)\right)}^{2}dt\right),}\hfill \end{array}$$

where ${\widehat{S}}_r\left(t\right|x)$ is the Beran survival estimation with pilot bandwidth r using the original sample ${\left\{(X_i,Z_i,{\delta }_i)\right\}}_{i=1}^n$, ${\widehat{S}}_h^{*\left(j\right)}\left(t\right|x)$ is the Beran survival estimation with bandwidth h using the bootstrap resample ${\left\{(X_i^{*\left(j\right)},Z_i^{*\left(j\right)},{\delta }_i^{*\left(j\right)})\right\}}_{i=1}^n$, and B the number of bootstrap resamples.

3. Bootstrap Confidence Intervals

Let $h\in I_h\subset \mathbb{R}$ be an appropriate smoothing parameter and fixed values $(t,x)\in [a,b]\times I$, the bootstrap confidence interval for a confidence level of $1-\alpha$ is given by

$$\left({\widehat{S}}_r\left(t\right|x)-{\displaystyle \frac{{\rho }_{1-\alpha /2}}{\sqrt{nh}}},{\widehat{S}}_r\left(t\right|x)-{\displaystyle \frac{{\rho }_{\alpha /2}}{\sqrt{nh}}}\right),$$

where ${\widehat{S}}_r\left(t\right|x)$ is the Beran estimation with the pilot bandwidth r that is used in the bootstrap resampling, and ${\rho }_{\alpha /2}$ and ${\rho }_{1-\alpha /2}$ are the $100\alpha /2$ and $100(1-\alpha /2)$ percentiles of the resampling distribution of $\sqrt{nh}\left({\widehat{S}}_h^{*}\left(t\right|x)-{\widehat{S}}_r\left(t\right|x)\right)$, being ${\widehat{S}}_h^{*}\left(t\right|x)$ the Beran survival estimation of the bootstrap resample.

4. Simulation Study

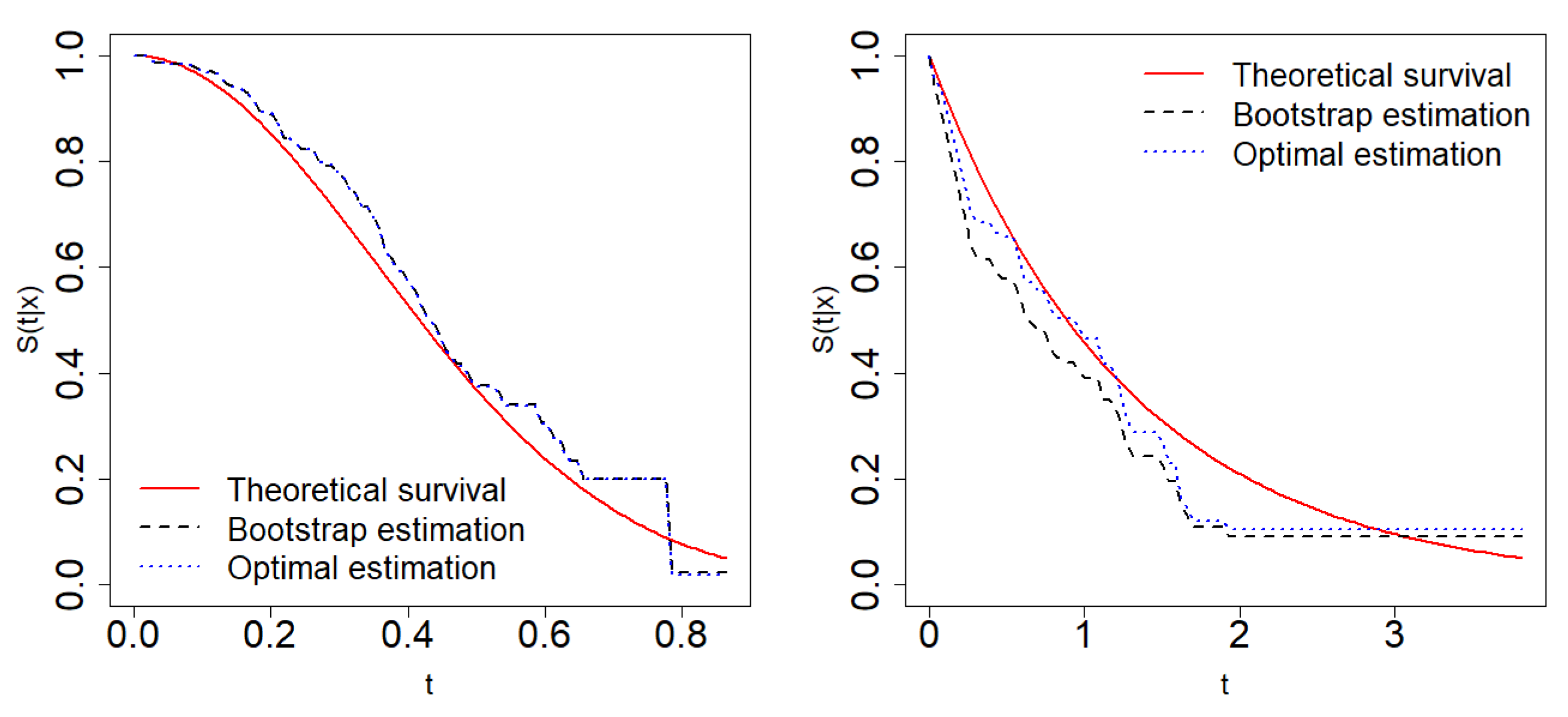
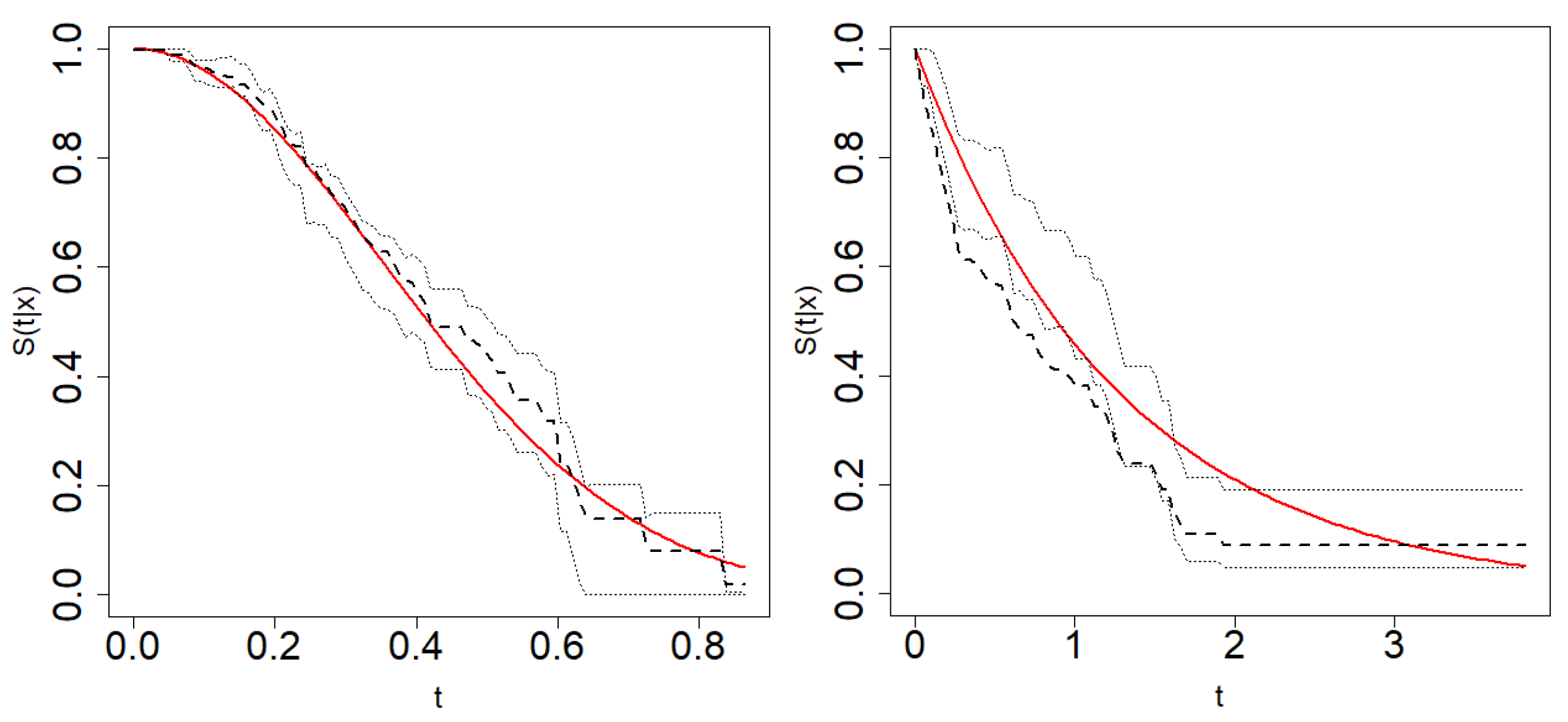
A simulation study is carried out to analyse the behaviour of the bootstrap algorithm previously described. Several models with different conditional probabilities of censoring were considered. Figure 1 shows the bootstrap estimations of the conditional survival function in two of these scenarios: Model 1 considers the Weibull distribution for life and censoring times and Model 2 considers exponential life and censoring times. Both models have a conditional probability of censoring equal to 0.5. Figure 2 shows the bootstrap confidence intervals in one sample from Models 1 and 2.

Figure 1. Theoretical survival function $S\left(t\right|x)$ (solid line), Beran’s estimation with optimal bandwidth (dotted line) and Beran’s estimation with bootstrap bandwidth (dashed line) for Model 1 (left) and Model 2 (right).

Figure 2. Theoretical survival function (solid line), Beran’s estimator with bootstrap bandwidth (dashed line) and the bootstrap confidence intervals (dotted line) for each t in a grid of size $n_t=100$ in Model 1 (left) and Model 2 (right).

5. Conclusions

The results of the simulations show that this bootstrap algorithm provides adequate smoothing parameters to estimate the survival function in this context. The bootstrap bandwidths obtained are similar to the optimal ones and the estimation errors of both are quite similar. Bootstrap confidence intervals have a reasonable behaviour.

Future lines of work focus on developing a method for choosing the bidimensional smoothing parameters involved in the doubly smoothed Beran estimator presented in [2]. In addition, we deal with the construction of confidence intervals for the conditional survival function based on the doubly smoothed Beran estimator.