Thermoporoelastoplastic Wellbore Breakout Modeling by Finite Element Method
Abstract
:1. Introduction
2. Model Structure and Methodology
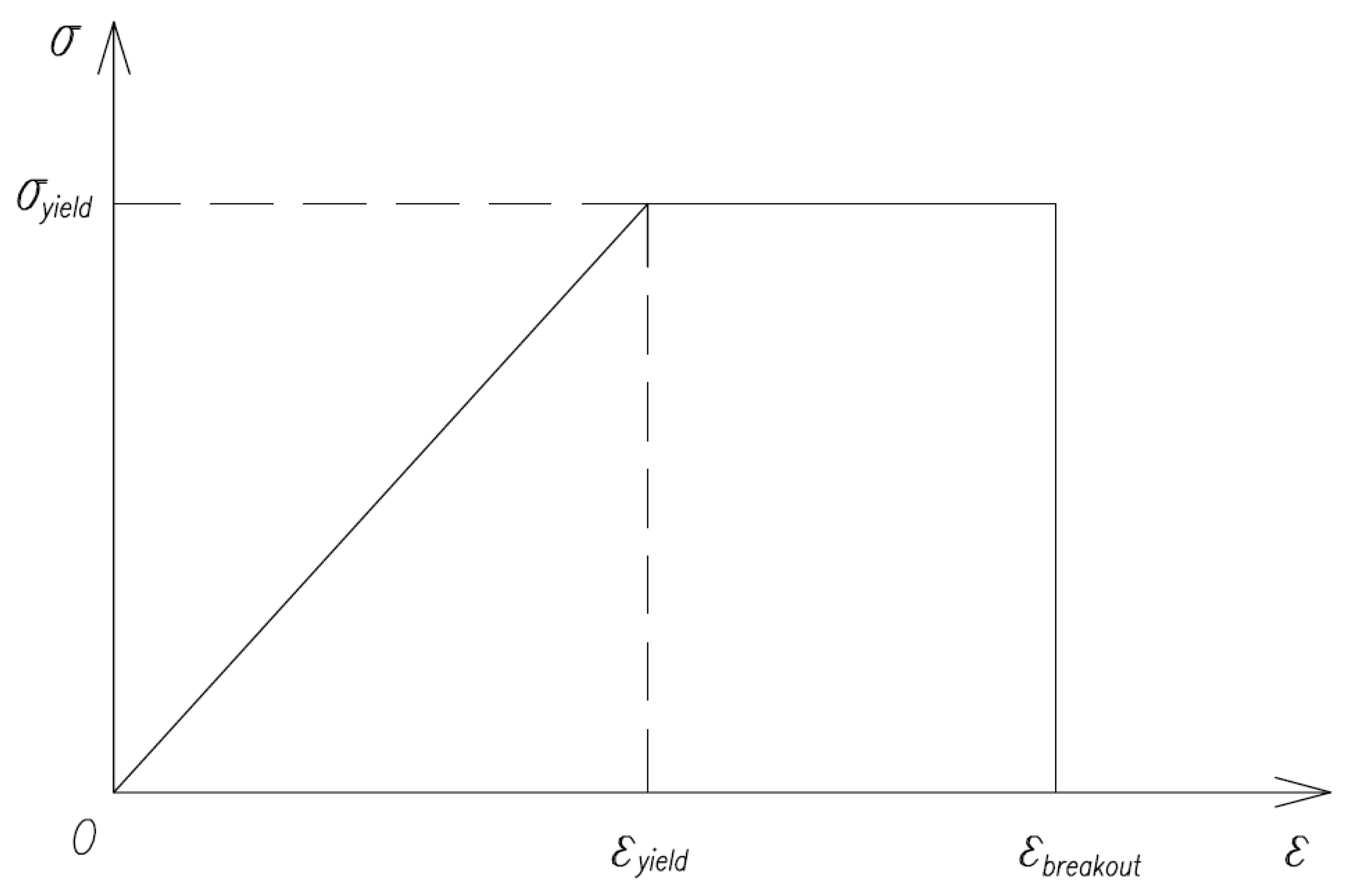
2.1. Rock Failure Criteria
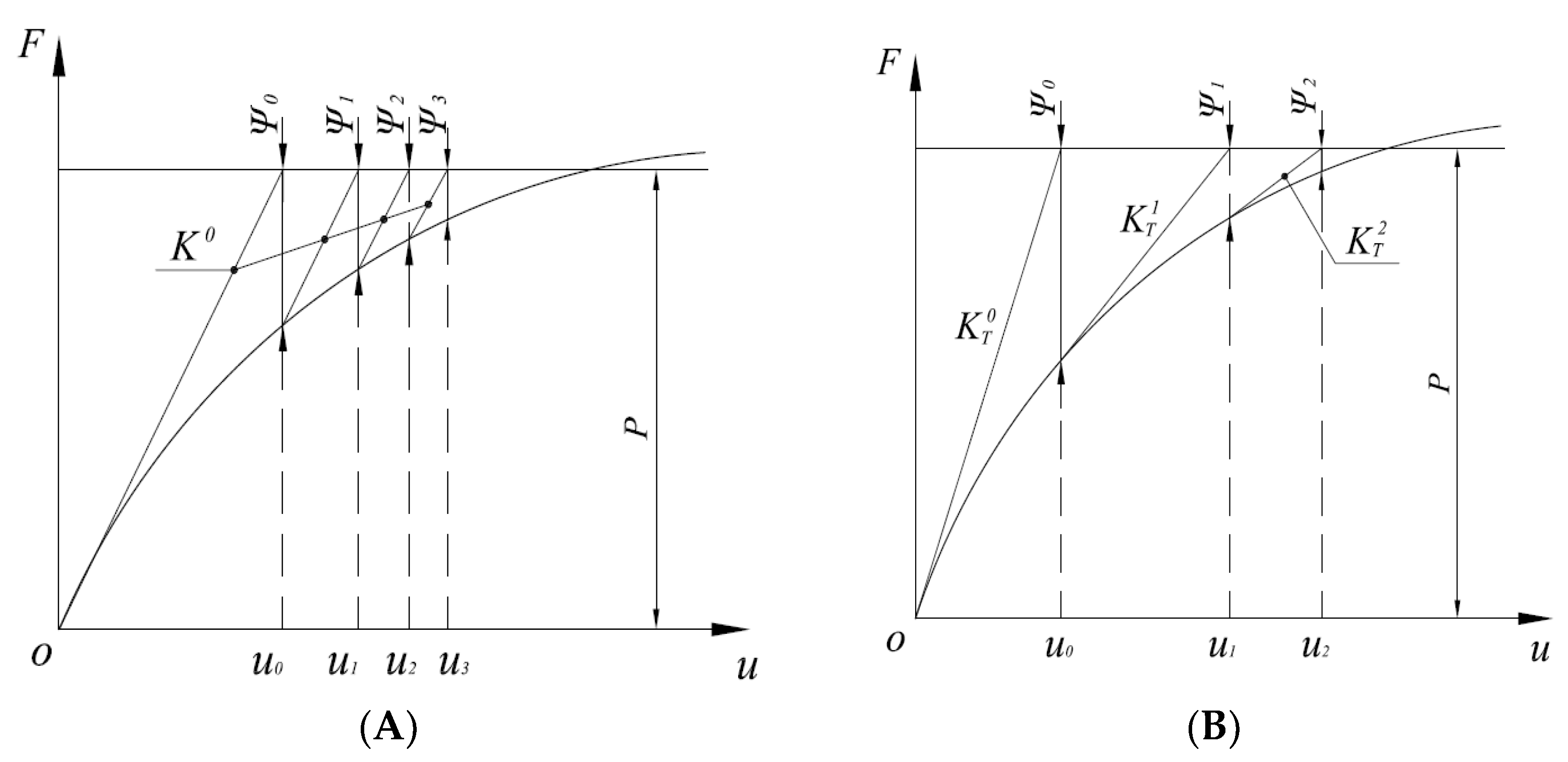
2.2. Finite Element Implementation
3. Numerical Experiments
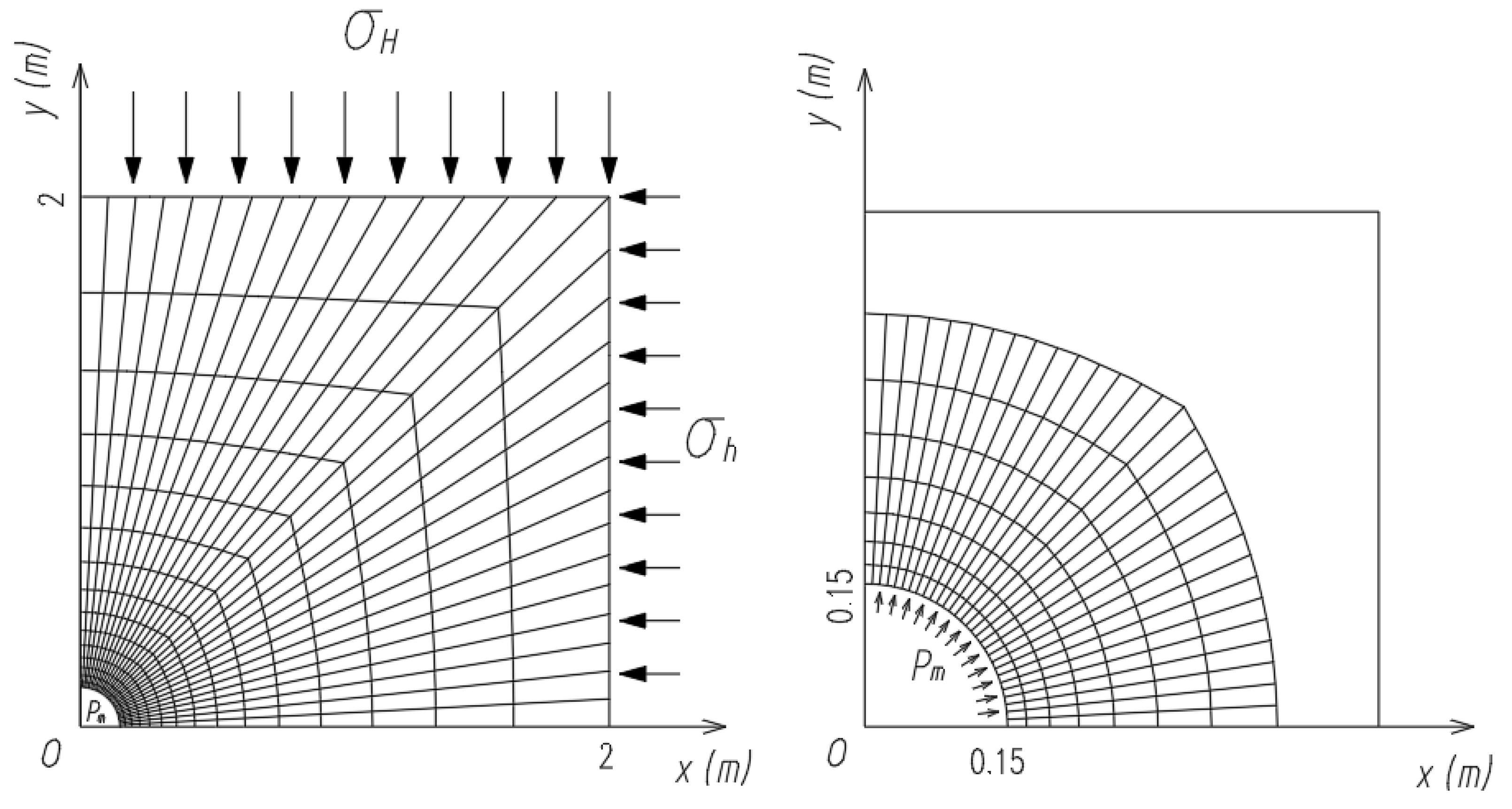
3.1. Thermoporoelastoplastic Finite Element Modeling of Wellbore Breakouts
3.2. Verification of Wellbore Breakout Process
3.3. Influence of Drilling Fluid Temperature
3.4. Comparison between Thermoporoelastic and Thermoporoelastoplastic Modeling
4. Discussion
5. Conclusions
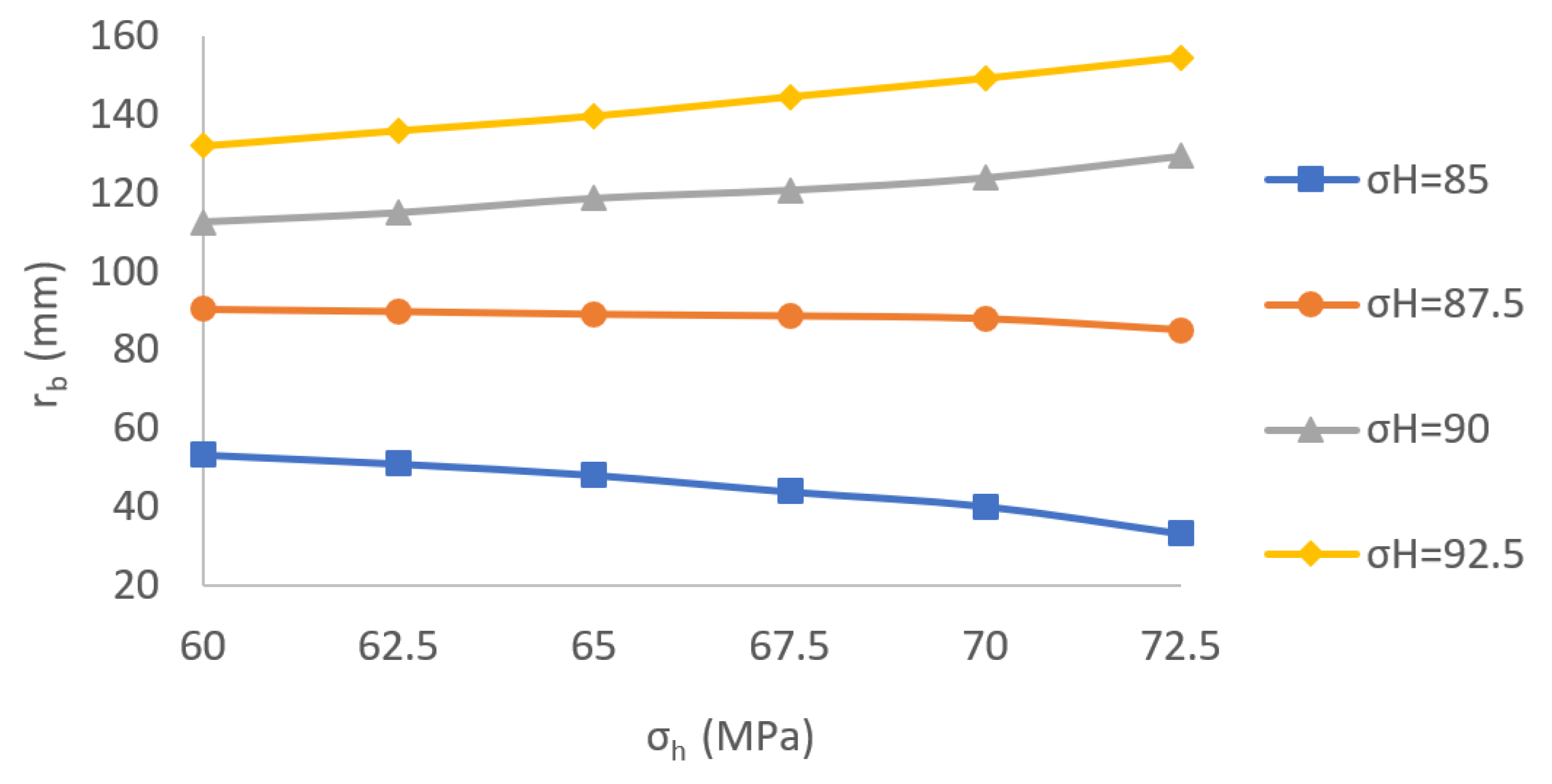
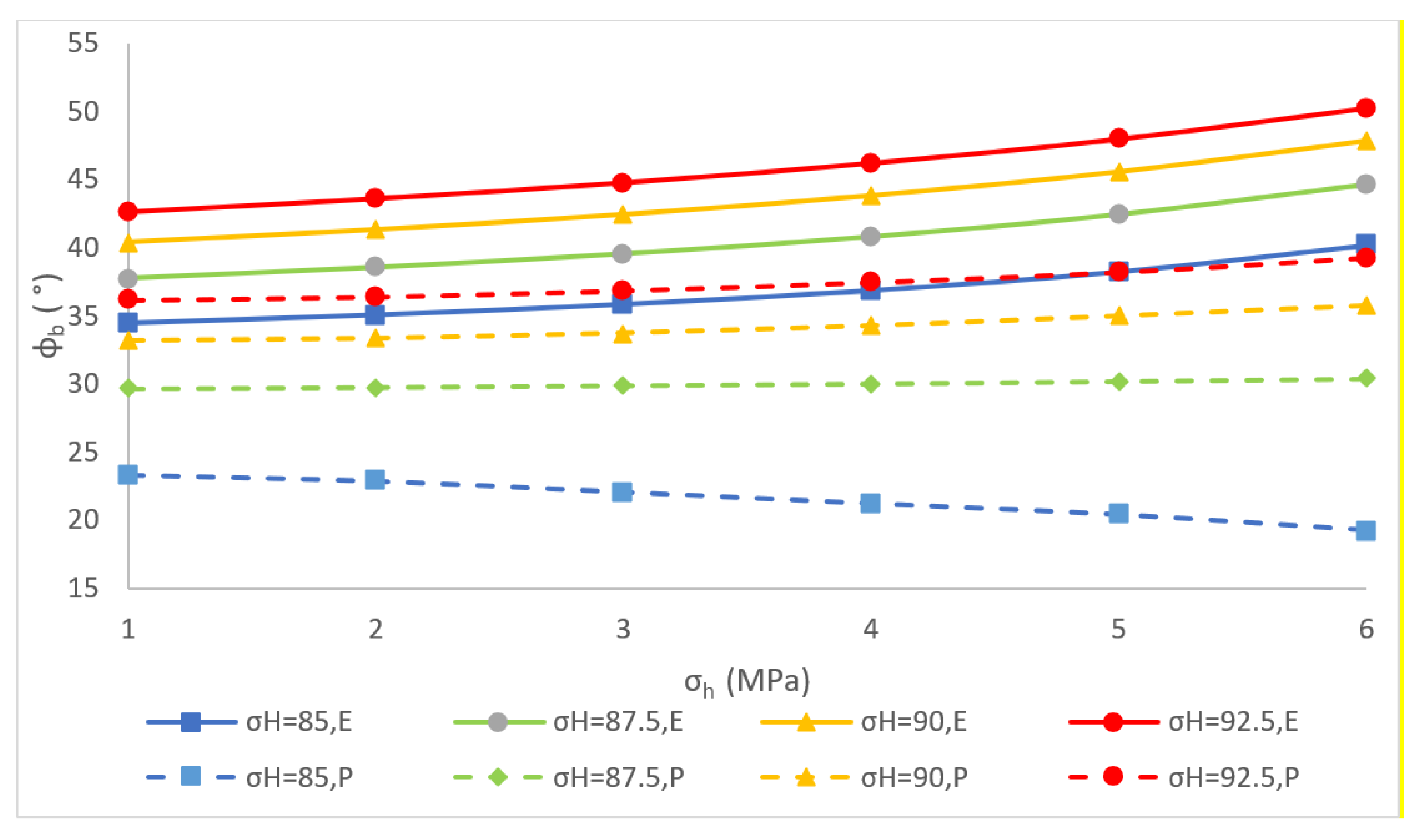
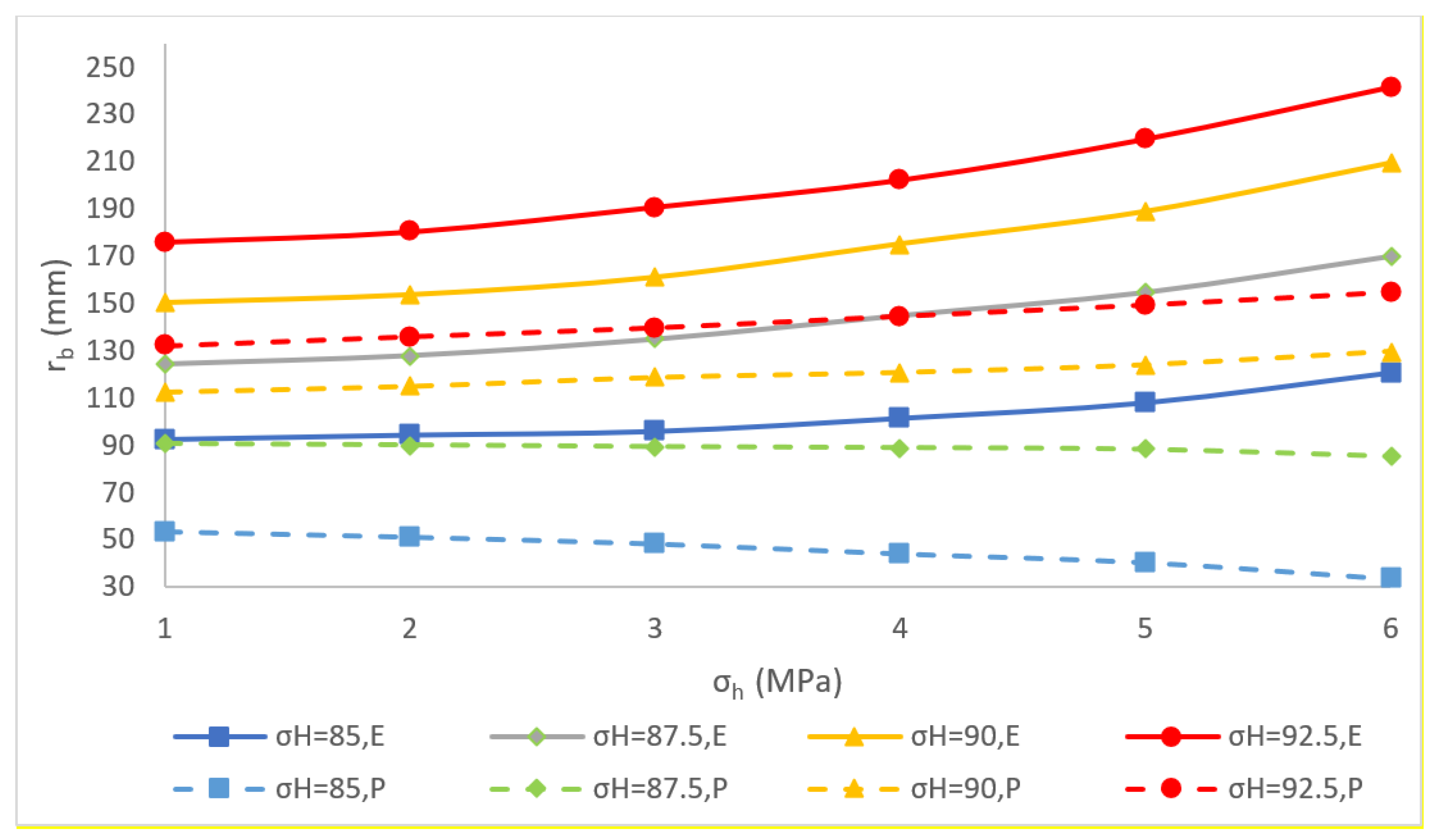
- The relationship between breakout shape and in situ stresses is nonlinear. If the is constant, as increases, the breakout width and depth become greater. If the is kept constant while the difference between and is relatively large, as increases, the breakout width and depth increase greater. However, if the is kept constant while the difference between and is relatively small, as increases, the breakout width and depth decrease instead.
- In the process of wellbore breakouts, the breakout depth increases till a stable state, but the breakout width remains unchanged.
- As temperature of drilling fluid increases, the breakout width and depth will increase.
- For different in situ stresses, the width and depth of wellbore breakouts for thermoporoelastoplastic model are smaller than those for thermoporoelastic model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bell, J.S. The stress regime of the scotian shelf offshore eastern Canada to 6 km depth and implications for rock mechanics and hydrocarbon migration. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, A88. [Google Scholar]
- Zoback, M.D.; Moos, D.L.; Mastin, L.; Anderson, R.N. Wellbore breakout and insitu stress. J. Geophys. Res. 1985, 90, 5523–5538. [Google Scholar] [CrossRef]
- Zheng, Z.; Kemeny, J.; Cook, N.G.W. Analysis of borehole breakouts. J. Geophys. Res. 1989, 94, 7171–7182. [Google Scholar] [CrossRef]
- Ito, T.; Zoback, M.D.; Peska, P. Utilization of mud weights in excess of the least principal stress to stabilize wellbores: Theory and practical examples. SPE Drill. Complet. 2001, 16, 221–229. [Google Scholar] [CrossRef]
- Haimson, B.C.; Herrick, C.G. In situ stress evaluation from borehole breakouts experimental studies. In Proceedings of the 26th US Rock Mechanics Symposium, Rapid City, South Dakota, 10 June 1985; Balkema: Rotterdam, The Netherlands, 1985; pp. 1207–1218. [Google Scholar]
- Haimson, B.C.; Herrick, C.G. Borehole breakouts-a new tool for estimating in situ stress? In Proceedings of the First International Symposium on Rock Stress and Rock Stress Measurement, Stockholm, Sweden, 1–3 September 1986; Centek Publications: Lulea, Sweden, 1986; pp. 271–281. [Google Scholar]
- Haimson, B.C. Micromechanisms of borehole instability leading to breakouts in rocks. Int. J. Rock Mech. Min. Sci. 2007, 44, 157–173. [Google Scholar] [CrossRef]
- Papamichos, E. Borehole failure analysis in a sandstone under anisotropic stresses. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 581–603. [Google Scholar] [CrossRef]
- Yuan, S.C.; Harrison, J.P. Modeling breakout and near-well fluid flow of a borehole in an anisotropic stress field. In Proceedings of the 41st ARMA/USRMS, Golden, Colorado, 17–21 June 2006; pp. 6–1157. [Google Scholar]
- Zhang, H.; Yin, S.; Aadnoy, B.S. Numerical investigation of the impacts of borehole breakouts on breakdown pressure. Energies 2019, 12, 888. [Google Scholar] [CrossRef] [Green Version]
- Biot, A. General theory of three dimensional consolidations. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Bratli, R.K.; Horsrud, P.; Risnes, R. Rock mechanics applied to the region near a wellbore. In Proceedings of the 5th ISRM Congress, International Society for Rock Mechanics, Melbourne, Australia, 10 April 1983. [Google Scholar]
- Abousleiman, Y.; Roegiers, J.C.; Cui, L.; Cheng, A.H.D. Poroelastic solution of an inclined borehole in a transversely isotropic medium. In Proceedings of the 35th U.S. Symposium on Rock Mechanics (USRMS), American Rock Mechanics Association, Lake Tahoe, CA, USA, 1 January 1995. [Google Scholar]
- Cui, L.; Cheng, A.H.D.; Abousleiman, Y. Poroelastic solution for an inclined borehole. J. Appl. Mech. 1997, 64, 32–38. [Google Scholar] [CrossRef]
- Fakhimi, A.; Carvalho, F.; Ishida, T.; Labuz, J.F. Simulation of failure around a circular opening in rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 507–515. [Google Scholar] [CrossRef]
- Cook, B.K.; Lee, M.Y.; DiGiovanni, A.A.; Bronowski, D.R.; Perkins, E.D.; Williams, J.R. Discrete element modeling applied to laboratory simulation of near-wellbore mechanics. Int. J. Geomech. 2004, 4, 19–27. [Google Scholar] [CrossRef]
- Rahmati, H. Micromechanical Study of Borehole Breakout Mechanism. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2013. [Google Scholar]
- Mostafa, G.; Goodarznia, I.; Shadizadeh, S.R. Transient thermo-poroelastic finite element analysis of borehole breakouts. Int. J. Rock Mech. Min. Sci. 2014, 71, 418–428. [Google Scholar]
- Lee, H.; Moon, T.; Haimson, B.C. Borehole breakouts induced in Arkosic sandstones and a discrete element analysis. Rock Mech. Rock Eng. 2016, 49, 1369–1388. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W. Fundamentals of Rock Mechanics; Chapman & Hall: London, UK, 1979. [Google Scholar]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis for limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Whittle, A.J.; Kavvadas, M. Formulation of the MIT-E3 constitutive model for overconsolidated clays. J. Geotech. Eng. 1994, 120, 173–198. [Google Scholar] [CrossRef]
- Akl, S.A.; Whittle, A.J. Analysis of horizontal wellbore stability in clay shale. In Proceedings of the 46th US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012. ARMA12-559. [Google Scholar]
- Zhang, H.; Yin, S. Poroelastoplastic borehole modeling by tangent stiffness matrix method. Int. J. Geomech. 2020, 20, 04020010. [Google Scholar] [CrossRef]
- Li, X.; ELMohtar, C.S.; Gray, K.E. Numerical modeling of borehole breakout in ductile formation considering fluid seepage and damage-induced permeability change. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. ARMA16-244. [Google Scholar]
- Mastin, L. The Development of Borehole Breakouts in Sandstone. Master’s. Thesis, Stanford University, Stanford, CA, USA, 1984. [Google Scholar]
- Yin, S.; Towler, B.F.; Dusseault, M.B.; Rothenburg, L. Fully coupled THMC modeling of wellbore stability with thermal and solute convection considered. Transp. Porous Media 2010, 84, 773–798. [Google Scholar] [CrossRef]
- Lewis, R.W.; Majorana, C.E.; Schrefler, B.A. A coupled finite element model for the consolidation of non-isothermal elastoplastic porous media. Transp. Porous Media 1986, 1, 155–178. [Google Scholar] [CrossRef]
- Aboustit, B.L.; Advani, S.H.; Lee, J.K. Variational principles and finite element simulations for thermo-elastic consolidation. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 49–69. [Google Scholar] [CrossRef]
- Vaziri, H.H.; Britto, A.M. Theory and application of a fully coupled thermalhydro-mechanical finite-element model. Comput. Struct. 1996, 61, 131–146. [Google Scholar]
- Yin, S. Geomechanics-Reservoir Modeling by Displacement Discontinuity-Finite Element Method. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2008; pp. 22–23. [Google Scholar]
- Zhu, B. The Finite Element Method; Tsinghua University Press: Beijing, China, 2018. [Google Scholar]
- Neto, E.S.; Peric, D.; Owen, D. Computational Methods for Plasticity; Wiley: Chichester, UK, 2008. [Google Scholar]





| Parameter | Value |
|---|---|
| Young’s Modulus, (MPa) | 14,400 |
| Poisson Ratio, | 0.2 |
| Cohesion, (MPa) | 6 |
| Inner friction angle, (°) | 35 |
| Radius of well, | 0.15 |
| Bulk modulus of skeleton, | 8000 |
| Bulk modulus of matrix, | 36,000 |
| Bulk modulus of fluid, | 2250 |
| Porosity of the porous medium, | 0.19 |
| Permeability of the porous medium, | 0.19 |
| Viscosity of the fluid, | 10−9 |
| Thermal conductivity, | 2.5 |
| Thermal expansion coefficient of solid, | 2.1 × 10−5 |
| Thermal expansion coefficient of liquid, | 2.0 × 10−4 |
| Specific heat of solid, | 800 |
| Specific heat of liquid, | 4200 |
| Maximum principal stress, | 85~92.5 |
| Minimum principal stress, | 60~72.5 |
| Vertical stress, | 80 |
| Drilling fluid pressure, | 45 |
| Temperature difference between drilling fluid and surrounding, | −50 |
| Maximum allowable tensile strain, | 0.002 |
| No. | σh | σH | rb | No. | σh | σH | rb | ||
|---|---|---|---|---|---|---|---|---|---|
| MPa | MPa | ° | mm | MPa | MPa | ° | mm | ||
| 1 | 85.0 | 60.0 | 23.3 | 53.5 | 13 | 90.0 | 67.5 | 33.2 | 112.7 |
| 2 | 85.0 | 62.5 | 22.9 | 51.2 | 14 | 90.0 | 70.0 | 33.3 | 115.1 |
| 3 | 85.0 | 65.0 | 22.1 | 48.3 | 15 | 90.0 | 72.5 | 33.7 | 118.8 |
| 4 | 85.0 | 67.5 | 21.2 | 44.1 | 16 | 90.0 | 60.0 | 34.3 | 120.9 |
| 5 | 85.0 | 70.0 | 20.4 | 40.3 | 17 | 90.0 | 62.5 | 35.0 | 124.0 |
| 6 | 85.0 | 72.5 | 19.3 | 33.4 | 18 | 90.0 | 65.0 | 35.8 | 129.6 |
| 7 | 87.5 | 60.0 | 29.7 | 90.6 | 19 | 92.5 | 67.5 | 36.2 | 132.2 |
| 8 | 87.5 | 62.5 | 29.8 | 90.1 | 20 | 92.5 | 70.0 | 36.4 | 136.1 |
| 9 | 87.5 | 65.0 | 29.9 | 89.3 | 21 | 92.5 | 72.5 | 36.9 | 139.8 |
| 10 | 87.5 | 67.5 | 30.0 | 88.9 | 22 | 92.5 | 60.0 | 37.5 | 144.6 |
| 11 | 87.5 | 70.0 | 30.2 | 88.2 | 23 | 92.5 | 62.5 | 38.2 | 149.3 |
| 12 | 87.5 | 72.5 | 30.4 | 85.2 | 24 | 92.5 | 65.0 | 39.3 | 154.6 |
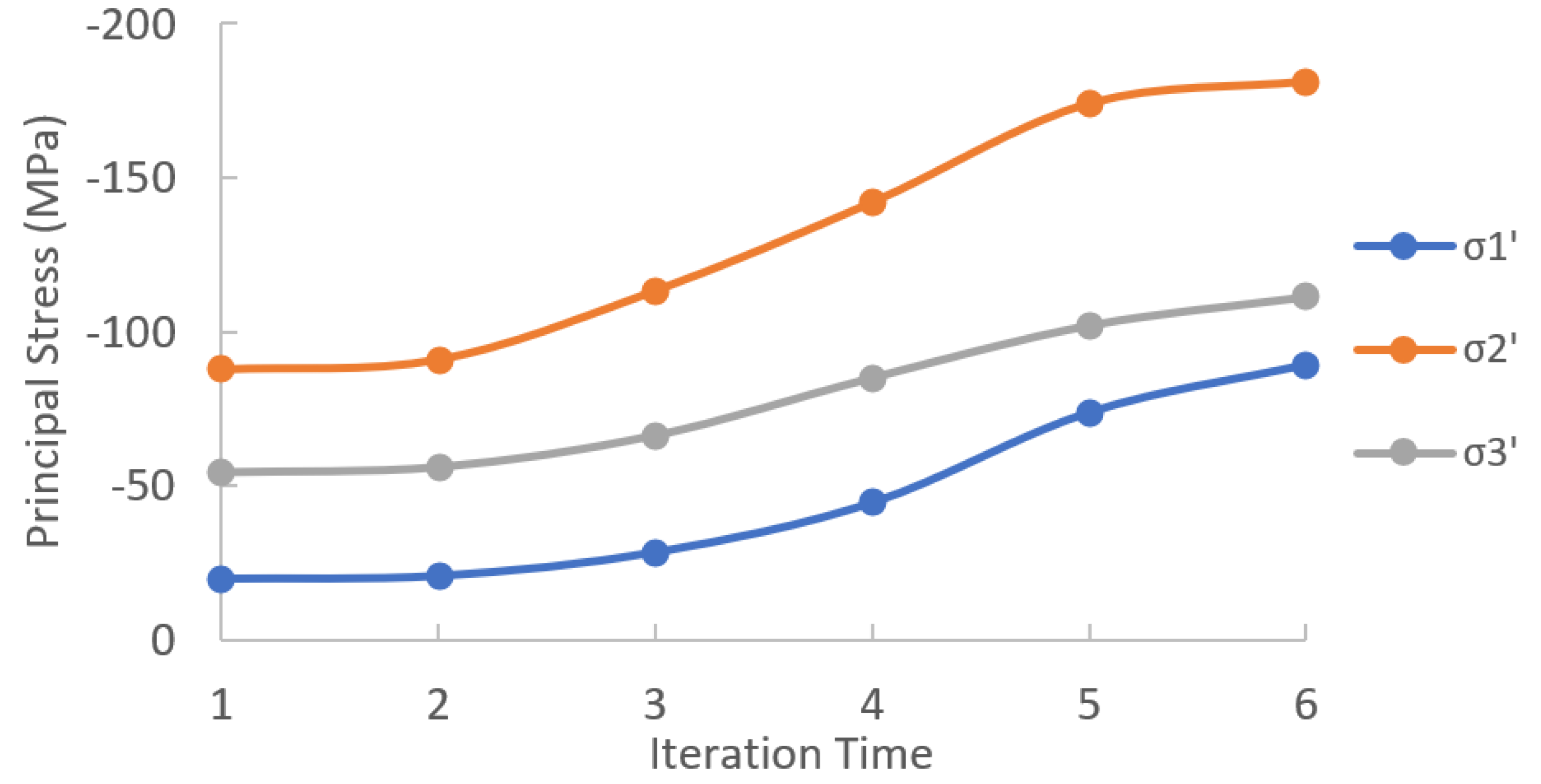
| Elem | Iteration1 | Iteration2 | Iteration3 | |||||||||
| σ1′ (MPa) | σ2′ (MPa) | σ3′ (MPa) | εmax | σ1′ (MPa) | σ2′ (MPa) | σ3′ (MPa) | εmax | σ1′ (MPa) | σ2′ (MPa) | σ3′ (MPa) | εmax | |
| 1 | −19.64 | −87.86 | −54.31 | 0.00294 | −20.56 | −91.03 | −55.97 | 0.00315 | −28.26 | −113.46 | −66.27 | 0.00397 |
| 2 | −19.86 | −87.44 | −54.21 | 0.00292 | −20.79 | −90.46 | −55.86 | 0.00314 | −28.98 | −111.17 | −65.55 | 0.00387 |
| 3 | −20.29 | −86.59 | −54.00 | 0.00288 | −21.28 | −89.41 | −55.64 | 0.00311 | −30.35 | −106.72 | −64.05 | 0.00362 |
| 4 | −20.93 | −85.35 | −53.70 | 0.00282 | −21.97 | −87.94 | −55.30 | 0.00305 | −31.98 | −99.88 | −61.76 | 0.00328 |
| 5 | −21.73 | −83.74 | −53.31 | 0.00275 | −23.08 | −86.13 | −54.89 | 0.00295 | −33.25 | −90.66 | −58.60 | 0.00290 |
| 6 | −22.67 | −81.78 | −52.84 | 0.00266 | −24.60 | −84.05 | −54.28 | 0.00277 | −33.25 | −79.86 | −54.76 | 0.00236 |
| 7 | −23.71 | −79.54 | −52.31 | 0.00257 | −26.56 | −81.64 | −53.33 | 0.00248 | −29.37 | −64.73 | −48.08 | 0.00168 |
| 8 | −24.85 | −77.08 | −51.74 | 0.00246 | −27.60 | −78.51 | −51.49 | 0.00211 | −25.69 | −53.71 | −43.49 | 0.00133 |
| 9 | −26.13 | −74.51 | −51.08 | 0.00231 | −27.75 | −73.95 | −50.08 | 0.00191 | −23.57 | −49.53 | −40.89 | 0.00094 |
| 10 | −27.67 | −71.91 | −50.22 | 0.00205 | −27.14 | −66.88 | −48.84 | 0.00199 | −23.10 | −47.39 | −40.83 | 0.00091 |
| Elem | Iteration4 | Iteration5 | Iteration6 | |||||||||
| σ1′ (MPa) | σ2′ (MPa) | σ3′ (MPa) | εmax | σ1′ (MPa) | σ2′ (MPa) | σ3′ (MPa) | εmax | σ1′ (MPa) | σ2′ (MPa) | σ3′ (MPa) | εmax | |
| 1 | −44.48 | −142.16 | −85.00 | 0.00501 | −73.96 | −174.26 | −101.91 | 0.00270 | −89.52 | −181.38 | −111.19 | 0.00196 |
| 2 | −44.71 | −128.38 | −76.66 | 0.00523 | −64.49 | −137.95 | −83.14 | 0.00305 | −58.62 | −116.89 | −72.32 | 0.00194 |
| 3 | −42.72 | −108.77 | −70.07 | 0.00433 | −39.34 | −69.62 | −54.19 | 0.00185 | −25.22 | −50.52 | −42.48 | 0.00083 |
| 4 | −40.12 | −87.33 | −61.17 | 0.00323 | −17.79 | −38.71 | −37.73 | 0.00080 | −15.15 | −29.09 | −35.71 | −0.00004 |
| 5 | −32.66 | −62.74 | −49.07 | 0.00195 | −17.15 | −29.80 | −36.13 | −0.00007 | −15.68 | −26.52 | −35.48 | −0.00014 |
| 6 | −23.86 | −45.66 | −40.42 | 0.00097 | −16.17 | −27.53 | −35.79 | −0.00006 | −15.10 | −24.65 | −34.91 | −0.00012 |
| 7 | −20.75 | −38.00 | −37.25 | 0.00014 | −15.95 | −25.85 | −35.30 | −0.00008 | −15.20 | −23.19 | −34.55 | −0.00014 |
| 8 | −19.36 | −36.17 | −37.26 | 0.00020 | −16.14 | −25.73 | −35.25 | −0.00006 | −15.57 | −23.52 | −34.70 | −0.00013 |
| 9 | −19.50 | −36.24 | −37.52 | 0.00019 | −16.71 | −26.65 | −35.51 | −0.00006 | −16.02 | −24.40 | −34.95 | −0.00012 |
| 10 | −19.25 | −36.35 | −37.60 | 0.00020 | −16.87 | −27.24 | −35.63 | −0.00004 | −16.25 | −25.08 | −35.11 | −0.00010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, H.; Hu, K.; Chen, Z.; Yin, S. Thermoporoelastoplastic Wellbore Breakout Modeling by Finite Element Method. Mining 2022, 2, 52-64. https://doi.org/10.3390/mining2010004
Zhang L, Zhang H, Hu K, Chen Z, Yin S. Thermoporoelastoplastic Wellbore Breakout Modeling by Finite Element Method. Mining. 2022; 2(1):52-64. https://doi.org/10.3390/mining2010004
Chicago/Turabian StyleZhang, Lijing, Hua Zhang, Kezhen Hu, Zhuoheng Chen, and Shunde Yin. 2022. "Thermoporoelastoplastic Wellbore Breakout Modeling by Finite Element Method" Mining 2, no. 1: 52-64. https://doi.org/10.3390/mining2010004
APA StyleZhang, L., Zhang, H., Hu, K., Chen, Z., & Yin, S. (2022). Thermoporoelastoplastic Wellbore Breakout Modeling by Finite Element Method. Mining, 2(1), 52-64. https://doi.org/10.3390/mining2010004






