Use of Local Resources in Plant-Based Concretes: Exploring Thermal Performance Through Multi-Scale Modeling

Abstract

The construction sector significantly impacts the environment, driving the development of sustainable materials like plant-based concretes. These materials offer low embodied energy, effective thermal insulation, and natural hygroscopicity. However, one of the major difficulties is that the diversity of formulations complicates the performance assessment. Furthermore, few studies model their insulating capacity based on composition. This research employs mean-field homogenization techniques (Mori–Tanaka and double inclusion schemes) to predict thermal conductivity, integrating formulation, aggregate orientation due to implementation methods, and morphological characteristics at several scales. The models analyze key factors—aggregate type, aspect ratio, and orientation—improving insulation beyond experimental limitations. A multi-criteria approach further explores binder and aggregate proportions, hygric and mechanical properties, and raw material availability. One of the major results is that a preferred orientation increases thermal efficiency by 60 percent, a difficult factor to assess experimentally today. This study enables the optimized thermal performance of plant-based concretes before production, fostering innovative manufacturing approaches for eco-friendly construction.

1. Introduction

The construction sector’s carbon footprint requires a rapid and sustained transition to limit the environmental and social consequences of global warming [1,2]. Bio-based building materials are increasingly recognized for their low environmental impact, providing viable alternatives to conventional high-impact materials [3]. Despite their potential, the large-scale adoption of these materials remains limited to date due to various technical, political, and societal barriers [4]. Plant-based concretes are made from a mixture of water, plant particles and lime or metakaolin-based binders. The choice of binder is crucial as it determines the mechanical, economic, and environmental properties of the composite [5]. Its impact on thermal conductivity is still under discussion in the literature [6,7]. Modeling can be a useful addition to the discussion.

Plant-based aggregates in building materials demonstrate great potential for enhancing hygrothermal comfort [8]. Their unique thermo-hydric coupling enables them to serve as both insulators and passive regulators of ambient humidity, significantly improving building energy efficiency [9]. This explains the recent interest in concretes incorporating plant aggregates—plant-based concretes, and the large number of experimental studies evaluating their thermal conductivity. The incorporation of plant aggregates in cementitious matrices reduces thermal conductivity and may achieve good thermal performance [10,11]. Despite their interesting thermal properties, the development of plant-based concretes is hindered by marked anisotropy and multi-scale porosity—complicating the understanding of their behavior [12,13]. The effect of aggregate size has been studied in mechanical terms [12], but not in their thermal properties. Measurement methods do not easily permit the study of this aspect and do not systematically provide access to the different components of thermal conductivity, which is in fact, a tensor in the case of anisotropic material.

The thermal conductivity of vegetal concrete varies according to formulation—type of aggregate, nature of binder, and binder/plant aggregate ratio [14]. Some authors conclude from experimental data that the binder has less influence while others indicate that it has a significant impact on the material’s thermal behavior [15,16]. Similar questions arise about the influence of the type of plant aggregate used [17]. The consensus seems to be that thermal conductivity is linearly dependent on material density [18,19], although other empirical exponential formulas can be put forward [20]. Thermal conductivity may decrease with density and with the concentration of plant aggregates. Nevertheless, the influence of the binder or the plant aggregate is not identified to date. Consequently, recent studies underline that density alone is not a good predictor of the thermal performance of bio-based materials [21]. Consequently, emerging research aims to efficiently predict the thermal conductivity of plant-based concretes [22,23]. To date, authors could not find any reported established correlation between the formulation (material implemented in the wet state) and the thermal conductivity of the stabilized material (i.e., in the wall before the significant aging and evolution of its physical properties).

Alternatively, it is important to highlight that the experimental linear relationship established between dry density does not consider the anisotropy of plant-based concretes [24]. The self-coherent model (n-sphere model) is generally in the literature [25]; however, its isotropic assumption contradicts the anisotropy observed both at the particle scale and at the material scale [26]. Modeling must be yet a powerful tool to study the impact of the preferential orientation of plant particles generated by processing techniques. In addition, a few models have been developed for hemp concretes [22,23,27], while numerous studies demonstrate the relevance of using locally available aggregates, such as pith or sunflower bark, which are more available than hemp shiv [23]. No literature references estimate the thermal conductivity of plant-based concrete using other agricultural by-products than hemp shiv.

Among the challenges that need to be overcome to encourage the emergence and use of plant-based concretes, the following are worth mentioning to understand the approach taken in this article:

-

The wide variety of plant aggregates, their availability, seasonal harvests, and the range of possible binders (hydraulic or raw-earth binders) and their characterization have become more complex formulation parameters [18,27].

-

The stabilization time in various environments combined with varying thermal conductivities depending on the formulation and external conditions (temperature and ambient relative humidity), make characterization challenging [21].

-

Anisotropic behavior at both the material and aggregate scales, influenced by implementation technique and the microstructure of aggregates complicates the thermal performance assessment [22,28].

-

Optimizing formulations is complex because reducing material density improves insulation but degrades mechanical properties [29].

This article aims to tackle these challenges through multi-scale modeling by considering the following:

• The variability of both the aggregate and the binder to easily study and compare different formulations even before the manufacturing stage.
• A relevant and fast-calculating modeling method to complete and guide time-consuming characterization processes.
• The anisotropic thermal behavior both at the particle and the plant-based concretes scales.
• Different models to link experiment and morphology data to the thermal conductivity of a stabilized plant-based concretes.

Firstly, this study proposes the analytical predictive models of the thermal conductivity of plant-based concretes. They are applied to plant-based concretes made with sunflower bark, sunflower pith, and hemp shiv but can be easily extended to a wide range of agricultural by-products. Firstly, analytical homogenization techniques are used as a continuation of work already carried out at the particle and material scales [15,30]. Experimental data from the literature have been rigorously selected, allowing discussions of modeling results with the experimental measurements for plant-based concretes under given measurement conditions. The variability of thermal conductivity according to external loads (effects of temperature and relative humidity) and different criteria (aggregate type, shape, and orientation) are considered. Models are first evaluated for adequacy, and the most appropriate ones are selected for further study.

Secondly, the selected models are used as optimization tools to study the effect of particle orientation, nature and shape. The approach aims to illustrate that modeling enables to control both the size and orientation of aggregates to study their effects, optimizing not only the formulation but also the implementation. However, the optimization cannot be confined to the thermal aspects of building materials. Other factors are considered, such as mechanical or hygroscopic aspects, or resource availability, to achieve a more global approach to optimizing formulations in line with the composite’s expected performance in use. Consequently, a multi-criteria approach is suggested, combining several factors studied in the literature such as mechanical properties, hygric properties, and the availability of plant aggregates. The intent is to assess the performance of plant-based concretes on a broader scale, beyond their thermal properties.

2. Materials and Methods

2.1. A Homogenization-Based Effective Thermal Conductivity

2.1.1. Thermal Conductivity Tensor

Micromechanics, involving numerical or analytical techniques, are efficient to assess the thermal conductivity of a heterogeneous material [30,31]. The choice of method used generally depends on the expected computation time, the accuracy of the prediction, and the availability of input data. It is important to specify that the arrangement of phases is not perfectly known in bio-based building materials because of a notably complex multiscale porosities [32]. In light of the available microstructural data, analytical homogenization methods are explored in this article to be applied to different plant-based concretes. They aim to determine their effective thermal behavior.

An external macroscopic load (temperature field) is applied to determine its thermal conductivity tensor, which requires information on the material’s microstructure. A representative volume element (RVE) of the considered material has to be defined. This corresponds to the sample of plant-based concrete on which the experimental thermal conductivity measurements were carried out. The dimensions must be sufficiently large for the microstructural heterogeneities for the RVE to be statistically representative of the real material. A macroscopic uniform thermal gradient field is applied to the boundary of the R.V.E. In this case, the thermal conduction problem can be written using the microscopic and macroscopic forms of Fourier’s law as follows:

$$\overrightarrow{q}=-\lambda ·\overrightarrow{\nabla } T$$

(1)

$$\overrightarrow{Q}=-{\underset{\_}{\underset{\_}{\Lambda }}}_{hom} ·\overrightarrow{\mathrm{E}}$$

(2)

where $\overrightarrow{q}$ and $\overrightarrow{Q}$ are, respectively, the microscopic and the macroscopic heat fluxes, $\underset{\_}{\underset{\_}{\lambda }}$ is the microscopic effective thermal conductivity tensor, ${\underset{\_}{\underset{\_}{\Lambda }}}_{hom}$ is the effective thermal conductivity tensor, $\overrightarrow{\nabla } T$ and $\overrightarrow{\mathrm{E}}$ are the microscopic and macroscopic heat gradient fields, respectively. Based on this, different methods can be used to determine the effective thermal conductivity tensor ${\underset{\_}{\underset{\_}{\Lambda }}}_{hom}$.

Information on phase arrangement at the microscopic level can only be given through volume fractions (f_i) of the constituents, defined as:

$$f_i={\displaystyle \frac{V_i}{V_{tot}}} with V_{tot}=\sum _i^r{V}_i+V_m$$

(3)

where $V_i$ and $V_m$ are the volumes of inclusions and the matrix, respectively, in the total volume $V_{tot}$ of the RVE.

The entire RVE microstructure is thus defined by the combination of volume fractions:

$$\sum _i^r{f}_{i }+f_m=1$$

(4)

where $f_{i }$ and $f_m$ are the volume fractions of the inclusions and the matrix, respectively.

However, in the literature, only the mass relationships between the constituents are typically specified in the material formulation. This presents a major obstacle to determining the input data for homogenization and thus calculating the effective thermal conductivity tensor. A correspondence between mass ratios and volume ratios is therefore sought as soon as possible, often using X-ray tomography images from the literature [33]. In the absence of this information, assumptions about volume fractions are required at the material scale, and calibration is then applied. For the particle scale, previously validated methods enable the consideration of relevant volume fractions (such as intra-particle porosity) [15,30].

In the case of an isotropic material, the thermal conductivity tensor can be reduced to its norm, i.e., the scalar value of each tensor component. If the material’s thermal conductivity is the same in any direction, the thermal conductivity is expressed as follows in Equation (3):

• Isotropic

$$\underset{\_}{\underset{\_}{\Lambda }}=\Lambda \left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

(5)

where Λ is in W·m⁻¹·K⁻¹.

If the material behavior is anisotropic regarding thermal conduction, two cases can be distinguished where the value of thermal conductivity depends on the direction considered (see Equation (4)):

• Transversely isotropic

$$\underset{\_}{\underset{\_}{\Lambda }}=\left(\begin{array}{ccc}{\lambda }_N& 0& 0\\ 0& {\lambda }_T& 0\\ 0& 0& {\lambda }_T\end{array}\right)$$

(6)

where λ_N and λ_T are, respectively, the normal and tangential components (W·m⁻¹·K⁻¹).

• Orthotropic

$$\underset{\_}{\underset{\_}{\Lambda }}=\left(\begin{array}{ccc}{\lambda }_i& 0& 0\\ 0& {\lambda }_j& 0\\ 0& 0& {\lambda }_k\end{array}\right)$$

(7)

where λ_i, λ_j, and λ_k are the components in the three directions of an orthonormal reference frame (W·m⁻¹·K⁻¹).

2.1.2. Homogenization Schemes

To gain access to the effective thermal conductivity tensor, mean-field theories use concentration tensors that relate the averaged fields at the microstructure level (i.e., inclusions and matrix) with the corresponding macroscopic fields. Considering an n-phase heterogeneous material, the effective thermal conductivity tensor ${\underset{\_}{\underset{\_}{L}}}_{hom}$ of the RVE is defined (according to the classical theory of Eshelby) as follows [34]:

$${\underset{\_}{\underset{\_}{\Lambda }}}_{hom}=\sum _{r=1}^N{f}_r {\underset{\_}{\underset{\_}{\Lambda }}}_r. {\mathbb{A}}_r$$

(8)

where ${\underset{\_}{\underset{\_}{\Lambda }}}_r$ is the thermal conductivity tensors of the r-th phase (matrix or inclusion), $f_r$ is the volume fractions of the r-th phase, and ${\mathbb{A}}_r$ the concentration tensor of the r-th phase.

The concentration tensor itself depends on a Hill tensor and a depolarization tensor, which accounts the variability of the microstructure in terms of the orientation and shape of the inclusions [35]. This is particularly relevant for bio-based building materials, where the implementation technique induces a preferential orientation of the plant aggregates (inclusions) [36]. An advantage of mean-field homogenization methods is that they provide analytical results requiring little computing time and memory. Knowledge of the concentration tensors ${\mathbb{A}}_i$ allows for the resolution of the homogenization problem, provided that the volume fractions of each phase and their thermal conductivity tensors are well defined. Several estimation schemes can then be used to perform the resolution.

• Mori–Tanaka scheme

The Mori–Tanaka model simplifies the localization problem by representing inclusions of the same shape, orientation, and behavior as a single ellipsoidal inclusion embedded in an infinite medium (Figure 1).

Interactions between inclusions are included in the Mori–Tanaka scheme. The infinite medium has the properties of the matrix and is subjected to the average deformation of the matrix within the composite. It derives the following expression:

$${\underset{\_}{\underset{\_}{\Lambda }}}_{hom}= \sum _{r=1}^N{f}_r {\underset{\_}{\underset{\_}{\Lambda }}}_r· {\mathbb{A}}_r^{MT} with {\mathbb{A}}_r^{MT}= {{\mathbb{A}}_r^O·\left(\sum _{r=0}^n{f}_i·{\mathbb{A}}_r^O \right)}^{-1}$$

(9)

This scheme has demonstrated its effectiveness in determining the effective thermal conductivity of building materials [30,37]. Therefore, this study explores its applicability to composite materials where the inclusions are plant aggregates incorporated into hydraulic binders. In particular, the relevance of the Mori-Tanaka scheme may have limitations for a high inclusion volume fraction.

• Double inclusion scheme

Hori and Nemat-Nasser [38] generalized Eshelby’s formula and Mori–Tanaka’s average theory to propose a double-inclusion model. In this model, inclusions are embedded in a fictitious reference matrix and coated with another material matrix to predict the effective properties of composites considering interphase effects (Figure 2).

The double inclusion model considers the shape and orientation of the double inclusion and the properties of the reference medium, which must be specified based on the morphological and microstructural considerations. The external geometry of the double inclusion should reflect the arrangement of inclusions within the material. The coating phase (binder) has the same shape and orientation as the original inclusion (plant aggregate). Then, this new coated inclusion is processed using the Mori–Tanaka model. The results differ from the previous model because the matrix enveloping the coated inclusions is air and not hydraulic binder. In the case of two-phase composites, the volume fraction of the double inclusion equals the volume fraction of the inclusion. The double inclusion model is particularly suited for multiphase materials [39]. However, applying it to bio-based building materials poses challenges in assessing the thickness of the coating, which is not well documented in the literature. Nevertheless, the macroscopic granular appearance of plant-based concretes is evident when the volume fraction of aggregates is significant; plant aggregates are coated by the binder and bonded together (Figure 3).

The apparent relevance of the double inclusion model’s description can be emphasized, in the face of the real morphology of the materials considered here, i.e., plant-based concretes. This study compares the results of this model and the Mori–Tanaka model in estimating the thermal conductivity of the materials considered.

2.1.3. Representative Volume Equivalent (RVE)

Determining the RVE a critical point in homogenization. Given the complexity of plant-based concretes, several possibilities are conceivable. An RVE consisting of a binder matrix with only aggregate inclusions is a first-line solution. It is particularly relevant when the volume fraction of plant aggregates is low as it can be assumed that they are largely enclosed by the binder matrix in the composite. This type of RVE is referred to as “HB-1”. When the aggregate volume fraction is more important, the additional porosity between the aggregate and the binder is more difficult to neglect. Indeed, the literature commonly refers to tri-modal porosity in the case of hemp concrete (intra-binder porosity, intra-particle porosity, and porosity at the interface between the binder and the plant particle) [27]. In this case, additional porosity is defined compared to the previous case. Without any particular indication found in the literature, the additional porosity (air) was considered to be anisotropic (spherical inclusion) in the case of plant-based concretes. This type of RVE is referred as “HB-2”. Finally, the plant particles may appear to be simply embedded in the binder and arranged in a relatively random way. From this point of view, an RVE describing coated particles bathed in an air matrix also seems relevant (cf. Section 2.1.2). The thickness of the binder layer around the particle represents in the first instance 20% of the total volume of the coated inclusion (cf. Section 2.2.1). This latter case is noted “HB-3”.

To provide a better understanding of the different RVE cases considered in this study for plant-based concretes, an illustration is provided in Figure 4.

The effective thermal conductivity, due to the anisotropy of each RVE, is a tensor whose components are described as follows:

$${\underset{\_}{\underset{\_}{\Lambda }}}_{HB}=\left(\begin{array}{ccc}{\lambda }_i^{HB}& 0& 0\\ 0& {\lambda }_j^{HB}& 0\\ 0& 0& {\lambda }_k^{HB}\end{array}\right)$$

(10)

Depending on the orientation of the particles, these components can differ or not. In the following, the tangential components (λ_T) are those in the (O, $\overrightarrow{i}$, $\overrightarrow{j}$) plane, while the normal component (λ_N) is that along the (O, $\overrightarrow{k }$) axis.

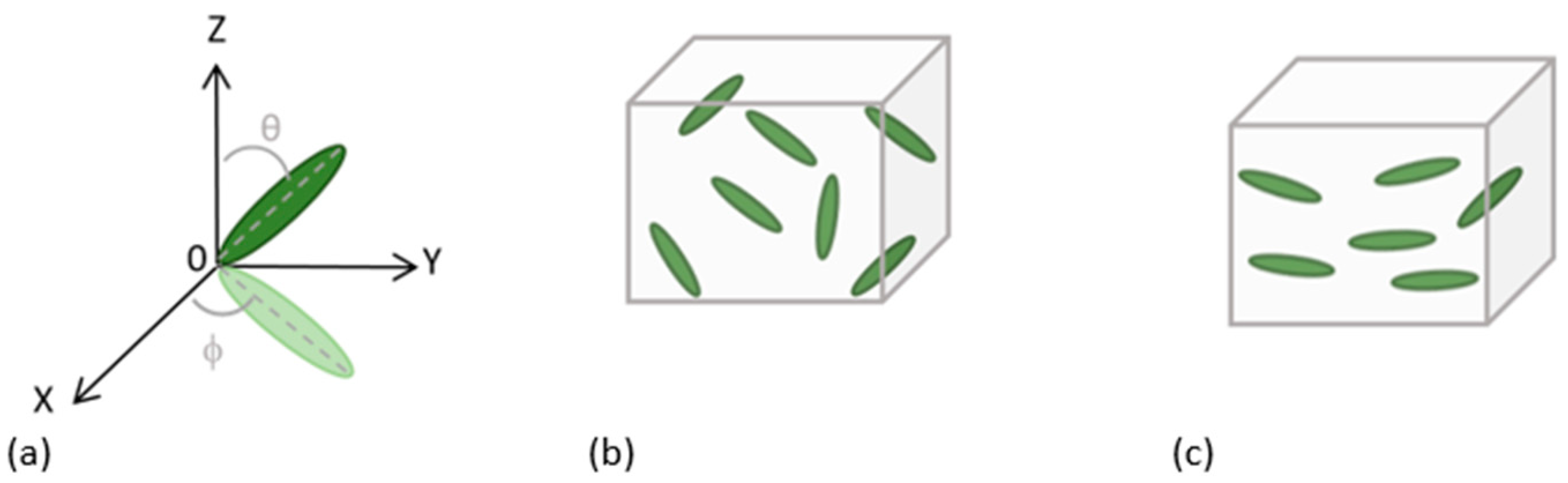
2.1.4. Microstructural Data

• Particulate shape

Hemp shiv and sunflower bark exhibit macroscopic cylindrical shapes and tubular pores. The ellipsoidal shape is consequently assumed for hemp shiv and sunflower bark according to the mean-field homogenization hypotheses. Sunflower pith, characterized by honeycomb pores, is predominantly spherical at the macroscopic scale [40]. The assumption of spherical inclusions for sunflower pith in mean-field homogenization was validated in previous research [30].

Table 1. Particulate values and assumptions for modeling.

Aggregate	Aspect Ratio	Assumption	Reference	Shape in Analytical Models
Hemp shiv	3.3	Transversely isotropic	Laborel-Preneron et al., 2018 [22]
Sunflower bark	3.4	Transversely isotropic	Lagouin et al., 2019 [11]
Sunflower pith	1	Isotropic	Magniont et al., 2012 [41] Arufe et al., 2021 [42] Rosa Latapie et al., 2023 [30]

summarizes the aspect ratios and shapes considered for the plant aggregates in mean-field homogenization.

The aspect ratios were calculated from the particle size analysis provided in the same study that provided thermal conductivities of the composites either by the same authors in preliminary works [11]. This ensures consistent input data and mitigates the impact of resource variability.

• Particulate orientation

The orientation of aggregates in composites can be defined by two angles. Θ is the angle between the main axis of the inclusion and the Z axis in global coordinates, while φ denotes the angle between the projection of the inclusion in the XY plane and the Y axis. Due to the lack of precise and exhaustive knowledge regarding the actual orientation of aggregates in the materials under consideration, this study makes two assumptions in line with X-ray tomography results [13]. Firstly, it assumes that aggregates are randomly oriented in all directions (“random 3D” assumption). Secondly, it assumes that compaction during placement induces random orientation only in the XY plane (“random 2D” assumption), illustrated in Figure 5.

• Particulate thermal conductivity

Particulate thermal conductivity is an essential input to the homogenization process as it translates local thermal behavior at the inclusion level. In the literature, only the thermal conductivity of the hemp shiv particles has been measured experimentally [32]. Given the difficulty of the measurement protocol at the particle scale and the variability of the resource, it is possible to determine the particle thermal conductivity from particle porosity or, by the inverse method, from the bulk thermal conductivity [15].

The macroscopic shape of the aggregates studied necessitates considering normal and tangential components for hemp shiv and sunflower bark: their thermal conductivity is a tensor with the assumption of a transversely isotropic inclusion (cf. Section 2.1.1). Sunflower pith, considered as an isotropic inclusion, is characterized by a single particulate thermal conductivity value, thus reducing its thermal conductivity to a scalar value (cf. Section 2.1.1).

In the following, details of each component of particle thermal conductivity will be given regarding the tensors in Figure 6.

2.1.5. Effect of Temperature and Relative Humidity

Plant aggregates are hygroscopic materials and naturally absorb water when ambient humidity rises. A part of the air trapped inside the particle, which contributes to its insulating capacity, is then replaced by water, whose thermal conductivity is almost twenty times greater than that of air. This significantly impacts particle thermal conductivity. To consider this phenomenon, it is necessary to quantify the water adsorbed in the plant aggregate using sorption isotherms. The sorption curves for hemp shiv and sunflower pith are selected from Ratsimbazafy’s work [43] to deduce the volume fraction of water in the plant particle at a given ambient humidity. Based on this, water volume fraction is determined in the pore space of the plant particle, and an analytical homogenization on this scale is used to correct the particulate thermal conductivity from the dry state.

Since both the thermal conductivity of air and the particle’s solid skeleton increase with temperature, a correction is also made as necessary. Particle thermal conductivities are first determined in dry conditions and at 20 °C (bulk thermal conductivity measurement conditions). They are then corrected according to the temperature and relative humidity conditions specified in the selected reference works for thermal conductivity measurements on the composite.

The method applied here has already demonstrated its suitability for predicting the evolution of the thermal conductivity in sunflower pith panels over the entire temperature and relative humidity range of use [30]. It is assumed that water-binding takes place only at the level of the plant particles, so any adsorption at the level of the binder is neglected in this study. Similarly, any variation in the thermal conductivity of the binder as a function of temperature is not considered.

2.2. Model Validation

2.2.1. Experimental Data

The studies selected for comparison and validation with the models are chosen based on several criteria. Firstly, specific data for each scale’s material are required as this forms the basis of the input data for modeling. This includes the thermal conductivity of the binder alone and that of the bulk aggregates (or their particular porosity if thermal conductivity is not available). Additionally, the temperature and relative humidity conditions for measuring the composite’s thermal conductivity have to be specified, which is not systematically done in the literature. An assessment, even if incomplete, of the volume proportions of each phase of the composite (inclusion, solid phase or total porosity) has to be provided in those references. Moreover, the material implementation must be clearly explained to assess the possibility of the preferential orientation of plant particles. Given these constraints, few works in the literature can be retained. The selected experimental work is one of the few to provide the key elements needed for modeling.

The chosen composites and corresponding characteristics for plant-based concretes are listed in

Table 2. Plant-based concretes selected for the study: experimental characteristics.

Plant-Based Concretes	Reference	Binder/Aggregate	Density (kg·m−3)	Open Porosity (%)	Thermal Conductivity (W·m−1·K−1)	Measurement Conditions
LSB-Lagouin	Lagouin et al., 2019 [11]	Lime/sunflower bark	539.64 ± 51.56	68.6 ± 1.7	0.127 ± 0.008	25 °C, 50% RH
MSB-Lagouin		Metakaolin/sunflower bark	511.07 ± 61.86	71.5 ± 5.3	0.128 ± 0.009

. It is interesting to note that the materials chosen have similar densities and thermal conductivities, but different binders. This enables the discussion of the influence or otherwise of the binder on the thermal conductivity of a composite, a point on which there is no consensus in the literature. It also allows the verification that the modeling gives comparable results in the two cases.

These materials are used as a basis for comparing the different modeling tools mentioned in Section 2.1. Open porosity is associated with the air volume fraction in the composite. Since porosity, which depends significantly on formulation [17], has a major impact on composite’s insulating capacity, it is important to specify the formulation of the selected plant-based concretes (

Table 3. Formulation of selected vegetal concretes from Lagouin et al. [19] to obtain one cubic meter of material.

Plant-Based Concretes	Binder (kg)	Aggregate (kg)	Water (kg)	Water/Binder	Aggregate/Binder
LSB-Lagouin	374.3	161.9	390.4	1.11	0.43
MSB-Lagouin	374.3	161.9	371.7	0.99	0.43

).

The information provided by the authors (mass proportions, constituent densities) is exploited and crosschecked with literature references [13,30] to estimate the volume fractions of the different phases. The consistency of these input data is evaluated with regard to the output data and by comparison with experimental data.

2.2.2. Modeling Input Data

• Particulate thermal conductivity

From the data available in the selected reference, each component of the particulate thermal conductivity tensors of sunflower bark is calculated in this work. These dry reference values at 20 °C were chosen as the reference values. In addition, to consider a change of aggregates in the modeling, the particulate thermal conductivity values of the hemp shiv are also calculated from the experimental results. This method can be extended to any other plant aggregate. For sunflower pith, the values was retained from previous work [30]. The method used and the dry reference values are listed in

Table 4. Particulate values calculated under 20 °C and in a dry state.

Reference	Type of Aggregate	Calculation Method	Modeled Particulate Thermal Conductivity (W·m−1·K−1)
			λT	λN
Lagouin et al., 2019 [11]	Sunflower Bark	From intra-particle porosity	0.139	0.208
Laborel et al., 2018 [22]	Hemp shiv	From measurement on bulk particles	0.044	0.066
Rosa Latapie e al., 2023 [30]	Sunflower pith	From intra-particle porosity	λiso = 0.04

.

The results for hemp shiv are relatively consistent with those found in the literature [22,26]. However, it is slightly lower, which can be explained by a slightly higher porosity of the aggregate used compared to the average of hemp aggregates. To our knowledge, no experimental reference exists for the particulate conductivity of the sunflower bark. However, since sunflower bark is less porous than hemp shiv, the result is consistent with expectations that there is very low thermal conductivity. Therefore, the high potential of sunflower pith should be emphasized, which is consistent with an intra-particle porosity of the order of 95% intra-particle porosity [43].

The dry particulate thermal conductivities are then corrected to suit the temperature and relative humidity conditions used to measure the composite’s thermal conductivity. The thermal conductivity of the binder is considered constant (i.e., independent of ambient humidity and temperature). Finally, the volume proportions of the aggregates are calculated from the mass ratios and densities of the constituents, initially assuming no additional porosity in the final composite.

The input data required for the various homogenization calculations carried out in this study are listed in

Table 5. Initial input data common for plant-based concretes under 25 °C and 50% HR.

	Hydraulic Binder		Aggregate
Composite	Density (kg·m−3)	Thermal Conductivity (W·m−1·K−1)	Particulate Density (kg·m−3)	Particulate Thermal Conductivity (W·m−1·K−1)		Volume Fraction	Aspect Ratio
				λT	λN
LSB-Lagouin	1052	0.366	425	0.139	0.209	0.82	3.4
MSB-Lagouin	1079	0.277				0.87

.

• Binder thermal conductivity

In order to investigate the possible correlation between the density and thermal conductivity of hydraulic binders (based on lime, metakaolin, and/or pozzolan), several references were selected from the literature [11,44,45,46,47,48,49,50,51]. A correlation link was investigated: the results are presented in Figure 7.

The experimental references indicate that hydraulic binders usually range in density from 800 to 1800 kg·m⁻³. While a linear correlation appears to be a good approximation, a polynomial equation more accurately relates thermal conductivity to the density of a hydraulic binder:

$${\lambda }_{hydraulic binder }={8.10}^{-7} {\rho }^2-{13.10}^{-4}\rho +0.7625$$

(11)

In the modeling, this relationship is used to study the impact of a binder change on the thermal conductivity of this phase in each RVE. It should be noted that this thermal conductivity necessarily includes the intra-binder porosity. To remain consistent with experimental data, three values of hydraulic binder density are tested: 800, 1300, and 1800 kg·m⁻³. It leads to a discussion of the influence of the binder on the effective thermal conductivity. The corresponding thermal conductivity is calculated using the relationship (10).

2.3. Optimization Factors of Effective Thermal Conductivity

2.3.1. Type of Plant Aggregate

Modeling is a powerful tool for simulating various RVE configurations and evaluating their impact on effective material properties. The analytical homogenization approach chosen in this study enables the study of the impact of a change in aggregate on a composite with relative ease and efficiency. Specifically, the incorporation of sunflower pith, sunflower bark or hemp shiv is tested while keeping the other parameters constant in the modeling, i.e., assuming both the same formulation and processing.

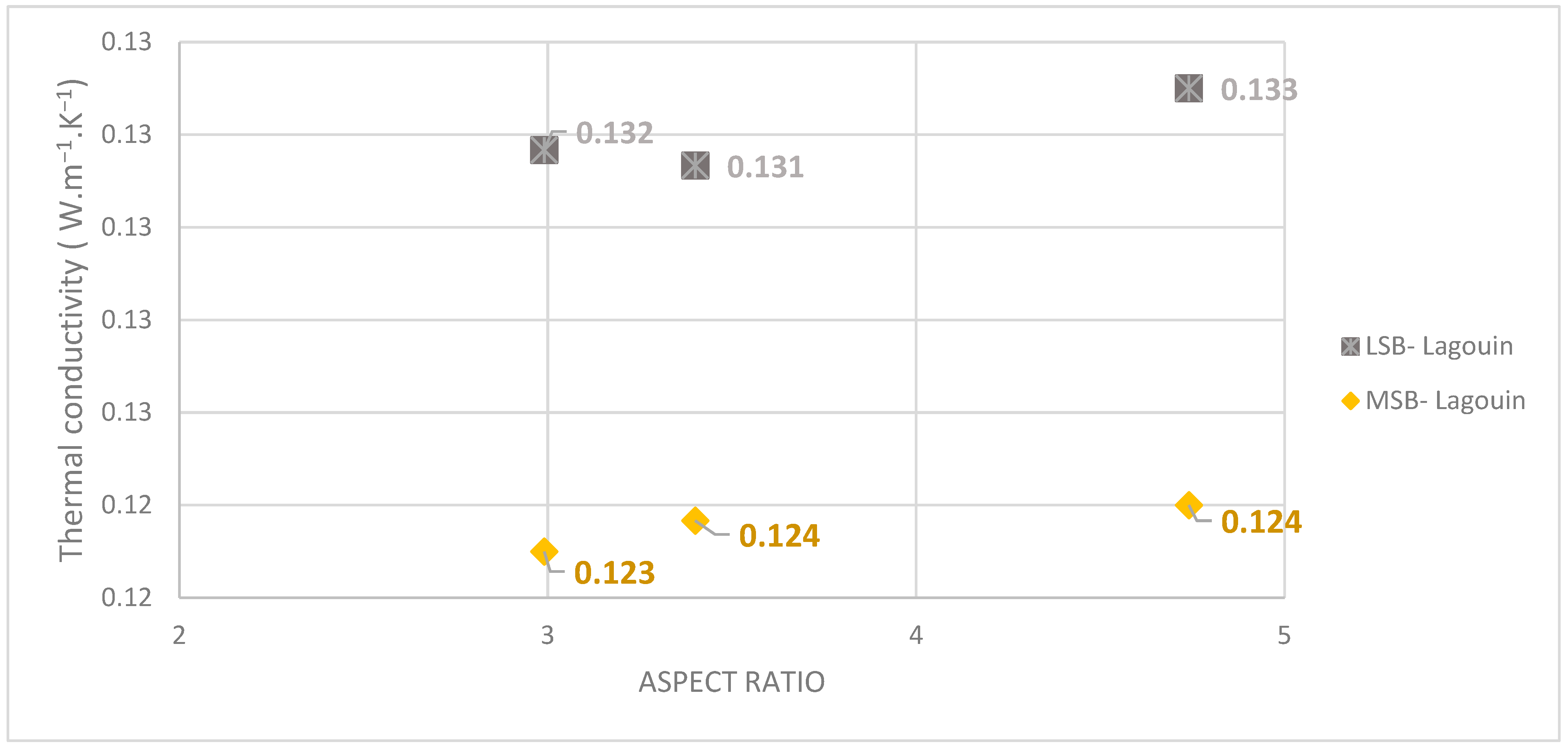
2.3.2. Aspect Ratio

Selecting plant aggregates with identical shapes for experimental study presents a significant challenge. Due to their natural origin and extraction methods, aggregates typically exhibit a certain size distribution, widely highlighted by granulometric analyses in the literature [52,53]. Modeling allows one to investigate the effects of plant particle aspect ratio on thermal properties. The range of aspect ratios chosen in this study aligns with data reported in the literature [54] (see

Table 6. Variability of the resource regarding the aspect ratio from Ratsimbazafy et al., 2021 [52].

Aggregate	Range of Aspect Ratio
Hemp shiv	2.28–8.75
Sunflower bark	2.99–4.74
Sunflower pith	1–1.50

).

2.3.3. Preferential Orientation

Due to the anisotropic thermal behavior of plant particles (see Section 2.1.4), the shape of the aggregate necessarily influences the effective thermal conductivity of the resulting bio-composite. In addition, the preferential orientation of these particles within the material—whether due to compaction or spray application—adds to the phenomenon and probably amplifies or compensates for the inherent anisotropy of the particles [53]. Regarding particle orientation, various cases are tested, ranging from random orientations to the extreme case of perfect alignment of all particles in the same direction. It is important to note that, while perfect alignment does not correspond to any practical implementation seen to date, exploring this extreme case allows for a more comprehensive discussion of the material’s thermal behavior.

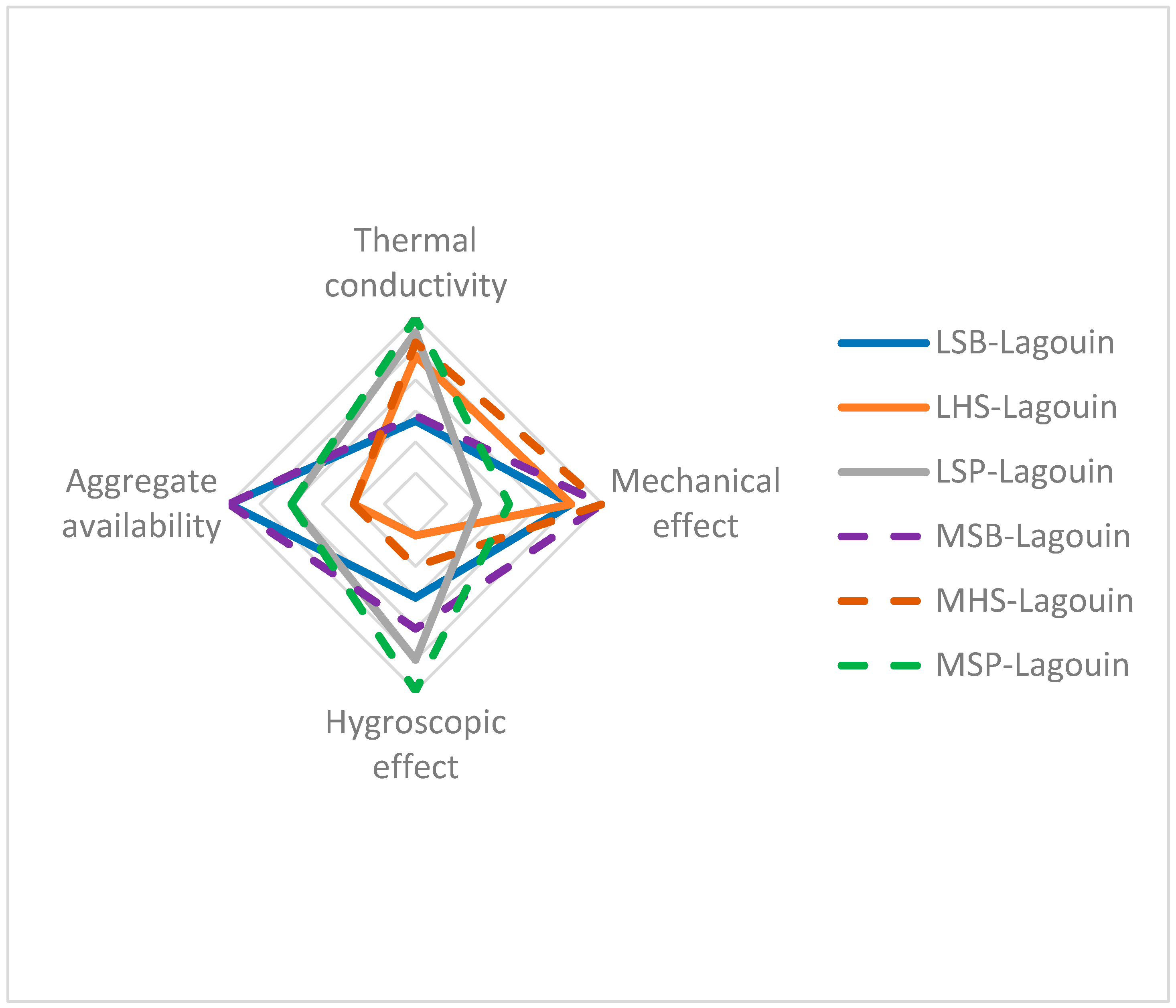
2.3.4. Multi-Criteria Optimization Parameters

While materials that incorporate plant aggregates in the hydraulic matrix are mainly used for distributed insulation, it is crucial to consider other criteria when optimizing their formulation [54,55]. This section suggests considering different aspects linked to the material’s extended performance, including mechanical and hygric properties, as well as environmental considerations related to the local availability of aggregates.

• Mechanical aspect

The binder content seems to be fundamental from a mechanical point of view for plant-based concretes: for a given type of hydraulic binder, the higher the concentrations of the binder, the lower the deformation levels [56]. Experimental studies have also demonstrated that smaller average aggregate sizes lead to improved mechanical performance [57]. In addition, the use of metakaolin-based binders improves the mechanical performance of plant-based concrete [58].

Due to the incomplete availability of mechanical data for all materials under consideration, this study relies on the trends reported in the literature. Nevertheless, to provide a visual multi-criteria analysis of the influence of varying binder or aggregate volume fractions, arbitrary values have been assigned to the mechanical properties (where a higher index indicates a greater value of the criterion). These parameter values are included in radar diagrams for comparative purposes between different formulations.

• Hygroscopic aspect

Plant-based concretes are capable of capturing, storing, and transporting moisture from the environment, a property related to their morphology, pore connectivity, and pore size [27]. As they naturally moderate indoor relative humidity fluctuations through water adsorption, these bio-composites contribute to the hygric comfort of buildings. The moisture buffer value (MBV) reflects this moisture regulation capacity.

Experimental findings suggest that the effect of formulations on sorption curves is fairly limited, as long as the composites are similar in terms of porosity [59,60]. The extent to which these materials can regulate moisture depends on their sorption curve. It can be argued that, for the same binder, the use of a more hygroscopic aggregate (i.e., one with a steeper sorption curve) increases the MBV, as it is proportional to hygric effusivity—a factor related to the slope of the material’s sorption curve. On the other hand, it has been established that using a binder based on metakaolin—rather than a hydraulic binder, improves the hygric regulating capacity of the composite [61]. Furthermore, to compare the effect of plant aggregate type on storage dynamics, Abbas et al. [62] introduced an interesting indicator, the ideal storage capacity of aggregates $x_{aggregate}^{ideal}$. This value was compared with a reference value for the dynamic storage capacity of the composite, noted $x_{aggregate}^{*}$, assuming no modification of the aggregate microstructure. Their study suggested that sunflower pith suffered microstructural alteration due to interactions with the hydraulic binder, whereas hemp shiv did not show such alterations. However, it is difficult to generalize this trend. Consequently, for simplicity, it is assumed here that aggregates with higher sorption/desorption capacities are more hygroscopic, based on the sorption curves of the aggregates considered in this study: hemp shiv, sunflower bark, and pith [62,63].

Given the incomplete availability of hygroscopic property data for the materials in this study, only trends reported from the literature have been considered. As for mechanical properties, arbitrary values have been assigned to hygroscopic criteria, based on the works of Ratsimbafazy et al. [52]. The aim is to provide a comparison across several formulations once thermal properties have been optimized.

• Resource availability criteria

The local availability of raw materials is an important factor in the lifecycle analysis of building materials [64]. Therefore, the local supply of plant aggregates used in plant-based concretes has to be examined. This study considers availability on a European scale, based on values reported in the literature [65,66]. Ideally, it would be necessary to have data on the quantities of waste available, both geographically (i.e., as close as possible to the construction site) and according to the seasonality of harvests (i.e., at the time of the construction phase) [67]. Nevertheless, the aim here is to compare different formulations, including the choice of aggregates.

Since specific data on the proportion of waste for a given crop are not available, a rate of return was calculated based on the number of hectares cultivated and the quantity of plants produced [68]. A higher ratio indicates more waste available per cultivated hectare. It is also important to assess the proportion of each crop compared to European cereal production, which was 543,061,000 tonnes in 2019 [69]. These indicators allow for a comparison of the potential of each agro-resource (see

Table 7. Indicators calculated for each agro-resource considered in the study based on literature data.

Raw Material	Cultivated Area in Europe (ha)	Annual European Production (t)	Reference	Rate of Return (t/ha)	Proportion Compared to European Total Cereal Production (%)
Hemp	15,700	85,000	Carus et al., 2016 [66]	5.4	0.01
Sunflower	18,073,170	68,655,795	Debaeke et al., 2017 [65]	3.8	12.6

).

In practice, separating pith from bark requires a mechanical process that must be repeated to improve pith purity (i.e., effective removal of traces of bark) [70]. The proportion of pith and bark obtained from a certain quantity of harvested stem waste is not well documented. However, it can be stressed that this process necessarily impacts the availability of pure pith. In this study, hemp by-products are considered less available globally compared to those from sunflower, in line with the literature [71]. In the case of sunflower, the bark is more readily available, and it can be extracted more easily than the pith.

3. Results and Discussion

3.1. Effective Thermal Conductivity of Plant-Based Concretes Concretes

One of the difficulties in analyzing results is that experimental measurements reported in the literature typically provide a single value for thermal conductivity, whereas the modeling can provide up to three components (in each direction of space) when considering an anisotropic distribution of plant particles. In the presentation of the results, the weighted average value of these components obtained through homogenization is compared with the measured value. Additionally, each component of the effective thermal conductivity tensor is compared with the experimental value to assess the relevance of accounting for anisotropy in the models. For randomly oriented composites (cf. Section 2.1.4), the thermal conductivity components are provided as a single common value for comparative purposes.

3.1.1. Lime-Based Composite

For the first plant-based reference concrete modeled in this study, denoted LSB-Lagouin, the results of the analytical homogenizations are presented in Figure 8. Each of the components (average, transverse and normal ones) given by the homogenization calculations are compared with the experimental value. This preliminary work aims to identify the model that gives the most consistent result when compared with the experimental value. This model is then used to optimize the thermal properties of the actual composite (Section 3.2).

The main observations that can be drawn are given as follows:

-

RVE HB-1 models: models without additional porosity show a significant relative deviation of over 40% from the experimental target value, indicating their limited relevance.

-

RVE HB-2 models: these models exhibit better results with a deviation of around 20% from the experiment value but it follows the trend of experimental data (i.e., predicted data are systematically below the experimental data). This could indicate a bias in the model.

-

Double inclusion scheme (HB-3): the most relevant results are obtained with homogenization considering the double inclusion scheme, with a deviation of less than 15% across all components. Given the measurement uncertainty, the thermal conductivity of this composite is estimated between 0.119 W·m⁻¹·K⁻¹ and 0.135 W·m⁻¹·K⁻¹. The predicted values of 0.132 W·m⁻¹·K^{−1 1} by both the HB-3-3D and HB-3-2D models (averaged) fit within this range.

The excellent results of the double inclusion model are probably due to a very good correspondence between the model’s assumptions and the real morphology of the material. Therefore, the LSB-Lagouin-HB-3 model is chosen for the rest of the study.

In addition, the anisotropy ratios between the normal and tangential components are 1.2, 1.1, and 1.3, respectively, for the HB-1-2D, HB-2-2D, and HB-3-2D models, respectively. While the considered composites are made of sunflower bark instead of hemp shiv, the literature reports an anisotropy effect on hemp concretes consistent with these values [72,73,74].

In addition, anisotropic effects vary depending on the formulation and the degree of compaction during processing [75]. Therefore, focusing on particle-scale anisotropy is crucial for predicting composite behavior. The impact of both form factor and particle-scale anisotropy has thus been considered in predictive models to optimize the insulating power of plant-based concrete. This approach could potentially guide the choice of aggregates used for manufacturing, enhancing the material’s overall performance.

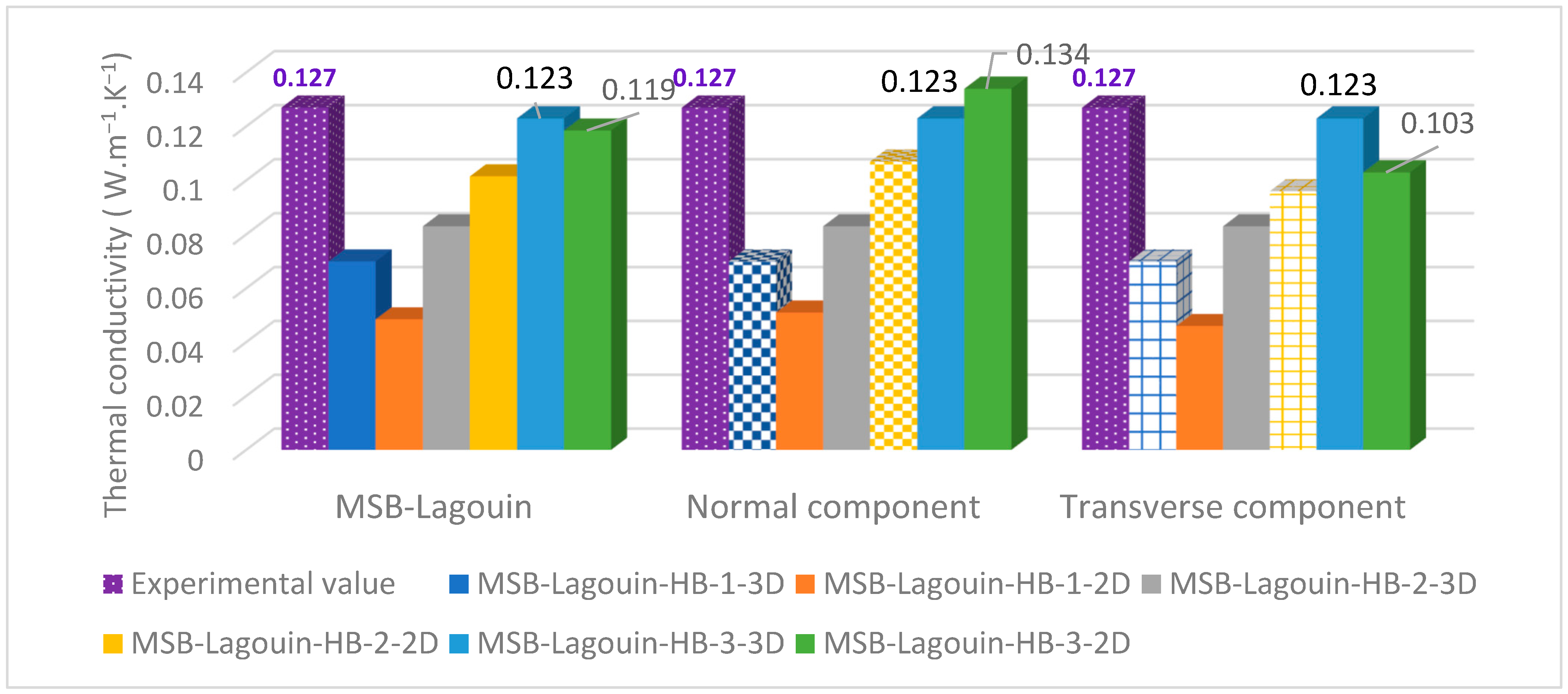
3.1.2. Metakaolin-Based Composite

The results of the analytical homogenizations for the MSB-Lagouin composite are presented in Figure 9 to select the model to be retained for the optimization phase. Modeled values are compared to experimental ones.

The observations are similar to previous one (for the lime-based composite):

-

RVE HB-1 models are irrelevant with a relative deviation of over 60% from the experimental target value.

-

Composites modeled by RVE HB-2 give unsatisfactory results with a deviation of around 40%, which is significantly below the experimental value.

-

Better results are obtained with homogenization using the double inclusion scheme, where both the HB-3-3D and HB-3-2D models show a deviation of less than 5% (considering the average value). Given the measurement uncertainty, this composite has a thermal conductivity value between 0.119 W·m⁻¹·K⁻¹ and 0.137 W·m⁻¹·K⁻¹. So, the values 0.123 and 0.124 W·m⁻¹·K⁻¹ predicted by the MSB-Lagouin-HB-3 models are therefore appropriate. The LMB-Lagouin-HB-3 is consequently retained for the optimization process. Similar conclusions can be drawn for those of the LSB composite concerning the alignment between the chosen model and the material structure, explaining the excellent fit between model and real composite behavior.

Finally, the anisotropy ratio between the normal and tangential components is 1.1 for the HB-1-2D and the HB-2-2D models and 1.3 for the HB-3-2D models, based on the experimental values from the literature [76]. It supports the idea that analytical homogenization is promising for predicting anisotropic effects in plant-based concretes.

The double-inclusion model is the most relevant for both of the plant-based concretes, showing its potential suitability for this type of composite. So, this model is retained, and calibrated (concerning the coating proportion applied on the plant aggregate) before the optimization phases.

3.2. Optimization of Thermal Conductivity

3.2.1. Reference Values and Models

For each study in this section, only the appropriate calibrated model for each composite is considered. As long as particle orientation is not investigated, a random distribution is retained if it offers a smaller relative deviation from the experimental value than in the case of orientation in a plane. To study the effect of an aggregate change (nature or shape factor), it was assumed that the other modeling parameters remained unchanged. For the optimizing process, the reference thermal conductivity-noted $l_{model}^{composite}$ for each model, is the one given by modeling. The results given by the selected models and their calibration values (concerning the percentage of coating) are listed and compared to the experimental data in

Table 8. Recapitulation of the models chosen for each composite and the reference thermal conductivity values before optimization.

Plant-Based Concretes
Composite	LSB-Lagouin	MSB-Lagouin
Model type	HB-3-2D	HB-3-2D
Calibrated value	20% coating	20% coating
λcomposite [W·m−1·K−1]	0.127	0.128
${\mathrm{l}}_{model}^{composite}$ [W·m−1·K−1]	0.132	0.124
Relative deviation	4%	4%

. Analysis of the formulations and the constituent densities provided an initial evaluation of the coating percentage. Calibration only serves to refine the results before the optimization stage.

From this point, simulations were carried out by varying various criteria: nature of the plant aggregate, aggregate shape factor, and aggregate orientation. Assuming that the other parameters remain unaltered and the selected models are reliable, thermal conductivity values modeled in the various optimization cases can be expected to be within 7% of the experimental value. This is entirely consistent with the measurement uncertainties given by the reference chosen for plant-based concretes [11], which is 6–7% depending on the composite considered.

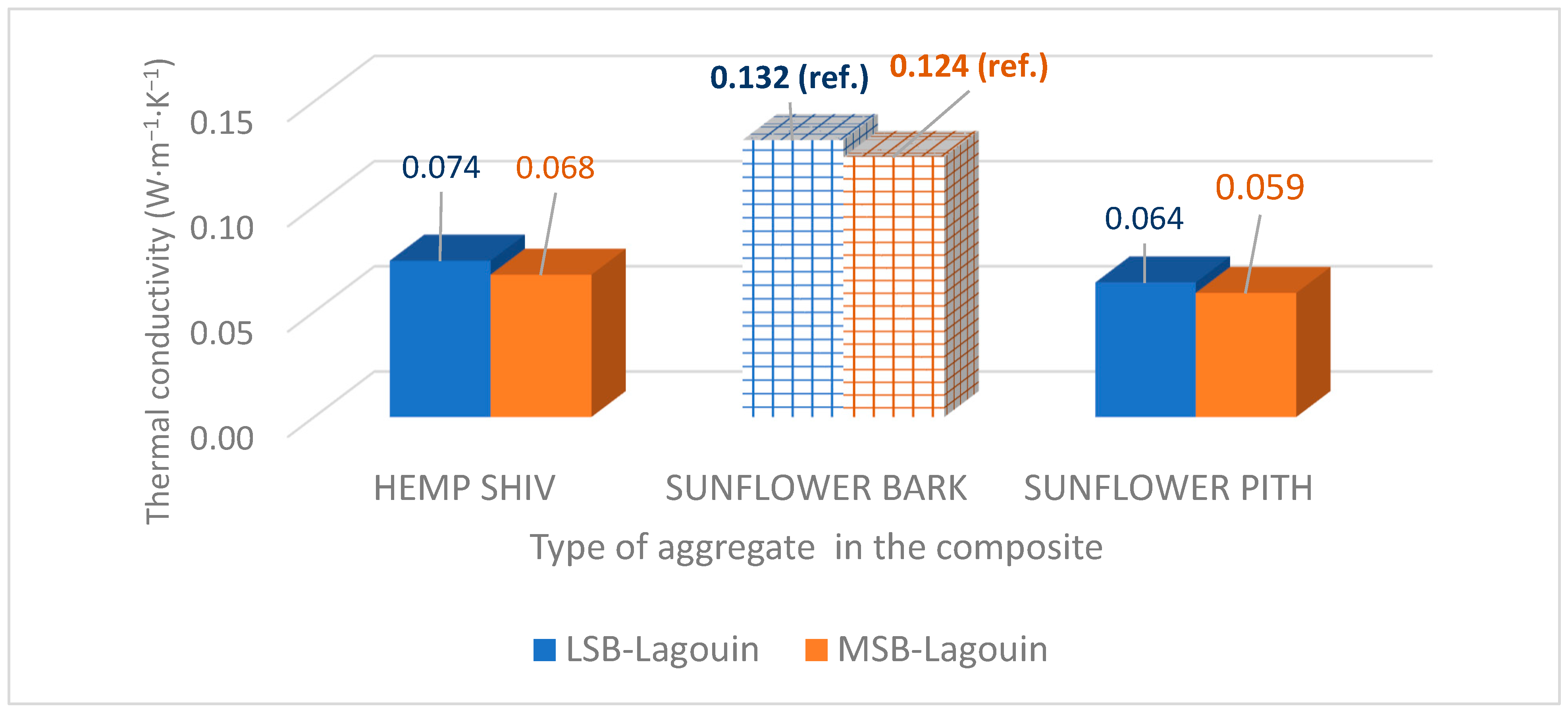
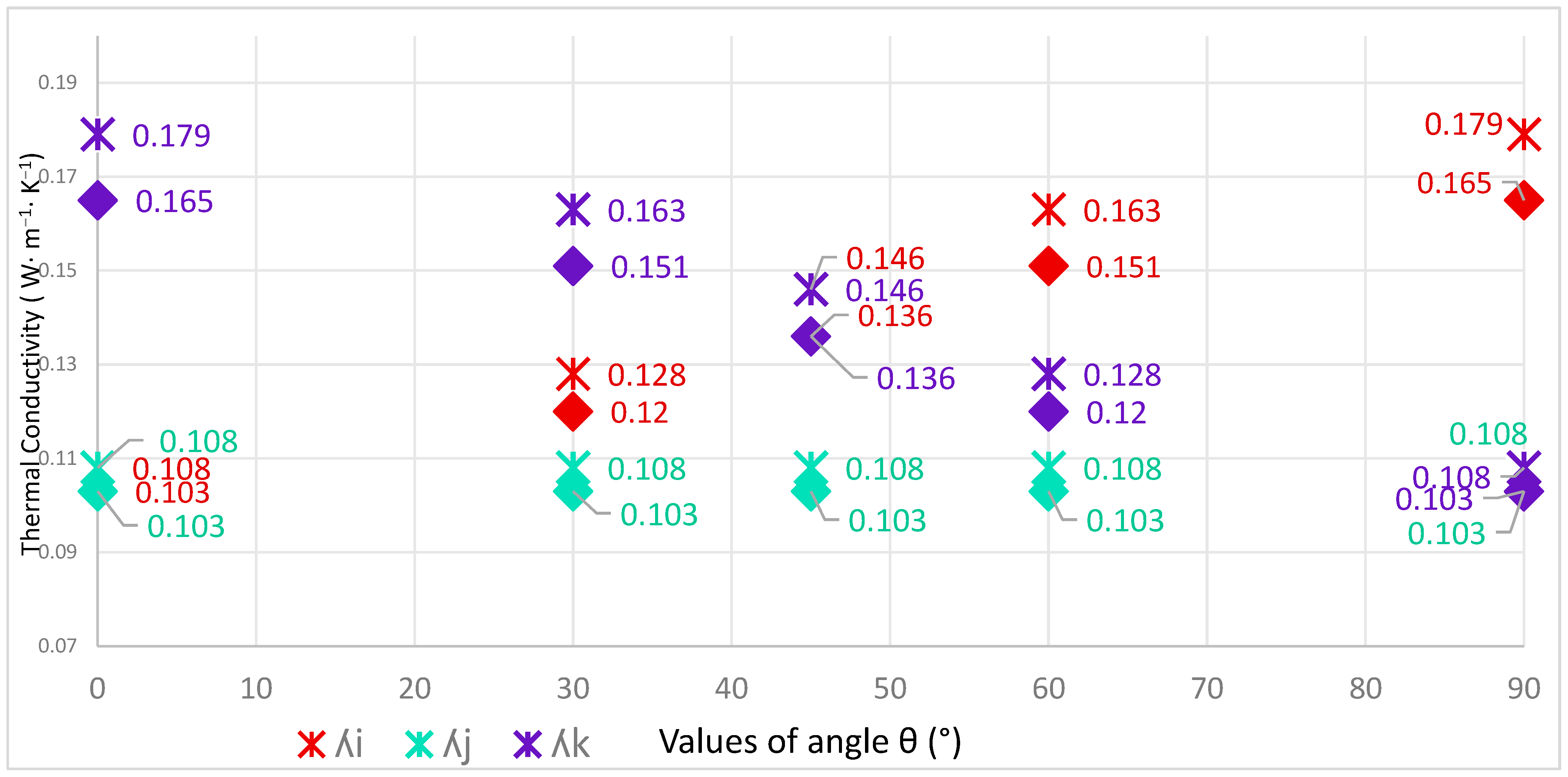
3.2.2. Influence of Aggregate Type

The simulations enable to envisage a change in the aggregate of each composite to compare the effect on the material’s thermal conductivity. The initial composites, LSB-Lagouin and MSB-Lagouin, are made from sunflower bark. Using the thermal conductivity value of plant aggregates (cf. Section 2.2.2) such as hemp shiv or sunflower pith, it was possible to simulate a change in aggregate in the composite. The names of the modeled composites indicate the letters H for hemp shiv, SP for sunflower pith, and SB for sunflower bark (reference). The simulation results are summarized in Figure 10 and enable the quantification of the effect of a change in aggregate type on the various composites tested.

According to the modeled values, replacing the bark in the LSB-Lagouin composite with sunflower pith reduced the initial thermal conductivity by half. The use of hemp shiv instead of sunflower bark reduced the initial value by 44% and 45% for the LSB and MSB-Lagouin composites, respectively. The situation is very similar for both composites which is consistent with their initial thermal conductivities (cf. Section 2.2.1). Consequently, the use of sunflower pith as a plant-based aggregate offers the best thermal performance irrespective of the composite type. It is consistent since this aggregate has the lowest particulate thermal conductivity. In contrast, composites with sunflower bark are the least thermally efficient due to the significantly higher particulate thermal conductivity of this aggregate compared to the hemp shiv and sunflower pith.

For further consideration, it is interesting to compare the results with hemp shiv, as it is the granulate reference in today’s literature. While sunflower pith aggregate is 30% more thermally efficient than hemp shiv, when used in plant-based concrete, the thermal gain is only 15% on average for the two formulations studied here (metakaolin-based and lime-based). This is due to the binder phase, which counterbalances the effect of the change in aggregate.

Furthermore, while sunflower bark aggregate is three times less thermally efficient than hemp shiv, when used in plant-based concrete, its thermal performance is improved. As previously observed, the effect of the binder attenuates the disparities associated with aggregates. However, it is important to note that the choice of aggregate is a key element in the expected performance, and therefore a key factor in the choice of formulation.

3.2.3. Influence of Aggregate Shape

Because of the variability of the resource, the literature reports different aspect ratios for a given type of plant aggregate. Thus, assuming the same particulate thermal conductivity, the shape factors of the aggregates in each composite were varied over the reported range in the literature (cf. Section 2.3.2). The results of the homogenization calculations are presented in Figure 11.

According to the homogenization calculations on the selected composites, the aspect ratio seems to have a very limited influence on their thermal conductivity. However, when compared with measurement uncertainties (see Section 3.2), this impact is largely negligible concerning the thermal conductivity of the studied composites. Also, the modeling was carried out with fixed aspect ratios, whereas in reality, a certain size distribution exists in plant aggregates. This study could therefore be extended by considering the results of granulometric analysis of aggregates used in plant-based concretes.

3.2.4. Influence of Aggregate Orientation

Current processing techniques tend to favor a preferential orientation of plant particles in the plane perpendicular to compaction or projection. In order to consider the development of new techniques that would enable plant aggregates to be oriented differently, the full range of possible orientations has been considered in this study. For reasons of symmetry, only the range from 0 to 90° is presented in this section. The results for average thermal conductivity values are presented in Figure 12.

Considering only the average thermal conductivity values, particle orientation appears to have less of an influence on thermal conductivity in the case of the composites studied (less than 1% difference among the values). Nevertheless, it is interesting to examine the variation in the component values of the thermal conductivity tensor as a function of particle orientation. For each space component (defined in Section 2.1.3) and each type of considered composite (LSB-Lagouin or MSB-Lagouin), the results are presented in Figure 13. The latter allow the quantification of how the thermal conductivity component can vary according to particle orientation.

Depending on the orientation of the plant particles, the composite’s thermal conductivity in a specific direction can vary by about 60% in both plant-based concretes. The marked anisotropy of thermal behavior may help to optimize the orientation of a prefabricated block of plant concrete in a wall, for example, to ensure the efficient insulation performance. In order to be explicit about the most favorable or unfavorable cases for each of the composites, the following table summarizes the extremum results (see

Table 9. Extreme thermal conductivities for each modeled composite.

Plant-Based Concretes
Composite (λ in W·m−1·K−1)	LSB-Lagouin	MSB-Lagouin
λmax/λmin	1.7	1.6

).

No values can be found in the literature concerning sunflower bark-based composites to assess the relevance of these results. However in the case of hemp-based composites, the ratio between normal and tangential thermal conductivity reported by experimental work is about 1.5 for non-optimized composites [76,77], i.e., where particle alignment is not necessarily the same. The results presented for optimized composites are therefore consistent with literature values. The influence of the binder is not considered as it has an isotropic thermal behavior according to the assumptions adopted in this study.

Finally, the results of this section highlight that processing techniques controlling particle orientation could be used to optimize the thermal properties of a bio-based material with a given formulation. These modeling results demonstrate how the exploration of a controlled preferential orientation could help optimize the thermal performance of plant-based concretes.

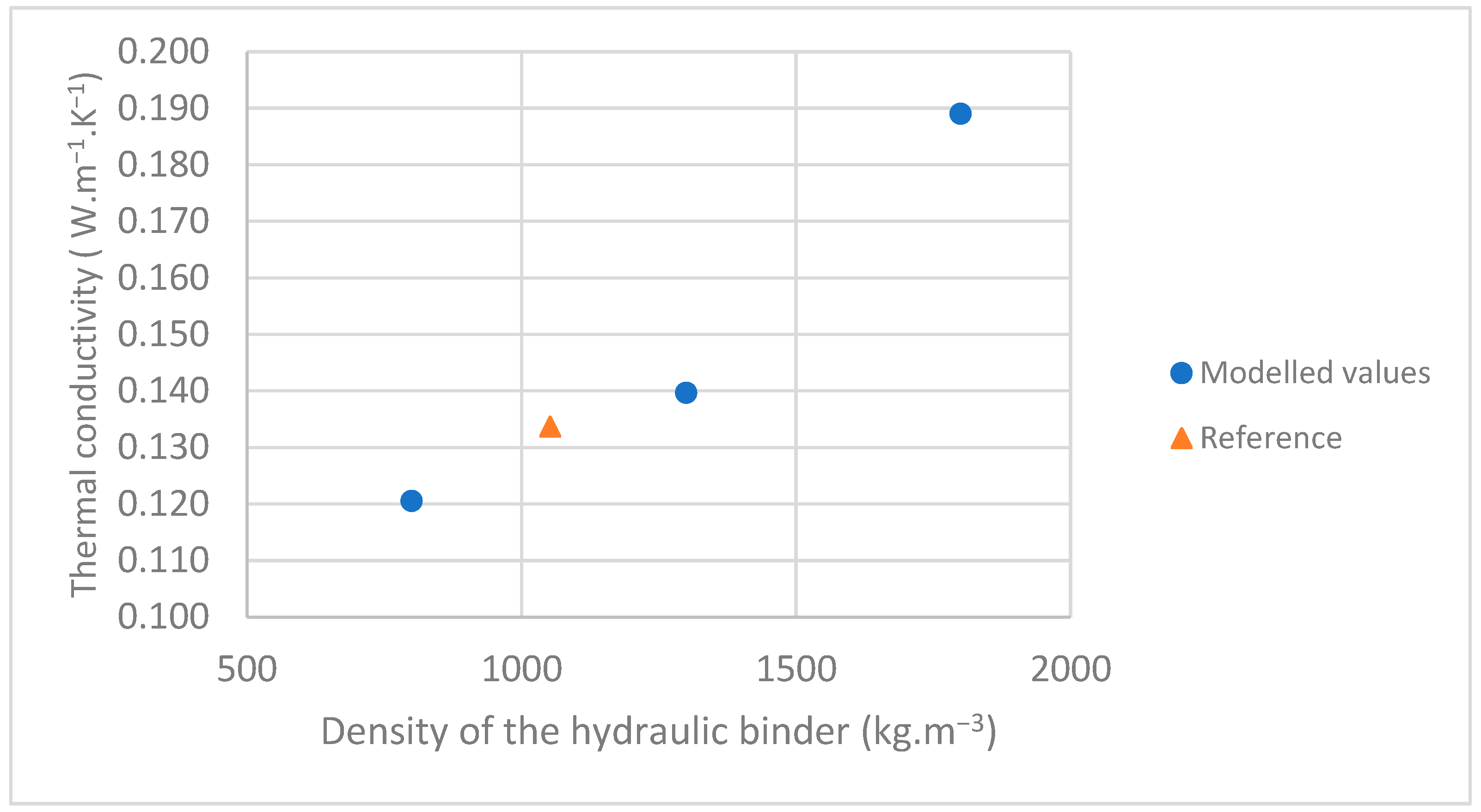
3.2.5. Influence of Binder

The change of hydraulic binder was tested on the LSB-Lagouin composite. The modeling results for three hydraulic binders differing in density and hence thermal conductivity are presented in Figure 14.

The results suggest that the binder can significantly influence the thermal conductivity of plant-based concrete in wall formulations. When the density of hydraulic binder is increased from 800 to 1800 kg·m⁻³, the thermal conductivity of the plant-based concrete increased by almost 60%. However, over a range from 800 to 1300 kg·m⁻³, this variation is only 16%. It can therefore be hypothesized that experimental observations and conclusions on the influence of binder on the thermal conductivity of hydraulic matrix plant-based concretes depend on the range of binder densities involved. This point could explain the different views expressed in the literature on the influence of binder type on the thermal conductivity of plant-based concretes.

3.3. Multi-Criteria Optimization of the Formulation

To compare the different possible formulations based on locally available raw materials, optimizing thermal properties does not simply mean achieving the lowest thermal conductivity. It involves weighing up a whole series of criteria that are more or less dependent on each other. A multi-criteria analysis is therefore proposed to suggest criteria for optimizing formulations prior to the manufacturing stage. It is based on the thermal behavior results presented in this article, as well as the mechanical, hygroscopic, and availability aspects discussed in Section 2.3.4. The optimization process is based on exploring the possibility of changing the plant aggregate in the initial composite. Since the only difference between LSB and MSB Lagouin composites is the binder type, the results are combined in a single graph to study the effect of both change in aggregate and change in binder (see Figure 15). This graph indicates how the thermal, hygroscopic and mechanical properties of the initial composites (LSB-Lagouin and MSB-Lagouin) can be optimized, taking into account local raw material availability.

This study enables decision making upstream of the manufacturing stage, depending on the objectives pursued. With a view to using widely available raw materials to minimize environmental impact, sunflower-based materials are of particular interest. In these circumstances, if mechanical performance is not a priority and a material with high hygro-thermal performance is required, the MSP-Lagouin composite based on metakaolin and sunflower pith is the best candidate. To achieve a material with good mechanical, hydric, and thermal performance, MSB-type composites are the most appropriate. Finally, it is interesting to note that the results illustrate the discussion conducted in Section 3.2.5 on the influence of binder. With a change of binder but retaining the same aggregate (lines of the same color in solid or dotted lines), the influence on the thermal conductivity of the composite is relatively low for binders with a density of around 1000 kg·m⁻³.

4. Conclusions

In this study, the aim is to propose a relevant tool for predicting and optimizing the thermal conductivity of plant-based concretes. This work demonstrates that modeling opens the way to an efficient tool to guide to choose formulation. The modeling is used to address a number of strategic points that are currently difficult to study under experimental conditions. Two composites rigorously selected from the literature are used to support the modeling work, lime-based and metakaolin-based, both using sunflower bark. This is particularly original in view of the few modeling studies reported in the literature, which only consider composites based on hemp shiv.

The proposed models account for both macro- and microstructure, with readily available input data at the particle scale. When data are difficult to finely assess, such as aggregate coating proportion, it is addressed through a first model calibration, ensuring that thermal conductivity predictions remain within a 5% margin of experimental values. The validated models then demonstrate their relevance to optimizing thermal behavior, while considering various aspects. The Mori–Tanaka model shows limitations for composites with high inclusion content, where the double inclusion model proves more suitable. Mean-field homogenization effectively models the thermal behavior of bio-sourced materials, but broader validation is hindered by limited microstructural data. Expanding this approach to a wider range of materials (considering the aggregates natural size distribution) requires further experimental and modeling work to refine conclusions.

However, in order to optimize the formulation for thermal performance, this study highlights the following points:

(i)

The nature of the aggregate is a fundamental criterion. Replacing sunflower bark with sunflower pith can halve the thermal conductivity of a bio-based composite, especially when the aggregate volume ratio is particularly significant as in plant-based concretes.

(ii)

The aggregate shape has a minor impact on the composite thermal conductivity on a macroscopic scale for the same type of aggregate.

(iii)

The orientation of plant particles has a significant impact on the thermal conductivity of the plant-based concrete. The difference between normal and tangential components (along or perpendicular to the compaction axis) can be as high as 60%. These results underline that appropriate processing techniques can make a major contribution to optimizing the thermal performance of bio-based materials.

(iv)

The impact of a binder change is limited as long as it remains within the same density range, since it has been revealed (from the experimental values) that a polynomial relationship exists between the thermal conductivity of the binder and its density.

It is especially important to note that, as long as the input data are available, these important conclusions are obtained without any time-consuming calculation step with the developed tool.

Finally, a simplified multi-criteria study provides a clearer picture of the impact (environmental impact, thermal, hygric and mechanical performance) of the choices concerning formulation that can be made upstream of the manufacturing phase.

Future research should explore mixing plant aggregates to adapt to local and seasonal availability. Refinements in modeling could account for variability in aspect ratios and integrate the impact of the humidity-induced swelling and shrinkage of plant aggregates on thermal insulation [78]. One of the limitations of the study is that it only takes into account a fixed particle size rather than a range of values. Furthermore, expanding the analysis from material to wall scale is promising, as thermal comfort depends on thermo-hygric interactions. Additionally, the virtual models of bio-based materials could incorporate new experimental data, such as fire resistance and sustainability indicators, paving the way for digital twins to anticipate complex material behaviors. Given the vast diversity of formulations, advanced data exploitation methods like Bayesian networks [79] may help to overcome the lack of data.