Fundamentals of Water Radiolysis
Definition
1. Introduction: Some History
2. Fundamentals of Water Radiolysis
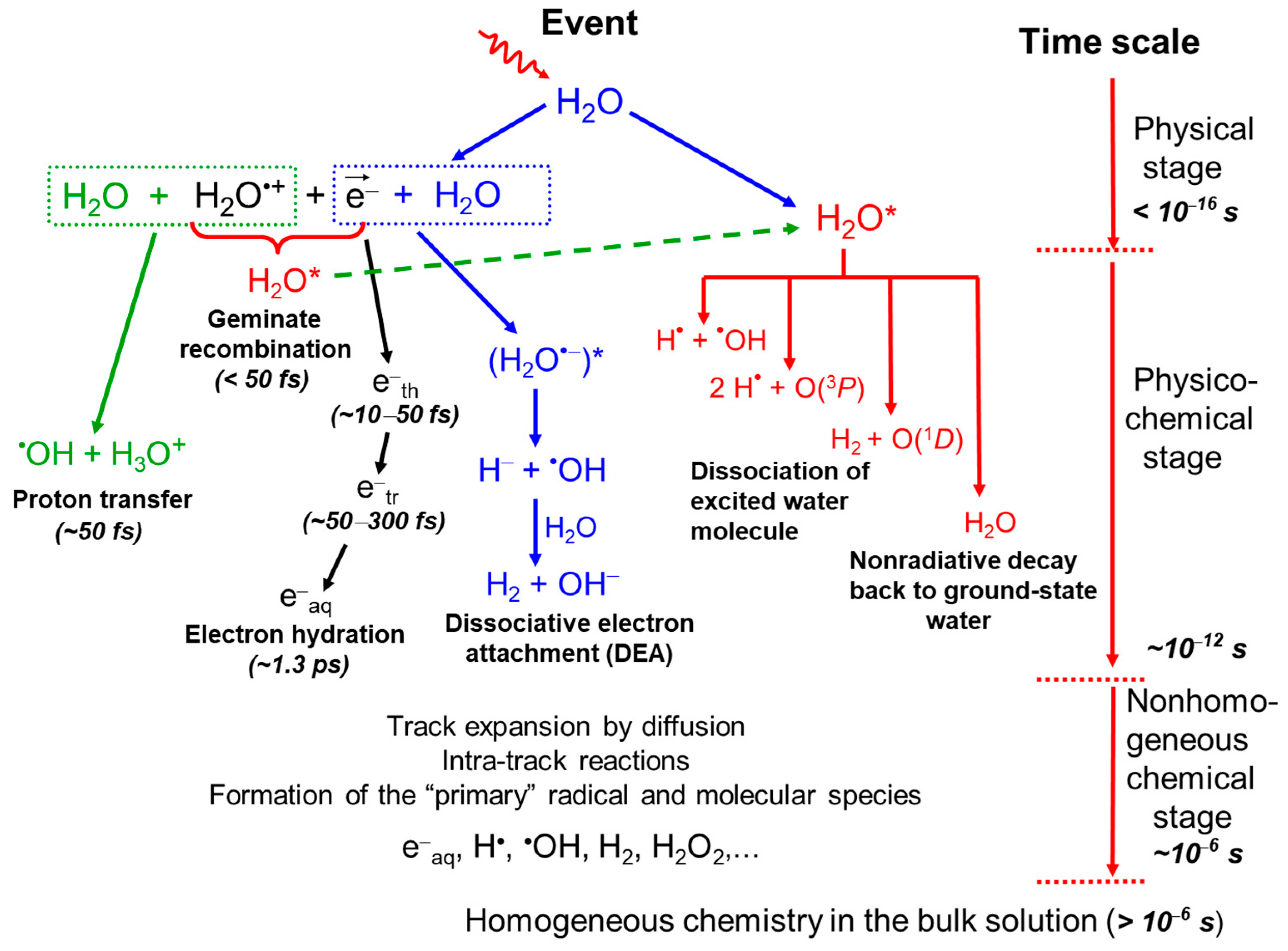
2.1. Radiolysis of Pure, Deaerated Water: Time Scale of Events and Formation of Primary Radical and Molecular Products
+ g(●OH) ●OH + g(H2O2) H2O2 + …,
g(●OH) = 2.80 g(H2O2) = 0.68 g(–H2O) = 4.15.
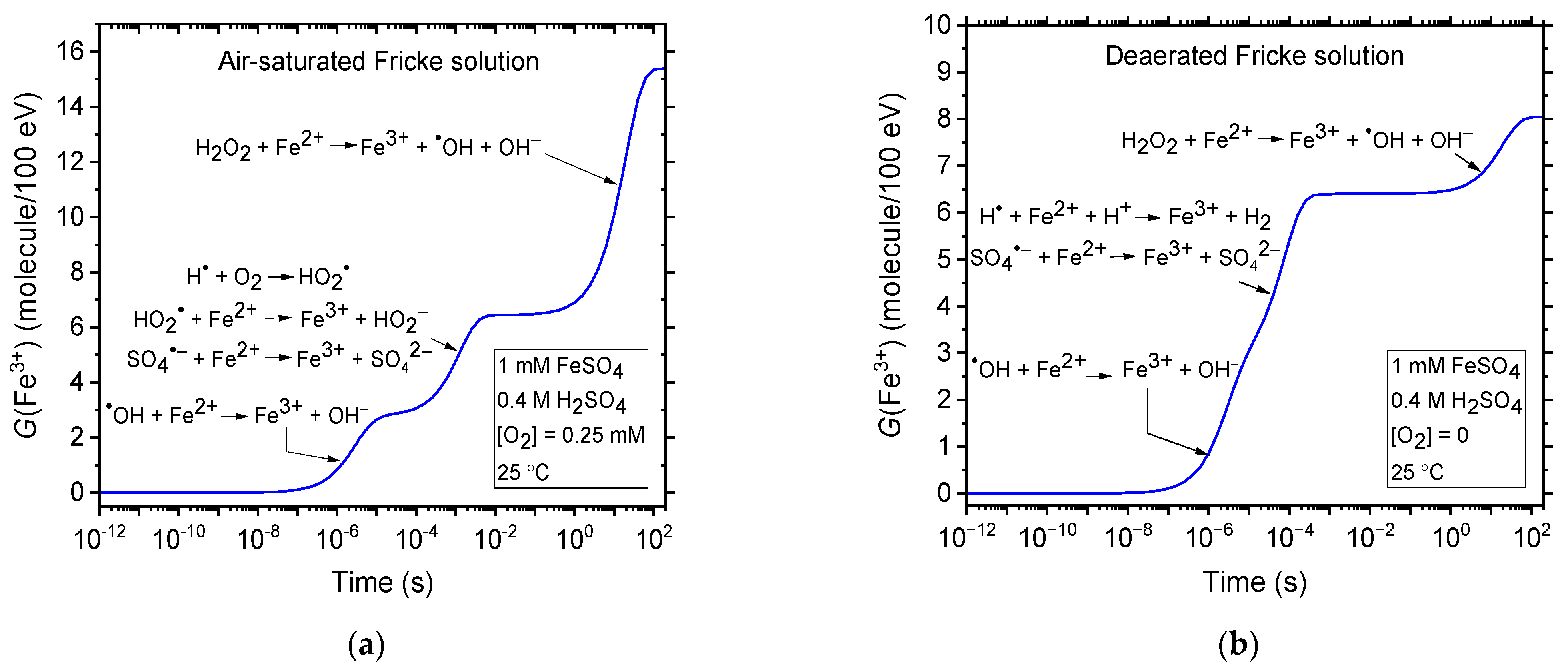
2.2. The Effect of Dissolved Oxygen
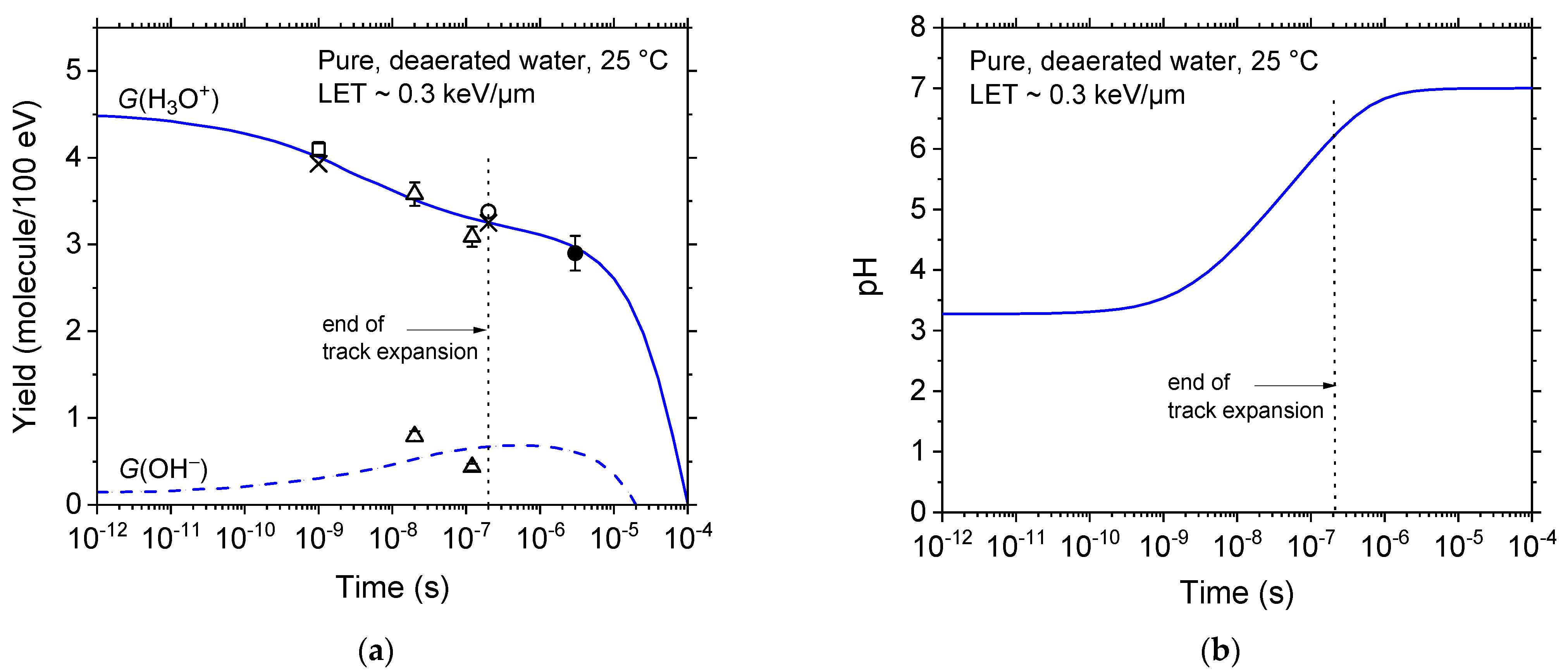
2.3. Spurs/Tracks Are Highly Acidic
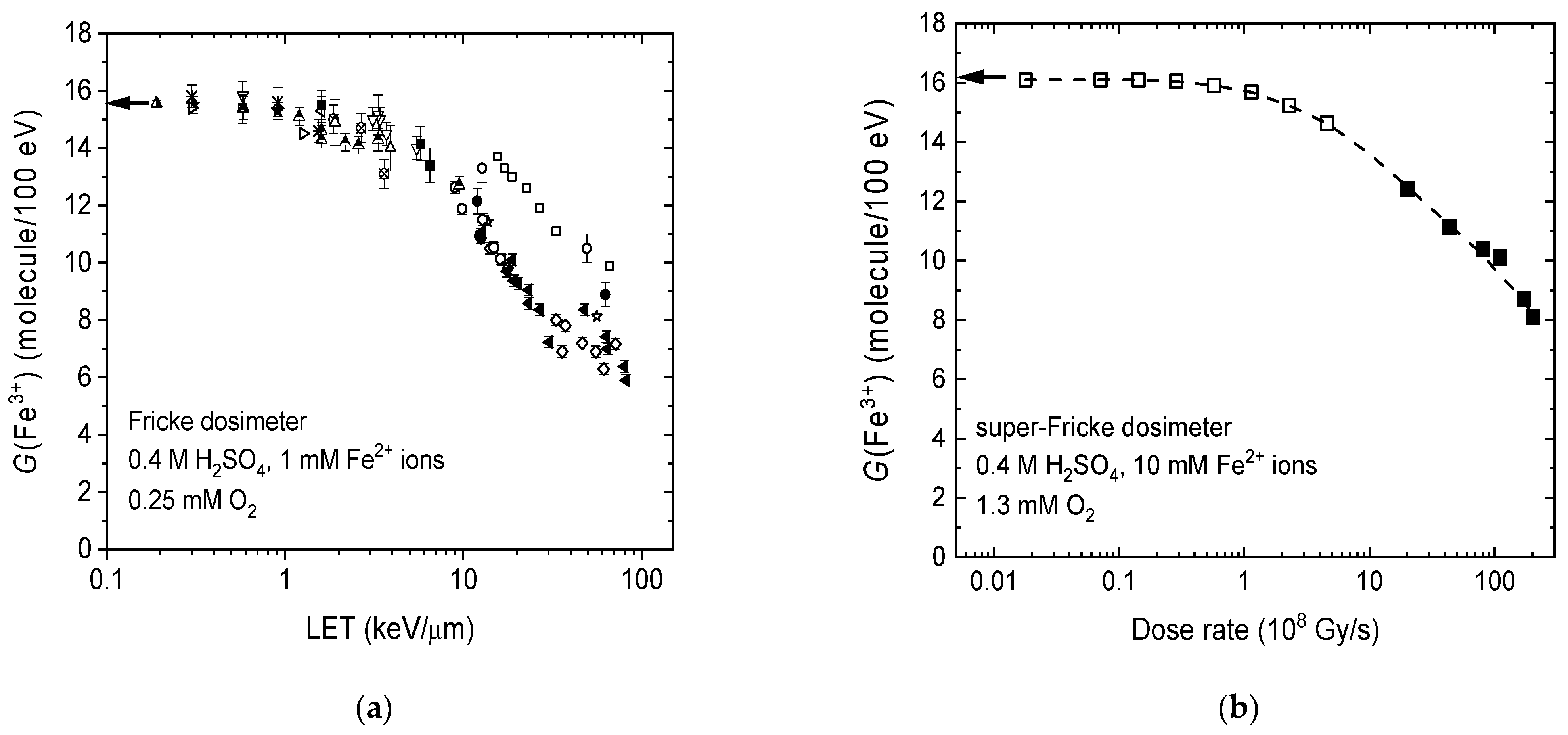
2.4. LET and Dose-Rate Effects
3. The Ferrous Sulfate (Fricke) Dosimeter: The Most Thoroughly Studied System in Radiation Chemistry
3.1. The Primary Radical and Molecular Yields in Irradiated 0.4 M H2SO4 Aqueous Solutions
g(●OH) = 2.90 g(H2O2) = 0.80 g(HO2●) = 0.02 g(–H2O) = 4.50,
3.2. The Ferrous Sulfate, or Fricke, Dosimeter
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferradini, C.; Pucheault, J. Biologie de l’Action des Rayonnements Ionisants; Masson: Paris, France, 1983. [Google Scholar]
- Buxton, G.V. Radiation chemistry of the liquid state: (1) Water and homogeneous aqueous solutions. In Radiation Chemistry: Principles and Applications; Farhataziz, Rodgers, M.A.J., Eds.; VCH: New York, NY, USA, 1987; pp. 321–349. [Google Scholar]
- Freeman, G.R. (Ed.) Kinetics of Nonhomogeneous Processes: A Practical Introduction for Chemists, Biologists, Physicists, and Materials Scientists; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Magee, J.L. Nonhomogeneous processes in radiation research: Radical diffusion models. Can. J. Phys. 1990, 68, 853–857. [Google Scholar] [CrossRef]
- Spinks, J.W.T.; Woods, R.J. An Introduction to Radiation Chemistry, 3rd ed.; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Tabata, Y.; Ito, Y.; Tagawa, S. (Eds.) CRC Handbook of Radiation Chemistry; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Klassen, N.V. Primary species in irradiated water. J. Chim. Phys. 1991, 88, 747–757. [Google Scholar] [CrossRef]
- Ferradini, C.; Jay-Gerin, J.-P. (Eds.) Excess Electrons in Dielectric Media; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Draganić, I.G.; Draganić, Z.D.; Adloff, J.-P. Radiation and Radioactivity on Earth and Beyond, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar] [CrossRef]
- Bensasson, R.V.; Land, E.J.; Truscott, T.G. Excited States and Free Radicals in Biology and Medicine; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Woods, R.J.; Pikaev, A.K. Applied Radiation Chemistry: Radiation Processing; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Getoff, N. Radiation-induced degradation of water pollutants—State of the art. Radiat. Phys. Chem. 1996, 47, 581–593. [Google Scholar] [CrossRef]
- McCracken, D.R.; Tsang, K.T.; Laughton, P.J. Aspects of the Physics and Chemistry of Water Radiolysis by Fast Neutrons and Fast Electrons in Nuclear Reactors; Report AECL-11895; Atomic Energy of Canada Limited: Chalk River, ON, Canada, 1998. [Google Scholar]
- Richter, H.W. Radiation chemistry: Principles and applications. In Photochemistry and Radiation Chemistry. Complementary Methods for the Study of Electron Transfer; Wishart, J.F., Nocera, D.G., Eds.; American Chemical Society: Washington, DC, USA, 1998; Chapter 2; pp. 5–33. [Google Scholar] [CrossRef]
- Pastina, B.; LaVerne, J.A.; Pimblott, S.M. Dependence of molecular hydrogen formation in water on scavengers of the precursor to the hydrated electron. J. Phys. Chem. A 1999, 103, 5841–5846. [Google Scholar] [CrossRef]
- Mozumder, A. Fundamentals of Radiation Chemistry; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- LaVerne, J.A. Radiation chemical effects of heavy ions. In Charged Particle and Photon Interactions with Matter: Chemical, Physicochemical, and Biological Consequences with Applications; Mozumder, A., Hatano, Y., Eds.; Marcel Dekker: New York, NY, USA, 2004; pp. 403–429. [Google Scholar]
- Garrett, B.C.; Dixon, D.A.; Camaioni, D.M.; Chipman, D.M.; Johnson, M.A.; Jonah, C.D.; Kimmel, G.A.; Miller, J.H.; Rescigno, T.N.; Rossky, P.J.; et al. Role of water in electron-initiated processes and radical chemistry: Issues and scientific advances. Chem. Rev. 2005, 105, 355–389. [Google Scholar] [CrossRef]
- von Sonntag, C. Free-Radical-Induced DNA Damage and Its Repair. A Chemical Perspective; Springer: Berlin, Germany, 2006. [Google Scholar]
- Elliot, A.J.; Bartels, D.M. The Reaction Set, Rate Constants and g-Values for the Simulation of the Radiolysis of Light Water over the Range 20 to 350 °C Based on Information Available in 2008; Report No. 153-127160-450-001; Atomic Energy of Canada Limited: Mississauga, ON, Canada, 2009. [Google Scholar]
- Lin, M.; Muroya, Y.; Baldacchino, G.; Katsumura, Y. Radiolysis of supercritical water. In Recent Trends in Radiation Chemistry; Wishart, J.F., Rao, B.S.M., Eds.; World Scientific: Hackensack, NJ, USA, 2010; pp. 255–277. [Google Scholar]
- Muroya, Y.; Lin, M.; de Waele, V.; Hatano, Y.; Katsumura, Y.; Mostafavi, M. First observation of picosecond kinetics of hydrated electrons in supercritical water. J. Phys. Chem. Lett. 2010, 1, 331–335. [Google Scholar] [CrossRef]
- Meesungnoen, J.; Jay-Gerin, J.-P. Radiation chemistry of liquid water with heavy ions: Monte Carlo simulation studies. In Charged Particle and Photon Interactions with Matter. Recent Advances, Applications, and Interfaces; Hatano, Y., Katsumura, Y., Mozumder, A., Eds.; CRC Press (Taylor & Francis Group): Boca Raton, FL, USA, 2011; pp. 355–400. [Google Scholar] [CrossRef]
- Bobrowski, K. Radiation-induced radical reactions. In Encyclopedia of Radicals in Chemistry, Biology and Materials; Chatgilialoglu, C., Studer, A., Eds.; Wiley: Chichester, UK, 2012; Volume 1, pp. 395–432. [Google Scholar] [CrossRef]
- Das, S. Critical review of water radiolysis processes, dissociation products, and possible impacts on the local environment: A geochemist’s perspective. Aust. J. Chem. 2013, 66, 522–529. [Google Scholar] [CrossRef]
- Wojnárovits, L.; Takács, E. Radiation induced degradation of organic pollutants in waters and wastewaters. Top. Curr. Chem. (Z) 2016, 374, 50. [Google Scholar] [CrossRef]
- Katsumura, Y.; Kudo, H. Radiation chemistry of aqueous solutions. In Radiation Applications; Kudo, H., Ed.; Springer Nature: Singapore, 2018; Chapter 6; pp. 37–49. [Google Scholar] [CrossRef]
- Wardman, P. Radiotherapy using high-intensity pulsed radiation beams (FLASH): A radiation-chemical perspective. Radiat. Res. 2020, 194, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, D.D.; Engelhardt, G.R.; Petrov, A. A critical review of radiolysis issues in water-cooled fission and fusion reactors: Part I, Assessment of radiolysis models. Corros. Mater. Degrad. 2022, 3, 470–535. [Google Scholar] [CrossRef]
- Fritsch, B.; Lee, S.; Körner, A.; Schneider, N.M.; Ross, F.M.; Hutzler, A. The influence of ionizing radiation on quantification for in situ and operando liquid-phase electron microscopy. Adv. Mater. 2025, 2415728. [Google Scholar] [CrossRef] [PubMed]
- Medin, J.; Ross, C.K.; Klassen, N.V.; Palmans, H.; Grusell, E.; Grindborg, J.-E. Experimental determination of beam quality factors, kQ, for two types of Farmer chamber in a 10 MV photon and a 175 MeV proton beam. Phys. Med. Biol. 2006, 51, 1503–1521. [Google Scholar] [CrossRef] [PubMed]
- Curie, P.; Curie, S. Sur une substance nouvelle radio-active, contenue dans la pechblende. C. R. Acad. Sci. Paris 1898, 127, 175–178. [Google Scholar]
- Curie, P.; Curie, P. (Mme); Bémont, G. Sur une nouvelle substance fortement radio-active, contenue dans la pechblende. C. R. Acad. Sci. Paris 1898, 127, 1215–1217. [Google Scholar]
- Curie, P.; Debierne, A. Sur la radio-activité induite et les gaz activés par le radium. C. R. Acad. Sci. Paris 1901, 132, 768–770. [Google Scholar]
- Giesel, F. Ueber Radium und radioactive Stoffe. Ber. Deutsch. Chem. Ges. (Berlin) 1902, 35, 3608–3611. [Google Scholar] [CrossRef]
- Giesel, F. Ueber den Emanationskörper aus Pechblende und über Radium. Ber. Deutsch. Chem. Ges. 1903, 36, 342–347. [Google Scholar] [CrossRef]
- Ramsey, W.; Soddy, F. Experiments in radioactivity, and the production of helium from radium. Proc. R. Soc. London 1903, 72, 204–207. [Google Scholar]
- Curie, P. Radioactivité; Hermann: Paris, France, 1935; p. 347. [Google Scholar]
- Rutherford, E.; Royds, T. The nature of the α particle from radioactive substances. Philos. Mag. 1909, 17, 281–286. [Google Scholar] [CrossRef]
- Ramsey, W. The chemical action of the radium emanation. Part I. Action on distilled water. J. Chem. Soc. Trans. 1907, 91, 931–942. [Google Scholar] [CrossRef]
- Cameron, A.T.; Ramsey, W. The chemical action of radium emanation. Part II. On solutions containing copper, and lead, and on water. J. Chem. Soc. Trans. 1907, 91, 1593–1606. [Google Scholar] [CrossRef]
- Usher, F.L. Die chemische Einzelwirkung und die chemische Gesamtwirkung der α- und der β-Strahlen. Jahrb. Radioakt. Elektr. 1911, 8, 323–334. [Google Scholar]
- Kernbaum, M. Action chimique sur l’eau des rayons pénétrants de radium. C. R. Acad. Sci. Paris 1909, 148, 705–706. [Google Scholar]
- Risse, O. Über die Röntgenphotolyse des Hydroperoxyds. Z. Phys. Chem. 1929, 140A, 133–157. [Google Scholar] [CrossRef]
- Fricke, H.; Brownscombe, E.R. Inability of X-rays to decompose water. Phys. Rev. 1933, 44, 240. [Google Scholar] [CrossRef]
- Debierne, A. Recherches sur les gaz produits par les substances radioactives. Décomposition de l’eau. Ann. Physique (Paris) 1914, 2, 97–127. [Google Scholar] [CrossRef]
- Risse, O. Einige Bemerkungen zum Mechanismus chemischer Röntgenreaktionen in wäβrigen Lösungen. Strahlentherapie 1929, 34, 578–581. [Google Scholar]
- Allen, A.O. Mechanism of the radiolysis of water by gamma rays or electrons. In Actions Chimiques et Biologiques des Radiations; Haïssinsky, M., Ed.; Masson: Paris, France, 1961; Volume 5, pp. 9–30. [Google Scholar]
- Gordon, S. Radiation chemistry at the Metallurgical Laboratory, Manhattan project, University of Chicago (1942–1947) and the Argonne National Laboratory, Argonne, IL (1947–1984). In Early Developments in Radiation Chemistry; Kroh, J., Ed.; The Royal Society of Chemistry, Thomas Graham House: Cambridge, UK, 1989; pp. 163–204. [Google Scholar]
- Weiss, J. Radiochemistry of aqueous solutions. Nature 1944, 153, 748–750. [Google Scholar] [CrossRef]
- Kroh, J. (Ed.) Early Developments in Radiation Chemistry; The Royal Society of Chemistry, Thomas Graham House: Cambridge, UK, 1989. [Google Scholar]
- Jonah, C.D. A short history of the radiation chemistry of water. Radiat. Res. 1995, 144, 141–147. [Google Scholar] [CrossRef]
- Ferradini, C.; Jay-Gerin, J.-P. Radiolysis of water and aqueous solutions: History and present state of the science. Can. J. Chem. 1999, 77, 1542–1575. [Google Scholar] [CrossRef]
- LaVerne, J.A. Track effects of heavy ions in liquid water. Radiat. Res. 2000, 153, 487–496. [Google Scholar] [CrossRef] [PubMed]
- Zimbrick, J.D. Radiation chemistry and the Radiation Research Society: A history from the beginning. Radiat. Res. 2002, 158, 127–140. [Google Scholar] [CrossRef]
- Buxton, G.V. The radiation chemistry of liquid water: Principles and Applications. In Charged Particle and Photon Interactions with Matter: Chemical, Physicochemical, and Biological Consequences with Applications; Mozumder, A., Hatano, Y., Eds.; Marcel Dekker: New York, NY, USA, 2004; pp. 331–363. [Google Scholar]
- Cooper, R. The history and development of radiation chemistry. Aust. J. Chem. 2011, 64, 864–868. [Google Scholar] [CrossRef]
- Le Caër, S. Water radiolysis: Influence of oxide surfaces on H2 production under ionizing radiation. Water 2011, 3, 235–253. [Google Scholar] [CrossRef]
- Baldacchino, G. The contribution of swift ions in the epic of radiation chemistry. Histoire de la Recherche Contemporaine 2017, Tome VI, 47–54. [Google Scholar] [CrossRef]
- Zimbrick, J.D. Radiation chemistry and Radiation Research: A history from the beginning to the Platinum edition. Radiat. Res. 2024, 202, 368–384. [Google Scholar] [CrossRef]
- Platzman, R.L. The physical and chemical basis of mechanisms in radiation biology. In Radiation Biology and Medicine. Selected Reviews in the Life Sciences; Claus, W.D., Ed.; Addison-Wesley: Reading, MA, USA, 1958; pp. 15–72. [Google Scholar]
- Kuppermann, A. Theoretical foundations of radiation chemistry. J. Chem. Educ. 1959, 36, 279–285. [Google Scholar] [CrossRef]
- Loh, Z.-H.; Doumy, G.; Arnold, C.; Kjellsson, L.; Southworth, S.H.; Al Haddad, A.; Kumagai, Y.; Tu, M.-F.; Ho, P.J.; March, A.M.; et al. Observation of the fastest chemical processes in the radiolysis of water. Science 2020, 367, 179–182. [Google Scholar] [CrossRef]
- Ogura, H.; Hamill, W.H. Positive hole migration in pulse-irradiated water and heavy water. J. Phys. Chem. 1973, 77, 2952–2954. [Google Scholar] [CrossRef]
- Cobut, V.; Frongillo, Y.; Patau, J.P.; Goulet, T.; Fraser, M.-J.; Jay-Gerin, J.-P. Monte Carlo simulation of fast electron and proton tracks in liquid water—I. Physical and physicochemical aspects. Radiat. Phys. Chem. 1998, 51, 229–243. [Google Scholar] [CrossRef]
- Cobut, V.; Frongillo, Y.; Jay-Gerin, J.-P.; Patau, J.P. A Monte Carlo calculation of subexcitation and vibrationally-relaxing electron spectra in irradiated liquid water. Radiat. Phys. Chem. 1992, 40, 589–591. [Google Scholar] [CrossRef]
- LaVerne, J.A.; Pimblott, S.M. Electron energy-loss distributions in solid, dry DNA. Radiat. Res. 1995, 141, 208–215. [Google Scholar] [CrossRef]
- Autsavapromporn, N. The Effects of pH and Radiation Quality (LET) on the Radiolysis of Liquid Water and Aqueous Solutions: A Monte Carlo Simulation Study. Master’s Thesis, Burapha University, Chonburi, Thailand, 2006. [Google Scholar]
- Michaud, M.; Cloutier, P.; Sanche, L. Low-energy electron-energy-loss spectroscopy of amorphous ice: Electronic excitations. Phys. Rev. A 1991, 44, 5624–5627. [Google Scholar] [CrossRef] [PubMed]
- Goulet, T.; Bernas, A.; Ferradini, C.; Jay-Gerin, J.-P. On the electronic structure of liquid water: Conduction-band tail revealed by photoionization data. Chem. Phys. Lett. 1990, 170, 492–496. [Google Scholar] [CrossRef]
- Migus, A.; Gauduel, Y.; Martin, J.L.; Antonetti, A. Excess electrons in liquid water: First evidence of a prehydrated state with femtosecond lifetime. Phys. Rev. Lett. 1987, 58, 1559–1562. [Google Scholar] [CrossRef]
- Pépin, C.; Goulet, T.; Houde, D.; Jay-Gerin, J.-P. Observation of a continuous spectral shift in the solvation kinetics of electrons in neat liquid deuterated water. J. Phys. Chem. A 1997, 101, 4351–4360. [Google Scholar] [CrossRef]
- LaForge, A.C.; Michiels, R.; Bohlen, M.; Callegari, C.; Clark, A.; von Conta, A.; Coreno, M.; Di Fraia, M.; Drabbels, M.; Huppert, M.; et al. Real-time dynamics of the formation of hydrated electrons upon irradiation of water clusters with extreme ultraviolet light. Phys. Rev. Lett. 2019, 122, 133001. [Google Scholar] [CrossRef]
- Sopena Moros, A.; Li, S.; Li, K.; Doumy, G.; Southworth, S.H.; Otolski, C.; Schaller, R.D.; Kumagai, Y.; Rubensson, J.-E.; Simon, M.; et al. Tracking cavity formation in electron solvation: Insights from X-ray spectroscopy and theory. J. Am. Chem. Soc. 2024, 146, 3262–3269. [Google Scholar] [CrossRef]
- Klassen, N.V. Primary products in radiation chemistry. In Radiation Chemistry: Principles and Applications; Farhataziz, Rodgers, M.A.J., Eds.; VCH Publishers: New York, NY, USA, 1987; pp. 29–64. [Google Scholar]
- Bernas, A.; Ferradini, C.; Jay-Gerin, J.-P. Excess electrons in homogeneous and heterogeneous polar media. Can. J. Chem. 1996, 74, 1–23. [Google Scholar] [CrossRef]
- Yamamoto, Y.-I.; Suzuki, T. Ultrafast dynamics of water radiolysis: Hydrated electron formation, solvation, recombination, and scavenging. J. Phys. Chem. Lett. 2020, 11, 5510–5516. [Google Scholar] [CrossRef]
- Platzman, R.L. Dissociative attachment of subexcitation electrons in liquid water, and the origin of radiolytic “molecular” hydrogen. In Book of Abstracts, Proceedings of the 2nd International Congress of Radiation Research (ICRR), Harrogate, UK, 5–11 August 1962; The University of Chicago: Chicago, IL, USA; p. 128.
- Rowntree, P.; Parenteau, L.; Sanche, L. Electron stimulated desorption via dissociative attachment in amorphous H2O. J. Chem. Phys. 1991, 94, 8570–8576. [Google Scholar] [CrossRef]
- Goulet, T.; Patau, J.P.; Jay-Gerin, J.-P. Influence of the parent cation on the thermalization of subexcitation electrons in solid water. J. Phys. Chem. 1990, 94, 7312–7316. [Google Scholar] [CrossRef]
- Swiatla-Wojcik, D.; Buxton, G.V. Modeling of radiation spur processes in water at temperatures up to 300 °C. J. Phys. Chem. 1995, 99, 11464–11471. [Google Scholar] [CrossRef]
- Taube, H. Photochemical reactions of ozone in solution. Trans. Faraday Soc. 1957, 53, 656–665. [Google Scholar] [CrossRef]
- Biedenkapp, D.; Hartshorn, L.G.; Bair, E.J. The O(1D) + H2O reaction. Chem. Phys. Lett. 1970, 5, 379–381. [Google Scholar] [CrossRef]
- Amichai, O.; Treinin, A. Chemical reactivity of O(3P) atoms in aqueous solution. Chem. Phys. Lett. 1969, 3, 611–613. [Google Scholar] [CrossRef]
- Nikogosyan, D.N.; Oraevsky, A.A.; Rupasov, V.I. Two-photon ionization and dissociation of liquid water by powerful laser UV radiation. Chem. Phys. 1983, 77, 131–143. [Google Scholar] [CrossRef]
- Crowell, R.A.; Bartels, D.M. Multiphoton ionization of liquid water with 3.0–5.0 eV photons. J. Phys. Chem. 1996, 100, 17940–17949. [Google Scholar] [CrossRef]
- Bernas, A.; Ferradini, C.; Jay-Gerin, J.-P. On the electronic structure of liquid water: Facts and reflections. Chem. Phys. 1997, 222, 151–160. [Google Scholar] [CrossRef]
- Faraggi, M. On the molecular hydrogen formation in the gamma radiolysis of water and aqueous solutions. Int. J. Radiat. Phys. Chem. 1973, 5, 197–206. [Google Scholar] [CrossRef]
- Cobut, V.; Jay-Gerin, J.-P.; Frongillo, Y.; Patau, J.P. On the dissociative electron attachment as a potential source of molecular hydrogen in irradiated liquid water. Radiat. Phys. Chem. 1996, 47, 247–250. [Google Scholar] [CrossRef]
- Sanguanmith, S. Breaking the Picosecond Barrier in the Physics and Chemistry of Water Radiolysis: Applications of Monte Carlo Modeling to High-Temperature Nuclear Reactors and Radiobiology. Ph.D. Thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, 2021. [Google Scholar]
- LaVerne, J.A.; Pimblott, S.M. New mechanism for H2 formation in water. J. Phys. Chem. A 2000, 104, 9820–9822. [Google Scholar] [CrossRef]
- Harris, R.E.; Pimblott, S.M. On 3H β-particle and 60Co γ irradiation of aqueous systems. Radiat. Res. 2002, 158, 493–504. [Google Scholar] [CrossRef]
- Horne, G.P.; Pimblott, S.M.; LaVerne, J.A. Inhibition of radiolytic molecular hydrogen formation by quenching of excited state water. J. Phys. Chem. B 2017, 121, 5385–5390. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, H.A. Applications of the spur diffusion model to the radiation chemistry of aqueous solutions. J. Phys. Chem. 1969, 73, 1928–1937. [Google Scholar] [CrossRef]
- Dobrovolskii, D.; Denisov, S.A.; Sims, H.E.; Mostafavi, M. Reactivity of quasi-free electrons towards N3− and its impact on H2 formation mechanism in water radiolysis. Phys. Chem. Chem. Phys. 2024, 26, 11604–11610. [Google Scholar] [CrossRef]
- Sims, H.E. (Central Laboratory, National Nuclear Laboratory, Sellafield, Seascale, UK). Personal communication, 2024.
- Hunt, J.W. Early events in radiation chemistry. In Advances in Radiation Chemistry; Burton, M., Magee, J.L., Eds.; Wiley: New York, NY, USA, 1976; Volume 5, pp. 185–315. [Google Scholar]
- Jonah, C.D.; Miller, J.R.; Matheson, M.S. The reaction of the precursor of the hydrated electron with electron scavengers. J. Phys. Chem. 1977, 81, 1618–1622. [Google Scholar] [CrossRef]
- Pimblott, S.M.; LaVerne, J.A. On the radiation chemical kinetics of the precursor to the hydrated electron. J. Phys. Chem. A 1998, 102, 2967–2975. [Google Scholar] [CrossRef]
- Lu, Q.-B.; Baskin, J.S.; Zewail, A.H. The presolvated electron in water: Can it be scavenged at long range? J. Phys. Chem. B 2004, 108, 10509–10514. [Google Scholar] [CrossRef]
- Ma, J.; Wang, F.; Denisov, S.A.; Adhikary, A.; Mostafavi, M. Reactivity of prehydrated electrons toward nucleobases and nucleotides in aqueous solution. Sci. Adv. 2017, 3, e1701669. [Google Scholar] [CrossRef]
- Ferradini, C.; Jay-Gerin, J.-P. Hypothesis of a possible chemical fate for the incompletely relaxed electron in water and alcohols. Chem. Phys. Lett. 1990, 167, 371–373. [Google Scholar] [CrossRef]
- Ferradini, C.; Jay-Gerin, J.-P. Does multiple ionization intervene for the production of HO2● radicals in high-LET liquid water radiolysis? Radiat. Phys. Chem. 1998, 51, 263–267. [Google Scholar] [CrossRef]
- Ferradini, C. Actions chimiques des radiations ionisantes. J. Chim. Phys. 1979, 76, 636–644. [Google Scholar] [CrossRef]
- Chatterjee, A.; Holley, W.R. Computer simulation of initial events in the biochemical mechanisms of DNA damage. Adv. Radiat. Biol. 1993, 17, 181–221. [Google Scholar] [CrossRef] [PubMed]
- Muroya, Y.; Plante, I.; Azzam, E.I.; Meesungnoen, J.; Katsumura, Y.; Jay-Gerin, J.-P. High-LET ion radiolysis of water: Visualization of the formation and evolution of ion tracks and relevance to the radiation-induced bystander effect. Radiat. Res. 2006, 165, 485–491. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Radiation Units and Measurements. Linear Energy Transfer; ICRU Report No. 16; International Commission on Radiation Units and Measurements: Washington, DC, USA, 1970. [Google Scholar]
- Magee, J.L. Radiation chemistry. Annu. Rev. Nucl. Sci. 1953, 3, 171–192. [Google Scholar] [CrossRef]
- Freeman, G.R. Basics of radiation chemistry. In The Study of Fast Processes and Transient Species by Electron Pulse Radiolysis; Baxendale, J.H., Busi, F., Eds.; Reidel Publishing: Dordrecht, The Netherlands, 1982; pp. 19–34. [Google Scholar]
- Plante, I.L.; Filali-Mouhim, A.; Jay-Gerin, J.-P. SIMULRAD: A JAVA interface for a Monte Carlo simulation code to visualize in 3D the early stages of water radiolysis. Radiat. Phys. Chem. 2005, 72, 173–180. [Google Scholar] [CrossRef]
- Sanguanmith, S.; Meesungnoen, J.; Muroya, Y.; Lin, M.; Katsumura, Y.; Jay-Gerin, J.-P. On the spur lifetime and its temperature dependence in the low linear energy transfer radiolysis of water. Phys. Chem. Chem. Phys. 2012, 14, 16731–16736. [Google Scholar] [CrossRef]
- Kuppermann, A.; Belford, G.G. Diffusion kinetics in radiation chemistry. I. Generalized formulation and criticism of diffusion model. J. Chem. Phys. 1962, 36, 1412–1426. [Google Scholar] [CrossRef]
- Dewhurst, H.A.; Burton, M. Radiolysis of aqueous solutions of hydrazine. J. Am. Chem. Soc. 1955, 77, 5781–5785. [Google Scholar] [CrossRef]
- Hart, E.J. Chemical effects of ionizing radiations on aqueous inorganic solutions. J. Chem. Educ. 1957, 34, 586–593. [Google Scholar] [CrossRef]
- Pastina, B.; LaVerne, J.A. Effect of molecular hydrogen on hydrogen peroxide in water radiolysis. J. Phys. Chem. A 2001, 105, 9316–9322. [Google Scholar] [CrossRef]
- Bepari, M.I.; Meesungnoen, J.; Jay-Gerin, J.-P. Early and transient formation of highly acidic pH spikes in water radiolysis under the combined effect of high dose rate and high linear energy transfer. Radiation 2023, 3, 165–182. [Google Scholar] [CrossRef]
- Schwarz, H.A. Reaction of the hydrated electron with water. J. Phys. Chem. 1992, 96, 8937–8941. [Google Scholar] [CrossRef]
- Elliot, A.J.; Chenier, M.P.; Ouellette, D.C. Temperature dependence of g values for H2O and D2O irradiated with low linear energy transfer radiation. J. Chem. Soc. Faraday Trans. 1993, 89, 1193–1197. [Google Scholar] [CrossRef]
- Ferradini, C.; Jay-Gerin, J.-P. The effect of pH on water radiolysis: A still open question—A minireview. Res. Chem. Intermed. 2000, 26, 549–565. [Google Scholar] [CrossRef]
- Buxton, G.V. An overview of the radiation chemistry of liquids. In Radiation Chemistry: From Basics to Applications in Material and Life Sciences; Spotheim-Maurizot, M., Mostafavi, M., Douki, T., Belloni, J., Eds.; EDP Sciences: Les Ulis, France, 2008; pp. 3–16. [Google Scholar] [CrossRef]
- Draganić, I.G.; Draganić, Z.D. The Radiation Chemistry of Water; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Draganić, I.G.; Nenadović, M.T.; Draganić, Z.D. Radiolysis of HCOOH + O2 at pH 1.3–13 and the yields of primary products in γ radiolysis of water. J. Phys. Chem. 1969, 73, 2564–2571. [Google Scholar] [CrossRef]
- Sehested, K.; Corfitzen, H.; Fricke, H. The cobalt-60 γ-ray radiolysis of aqueous solutions of H2 + O2. Determination of Ge−aq + GH at pH 0.46–6.5. J. Phys. Chem. 1970, 74, 211–213. [Google Scholar] [CrossRef]
- O’Donnell, J.H.; Sangster, D.F. Principles of Radiation Chemistry; American Elsevier Publishing Company: New York, NY, USA, 1970; pp. 80–98. [Google Scholar]
- Bielski, B.H.J.; Cabelli, D.E.; Arudi, R.L.; Ross, A.B. Reactivity of HO2/O2− radicals in aqueous solution. J. Phys. Chem. Ref. Data 1985, 14, 1041–1100. [Google Scholar] [CrossRef]
- Pastina, B.; Isabey, J.; Hickel, B. The influence of water chemistry on the radiolysis of the primary coolant water in pressurized water reactors. J. Nucl. Mater. 1999, 264, 309–318. [Google Scholar] [CrossRef]
- Marin, T.W.; Jonah, C.D.; Bartels, D.M. Reaction of ●OH radicals with H2 in sub-critical water. Chem. Phys. Lett. 2003, 371, 144–149. [Google Scholar] [CrossRef]
- Liu, G.; Du, T.; Toth, L.; Beninger, J.; Ghandi, K. Prediction of rate constants of important reactions in water radiation chemistry in sub- and supercritical water: Equilibrium reactions. CNL Nucl. Rev. 2016, 5, 345–361. [Google Scholar] [CrossRef]
- Allen, A.O. The Radiation Chemistry of Water and Aqueous Solutions; D. Van Nostrand Co.: Princeton, NJ, USA, 1961. [Google Scholar]
- Allen, A.O. The story of the radiation chemistry of water. In Early Developments in Radiation Chemistry; Kroh, J., Ed.; Royal Society of Chemistry, Thomas Graham House: Cambridge, UK, 1989; pp. 1–6. [Google Scholar]
- Ingraham, L.L.; Meyer, D.L. Biochemistry of Dioxygen; Plenum Press: New York, NY, USA, 1985. [Google Scholar]
- Halliwell, B.; Gutteridge, J.M.C. Free Radicals in Biology and Medicine; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Jay-Gerin, J.-P.; Ferradini, C. Are there protective enzymatic pathways to regulate high local nitric oxide (●NO) concentrations in cells under stress conditions? Biochimie 2000, 82, 161–166. [Google Scholar] [CrossRef]
- Smith, D.R.; Stevens, W.H. Radiation-induced hydrolysis of acetal: Evidence for the reaction of H3O+ ions in spurs in the radiolysis of water. Nature 1963, 200, 66–67. [Google Scholar] [CrossRef]
- Anbar, M.; Thomas, J.K. Pulse radiolysis studies of aqueous sodium chloride solutions. J. Phys. Chem. 1964, 68, 3829–3835. [Google Scholar] [CrossRef]
- Schneider, N.M.; Norton, M.M.; Mendel, B.J.; Grogan, J.M.; Ross, F.M.; Bau, H.H. Electron-water interactions and implications for liquid cell electron microscopy. J. Phys. Chem. C 2014, 118, 22373–22382. [Google Scholar] [CrossRef]
- Kanike, V.; Meesungnoen, J.; Jay-Gerin, J.-P. Acid spike effect in spurs/tracks of the low/high linear energy transfer radiolysis of water: Potential implications for radiobiology. RSC Adv. 2015, 5, 43361–43370. [Google Scholar] [CrossRef]
- Islam, M.M.; Kanike, V.; Meesungnoen, J.; Lertnaisat, P.; Katsumura, Y.; Jay-Gerin, J.-P. In situ generation of ultrafast transient “acid spikes” in the 10B(n,α)7Li radiolysis of water. Chem. Phys. Lett. 2018, 693, 210–215. [Google Scholar] [CrossRef]
- Meesungnoen, J.; Jay-Gerin, J.-P.; Filali-Mouhim, A.; Mankhetkorn, S. Low-energy electron penetration range in liquid water. Radiat. Res. 2002, 158, 657–660. [Google Scholar] [CrossRef]
- Lea, D.E. Actions of Radiations on Living Cells; Cambridge University Press: Cambridge, UK, 1946; Chapter 2. [Google Scholar]
- Lea, D.E. The action of radiations on dilute aqueous solutions: The spatial distribution of H and OH. Brit. J. Radiol. 1947, 1, 59–64. [Google Scholar]
- Morrison, P. Radiation in living matter: The physical processes. In Symposium on Radiobiology. The Basic Aspects of Radiation Effects on Living Systems; Nickson, J.J., Ed.; Wiley: New York, NY, USA, 1952; pp. 1–12. [Google Scholar]
- Čerček, B.; Kongshaug, M. Hydrogen ion yields in the radiolysis of neutral aqueous solutions. J. Phys. Chem. 1969, 73, 2056–2058. [Google Scholar] [CrossRef] [PubMed]
- Barker, G.C.; Fowles, P.; Sammon, D.C.; Stringer, B. Pulse radiolytic induced transient electrical conductance in liquid solutions. Part 1. Technique and the radiolysis of water. Trans. Faraday Soc. 1970, 66, 1498–1508. [Google Scholar] [CrossRef]
- Pikaev, A.K.; Kabakchi, S.A.; Zansokhova, A.A. Yields and reactions of hydrogen ions on radiolysis of water and aqueous solutions. Faraday Discuss. Chem. Soc. 1977, 63, 112–123. [Google Scholar] [CrossRef]
- Anderson, R.F.; Vojnovic, B.; Michael, B.D. The radiation-chemical yields of H3O+ and OH− as determined by nanosecond conductimetric measurements. Radiat. Phys. Chem. 1985, 26, 301–303. [Google Scholar] [CrossRef]
- Schmidt, K.H.; Ander, S.M. Formation and recombination of H3O+ and hydroxide in irradiated water. J. Phys. Chem. 1969, 73, 2846–2852. [Google Scholar] [CrossRef]
- Byakov, V.M.; Stepanov, S.V. The mechanism for the primary biological effects of ionizing radiation. Phys. Usp. 2006, 49, 469–487. [Google Scholar] [CrossRef]
- Kanike, V. “Acid-Spike” Effect in Spurs/Tracks of the Low/High Linear Energy Transfer Radiolysis of Water: Potential Implications for Radiobiology and Nuclear Industry. Master’s Thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, 2016. Available online: https://savoirs.usherbrooke.ca/handle/11143/9711 (accessed on 31 December 2024).
- Meesat, R.; Belmouaddine, H.; Allard, J.-F.; Tanguay-Renaud, C.; Lemay, R.; Brastaviceanu, T.; Tremblay, L.; Paquette, B.; Wagner, J.R.; Jay-Gerin, J.-P.; et al. Cancer radiotherapy based on femtosecond IR laser-beam filamentation yielding ultra-high dose rates and zero entrance dose. Proc. Natl. Acad. Sci. USA 2012, 109, E2508–E2513. [Google Scholar] [CrossRef]
- Kuppermann, A. Diffusion kinetics in radiation chemistry. In Actions Chimiques et Biologiques des Radiations; Haïssinsky, M., Ed.; Masson: Paris, France, 1961; Volume 5, pp. 85–166. [Google Scholar]
- Burns, W.G.; Barker, R. Dose-rate and linear energy transfer effects in radiation chemistry. In Progress in Reaction Kinetics; Porter, G., Ed.; Pergamon: Oxford, UK, 1965; Volume 3, pp. 303–368. [Google Scholar]
- Alanazi, A.; Meesungnoen, J.; Jay-Gerin, J.-P. A computer modeling study of water radiolysis at high dose rates. Relevance to FLASH radiotherapy. Radiat. Res. 2021, 195, 149–162. [Google Scholar] [CrossRef]
- Fricke, H.; Morse, S. The chemical action of roentgen rays on dilute ferrosulphate solutions as a measure of dose. Am. J. Roentgenol. Radium Ther. 1927, 18, 430–432. [Google Scholar]
- Fricke, H.; Morse, S. The action of X-rays on ferrous sulphate solutions. Philos. Mag. 1929, 7th Ser. 7, 129–141. [Google Scholar] [CrossRef]
- Allen, A.O. Hugo Fricke and the development of radiation chemistry: A perspective view. Radiat. Res. 1962, 17, 255–261. [Google Scholar] [CrossRef]
- Fricke, H.; Hart, E.J. Chemical dosimetry. In Radiation Dosimetry, 2nd ed.; Attix, F.H., Roesch, W.C., Eds.; Academic Press: New York, NY, USA, 1966; Volume II, pp. 167–239. [Google Scholar]
- Allen, A.O. Radiation chemistry of aqueous solutions. J. Phys. Colloid Chem. 1948, 52, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Hochanadel, C.J.; Lind, S.C. Radiation chemistry. Annu. Rev. Phys. Chem. 1956, 7, 83–106. [Google Scholar] [CrossRef]
- Klassen, N.V.; Shortt, K.R.; Seuntjens, J.; Ross, C.K. Fricke dosimetry: The difference between G(Fe3+) for 60Co γ-rays and high-energy X-rays. Phys. Med. Biol. 1999, 44, 1609–1624. [Google Scholar] [CrossRef]
- McEwen, M.; El Gamal, I.; Mainegra-Hing, E.; Cojocaru, C. Determination of the Radiation Chemical Yield (G) for the Fricke Chemical Dosimetry System in Photon and Electron Beams; Report NRC-PIRS-1980; National Research Council Canada: Ottawa, ON, Canada, 2014. [Google Scholar]
- International Commission on Radiation Units and Measurements. The Dosimetry of Pulsed Radiation; ICRU Report No. 34; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1982. [Google Scholar]
- Autsavapromporn, N.; Meesungnoen, J.; Plante, I.; Jay-Gerin, J.-P. Monte Carlo simulation study of the effects of acidity and LET on the primary free-radical and molecular yields of water radiolysis–Application to the Fricke dosimeter. Can. J. Chem. 2007, 85, 214–229. [Google Scholar] [CrossRef]
- Tippayamontri, T.; Sanguanmith, S.; Meesungnoen, J.; Sunaryo, G.R.; Jay-Gerin, J.-P. Fast neutron radiolysis of the ferrous sulfate (Fricke) dosimeter: Monte Carlo simulations. Recent Res. Dev. Phys. Chem. 2009, 10, 143–211. [Google Scholar]
- International Commission on Radiation Units and Measurements. Radiation Dosimetry: X Rays and Gamma Rays with Maximum Photon Energies Between 0.6 and 50 MeV; ICRU Report No. 14; International Commission on Radiation Units and Measurements: Washington, DC, USA, 1969. [Google Scholar]
- Sehested, K.; Bjergbakke, E.; Holm, N.W.; Fricke, H. The reaction mechanism of the ferrous sulphate dosimeter at high dose rates. In Dosimetry in Agriculture, Industry, Biology and Medicine, Proceedings of a Symposium on Dosimetry Techniques Applied to Agriculture, Industry, Biology and Medicine, Vienna, Austria, 16–20 April 1972; International Atomic Energy Agency Publication STI/PUB/311; International Atomic Energy Agency: Vienna, Austria, 1973; pp. 397–404. [Google Scholar]
- Bĕgusová, M.; Pimblott, S.M. Stochastic simulation of γ radiolysis of acidic ferrous sulfate solution at elevated temperatures. Radiat. Prot. Dosim. 2002, 99, 73–76. [Google Scholar] [CrossRef]
- Sepulveda, E.; Sanguanmith, S.; Meesungnoen, J.; Jay-Gerin, J.-P. Evaluation of the radioprotective ability of cystamine for 150 keV–500 MeV proton irradiation: A Monte Carlo track chemistry simulation study. Can. J. Chem. 2019, 97, 100–111. [Google Scholar] [CrossRef]
- Penabeï, S.; Meesungnoen, J.; Jay-Gerin, J.-P. Assessment of cystamine’s radioprotective/antioxidant ability under high-dose-rate irradiation: A Monte Carlo multi-track chemistry simulation study. Antioxidants 2023, 12, 776. [Google Scholar] [CrossRef]
- Ražem, D.; Miljanić, S.; Dvornik, I. Chemical dosimetry. In Ionizing Radiation: Protection and Dosimetry; Paić, G., Ed.; CRC Press: Boca Raton, FL, USA, 1988; pp. 157–186. [Google Scholar]
- Trupin-Wasselin, V. Processus Primaires en Chimie Sous Rayonnement. Influence du Transfert d’Énergie Linéique sur la Radiolyse de l’Eau. Ph.D. Thesis, Université Paris XI, Orsay, France, 2000. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jay-Gerin, J.-P. Fundamentals of Water Radiolysis. Encyclopedia 2025, 5, 38. https://doi.org/10.3390/encyclopedia5010038
Jay-Gerin J-P. Fundamentals of Water Radiolysis. Encyclopedia. 2025; 5(1):38. https://doi.org/10.3390/encyclopedia5010038
Chicago/Turabian StyleJay-Gerin, Jean-Paul. 2025. "Fundamentals of Water Radiolysis" Encyclopedia 5, no. 1: 38. https://doi.org/10.3390/encyclopedia5010038
APA StyleJay-Gerin, J.-P. (2025). Fundamentals of Water Radiolysis. Encyclopedia, 5(1), 38. https://doi.org/10.3390/encyclopedia5010038





