Analytical Solutions of Symmetric Isotropic Spin Clusters Using Spin and Point Group Projectors
Abstract
:1. Introduction
2. Theory
3. Results
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Construction of Point Group Projectors
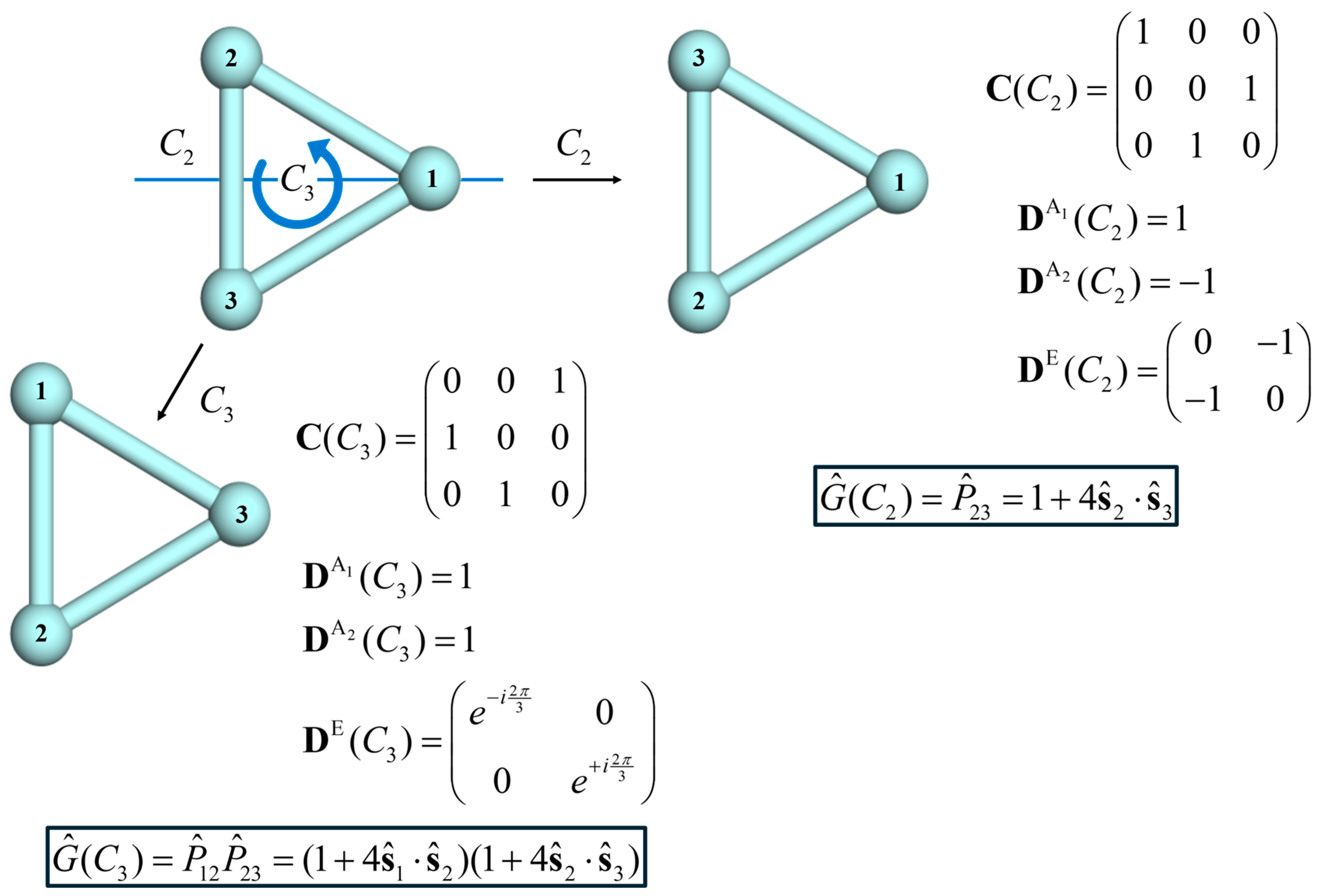
References
- Bencini, A.; Gatteschi, D. Electron Paramagnetic Resonance of Exchange Coupled Systems; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Schnack, J. Exact Diagonalization Techniques for Quantum Spin Systems. In Computational Modelling of Molecular Nanomagnets; Springer: Berlin/Heidelberg, Germany, 2023; pp. 155–177. [Google Scholar]
- Tinkham, M. Group Theory and Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Atkins, P.W.; Friedman, R. Molecular Quantum Mechanics, 5th ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Bonner, J.C.; Fisher, M.E. Linear Magnetic Chains with Anisotropic Coupling. Phys. Rev. 1964, 135, 640. [Google Scholar] [CrossRef]
- Bernu, B.; Lecheminant, P.; Lhuillier, C.; Pierre, L. Exact Spectra, Spin Susceptibilities, and Order Parameter of the Quantum Heisenberg Antiferromagnet on the Triangular Lattice. Phys. Rev. B 1994, 50, 10048. [Google Scholar] [CrossRef] [PubMed]
- Delfs, C.; Gatteschi, D.; Pardi, L.; Sessoli, R.; Wieghardt, K.; Hanke, D. Magnetic Properties of an Octanuclear Iron (III) Cation. Inorg. Chem. 1993, 32, 3099. [Google Scholar] [CrossRef]
- Waldmann, O. Symmetry and Energy Spectrum of High-Nuclearity Spin Clusters. Phys. Rev. B 2000, 61, 6138. [Google Scholar] [CrossRef]
- Raghu, C.; Rudra, I.; Sen, D.; Ramasesha, S. Properties of Low-Lying States in Some High-Nuclearity Mn, Fe, and V Clusters: Exact Studies of Heisenberg Models. Phys. Rev. B 2001, 64, 064419. [Google Scholar] [CrossRef]
- Schnalle, R.; Schnack, J. Calculating the Energy Spectra of Magnetic Molecules: Application of Real-and Spin-Space Symmetries. Int. Rev. Phys. Chem. 2010, 29, 403. [Google Scholar] [CrossRef]
- Heitmann, T.; Schnack, J. Combined Use of Translational and Spin-Rotational Invariance for Spin Systems. Phys. Rev. B 2019, 99, 134405. [Google Scholar] [CrossRef]
- Schnack, J.; Ummethum, J. Advanced Quantum Methods for the Largest Magnetic Molecules. Polyhedron 2013, 66, 28. [Google Scholar] [CrossRef]
- Kambe, K. On the Paramagnetic Susceptibilities of Some Polynuclear Complex Salts. J. Phys. Soc. Jpn. 1950, 5, 48. [Google Scholar] [CrossRef]
- Steinigeweg, R.; Schmidt, H.-J. Heisenberg-Integrable Spin Systems. Math. Phys. Anal. Geom. 2009, 12, 19. [Google Scholar] [CrossRef]
- Kouzoudis, D. Heisenberg s = 1/2 Ring Consisting of a Prime Number of Atoms. J. Magn. Magn. Mater. 1997, 173, 259. [Google Scholar] [CrossRef]
- Kouzoudis, D. Exact Analytical Partition Function and Energy Levels for a Heisenberg Ring of N = 6 Spin 1/2 Sites. J. Magn. Magn. Mater. 1998, 189, 366. [Google Scholar] [CrossRef]
- Bärwinkel, K.; Schmidt, H.-J.; Schnack, J. Structure and Relevant Dimension of the Heisenberg Model and Applications to Spin Rings. J. Magn. Magn. Mater. 2000, 212, 240. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S.; Jiménez-Hoyos, C.A. Ground States of Heisenberg Spin Clusters from Projected Hartree-Fock Theory. Phys. Rev. B 2022, 105, 35147. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S. Systematic Determination of Coupling Constants in Spin Clusters from Broken-Symmetry Mean-Field Solutions. J. Chem. Phys. 2023, 159, 154106. [Google Scholar] [CrossRef]
- Schmidt, H.-J.; Schröder, C. Thermodynamics of the Spin Square. Few-Body Syst. 2023, 64, 16. [Google Scholar] [CrossRef]
- Borrás-Almenar, J.J.; Clemente-Juan, J.M.; Coronado, E.; Tsukerblat, B.S. High-Nuclearity Magnetic Clusters: Generalized Spin Hamiltonian and Its Use for the Calculation of the Energy Levels, Bulk Magnetic Properties, and Inelastic Neutron Scattering Spectra. Inorg. Chem. 1999, 38, 6081. [Google Scholar] [CrossRef]
- Borrás-Almenar, J.J.; Clemente-Juan, J.M.; Coronado, E.; Tsukerblat, B.S. MAGPACK 1 A Package to Calculate the Energy Levels, Bulk Magnetic Properties, and Inelastic Neutron Scattering Spectra of High Nuclearity Spin Clusters. J. Comput. Chem. 2001, 22, 985. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S. Point-Group Selection Rules and Universal Momentum-Transfer Dependencies for Inelastic Neutron Scattering on Molecular Spin Clusters. Phys. Rev. B 2021, 103, 214422. [Google Scholar] [CrossRef]
- Klemm, R.A.; Efremov, D.V. Single-Ion and Exchange Anisotropy Effects and Multiferroic Behavior in High-Symmetry Tetramer Single-Molecule Magnets. Phys. Rev. B 2008, 77, 184410. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S. Theoretische Untersuchung der Spektroskopischen Eigenschaften Biologischer und Synthetischer Molekularer Spincluster. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2017. [Google Scholar]
- Ghassemi Tabrizi, S.; Arbuznikov, A.V.; Kaupp, M. Exact Mapping from Many-Spin Hamiltonians to Giant-Spin Hamiltonians. Chem. Eur. J. 2018, 24, 4689. [Google Scholar] [CrossRef] [PubMed]
- Konstantinidis, N.P. Antiferromagnetic Heisenberg Model on Clusters with Icosahedral Symmetry. Phys. Rev. B 2005, 72, 64453. [Google Scholar] [CrossRef]
- Konstantinidis, N.P. Unconventional Magnetic Properties of the Icosahedral Symmetry Antiferromagnetic Heisenberg Model. Phys. Rev. B 2007, 76, 104434. [Google Scholar] [CrossRef]
- Sahoo, S.; Rajamani, R.; Ramasesha, S.; Sen, D. Fully Symmetrized Valence-Bond Based Technique for Solving Exchange Hamiltonians of Molecular Magnets. Phys. Rev. B 2008, 78, 054408. [Google Scholar] [CrossRef]
- Dobrautz, W.; Katukuri, V.M.; Bogdanov, N.A.; Kats, D.; Li Manni, G.; Alavi, A. Combined Unitary and Symmetric Group Approach Applied to Low-Dimensional Heisenberg Spin Systems. Phys. Rev. B 2022, 105, 195123. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Quantum Theory of Many-Particle Systems. III. Extension of the Hartree-Fock Scheme to Include Degenerate Systems and Correlation Effects. Phys. Rev. 1955, 97, 1509. [Google Scholar] [CrossRef]
- Schumann, R. Thermodynamics of a 4-Site Hubbard Model by Analytical Diagonalization. Ann. Phys. 2002, 11, 49. [Google Scholar] [CrossRef]
- Brumfield, A.; Haraldsen, J.T. Thermodynamics and Magnetic Excitations in Quantum Spin Trimers: Applications for the Understanding of Molecular Magnets. Crystals 2019, 9, 93. [Google Scholar] [CrossRef]
- Griffith, J.S. On the General Theory of Magnetic Susceptibilities of Polynuclear Transition-Metal Compounds. In Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 1972; pp. 87–126. [Google Scholar]
- Dyszel, P.; Haraldsen, J.T. Thermodynamics of General Heisenberg Spin Tetramers Composed of Coupled Quantum Dimers. Magnetochemistry 2021, 7, 29. [Google Scholar] [CrossRef]
- Boča, R.; Rajnák, C.; Titiš, J. Spin Symmetry in Polynuclear Exchange-Coupled Clusters. Magnetochemistry 2023, 9, 226. [Google Scholar] [CrossRef]
- Noce, C.; Cuoco, M. Exact-Diagonalization Method for Correlated-Electron Models. Phys. Rev. B 1996, 54, 13047. [Google Scholar] [CrossRef] [PubMed]
- Ghassemi Tabrizi, S.; Arbuznikov, A.V.; Kaupp, M. Understanding Thermodynamic and Spectroscopic Properties of Tetragonal Mn12 Single-Molecule Magnets from Combined Density Functional Theory/Spin-Hamiltonian Calculations. J. Phys. Chem. A 2016, 120, 6864. [Google Scholar] [CrossRef] [PubMed]
- Ghassemi Tabrizi, S. Symmetry-Induced Universal Momentum-Transfer Dependencies for Inelastic Neutron Scattering on Anisotropic Spin Clusters. Phys. Rev. B 2021, 104, 14416. [Google Scholar] [CrossRef]
- Waldmann, O. Q Dependence of the Inelastic Neutron Scattering Cross Section for Molecular Spin Clusters with High Molecular Symmetry. Phys. Rev. B 2003, 68, 174406. [Google Scholar] [CrossRef]
- Katzer, G. Character Tables for Point Groups Used in Chemistry. Available online: http://gernot-katzers-spice-pages.com/character_tables/ (accessed on 30 April 2024).
- Zee, A. Group Theory in a Nutshell for Physicists; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Altmann, S.L.; Herzig, P. Point-Group Theory Tables; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Sakurai, J.J. Modern Quantum Mechanics, 2nd ed.; Tuan, S.F., Ed.; Addison Wesley: Reading, MA, USA, 1993. [Google Scholar]
- Brown, H.A. A Simple Derivation of the Spin-Exchange Operator. Am. J. Phys. 1972, 40, 1696. [Google Scholar] [CrossRef]
| s | E | ||
|---|---|---|---|
| 1/2 | 0 1 0 | 0 0 0 | 1 0 0 |
| 1 | 0 1 0 1 | 1 0 0 0 | 0 1 1 0 |
| 3/2 | 0 1 1 0 1 | 0 1 0 0 0 | 1 1 1 1 0 |
| 2 | 1 0 1 1 1 0 1 | 0 1 0 1 0 0 0 | 0 1 2 1 1 1 0 |
| 5/2 | 0 1 1 1 1 1 0 1 | 0 1 1 0 1 0 0 0 | 1 1 2 2 1 1 1 0 |
| 3 | 0 1 0 2 1 1 1 1 0 1 | 1 0 1 1 1 0 1 0 0 0 | 0 1 2 2 2 2 1 1 1 0 |
| 7/2 | 0 1 1 1 2 1 1 1 1 0 1 | 0 1 1 1 1 1 0 1 0 0 0 | 1 1 2 3 2 2 2 1 1 1 0 |
| 4 | 1 0 1 1 2 1 2 1 1 1 1 0 1 | 0 1 0 2 1 1 1 1 0 1 0 0 0 | 0 1 2 2 3 3 2 2 2 1 1 1 0 |
| 9/2 | 0 1 1 1 2 2 1 2 1 1 1 1 0 1 | 0 1 1 1 2 1 1 1 1 0 1 0 0 0 | 1 1 2 3 3 3 3 2 2 2 1 1 1 0 |
| 5 | 0 1 0 2 1 2 2 2 1 2 1 1 1 1 0 1 | 1 0 1 1 2 1 2 1 1 1 1 0 1 0 0 0 | 0 1 2 2 3 4 3 3 3 2 2 2 1 1 1 0 |
| 11/2 | 0 1 1 1 2 2 2 2 2 1 2 1 1 1 1 0 1 | 0 1 1 1 2 2 1 2 1 1 1 1 0 1 0 0 0 | 1 1 2 3 3 4 4 3 3 3 2 2 2 1 1 1 0 |
| 6 | 1 0 1 1 2 1 3 2 2 2 2 1 2 1 1 1 1 0 1 | 0 1 0 2 1 2 2 2 1 2 1 1 1 1 0 1 0 0 0 | 0 1 2 2 3 4 4 4 4 3 3 3 2 2 2 1 1 1 0 |
| 13/2 | 0 1 1 1 2 2 2 3 2 2 2 2 1 2 1 1 1 1 0 1 | 0 1 1 1 2 2 2 2 2 1 2 1 1 1 1 0 1 0 0 0 | 1 1 2 3 3 4 5 4 4 4 3 3 3 2 2 2 1 1 1 0 |
| # | Energy | Ground State | |
|---|---|---|---|
| (0, A1) | 1 | ||
| (1, A2) | 2 | ||
| (1, E) | 3 | ||
| (2, A1) | 4 | ||
| (2, E) | 5 6 | ||
| (3, A1) | 7 | ||
| (3, A2) | 8 | ||
| (3, E) | 9 | ||
| (4, A1) | 10 | ||
| (4, E) | 11 | ||
| (5, E) | 12 | ||
| (6, A1) | 13 |
| # | Energy | Ground State | |
|---|---|---|---|
| (1/2, E) | 1 | ||
| (3/2, A1) | 2 | ||
| (3/2, A2) | 3 | ||
| (3/2, E) | 4 | ||
| (5/2, A1) | 5 | ||
| (5/2, A2) | 6 | ||
| (5/2, E) | 7 8 | ||
| (7/2, A1) | 9 | ||
| (7/2, E) | 10 11 | ||
| (9/2, A1) | 12 | ||
| (9/2, A2) | 13 | ||
| (9/2, E) | 14 | ||
| (11/2, A1) | 15 | ||
| (11/2, E) | 16 | ||
| (13/2, E) | 17 | ||
| (15/2, A1) | 18 |
| s | E | ||||
|---|---|---|---|---|---|
| 1 | 2 0 2 0 1 | 0 1 0 0 0 | 1 0 1 0 0 | 0 1 1 1 0 | 0 2 1 1 0 |
| 3/2 | 2 0 3 1 2 0 1 | 0 1 1 1 0 0 0 | 2 0 2 0 1 0 0 | 0 2 1 2 1 1 0 | 0 3 2 3 1 1 0 |
| 2 | 3 0 4 1 4 1 2 0 1 | 0 2 1 2 1 1 0 0 0 | 2 0 3 1 2 0 1 0 0 | 0 2 2 3 2 2 1 1 0 | 0 4 3 5 3 3 1 1 0 |
| 5/2 | 3 0 5 2 5 2 4 1 2 0 1 | 0 2 2 3 2 2 1 1 0 0 0 | 3 0 4 1 4 1 2 0 1 0 0 | 0 3 2 4 3 4 2 2 1 1 0 | 0 5 4 7 5 6 3 3 1 1 0 |
| # | Energy | Ground State | Ground State | |
|---|---|---|---|---|
| (0, A1) | 1 2 | |||
| (0, B1) | 3 | |||
| (1, A2) | 4 | |||
| (1, B2) | 5 | |||
| (1, E) | 6 7 | |||
| (2, A1) | 8 9 | |||
| (2, B1) | 10 | |||
| (2, B2) | 11 | |||
| (2, E) | 12 | |||
| (3, B2) | 13 | |||
| (3, E) | 14 | |||
| (4, A1) | 15 |
| s | E | ||||
|---|---|---|---|---|---|
| 1/2 | 0 0 1 | 0 0 0 | 1 0 0 | 0 0 0 | 0 1 0 |
| 1 | 1 0 1 0 1 | 0 0 0 0 0 | 1 0 1 0 0 | 0 1 0 0 0 | 0 1 1 1 0 |
| 3/2 | 1 0 1 1 1 0 1 | 1 0 0 0 0 0 0 | 1 0 2 0 1 0 0 | 0 1 1 1 0 0 0 | 0 2 1 2 1 1 0 |
| 2 | 1 0 2 0 2 1 1 0 1 | 0 0 1 0 0 0 0 0 0 | 2 0 2 1 2 0 1 0 0 | 0 2 1 2 1 1 0 0 0 | 0 2 2 3 2 2 1 1 0 |
| 5/2 | 1 0 2 1 2 1 2 1 1 0 1 | 1 0 1 0 1 0 0 0 0 0 0 | 2 0 3 1 3 1 2 0 1 0 0 | 0 2 2 3 2 2 1 1 0 0 0 | 0 3 2 4 3 4 2 2 1 1 0 |
| 3 | 2 0 2 1 3 1 3 1 2 1 1 0 1 | 1 0 1 1 1 0 1 0 0 0 0 0 0 | 2 0 4 1 4 2 3 1 2 0 1 0 0 | 0 3 2 4 3 4 2 2 1 1 0 0 0 | 0 3 3 5 4 5 4 4 2 2 1 1 0 |
| # | Energy | |
|---|---|---|
| (0, A1) | 1 | |
| (0, A2) | 2 | |
| (0, E) | 3 | |
| (1, T1) | 4 | |
| (1, T2) | 5 6 | |
| (2, A1) | 7 | |
| (2, E) | 8 9 | |
| (2, T1) | 10 | |
| (2, T2) | 11 | |
| (3, A1) | 12 | |
| (3, T1) | 13 | |
| (3, T2) | 14 15 | |
| (4, A1) | 16 | |
| (4, E) | 17 | |
| (4, T2) | 18 | |
| (5, T2) | 19 | |
| (6, A1) | 20 |
| s | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1/2 | 0 1 0 1 | 1 0 0 0 | 0 0 0 0 | 1 0 0 0 | 0 1 1 0 | 0 0 0 0 | 0 0 0 0 | 0 1 0 0 | 1 0 1 0 | 0 1 0 0 |
| 1 | 3 0 3 1 2 0 1 | 0 2 0 2 0 0 0 | 1 0 0 0 0 0 0 | 0 1 0 1 0 0 0 | 1 2 4 2 2 1 0 | 0 1 1 0 0 0 0 | 0 2 1 1 0 0 0 | 2 1 3 1 1 0 0 | 0 4 2 3 1 1 0 | 1 2 3 2 1 0 0 |
| 3/2 | 0 5 2 7 3 4 2 2 0 1 | 3 1 4 3 4 1 2 0 0 0 | 0 2 0 2 0 0 0 0 0 0 | 3 0 3 1 2 0 1 0 0 0 | 1 6 8 8 7 6 3 2 1 0 | 1 2 4 2 2 1 0 0 0 0 | 2 4 6 5 4 2 1 0 0 0 | 0 7 5 8 4 4 1 1 0 0 | 5 4 11 7 9 4 4 1 1 0 | 1 7 7 9 6 5 2 1 0 0 |
| 3 0 2 0 1 | 0 0 0 0 0 | 1 0 0 0 0 | 0 2 0 1 0 | 2 0 2 0 0 | 0 1 1 0 0 | 0 2 0 0 0 | 1 2 2 1 0 | 0 3 1 1 0 | 1 1 1 0 0 |
| # | Energy | |
|---|---|---|
| (0, A1g) | 1 2 3 | |
| (0, A1u) | 4 | 0 |
| (0, Eg) | 5 6 | |
| (0, T2g) | 7 | −1 |
| (0, T2u) | 8 | −2 |
| (1, A2u) | 9 10 | −4 0 |
| (1, Eu) | 11 | −1 |
| (1, T1g) | 12 13 | |
| (1, T2g) | 14 15 | |
| (1, T1u) | 16 17 18 | |
| (1, T2u) | 19 | 0 |
| (2, A1g) | 20 21 | |
| (2, Eg) | 22 23 | |
| (2, Eu) | 24 | 0 |
| (2, T2g) | 25 26 | |
| (2, T1u) | 27 | −1 |
| (2, T2u) | 28 | 1 |
| (3, A2u) | 29 | 0 |
| (3, T2g) | 30 | 1 |
| (3, T1u) | 31 | 2 |
| (4, A1g) | 32 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghassemi Tabrizi, S.; Kühne, T.D. Analytical Solutions of Symmetric Isotropic Spin Clusters Using Spin and Point Group Projectors. Magnetism 2024, 4, 183-199. https://doi.org/10.3390/magnetism4030013
Ghassemi Tabrizi S, Kühne TD. Analytical Solutions of Symmetric Isotropic Spin Clusters Using Spin and Point Group Projectors. Magnetism. 2024; 4(3):183-199. https://doi.org/10.3390/magnetism4030013
Chicago/Turabian StyleGhassemi Tabrizi, Shadan, and Thomas D. Kühne. 2024. "Analytical Solutions of Symmetric Isotropic Spin Clusters Using Spin and Point Group Projectors" Magnetism 4, no. 3: 183-199. https://doi.org/10.3390/magnetism4030013
APA StyleGhassemi Tabrizi, S., & Kühne, T. D. (2024). Analytical Solutions of Symmetric Isotropic Spin Clusters Using Spin and Point Group Projectors. Magnetism, 4(3), 183-199. https://doi.org/10.3390/magnetism4030013




