Relationship between Inverse Langevin Function and r0-r1-Lambert W Function
Abstract
1. Introduction
2. Definitions
2.1. Link: Inverse Langevin Function and Generalized Lambert W Function
2.2. Published Approximations
2.2.1. Relative Error Bound
3. Relationship between Inverse Langevin and r0-r1-Lambert W Function
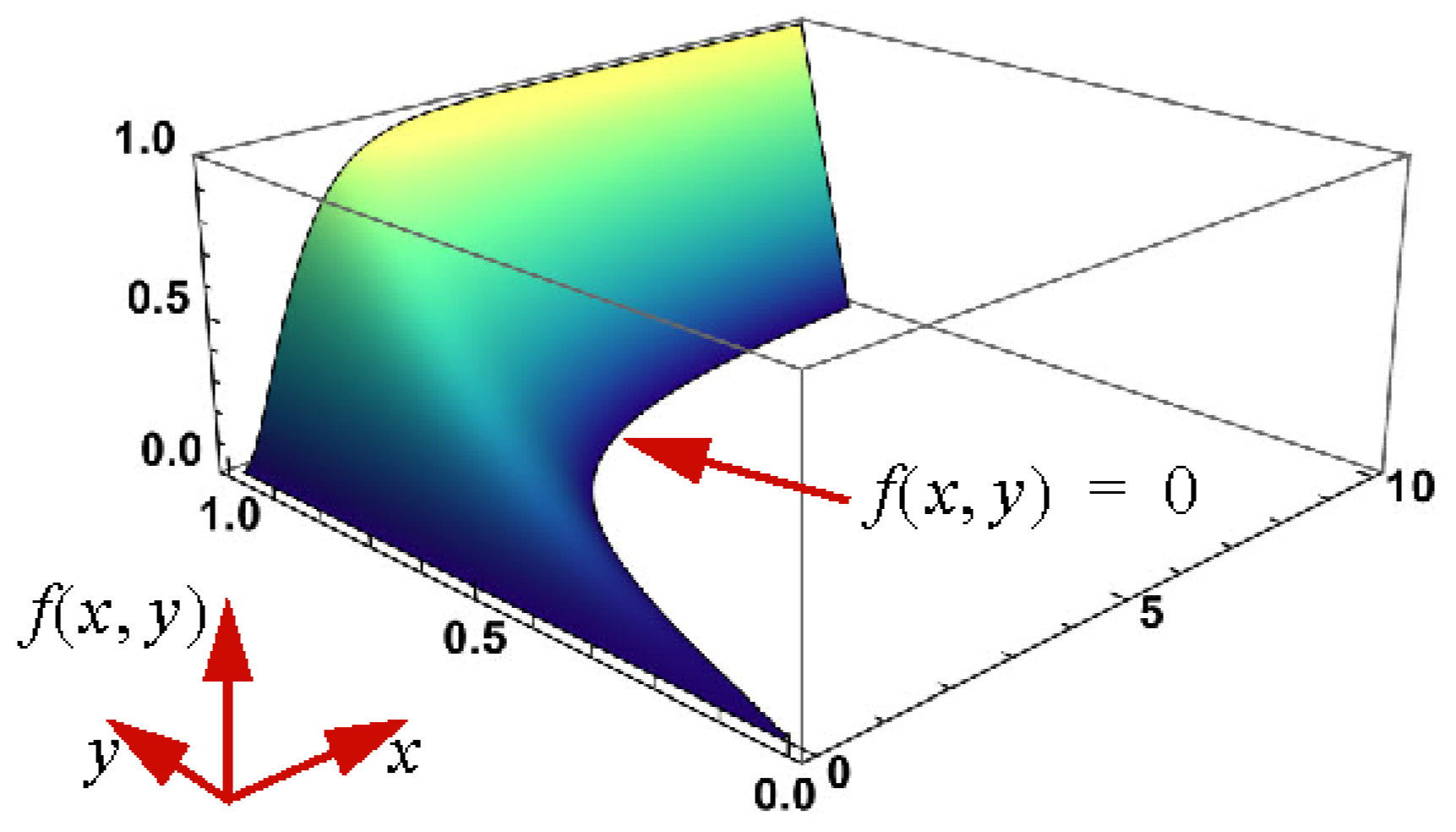
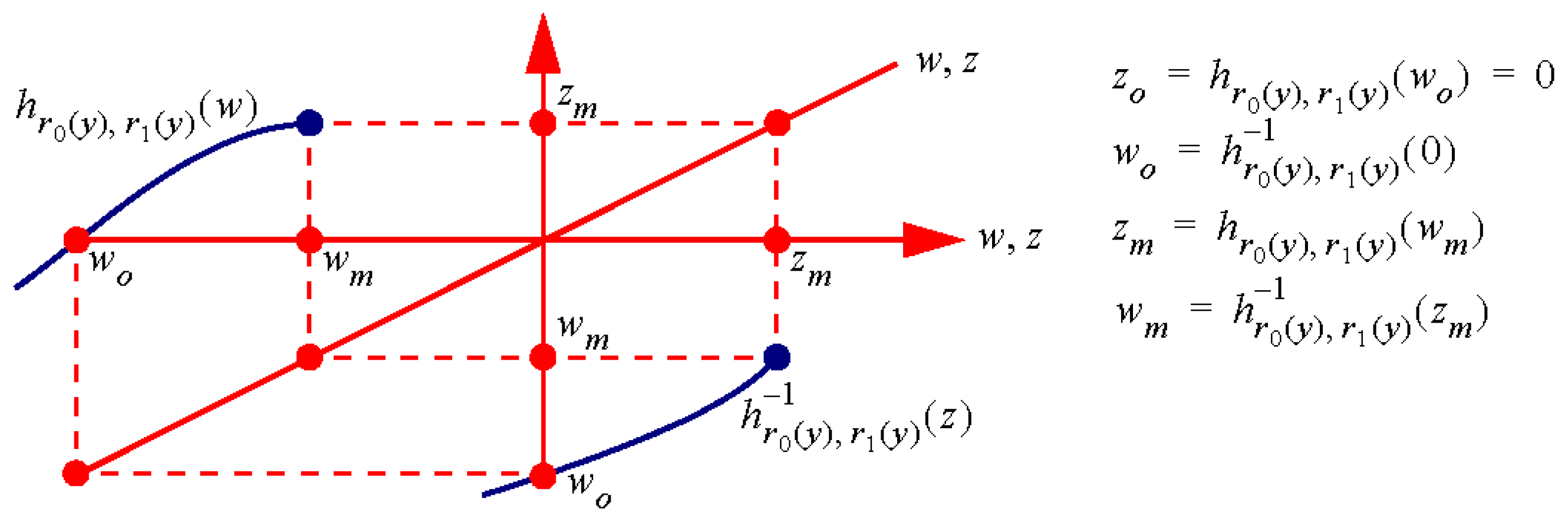
3.1. Determining Root of h
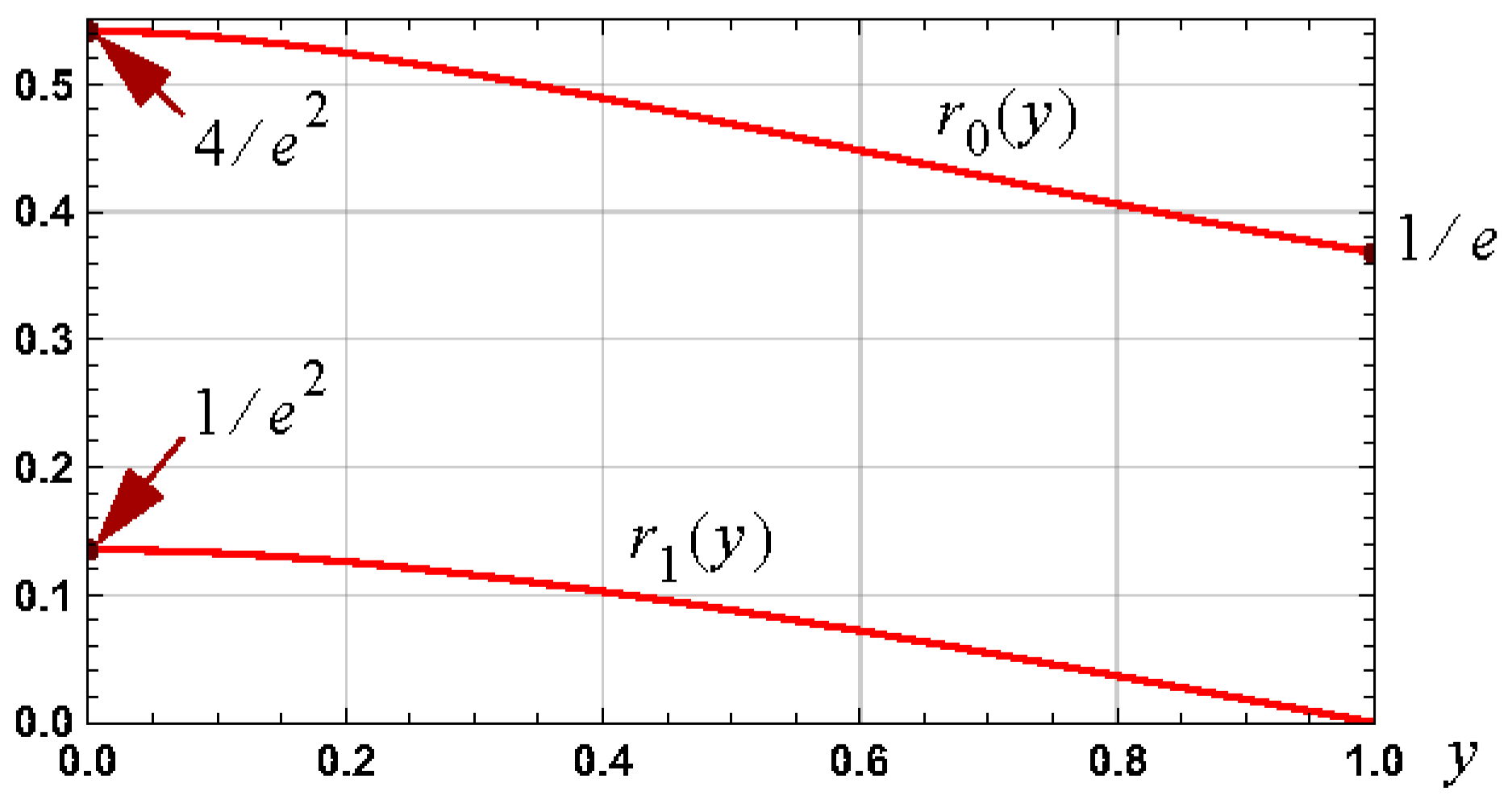
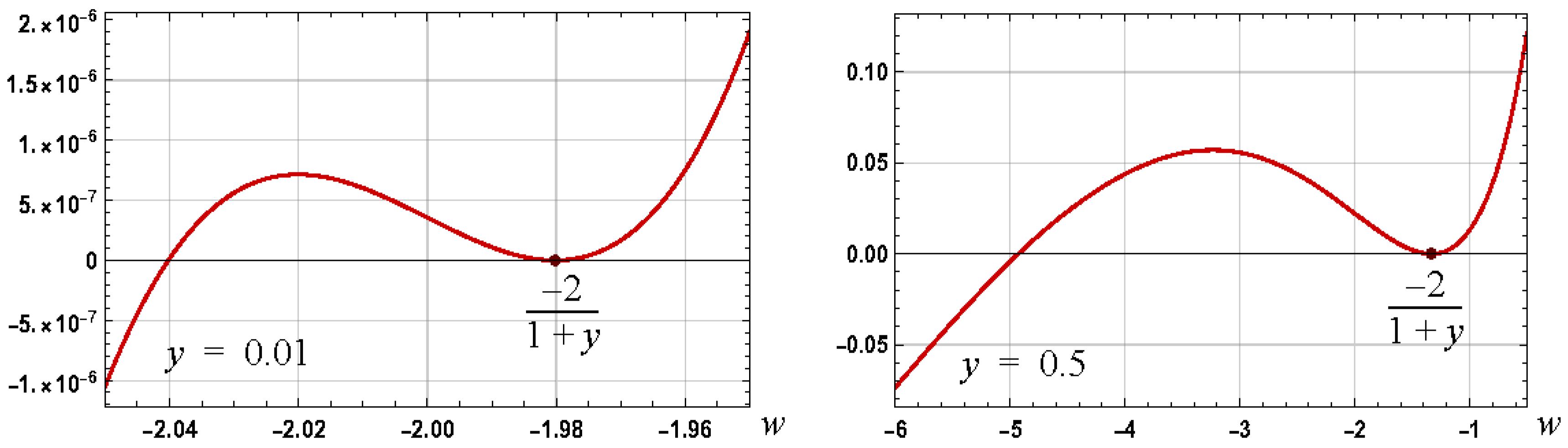
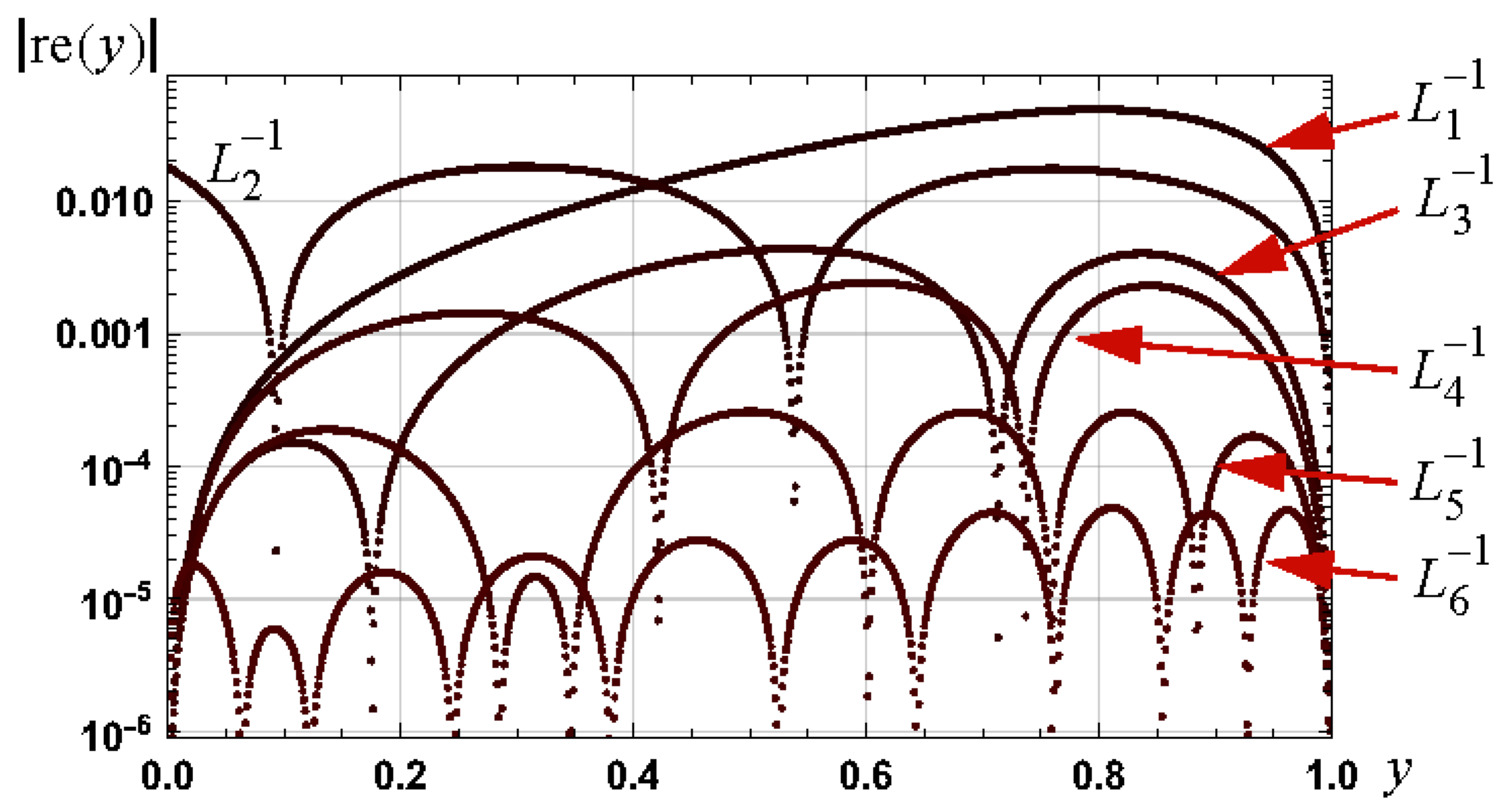
3.1.1. Graphs
3.1.2. Required Branch for Root of h
4. Approximations for Inverse Langevin Function
4.1. Associated Langevin Approximations
Notes
5. Schröder Based Higher Order Approximations
5.1. First, Second and Third Order Approximations for h−1(0)
Results
5.2. First Order Approximations: Explicit Cases
5.2.1. Case 1
5.2.2. Case 2
5.2.3. Case 3
5.2.4. Case 4
5.3. Second Order Approximations
5.4. Direct First Order Schröder Approximation to Inverse Langevin Function
Comparison
6. Applications
6.1. Limit Approximations
6.2. Integral Results
6.3. Roots of
Linear System Impulse Response
7. Summary of Results and Conclusion
7.1. Summary of Results
| Approximation | Definition | Relative Error Bound | Relative Error Bound: 1st Order—(42) | Relative Error Bound: 2nd Order—(43) | Relative Error Bound: 3rd Order—(44) |
|---|---|---|---|---|---|
| 4.07 |
| Approx. | Definition | Relative Error Bound | Relative Error Bound: First Order | Relative Error Bound: Second Order | Relative Error Bound: Third Order |
|---|---|---|---|---|---|
7.2. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Restricted Domain Approximations for
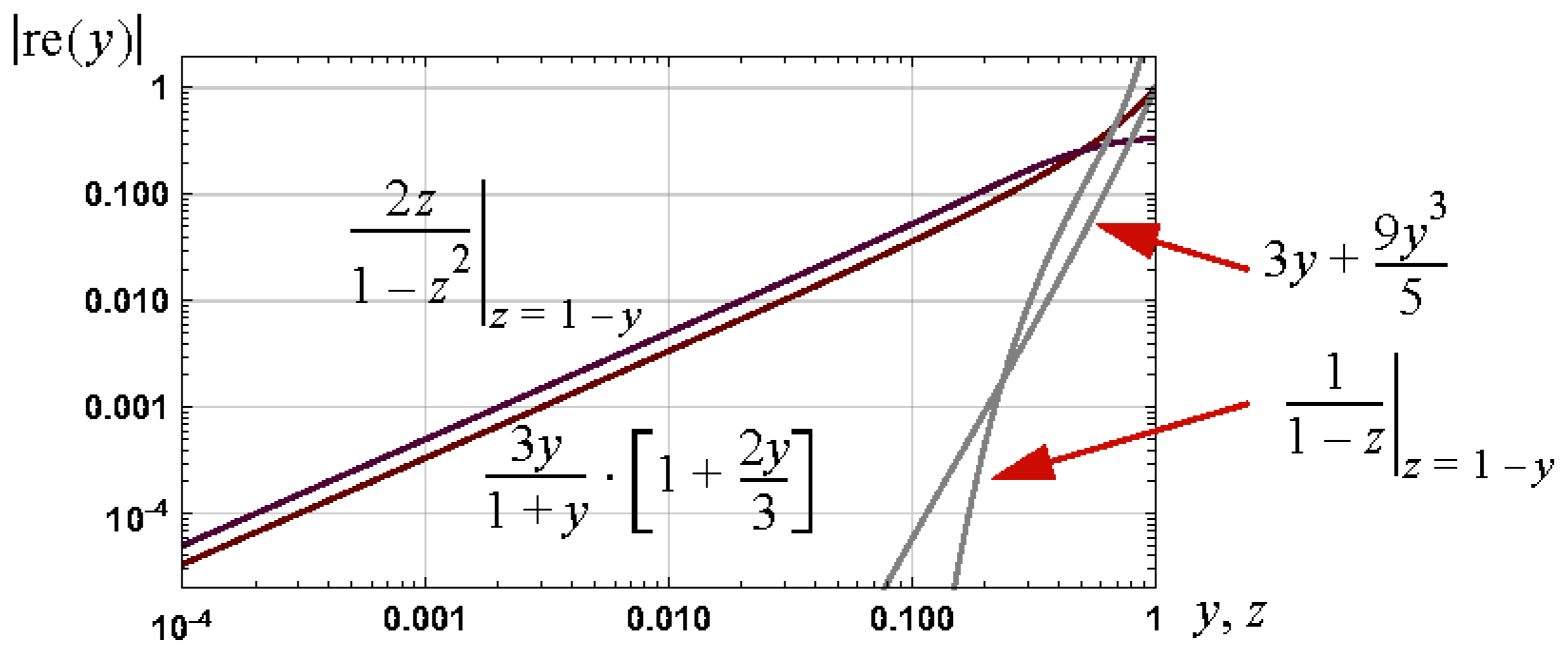
Appendix B.1. Case 1: 0 < y << 1
Appendix B.2. Case 2: y -> 1
Appendix C. Proof for First, Second, and Third Order Schröder Approximations
Appendix C.1. Second Order
Appendix C.2. Third Order
References
- Langevin, P. Sur la théorie du magnétisme. J. Phys. Theor. Appl. 1905, 4, 678–693. [Google Scholar] [CrossRef]
- Fiasconaro, A.; Falo, F. Analytical results of the extensible freely jointed chain model. Phys. A Stat. Mech.Appl. 2019, 532, 121929. [Google Scholar] [CrossRef]
- Iliafar, S.; Vezenov, D.; Jagota, A. Stretching of a Freely Jointed Chain in Two-Dimensions. arXiv 2013, arXiv:1305.5951. [Google Scholar]
- Itskov, M.; Dargazany, R.; Hornes, K. Taylor expansion of the inverse function with application to the Langevin function. Math. Mech. Solids 2012, 17, 693–701. [Google Scholar] [CrossRef]
- Nguessong, A.N.; Beda, T.; Peyraut, F. A new based error approach to approximate the inverse Langevin function. Rheol. Acta 2014, 53, 585–591. [Google Scholar] [CrossRef]
- Darabi, E.; Itskov, M. A simple and accurate approximation of the inverse Langevin function. Rheol. Acta 2015, 54, 455–459. [Google Scholar] [CrossRef]
- Jedynak, R. Approximation of the inverse Langevin function revisited. Rheol. Acta 2015, 54, 29–39. [Google Scholar] [CrossRef]
- Kröger, M. Simple, admissible, and accurate approximants of the inverse Langevin and Brillouin functions, relevant for strong polymer deformations and flows. J. Non-Newton. Fluid Mech. 2015, 223, 77–87. [Google Scholar] [CrossRef]
- Marchi, B.C.; Arruda, E.M. An error-minimizing approach to inverse Langevin approximations. Rheol. Acta 2015, 54, 887–902. [Google Scholar] [CrossRef]
- Rickaby, S.R.; Scott, N.H. A comparison of limited-stretch models of rubber elasticity. Int. J. Non-Linear Mech. 2015, 68, 71–86. [Google Scholar] [CrossRef]
- Petrosyan, R. Improved approximations for some polymer extension models. Rheol. Acta 2017, 56, 21–26. [Google Scholar] [CrossRef]
- Jedynak, R. A comprehensive study of the mathematical methods used to approximate the inverse Langevin function. Math. Mech. Solids 2018, 24, 1992–2016. [Google Scholar] [CrossRef]
- Marchi, B.C.; Arruda, E.M. Generalized error-minimizing, rational inverse Langevin approximations. Math. Mech. Solids 2019, 24, 1630–1647. [Google Scholar] [CrossRef]
- Howard, R.M. Analytical approximations for the inverse Langevin function via linearization, error approximation and iteration. Rheol. Acta 2020, 59, 521–544. [Google Scholar] [CrossRef]
- Mező, I.; Keady, G. Some physical applications of generalized Lambert functions. Eur. J. Phys. 2016, 37, 065802. [Google Scholar] [CrossRef]
- Mező, I. On the structure of the solution set of a generalized Euler–Lambert equation. J. Math. Anal. Appl. 2017, 455, 538–553. [Google Scholar] [CrossRef]
- Mező, I.; Baricz, Á. On the generalization of the Lambert W function. Trans. Am. Math. Soc. 2017, 369, 7917–7934. [Google Scholar] [CrossRef]
- Jamilla, C.; Mendoza, R.; Mező, I. Solutions of neutral delay differential equations using a generalized Lambert W function. Appl. Math. Comput. 2020, 382, 125334. [Google Scholar] [CrossRef]
- Petković, M.S.; Petković, L.D.; Herceg, Ð. On Schröder’s families of root-finding methods. J. Comput. Appl. Math. 2010, 233, 1755–1762. [Google Scholar] [CrossRef][Green Version]
- Dubeau, F. Polynomial and rational approximations and the link between Schröder’s processes of the first and second kind. Abstr. Appl. Anal. 2014, 2014, 719846. [Google Scholar] [CrossRef]
- Howard, R.M. Schröder based inverse function approximation. Axioms 2023, 12, 1042. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Howard, R.M. Analytical Approximations for the Principal Branch of the Lambert W Function. Eur. J. Math. Anal. 2022, 2, 14. [Google Scholar] [CrossRef]
- Lóczi, L. Guaranteed-and high-precision evaluation of the Lambert W function. Appl. Math. Comput. 2022, 433, 127406. [Google Scholar]
- Schröder, E. Über unendlich viele Algorithmen zur Auflösung der Gleichungen. Math. Ann. 1870, 2, 317–365. [Google Scholar] [CrossRef]
- Berinde, V.; Takens, F. Iterative Approximation of Fixed Points; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Polynomiography based on the nonstandard Newton-like root finding methods. Abstr. Appl. Anal. 2015, 2015, 797594. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Howard, R.M. Relationship between Inverse Langevin Function and r0-r1-Lambert W Function. AppliedMath 2024, 4, 743-762. https://doi.org/10.3390/appliedmath4020040
Howard RM. Relationship between Inverse Langevin Function and r0-r1-Lambert W Function. AppliedMath. 2024; 4(2):743-762. https://doi.org/10.3390/appliedmath4020040
Chicago/Turabian StyleHoward, Roy M. 2024. "Relationship between Inverse Langevin Function and r0-r1-Lambert W Function" AppliedMath 4, no. 2: 743-762. https://doi.org/10.3390/appliedmath4020040
APA StyleHoward, R. M. (2024). Relationship between Inverse Langevin Function and r0-r1-Lambert W Function. AppliedMath, 4(2), 743-762. https://doi.org/10.3390/appliedmath4020040






