Development of Deployable Reflector Antenna for the SAR-Satellite: Part 1. Design and Analysis of the Main Reflector Using Honeycomb Sandwich Composite Structure
Abstract
:1. Introduction
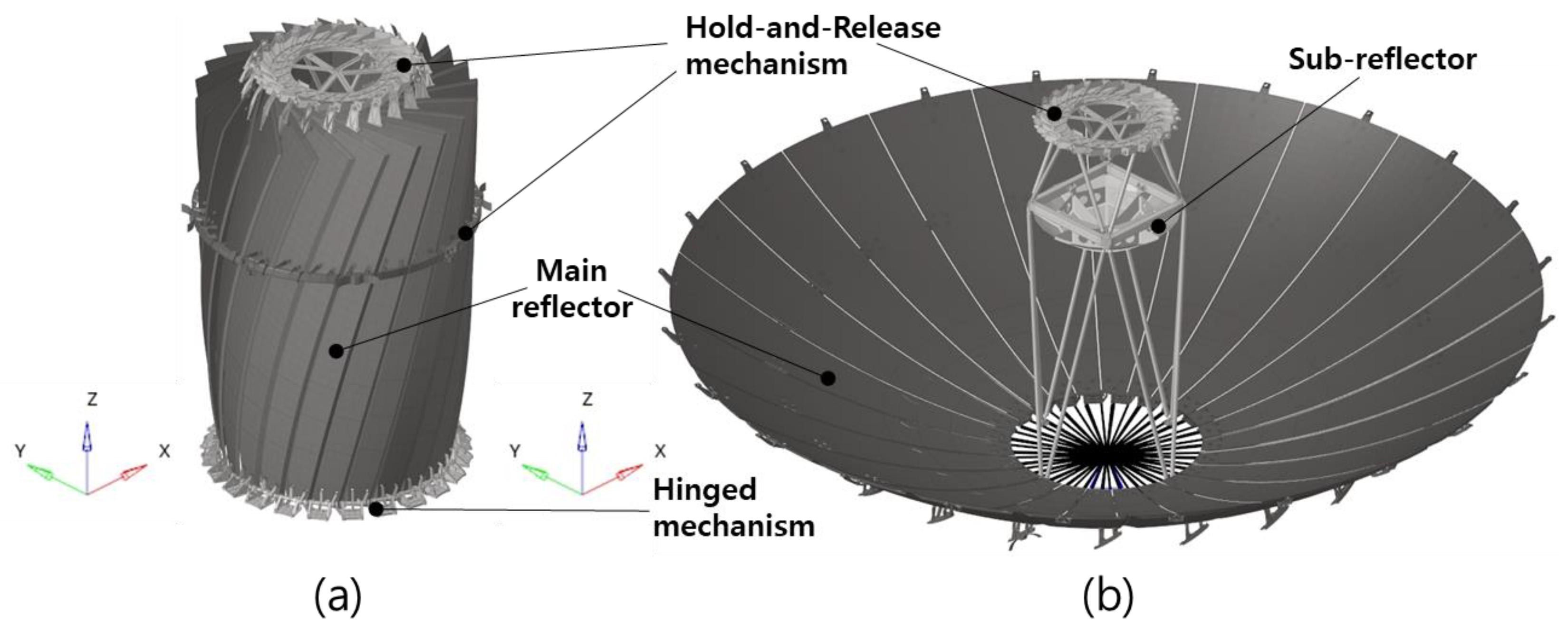
2. Design Approach of Deployable Reflector Antenna
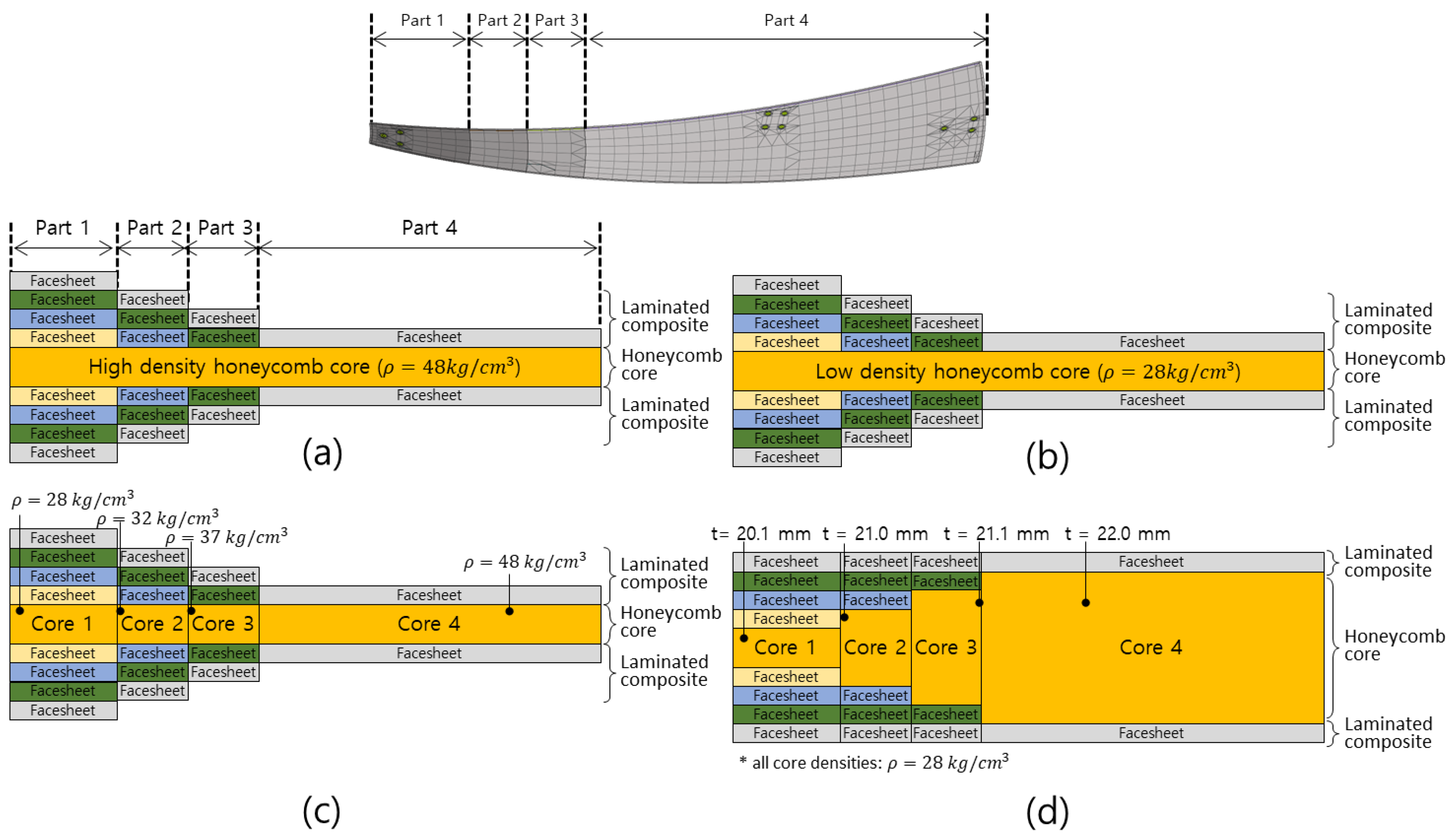
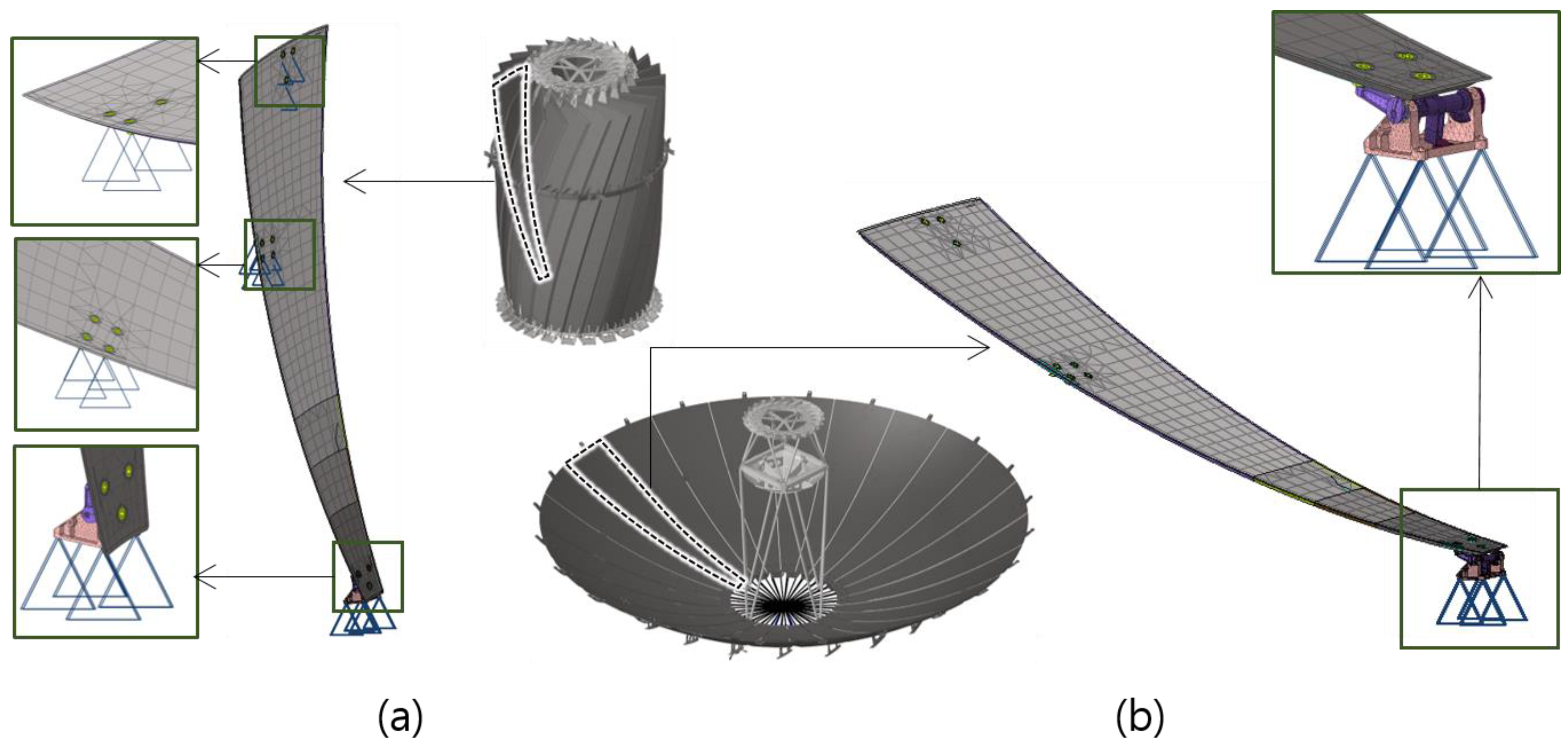
3. Design of the Unit Structure of the Main Reflector in the Deployable Reflector Antenna
3.1. Performance Evaluation According to Stacking Sequence of Facesheet
3.2. Performance Evaluation According to Honeycomb Core of Reflector Antenna
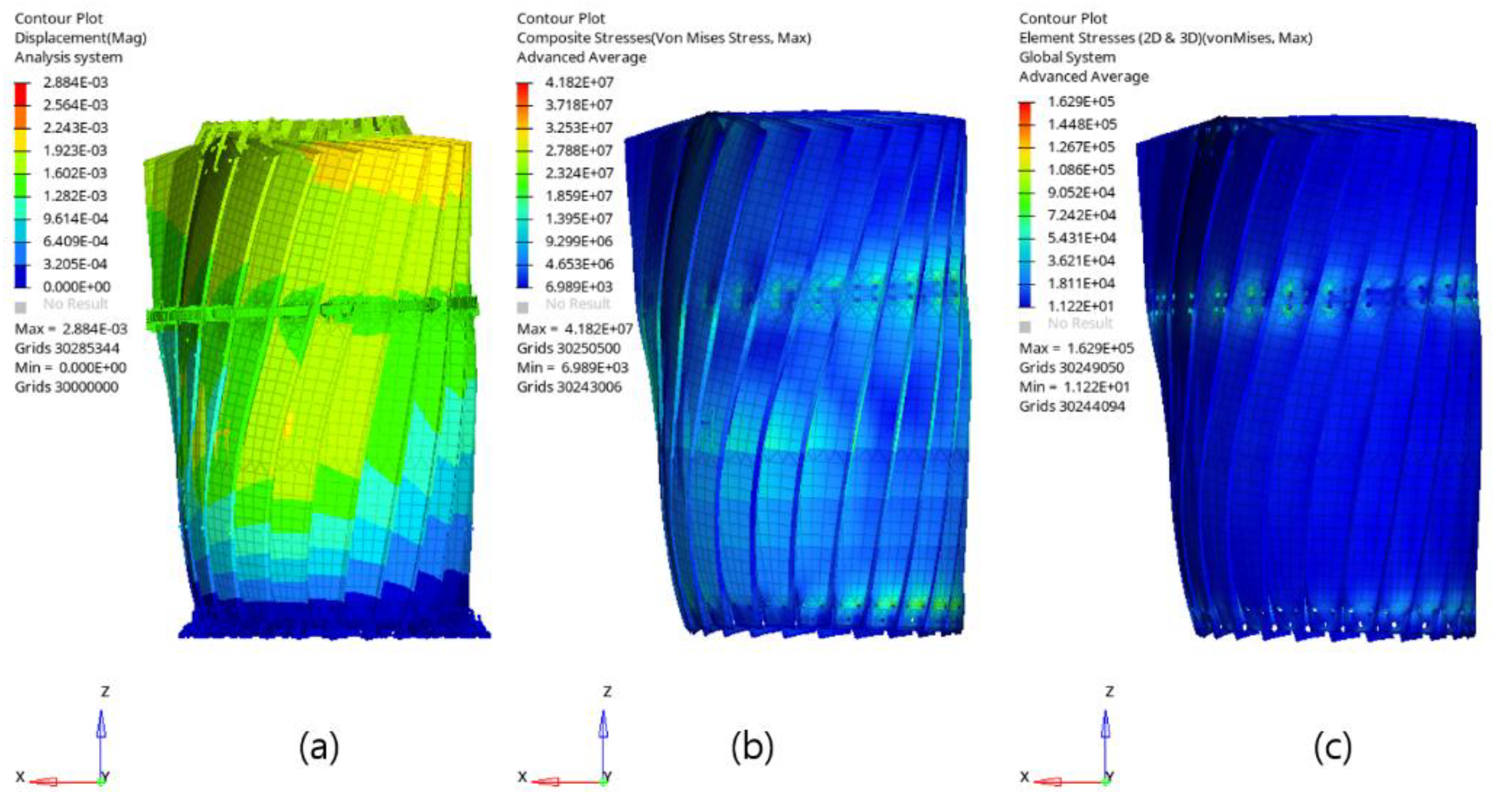
4. Structural Analysis of Unit Structure of Deployable Reflector Antenna
5. Structural Analysis of the Full Model of Deployable Reflector Antenna
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paulis, F.; Giuliomaria, D.D.; Fina, A.; Amici, M.; Mannocchi, G.; Carlofelice, A.D.; Fiaschetti, A.; Tognolatti, P.; Orlandi, A. Highly Integrated Wideband Transmit/Receive Module for X-Band SAR Applications. Appl. Sci. 2023, 13, 801. [Google Scholar] [CrossRef]
- Nasirzadehdizaji, R.; Sanli, F.B.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity Analysis of Multi-Temporal Sentinel-1 SAR Parameters to Crop Height and Canopy Coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef]
- Xia, Z.; Jin, S.; Yue, F.; Yang, J.; Zhang, Q.; Zhao, Z.; Zhang, C.; Gao, W.; Zhang, T.; Zhang, Y.; et al. A Novel Space-Borne High-Resolution SAR System with the Non-Uniform Hybrid Sampling Technology for Space Targets Imaging. Appl. Sci. 2022, 12, 4848. [Google Scholar] [CrossRef]
- Zhao, H.; Hao, Z.; Liu, W.; Ding, J.; Sun, Y.; Zhang, Q.; Liu, Y. The shock environment prediction of satellite in the process of satellite-rocket separation. Acta Astronaut. 2019, 159, 112–122. [Google Scholar] [CrossRef]
- Rizzo, F.; Franco, A.; Bonati, A.; Maddaloni, G.; Caterino, N.; Occhiuzzi, A. Predictive analyses for aerodynamic investigation of curtain walls. Structures 2021, 29, 1059–1077. [Google Scholar] [CrossRef]
- Dennison, J.R.; Hartley, K.; Phillipps, L.M.; Dekany, J.; Dyer, J.S.; Johnson, R.H. Small Satellite Space Environments Effects Test Facility. In Proceedings of the 28th Annual AIAA/USU Conference on Small Satellite, Logan, UT, USA, 4–7 August 2014. [Google Scholar]
- Cho, M.; Masui, H.; Hatamura, T.; Date, K.; Horii, S.; Obata, S. Overview of the Nano-satellite Environmental Test Standardization: Test Campaign and Standard Draft, SSC12-VII-10. In Proceedings of the 26th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 13–16 August 2012. [Google Scholar]
- Koo, K.-R.; Kim, H.-G.; Kim, D.-G.; Kwon, S.-C.; Oh, H.-U. Lightweight Design for Active Small SAR S-STEP Satellite Using Multilayered High-Damping Carbon Fiber-Reinforced Plastic Patch. Aerospace 2023, 10, 774. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, C.; Li, J.; Guan, Y.; Chen, S.; Zhang, L. Research on Design, Simulation, and Experiment of Separation Mechanism for Micro-Nano Satellites. Appl. Sci. 2022, 12, 5997. [Google Scholar] [CrossRef]
- Kim, H.-G.; Kwon, S.-C.; Koo, K.-R.; Song, S.-C.; Yu, Y.; Song, Y.; Park, Y.-H.; Oh, H.-U. Performance Investigation of Superplastic Shape Memory Alloy-Based Vibration Isolator for X-Band Active Small SAR Satellite of S-STEP under Acoustic and Random Vibration Environments. Aerospace 2022, 9, 642. [Google Scholar] [CrossRef]
- Angevain, J.; Ihle, A.; Rodrigues, G.; Santiago-Prowald, J. Present Status and Future Outlook of the Large Deployable Space Borne Reflector Antennas in Europe. In Proceedings of the 3rd International Conference, Tbilisi, Georgia, 19–21 September 2018. [Google Scholar]
- Datashvili, L.; Maghaldadze, N.; Friemel, M.; Luo, T.; Rocha-Schmidt, L.D.; Cappellin, C.; Lasson, J.R.; Jørgensen, R.; Angevain, J.; Ihle, A.; et al. Large deployable reflectors: Enhancing the mesh reflector RF performances. In Proceedings of the 3rd International Conference “Advanced Lightweight Structures and Reflector Antennas”, Tbilisi, Georgia, 19–21 September 2018. [Google Scholar]
- Snyder, J.F.; Wong, E.L.; Hubbard, C.W. Evaluation of Commercially Available Carbon Fibers, Fabrics, and Papers for Potential Use in Multifunctional Energy Storage Applications. J. Electrochem. Soc. 2009, 156, A215–A224. [Google Scholar] [CrossRef]
- Euro-Composites. Mechanical Properties of ECK Honeycomb. 2010. Available online: https://www.nzcomposites.com/site/nzcomposites/ECK%20Honeycomb%20Properties.pdf (accessed on 13 December 2023).
- Contu, S.; Meschini, A.; Rigato, R. Development status of Large Reflectors at TAS-I. In Proceedings of the IEEE Indian Conference on Antennas and Propogation (InCAP), Jaipur, Rajasthan, India, 19–22 December 2019. [Google Scholar]
- Schmid, M.; Barho, R. Development Summary and Test Results of a 3 Meter Unfurlable CFRP Skin Antenna Reflector. In Proceedings of the 10th European Space Mechanisms and Tribology Symposium, San Sebastián, Spain, 20—24 September 2021. [Google Scholar]
- Andrew, Q. Design Allowables Re-evaluation of Ten Composite Materials; Mechanical Testing and Porosity Examination of M55J Fabric Coupons”, Space Systems/Loral, June, 2013. Available online: https://digitalcommons.calpoly.edu/matesp/61 (accessed on 13 December 2023).
- Jones, R.M. Mechanics of Composite Materials; Scientific & Technical Conference; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Kim, S.; Song, C.-M.; Lee, S.-H.; Song, S.-C.; Oh, H.-U. Design and Performance of X-Band SAR Payload for 80 kg Class Flat-Panel-Type Microsatellite Based on Active Phased Array Antenna. Aerospace 2022, 9, 213. [Google Scholar] [CrossRef]
- Lavigne, L.; Cazaurang, F.; Maini, M.; Zerar, M. Satellite Path Planning by Flatness Approach. Int. Rev. Aerosp. Eng. 2009, 2, 123–132. [Google Scholar]





| Requirement | Value | |
|---|---|---|
| Mass | Antenna assembly | ≤110 kg |
| Diameter | Deployed main reflector | ≥5000 mm |
| Fundamental frequency | (Stowed condition) | |
| Lateral direction | ≥33 Hz | |
| Longitudinal direction | ≥80 Hz | |
| (Deployed condition) | ||
| Bending mode | ≥3 Hz |
| Case | Laminate Sequence | Effective Properties (Pa) | |||||
|---|---|---|---|---|---|---|---|
| E1 | E2 | G12 | v12 | Efx | Efy | ||
| 1.1 | 0.315 | ||||||
| 1.2 | 0.040 | ||||||
| 1.3 | 0.789 | ||||||
| 1.4 | 0.233 | ||||||
| 1.5 | 0.516 | ||||||
| Case | Laminated Pattern | Effective Properties (Pa) | ||
|---|---|---|---|---|
| First Bending Mode | Second Bending Mode | Third Twisting Mode | ||
| 1.1 | 27.93 Hz | 78.09 Hz | 94.81 Hz | |
| 1.2 | 30.75 Hz | 70.22 Hz | 41.73 Hz | |
| 1.3 | 16.15 Hz | 48.75 Hz | 57.97 Hz | |
| 1.4 | 28.28 Hz | 76.39 Hz | 80.03 Hz | |
| 1.5 | 24.37 Hz | 71.94 Hz | 116.95 Hz | |
| Property | 2.1 (High Density) | 2.2 (Low Density) | 2.3 (Various Densities) | 2.4 (Various Thickness) |
|---|---|---|---|---|
| Mass (kg) | 2.73 | 2.49 | 2.51 | 2.71 |
| 1st mode (Hz) | 3.66 | 3.86 | 3.89 | 3.59 |
| 2nd mode [Hz] | 11.29 | 11.95 | 11.97 | 10.96 |
| Unit Structure of Main Reflector | 2.1; High-Density HC | 2.2; Low-Density HC | |
|---|---|---|---|
| Mass (kg) | 2.725 | 2.487 | |
| Mode analysis | 1st mode (Hz) | 93.42 | 97.94 |
| (Stowed condition) | 2nd mode (Hz) | 123.24 | 130.95 |
| Mode analysis | 1st mode (Hz) | 3.66 | 3.84 |
| (Deployed condition) | 2nd mode (Hz) | 11.29 | 11.77 |
| 1g Gravity | (m) | ||
| Thermal deformation | (Pa) | ||
| Maximum Stress (Unit: MPa) | MOS | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case 2.1 | Laminate stress | 56.7 | −39.92 | 2.47 | 0.52 | ||||
| 37.85 | −33.29 | 4.19 | 0.82 | ||||||
| 1.54 | 6.31 | ||||||||
| Core stress | Longitudinal direction (L-dir.) | 0.13 | L-dir. | 76.5 | |||||
| Width direction (W-dir.) | 0.08 | W-dir. | 4.71 | ||||||
| Thickness-dir. | 0.01 | Thickness-dir. | 0.013 | ||||||
| Case 2.2 | Laminate stress | 50.87 | −36.15 | 2.86 | 0.67 | ||||
| 32.83 | −29.71 | 4.99 | 1.04 | ||||||
| 1.44 | 6.81 | ||||||||
| Core stress | L-dir. | 0.09 | L-dir. | 6.98 | |||||
| W-dir. | 0.05 | W-dir. | 12.89 | ||||||
| Thickness-dir. | 0.01 | Thickness-dir. | 93.75 | ||||||
| Antenna Assembly | Case 2.1 Stacking Sequence with the High-Density Honeycomb Core | Case 2.2 Stacking Sequence with the Low-Density Honeycomb Core | |
|---|---|---|---|
| Mass | 100.25 | 94.54 | |
| Modal analysis | 1st mode (Hz) | 35.38 | 36.47 |
| (Stowed condition) | 2nd mode (Hz) | 51.76 | 54.26 |
| Modal analysis | 1st mode (Hz) | 3.34 | 3.47 |
| (Deployed condition) | 2nd mode (Hz) | 10.93 | 11.77 |
| Quasi-static analysis | (Facesheet MOS (Fiber direction) | 0.52 | 0.67 |
| Core MOS (Shear direction) | 4.81 | 6.89 | |
| Micro-vibration analysis | RMS (m) | 1.90 × 10−4 | 1.34 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-G.; Kim, D.-G.; Do, R.-H.; Koo, K.-R.; Yu, Y.-J. Development of Deployable Reflector Antenna for the SAR-Satellite: Part 1. Design and Analysis of the Main Reflector Using Honeycomb Sandwich Composite Structure. Appl. Sci. 2024, 14, 1590. https://doi.org/10.3390/app14041590
Kim H-G, Kim D-G, Do R-H, Koo K-R, Yu Y-J. Development of Deployable Reflector Antenna for the SAR-Satellite: Part 1. Design and Analysis of the Main Reflector Using Honeycomb Sandwich Composite Structure. Applied Sciences. 2024; 14(4):1590. https://doi.org/10.3390/app14041590
Chicago/Turabian StyleKim, Hyun-Guk, Dong-Geon Kim, Ryoon-Ho Do, Kyung-Rae Koo, and Young-Joon Yu. 2024. "Development of Deployable Reflector Antenna for the SAR-Satellite: Part 1. Design and Analysis of the Main Reflector Using Honeycomb Sandwich Composite Structure" Applied Sciences 14, no. 4: 1590. https://doi.org/10.3390/app14041590
APA StyleKim, H.-G., Kim, D.-G., Do, R.-H., Koo, K.-R., & Yu, Y.-J. (2024). Development of Deployable Reflector Antenna for the SAR-Satellite: Part 1. Design and Analysis of the Main Reflector Using Honeycomb Sandwich Composite Structure. Applied Sciences, 14(4), 1590. https://doi.org/10.3390/app14041590





