Mathematical Analysis of a Discrete System Modeling COVID-19 ^†

Abstract

COVID-19 is one of the worst pandemics ever; it is spreading rapidly and creating a health crisis around the world. This disease continues to seriously threaten human life and has caused more than 759 million infections and over 6.8 million deaths worldwide. In this work, we propose a discrete mathematical model of COVID-19 to predict the evolution of the dynamics of this pandemic. We calculate the basic reproduction number and the equilibrium points, and then perform the stability analysis theoretically and numerically. Finally, we conclude with local sensitivity analysis.

1. Introduction

In December, 2019, a mysterious pneumonia appeared in the city of Wuhan, China [1]. By 3 January, 2020, 44 cases of this disease had been diagnosed [1]. A month later, it was determined that this was caused by a new coronavirus [2], which was named SARS-CoV-2 and whose disease is known as COVID-19 (coronavirus disease 2019) [3]. In March, 2020, the World Health Organization declared COVID-19 a pandemic due to its spread to most continents [2], creating a global health crisis with over 118 thousand confirmed cases and 4292 deaths worldwide [2]. By the end of the following month, the number of infected people had exceeded 3 million with 217,769 deaths. COVID-19 had affected almost every corner of the world. Many countries announced the closure of places where the virus could spread easily pandemic, such as schools, universities, markets, and places of entertainment. They also went on lockdown and closed their borders to reduce the spread of the virus. However, the number of infected cases continued to increase, and no ways to end the pandemic had been found. Three years later, this pandemic, which initially only raised a few concerns, has killed over 6.8 million people [4] and changed the world forever.

Since the beginning of the pandemic, all sectors have been mobilized in the fight against the highly transmissible SARS-CoV-2, including mathematics, specifically modeling. Many models have been proposed to predict the evolution of the dynamics and behavior of this disease such as those in [2,3,5,6]. These models allow for the estimation of lethality and the basic reproduction number, especially to find ways to minimize the number of infected individuals and deaths and to control scenarios responsible for transmission. In this work, a discrete SEIR model was proposed to predict the dynamics of COVID-19, including asymptomatic infected individuals, those infected with moderate symptoms, and those developing a severe form of the disease, which requires hospitalization. The model calculates the basic reproduction rate, $R_0$, and the equilibrium points. Stability analysis was performed, followed by a local sensitivity analysis.

2. Materials and Methods

We developed a compartmental model for COVID-19 using a discrete deterministic system based on epidemiological data. The model was used to analyze the disease and predict its evolution. We calculated the basic reproduction number using the next-generation method. The local stability theorem of Lyapunov was used for stability analysis. To perform the local sensitivity analysis, we calculated the sensitivity indexes for $R_0$.

3. Results and Discussion

3.1. Stability Analysis

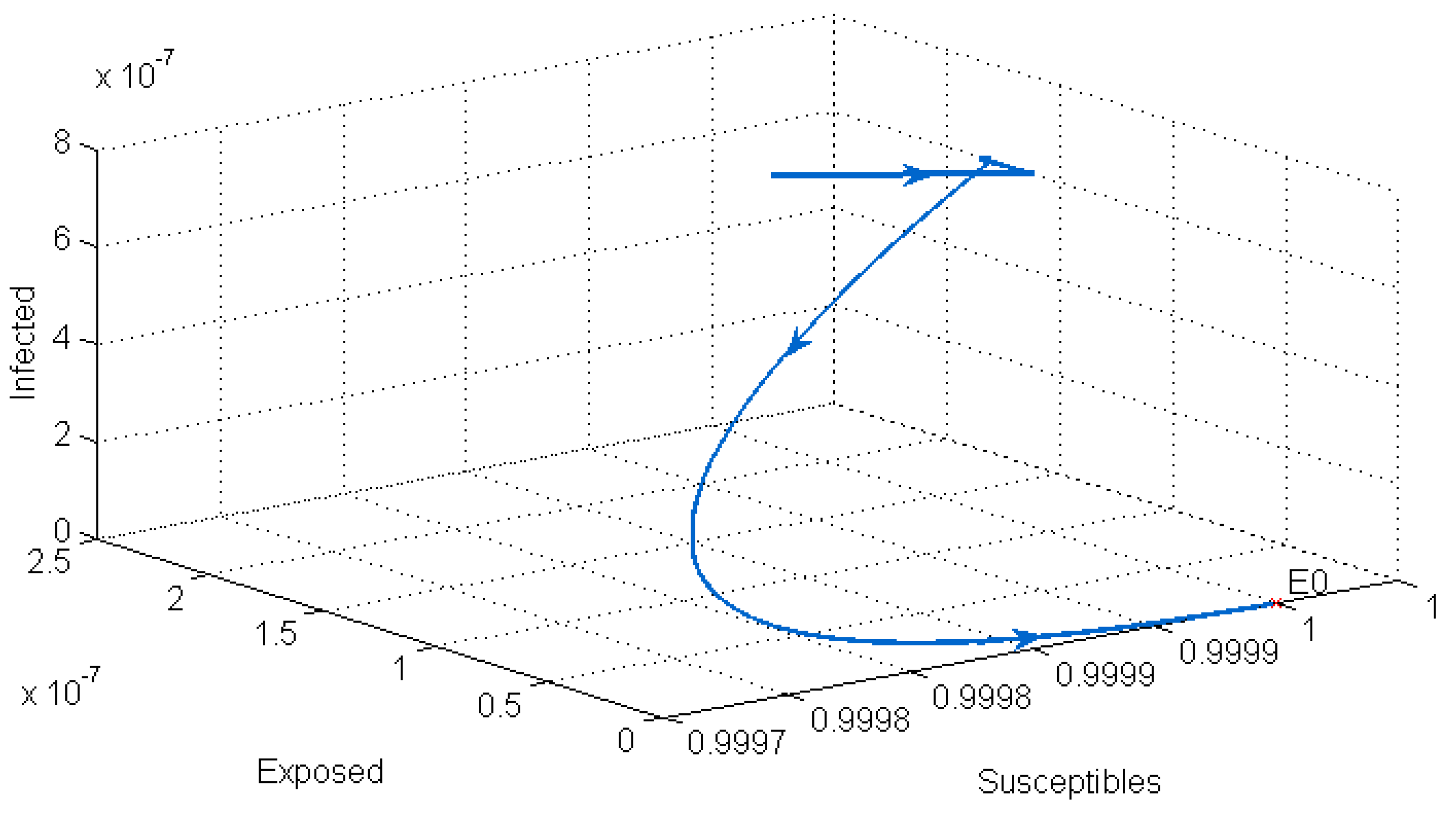
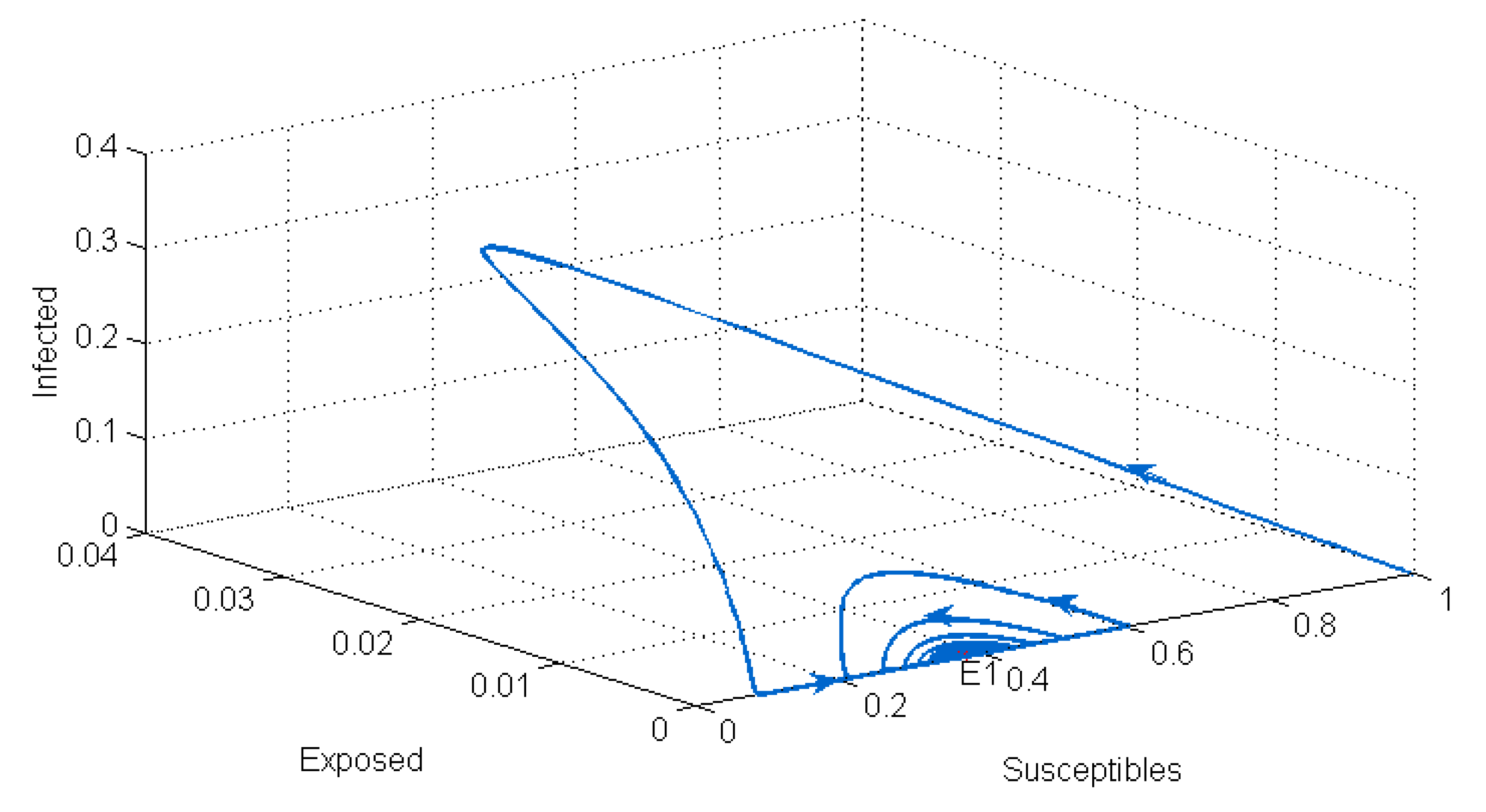
After performing the stability analysis of our system, we found that it has two equilibrium points: the disease-free equilibrium $E_0$, which is locally asymptotically stable when $R_0<1$ (see Figure 1), and the endemic equilibrium $E_1$, which is locally asymptotically stable when $R_0>1$ (see Figure 2).

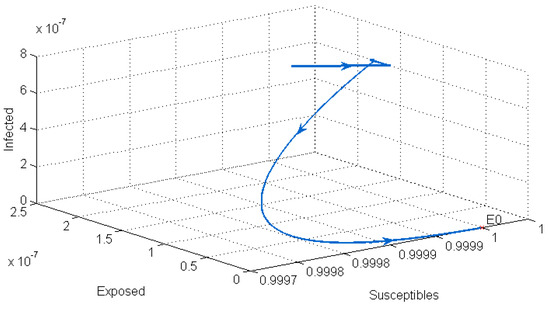
Figure 1. Stability of the disease-free point $E_0$.

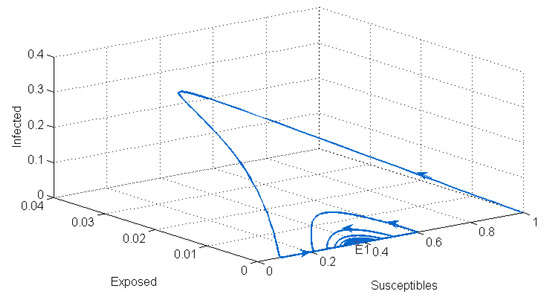
Figure 2. Stability of the endemic equilibrium point $E_1$.

3.2. Sensitivity Analysis

We performed a sensitivity analysis by calculating the sensitivity indices of $R_0$ (see Table 1). Our analysis showed that $R_0$ is most sensitive to the transmission rate of COVID-19 and the recovery rate of asymptomatic infected people. An increase in the transmission rate leads to an increase in $R_0$, while an increase in the recovery rate leads to a decrease in $R_0$.

Table 1. Sensitivity indices of $R_0$.

Parameters	Description	Sensitivity Index
α	The transmission rate of COVID-19	+1.0000
${\mathsf{\gamma }}_1$	The recovery rate of asymptomatic infected people	−0.6139
${\mathsf{\gamma }}_2$	The recovery rate of infected with moderate symptoms	−0.3346
${\beta }_3$	The rate at which exposed people become infected with severe symptoms need hospitalization	−0.1500
${\beta }_2$	The rate at which exposed become infected with moderate symptoms	+0.0855
ⱷ	The rate at which a symptomatic infected develops severe symptoms and enters the hospital	−0.0711
${\beta }_1$	The rate at which exposed individuals become asymptomatic infected	+0.0647
${\lambda }_1$	The transition rate from the first to the second phase of infection	+0.0268