Variable Guide Vane Scheduling Method Based on the Kinematic Model and Dual Schedule Curves
Abstract
:1. Introduction
2. Mechanical Structure of the VGVS
2.1. Component of the Link Mechanisms
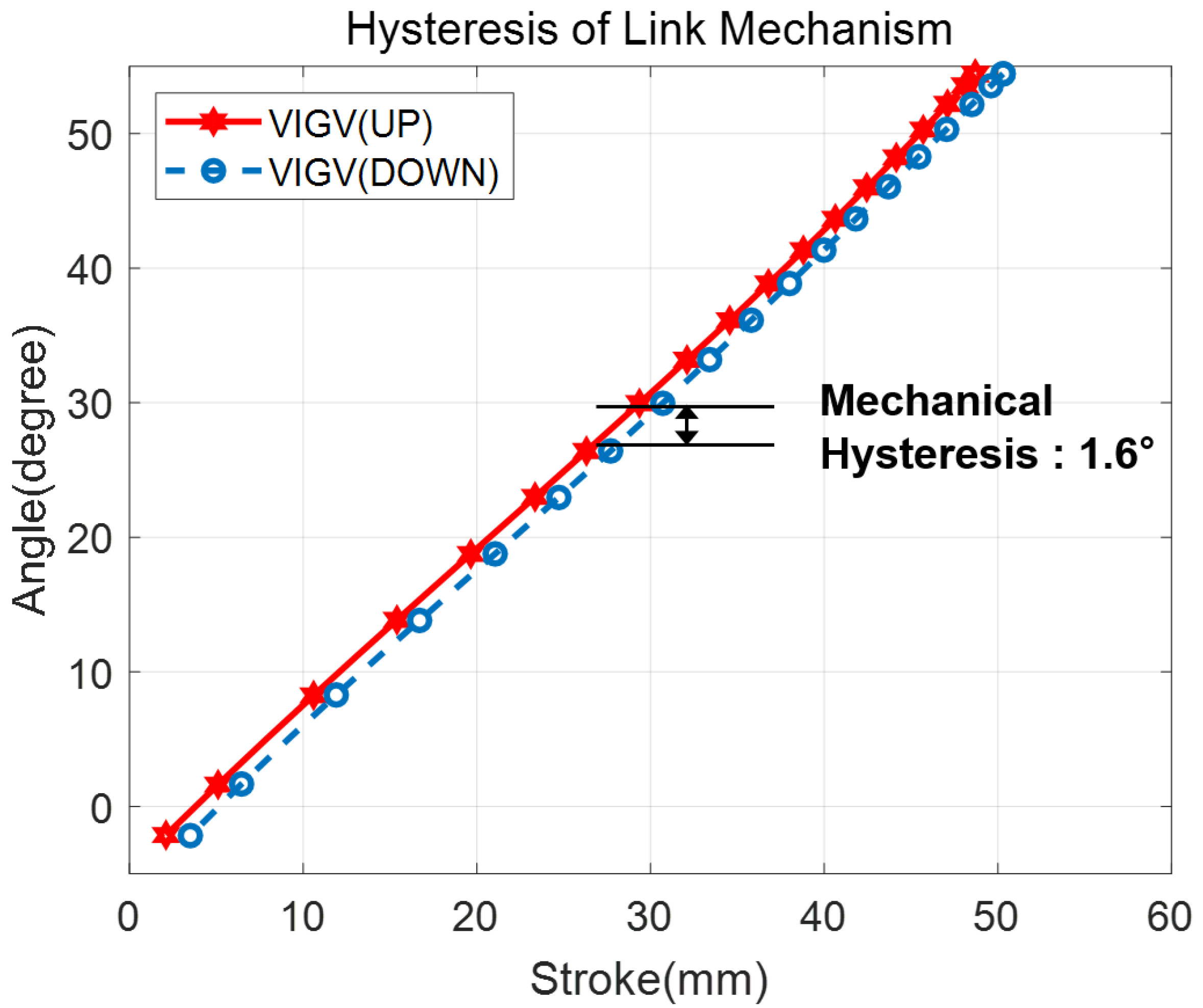
2.2. DOFs and Hysteresis of the VGV Link Mechanisms
3. Analytical Model of the VGV Link Mechanism
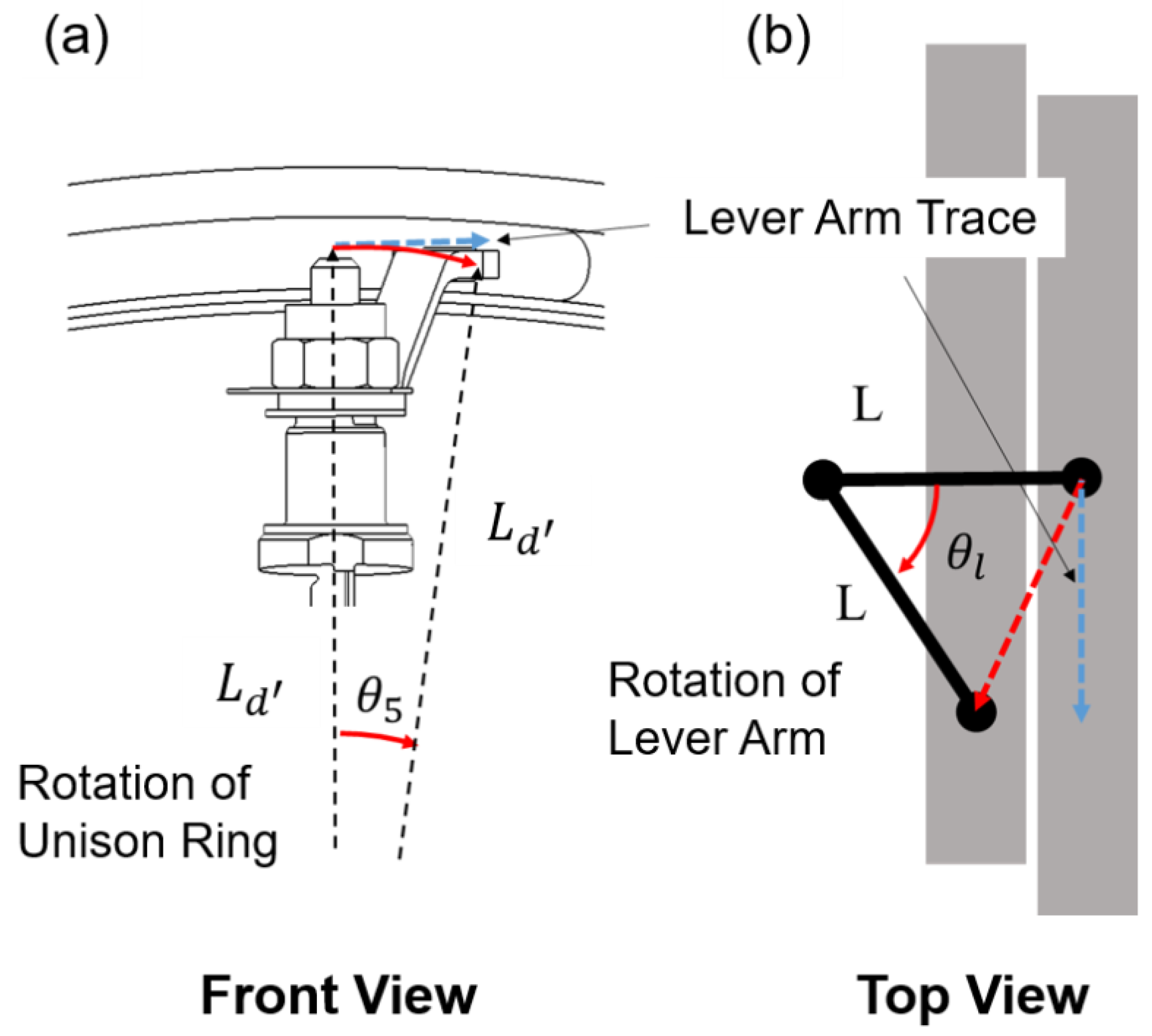
3.1. Model for the Links from Actuator to Unison Ring
3.2. Model for the Links from the Unison Ring to the Vane
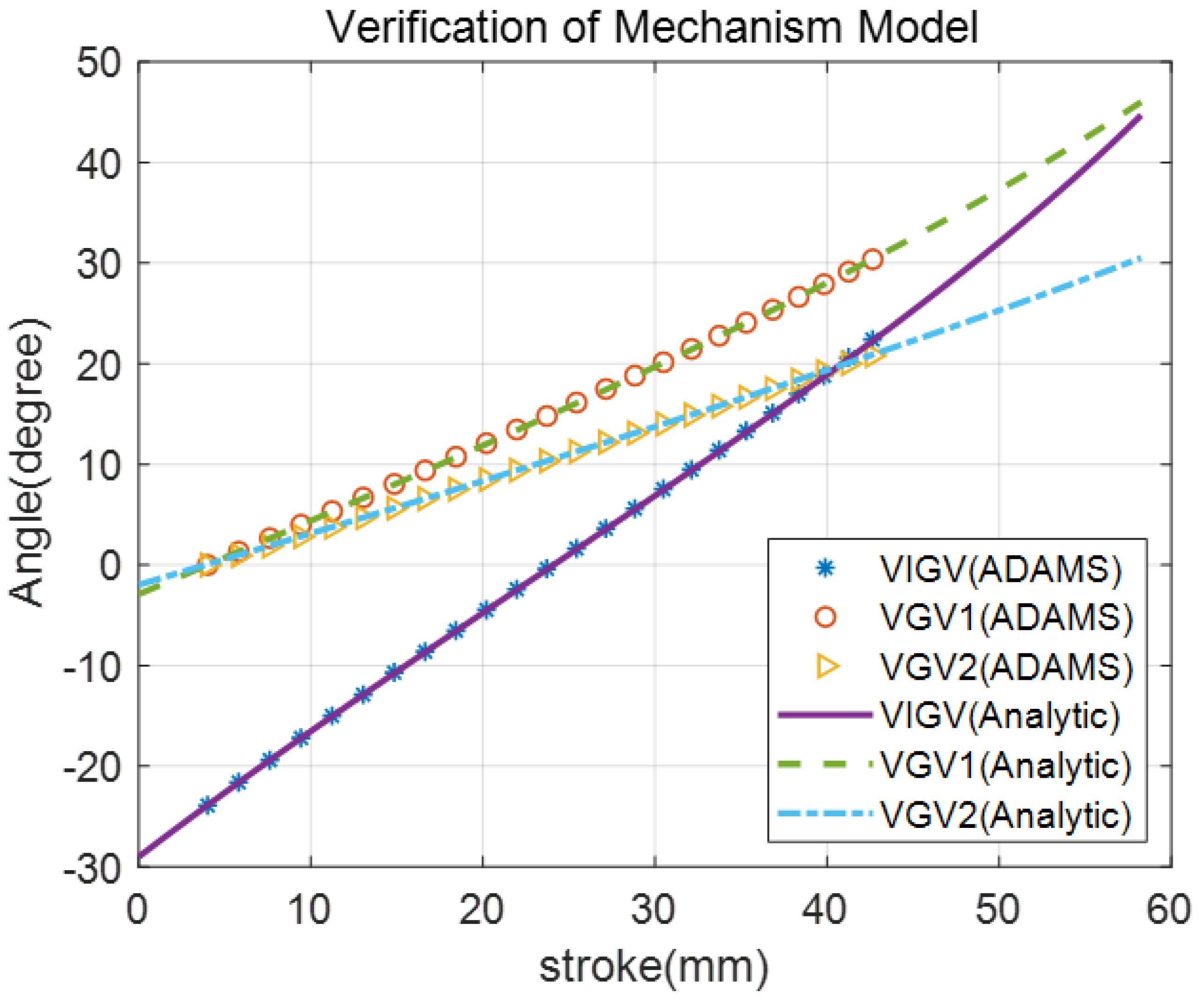
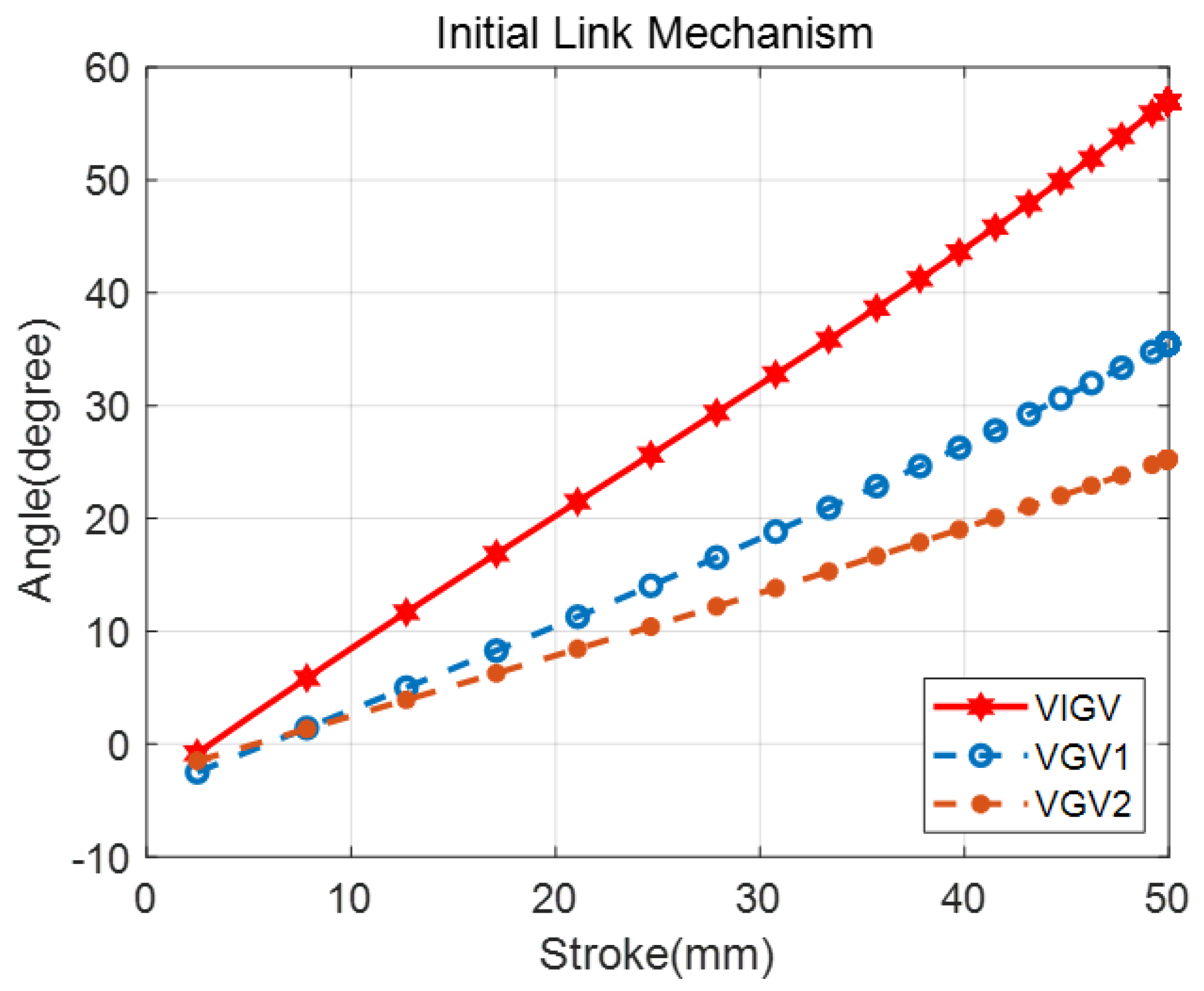
3.3. Model Validation by ADAMS Simulation
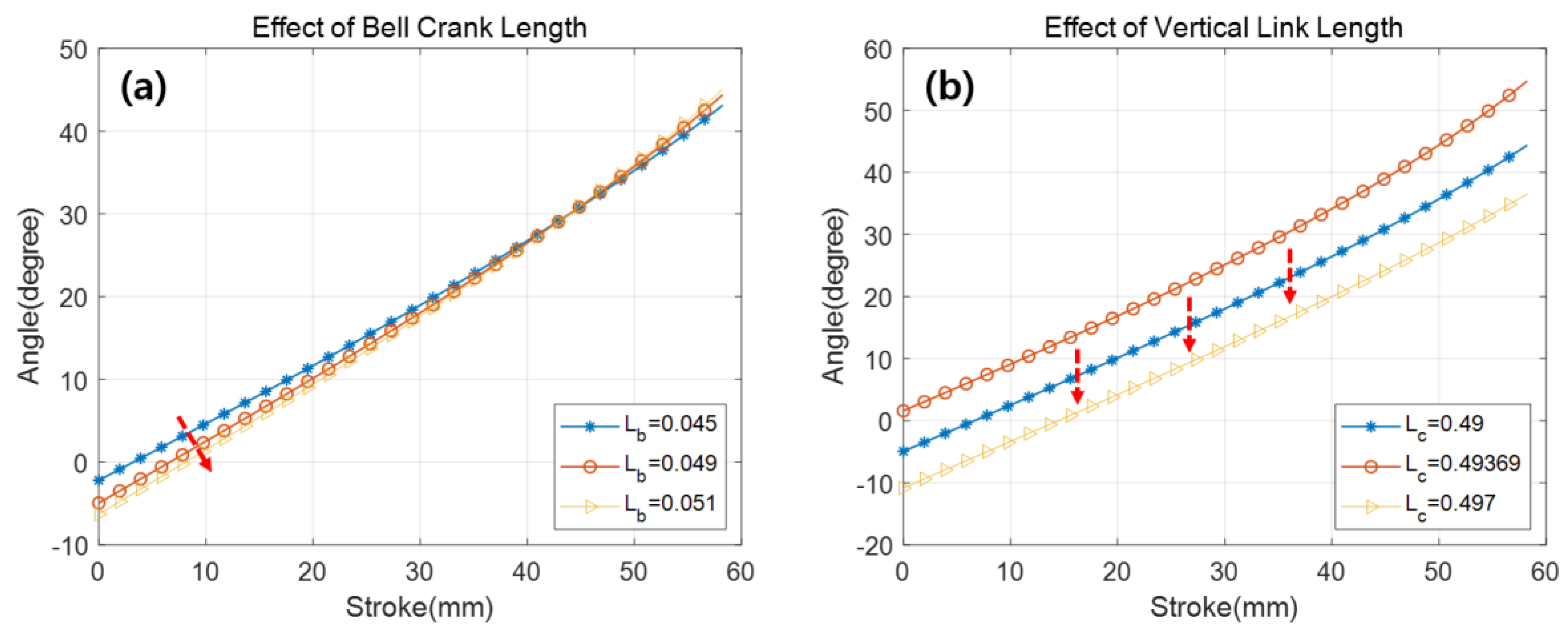
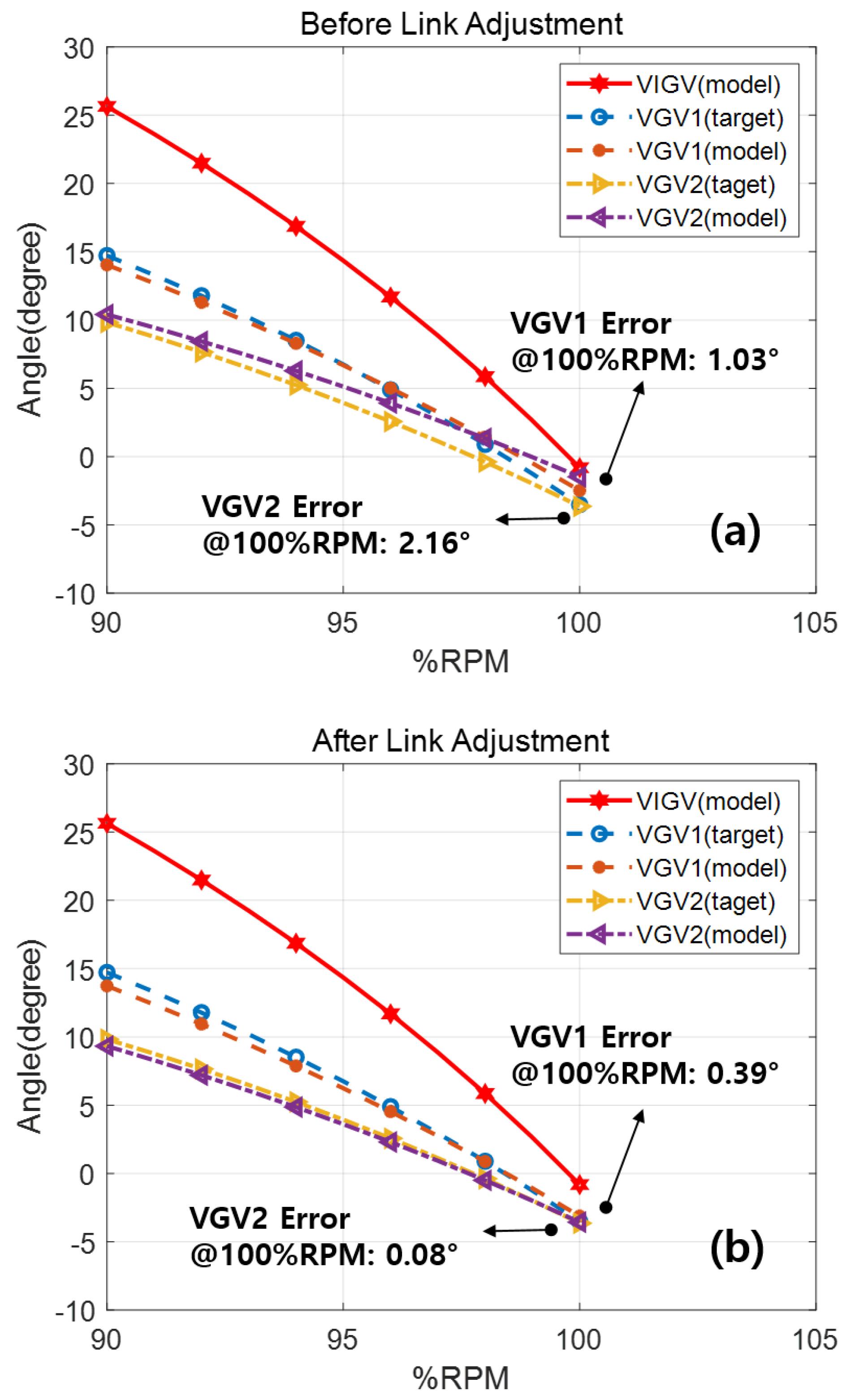
3.4. Parameters for Adjusting the Link Mechanism
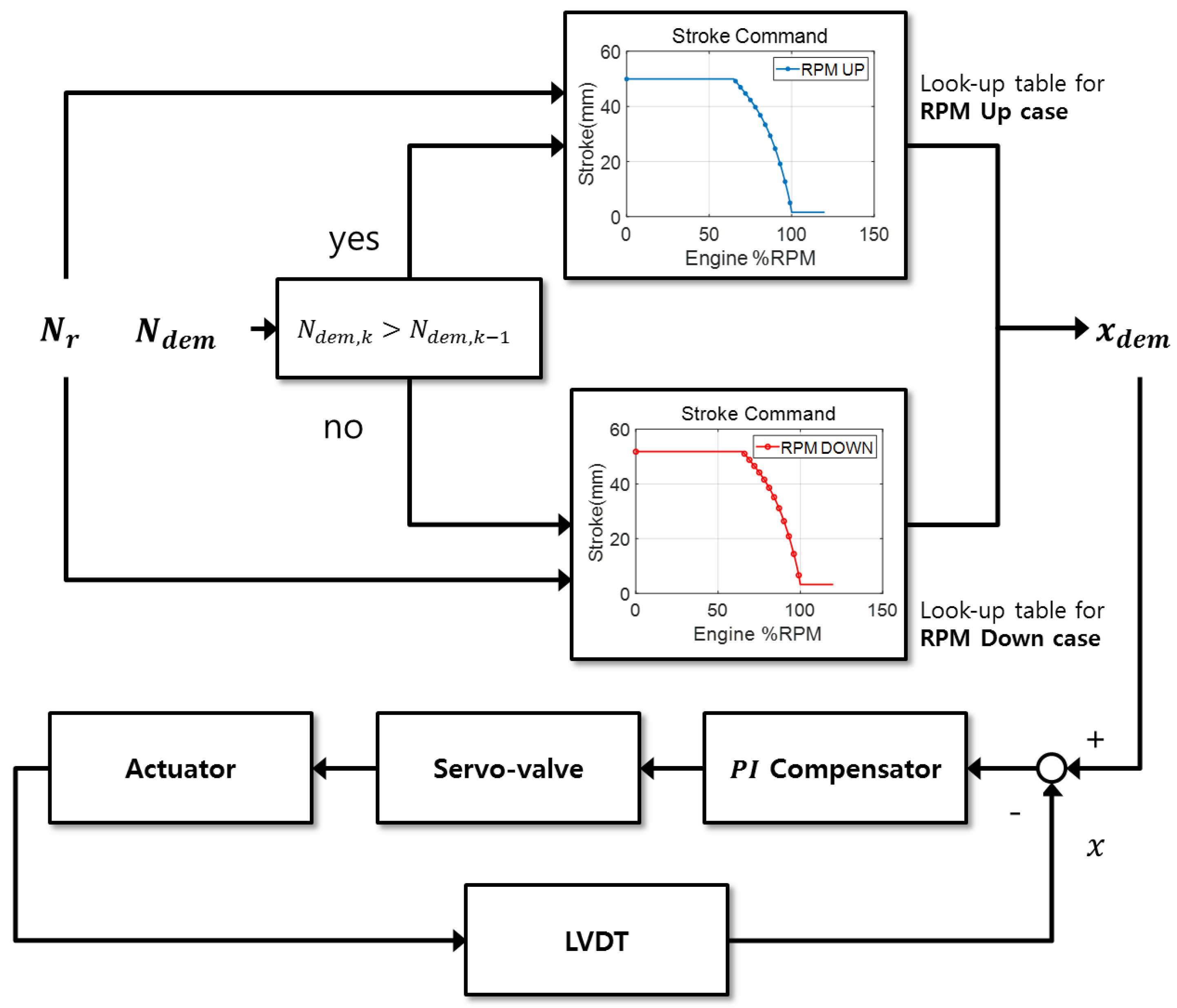
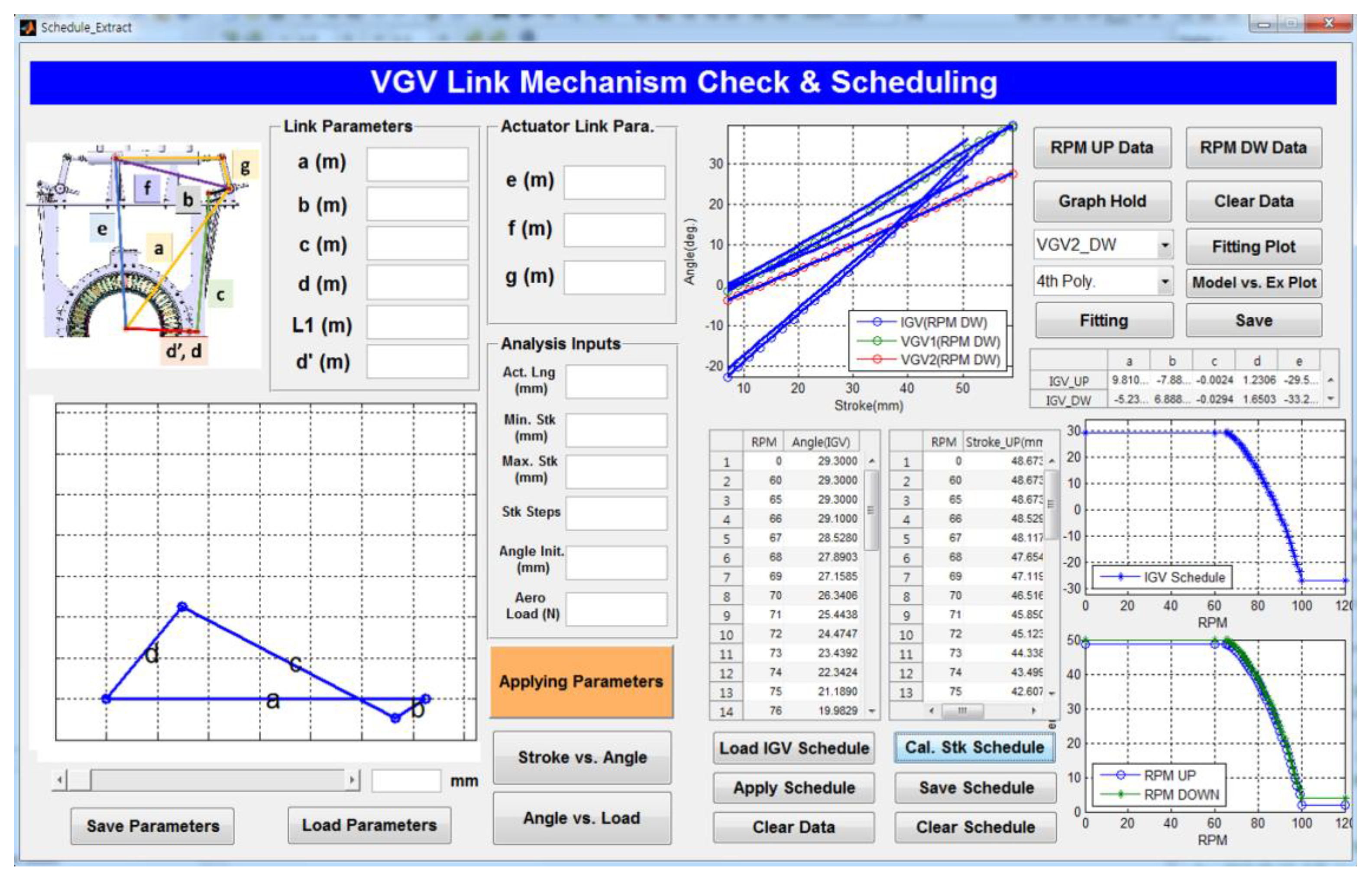
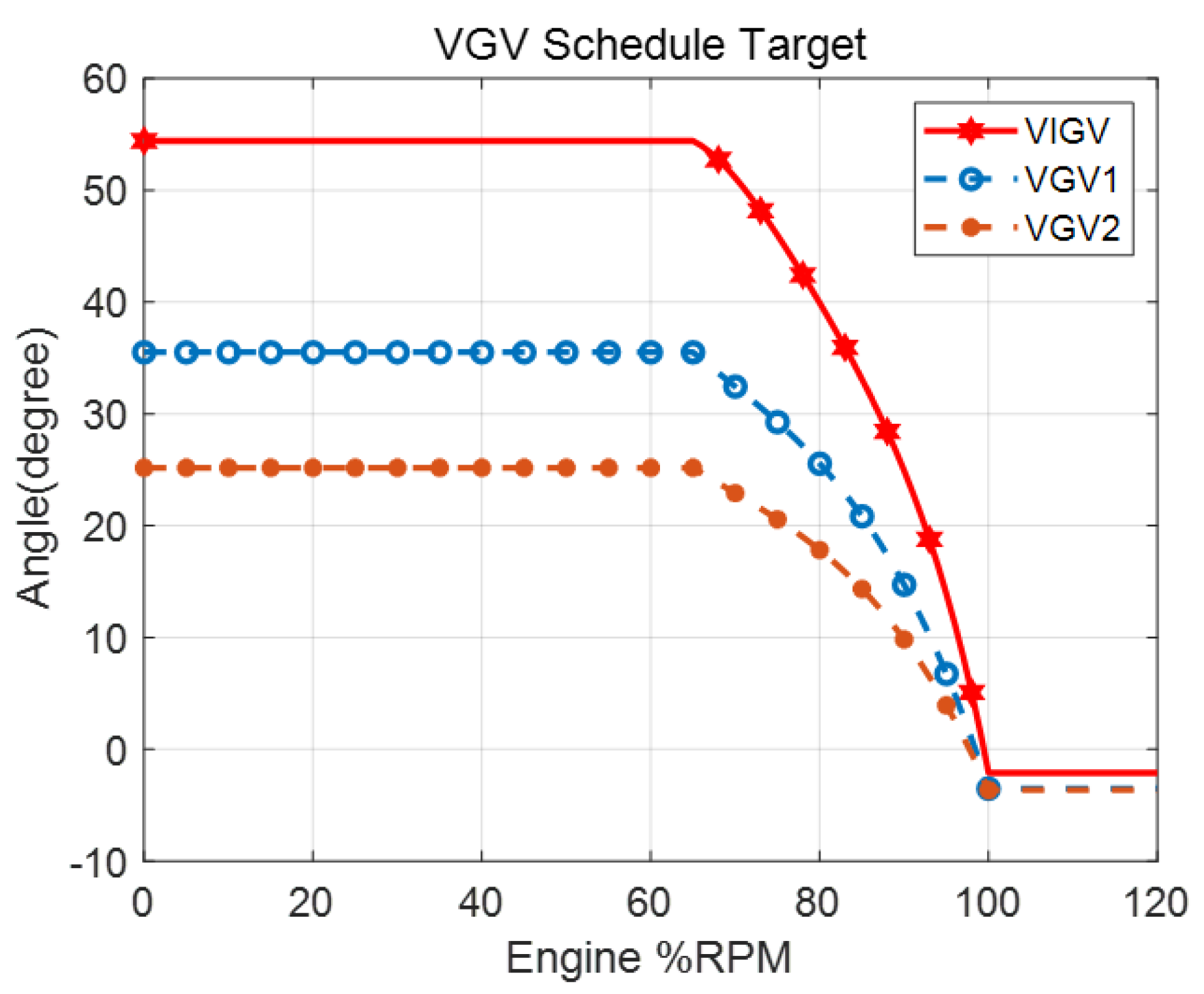
4. VGV Scheduling Method
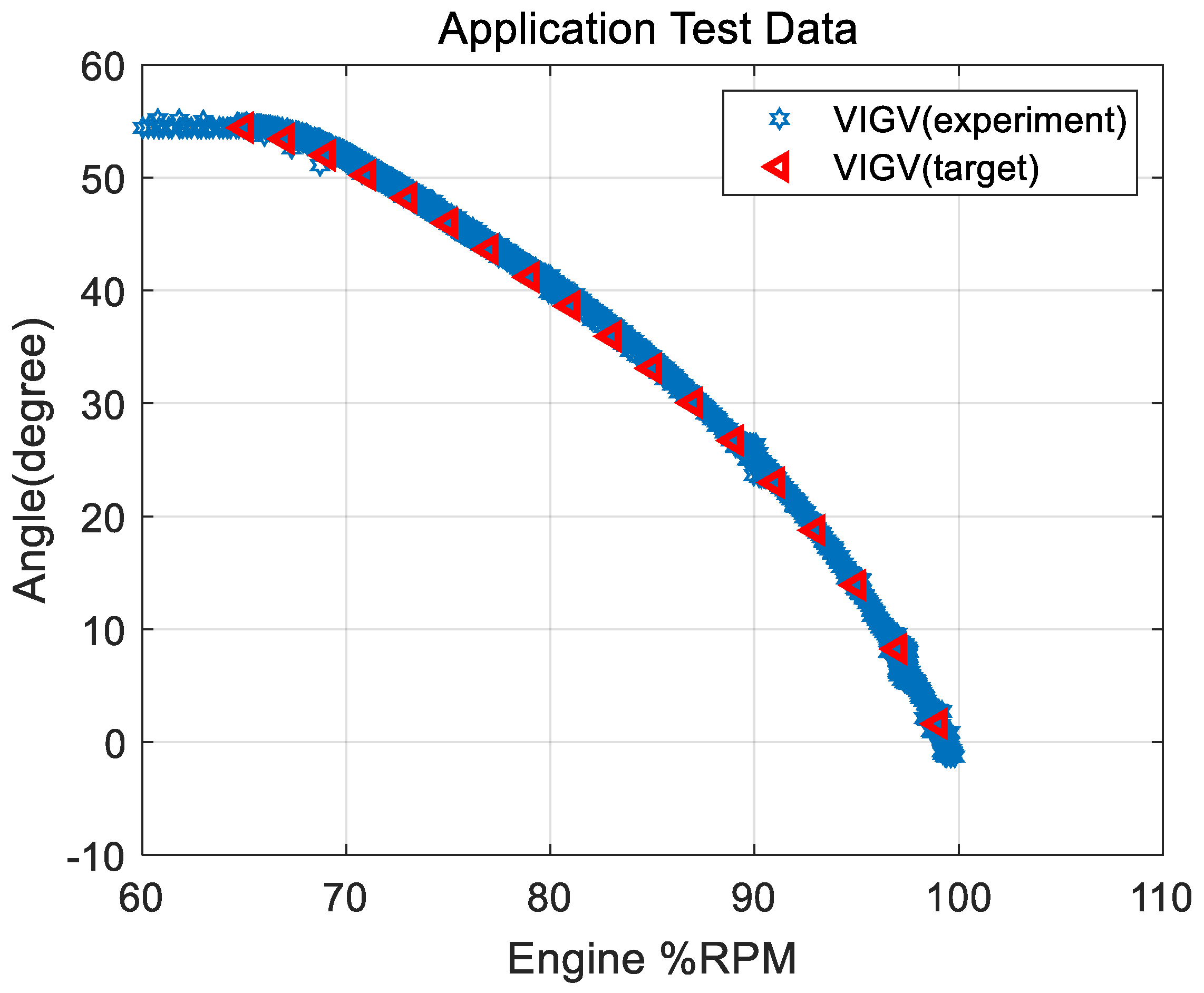
5. Engine Application Test
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclatures
| Acronym/Nomenclature | Definition |
| VGV | Variable guide vanes |
| VIGV | Variable inlet guide vane |
| IGV | Inlet guide vane |
| DOF | Degree of Freedom |
| VGV1 | First-stage variable guide vane |
| VGV2 | Second-stage variable guide vane |
| J0, J1, J2, J3, J4, and J5 | Joint 0, 1, 2, 3, 4, and 5 |
| ADAMS | Multi-body dynamics analysis software |
| LVDT | Linear Variable Displacement Transducer |
| RPM | Rotations per minute |
| MATLAB GUI | MATLAB Graphical user interface |
| Length of link a, b, c, d | |
| Length of link x (actuator stroke) | |
| Length of link e (length of upper link of bell crank) | |
| Length of lever arm | |
| Radial distance of the end of the lever arm from the center of the engine | |
| Total number of links in the mechanism | |
| Number of joints having k DOF | |
| Transformation matrix from P1 to P2 | |
| cθ | Cosine θ |
| sθ | Sine θ |
| , | xx-directional values of the links(x: 1 for x-axis, 2 for y-axis, 3 for z-axis) |
| ( | Position of Joint 2 |
| ( | Position of Joint 5w.r.t. local coordinate based on Joint 2 |
| ∆x, ∆y | Distance of Joint 5 from Joint 2 according to x or y axis |
| Angle value represented in Figure 2 | |
| Lever arm rotational angle | |
| Axial displacement of the clevis (unison ring) | |
| Slope of the linear regression between vane angle and actuator stroke | |
| Offset of the linear regression between vane angle and actuator stroke | |
| Engine rotor RPM | |
| Engine rotor RPM demand | |
| Engine rotor RPM demand at k-th step | |
| Actuator stroke demand |
References
- Rolls Royce. The Jet Engines, 4th ed.; Rolls Royce Limited: London, UK, 1986. [Google Scholar]
- Wirkowski, P. Modelling the Characteristics of Axial Compressor of Variable Flow Passage Geometry Working in the Gas Turbine Engine System. Pol. Marit. Res. 2007, 14, 27–32. [Google Scholar] [CrossRef]
- Salvage, J.W. Development of a Centrifugal Compressor with a Variable Geometry Split-Ring Pipe Diffuse. J. Turbomach. 1999, 121, 295–304. [Google Scholar] [CrossRef]
- Tibrewala, A.P.; Padave, T.J.; Wagh, T.P.; Gajare, C.M. Flow Aanlysis of Upstream Fluid Flow using Simulation for Different Positions of Optimized Inlet Guide Vane in Centrifugal Air Compressor. Am. J. Eng. Res. 2014, 3, 148–156. [Google Scholar]
- Mohseni, A.; Goldhahn, E.; Braembussche, R.A.V.D.; Seume, J.R. Novel IGV Designs for Centrifugal Compressors and Their Interaction with the Impeller. J. Turbomach. 2011, 134, 021006. [Google Scholar] [CrossRef]
- Ziegler, K.U.; Justen, F.; Rothstein, M.; Gallus, H.E.; Niehuis, R. Research on a Centrifugal Compressor of Variable Geometry. In Proceedings of the 15th International Compressor Engineering Conference, West Lafayette, IN, USA, 25–28 July 2000; pp. 89–96. [Google Scholar]
- Harrold, M.C. Stator Vane Actuator in Gas Turbine Engine. U.S. Patent 6769868 B2, 3 August 2004. [Google Scholar]
- Rusovici, R.; Feys, J.; Sepri, P.; Subramanian, C. Smart Actuation of Inlet Guide Vanes for Small Turbine Engine. ICAST 2014, 2014. [Google Scholar] [CrossRef]
- Robert, W. Duct with Vanes having Selectively Variable Pitch. U.S. Patent 3861822, 27 February 1974. [Google Scholar]
- Tsalavoutas, A.; Mathioudakis, K.; Stamatis, A.; Smith, M. Identifying Faults in the Variable Geometry System of a Gas Turbine Compressor. J. Turbomach. 2001, 123, 33–39. [Google Scholar] [CrossRef] [Green Version]
- Muir, D.E.; Saravanamuttoo, H.I.H.; Marshall, D.J. Health Monitoring of Variable Geometry Gas Turbine for the Canadian Navy. ASME J. Eng. Gas Turbines Power 1989, 111, 244–250. [Google Scholar] [CrossRef]
- Hashmi, M.; Lemma, T.A.; Karim, Z.A.A. Investigation of the Combined Effect of Variable Inlet Guide Vane Drift, Fouling, and Inlet Air Cooling on Gas Turbine Performance. Entropy 2019, 21, 1186. [Google Scholar] [CrossRef] [Green Version]
- Song, T.; Kim, T.; Kim, J.; Ro, S. Performance Prediction of Axial Flow Compression using Stage Characteristics and Simultaneous Calculation of Interstage Parameters. Proc. Inst. Mech. Eng. Part A J. Power Energy 2001, 215, 89–98. [Google Scholar] [CrossRef]
- Ishak, S.; Ahmad, A. Improving VIGV Predictive Monitoring by Developing a Failure Mode Virtual Snesor. In Proceedings of the 2017 7th IEEE ICCSCE, Penang, Malaysia, 24–26 November 2017; pp. 144–149. [Google Scholar]
- Hensges, M. Simulation and Optimization of an Adjustable Inlet Guide Vane for Industrial Turbo Compressors. In Proceedings of the ASME Turbo Expo 2008, GT2008-50242, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Uicker, J.J.; Pennock, G.R.; Shigley, J.E.; McCarthy, J.M. Theory of Machines and Mechanisms; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Al-Bender, F.; Lampaert, V.; Swevers, J. A Novel Generic Model at Asperity Level for Dry Friction Force Dynamics. Tribol. Lett. 2004, 16, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Wojewoda, J.; Stefanski, A.; Wiercigroch, M.; Kapitaniak, T. Hysteretic Effects of dry friction: Modelling and Experimental Studies. Phil. Trans. R. Soc. A 2007, 366, 747–765. [Google Scholar] [CrossRef] [PubMed]
- Marques, F.; Flores, P.; Claro, J.C.P.; Lankarani, H.M. Modeling and Analysis of Friction including Rolling Effects in Multibody Dynamics: A review. Multibody Syst. Dyn. 2018, 45, 223–244. [Google Scholar] [CrossRef]
- Tan, H.; Hu, Y.; Li, L. Effect of Friction on the Dynamic Analysis of Slider-crank Mechanism with Clearance Joint. Int. J. Non-Linear Mech. 2019, 115, 20–40. [Google Scholar] [CrossRef]
- Xiang, W.; Yan, S.; Wu, J. Dynamic Analysis of Planar Mechanical Systems Considering Stick-slip and Stribeck Effect in Revolute Clearance Joints. Nonlinear Dyn. 2018, 95, 321–341. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A Comprehensive Survey of the Analytical, Numerical and Experimental Methodologies for Dynamics of Multibody Mechanical Systems with Clearance or Imperfect Joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Lai, X.; He, H.; Lai, Q.; Wang, C.; Yang, J.; Zhang, Y.; Fang, H.; Liao, S. Computational Prediction and Experimental Validation of Revolute Joint Clearance Wear in the Low-velocity Planar Mechanism. Mech. Syst. Signal Process. 2017, 85, 963–976. [Google Scholar] [CrossRef]
- Erkaya, S. Experimental Investigation of Flexible Connection and Clearance Joint Effects on the Vibration Response of Mechanisms. Mech. Mach. Theory 2018, 121, 515–529. [Google Scholar] [CrossRef]
- Ohe, T.; Lee, J.H.; Okamoto, S. Experimental Verification of Nonlinear Characteristics with Hysteresis in Variable Stiffness Robotic Joint. In Proceedings of the 16th International Conference on Ubiquitous Robots, Jeju, Korea, 24–27 June 2019. [Google Scholar]




| Description | Type | Numbers | |
|---|---|---|---|
| Number of 3 DOF Joint | Spherical Joint (2 x bell crank-vertical link) (2 x clevis-vertical link) | 4 | |
| Number of Parts | Links (2 vertical links, 1 unison ring, ground) | 4 |
| Variables | |
|---|---|
| Constants | , , , , |
| State variables | |
| Inputs | |
| Outputs |
| Number in Figure 4 | Joint | Parts | DOFs |
|---|---|---|---|
| ① | Spherical | Bell Crank, Vertical Link | 3 |
| ② | Revolute | Bell Crank, Ground | 1 |
| ③ | Slide + Revolute | Clevis, Ground | 2 |
| ④ | Spherical | Vertical Link, Clevis | 3 |
| Parameters | VIGV | VGV1 | VGV2 |
|---|---|---|---|
| 112.3 | 112.3 | 112.3 | |
| 74.0 | 48.0 | 35.0 | |
| 497.1 | 493.7 | 498.8 |
| Max. Error | Overall Mean Error | Mean Error (99% RPM < RPM < 100% RPM) |
|---|---|---|
| 2.17 | 0.55 | 0.47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.J.; Ki, T. Variable Guide Vane Scheduling Method Based on the Kinematic Model and Dual Schedule Curves. Appl. Sci. 2020, 10, 6643. https://doi.org/10.3390/app10196643
Kim SJ, Ki T. Variable Guide Vane Scheduling Method Based on the Kinematic Model and Dual Schedule Curves. Applied Sciences. 2020; 10(19):6643. https://doi.org/10.3390/app10196643
Chicago/Turabian StyleKim, Sun Je, and Taeseok Ki. 2020. "Variable Guide Vane Scheduling Method Based on the Kinematic Model and Dual Schedule Curves" Applied Sciences 10, no. 19: 6643. https://doi.org/10.3390/app10196643
APA StyleKim, S. J., & Ki, T. (2020). Variable Guide Vane Scheduling Method Based on the Kinematic Model and Dual Schedule Curves. Applied Sciences, 10(19), 6643. https://doi.org/10.3390/app10196643




