Considering the Effect of Non-Propagating Cracks on Fatigue Limit Prediction in the Critical Distance Method Framework

Abstract

Although the material has developed micro-scale cracks, the micro-cracks stop propagating and transform into non-propagating cracks (NPCs) under fatigue limit loading. The movement of the crack tip position caused by the non-propagating crack will generate a small change in the notch geometry, which easily triggers the geometric size effect. Since the critical distance method focuses on evaluating the limit of fatigue in terms of the material’s cracking conditions, the present study attempted to develop a notched fatigue analysis model to consider the effect of non-propagating cracks on fatigue limit prediction in the critical distance method framework. The effectiveness and capability of the proposed model were demonstrated by the fatigue experimental data of Q345qD low carbon steel.

1. Introduction

Due to the limitations of construction technology and design, engineering structures will inevitably form some notch features (such as holes, grooves, corners, welding, etc.) on components or structures. The complicated stress characteristics of the notch position will significantly weaken the fatigue resistance of the components [1,2,3,4,5]. Therefore, how to accurately evaluate the fatigue performance of the notch position under cyclic loading has become an important research project, especially for the long-term operation of mechanical and civil engineering.

The theory of critical distance (TCD) has been a popular fatigue analysis method in the last two decades [6,7,8,9,10,11,12]. TCD was proposed by Taylor [13,14,15] in the late 1990s by summarizing the views of Neuber [3] and Peterson [16]. Since the critical distance theory takes into account the effect of the stress gradient at the notch root on fatigue damage, the critical distance method has better predictive power than the relatively conservative peak stress method in notch fatigue analysis. However, the expected effect of critical distance theory is not ideal in some small notches and low/medium cycle fatigue. Lanning et al. [17,18] pointed out that the size effect exists in some very small notches, showing the critical distance theory to be inapplicable to very small notches. Yamashita et al. [19] have illustrated that due to the volume effect of the notch, the conventional critical distance method does not work well for small notch fatigue problems. In view of this, some researchers have also carried out research on the critical distance size effect and proposed a corresponding correction model. Among these, Wang et al. [20] considered that the fatigue process region depends on the severity of stress concentration and put forward the idea of superimposing the Kt coefficient on the critical length to deal with the critical distance size effect. From the perspective of fracture mechanics, Hertel et al. [21] provided a rigorous interpretation of the geometric size effect and corrected the critical distance length. Wang et al. [22] and Li et al. [23] suggested that the size effect of the notch can be analyzed by combining TCD and highly-stressed-volume (HSV) methods. Zhu et al. [11] proposed a specific mathematical quantification of the relationship between hole radius and critical distance to account for the effect of notch size. Sun et al. [24] pointed out that the critical dimension effect of the crankshaft can be considered by superimposing the stress gradient over the conventional critical distance.

Numerous evidence [25,26,27,28,29,30,31,32,33] has revealed that although components may already have generated microcracks, the microcracks stopped propagating and transformed into non-propagating cracks (NPC) under fatigue limit load. In many engineering applications, the crack initiation stage does not exist, and some initial microcracks generated by the manufacturing or processing process pre-exist in the engineering component. Therefore, the fatigue limit of materials in practical structural engineering, such as steel [33,34], is mainly determined by non-propagating fatigue crack behavior. Different studies have shown that the fatigue limit of materials should be evaluated based on the threshold stress of microscopic non-propagating crack growth [33,35]. In view of this, numerous models based on the NPC concept have been established for fatigue analysis. Among these, Asai et al. [36] proposed a fracture mechanics model for evaluating fretting fatigue strength with non-propagating cracks. Molokov et al. [37] used the non-propagating crack criterion to estimate the durability limit of welded joints. Steimbreger et al. [38] provided a model that combines undercut depth, maximum non-propagating crack length and threshold stress value to determine the minimum durability limit.

Although Susmel and Taylor later illustrated that the fatigue limit can be defined in terms of the formation of non-propagating cracks emanating from components’ weakest points [39], they did not consider the movement of the crack tip position caused by the non-propagating crack and its effect. In addition, the movement of the crack position changes the original geometry of the notch, which easily triggers the geometric size effect. Therefore, the present study attempted to develop a notched fatigue analysis model to consider the effect of non-propagating cracks on fatigue limit prediction in the critical distance method framework. The paper is organized as follows: in Section 2, the details and results of fatigue test for Q345qD low carbon steel are described; in Section 3, the critical distance theory is briefly reviewed, and the fatigue limit of Q345qD low carbon steel is predicted by the critical distance method; in Section 4, the critical distance model recommended in this study is proposed, and related analysis and discussion are carried out; finally, some conclusions are drawn from the current study in Section 5.

2. Experiment

2.1. Material and Specimen

The material used in the present study is Q345qD low carbon steel. The specimen for fatigue test is a plate structure with a thickness of 4 mm. The specimen is 181 mm in length and has a double-sided V-notch angle of 60°. Figure 1 shows the geometry and dimensions of the specimens in the fatigue test. The detailed dimensions of the small notches for different specimens are listed in

Table 1. Summary of notch depth and root radius of specimens.

Specimen No.	Type	Notch Depth (mm)	Root Radius (mm)
V0	smooth	0	∞
V1	notch	2	1
V2	notch	4	1
V3	notch	2	2
V4	notch	4	2

. The mechanical properties of material were obtained by axial tensile tests of 3 replicate specimens. The test machine is a SUST universal testing machine, and the test speed was 0.5 mm/min. An extensometer was clamped on the tensile specimens to obtain more accurate test results. The mechanical properties of the low carbon steel Q345qD are listed as follows: the elastic modulus is 207GPa, the yield stress is 381MPa, the ultimate stress is 522MPa, and the percentage reduction of area is 64.3%. The stress–strain relationship of the Q345qD specimen obtained from the experimental test is shown in Figure 2.

2.2. Fatigue Test Method and Results

All the fatigue tests were carried out under constant stress amplitude using an CCQB electro-hydraulic servo fatigue testing system at a nominal frequency of 20 Hz, as shown in Figure 3. Specimens were cycled under tension fatigue loading of stress ratio of 0.1. The fatigue tests were performed at room temperature. A 1600-fold observation instrument was used to simultaneously monitor the crack state at the root of the notch in the test. An example of crack initiation at the notch root of the specimen is shown in Figure 4. When the specimen V2 was loaded with 220 MPa, obvious crack initiation was observed on the surface of notch root after 95,237 cycles, as shown in Figure 4a. Because the stress was large enough, there was no crack closure effect. However, when the specimen was loaded with 200 MPa, non-propagating cracks were observed and crack closure was found at local locations, as shown in Figure 4b. These also led to no obvious crack growth behavior from 37,524 cycles to 10⁶ cycles. The detailed results of the fatigue test are shown in Figure 5. It can be found from Figure 5 that the fatigue strength of the notched specimen is significantly lower than that of the smooth specimen. At the same time, the larger the radius of the notch root, the higher the fatigue strength such as V1 vs. V3, V2 vs. V4. Different studies [17,18] have also reached the same conclusion.

3. The Conventional Critical Distance Method

3.1. Theory of Critical Distance (TCD)

The concept of the critical distance was originally proposed by Peterson [16] and Neuber [3], who considered that the effective stress for notch fatigue does not depend entirely on the peak stress at the notch root, but on the stress distribution near the notch root. Taylor summarized and developed their views and proposed the classical critical distance method based on the theory of linear elastic fracture mechanics (LEFM). According to the range of effective stress selection, the critical distance method is divided into the critical point method (PM), the critical distance line method (LM), critical area method (AM) and critical volume method (VM), as shown in Figure 6. Specifically, PM defines the stress at L/2 from the root of the notch as the effective stress for notch fatigue. When the effective stress of notch fatigue is equal to the fatigue strength of the smooth specimen, the corresponding applied load is the notch fatigue limit; LM is the average stress within the 2L length of the notch root as the effective stress of notch fatigue. AM and VM take the average stress in the critical semicircle and critical volume as the effective stress, respectively.

The mechanical expression of the critical distance method is as follows:

$${\sigma }_{eff}\left(PM\right)=\sigma \left(L/2\right)={\sigma }_0$$

(1)

$${\sigma }_{eff}\left(LM\right)=\frac{1}{2L}{\displaystyle {\int }_0^{2L}\begin{array}{cc}\sigma \left(r\right)dr& ={\sigma }_0\end{array}}$$

(2)

$${\sigma }_{eff}\left(AM\right)=\frac{2}{\pi {\left(1.32L\right)}^2}{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\displaystyle {\int }_0^{1.32L}\begin{array}{cc}\sigma \left(r,\theta \right)rdrd\theta & ={\sigma }_0\end{array}}}$$

(3)

$${\sigma }_{eff}\left(VM\right)=\frac{3}{2\pi {\left(1.54L\right)}^3}{\displaystyle {\int }_0^{\pi }{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\displaystyle {\int }_0^{1.54L}\begin{array}{cc}\sigma \left(r,\theta ,\phi \right)r^{2}drd\theta d\phi & ={\sigma }_0\end{array}}}}$$

(4)

where L is material constant, which can be expressed as:

$$L=\frac{1}{\pi }{\left(\frac{K_{th}}{{\sigma }_0}\right)}^2$$

(5)

where K_th is the stress intensity factor threshold, σ₀ is the fatigue strength of the smooth specimen.

3.2. Predicting Fatigue Strength Using the Conventional TCD

The critical distance method to predict the fatigue limit of the notch usually requires the assistance of finite element analysis software. In the present study, the commercial finite element software Abaqus was used to obtain the stress distribution near the notched specimen. The ratio of the finite element size of the specimen to the actual size was set to 1:1. The 8-node hexahedral C3D8R solid element was used in the finite element simulation. Since the critical distance method needs to extract detailed stress data near the notch, the mesh size refinement was performed at the critical location of the notched specimens and the minimum size of the mesh was 0.1 mm, as shown in Figure 7. The model has a total of 5,063,121 nodes and 8,400,000 elements. A fixed constraint was applied at one end of the Q345 flat plate, and an axial tensile load was applied at the other end. The elastic stress distribution near the notch of V2 specimen is shown in Figure 8. Stress analysis was carried out in the notch area using element sizes of 0.1 mm, 0.05 mm, and 0.02 mm to evaluate the effect of mesh size. Figure 8 shows that finite element meshing has good convergence. The stress concentration factor Kt of each notch can be determined from the finite element results, as shown in

Table 2. Stress concentration factor for all Q345qD notched specimens.

NO.	V1	V2	V3	V4
Kt-FEA	2.91	2.64	2.26	1.99
Kt-Noda [40]	2.92	2.64	2.23	1.98
Deviation	−0.3%	0%	1.3%	0.5%

. The stress concentration factor of the Q345qD notched specimen obtained by the stress concentration factor expression of Noda’s double-sided V-notch [40] is also listed in Table 2. The results show that the two are almost identical, with a maximum deviation of only 1.3%. Zong et al. [41] have given the stress intensity factor threshold for Q345qD material when the stress ratio was 0.1 (K_th = 11.07 MPa·m^0.5). Therefore, the conventional critical distance under 1 million cyclic loading can be obtained, L = 0.498 mm, for the Q345qD steel used. According to the characteristics of the critical distance method, when the stress in the critical distance range is equal to the fatigue strength of the smooth specimen, the corresponding applied load is the fatigue strength of the notch.

Table 3. Comparing the predicted values of PM and LM with the fatigue experimental results.

Specimen No.	Experimental Value (MPa)	PM (MPa)	Deviation	LM (MPa)	Deviation
V1	180	139	−22.65%	163	−9.45%
V2	200	149	−25.38%	177	−11.70%
V3	215	153	−28.84%	175	−18.60%
V4	235	169	−28.18%	192	−18.14%

shows the prediction results of the notched specimens V1~V4 based on PM and LM and compares them with the test results. It can be seen from Table 3 that the conventional critical distance method does not provide reasonable fatigue strength prediction results for the low-carbon steel Q345qD small-notch plate specimen. In particular, the prediction ability of the point method is obviously inferior to that of the line method, something which has been supported by other researchers [11,19,22].

4. Proposed Method for Notch Fatigue Analysis

4.1. Theoretical Background of the Proposed Model

As mentioned in the introduction, in many engineering applications, the crack initiation stage does not exist, and some initial microcracks generated by the manufacturing or processing process pre-exist in the engineering component, causing the fatigue limit of materials in practical structural engineering, such as steel [33,34], to be mainly determined by non-propagating fatigue crack behavior. It is well known that the formation of non-propagating cracks is attributed to the crack closure effect [42,43,44]. After the initial microcrack propagates for a short distance, when the applied load is insufficient to overcome the crack closure resistance caused by the plastic wake at the crack tip, the crack stops growing and forms a non-propagating crack, as shown in Figure 9. Therefore, the critical state is reached when the elastic stress of the non-propagating crack wake (point B) is equal to the opening stress (σ_op) of the crack closure effect. Which can be expressed as:

$${\sigma }_{\max }\sqrt{\frac{a}{2S}}={\sigma }_{op}$$

(6)

where S is the length of the non-propagating crack; the crack length of the notch (a) can be expressed as [45,46,47]:

$$a=\frac{1}{\pi }{\left(\frac{K_{th,eff}}{{\sigma }_0}\right)}^2=\frac{1}{\pi }{\left(\frac{K_{th}}{{\sigma }_0}\right)}^2{\left(\frac{1-\lambda }{1-R}\right)}^2$$

(7)

where crack opening stress coefficient λ= σ_op/σ_max; stress ratio R = σ_min/σ_max.

Substituting Equation (7) into Equation (6), the length of the non-propagating crack can be obtained:

$$S=\frac{1}{\pi }{\left(\frac{K_{th}}{{\sigma }_0}\right)}^2{\left(\frac{1-\lambda }{\sqrt{2}\lambda \left(1-R\right)}\right)}^2$$

(8)

The formation of the non-propagating crack changes the position of the crack and causes the crack tip to extend from the initial position (point A) to the non-propagating crack tail (point B) as shown in Figure 9. Since the conventional critical distance method is based on the theory of linear elastic fracture mechanics, the change of the crack position will affect the calculation of the critical length, thereby affecting the accuracy of the fatigue strength prediction. Therefore, the present study attempts to combine the length of the non-propagating crack and the conventional critical distance as a new critical distance.

$${\sigma }^{*}{}_{eff}\left(PM\right)=\sigma \left(L/2+S\right)={\sigma }_0$$

(9)

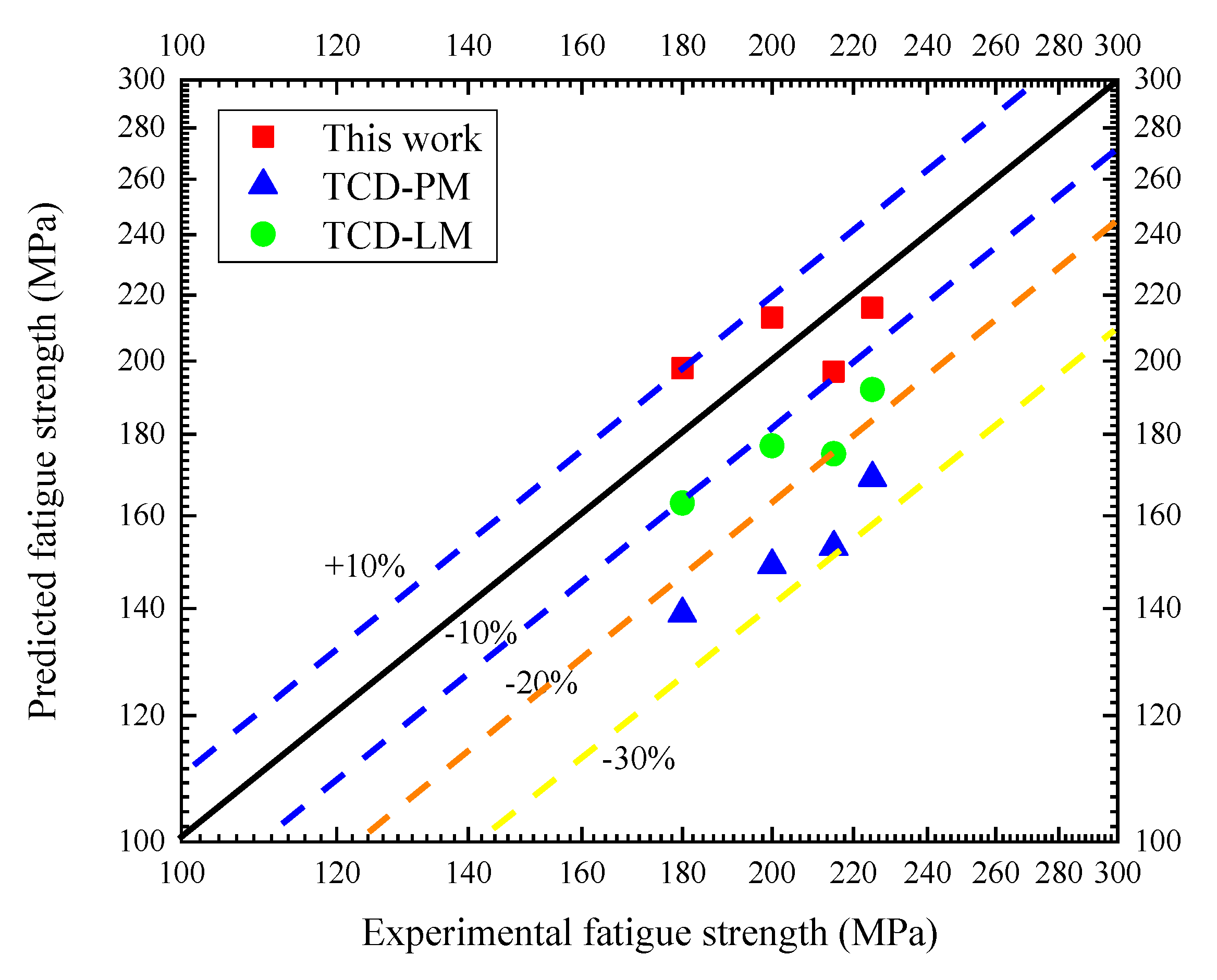
4.2. Model Verification and Analysis

In the present study, the new critical distance length was obtained by coupling NPC and TCD. The length of the non-propagating crack of the proposed model was determined by the crack closure effect. Therefore, the standard ASTM [48] was used to determine the opening stress coefficient of the crack closure effect in the present study, as shown in Equation (10).

$$\lambda =\frac{{\sigma }_{op}}{{\sigma }_{\max }}=0.424+0.561R-0.394R^2+0.409R^3\begin{array}{cc}& R\ge 0\end{array}$$

(10)

Taking the stress within the new critical distance as the effective stress, the fatigue limit prediction result of the proposed theory can be obtained. Figure 10 compares the prediction results of the proposed model and conventional TCD. As can be seen from Figure 10, all predictions of the proposed model fall within the ±10% scattering band, while the conventional TCD-LM falls within the −20% range, TCD-PM falls within the −30% range. Obviously, the prediction result of the proposed model is better than that of the traditional critical distance method. The result can also be explained from a microscopic perspective. Miller [34,35] have illustrated that the fatigue limit refers to the stress level required to overcome the strongest propagation barriers, which will be determined by microstructural barriers such as grain boundaries, twin boundaries, phase boundaries and pearlite bands. However, machining of components destroys the structure of the grains near the notch and produces some overlapping/branched microcracks. The complete closure near the tip for the overlapped/branched crack path shields the crack tip from the applied stress [49], producing a phenomenon in which the interaction of adjacent or surrounding microstructures and crack grains affects crack propagation [50,51]. In a recent study, Lia et al. [52] also obtained similar conclusions through their studies and pointed out that the notch fatigue limit depends on the interaction between the initial effective driving force and crack closure. Therefore, considering the crack closure phenomenon caused by short cracks at the notch root in the framework of the critical distance method is conducive to improving the accuracy of fatigue prediction.

4.3. Size Effect of Critical Distance

Due to the existence of the critical distance size effect, the critical distance theory does not apply to some small notches [17,18,19]. The non-propagating crack will change the original position of the crack, causing a small change in the notch geometry, which in turn triggers the geometric size effect. Therefore, size effect of the critical distance might originate from the non-propagating cracks generated in the small notch. In view of this, the present study compared the proposed critical distance method with the model of Yang et al. [21] and Hertel et al. [22], both of whom take into account the critical distance size effect. The critical distance point method expressions of Yang and Hertel are respectively as follows:

$$\mathrm{Yang}\text{:} L/2=Kt\times \frac{1}{2\pi }{\left(\frac{K_{th}}{{\sigma }_0}\right)}^2$$

(11)

$$\mathrm{Hertel}\text{:} L/2=\frac{1}{2\pi }{\left(\frac{K_{th}}{0.66{\sigma }_0}\right)}^2$$

(12)

Table 4. Critical distance of Q345qD notched specimens based on different critical distance method.

Specimen No.	Critical Distance (mm)
	Yang	Hertel	Proposed
V1	0.725	0.572	0.620
V2	0.657	0.572	0.620
V3	0.563	0.572	0.620
V4	0.496	0.572	0.620

presents critical distance values of notched Q345qD specimens based on different critical distance point methods. Figure 11 shows the prediction results of three different critical distance methods. It can be seen from Figure 10 that the predictions of the proposed model and Hertel’s model fall within the ±10% scattering band; Yang’s model is within the ±15% scattering band. The three methods have almost the same prediction accuracy. This shows that the proposed model can provide a reference for dealing with the critical distance size effect.

4.4. Correlation of Critical Distance Size Effects and Notch Geometry Size

Although related studies have shown that the critical distance size effect will affect the application of the critical distance method [18,19,20,21,22,23,24], the correlation of critical distance size effects and notch geometry size is unclear. In this section, the relationship between the root radius or depth of notch and the critical distance size effect will be analyzed through the size effect parameter ψ. The size effect parameter ψ is defined as:

$$\psi =\frac{{\sigma }_{TCD-SE}-{\sigma }_{\mathrm{TCD}}}{{\sigma }_{TCD-SE}}$$

(13)

where σ_TCD-SE is the notched fatigue strength obtained by the TCD considering the size effect; σ_TCD is the notched fatigue strength obtained by the conventional TCD.

The results of size effect parameters for different notched specimens were obtained by different critical distance correction methods as shown in Figure 12. At the same notch depth, the influence of size effect on fatigue limit is negatively correlated with root radius such as with V1 vs. V3, V2 vs. V4. However, for the notch specimens with the same notch radius, with the increase of notch depth, the effect of size effect on the fatigue limit is not apparent such as with V1 vs. V2, V3 vs. V4. Therefore, the notch root radius is the main factor in the influence of size effect on the fatigue limit.

5. Conclusions

In the present study, a notched fatigue analysis model for considering the effect of non-propagating cracks on fatigue limit prediction in the critical distance method framework was developed. Experimental results of Q345qD low carbon steel with different notch geometries were used for model validation and comparison. Based on the current investigation, the following conclusions can be drawn.

• For the fatigue limit of the V-shaped small notch of Q345qD material, the prediction results of the conventional critical distance method are conservative, and the model proposed in the present study is in good agreement with the experimental results.
• The proposed model can provide a reference for dealing with the critical distance size effect, and the recommended model in present study has almost the same prediction accuracy as the published model that considering the critical size effect.
• The influence of the size effect on the fatigue limit is negatively correlated with the root radius, and the notch radius is the main factor in the influence of size effect on the fatigue limit.