Deep Learning for Brain Tumor Segmentation: A Survey of State-of-the-Art
Abstract
1. Introduction
2. Overview of Brain Tumor Segmentation
2.1. Image Segmentation
- active tumorous tissue;
- necrotic (dead) tissue; and,
- edema (swelling near the tumor).
2.2. Types of Segmentation
2.2.1. Manual Segmentation
2.2.2. Semi-Automatic Segmentation
2.2.3. Fully Automatic Segmentation
3. Deep Learning
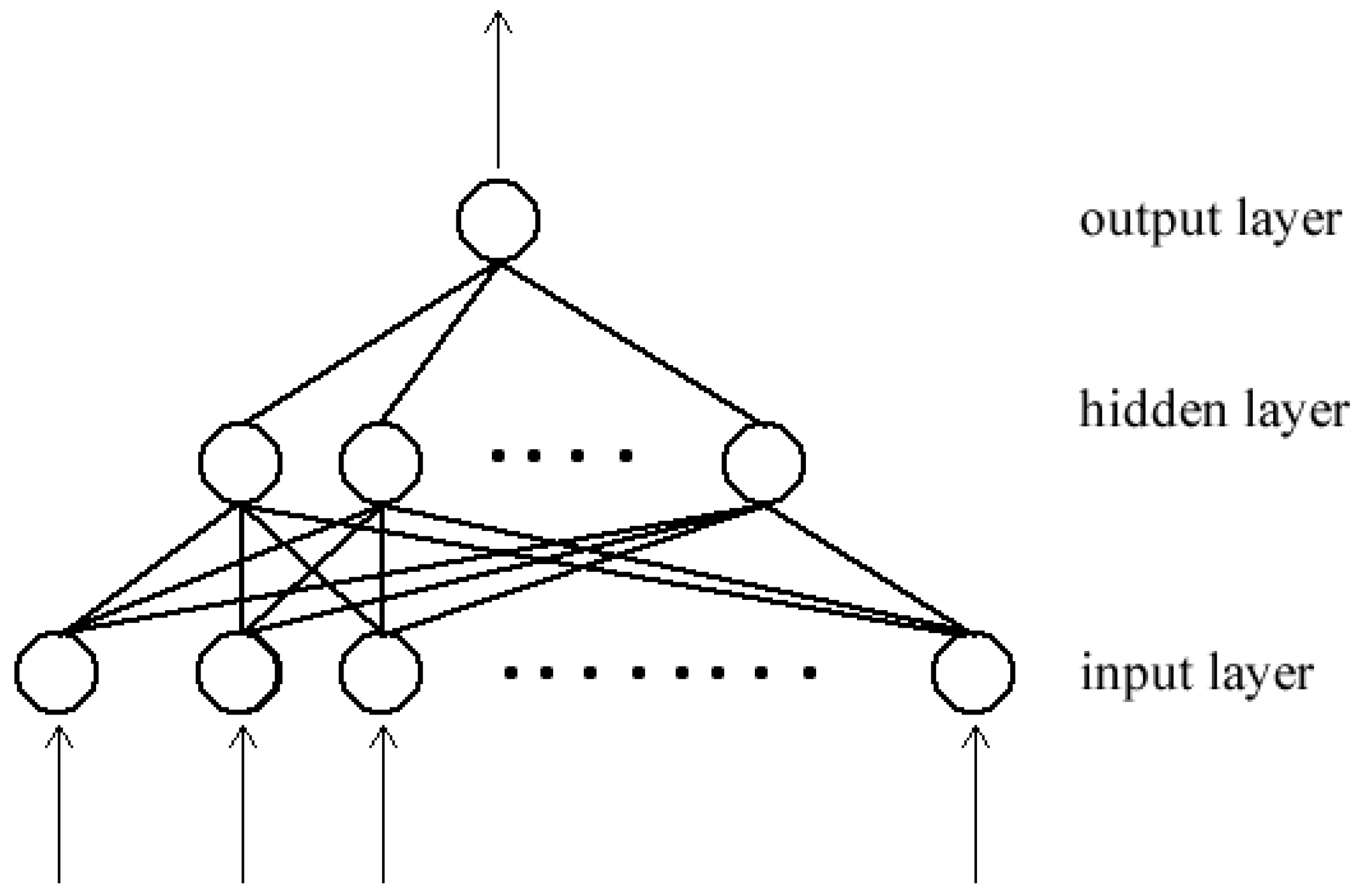
3.1. Neural Networks
3.2. Convolutional Neural Network (CNN)
3.3. Building Blocks CNN
3.3.1. Convolutional Layer
3.3.2. Pooling Layer
3.3.3. Non-Linearity Layer
3.3.4. Fully Connected Layer
3.3.5. Optimization
3.3.6. Loss Function
3.3.7. Parameter Initialization
3.3.8. Hyperparameter Tuning
3.3.9. Regularization
3.4. Deep CNN Architectures
3.4.1. Single Pathway
3.4.2. Dual Pathway
3.4.3. Cascaded Architecture
3.4.4. UNET
3.5. Techniques for Brain Tumor Segmentation
3.5.1. Pre-Processing
3.5.2. Post-Processing
3.5.3. Class Imbalance
3.5.4. Data Augmentation
3.6. Datasets
3.7. Performance Evaluation Metrics
- the whole tumor (includes all tumor structures);
- the tumor core (exclusive of edema); and,
- the active tumor (only consists of the "enhancing core").
3.8. Software and Frameworks
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Havaei, M.; Davy, A.; Warde-Farley, D.; Biard, A.; Courville, A.; Bengio, Y.; Pal, C.; Jodoin, P.M.; Larochelle, H. Brain tumor segmentation with Deep Neural Networks. Med. Image Anal. 2017, 35, 18–31. [Google Scholar] [CrossRef] [PubMed]
- Menze, B.H.; Jakab, A.; Bauer, S.; Kalpathy-Cramer, J.; Farahani, K.; Kirby, J.; Burren, Y.; Porz, N.; Slotboom, J.; Wiest, R.; et al. The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS). IEEE Trans. Med. Imaging 2015, 34, 1993–2024. [Google Scholar] [CrossRef] [PubMed]
- Işın, A.; Direkoğlu, C.; Şah, M. Review of MRI-Based Brain Tumor Image Segmentation Using Deep Learning Methods. Procedia Comput. Sci. 2016, 102, 317–324. [Google Scholar] [CrossRef]
- Kamnitsas, K.; Ledig, C.; Newcombe, V.F.J.; Simpson, J.P.; Kane, A.D.; Menon, D.K.; Rueckert, D.; Glocker, B. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Med. Image Anal. 2017, 36, 61–78. [Google Scholar] [CrossRef] [PubMed]
- Razzak, M.I.; Imran, M.; Xu, G. Efficient Brain Tumor Segmentation With Multiscale Two-Pathway-Group Conventional Neural Networks. IEEE J. Biomed. Health Inform. 2019, 23, 1911–1919. [Google Scholar] [CrossRef]
- Muhammad, K.; Khan, S.; Ser, J.D.; de Albuquerque, V.H.C. Deep Learning for Multigrade Brain Tumor Classification in Smart Healthcare Systems: A Prospective Survey. IEEE Trans. Neural Netw. Learn. Syst. 2020, 1–16. [Google Scholar] [CrossRef]
- Wadhwa, A.; Bhardwaj, A.; Singh Verma, V. A review on brain tumor segmentation of MRI images. Magn. Reson. Imaging 2019, 61, 247–259. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory andArchitectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Zikic, D.; Ioannou, Y.; Brown, M.; Criminisi, A. Segmentation of Brain Tumor Tissues with Convolutional Neural Networks. In Proceedings of the BRATS-MICCAI, Boston, MA, USA, 14 September 2014; pp. 36–39. [Google Scholar]
- Urban, G.; Bendszus, M.; Hamprecht, F.A.; Kleesiek, J. Multi-Modal Brain Tumor Segmentation Using Deep Convolutional Neural Networks. In Proceedings of the BRATS-MICCAI, Boston, MA, USA, 14 September 2014; pp. 31–35. [Google Scholar]
- Shen, D.; Wu, G.; Suk, H.I. Deep learning in medical image analysis. Annu. Rev. Biomed. 2017, 19, 221–248. [Google Scholar] [CrossRef]
- Havaei, M.; Guizard, N.; Larochelle, H.; Jodoin, P.M. Deep Learning Trends for Focal Brain Pathology Segmentation in MRI. In Machine Learning for Health Informatics; Holzinger, A., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 9605, pp. 125–148. [Google Scholar] [CrossRef]
- Corso, J.J.; Sharon, E.; Dube, S.; El-Saden, S.; Sinha, U.; Yuille, A. Efficient Multilevel Brain Tumor Segmentation With Integrated Bayesian Model Classification. IEEE Trans. Med. Imaging 2008, 27, 629–640. [Google Scholar] [CrossRef]
- Gordillo, N.; Montseny, E.; Sobrevilla, P. State of the Art Survey on MRI Brain Tumor Segmentation. Magn. Reson. Imaging 2013, 31, 1426–1438. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Bentley, P.; Mori, K.; Misawa, K.; Fujiwara, M.; Rueckert, D. DRINet for Medical Image Segmentation. IEEE Trans. Med. Imaging 2018, 37, 2453–2462. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning Publications Co.: Shelter Island, NY, USA, 2018. [Google Scholar]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to Multi-Layer Feed-Forward Neural Networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 25, pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. arXiv 2019, arXiv:1709.01507. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the ICML Workshop on Deep Learning for Audio, Speech and Language Processing, Atlanta, GA, USA, 16 June 2013. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv 2015, arXiv:1502.01852. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv 2015, arXiv:1411.4038. [Google Scholar]
- Bernal, J.; Kushibar, K.; Asfaw, D.S.; Valverde, S.; Oliver, A.; Martí, R.; Lladó, X. Deep Convolutional Neural Networks for Brain Image Analysis on Magnetic Resonance Imaging: A Review. Artif. Intell. Med. 2019, 95, 64–81. [Google Scholar] [CrossRef]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the Importance of Initialization and Momentum in Deep Learning. In Proceedings of the 30th International Conference on Machine Learning; Dasgupta, S., McAllester, D., Eds.; PMLR: Atlanta, GA, USA, 2013; Volume 28, pp. 1139–1147. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, G.; Li, W.; Ourselin, S.; Vercauteren, T. Automatic Brain Tumor Segmentation Based on Cascaded Convolutional Neural Networks with Uncertainty Estimation. Front. Comput. Neurosci. 2019, 13, 56. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Li, A.; Wang, M. A novel end-to-end brain tumor segmentation method using improved fully convolutional networks. Comput. Biol. Med. 2019, 108, 150–160. [Google Scholar] [CrossRef]
- Cahall, D.E.; Rasool, G.; Bouaynaya, N.C.; Fathallah-Shaykh, H.M. Inception Modules Enhance Brain Tumor Segmentation. Front. Comput. Neurosci. 2019, 13, 44. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. [Google Scholar]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy Layer-Wise Training of Deep Networks. In Advances in Neural Information Processing Systems 19; Schölkopf, B., Platt, J.C., Hoffman, T., Eds.; MIT Press: Cambridge, MA, USA, 2007; pp. 153–160. [Google Scholar]
- Claesen, M.; De Moor, B. Hyperparameter Search in Machine Learning. arXiv 2015, arXiv:1502.02127. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Pereira, S.; Pinto, A.; Alves, V.; Silva, C.A. Brain Tumor Segmentation Using Convolutional Neural Networks in MRI Images. IEEE Trans. Med. Imaging 2016, 35, 1240–1251. [Google Scholar] [CrossRef] [PubMed]
- Myronenko, A. 3D MRI Brain Tumor Segmentation Using Autoencoder Regularization. arXiv 2018, arXiv:1810.11654. [Google Scholar]
- Rezaei, M.; Harmuth, K.; Gierke, W.; Kellermeier, T.; Fischer, M.; Yang, H.; Meinel, C. Conditional Adversarial Network for Semantic Segmentation of Brain Tumor. arXiv 2017, arXiv:1708.05227. [Google Scholar]
- Rao, V.; Sarabi, M.S.; Jaiswal, A. Brain tumor segmentation with deep learning. In Proceedings of the MICCAI Multimodal Brain Tumor Segmentation Challenge (BraTS), 2015; pp. 56–59. Available online: https://www.researchgate.net/profile/Mona_Sharifi2/publication/309456897_Brain_tumor_segmentation_with_deep_learning/links/5b444445458515f71cb8a65d/Brain-tumor-segmentation-with-deep-learning.pdf (accessed on 1 June 2020).
- Casamitjana, A.; Puch, S.; Aduriz, A.; Sayrol, E.; Vilaplana, V. 3D Convolutional Networks for Brain Tumor Segmentation. In Proceedings of the MICCAI Challenge on Multimodal Brain Tumor Image Segmentation (BRATS), 2016; pp. 65–68. Available online: https://imatge.upc.edu/web/sites/default/files/pub/cCasamitjana16.pdf (accessed on 1 June 2020).
- Hussain, S.; Anwar, S.M.; Majid, M. Brain Tumor Segmentation Using Cascaded Deep Convolutional Neural Network. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017; pp. 1998–2001. [Google Scholar] [CrossRef]
- Pereira, S.; Oliveira, A.; Alves, V.; Silva, C.A. On hierarchical brain tumor segmentation in MRI using fully convolutional neural networks: A preliminary study. In Proceedings of the 2017 IEEE 5th Portuguese Meeting on Bioengineering (ENBENG), Coimbra, Portugal, 16–18 February 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Sled, J.; Zijdenbos, A.; Evans, A. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imaging 1998, 17, 87–97. [Google Scholar] [CrossRef]
- Tustison, N.J.; Avants, B.B.; Cook, P.A.; Zheng, Y.; Egan, A.; Yushkevich, P.A.; Gee, J.C. N4ITK: Improved N3 Bias Correction. IEEE Trans. Med. Imaging 2010, 29, 1310–1320. [Google Scholar] [CrossRef]
- Nyul, L.; Udupa, J.; Zhang, X. New variants of a method of MRI scale standardization. IEEE Trans. Med. Imaging 2000, 19, 143–150. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, Y.; Song, G.; Li, Z.; Zhang, Y.; Fan, Y. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation. Med. Image Anal. 2018, 43, 98–111. [Google Scholar] [CrossRef]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. arXiv 2016, arXiv:1606.04797. [Google Scholar]
- Vaidhya, K.; Thirunavukkarasu, S.; Alex, V.; Krishnamurthi, G. Multi-Modal Brain Tumor Segmentation Using Stacked Denoising Autoencoders. In Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Menze, B., Maier, O., Reyes, M., Handels, H., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 181–194. [Google Scholar] [CrossRef]
- Pereira, S.; Pinto, A.; Alves, V.; Silva, C.A. Deep Convolutional Neural Networks for the Segmentation of Gliomas in Multi-Sequence MRI. In Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Menze, B., Maier, O., Reyes, M., Handels, H., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 131–143. [Google Scholar] [CrossRef]
- Hussain, S.; Anwar, S.M.; Majid, M. Segmentation of glioma tumors in brain using deep convolutional neural network. Neurocomputing 2018, 282, 248–261. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. arXiv 2018, arXiv:1708.02002. [Google Scholar]
- Sun, L.; Zhang, S.; Chen, H.; Luo, L. Brain Tumor Segmentation and Survival Prediction Using Multimodal MRI Scans with Deep Learning. Front. Neurosci. 2019, 13, 810. [Google Scholar] [CrossRef] [PubMed]
- Mlynarski, P.; Delingette, H.; Criminisi, A.; Ayache, N. Deep learning with mixed supervision for brain tumor segmentation. J. Med. Imaging 2019, 6, 034002. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, S.; Ghani Khan, M.U.; Saba, T.; Mehmood, Z.; Javaid, N.; Rehman, A.; Abbasi, R. Deep learning model integrating features and novel classifiers fusion for brain tumor segmentation. Microsc. Res. Tech. 2019, 82, 1302–1315. [Google Scholar] [CrossRef] [PubMed]
- Kuzina, A.; Egorov, E.; Burnaev, E. Bayesian Generative Models for Knowledge Transfer in MRI Semantic Segmentation Problems. Front. Neurosci. 2019, 13, 844. [Google Scholar] [CrossRef]
- Kao, P.Y.; Ngo, T.; Zhang, A.; Chen, J.W.; Manjunath, B.S. Brain Tumor Segmentation and Tractographic Feature Extraction from Structural MR Images for Overall Survival Prediction. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Kuijf, H., Keyvan, F., Reyes, M., van Walsum, T., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; Volume 11384, pp. 128–141. [Google Scholar] [CrossRef]
- Kao, P.Y.; Shailja, F.; Jiang, J.; Zhang, A.; Khan, A.; Chen, J.W.; Manjunath, B.S. Improving Patch-Based Convolutional Neural Networks for MRI Brain Tumor Segmentation by Leveraging Location Information. Front. Neurosci. 2020, 13, 1449. [Google Scholar] [CrossRef]
- Nalepa, J.; Marcinkiewicz, M.; Kawulok, M. Data Augmentation for Brain-Tumor Segmentation: A Review. Front. Comput. Neurosci. 2019, 13, 83. [Google Scholar] [CrossRef]
- Shin, H.C.; Tenenholtz, N.A.; Rogers, J.K.; Schwarz, C.G.; Senjem, M.L.; Gunter, J.L.; Andriole, K.; Michalski, M. Medical Image Synthesis for Data Augmentation and Anonymization Using Generative Adversarial Networks. arXiv 2018, arXiv:1807.10225. [Google Scholar]
- Han, C.; Rundo, L.; Araki, R.; Nagano, Y.; Furukawa, Y.; Mauri, G.; Nakayama, H.; Hayashi, H. Combining Noise-to-Image and Image-to-Image GANs: Brain MR Image Augmentation for Tumor Detection. IEEE Access 2019, 7, 156966–156977. [Google Scholar] [CrossRef]
- Han, C.; Murao, K.; Noguchi, T.; Kawata, Y.; Uchiyama, F.; Rundo, L.; Nakayama, H.; Satoh, S. Learning More with Less: Conditional PGGAN-Based Data Augmentation for Brain Metastases Detection Using Highly-Rough Annotation on MR Images. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing China, 3–7 November 2019; pp. 119–127. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar]
- Simpson, A.L.; Antonelli, M.; Bakas, S.; Bilello, M.; Farahani, K.; van Ginneken, B.; Kopp-Schneider, A.; Landman, B.A.; Litjens, G.; Menze, B.; et al. A Large Annotated Medical Image Dataset for the Development and Evaluation of Segmentation Algorithms. arXiv 2019, arXiv:1902.09063. [Google Scholar]
- Team, T.T.D.; Al-Rfou, R.; Alain, G.; Almahairi, A.; Angermueller, C.; Bahdanau, D.; Bastien, F.; Bayer, J.; Belikov, A.; Belopolsky, A.; et al. Theano: A Python Framework for Fast Computation of Mathematical Expressions. arXiv 2016, arXiv:1605.02688. [Google Scholar]
- Goodfellow, I.J.; Warde-Farley, D.; Lamblin, P.; Dumoulin, V.; Mirza, M.; Pascanu, R.; Bergstra, J.; Bastien, F.; Bengio, Y. Pylearn2: A Machine Learning Research Library. arXiv 2013, arXiv:1308.4214. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional Architecture for Fast Feature Embedding. arXiv 2014, arXiv:1408.5093. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Chollet, F. Keras: The Python Deep Learning API. 2020. Available online: https://keras.io/ (accessed on 1 June 2020).
- Zhang, J.; Shen, X.; Zhuo, T.; Zhou, H. Brain tumor segmentation based on refined fully convolutional neural networks with a hierarchical dice loss. arXiv 2017, arXiv:1712.09093. [Google Scholar]
- Kayalibay, B.; Jensen, G.; Smagt, P.V.D. CNN-based segmentation of medical imaging data. arXiv 2017, arXiv:1701.03056. [Google Scholar]
- Kamnitsas, K.; Bai, W.; Ferrante, E.; McDonagh, S.; Sinclair, M.; Pawlowski, N.; Rajchl, M.; Lee, M.; Kainz, B.; Rueckert, D.; et al. Ensembles of Multiple Models and Architectures for Robust Brain Tumour Segmentation. arXiv 2017, arXiv:1711.01468. [Google Scholar]
- Dong, H.; Yang, G.; Liu, F.; Mo, Y.; Guo, Y. Automatic Brain Tumor Detection and Segmentation Using U-Net Based Fully Convolutional Networks. In Proceedings of the Medical Image Understanding and Analysis; Valdés Hernández, M., González-Castro, V., Eds.; Communications in Computer and Information Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 506–517. [Google Scholar] [CrossRef]
- Alex, V.; Safwan, M.; Krishnamurthi, G. Automatic Segmentation and Overall Survival Prediction in Gliomas Using Fully Convolutional Neural Network and Texture Analysis. arXiv 2017, arXiv:1712.02066. [Google Scholar]
- Erden, B.; Gamboa, N.; Wood, S. 3D Convolutional Neural Network for Brain Tumor Segmentation; Technical Report; Computer Science, Stanford University: Stanford, CA, USA, 2017. [Google Scholar]
- Isensee, F.; Kickingereder, P.; Wick, W.; Bendszus, M.; Maier-Hein, K.H. Brain Tumor Segmentation and Radiomics Survival Prediction: Contribution to the BRATS 2017 Challenge. arXiv 2018, arXiv:1802.10508. [Google Scholar]
- Meng, Z.; Fan, Z.; Zhao, Z.; Su, F. ENS-Unet: End-to-End Noise Suppression U-Net for Brain Tumor Segmentation. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 5886–5889. [Google Scholar] [CrossRef]
- Liu, J.; Chen, F.; Pan, C.; Zhu, M.; Zhang, X.; Zhang, L.; Liao, H. A Cascaded Deep Convolutional Neural Network for Joint Segmentation and Genotype Prediction of Brainstem Gliomas. IEEE Trans. Bio-Med. Eng. 2018, 65, 1943–1952. [Google Scholar] [CrossRef] [PubMed]
- Pereira, S.; Pinto, A.; Amorim, J.; Ribeiro, A.; Alves, V.; Silva, C.A. Adaptive feature recombination and recalibration for semantic segmentation with Fully Convolutional Networks. IEEE Trans. Med. Imaging 2019. [Google Scholar] [CrossRef] [PubMed]
- Kermi, A.; Mahmoudi, I.; Khadir, M.T. Deep Convolutional Neural Networks Using U-Net for Automatic Brain Tumor Segmentation in Multimodal MRI Volumes. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Kuijf, H., Keyvan, F., Reyes, M., van Walsum, T., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 37–48. [Google Scholar] [CrossRef]
- Isensee, F.; Kickingereder, P.; Wick, W.; Bendszus, M.; Maier-Hein, K.H. No New-Net. arXiv 2019, arXiv:1809.10483. [Google Scholar]
- Wang, L.; Wang, S.; Chen, R.; Qu, X.; Chen, Y.; Huang, S.; Liu, C. Nested Dilation Networks for Brain Tumor Segmentation Based on Magnetic Resonance Imaging. Front. Neurosci. 2019, 13, 285. [Google Scholar] [CrossRef]
- Ribalta Lorenzo, P.; Nalepa, J.; Bobek-Billewicz, B.; Wawrzyniak, P.; Mrukwa, G.; Kawulok, M.; Ulrych, P.; Hayball, M.P. Segmenting brain tumors from FLAIR MRI using fully convolutional neural networks. Comput. Methods Programs Biomed. 2019, 176, 135–148. [Google Scholar] [CrossRef]
- Jiang, Z.; Ding, C.; Liu, M.; Tao, D. Two-Stage Cascaded U-Net: 1st Place Solution to BraTS Challenge 2019 Segmentation Task. In Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 231–241. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Zhang, Y.M.; Liu, C.L. Bag of Tricks for 3D MRI Brain Tumor Segmentation. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Eds.; Lecture Notes in Computer, Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 210–220. [Google Scholar] [CrossRef]
- Zhuge, Y.; Krauze, A.V.; Ning, H.; Cheng, J.Y.; Arora, B.C.; Camphausen, K.; Miller, R.W. Brain tumor segmentation using holistically nested neural networks in MRI images. Med. Phys. 2017, 44, 5234–5243. [Google Scholar] [CrossRef]
- Liu, Y.; Stojadinovic, S.; Hrycushko, B.; Wardak, Z.; Lau, S.; Lu, W.; Yan, Y.; Jiang, S.B.; Zhen, X.; Timmerman, R.; et al. A deep convolutional neural network-based automatic delineation strategy for multiple brain metastases stereotactic radiosurgery. PLoS ONE 2017, 12, e0185844. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Yu, J.; Guo, Y.; Cao, W. Deep Learning based Radiomics (DLR) and its usage in noninvasive IDH1 prediction for low grade glioma. Sci. Rep. 2017, 7, 5467. [Google Scholar] [CrossRef]
- Kamnitsas, K.; Chen, L.; Ledig, C.; Rueckert, D.; Glocker, B. Multi-Scale 3D Convolutional Neural Networks for Lesion Segmentation in Brain MRI. Ischemic Stroke Lesion Segm. 2015, 13, 46. [Google Scholar]
- Hoseini, F.; Shahbahrami, A.; Bayat, P. AdaptAhead Optimization Algorithm for Learning Deep CNN Applied to MRI Segmentation. J. Digit. Imaging 2019, 32, 105–115. [Google Scholar] [CrossRef]
- Naceur, M.B.; Saouli, R.; Akil, M.; Kachouri, R. Fully Automatic Brain Tumor Segmentation using End-To-End Incremental Deep Neural Networks in MRI images. Comput. Methods Programs Biomed. 2018, 166, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Yi, D.; Zhou, M.; Chen, Z.; Gevaert, O. 3-D convolutional neural networks for glioblastoma segmentation. arXiv 2016, arXiv:1611.04534. [Google Scholar]
- Cui, S.; Mao, L.; Jiang, J.; Liu, C.; Xiong, S. Automatic Semantic Segmentation of Brain Gliomas from MRI Images Using a Deep Cascaded Neural Network. J. Healthc. Eng. 2018, 2018, 4940593. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Ou, Y.; Huang, T. Automatic Segmentation of Brain Tumor from MR Images Using SegNet: Selection of Training Data Sets. In Proceedings of the 6th MICCAI BraTS Challenge, Quebec City, QC, Canada, 14 September 2017; pp. 309–312. [Google Scholar]
- McKinley, R.; Meier, R.; Wiest, R. Ensembles of Densely-Connected CNNs with Label-Uncertainty for Brain Tumor Segmentation. In Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Kuijf, H., Keyvan, F., Reyes, M., van Walsum, T., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 456–465. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, S.; Ding, C.; Tao, D. Learning Contextual and Attentive Information for Brain Tumor Segmentation. In Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Kuijf, H., Keyvan, F., Reyes, M., van Walsum, T., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 497–507. [Google Scholar] [CrossRef]
- McKinley, R.; Rebsamen, M.; Meier, R.; Wiest, R. Triplanar Ensemble of 3D-to-2D CNNs with Label-Uncertainty for Brain Tumor Segmentation. In Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 379–387. [Google Scholar] [CrossRef]
- Bakas, S.; Reyes, M.; Jakab, A.; Bauer, S.; Rempfler, M.; Crimi, A.; Shinohara, R.T.; Berger, C.; Rozycki, M.; Prastawa, M.; et al. Identifying the Best Machine Learning Algorithms for Brain Tumor Segmentation, Progression Assessment, and Overall Survival Prediction in the BRATS Challenge. arXiv 2019, arXiv:1811.02629. [Google Scholar]
- Ji, Z.; Shen, Y.; Ma, C.; Gao, M. Scribble-Based Hierarchical Weakly Supervised Learning for Brain Tumor Segmentation. arXiv 2019, arXiv:1911.02014. [Google Scholar]
- Pavlov, S.; Artemov, A.; Sharaev, M.; Bernstein, A.; Burnaev, E. Weakly Supervised Fine Tuning Approach for Brain Tumor Segmentation Problem. arXiv 2019, arXiv:1911.01738. [Google Scholar]
- Wu, K.; Du, B.; Luo, M.; Wen, H.; Shen, Y.; Feng, J. Weakly Supervised Brain Lesion Segmentation via Attentional Representation Learning. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2019; Shen, D., Liu, T., Peters, T.M., Staib, L.H., Essert, C., Zhou, S., Yap, P.T., Khan, A., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 211–219. [Google Scholar] [CrossRef]


| Name | Total | Training Data | Validation Data | Testing Data |
|---|---|---|---|---|
| BRATS 2012 [2] | 50 | 35 | - | 15 |
| BRATS 2013 [2] | 60 | 35 | - | 25 |
| BRATS 2014 [2] | 238 | 200 | - | 38 |
| BRATS 2015 [2] | 253 | 200 | - | 53 |
| BRATS 2016 [2] | 391 | 200 | - | 191 |
| BRATS 2017 [2] | 477 | 285 | 46 | 146 |
| BRATS 2018 [2] | 542 | 285 | 66 | 191 |
| BRATS 2019 [2] | 653 | 335 | 127 | 191 |
| Decathlon [70] | 750 | 484 | - | 266 |
| Reference | Input | Preprocessing | Regulization | Loss | Optimizer | Activation |
|---|---|---|---|---|---|---|
| Unet Architecture | ||||||
| [47] | 3D | Z-score | ReLu | |||
| [77] | 2D | BN | Dice, WCE, | Adam | ReLU | |
| BS, SS | ||||||
| [34] | 2D | Z-score, hist-norms | dropout | CE | SDG | LReLU |
| [78] | 3D | cropping | BN | Jaccard loss, CE | PReLU | |
| [79] | Z-score, N4ITK, lin-norm | |||||
| [80] | 2D | Dice | Adam | |||
| [81] | 2D | Z-score, HM | BN | CE | Adam | ReLU |
| [82] | 3D | bounding box | dropout | Dice | Adam | |
| [83] | 3D | Z-score, rescaling, outliers | IN, L2 | Dice | Adam | LReLU |
| [84] | 2D | slice-norm | CE | Adam | ||
| [85] | 3D | BN | Dice | Adam | ||
| [15] | 2D | Z-score | BN | CE | Adam | ReLU |
| [63] | 3D | Z-score | GN | CE, neg-mining | SGD | |
| [36] | 2D | bounding-box, cropping, | BN | Dice | Adam | Relu |
| Z-score, intensity-windowing | ||||||
| [86] | 2D | N4ITK, Nyúl | BN, spatial-dropout | CE | Adam | ReLU |
| [60] | 2D | BN | CE | ReLU | ||
| [87] | 2D | Z-score, remove outliers | BN | WCE, Dice | SGD | PReLU |
| [88] | 3D | Z-score | IN, L2 | CE, Dice | Adam | LReLU |
| [5] | N4ITK, remove outliers | WCE | Adam | |||
| [35] | 2D | Z-score | BN | Dice | Adam | Relu |
| [59] | 3D | Z-score | BN | Dice | Adam | PReLU |
| [89] | 3D | Z-score | BN, L2 | CE, Dice, focal | Adam | ReLU |
| [90] | Z-score | Adam | RelU | |||
| [91] | 3D | Z-score | GN, L2, Dropout | Dice | Adam | ReLU |
| [92] | 3D | RN, random axis mirror | CE, Dice | SDG | ||
| [64] | 3D | Z-score, N4ITK | BN, L2 | CE, NM | Adam | ReLU |
| Dual-pathay Architecture | ||||||
| [10] | 2D | L1, L2 Dropout | SDG | |||
| [1] | 2D | Z-score, N4ITK, outliers | L1, L2, Dropout | log-loss | Maxout | ReLU |
| [47] | 2D | Z-score | Adam | ReLU | ||
| [57] | 2D | Z-score, N4ITK | BN, Dropout | log-loss | SDG | ReLU |
| [63] | 3D | GN | CE, NM | SDG | ||
| [53] | 2D | N4ITK | PReLU | |||
| [5] | N4ITK, outliers | WCE | SGD | |||
| [93] | 3D | N4ITK, LIN | ReLU | |||
| [94] | 3D | Dropout | log-loss | SDG | PReLU | |
| [95] | 2D | N4ITK | Dropout | SGD | ReLU | |
| [4] | 3D | Z-score | log-loss | ReLU | ||
| [79] | Z-score, N4ITK, PLN | |||||
| [96] | 3D | Z-score | BN, L2, Dropout | ReLU | ||
| Single-pathway Architecture | ||||||
| [9] | 2D | log-loss | SGD | ReLU | ||
| [46] | 2D | Dropout | CE | SGD | ReLU | |
| [43] | 2D | SGD | ReLU | |||
| [64] | 3D | Z-score, N4ITK | BN | CE, NM | Adam | ReLU |
| [97] | 2D | CE | Nesterov, RMSProp | ReLu | ||
| [98] | 2D | Z-score, outliers | Adam, SGD, RMSProp | ReLu | ||
| [99] | 3D | ReLU | ||||
| [43] | 3d | Z-score, N4ITK, Nyúl | Dropout | CE | Nesterov | LReLU |
| Ensemble Architecture | ||||||
| [59] | 3D | Z-score | BN | dice | Adam | PReLU |
| [64] | 3D | Z-score, N4ITK | BN | CE, NM | Adam | ReLU |
| [63] | 3D | GN | CE, NM | SDG | ||
| [61] | 2D | Z-score, N4ITK, HN, | Dropout | CE | Adam | |
| [98] | 2D | Z-score, outliers | Adam, SGD, RMSProp | ReLu | ||
| [44] | 3D | Z-score | GN, L2, spatial dropout | Dice | Adam | ReLU |
| [79] | Z-score, N4ITK, PLN | |||||
| Cascaded Architecture | ||||||
| [34] | 2D | HS, Z-score | dropout | CE | SGD | LReLU |
| [1] | 2D | Z-score, N4ITK, remove outliers | Dropout L2, L1 | log-loss | Maxout | |
| [48] | 2D | Maxout | RelU | |||
| [85] | 3D | BN | Dice | Adam | LReLU | |
| [100] | 2D | Z-score, BN, outliers | L2, dropout | CE | SGD | ReLU |
| [34] | 2.5D | Z-score | BN | Dice | Adam | PReLU |
| [59] | 3D | Z-score | BN | Dice | Adam | PReLU |
| [89] | 3D | Z-score | Adam | ReLU | ||
| [86] | 2D | Z-score, N4ITK | BN, spatial dropout | CE | SDG | ReLU |
| [34] | 3D | Z-score | BN | Dice | Adam | PReLU |
| [86] | N4ITK, Nyúl | BN, dropout | CE | Adam | ReLU | |
| [35] | 2D | Z-score | BN | Dice | Adam | ReLU |
| [91] | 3D | Z-score | GN, L2, dropout | Dice | Adam | ReLU |
| Rank | Reference | Architecture | Dice | Sensitivity | Specificity | Hausdorff 95 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ET | WT | TC | ET | WT | TC | ET | WT | TC | ET | WT | TC | |||
| BraTS 2017 | ||||||||||||||
| 1 | [79] | Ensemble | 0.738 | 0.901 | 0.797 | 0.783 | 0.895 | 0.762 | 0.998 | 0.995 | 0.998 | 4.499 | 4.229 | 6.562 |
| 2 | [34] | Cascaded | 0.786 | 0.905 | 0.838 | 0.771 | 0.915 | 0.822 | 0.999 | 0.995 | 0.998 | 3.282 | 3.890 | 6.479 |
| 3 | [83] | Unet | 0.776 | 0.903 | 0.819 | 0.803 | 0.902 | 0.786 | 0.998 | 0.996 | 0.999 | 3.163 | 6.767 | 8.642 |
| 3 | [101] | SegNet | 0.706 | 0.857 | 0.716 | 0.687 | 0.811 | 0.660 | 0.999 | 0.997 | 0.999 | 6.835 | 5.872 | 10.925 |
| BraTS 2018 | ||||||||||||||
| 1 | [44] | Ensemble | 0.825 | 0.912 | 0.870 | 0.845 | 0.923 | 0.864 | 0.998 | 0.995 | 0.998 | 3.997 | 4.537 | 6.761 |
| 2 | [88] | Unet | 0.809 | 0.913 | 0.863 | 0.831 | 0.919 | 0.844 | 0.998 | 0.995 | 0.999 | 2.413 | 4.268 | 6.518 |
| 3 | [102] | Ensemble | 0.792 | 0.901 | 0.847 | 0.829 | 0.911 | 0.836 | 0.998 | 0.994 | 0.998 | 3.603 | 4.063 | 4.988 |
| 3 | [103] | Ensemble | 0.814 | 0.909 | 0.865 | 0.813 | 0.914 | 0.868 | 0.998 | 0.995 | 0.997 | 2.716 | 4.172 | 6.545 |
| BraTS 2019 | ||||||||||||||
| 1 | [91] | two-stage Unet | 0.802 | 0.909 | 0.865 | 0.804 | 0.924 | 0.862 | 0.998 | 0.994 | 0.997 | 3.146 | 4.264 | 5.439 |
| 2 | [92] | Unet | 0.746 | 0.904 | 0.840 | 0.780 | 0.901 | 0.811 | 0.990 | 0.987 | 0.990 | 27.403 | 7.485 | 9.029 |
| 3 | [104] | Ensemble | 0.634 | 0.790 | 0.661 | 0.604 | 0.727 | 0.587 | 0.983 | 0.980 | 0.983 | 47.059 | 14.256 | 26.504 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magadza, T.; Viriri, S. Deep Learning for Brain Tumor Segmentation: A Survey of State-of-the-Art. J. Imaging 2021, 7, 19. https://doi.org/10.3390/jimaging7020019
Magadza T, Viriri S. Deep Learning for Brain Tumor Segmentation: A Survey of State-of-the-Art. Journal of Imaging. 2021; 7(2):19. https://doi.org/10.3390/jimaging7020019
Chicago/Turabian StyleMagadza, Tirivangani, and Serestina Viriri. 2021. "Deep Learning for Brain Tumor Segmentation: A Survey of State-of-the-Art" Journal of Imaging 7, no. 2: 19. https://doi.org/10.3390/jimaging7020019
APA StyleMagadza, T., & Viriri, S. (2021). Deep Learning for Brain Tumor Segmentation: A Survey of State-of-the-Art. Journal of Imaging, 7(2), 19. https://doi.org/10.3390/jimaging7020019







