1. Introduction
Quantum Theory is booming: It allows us to describe elementary particles and fundamental forces, to predict the colour of the light emitted by excited atoms and molecules, to explain the black body spectrum and the photoelectric effect, to determine the specific heat and the speed of sound in solids, to understand chemical and biochemical reactions, to construct lasers, transistors, and computers. This extraordinary experimental and technological success, however, is dimmed by huge conceptual difficulties. After more than hundred years from the birth of Quantum Theory, we still struggle to understand its puzzles and hotly debate on its interpretations. Even leaving aside the vexed issue of interpretations, there is a more basic (and embarrassing) problem: We cannot even tell what Quantum Theory is without resorting to the abstract language of Hilbert spaces! Compare quantum mechanics with the classical mechanics of Newton and Laplace: Intuitive notions, such as position and velocity of a particle, are now replaced by abstract ones, such as unit vector in a complex Hilbert space. Physical systems are now represented by Hilbert spaces, pure states by unit vectors, and physical quantities by self-adjoint operators. What does this mean? Why should Nature be described by this very special piece of mathematics?
It is hard not to suspect that, despite all our experimental and technological advancement, we are completely missing the big picture. The situation was vividly portrayed by John Wheeler in a popular article in the New York Times, where he tried to attract the attention of the general public to what he was considering “the greatest mystery in physics today” [
1]: “Balancing the glory of quantum achievements, we have the shame of not knowing ‘how come’. Why does the quantum exist?”
The need for a more fundamental understanding was clear since the early days of Quantum Theory. The first to be dissatisfied with the Hilbert space formulation was its founder himself, John von Neumann [
2]. Few years after the completion of his monumental book [
3], von Neumann tried to understand Quantum Theory as a new form of logics. His seminal work in collaboration with Birkhoff [
4] originated the field of quantum logics, which however did not succeed in producing a clear-cut picture capable to cross the borders of a small community of specialists. More recently, a fresh perspective on the origin of the quantum came from Wheeler. In his programme
It from Bit, Wheeler argued that information should be the fundamental notion in our understanding of the whole of physics, based on the premise that “all things physical are information-theoretic in origin” [
5]. If we accept this premise, then nothing is more natural then looking for an information-theoretic understanding of
quantum physics. Indeed, one of the most noteworthy features of quantum theory is the peculiar way in which it describes the extraction of information through measurements. This remarkable feature and its foundational import were discussed in depth by Wootters in his PhD thesis [
6]. In different guises, the idea of information being the core of Quantum Theory has been explored by several authors, notably by Weizsacker [
7], Zeilinger [
8], and Brukner [
9].
The idea that Quantum Theory is in its backbone a new theory of information became very concrete with the rise of Quantum Information. This revolutionary discipline revealed that Quantum Theory is not just a theory of unavoidable indeterminacy, as emphasized by its founders, but also a theory of new exciting ways to process information, ways that were unimaginable in the old classical world of Newton and Laplace. Quantum Information unearthed a huge number of operational consequences of Quantum Theory: quantum states cannot be copied [
10,
11] but they can be teleported [
12], the quantum laws allow for secure key distribution [
13,
14], for fast database search [
15], and for the factorization of large numbers in polynomial time [
16]. These facts are so impressive that one may be tempted to promote some of them to the role of fundamental principles, trying to derive the obscure mathematics of Quantum Theory from them. The idea that the new discoveries of Quantum Information could offer the key to the mystery of the quantum was enthusiastically championed by Fuchs [
17] and Brassard [
18] and rapidly led to a feverish quest for new information-theoretic principles, like
information causality [
19], and to the reconstructions of quantum theory from various informational ideas, like those of [
20,
21,
22,
23,
24,
25].
Recently, a new derivation of Quantum Theory from purely information-theoretic principles has been presented in [
26] (see also [
27] for a short introduction to the background). In this work, which marks a first step towards the realization of Wheeler’s dream, Quantum Information is shown to maintain its promise for the understanding of fundamental physics: indeed, the key principle that identifies Quantum Theory is the
Purification Principle [
28], which is directly inspired by the research in Quantum Information. Quantum Theory is now captured by a complete set of information-theoretic principles, which can be stated using
only the elementary language of systems, processes, and probabilities. With respect to related reconstructive works, the new derivation of [
26] has the advantage of offering a clear-cut picture that nails down in few simple words what is special about of Quantum Theory: Quantum Theory is, in the first place, a theory of information, which shares some basic features with classical information theory, but differs from it on a crucial point, the
purity and reversibility of information processing. In a standard set of theories of information, Quantum Theory appears to be the only theory where the limited knowledge about the processes that we observe in nature is enough to reconstruct a picture of the physical world where all processes are pure and reversible.
More precisely, when we state that Quantum Theory is a theory of information, we mean that the mathematical framework of the theory can be expressed by using only concepts and statements that have an informational significance, such as the concept of signalling, of distinguishability of states, or of encoding/decoding. Here we refer to “information” and “informational significance” in a very basic, primitive sense: in this paper we will not rely on specific measures of information, such as the Shannon, von Neumann, or Renyi entropies. In fact, the very possibility of defining such quantitative measures is based on the specific mathematical structure of classical and quantum theory (chiefly, on the fact that in these theories every mixed state is a probabilistic mixture of perfectly distinguishable states), which, for the quantum case, is exactly what we want to pin down with our principles.
The informational concepts used in this paper are connected to the more traditional language of physics by viewing the possible physical processes as information processing events. For example, a scattering process can be viewed as an event—the interaction—that transforms the input information encoded in the momenta of the incoming particles into the output information encoded in the momenta of the scattered particles. From this perspective, the properties of the particular theory of information that we adopt immediately translate into properties of our physical description of the world. The natural question that we address here is: which properties of a theory of information imply that the description of the world must be quantum?
The purpose of this paper is to give a short, non-technical answer to the question, providing an account of the informational principles of Quantum Theory presented in [
26] and of the worldview emerging from them. Hence, we will focus on the broad picture and on the connection of the principles with other fundamental areas of theoretical physics, while referring the reader to the comprehensive work of [
26] for the mathematical definitions and for the rigorous proofs of the claims.
2. A Complete Set of Information-Theoretic Principles for Quantum Theory
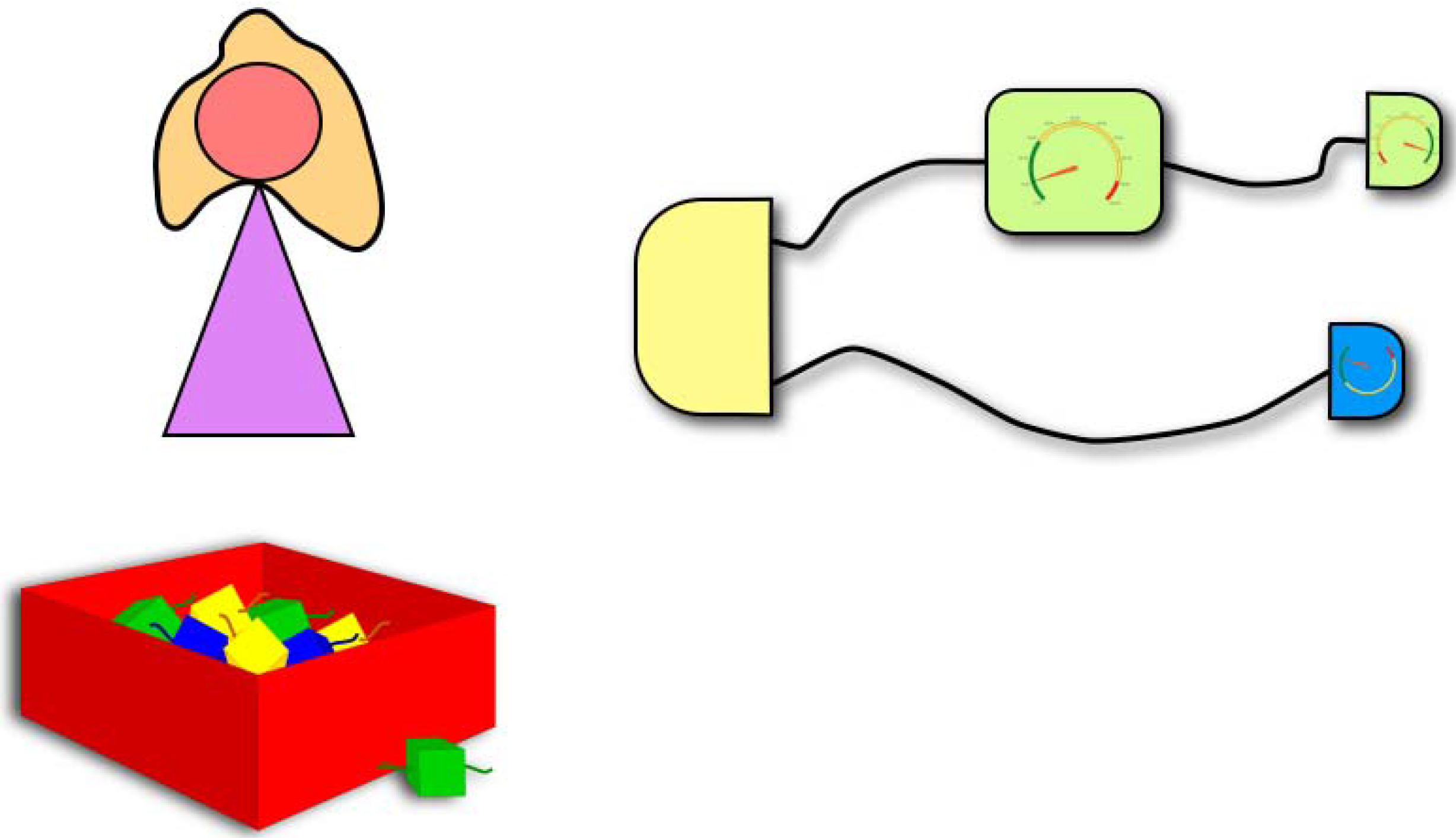
To portray Quantum Theory, we set up a scene where an experimenter, Alice, has many devices in her laboratory and can connect them in series and in parallel to build up circuits (
Figure 1). In Alice’s laboratory, any device can have an input and an output system, and possibly some outcomes that Alice can read out. Each outcome labels a different
process transforming the input into the output: the device itself can be viewed as a
random process. Some devices have no input: they are
preparations, which initialize the system in some state. Other devices have no output: they are
measurements, which absorb the system and produce an outcome with some probability.
Figure 1.
Alice’s laboratory. Alice has at disposal many devices, each of them having an input system and an output system (represented by different wires) and possibly a set of outcomes labelling different processes that can take place. The devices can be connected in series and in parallel to form circuits. A circuit with no input and no output wires represents an experiment starting from the preparation of a state with a given source and ending with some measurement(s). Specifying a theory for Alice’s laboratory means specifying which are the allowed devices and specifying a rule to predict the probability of outcomes in such experiments.
Figure 1.
Alice’s laboratory. Alice has at disposal many devices, each of them having an input system and an output system (represented by different wires) and possibly a set of outcomes labelling different processes that can take place. The devices can be connected in series and in parallel to form circuits. A circuit with no input and no output wires represents an experiment starting from the preparation of a state with a given source and ending with some measurement(s). Specifying a theory for Alice’s laboratory means specifying which are the allowed devices and specifying a rule to predict the probability of outcomes in such experiments.
From a slightly more formal point of view, Alice’s circuits can be described with a graphical language where boxes represent different devices and wires represent physical systems travelling from one device to the next [
28], in a way that is inspired by the picturalist framework by Coecke [
29]. These circuits are essentially the same circuits that are commonly used in Quantum Information [
30], except for the fact that here we do not specify from the beginning the mathematical representation of the devices: we do not specify that the possible states are described by density matrices on some complex Hilbert space, or that the possible reversible evolutions are described by unitary operators. Retrieving these specific mathematical prescriptions from operationally meaningful assumptions is indeed the main technical point of [
26] and of the other quantum reconstructions [
20,
21,
22,
23,
24,
25].
Since the devices in Alice’s laboratory can have different outcomes, there are two natural ways to associate circuits to an experiment. First, a circuit can represent the schematic of Alice’s experimental setup. For example, the circuit
represents a setup where Alice connects a preparation device that outputs system
, a transformation device that turns system
into system
, and, finally a measurement device that measures system
. Here all the devices are allowed to have outcomes: outcome
will herald the fact that the first device prepared the state
,
will herald that the second device performed the transformation
, and outcome
will herald the event
in the final measurement. In the specific case of Quantum Theory,
is going to be an
ensemble of quantum states of system
(that is, a collection of unnormalized density matrices on a suitable Hilbert space
with the property
),
is going to be a
quantum instrument (a collection of completely positive maps sending states on
to states on
with the property that the map
is trace-preserving), and
is going to be a
quantum measurement (a collection of positive operators on
with the property
, the identity on
). A reader who is not familiar with these notions can find a didactical presentation in Chapter 8 of [
30]. Note that the graphical representation of the circuit has a privileged direction (from left to right in our convention) corresponding to the
input-output arrow: wires on the left of a box represent its inputs, wires on the right of a box represent its outputs. Such a preferred input-output arrow will be important later in the statement of the Causality principle.
The second way to associate a circuit to an experiment is to represent the instance of the experiment corresponding to a particular sequence of outcomes. For example, the circuit
represents a particular instance of the experiment with the setup in Equation (
1), corresponding to the particular sequence of outcomes
. In this specific instance, the first device has prepared the state
, the second device has implemented the transformation
, and the final measurement has given outcome
z. A circuit with no open wires, like the circuit in Equation (
2), will be associated to a joint probability
, namely the joint probability of obtaining the outcomes
in the experiment with setup (
1). Notice however that nothing prevents us from drawing circuits with open wires, such as
which represents a “non-demolition measurement”, where the system
(initially in the state
ρ) interacts with a probe
(initially in state
σ) through some transformation
, after which the probe undergoes a measurement, giving outcome
i.
In summary, our basic framework to treat general theories of information is based on the combination of the graphical language of circuits with elementary probability theory. Such a combination of circuits and probabilities, originally introduced in [
28] and discussed in [
31], offers a simple ground for the study of generalized probabilistic theories [
20,
21,
32,
33,
34,
35], and allows one to avoid some of the technicalities of the more traditional “convex sets framework”, such as the choice to the tensor product (see e.g., [
35]).
The features of the probability distributions arising in Alice’s experiments depend on the particular physical theory describing her laboratory: At this basic level, the theory could be classical or quantum, or any other fictional theory that we may be able to invent. We now start restricting the circle of possible theories: first of all, we make sure that Alice’s laboratory is not in a fictional Wonderland, but in a standard world enjoying some elementary properties common to Classical and Quantum Theory. The first property is:
Principle 1 (Causality) The probability of an outcome at a certain step does not depend on the choice of experiments performed at later steps.
The word
later in the statement of the principle refers to the ordering of the computational steps in a circuit induced by the input-output connections: in our graphical representation the ordering goes from the left to the right and a box connected to the output of another represents a later computational step (
cf. Equations (
1) and (
2)). The causality principle identifies the input-output ordering of a circuit with the
causal ordering, namely the direction along which information flows, without any refluence. In more physical terms, we could informally replace the word “step” with the word “time” in the formulation of causality. In this language, Causality is the requirement that Alice’s future choices do not affect the outcomes of her present experiments
(no-signalling from the future).
Causality is implicit in the framework in most works in the tradition of generalized probabilistic theories [
20,
23,
24,
32,
33,
34,
35]. The reason why we are stating it explicitly as the first principle of our list is that we would like it to be a reminder that the formulation of Quantum Theory, in the way it is presently known, requires a well-defined causal structure in the background. This immediately opens the question whether it is possible to formulate a general version of Quantum Theory in scenarios where such a well-defined causal structure cannot be taken for granted. As it was observed by Hardy [
36], the formulation of such a generalized Quantum Theory with indefinite causal structure could be a route to the formulation of a quantum theory of gravity. In this spirit, the information-theoretic principles presented here are very appealing, because they suggest to construct a generalized Quantum Theory on indefinite causal structure by weakening the Causality principle while keeping the other principles unaltered.
Let us set more requirements on the processes taking place in Alice’s laboratory. For every random process, there is also a coarse-grained process where some random outcomes are joined together, thus neglecting some information. A fine-grained process is instead a process where no information has been neglected: in this case Alice has maximal knowledge about the process taking place in her laboratory. For example, in the roll of a die the fine-grained processes are “the roll yielded the number n”, with , while “the roll yielded an even number” is a coarse-grained process. When Alice declares outcome “even” she is joining together the outcomes 2, 4 and 6, thus neglecting the corresponding information. For preparation processes, the coarse-grained processes are called mixed states and fine-grained processes are called pure states.
Our second principle is:
Principle 2 (Fine-Grained Composition) The sequence of two fine-grained processes is a fine-grained process.
This principle establishes that “maximal knowledge of the episodes implies maximal knowledge of the history”: if Alice possesses maximal knowledge about all processes in a sequence, then she also possesses maximal information about the whole sequence. A physical theory where this did not hold would be highly pathological, because the mere composition of two processes, which considered by themselves are specified with the maximum degree of accuracy possible, would generate some global information that cannot be accessed on a step-by-step basis. For preparation processes, this would mean that by putting together two systems that individually are in a pure state, we would get a compound system that, considered as a whole, is in a mixed state. We will come back to this point in more detail in the discussion of our fifth principle, Local Tomography, which has a similar yet different and logically independent content.
If Alice describes the system as being in a pure state, then this means that she has maximal knowledge about the system’s preparation. Instead, if Alice describes the system as being in a mixed state, then she is ignoring (or choosing to ignore) some information about the preparation. When Alice describes the preparation of her system with a mixed state ρ, her description is compatible with the system being prepared in any of the pure states from which ρ results as a coarse-graining. This concept can be easily exemplified for the roll of a (generally unfair) die: here the pure states are numbers from 1 to 6, while the mixed states are probability distributions over . A mixed state p is compatible with every pure state such that , while it is not compatible with those x such that . If a mixed state p is not compatible with some pure states , then it is possible to distinguish perfectly between p and any other probability distribution q that has support contained in . The same feature holds in Quantum Theory: if a density matrix ρ on some Hilbert space is not compatible with some pure state φ [that is, if there is no probability and no density matrix σ such that ] then the the density matrix ρ should have a non-trivial kernel, defined as the set of all vectors such that . Hence ρ will be perfectly distinguishable from any pure state in its kernel, and, more generally, from any mixture of pure states in its kernel. Abstracting from these specific examples, we can state the following general principle:
Principle 3 (Perfect Distinguishability) If a state is not compatible with some preparation, then it is perfectly distinguishable from some other state.
In other words, “possessing definite information about the preparation implies the ability to experimentally falsify some proposition”. Indeed, suppose that knowing that the system is prepared in the state allows us to exclude that the system is in a pure state φ. Then, Perfect Distinguishability guarantees that is perfectly distinguishable from some other state, call it . The proposition “the system was prepared in the state ” can then be falsified by performing the measurement that distinguishes perfectly between and . Note that, thanks to Perfect Distinguishability, Alice can use and to encode the value of a classical bit in a physical support without errors.
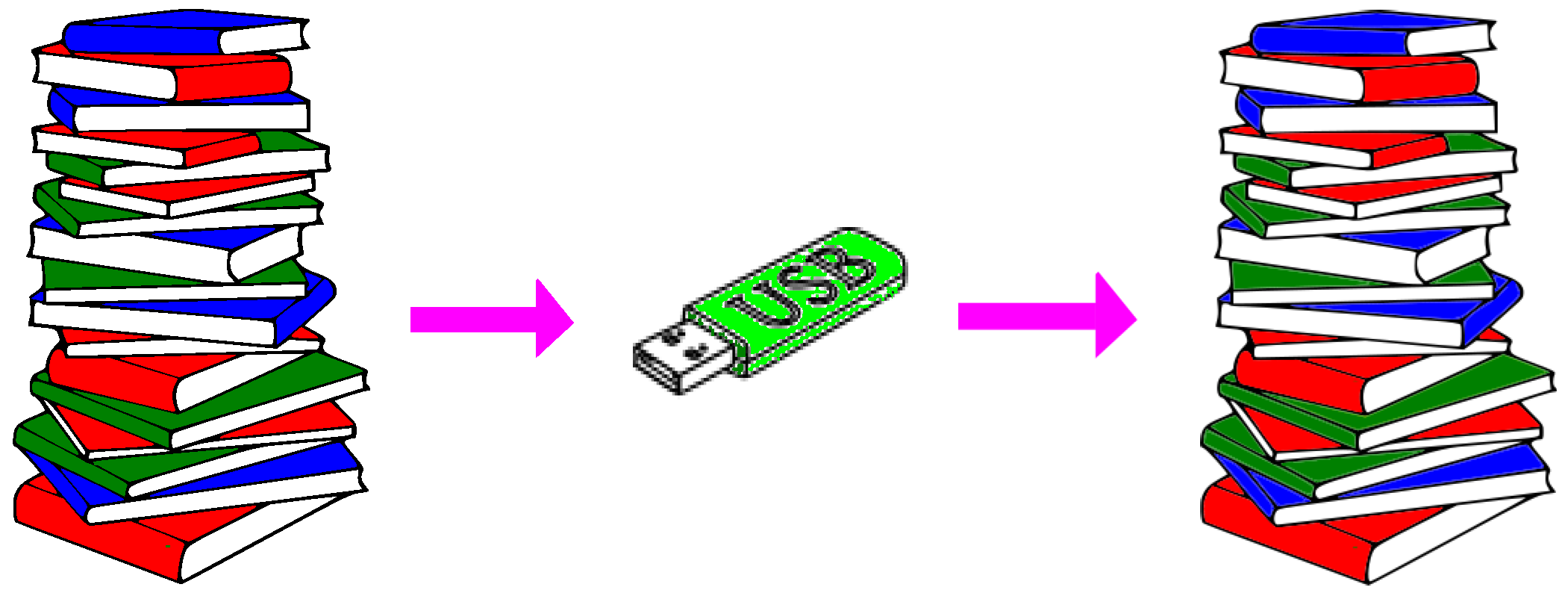
Suppose that Alice wants to transfer to another experimenter Bob all the information she possesses about a system. If the system’s state
ρ is mixed, then Alice ignores the exact preparation: with some non-zero probability the system could be in any of the pure states compatible with
ρ. Hence, in order for her transmission to be successful, the transmission should work for every pure state compatible with
ρ. Moreover, since transferring data has a cost, Alice would better
compress the information (
Figure 2).
Our fourth principle guarantees the possibility of such an ideal compression:
Principle 4 (Ideal Compression) Information can be compressed in a lossless and maximally efficient fashion.
Due to the Ideal Compression principle, Alice can transfer information without transferring the particular physical system in which information is embodied. In the example of the roll of the die, Ideal Compression principle can be illustrated as follows: if our information about the outcome of the roll is described by a probability distribution
p with
and
, then we can faithfully encode this information in the state of a coin, by encoding 1 into “heads” and 2 into “tails”. This compression is perfectly lossless and maximally efficient in the sense of our definition. Note that this elementary notion of ideal compression differs from the more articulate notion used in Shannon’s theory [
37], in Schumacher’s quantum theory of compression, and in everyday information technology, where one is often willing to tolerate some losses in order to further reduce the size of the physical support in which information is encoded. In that case, the compression is required to be lossless only in the asymptotic limit of many identical uses of the same information source, and the efficiency is defined among the set of compression protocols that are asymptotically lossless [
37,
38].
Figure 2.
Compressing information. Alice encodes information (here represented by a pile of books) in a suitable system carrying the smallest possible amount of data (here a USB stick). The most advantageous situation is when the compression is lossless (after the encoding Bob is able to perfectly retrieve the information) and maximally efficient (the encoding system contains only the pure states needed to convey the information compatible with ρ).
Figure 2.
Compressing information. Alice encodes information (here represented by a pile of books) in a suitable system carrying the smallest possible amount of data (here a USB stick). The most advantageous situation is when the compression is lossless (after the encoding Bob is able to perfectly retrieve the information) and maximally efficient (the encoding system contains only the pure states needed to convey the information compatible with ρ).
The next principle concludes our list of requirements that are satisfied both by Classical and Quantum Theory:
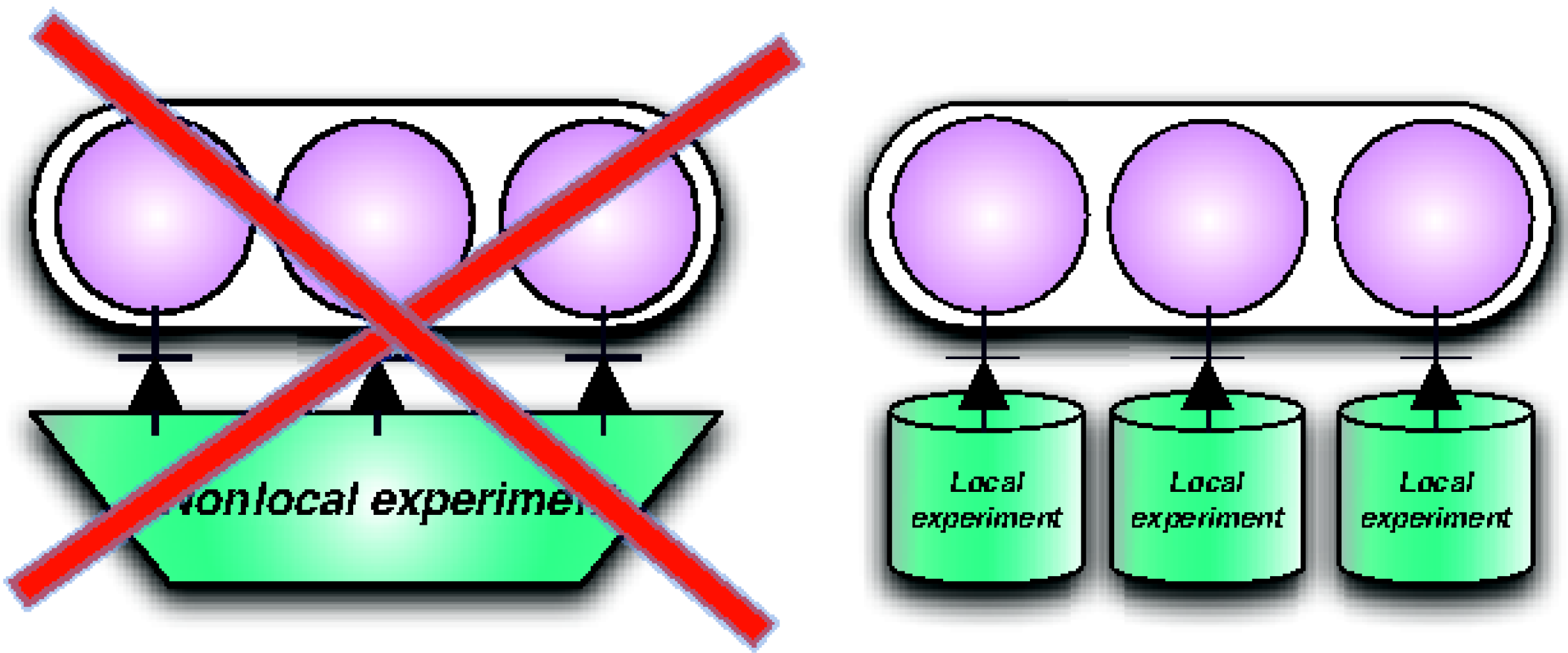
Principle 5 (Local tomography) The state of a composite system is determined by the statistics of local measurements on the components.
Local Tomography plays a crucial role in reducing the complexity of experimental setups needed to characterize the state of multi-partite systems, ensuring that all the information contained in a composite system is accessible to joint local measurements, as illustrated in
Figure 3. Mathematically, this principle is the key reason for the choice of
complex (instead of real) Hilbert spaces: in real Hilbert space Quantum Theory, there are some bipartite states that can be distinguished perfectly with global measurements but give the same statistics for all possible local measurements, as it was noted by Wootters [
39]. It is worth noticing that Quantum Theory on real Hilbert spaces still satisfies the Local Tomography principle
if we restrict our attention to pure states [
28]. Finally, it is interesting to comment on the relation between Fine-Grained Composition and Local Tomography. Although these two principles have a similar flavour (both of them exclude the possibility of having some inaccessible global information), they are actually very different. Fine-Grained Composition states that if we put together two processes of which we have maximal knowledge, then we obtain a process of which we have maximal knowledge as well. In particular, for preparation processes this means that if we prepare two systems
and
in two pure states, then the composite system
will be in a pure state as well. This is a much weaker statement than Local Tomography! Indeed, it is quite simple to see that Quantum Theory on real Hilbert spaces satisfies Fine-Grained Composition, but not Local Tomography. In principle, it is also conceivable to have fictional theories that satisfy Local Tomography, but not Fine-Grained Composition: although Local Tomography implies Fine-Grained composition in the particular case of preparation processes, it is possible to construct locally tomographic theories where Fine-Grained Composition fails at the level of general processes (processes that have both a non-trivial input and a non-trivial output).
Figure 3.
Local Tomography. Alice can reconstruct the state of compound systems using only local measurements on the components. A world where this property did not hold would contain global information that cannot be accessed with local experiments.
Figure 3.
Local Tomography. Alice can reconstruct the state of compound systems using only local measurements on the components. A world where this property did not hold would contain global information that cannot be accessed with local experiments.
The five principles presented so far define a family of theories of information that can be regarded as a standard. If it were just for these principles, Alice’s experiments could still be described, for example, by Classical Theory. What is then special about Quantum Theory? What makes it different from any other theory of information satisfying the five basic principles presented so far? Our answer is the following: Quantum Theory is the only theory of information that is compatible with a description of physical processes only in terms of pure states and reversible interactions. In a sense, Quantum Theory is the only physical theory of information: the only theory where Alice’s ignorance about processes happening in her laboratory is compatible with a complete picture of the physical world. Colourfully reinterpreting Einstein’s quote: God does not play dice, but we definitely do, and God must be able to describe our game!
Let us spell out our last principle precisely. In Quantum Theory, every random process can be simulated as a reversible interaction of the system with a pure environment (i.e., with an environment in a pure state). This simulation is essentially unique: once we fix the environment, two simulations of the same random process can only differ by a reversible transformation acting on the environment. Essential uniqueness is a very important feature: it means that Alice’s information about a random process happening in her laboratory is sufficient for her to determine the system-environment interaction in the most precise way possible (compatibly with the fact that Alice has no access to the environment). Distilling these ideas in a principle, we obtain the following:
Principle 6 (Purity and Reversibility of Physical Processes) Every random process can be simulated in an essentially unique way as a reversible interaction of the system with a pure environment.
The Purity and Reversibility principle is closely connected with the idea of
reversible computation, introduced in the seminal works by Bennett [
41] and Fredkin–Toffoli [
42]. In the world of classical computers, it was shown that every deterministic function (even a non-invertible function) can be computed in a reversible way, by suitably enlarging the space of the computation with additional bits initialized in a fixed pure state. This is a fundamental observation because it hints at the possibility of computing without erasing information, which, by Landauer’s principle [
43], would imply an energy cost and an increase of entropy in the environment (see also pp. 153–161 of [
30] for an easy introduction to these topics). In the classical world, however, only deterministic functions can be computed through a reversible interaction of the input system with a pure environment, whereas classical stochastic processes require the environment to be initialized in a mixed state. In other words, the realization of classical stochastic processes requires a source of randomness in the environment, which, loosely speaking, has to “pump entropy” into the system. This is unfortunate, because stochastic processes are also computationally interesting and useful for a number of applications in the the most disparate disciplines (e.g., think of the wide application of the Monte-Carlo and Metropolis algorithms). Instead, the bonus offered by Quantum Theory, as stated by the Purity and Reversibility principle, is that
every allowed process (including those of a stochastic nature) can be realized in a pure and reversible fashion, thus allowing for a fully reversible model of information processing.
The Purity and Reversibility principle concludes our list. For finite systems (systems whose state is determined by a finite number of outcome probabilities) the six principles presented above describe Quantum Theory completely [
26]: complex Hilbert spaces, superposition principle, Heisenberg’s uncertainty relations, entanglement, no-cloning, teleportation, violation of Bell’s inequalities, quantum cryptography—every quantum feature is already here, encapsulated in the principles. The detailed proof can be found in [
26]. The surprising result here is that, although our sketch of Alice’s laboratory may seem too simplistic, especially to physicists (after all, the Universe is not a big laboratory where we can choose the preparations and measurements at will!), this scenario is rich enough to capture the basic language of Quantum Theory. Technically, our information-theoretic principles imply the following mathematical statements:
physical systems are associated to complex Hilbert spaces;
the maximum number of perfectly distinguishable states of the system is equal to the dimension of the corresponding Hilbert space;
the pure states of a system are described by the unit vectors in the corresponding Hilbert space (up to a global phase);
the reversible processes on a system are described by the unitary operators on the corresponding Hilbert space (up to a global phase);
the measurements on a system are described by resolutions of the identity in terms of positive operators
on the corresponding Hilbert space (aka POVMs, see, e.g., [
30] for a didactical presentation);
the mixed states of a system are described by density matrices on the corresponding Hilbert space;
the probabilities of outcomes in a measurement are given by the Born rule , where ρ is the density matrix representing the system’s state and denotes the trace of a matrix;
the Hilbert space associated to a composite system is the tensor product of the Hilbert spaces associated to the components;
random processes are described by completely positive trace-preserving maps.
Remarkably, these statements are exactly the mathematical features mentioned in the original paper by Fuchs [
17], which was calling for an information-theoretic reason thereof.
Although the derivation of [
26] holds for finite systems, it is natural to expect that the principles discussed here will identify Quantum Theory also in infinite dimension: in that case one has to take care of many technicalities, which however have more to do with the mathematical problem of infinity rather than with the conceptual problems of Quantum Theory.
4. Discussion and Conclusions
Before concluding, some remarks are in order. First of all, it is important to stress that the principles in [
26] are about the syntax of physical experiments, and not about their semantics. When we discuss about systems, transformations, and measurements, we take a general information-theoretic standpoint that abstracts from the specific physical realization of these notions. From the information-theoretic standpoint, all two-level systems are equivalent, no matter if they are implemented with the polarization of a photon, the magnetic moment of a nucleus, or the charge in a superconductor. This is at the same time a strength and a limitation of the information-theoretic approach. On the one hand, forgetting about the specific details of the physical implementation is a very powerful abstraction: it is the abstraction that allows us to talk about “software” without specifying the details of the “hardware”, and to prove high-level statements that are implementation-independent (think, for example to the no-cloning theorem [
10,
11]). On the other hand, in physics it is also fruitful to attach a specific physical meaning to the abstract information-theoretic entities of the theory: for example, among all possible measurements, one would like to single out a particular one as the measurement of the “energy” or another one as the measurement of “angular momentum”. Likewise, among all allowed states of the system, one would like to know which ones are “ground states of the energy”, or which ones are states where “the angular momentum is aligned in the
x direction”. The basic information-theoretic framework of [
26] does not address these issues: to include physical notions like “energy”, “angular momentum”, “polarization”, “mass”, “charge”, “position”, “velocity”, one would have to enrich to the basic language in which our principles are phrased. There is no doubt that this is a very worthwhile thing to do, because, all in all, physical laws are quantitative relations involving these notions. However, one important lesson of [
26] (and, more generally of the recent information-based quantum reconstructions [
23,
24,
25]) is that the basic mathematical structure of Quantum Theory can be completely characterized without referring to traditional physical notions such as “position”, “velocity”, or “mass”.
The difference between the information-theoretic syntax and physical semantics can be well exemplified by discussing how much of the Schrödinger equation can be reconstructed in the information-theoretic approach. As we already mentioned, from our principles we can derive that the reversible transformations of a system are described by unitary operators on the corresponding Hilbert space. As a consequence, a reversible time-evolution in continuous time will be described by a family of unitary transformations . It is then immediate to show that the unitaries should satisfy the equation , where is some Hermitian operator that we can call the “Hamiltonian” of the system. This is exactly the mathematical structure of the Schrödinger’s equation. However, the physical interpretation of H as the “energy” of the system is not included in the information-theoretic framework, but instead it is part of the physical content of the Schrödinger equation. Likewise, it is important to note that in our framework there is no fundamental scale: no “far vs. close”, nor “slow vs. fast”. Again, the actual value of the Plank’s constant ℏ is part of the physical semantics of Quantum Mechanics, and not of the basic syntax of Quantum Theory.
It is important to note that also the very scope of the information-theoretic derivations focuses on the syntax, rather than on the semantics: Questions like “What is an observer?” or “What is a measurement?” are not addressed by the principles. Neither [
26] nor the other reconstruction works [
23,
24,
25] aim to solve the measurement problem or any related interpretational issue.
In conclusion, building on the results of [
26], in this paper we presented six informational principles that completely capture the world of Quantum Theory. The theory can now be described with the elementary language of Physics, without appealing to external
ad hoc notions. The view emerging from the principles is that Quantum Theory is
the only physical theory of information: the only theory where the limited information possessed by the experimenter is enough to construct a picture of the world where all states are pure and all processes are reversible.
Now that our portrait of Quantum Theory has been completed, a natural avenue of future research consists in exploring the alternative theories that are allowed if we relax some of the principles. Given the structure of our work, which highlights Purity and Reversibility as “the characteristic trait” of Quantum Theory, it becomes interesting to study theories in which one weakens some of the first five (standard) principles while keeping Purity and Reversibility. All these alternative theories could be rightfully called “quantum”, for they share with the standard Quantum Theory its distinctive feature. One natural weakening of the principles would be to relax Local Tomography, thus allowing Quantum Theory on real Hilbert spaces, an interesting toy theory which exhibits quite peculiar information-theoretic features [
55]. More challenging and more exciting at the same time would be to venture in the realm of non-causal theories that satisfy the Purity and Reversibility principle, a much broader family of theories that are interesting in view of a formulation of quantum theory in the absence of a definite causal structure. The study of quantum theories with indefinite causal structure is a completely new avenue of research that has just begun to be investigated [
56,
57,
58,
59,
60], and we believe that it will lead to the discovery of new quantum effects and interesting information processing protocols.