Distributed Rateless Codes with Unequal Error Protection Property for Space Information Networks

Abstract

In this paper, we propose a novel distributed unequal error protection (UEP) rateless coding scheme (DURC) for space information networks (SIN). We consider the multimedia data transmissions in a dual-hop SIN communication scenario, where multiple disjoint source nodes need to transmit their UEP rateless coded data to a destination via a dynamic relay. We formulate the optimization problems to provide optimal degree distributions on the direct links and the dynamic relay links to satisfy the required error protection levels. The optimization methods are based on the And–Or tree analysis and can be solved by multi-objective programming. In addition, we evaluate the performance of the optimal DURC scheme, and simulation results show that the proposed DURC scheme can effectively provide UEP property under a variety of error requirements.

1. Introduction

With the development of space exploration and the evolution of future space information networks (SIN), erasure correcting codes have attracted considerable research interest to enhance the information transmission capacity under the extremely challenging space communication environments [1], which are characterized by the frequent and lengthy link disruptions, high data loss and a long link delay [2]. In 2014, Consultative Committee for Space Data Systems (CCSDS) released an experimental specification of long erasure correcting (LEC) codes for near earth and deep-space communications [3], in which near-optimum fixed code rate Irregular-Repeat-Accumulate (IRA) codes are proposed. In [4], a joint design of the CCSDS file delivery protocol (CFDP) and IRA codes is discussed, and such erasure codes can be decoded efficiently with the Maximum-Likelihood algorithm [5], and the code rate can be selected from several values [6,7].

Rateless codes (RC), also termed fountain codes, are capacity-achieving loss-resilient codes for erasure channels. Luby-Transform (LT) codes with a well-designed robust Soliton degree distribution (RSD) are the first practical realization of fountain codes [8]. They can recover the original k information (input) symbols from any $N=k+O(\sqrt{k}{ln}^2(k/\theta ))$ received coded (output) symbols with probability $1-\theta$ and the decoding cost of $O(kln(k/\theta ))$ operations, where θ is the allowable failure probability to recover the original message after N coded symbols have been received. To further reduce the decoding complexity and to address the issue of high error floor in LT codes, Shokrollahi proposed Raptor codes that concatenate the LT code with a weakened robust Soliton degree distribution (WRSD) with a high-rate pre-code [9]. In [10,11], LT codes are incorporated into the CFDP implementation, and both of the Packets Interleaving CCSDS File Delivery Protocol and the Loss-Tolerant File Delivery Protocol are able to resist channel erasures and can further reduce obvious overhead in CFDP.

Moreover, the line of sight (LOS) link is often unavailable for the space exploration rovers communicating to the base station directly [12]. The space exploration rovers and relay satellites can form a typical multi-access relaying SIN, which has a dynamic time-varying property of multi-hop links [13]. For example, the data from disjoint rovers/explorers need to be collected at the base station through a periodic relaying satellite [14]. Therefore, rateless codes have been considered in increasingly complicated SIN to provide an efficient distributed transmission scheme [15].

The first distributed LT (DLT) codes is proposed in [16]. The degree distribution for the distributed sources is designed as a way of decomposing the standard RSD, which is suited for a pre-fixed number of source nodes communicating with a single destination via a relay. In [17], selective distributed LT (SDLT) code is proposed by applying the And-Or tree analysis and linear programming, which can find some optimal combination at the relay node for an arbitrarily number of sources. In [18], soliton-like rateless coding (SLRC) scheme is designed for a Y-network, and SLRC scheme can provide degree distributions that generate LT-like output symbols in a relay with simple network coding protocol. It was shown through Monte Carlo simulations that the SLRC outperforms the DLT and SDLT. In [19], an improved approach of SLRC is proposed for the relay buffer-limited situation to ensure more effective decoding. The SIN is considered in the scenario that direct links and relay links are all existing, and an available degree distribution optimization scheme is proposed based on the And–Or tree analysis in [20]. The rateless network coding (NC) for dynamic relay topology based on [20] is investigated preliminarily for increasing the system throughput in this paper.

Furthermore, there are several scenarios where the conventional rateless codes cannot perform optimally due to the lack of unequal error protection (UEP). For example, when transmitting the data blocks of discrete wavelet-transform encoded images in SIN, the lower frequency part of data blocks are more important than the higher frequency parts. Thus, it is more desirable to use rateless codes with UEP to protect the important parts. The first scheme of rateless codes with UEP property is proposed in [21], and message symbols are allocated two different weights according to their importance levels. In [22], expanding window fountain codes is proposed to generate output symbols only from message symbols within a certain window. Two overlapping and expanding windows are pre-designed, such that the smaller window contains important message symbols, and the larger window contains all the symbols. A distributed rateless code with an unequal error protection (UEP) property has been proposed in [23] for a Y-network, and it can provide different data importance levels with different error probabilities for two sources. The generalized UEP rateless code (GURC) for distributed relay networks is proposed in [24], and the relationship between UEP property and decoding error rate (DER) of LT codes is obtained by the And-Or tree analysis [25]. However, the UEP property for multiple source nodes and original data in a dynamic network topology of SIN is still lacking research.

Considering a relay has its own orbit around the mission planet, which makes the links between landed rovers and the relay being periodically available. Since the space explorers have limited energy, broadcasting is prohibited. Thus, the rovers cannot communicate with the relay and destination simultaneously. In this paper, to improve the throughput of the multimedia service in future SIN communications, we proposed a novel distributed UEP rateless coding (DURC) scheme for the multimedia data transmission in a multi-access relaying SIN, which could obtain a lower DER under the pre-selected parameters of UEP property. Specifically, the RC degree distributions and network coding rules are designed to match the duration of the link access conditions.

The rest of the paper is organized as follows. In Section 2, we present the system model and our DURC scheme. In Section 3, we derive the asymptomatic performance based on the And-Or tree analysis and optimize the degree distributions and network coding rules by using multi-objective programming. In Section 4, we employ NSGA-II to design DURC codes and evaluate the performance of the DURC under different channel conditions. Finally, we conclude the paper in Section 5.

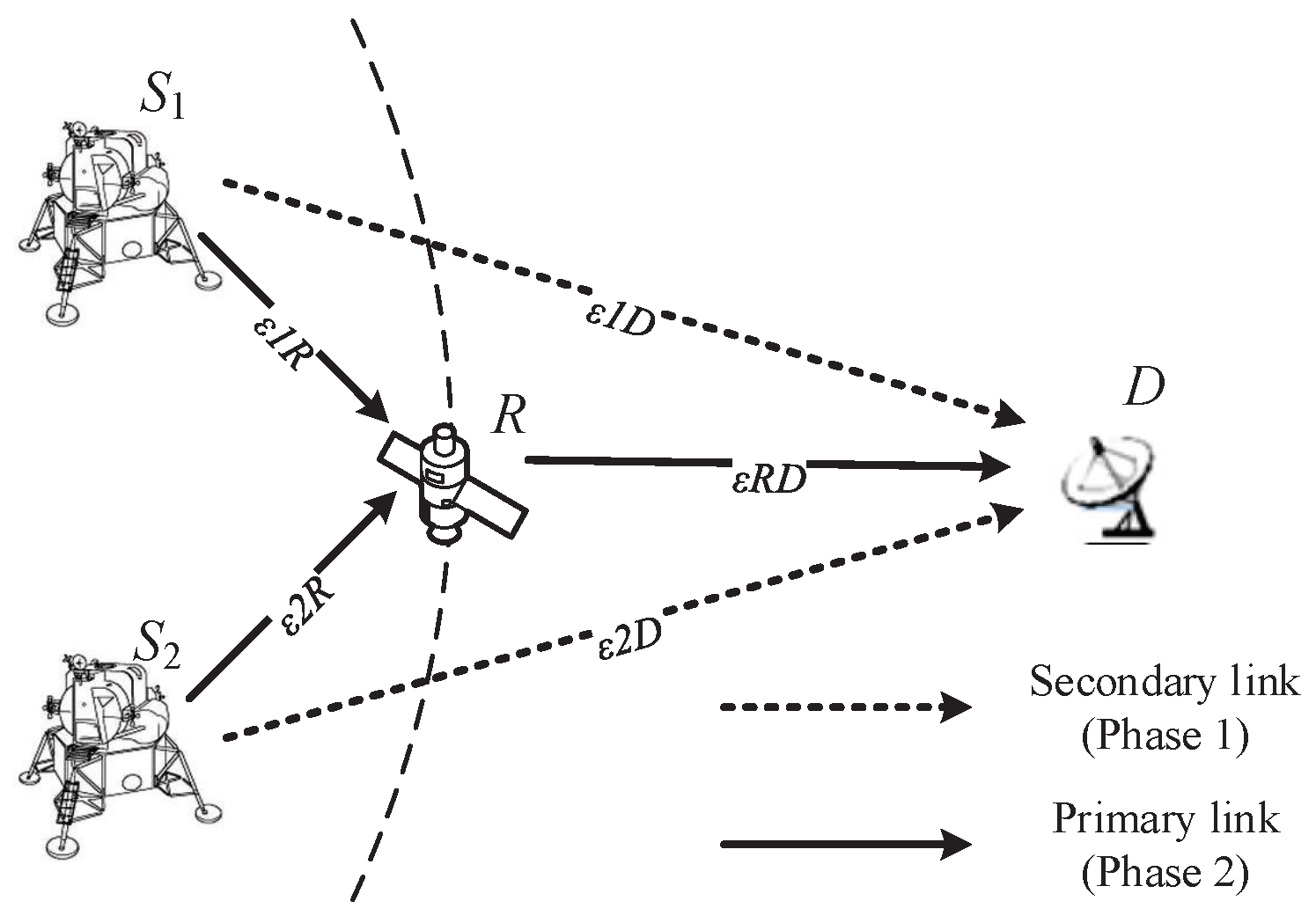
2. System Model

We consider a communication scenario in SIN as shown in Figure 1: two disjoint exploration rovers with sources $s_1$ and $s_2$ with data block of length $k_1$ and $k_2$ input symbols, respectively. Let $S_1$ and $S_2$ denote the set of $s_1$ and $s_2$ input symbols, respectively. $S_1$ and $S_2$ transmit to a base station D with the assistance of a periodic moving relay satellite/orbiter R. Due to the periodic motion, R has limited access time, and the source nodes have the knowledge of the accessing period in the SIN. Note that, without loss of generality, the output symbols transmission in Figure 1 are on binary erasure channels (BEC), and the erasure probabilities between the four nodes are denoted by ${\epsilon }_{ij}$, where $i\in \{1,2,R\}$ and $j\in \{R,D\}$. Note that the qualities of direct links are much worse than the relay links in SIN, i.e., $\{{\epsilon }_{1D},{\epsilon }_{2D}\}>>\{{\epsilon }_{1R},{\epsilon }_{2R},{\epsilon }_{RD}\}$. We define the relay links $S_1-R$, $S_2-R$, and $R-D$ (Y-network in Figure 1) as primary links, and the direct links between sources to destination, $S_1-D$, $S_2-D$, as secondary links.

We define each period of the relay in the SIN as a transmission session, and each transmission session period is divided into two Phases.

In Phase 1, R is invisible to $S_1$, $S_2$, and D, then $S_1$ and $S_2$ performs LT coding over their information set $s_1$ and $s_2$ with degree distribution ${\mathrm{\Omega }}_1(x)$ and ${\mathrm{\Omega }}_2(x)$, respectively, and transmits the coded symbols on the secondary links $S_1-D$ and $S_2-D$ to the destination D; in Phase 2, once primary links $S_1-R$ and $S_2-R$ are available, the secondary link is closed to save energy immediately. $S_1$ and $S_2$ performs LT coding over its information set $s_1$ and $s_2$ with degree distribution ${\mathrm{\Psi }}_1(x)$ and ${\mathrm{\Psi }}_2(x)$, respectively, and transmits the coded symbols to the relay R, and a rateless NC is performed at R and then transmitted to D on $R-D$. The connections and durations are illustrated in Figure 2. The number of coded symbols transmitted on each link are denoted by $N_1$ and $N_2$. For this dynamic SIN network model, the detail of our DURC scheme is illustrated below:

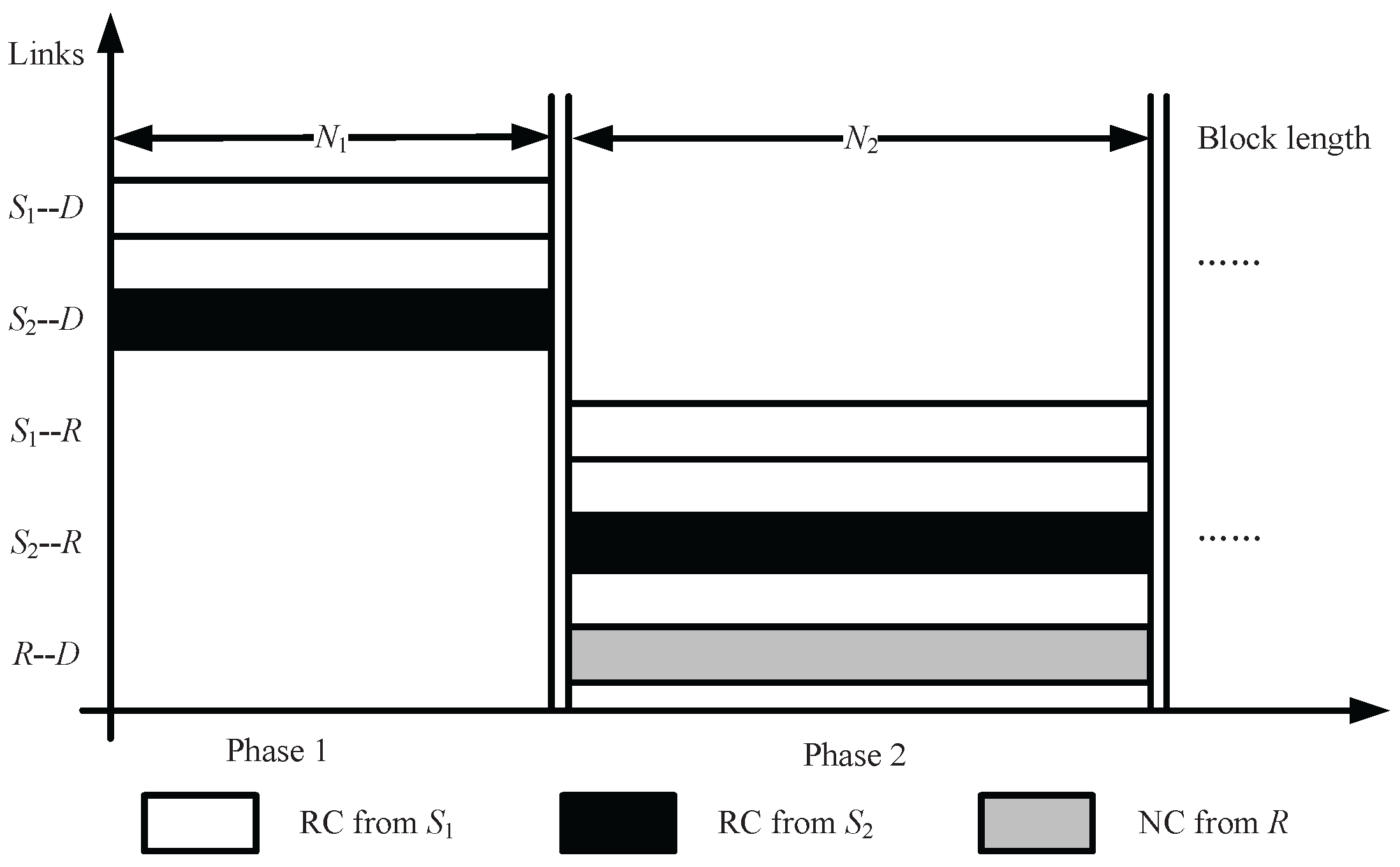
• Initialization Suppose that the information symbol lengths of $s_1$ and $s_2$ are $k_1$ and $k_2$, respectively. The $k_m$ ($m\in \{1,2\}$) symbols are divided into n subsets according to their importance levels, expressed as $I_{m1},I_{m2},...,I_{mn}$ and $k_m={\sum }_{i=1}^n{I}_{mi}$, the fraction of the $I_{mi}$ information symbols in $k_m$ is ${\pi }_{mi}$ and ${\sum }_{i=1}^n{\pi }_{mi}=1$. $S_m$ selects the i-th importance level from subset $I_{mi}$ with probability $w_{mi}$, which is called symbol-selection weight [21]. $S_m$ employs an LT-coding degree distribution ${\mathrm{\Omega }}_m(x)={\sum }_{d_m=1}^{D_m}{\mathrm{\Omega }}_{m,d_m}{x}^{d_m}$ in Phase 1, and ${\mathrm{\Psi }}_m(x)={\sum }_{d_m=1}^{D_m}{\mathrm{\Psi }}_{m,d_m}{x}^{d_m}$ in Phase 2, where $D_m$ denotes a pre-selected maximum value of $d_m$.
• Phase 1 R is invisible, and $S_1$ and $S_2$ generate distributed rateless coded symbols from $k_m$ information symbols using LT-coding degree distribution ${\mathrm{\Omega }}_m(x)$, and transmit $N_1$ coded symbols to D by secondary links. In an encoding process at $S_m$, if a degree $d_m$ is randomly selected with probability ${\mathrm{\Omega }}_{m,d_m}$ using the degree distribution ${\mathrm{\Omega }}_m(x)={\sum }_{d_m=1}^{D_m}{\mathrm{\Omega }}_{m,d_m}{x}^{d_m}$, then $d_m$ information symbols are selected uniformly at random and are bitwise XORed to form the coded symbol.
• Phase 2.1 R is visible, and $S_1$ and $S_2$ generate distributed UEP rateless coded symbols from information symbols using LT-coding degree distribution ${\mathrm{\Psi }}_m(x)$, and transmit $N_2$ coded symbols to R by primary links. In an encoding process at $S_m$, if a degree $d_m$ is randomly selected with probability ${\mathrm{\Psi }}_{m,d_m}$ using the degree distribution ${\mathrm{\Psi }}_m(x)={\sum }_{d_m=1}^{D_m}{\mathrm{\Psi }}_{m,d_m}{x}^{d_m}$, then $d_m$ information symbols are selected with probability $\frac{w_{mi}}{{\pi }_{mi}{k}_m}$ in $I_{mi}$ and are bitwise XORed to form the coded symbol.
• Phase 2.2 The coded symbols are transmitted to relay R from $S_1$ and $S_2$, and based on the network coding rule $P=\{p_1,p_2,p_3\}$ and ${\sum }_{i=1}^3{p}_i=1$, R generates three types of network coded symbols and forwards them to the destination D. R forwards $S_1$’s output symbol directly with the probability $p_1$, while forwarding $S_2$’s output symbol directly with the probability $p_2$, and XORs the two incoming symbols with the probability $p_3$ and then forwards to D .
• Decoding After receiving enough coded symbols from $S_1$, $S_2$ and R, a joint decoding is performed on D to recover the information symbols of $S_1$ and $S_2$.

Considering the erasure probabilities of the links, in Phase 1 and Phase 2, the expected number of the coded symbols successfully received at D can be expressed as $n_1=N_1(1-{\epsilon }_{1D})$, $n_2=N_1(1-{\epsilon }_{2D})$ and $n_{NC}=N_2(1-{\epsilon }_{RD})$, where $n_1$ and $n_2$ are the number of the received coded symbols on the $S_1-D$ and $S_2-D$ links in Phase 1, respectively, and $n_{NC}$ is the number of the received output coded symbols on the link $R-D$ in Phase 2.

3. Design of Distributed Unequal Error Protection Rateless Codes

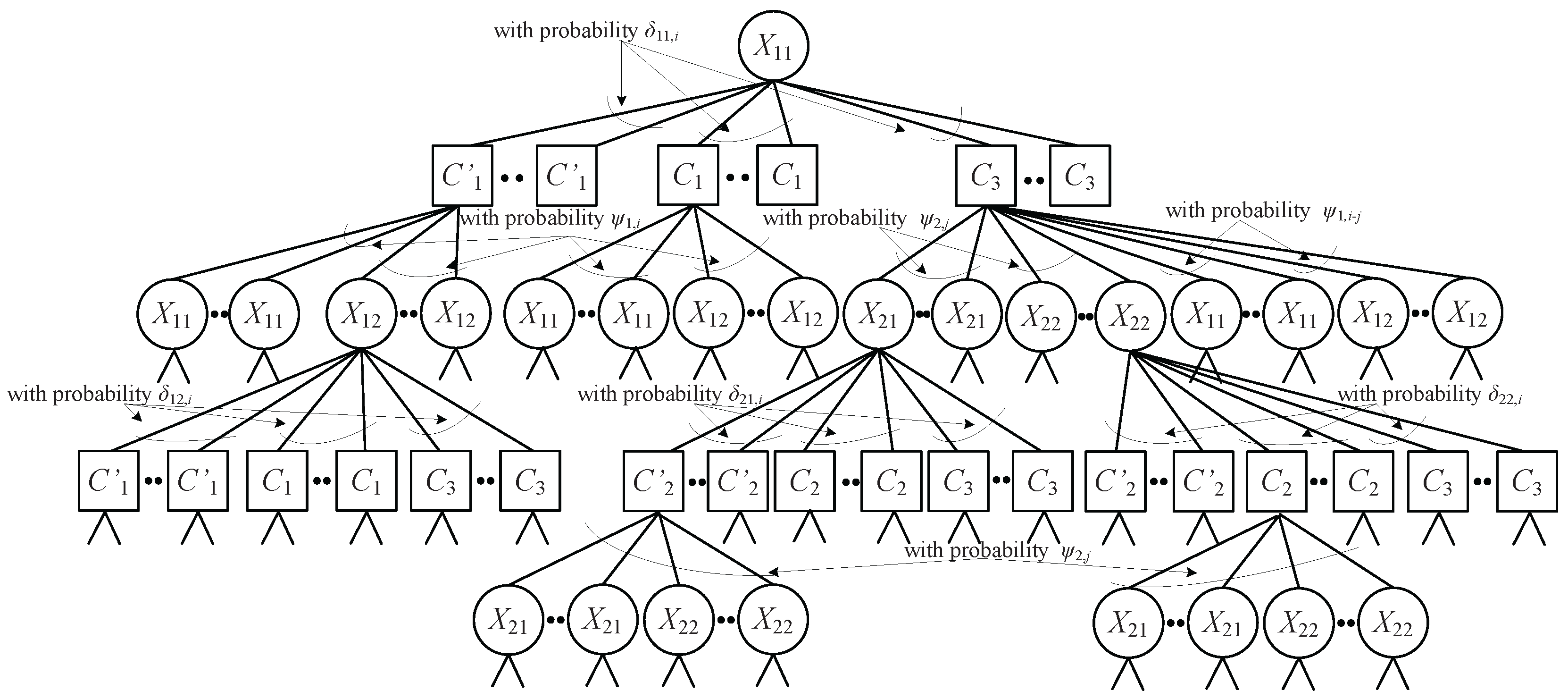
3.1. Analysis of RC and NC Degree Distributions by the And-Or Tree Technique

In one transmission session, D will receive multi-path coded blocks in Phase 1 and Phase 2, and a joint decoding to restore the sources’ original symbols via the belief propagation (BP) algorithm. In this paper, we assume that the original symbols in one source node are divided into more important bits (MIB) and less important bits (LIB), which means that $n=2$ in the flowchart.

Based on the And-Or tree analysis [26], let $\delta (x)$ and $\psi (x)$ denote the edge distributions of the input node and the output node in a rateless codes, respectively. The DER after l BP decoding iterations is expressed as $y_l=\delta \left(1-\psi (1-y_{l-1})\right)$, where $y_0=1$. When k approaches infinity, the edge distribution of input nodes become a Poisson distribution, and the DER becomes $y_l=exp(-\gamma \times {\mathrm{\Psi }}^{\prime }(1-y_{l-1})$), where ${\mathrm{\Psi }}^{\prime }(x)$ is the derivative of the output degree distribution, and γ is the decoding overhead defined as the ratio of the number of information symbols recovered by the destination decoder to the number of coded symbols. Thus, the decoding performance is only determined by γ and $\mathrm{\Psi }(x)$.

With the addition of the UEP property, the decoding overhead of the j-th importance level in the GURC [24] becomes ${\gamma }_j=\gamma \times w_j/{\pi }_j$, where $j\in \{1,2,...,n\}$. The success decoding probability after $l-1$ iterations becomes $(1-{\sum }_{n=1}^u{p}_n{y}_{l-1,n})$.

Thus, the DER $y_{l,j}$ of message symbols from the j-th importance level for an ensemble $(\mathrm{\Psi }(x),{\{w_j\}}_{j=1,2,...,n},{\{{\pi }_j\}}_{j=1,2,...,n})$ at l-th iteration is expressed as

$$\begin{array}{cc}& y_{l,j}=exp\left(-{\gamma }_j\times {\mathrm{\Psi }}^{\prime }(1-y_{l-1,j})\right)=exp[-\gamma \frac{w_j}{{\pi }_j}{\mathrm{\Psi }}^{\prime }(1-\sum _{j=1}^n{p}_j{y}_{l-1,j})],\hfill \end{array}$$

(1)

where $y_{0,j}=1$.

In order to analyze the decoding performance of our DURC scheme, we should derive the relationship between degree distribution ${\mathrm{\Omega }}_m(x)$, ${\mathrm{\Psi }}_m(x)$ and network coding rule P. We consider an And-Or tree as shown in Figure 3, and the received coded symbols can be divided into five groups. The first two groups are received on the secondary links $S_1-D$ and $S_2-D$, termed $C_1^{\prime }$ and $C_2^{\prime }$.

The other three groups are received on the primary links, termed $C_1$, $C_2$ and $C_3$. $C_1$ and $C_2$ are the coded blocks forwarded by R with the probabilities $p_1$ and $p_2$, respectively. $C_3$ is the coded symbol transmitted from R after the XOR operation with the probability $p_3$. $C_1^{\prime }$ and $C_2^{\prime }$ are generated with degree distributions ${\mathrm{\Omega }}_1(x)$ and ${\mathrm{\Omega }}_2(x)$ , respectively. $C_1$ and $C_2$ are generated with degree distributions ${\mathrm{\Psi }}_1(x)$ and ${\mathrm{\Psi }}_2(x)$, respectively. $C_3$ is generated with the convolution degree distribution ${\mathrm{\Psi }}_1(x)\times {\mathrm{\Psi }}_2(x)$.

The input nodes can be divided into four groups, termed $X_{11}$, $X_{12}$, $X_{21}$ and $X_{22}$. $X_{11}$ and $X_{12}$ are the MIB and LIB of $S_1$, respectively. Similarly, $X_{21}$ and $X_{22}$ are the MIB and LIB of $S_2$, respectively. Thus, $T_{l,11}$ with depth $2l$ as shown in Figure 3, with the root $X_{11}$. Similarly, we can construct And-Or trees $T_{l,12}$, $T_{l,21}$ and $T_{l,22}$ with the roots $X_{12}$, $X_{21}$ and $X_{22}$ by using the same method.

Theorem 1.

Let $y_{l,1,n}$ (or $y_{l,2,n}$) be the probability that the root of $S_1$ (or $S_2$) evaluates to 0, indicating one input node not being recovered after l-th BP decoding iterations. Then, we have

$$\begin{array}{cc}& y_{l,1,n}={\delta }_1(1-{\omega }_1(1-\sum _{n=1}^2{w}_{1,n}{y}_{l-1,1,n}))\times {\tau }_{1,n}\{1-P_1{\psi }_1(1-\sum _{n=1}^2{w}_{1,n}{y}_{l-1,1,n})\hfill \\ & -P_3\sum _{i=1}^{D_1+D_2-1}\sum _{j=0}^{i-1}[{\psi }_{1,j}{(1-\sum _{n=1}^2{w}_{1,n}{y}_{l-1,1,n})}^j{\psi }_{2,i-j}{(1-\sum _{n=1}^2{w}_{2,n}{y}_{l-1,2,n})}^{i-j}]\},\hfill \end{array}$$

(2)

$$\begin{array}{cc}& y_{l,2,n}={\delta }_2(1-{\omega }_2(1-\sum _{n=1}^2{w}_{2,n}{y}_{l-1,2,n}))\times {\tau }_{2,n}\{1-P_2{\psi }_2(1-\sum _{n=1}^2{w}_{2,n}{y}_{l-1,2,n})\hfill \\ & -P_4\sum _{i=1}^{D_1+D_2-1}\sum _{j=0}^{i-1}[{\psi }_{2,j}{(1-\sum _{n=1}^2{w}_{2,n}{y}_{l-1,2,n})}^j{\psi }_{1,i-j}{(1-\sum _{n=1}^2{w}_{1,n}{y}_{l-1,1n})}^{i-j}]\},\hfill \end{array}$$

(3)

where $y_{0,1,n}=y_{0,2,n}=1$, and

$${\delta }_1(x)=\sum _{i=0}{\delta }_{1,i}{x}^i=exp({\alpha }_1(x-1)),{\alpha }_1=\frac{{\lambda }_1{n}_1}{k_1},$$

(4)

$${\delta }_2(x)=\sum _{i=0}{\delta }_{2,i}{x}^i=exp({\alpha }_2(x-1)),{\alpha }_2=\frac{{\lambda }_2{n}_2}{k_2},$$

(5)

$${\tau }_{1,n}(x)=\sum _{i=0}{\tau }_{1,n,i}{x}^i=exp({\beta }_{1,n}(x-1)),{\beta }_{1,n}=\frac{{\mu }_1{n}_{NC}(p_1+p_3)w_n}{k_1{\pi }_n},$$

(6)

$${\tau }_{2,n}(x)=\sum _{i=0}{\tau }_{2,n,i}{x}^i=exp({\beta }_{2,n}(x-1)),{\beta }_{2,n}=\frac{{\mu }_2{n}_{NC}(p_2+p_3)w_n}{k_2{\pi }_n},$$

(7)

$$\left\{\begin{array}{c}{P}_1=\frac{p_1}{1-p_2},P_3=1-P_1\hfill \\ P_2=\frac{p_2}{1-p_1},P_4=1-P_2\hfill \end{array}\right..$$

(8)

Proof of Theorem 1.

In (2) and (3), the first product term means $y_l$ of Phase 1, and the second one means $y_l$ of Phase 2. For every importance level of the information symbols in a single source node, their input edge distribution and average degree are different. Thus, the parameters used in (2) and (3) can be defined as follows. The input edge distribution of primary link is expressed as ${\tau }_{m,n}(x)=exp({\beta }_{m,n}(x-1))$, where ${\beta }_{m,n}={\mu }_m{n}_{NC}(p_i+p_3)w_{m,n}/(k_i{\pi }_{m,n})$ is the input average degree, and where ${\mu }_m={\sum }_{d_m=1}^{D_m}{d}_m{{\mathrm{\Psi }}_m}_{d_m}$ is its output average degree.

The input edge distribution of secondary link is expressed as ${\delta }_m(x)=exp({\alpha }_m(x-1))$, where ${\alpha }_m={\lambda }_m{n}_m/k_m$, and the output edge distribution of secondary link is expressed as ${\lambda }_m(x)={{\mathrm{\Omega }}_m}^{\prime }(x)/{\mathrm{\Omega }}_1$. ${\psi }_{1,i}$ is defined as the probability that $C_1$ has i children of input nodes, and ${\psi }_{2,i}$ is defined as the probability that $C_2$ has i children of input nodes. Moreover, ${\psi }_{1,i}$ also refers to the probability that $C_3$ has i children of $X_1$ (including $X_{11}$ and $X_{12}$), and ${\psi }_{2,i}$ refers to the probability that $C_3$ has i children of $X_2$ (including $X_{21}$ and $X_{22}$). Every $C_1$ only has the children of $X_1$, and the probability of any $X_1$ evaluating to 1 is $1-{\sum }_{n=1}^2{w}_{1,n}{y}_{l-1,1,n}$. Thus, if a $C_1$ has i children of $X_1$, the probability of $C_1$ evaluating to 1 is ${\sum }_{i=0}^{D_1-1}{{\psi }_{1,}}_i{(1-{\sum }_{n=1}^2{w}_{1,n}{y}_{l-1,1,n})}^i$. In the same way, if a $C_3$ node has i children of $X_1$ and j children of $X_2$, the probability of $C_3$ evaluating to 1 is ${\sum }_{i=1}^{D_1+D_2-1}{\sum }_{j=0}^{i-1}[{\psi }_{1,j}{(1-{\sum }_{n=1}^2{w}_{1,n}{y}_{l-1,1,n})}^j{\psi }_{2,i-j}{(1-{\sum }_{n=1}^2{w}_{2,n}{y}_{l-1,2,n})}^{i-j}]$.

In the And-Or tree $T_{l,11}$, $P_1$ and $P_3$ are the proportions of $X_1$ connecting with $C_1^{\prime }+C_1$ and $C_3$, respectively. $P_2$ and $P_4$ are the proportions of $X_2$ connect with $C_2^{\prime }+C_2$ and $C_3$, respectively. The relationships are expressed as (8). When $n_1$, $n_2$ and $n_{NC}$ are given, the DER $y_l$ in (2) and (3) monotonically decrease with l, and converge to fixed values, which can be regarded as the final DER. ☐

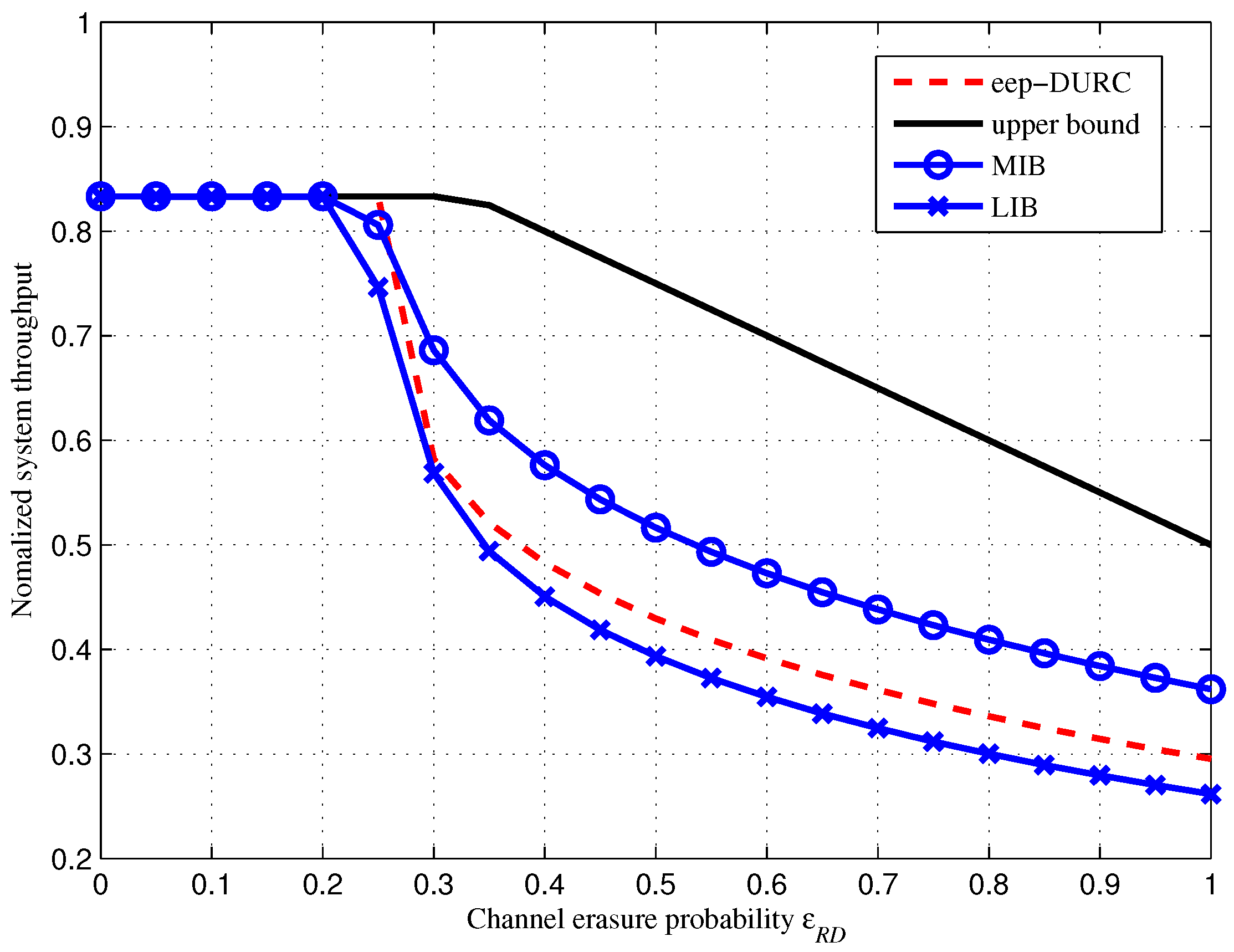
3.2. Analysis of System Throughput

The system throughput is defined as the ratio of the total number of recovered information symbols k and the sum of received output symbols n in one transmission session period. Since $y_l$ is the asymptotic DER, there exists a unique ideal throughput upper bound for a certain system model that is related to $y_l$. For the LT code, the ideal DER tends to 0 when $\gamma \ge 1$, which means that the upper bound is only affected by the overhead γ. In this way, we can derive the throughput upper bound for a typical BEC model as shown in Figure 1, which is given by

$$thr\_up=min\left\{\frac{k}{n},\frac{n(1-\epsilon )}{n}\right\}.$$

(9)

In (9), ε is the channel erasure probability, which affects the overhead γ. Moreover, by considering the periodic motion of relay R in the dynamic SIN scenario, we can derive the throughput upper bound of system model in this paper as

$$thr\_up=min\left\{\frac{k_1+k_2}{N_1+N_2},\frac{N_1(2-{\epsilon }_{1D}-{\epsilon }_{2D})+N_2(1-{\epsilon }_{RD})}{N_1+N_2}\right\}.$$

(10)

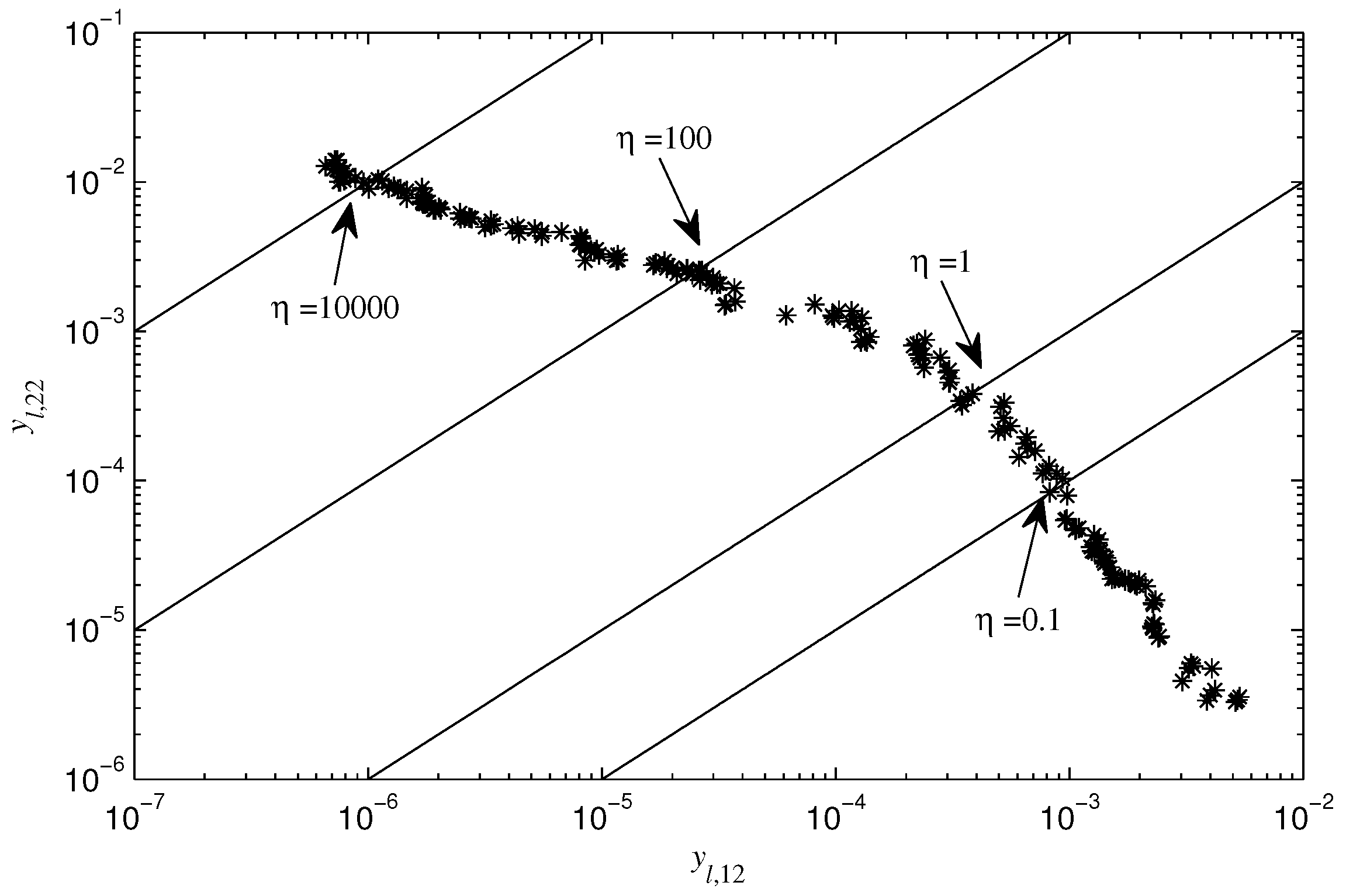
3.3. Optimizations of Rateless Coding Scheme and Network Coding Rule

To optimize the system performance, we construct a decision variables set about degree distribution, symbol selection weight and network coding rule in (2) and (3), $Q=({\mathrm{\Omega }}_m,{\mathrm{\Psi }}_{m,1},{\mathrm{\Psi }}_{m,2},...,{\mathrm{\Psi }}_{m,d_m},w_{m,n},P)$, where ${\mathrm{\Psi }}_{m,d_m}$ denotes the coefficient of degree distribution, $w_{m,n}$ denotes symbol selection weight for different importance level, and P is the network coding rule. Since the channel state information of the links are unknown, we cannot obtain the exact number of coded symbols at D in each phase. Therefore, sub-optimal Q should be acquired for minimizing the BP DER at the destination D. Therefore, we give the optimizations as follows.

We first consider the secondary link in our scenario. The erasure probability ${\epsilon }_{1D}$ or ${\epsilon }_{2D}$ is much too high, which may lead to the received coded symbols being less than the information symbols at the destination D, i.e., $n_1<k_1$ and $n_2<k_2$. Thus, as a supplementation to enhance the decoding performance of the whole transmission session, the optimization problem of ${\mathrm{\Omega }}_1(x)$ or ${\mathrm{\Omega }}_2(x)$ is to guarantee that the received coded symbols can recover part of the information symbols instead of recovering the total original information symbol sets or UEP, and similar optimal formulations can be found in [25] and [27]. The optimization problem of ${\mathrm{\Omega }}_1(x)={\sum }_{m_1=1}^{M_1}{\mathrm{\Omega }}_{1,m_1}{x}^{m_1}$ to minimize the decoding error probability can be formulated as follows:

$$\begin{array}{cc}\hfill \underset{{\mathrm{\Omega }}_1}{\min }& \exp \left(-{\alpha }_1{\mathrm{\Omega }}_1^{\prime }(1-y_{l-1,1})\right),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \sum _{i=1}^{M_1}{\mathrm{\Omega }}_{1,i}=1,\hfill \\ & y_{0,1}=1,l\to \infty ,\hfill \\ & 0\le {\mathrm{\Omega }}_{1,i}\le 1.\hfill \end{array}$$

(11)

Without the exact knowledge of $n_1$, the values of ${\alpha }_1$ for different channel erasure probabilities are unknown. Problem (11) is thus a constrained nonlinear optimization problem and generally non-convex. Therefore, it is a simplified method to solve this problem instead, by considering the most important coded symbols at the LT BP-decoder. In each BP decoding iteration, degree-1 and degree-2 symbols are most important, as they can help other unrecovered coded symbols to reduce the number of edges connected with them. In this case, we could restrict the maximum degree $M_1$ and $M_2$ to 2, i.e., ${\mathrm{\Omega }}_1(x)={\mathrm{\Omega }}_{1,1}{x}^1+{\mathrm{\Omega }}_{1,2}{x}^2$ and ${\mathrm{\Omega }}_2(x)={\mathrm{\Omega }}_{2,1}{x}^1+{\mathrm{\Omega }}_{2,2}{x}^2$. In [27], a theoretical analysis is given to demonstrate that the partial decoding performance of the degree distribution with only degree-1 and degree-2 nodes is acceptable, when the received overhead $\frac{n}{k}$ is lower than 1.

In addition, these low-degree coded symbols are to be jointed with the coded symbols on the primary links to assist in full decoding. Therefore, to minimize the DER of the joint decoding at the destination D with a pre-selected decoding overhead $\gamma =\frac{n_1+n_2+n_{NC}}{k_1+k_2}$, and the And-Or tree asymptotic performances of $y_{l,1}$ and $y_{l,2}$ in (2) and (3) can be easily computed by choosing the remaining parameters ${\mathrm{\Omega }}_{1,1}$, ${\mathrm{\Omega }}_{1,2}$, ${\mathrm{\Omega }}_{2,1}$, ${\mathrm{\Omega }}_{2,2}$, $p_1$, $p_2$ and $p_3$, with $n_1:n_2:n_{NC}$, and ${\mathrm{\Psi }}_{m,n}(x)$ is known beforehand. It is not difficult to show that $y_{l,1}$ and $y_{l,2}$ are two conflicting objective functions by investigating (2) and (3). Therefore, we have a multi-objective optimization (MOP) problem about the objective function $y(S)=(y_1(S),y_2(S))$ to minimize them concurrently, where S is the set of decision variables, i.e., $S=({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2,p_1,p_2,p_3)$

$$\begin{array}{cc}\hfill \min & y=(y_1,y_2),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\mathrm{\Omega }}_{1,1}+{\mathrm{\Omega }}_{1,2}=1,\hfill \\ & {\mathrm{\Omega }}_{2,1}+{\mathrm{\Omega }}_{2,2}=1,\hfill \\ & p_1+p_2+p_3=1.\hfill \end{array}$$

(12)

Then, consider the primary links in our scheme, although the actual values of $n_1$, $n_2$ and $n_{NC}$ are unknown, and the expected ratio of the numbers of the received coded symbols on different links, $n_1$: $n_2$ : $n_{NC}$, can be derived by given the block lengths and erasure probabilities. If a desired overhead $\gamma *$ and proportion of every importance level are given, the decoding performance of MIB and LIB only depend on the degree distribution and symbol selection weight. Thus, if we limit the decoding performance relation between LIB and MIB, the optimizations of rateless coding scheme of one source are finished when we finish optimizing the decoding performance of LIB. Furthermore, it is not difficult to show that $y_{l,1,2}$ and $y_{l,2,2}$ are two conflicting objective functions by investigating (2) and (3). Therefore, we have a multi-objective optimization (MOP) problem, MOP1, about the objective function $y_{l,1,2}(Q)$ and $y_{l,2,2}(Q)$ to minimize them concurrently, where Q is the set of decision variables shown above:

$$\begin{array}{cc}\hfill \underset{Q}{\min }& y(Q)=(y_{l,1,2}(Q),y_{l,2,2}(Q)),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& I_{1,1}{y}_{l,1,1}\le I_{1,2}{y}_{l,1,2},I_{2,1}{y}_{l,2,1}\le I_{2,2}{y}_{l,2,2},\hfill \\ & \sum _{d_m}^{D_m}{\mathrm{\Psi }}_{m{d}_m}=1,{\mathrm{\Psi }}_{m{d}_m}\ge 0,\hfill \\ & 0\le w_{mn}\le 1,\hfill \\ & p_1+p_2+p_3=1,\hfill \\ & m\in \{1,2\},n\in \{1,2\},d_m\in \{1,2,...,D_m\}.\hfill \end{array}$$

(13)

Note that the inequalities on the second line of (13) are added to guarantee UEP property, which limits the decoding performance relation between LIB and MIB. Thus, it should be noted that when the original information in any source is divided into $n(n>2)$ importance levels, optimization can also be in the same way due to the same degree distribution and network coding rule for every importance level. The MOP2 can be formulated as follows, in which it will have $2n$ importance levels for the whole system:

$$\begin{array}{cc}\hfill \underset{Q}{\min }& y(Q)=(y_{l,1,2}(Q),y_{l,2,2}(Q)),\hfill \\ \hfill \mathrm{s}.\mathrm{t}& I_{1,1}{y}_{l,1,1}\le I_{1,2}{y}_{l,1,2}\le ...\le I_{1,u}{y}_{l,1,u},\hfill \\ & I_{2,1}{y}_{l,2,1}\le I_{2,2}{y}_{l,2,2}\le ...\le I_{2,u}{y}_{l,2,u},\hfill \\ & \sum _{d_m}^{D_m}{\mathrm{\Psi }}_{m{d}_m}=1,{\mathrm{\Psi }}_{m{d}_m}\ge 0,\hfill \\ & 0\le w_{mn}\le 1,\hfill \\ & p_1+p_2+p_3=1,\hfill \\ & m\in \{1,2\},n\in \{1,2,...,u\},d_m\in \{1,2,...,D_m\}.\hfill \end{array}$$

(14)

A fast non-dominated sorting genetic algorithm (NSGA-II) [28] is one of the many algorithms that could give a Pareto front of MOP with an outstanding performance. Thus, we employ this algorithm to solve the set Q.

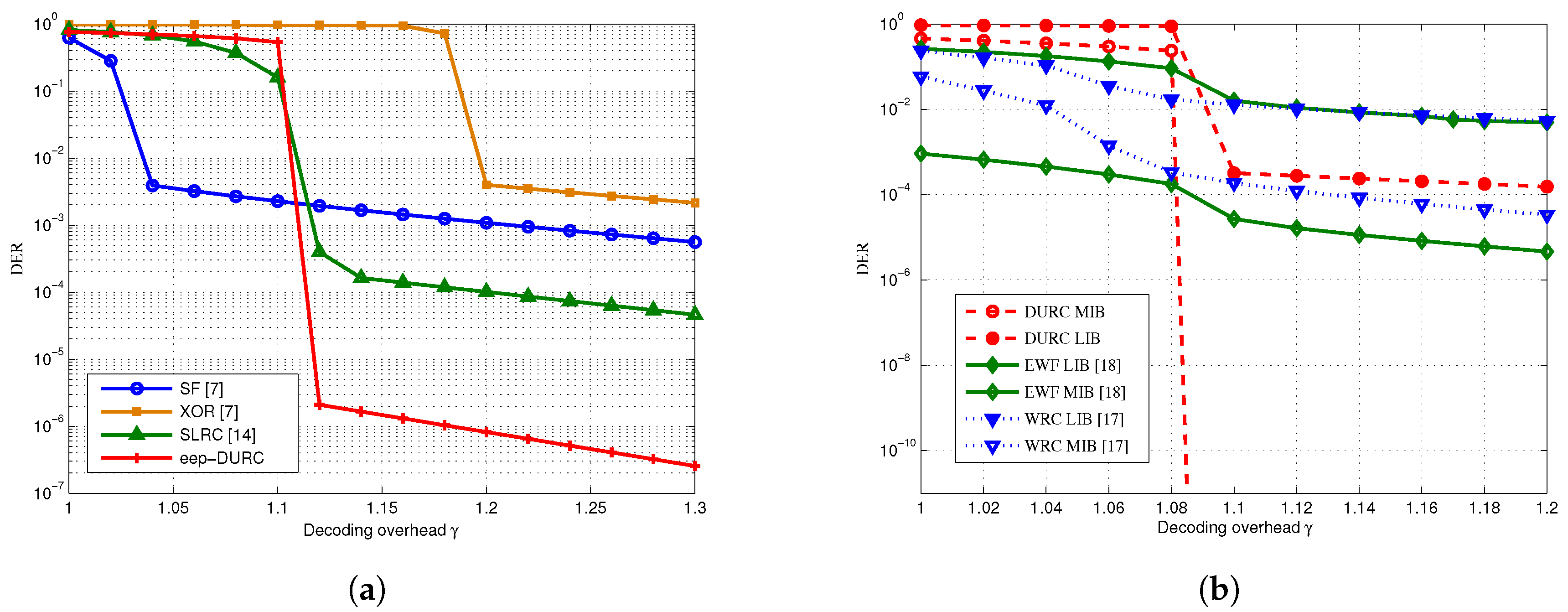
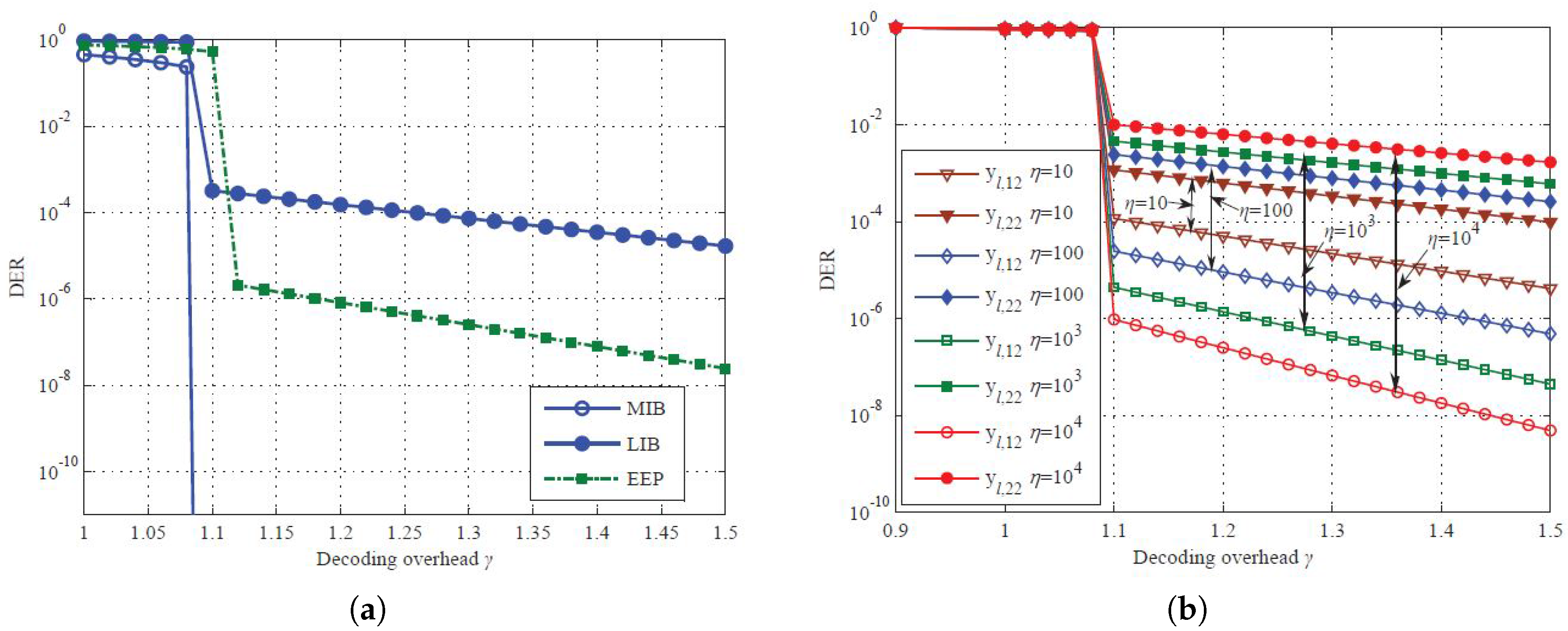
4. Simulation and Comparison

Let us investigate the DURC parameters under a totally symmetric network model, where the block lengths are $N_1=N_2=1200$, the information symbols lengths are $k_1=k_2=1000$, and the erasure probabilities of channel links are ${\epsilon }_{1D}={\epsilon }_{2D}=0.5$, ${\epsilon }_{1R}={\epsilon }_{2R}=0$, and ${\epsilon }_{RD}=0.1$. Setting the maximal value of the degree $D_1=D_2=50$, desired total overhead $\gamma *=1.1$, the proportion of MIB in every source is ${\pi }_{m1}=0.5$, and the decoding performance relationship between MIB and LIB is $I_{m,1}\ge 10I_{m,2}$. To obtain the optimized degree distribution ${\mathrm{\Psi }}_1(x)$ and ${\mathrm{\Psi }}_2(x)$, we solved the MOP1 and finally get a Pareto front about the optimized $y_{l,12}$ and $y_{l,22}$. We plot the Pareto fronts obtained from our optimizations in Figure 4, where $\eta =y_{l,2,2}/y_{l,1,2}$. It is obviously that the protection of $S_1$ is increasing with the increasing of η.

The partial optimization results are shown in

Table 1. Optimal network coding rule, selection weights and degree distributions for DURC with different importance levels.

Importance Levels	Network Coding Rule	Selection Weights	Degree Distributions
$y_{l,1,2}=y_{l,2,2}$	$p_1=0.15$ $p_2=0.15$ $p_3=0.70$	$w_{1,1}=0.923$ $w_{1,2}=0.077$ $w_{2,1}=0.923$ $w_{2,2}=0.077$	${\mathrm{\Psi }}_1(x)={\mathrm{\Psi }}_2(x)=0.0523x+0.4733x^2+0.0174x^3$ $+0.0124x^4+0.0146x^5+0.0194x^6+0.0237x^8$ $+0.0142x^{10}+0.0237x^{12}+0.0196x^{16}+0.0069x^{18}$ $+0.0068x^{19}+0.0306x^{22}+0.038x^{28}+0.0515x^{36}$ $+0.041x^{45}+0.1547x^{50}$
$y_{l,1,2}={10}^4{y}_{l,2,2}$	$p_1=0.178$ $p_2=0.122$ $p_3=0.700$	$w_{1,1}=0.860$ $w_{1,2}=0.140$ $w_{2,1}=0.952$ $w_{2,2}=0.048$	${\mathrm{\Psi }}_1(x)=0.059x+0.484x^2+0.0216x^3+0.0196x^4$ $+0.0087x^6+0.0074x^7+0.0223x^8+0.019x^{11}$ $+0.014x^{14}+0.022x^{19}+0.0335x^{22}+0.0384x^{30}$ $+0.0355x^{37}+0.0387x^{42}+0.0174x^{49}+0.146x^{50}$ ${\mathrm{\Psi }}_2(x)=0.045x+0.4637x^2+0.0156x^3$ $+0.0104x^4+0.0247x^5+0.0357x^6+0.0197x^8$ $+0.0175x^{10}+0.011x^{12}+0.0286x^{14}+0.034x^{19}$ $+0.031x^{25}+0.024x^{29}+0.052x^{35}+0.028x^{41}$ $+0.0229x^{49}+0.137x^{50}$

. Furthermore, we select an equal error protect (eep) degree distribution from the sets of our optimized DURC scheme, i.e., $\eta =1$ and $n=1$, the optimized ${\mathrm{\Psi }}_1(x)$ and ${\mathrm{\Psi }}_2(x)$ at sources are identical as ${\mathrm{\Psi }}_1(x)={\mathrm{\Psi }}_2(x)=0.0111x+0.4944x^2+0.1787x^3+0.1653x^5+0.0053x^6+0.0978x^{12}+0.0474x^{50}$. Furthermore, we substitute ${\mathrm{\Psi }}_m(x)$ into the MOP problem (12) with a desired total overhead ${\gamma }^{*}=1.1$ to solve for the RC degree distribution on secondary links as ${\mathrm{\Omega }}_1(x)={\mathrm{\Omega }}_2(x)=0.054x+0.946x^2$, and NC relaying probabilities as $p_1=0.045$, $p_2=0.045$ and $p_3=0.91$, and we can use these eep-DURC scheme to compare with three existing distributed rateless coding schemes in the same network model as described before. The store-and-forward (SF) scheme is that the RC degree distributions on secondary and primary links are both set as the classical degree distributions used for Raptor codes in [9], and the relay node R randomly forwards the received coded symbols from $S_1$ and $S_2$ with equal probability. Simple network coding scheme (XOR) is that R always sends a new coded symbol to D, which is generated by XORing the two coded symbols from $S_1$ and $S_2$. The SLRC scheme uses the network coding relay protocol as in [18], the relay node R only forwards coded symbols with degree-1 and degree-2 with a threshold probability, and RC degree distributions on secondary and primary links are also the Raptor degree distributions.

Figure 5a shows the DER versus the total overhead for various distributed rateless codes (DRC) schemes, which are obtained by the asymptotical performances formed by And-Or tree analysis. It is noted that the XOR scheme has the worst decoding performance because of the lack of lower degree symbols (1 and 2) received by D. The SLRC scheme has better performance than the SF scheme when the overhead is larger than 1.15. The DER of the eep-DURC scheme, which is the basic of our proposed UEP, is clearly the lowest. Figure 5b shows the DER versus the total overhead for various UEP schemes. It is noted that the DURC schemes achieved the lowest DER for both MIB and LIB, which gives great support for information transmission in SIN.

Figure 6a shows the DER versus the total overhead of inner information in one source node for DURC and eep-DURC schemes from the And-Or tree performance evaluation. It is obvious that the DURC scheme can achieve marvel decoding performance of MIB with about two orders of the decoding performance of LIB decreasing, which gives great protection for MIB than eep-DURC scheme. Figure 6b shows the LIB performance of different sources for $\eta =10,{10}^2,{10}^3,{10}^4$. The result shows that when decoding performance of $S_1$ increases, the performance of related $S_2$ will decrease, that is to say, the performance increase of one source is on the price of performance decrease of another source. Therefore, we only have to set desired parameters, and the scheme proposed in this paper will then satisfy different needs.

We also estimate the throughput performance of the DURC scheme. To substitute the parameter setting in this section into (10), we can derive the system throughput upper bound as

$$thr\_up=\left\{\begin{array}{c}\frac{5}{6},0\le {\epsilon }_{RD}\le \frac{1}{3},\hfill \\ \frac{1+(1-{\epsilon }_{RD})}{2},\frac{1}{3}<{\epsilon }_{RD}\le 1.\hfill \end{array}\right.$$

(15)

Figure 7 shows the system throughput versus erasure probability of channel $R-D$ for information in one source and eep-DURC. To match the system setting of primary link and secondary link, we set $\epsilon \le 0.5$.

The result in Figure 7 demonstrated the same trend of Figure 6a, where the throughput of MIB is much higher than eep-DURC, but the throughput of LIB is decreased. However, for the systems that need higher protection of MIB, this tradeoff is meaningful.

5. Conclusions

We have investigated the design and optimization of the DURC over a dynamic energy-limited satellite relay network with multiple sources in SIN. The decoding performance has been analyzed by the And-Or tree technique, and the optimizations of parameters are solved by the MOP. The DURC can adapt the degree distribution, symbol selection weight and network coding rule to various erasure probabilities in different links. Simulation results show that, in the DURC, the information of any source can be divided into different arbitrary importance levels. The DURC can give great protection for the MIB without a large sacrifice of LIB. Furthermore, we can set different UEP levels for different sources to satisfy the requirement of system, which improves the flexibility of screening information for ground stations and makes the system more practical.