We developed many experiments to assess the performance of the presented CSO algorithm. Many runs of the proposed approach were executed and the solution quality was taken into account. We have prepared seven benchmarks for the construction of problems of varying complexity (see
Table 1). The time-expanded model was simulated. We assumed that all lines had regular departures (12 or 48 daily) at equal intervals, regardless of the time of day. In order to test the effectiveness of the CSO algorithm, experiments were performed 10 times for each test instance, with the same setting of parameters. In all experiments we assumed fixed parameters of the CSO algorithm during all iterations. The performance of our CSO adaptation was evaluated in comparison with Dijkstra’s [
1,
29] and the particle swarm optimization [
15,
38,
39] algorithms. All algorithms were implemented in the Java programming language, using a Linux operating system. We ran all experiments using an Intel Core i5-5200U 2.20 GHz processor with 16 GB RAM.
4.1. Description of the Considered Test Instances
In order to verify the correctness and the quality of the implemented algorithm, we designed several test instances with simple timetables. Below, we present a short description of those.
In the first case, we constructed only one transportation line, containing 21 stops with 12 departures per day. It is worth noting that, for this line, a graph with 674 vertices will be chosen. Consequently, the increase of the number of departures to 48 per day required a more complex graph to be adopted, as shown in
Table 1. On this basis, the implemented solutions and processes of graph construction were validated.
In the second experiment, we decided to investigate the correct detection of transfers between the transportation lines, also for the two versions of timetables (12 and 48 departures). For this purpose, the second transportation line intersecting with the first one at a single stop was added. It should be emphasized that the only possible route between the desired points required transfer operations.
In another experiment, the area of travel was slightly expanded. Therefore, we increased the number of public transportation lines to six. In addition, we assumed that at least two transfers were required to reach the target point.
In the last experiment, we set the number of transportation lines at seven. In that case, one night line was also taken into account, which was necessary to ensure diversity among instances.
All of the test instances conducted in the context of the time-expanded model are summarized in
Table 1. Therefore, we have a summary describing the dependence of the number of created nodes in the graph on the complexity of the transportation plan. Note that the number of transfer nodes is always one less than the number of departure nodes.
4.2. CSO Performance
By implementing the CSO algorithm described in the previous section, its performance was obtained and then compared with Dijkstra’s and PSO algorithms. In addition, the variance analysis (ANOVA) was applied in the statistical evaluation of the CSO results. We checked how the variable containing the travel time obtained was influenced by the population size and the
visual coefficient. We tested the settings of the parameter:
visual = 1, 2, 3, 4 and the population size: 5, 15, and 50 individuals. Depending on the test instance, our analysis indicated either an essential influence or no essential influence of the
visual parameter on the travel time obtained. For each test instance, there existed, however, an essential dependence of that variable that contained the travel time obtained on the population size. However, no interactions between the
visual and population size factors occurred. Selected results of the significance levels
p for two analyses (instances with six lines, marked as 6/12 and 6/48) and the measures of the effect magnitude are presented in
Table 2.
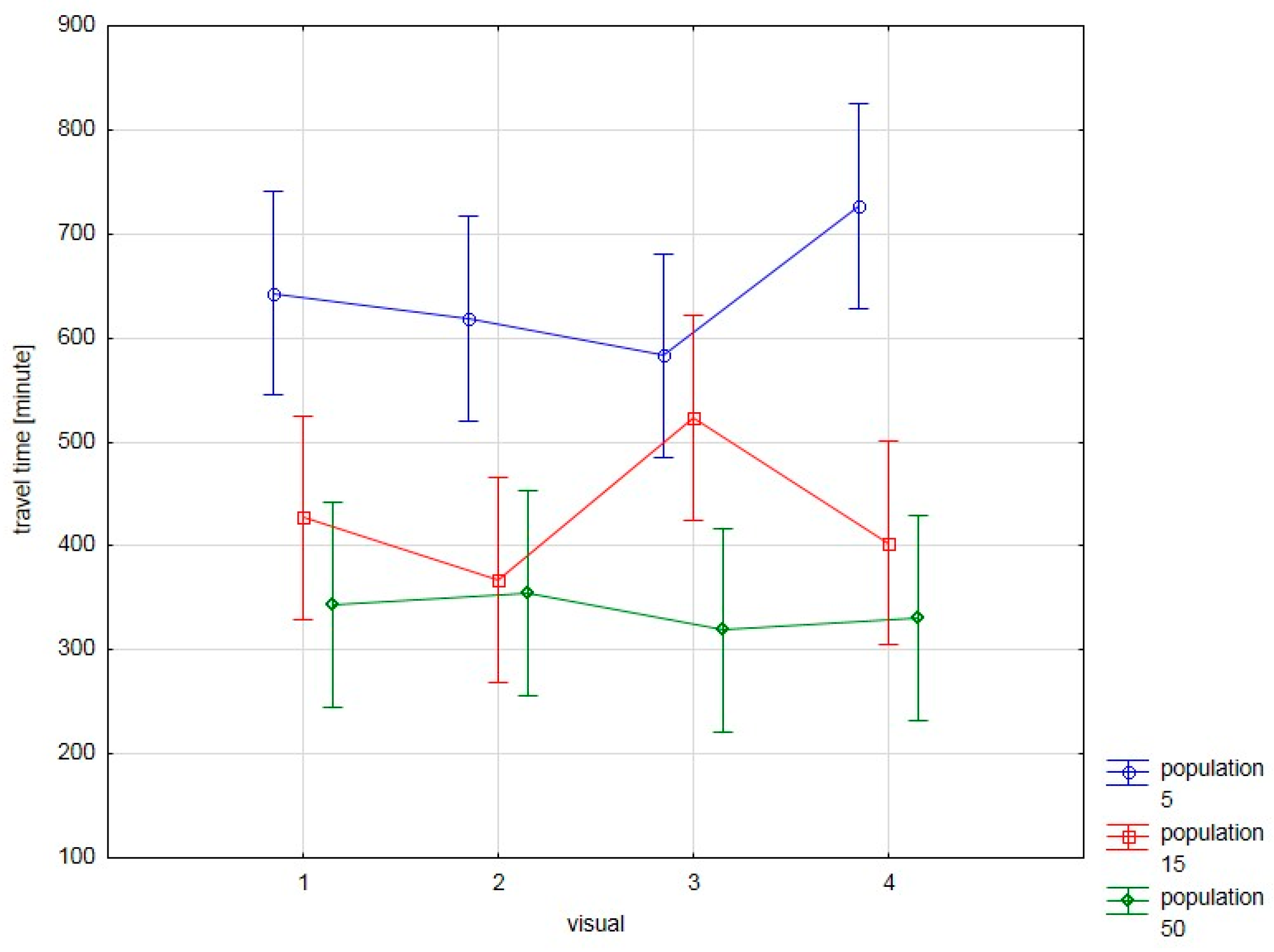
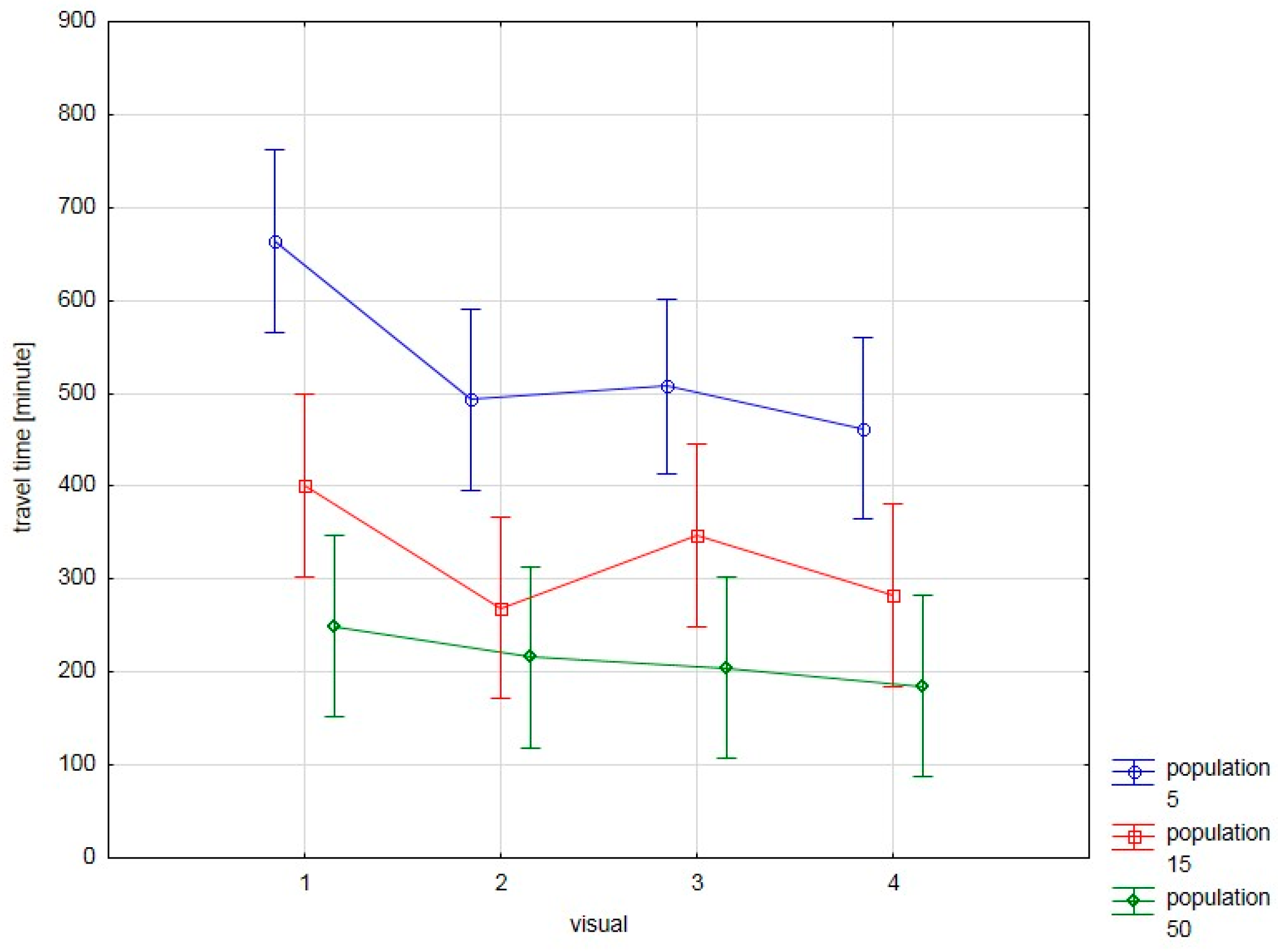
As we can see, the population size presents a strong effect (the
travel time variable is explained by the population size variable in the proportion of more than 40%) in both cases; however, the
visual either fails to indicate any influence (test instance 6/12) or shows a medium-size effect (test instance 6/48). The influence of the
visual and population size parameters on the travel time obtained (vertical bars refer to 0.95 confidence intervals) are presented for both test instances in
Figure 2 and
Figure 3.
To investigate which of the parameters being tested,
visual or population size, are different from each other, post hoc tests (Tukey tests) were conducted. Selected test results for test instance 6/48 are presented in
Table 3. For the
visual parameter, Tukey test showed essential differences of the average values between 1 and 2 and 4. In turn, for the population size parameter, tests showed essential differences between all the groups. For test instance 6/12, essential differences also occurred in all of the values of the population size parameter. Therefore, in our following tests, we assumed various sizes of population (5, 15, and 50) and
visual = 3.
Each run of the CSO approach was terminated after 1000 iterations or if there was no improvement of the best solution through 25 iterations. In all tests:
maxStep = 15,
maxAttempt = 100.
Table 4 shows the selected results of the CSO algorithm for the test instance with only one line, relating, however, to various sizes of population. For one line with 12 departures per day (marked as 1/12), the population consisting of 5 individuals is sufficient to find the best solution of travel time. Through 10 independent runs of the CSO approach, that solution was found in four cases. It turned out, however, that such a small number of solutions was not enough to solve the problem with 48 departures. The shortest travel time amounted to 1 h and 9 min. That value was obtained in three runs of the CSO algorithm. In the same test instance, the longest travel time amounted to 5 h and 21 min. Upon the increase of the population of individuals up to 15, we obtained the shortest travel time of 41 min in three runs. It is worth noting that the CSO algorithm, with the population of 50 solutions, generated the shortest travel time (41 min) in eight runs. What is interesting is that the worst solution for said population size was the same as the best solution for the population equal to 5.
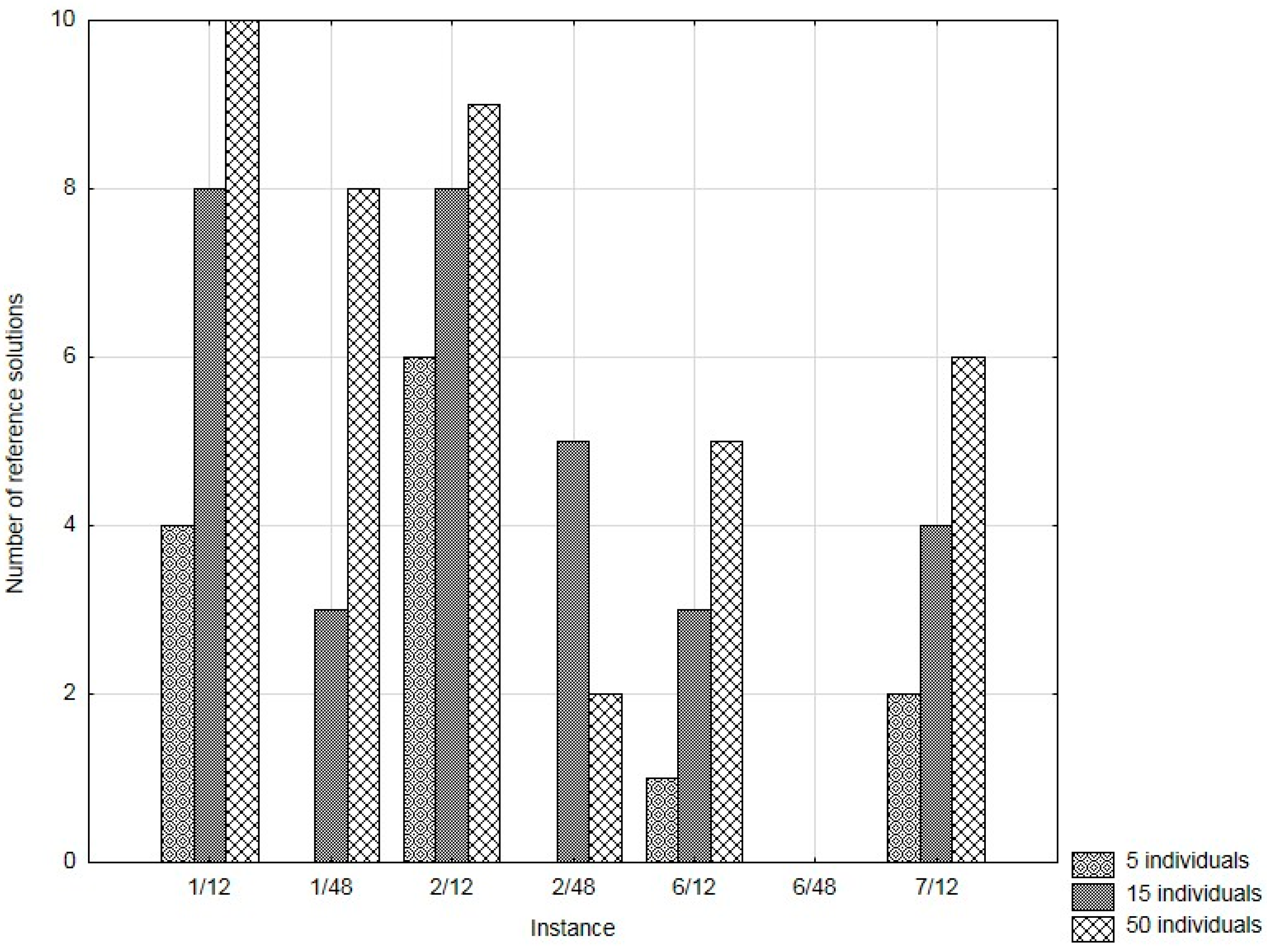
The number of correct solutions obtained during 10 runs, depending on the population size, is shown in
Figure 4. As expected, the increased population improved the chance of finding the best solution. Note that in the test instance 6/48 (six lines and 48 departures per day), the best result could not be attained anyway.
For simpler TE models, relating to 12 departures a day, we obtained the best solution, although only in several runs.
However, with the population composed of five solutions, it was not possible to obtain the best known solution for any of the test instances in which 48 departures a day were taken into account (marked as 1/48, 2/48, and 6/48, respectively).
In addition, we implemented the particle swarm optimization algorithm. We assume that following the neighboring particles consist of attempts at “taking over” part of the graph edge from the solution of a better particle; that is, the particle that “follows” another one is trying to add to its route a node from the particle being followed. The number of nodes that is tried to be added is determined by the particle’s velocity. Moreover, we assumed that the difference of one hour in reaching the target node caused the increase of one node in the particle’s velocity.
Table 5 shows the experimental results of the CSO algorithm performance in comparison with the results obtained by Dijkstra’s and PSO algorithms for each test instance. Among the results obtained from the swarm algorithms, the best and the worst values of travel time were gathered. The first column shows the population size, the second one presents specific test instances, described by the numbers of lines and departures. The columns “Best travel” and “Worst travel” represent the best and worst travel times found by the CSO and the PSO algorithms, respectively. The fifth and the eighth columns give the average computational times of 10 independent runs of swarm algorithms. The last column shows reference solutions obtained by Dijkstra’s algorithm.
Depending on particular tests, and upon comparison with Dijkstra’s algorithm, the best results obtained with the CSO algorithm were similar to those of the second algorithm. In all of the test instances the results show that application of a larger population (50 individuals) reduced travel time, and produced the same solutions as Dijkstra’s algorithm in most cases. It needs to be pointed out that such an improvement was reached at the expense of computational time. Note that it does not imply that the optimum result was achieved. In the cases presented here, the result was not satisfying in one test instance with six lines and 48 departures per day.
When analyzing the results obtained with the use of the PSO algorithm, one can conclude that the CSO algorithm performs better than the PSO does. We should notice that the best travel times obtained with the PSO algorithm for two instances (6/12 and 6/48) are worse than those obtained with the use of the CSO algorithm. We should further consider the worst solutions, in all of the analyzed cases, there was a distinct domination of the CSO algorithm over the PSO one. Additionally, the average time of calculation performance, with the population increased to 50 individuals, indicates that the CSO algorithm provides a better solution when such specific parameters have been selected.