Local Information as an Essential Factor for Quantum Entanglement
Abstract
:1. Introduction
2. The Qualitative and Quantitative Analysis of Quantum Entanglement
2.1. Qualitative Detection of Quantum Entanglement
2.2. Quantitative Measure of Quantum Entanglement
3. The Equivalent Simplification of Geometric Representation
3.1. Simplified Geometric Representation in Generalized Basis
3.2. Geometric Transformations of Quantum States by Local Unitary Operations
3.3. Simplification of Geometric Representation by Local Unitary Operation
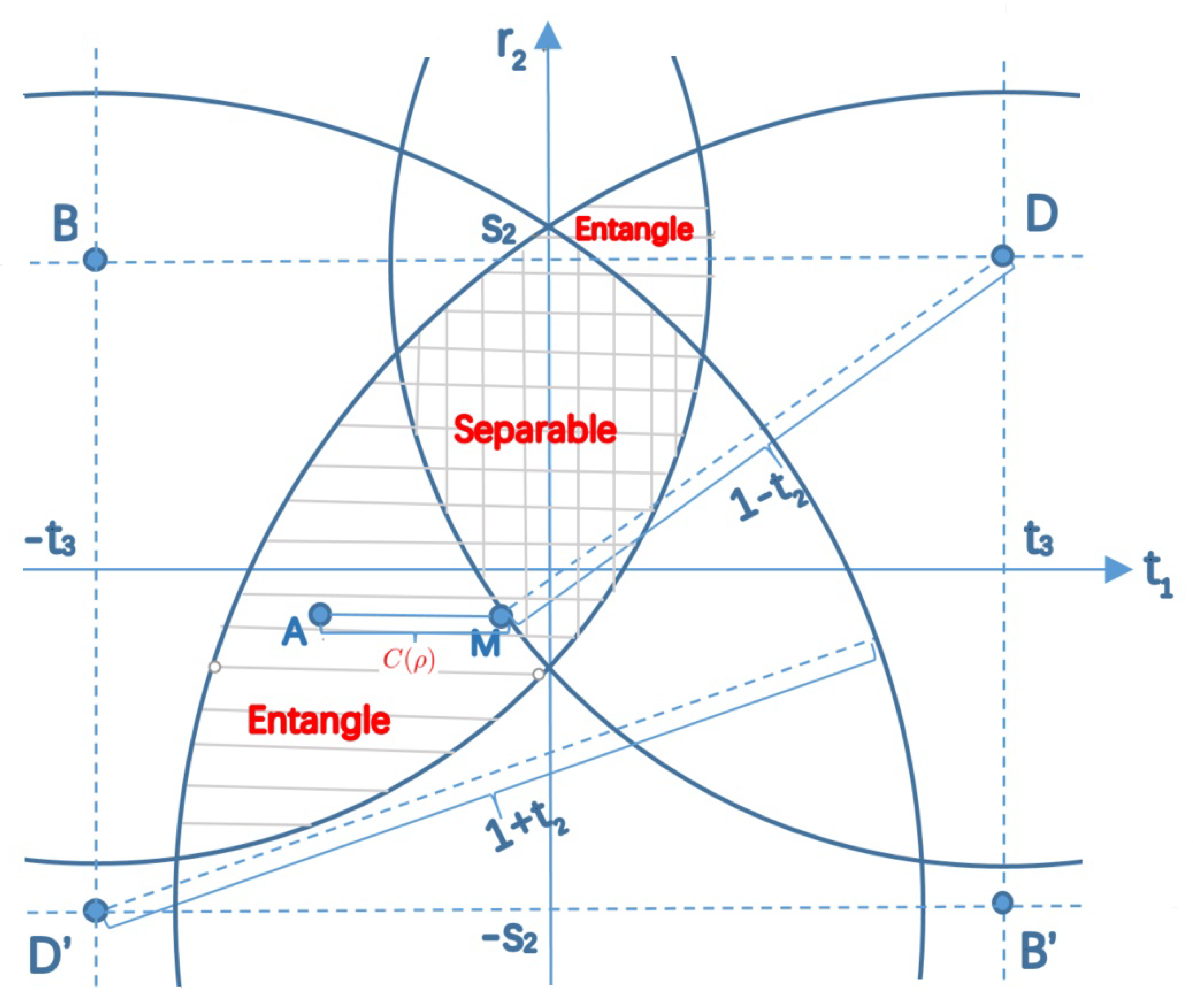
4. Geometric Bounds for Concurrence
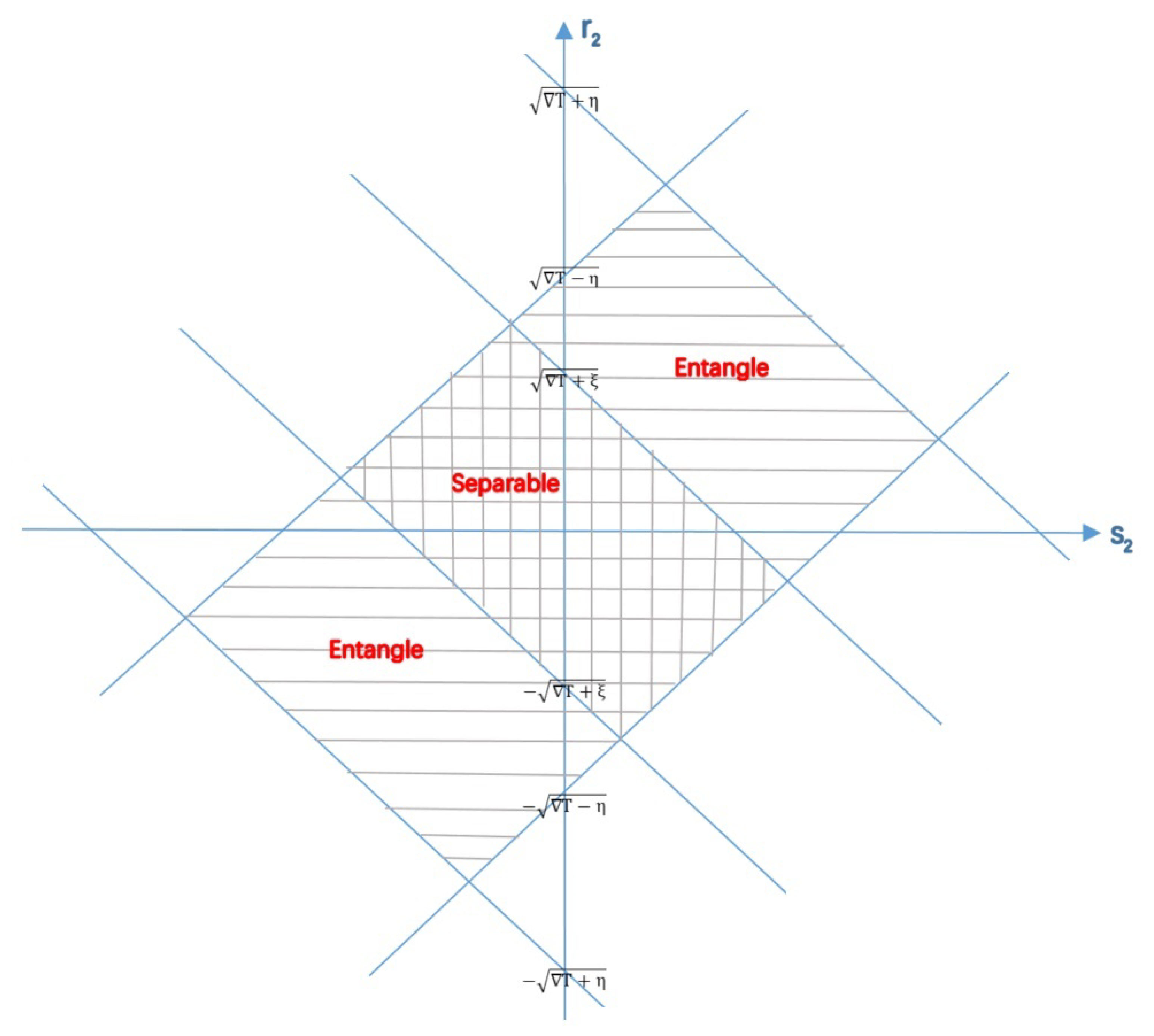
5. The Local Parameters and Separability
5.1. Permutation of Pauli Matrices by Local Unitary
5.2. Two Classes of Separable States
5.3. Local Parameters as an Indispensable Role for Entanglement
6. Conclusions and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef] [Green Version]
- Schrödinger, E. Discussion of probability relations between separated systems. Math. Proc. Camb. Philos. 1935, 31, 555–563. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef] [Green Version]
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2002, 361, 1655–1674. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on einstein-podolsky-rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Briegel, H.J.; Dur, W.; Cirac, J.I.; Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 1998, 81, 5932. [Google Scholar] [CrossRef]
- Su, Z.; Guan, J.; Li, L. Efficient quantum repeater with respect to both entanglement-concentration rate and complexity of local operations and classical communication. Phys. Rev. A 2018, 97, 012325. [Google Scholar] [CrossRef]
- Gurvits, L. Classical complexity and quantum entanglement. J. Comput. Syst. Sci. 2004, 69, 448–484. [Google Scholar] [CrossRef] [Green Version]
- Hioe, F.T.; Eberly, J.H. n-level coherence vector and higher conservation laws in quantum optics and quantum mechanics. Phys. Rev. Lett. 1981, 47, 838. [Google Scholar] [CrossRef]
- Gamel, O. Entangled Bloch spheres: Bloch matrix and two-qubit state space. Phys. Rev. A 2016, 93, 062320. [Google Scholar] [CrossRef] [Green Version]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, R.; Horocecki, P.; Horodecki, M. Violating Bell inequality by mixed spin-1/2 states: Necessary and sufficient condition. Phys. Lett. A 1995, 200, 340–344. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, M. Information-theoretic aspects of inseparability of mixed states. Phys. Rev. A 1996, 54, 1838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Vicente, J.I. Separability criteria based on the Bloch representation of density matrices. Quantum Inf. Comput. 2007, 7, 624–638. [Google Scholar]
- Badziag, P.; Brukner, C.; Laskowski, W.; Paterek, T.; Zukowski, M. Experimentally friendly geometrical criteria for entanglement. Phys. Rev. Lett. 2008, 100, 140403. [Google Scholar] [CrossRef] [Green Version]
- De Vicente, J.I.; Huber, M. Multipartite entanglement detection from correlation tensors. Phys. Rev. A 2011, 84, 062306. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Yu, J.; Li, M.; Fei, S. Improved separability criteria based on Bloch representation of density matrices. Sci. Rep. 2016, 6, 28850. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peres, A. Separability criterion for density matrices. Phys. Rev. Lett. 1996, 77, 1413–1415. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Wu, L. The generalized partial transposition criterion for separability of multipartite quantum states. Phys. Lett. A 2002, 306, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Chruściński, D.; Jurkowski, J.; Kossakowski, A. Quantum states with strong positive partial transpose. Phys. Rev. A 2008, 77, 022113. [Google Scholar] [CrossRef] [Green Version]
- Bohnet-Waldraff, F.; Braun, D.; Giraud, O. Partial transpose criteria for symmetric states. Phys. Rev. A 2016, 94, 042343. [Google Scholar] [CrossRef] [Green Version]
- Designolle, S.; Giraud, O.; Martin, J. Genuinely entangled symmetric states with no n-partite correlations. Phys. Rev. A 2017, 96, 032322. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S. Benjamin Schumacher Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046–2052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hill, S.; Wootters, W.K. Entanglement of a pair of quantum bits. Phys. Rev. Lett. 1997, 78, 5022–5025. [Google Scholar] [CrossRef] [Green Version]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef] [Green Version]
- Su, Z.; Tan, H.; Li, X. Entanglement as upper bound for the nonlocality of a general two-qubit system. Phys. Rev. A 2018, 101, 042112. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z. Local Information as an Essential Factor for Quantum Entanglement. Entropy 2021, 23, 728. https://doi.org/10.3390/e23060728
Su Z. Local Information as an Essential Factor for Quantum Entanglement. Entropy. 2021; 23(6):728. https://doi.org/10.3390/e23060728
Chicago/Turabian StyleSu, Zhaofeng. 2021. "Local Information as an Essential Factor for Quantum Entanglement" Entropy 23, no. 6: 728. https://doi.org/10.3390/e23060728





