A Model for Material Metrics in Thermoelectric Thomson Coolers
Abstract
:1. Introduction
2. Analysis
2.1. Thermoelectric Modules
2.2. Thomson Modules
2.2.1. Maximum Temperature Difference
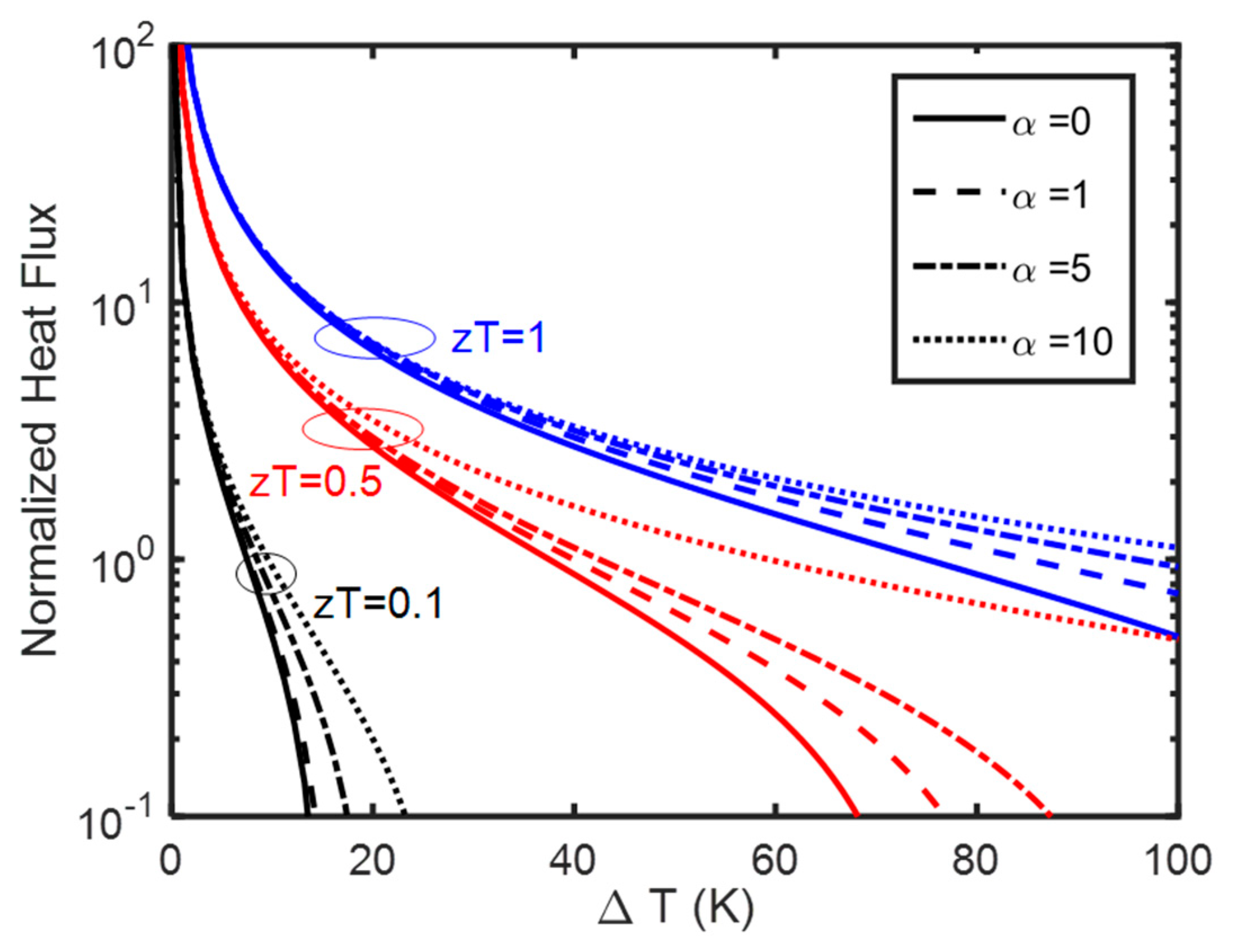
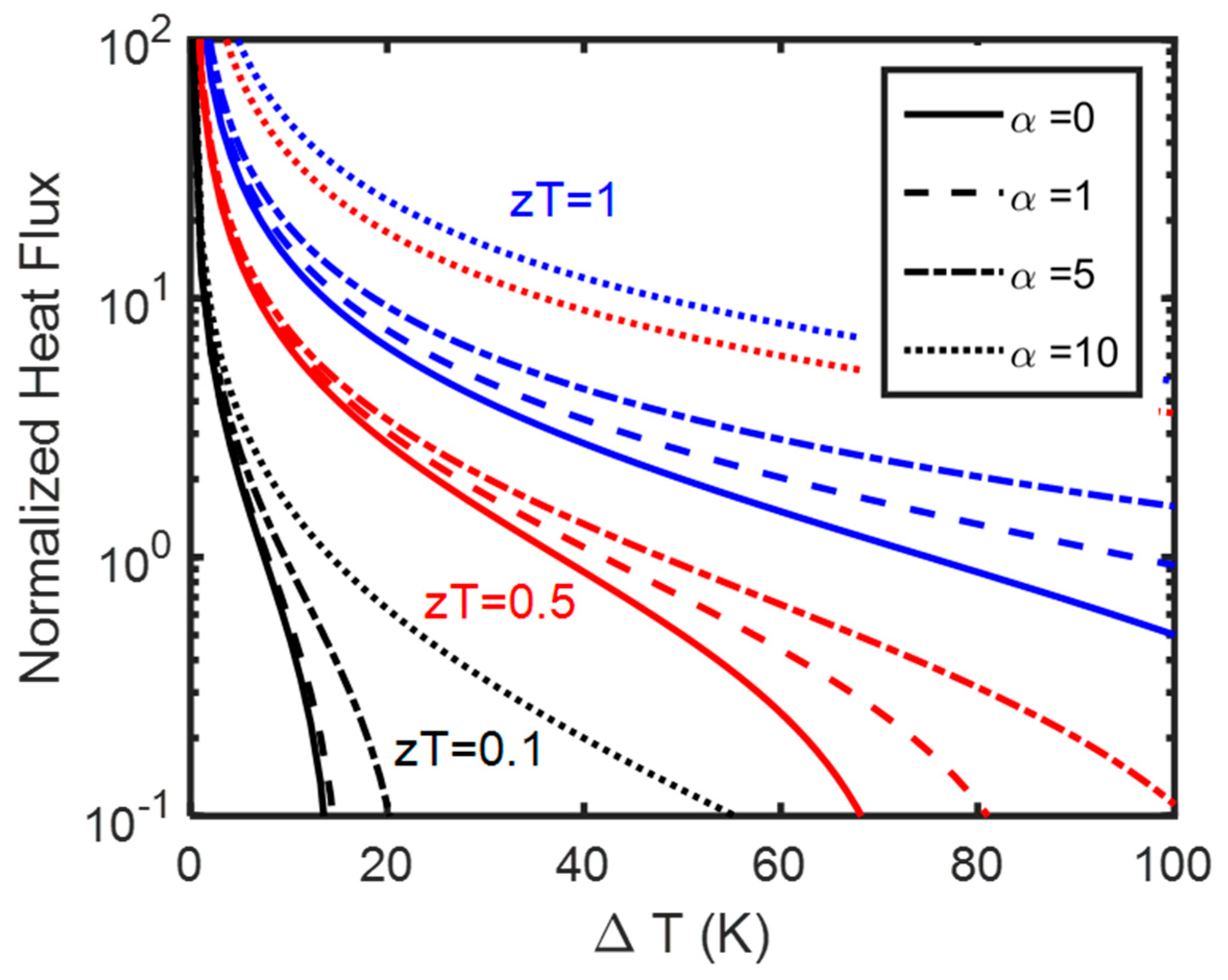
2.2.2. Maximum Heat Flux
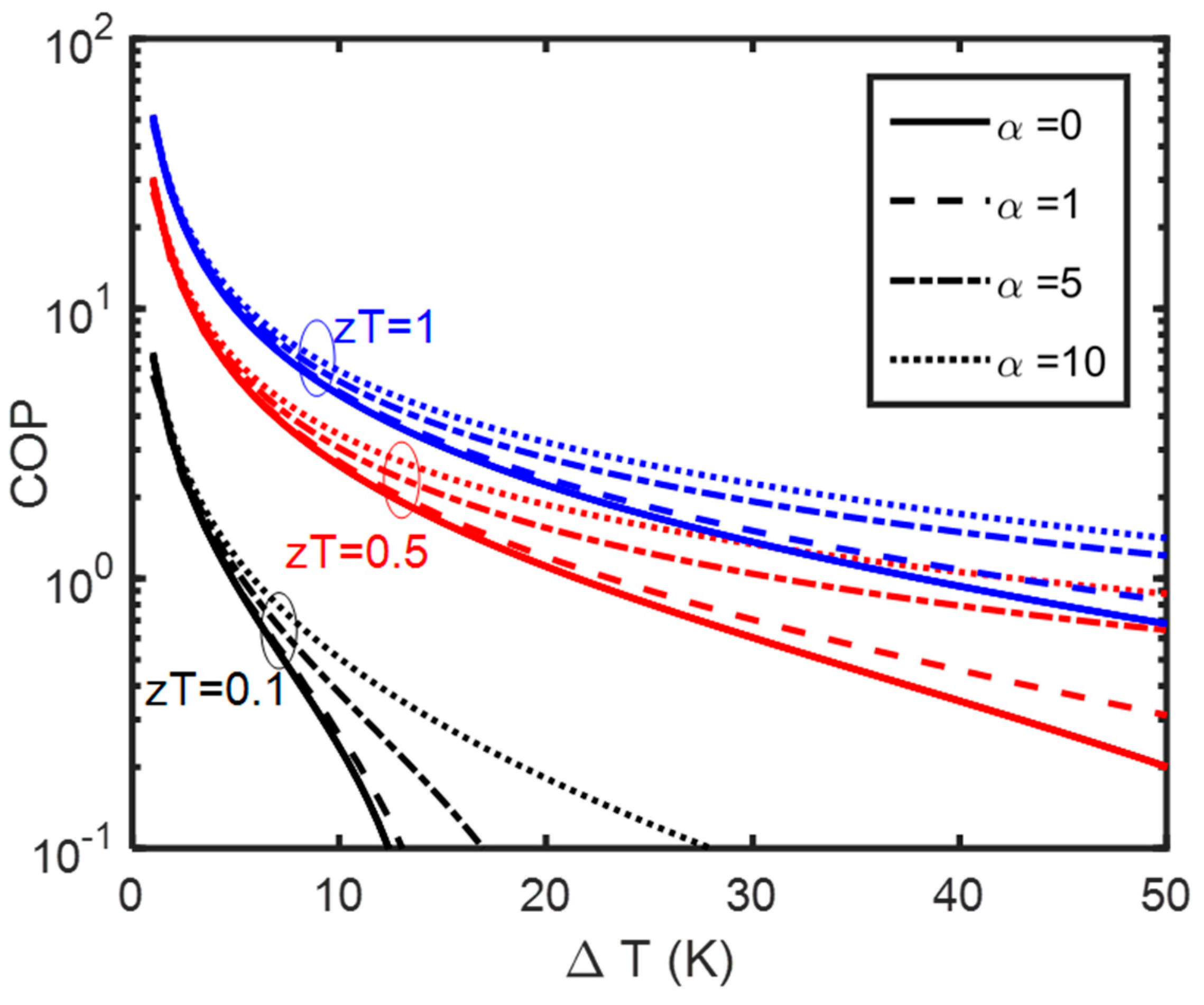
2.2.3. Maximum Coefficient of Performance, COP
3. Thomson Materials
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bell, L.E. Cooling, Heating, Generating Power, and Recovering Waste Heat with Thermoelectric Systems. Science 2008, 321, 1457–1461. [Google Scholar] [CrossRef] [PubMed]
- Goldsmid, H. Thermoelectric Refrigeration; Springer: New York, NY, USA, 1964. [Google Scholar]
- Ioffe, A.F. Semiconductor Thermoelements, and Thermoelectric Cooling; Infosearch, Ltd.: London, UK, 1957. [Google Scholar]
- Adams, M.J.; Verosky, M.; Zebarjadi, M.; Heremans, J.P. Active Peltier Coolers Based on Correlated and Magnon-Drag Metals. Phys. Rev. Appl. 2019, 11, 054008. [Google Scholar] [CrossRef]
- Li, S.; Snyder, K.; Akhanda, M.S.; Martukanitz, R.; Mitra, M.; Poon, J.; Zebarjadi, M. Cost-Efficient Copper-Nickel Alloy for Active Cooling Applications. Int. J. Heat Mass Transf. 2022, 195, 123181. [Google Scholar] [CrossRef]
- Zebarjadi, M. Electronic Cooling Using Thermoelectric Devices. Appl. Phys. Lett. 2015, 106, 203506. [Google Scholar] [CrossRef]
- Adams, M.J.; Verosky, M.; Zebarjadi, M.; Heremans, J.P. High Switching Ratio Variable-Temperature Solid-State Thermal Switch Based on Thermoelectric Effects. Int. J. Heat Mass Transf. 2019, 134, 114–118. [Google Scholar] [CrossRef]
- Mahan, G.D. Figure of Merit for Thermoelectrics. J. Appl. Phys. 1989, 65, 1578–1583. [Google Scholar] [CrossRef]
- Bian, Z.; Shakouri, A. Beating the Maximum Cooling Limit with Graded Thermoelectric Materials. Appl. Phys. Lett. 2006, 89, 212101. [Google Scholar] [CrossRef]
- Schilz, J.; Helmers, L.; Müller, W.E.; Niino, M. A Local Selection Criterion for the Composition of Graded Thermoelectric Generators. J. Appl. Phys. 1998, 83, 1150. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Saber, H.H.; Caillat, T. Efficient Segmented Thermoelectric Unicouples for Space Power Applications. Energy Convers. Manag. 2003, 44, 1755–1772. [Google Scholar] [CrossRef]
- Zeng, G.; Bahk, J.-H.; Bowers, J.E.; Lu, H.; Gossard, A.C.; Singer, S.L.; Majumdar, A.; Bian, Z.; Zebarjadi, M.; Shakouri, A. Thermoelectric Power Generator Module of 16×16 Bi2Te3 and 0.6% ErAs:(InGaAs)1−x(InAlAs)x Segmented Elements. Appl. Phys. Lett. 2009, 95, 083503. [Google Scholar] [CrossRef]
- El-Genk, M.; Saber, H.; Caillat, T. A Performance Comparison of SiGe and Skutterudite Based Segmented Thermoelectric Devices. Space Technol. Appl. Int. Forum-Staif 2002, 608, 1007–1015. [Google Scholar]
- Müller, E.; Walczak, S.; Seifert, W. Optimization Strategies for Segmented Peltier Coolers. Phys. Status Solidi (a) 2006, 203, 2128–2141. [Google Scholar] [CrossRef]
- Wehmeyer, G.; Yabuki, T.; Monachon, C.; Wu, J.; Dames, C. Thermal Diodes, Regulators, and Switches: Physical Mechanisms and Potential Applications. Appl. Phys. Rev. 2017, 4, 041304. [Google Scholar] [CrossRef]
- Liu, Z.C.; Wang, L. Applications of Phase Change Materials in Electrical Regime from Conventional Storage Memory to Novel Neuromorphic Computing. IEEE Access 2020, 8, 76471–76499. [Google Scholar] [CrossRef]
- Liangruksa, M.; Puri, I.K. Influence of Temperature-Dependent Thomson Coefficient on Thermal Transport in a Low-Dimensional Nanostructure. Nanoscale Microscale Thermophys. Eng. 2012, 16, 260–273. [Google Scholar] [CrossRef]
- Yamamoto, T.; Hatayama, S.; Song, Y.H.; Sutou, Y. Influence of Thomson Effect on Amorphization in Phase-Change Memory: Dimensional Analysis Based on Buckingham’s Π Theorem for Ge2Sb2Te5. Mater. Res. Express 2021, 8, 115902. [Google Scholar] [CrossRef]
- Ma, C.; He, J.; Lu, J.; Zhu, J.; Hu, Z. Modeling of the Temperature Profiles and Thermoelectric Effects in Phase Change Memory Cells. Appl. Sci. 2018, 8, 1238. [Google Scholar] [CrossRef]
- Thomson, W. On a Mechanical Theory of Thermo-Electric Currents. Proc. R. Soc. Edinb. 1851, 3, 91–98. [Google Scholar] [CrossRef]
- Modak, R.; Murata, M.; Hou, D.; Miura, A.; Iguchi, R.; Xu, B.; Guo, R.; Shiomi, J.; Sakuraba, Y.; Uchida, K.I. Phase-Transition-Induced Giant Thomson Effect for Thermoelectric Cooling. Appl. Phys. Rev. 2022, 9, 11414. [Google Scholar] [CrossRef]
- Akhanda, M.S.; Krylyuk, S.; Dickie, D.A.; Davydov, A.V.; Han, F.; Li, M.; Zebarjadi, M. Phase-Transition-Induced Thermal Hysteresis in Type-II Weyl Semimetals MoTe2 and Mo1−xWxTe2. Mater. Today Phys. 2022, 29, 100918. [Google Scholar] [CrossRef]
- Kuo, Y.K.; Sivakumar, K.M.; Su, T.H.; Lue, C.S. Phase Transitions in Lu2Ir3Si5: An Experimental Investigation by Transport Measurements. Phys. Rev. B Condens Matter Mater. Phys. 2006, 74, 045115. [Google Scholar] [CrossRef]
- Nakagawa, K.; Yokouchi, T.; Shiomi, Y. Reconfigurable Single-Material Peltier Effect Using Magnetic-Phase Junctions. Sci. Rep. 2021, 11, 24216. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Asheghi, M.; Goodson, K.E. Impact of Thermoelectric Phenomena on Phase-Change Memory Performance Metrics and Scaling. Nanotechnology 2012, 23, 205201. [Google Scholar] [CrossRef] [PubMed]
- Snyder, G.J.; Toberer, E.S.; Khanna, R.; Seifert, W. Improved Thermoelectric Cooling Based on the Thomson Effect. Phys. Rev. B Condens Matter Mater. Phys. 2012, 86, 045202. [Google Scholar] [CrossRef]
- Chiba, T.; Iguchi, R.; Komine, T.; Hasegawa, Y.; Uchida, K.I. Temperature Profile of the Thomson-Effect-Induced Heat Release/Absorption in Junctionless Single Conductors. Jpn. J. Appl. Phys. 2023, 62, 037001. [Google Scholar] [CrossRef]
- Huang, M.J.; Yen, R.H.; Wang, A.B. The Influence of the Thomson Effect on the Performance of a Thermoelectric Cooler. Int. J. Heat Mass Transf. 2005, 48, 413–418. [Google Scholar] [CrossRef]
- Sun, D.; Shen, L.; Chen, H.; Jiang, B.; Jie, D.; Liu, H.; Yao, Y.; Tang, J. Modeling and Analysis of the Influence of Thomson Effect on Micro-Thermoelectric Coolers Considering Interfacial and Size Effects. Energy 2020, 196, 117116. [Google Scholar] [CrossRef]
- Gong, T.; Gao, L.; Wu, Y.; Tan, H.; Qin, F.; Xin, X.; Shen, L.; Li, J.; Ming, T. A Model to Evaluate the Device-Level Performance of Thermoelectric Cooler with Thomson Effect Considered. J. Therm. Sci. 2022, 31, 712–726. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 121. [Google Scholar]
- da Rosa, A.; da Rosa, A.V. Fundamentals of Renewable Energy Processes, 3rd ed.; Elsevier Science & Technology: Waltham, MA, USA, 2013. [Google Scholar]
- Iwasaki, K.; Shimada, M.; Yamane, H.; Takahashi, J.; Kubota, S.; Nagasaki, T.; Arita, Y.; Yuhara, J.; Nishi, Y.; Matsui, T. Electrical Resistivity and Seebeck Coefficient of Sr6Co5O15. J. Alloys Compd. 2004, 377, 272–276. [Google Scholar] [CrossRef]
- Uchida, K.I.; Murata, M.; Miura, A.; Iguchi, R. Observation of the Magneto-Thomson Effect. Phys. Rev. Lett. 2020, 125, 106601. [Google Scholar] [CrossRef]
- Byeon, D.; Sobota, R.; Delime-Codrin, K.; Choi, S.; Hirata, K.; Adachi, M.; Kiyama, M.; Matsuura, T.; Yamamoto, Y.; Matsunami, M.; et al. Discovery of Colossal Seebeck Effect in Metallic Cu2Se. Nat. Commun. 2019, 10, 72. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zebarjadi, M.; Akbari, O. A Model for Material Metrics in Thermoelectric Thomson Coolers. Entropy 2023, 25, 1540. https://doi.org/10.3390/e25111540
Zebarjadi M, Akbari O. A Model for Material Metrics in Thermoelectric Thomson Coolers. Entropy. 2023; 25(11):1540. https://doi.org/10.3390/e25111540
Chicago/Turabian StyleZebarjadi, Mona, and Omid Akbari. 2023. "A Model for Material Metrics in Thermoelectric Thomson Coolers" Entropy 25, no. 11: 1540. https://doi.org/10.3390/e25111540




