Integrated Energy Micro-Grid Planning Using Electricity, Heating and Cooling Demands
Abstract
:1. Introduction
2. The Integrated Energy Micro-Grid
2.1. Structure of the Integrated Energy System (IES) and the Integrated Energy Micro-Grid (IEMG)
2.2. The Principle Elements of the IEMG
2.2.1. The Generation Equipment
2.2.2. Energy Network Model
2.3. Energy Balance of the IEMG
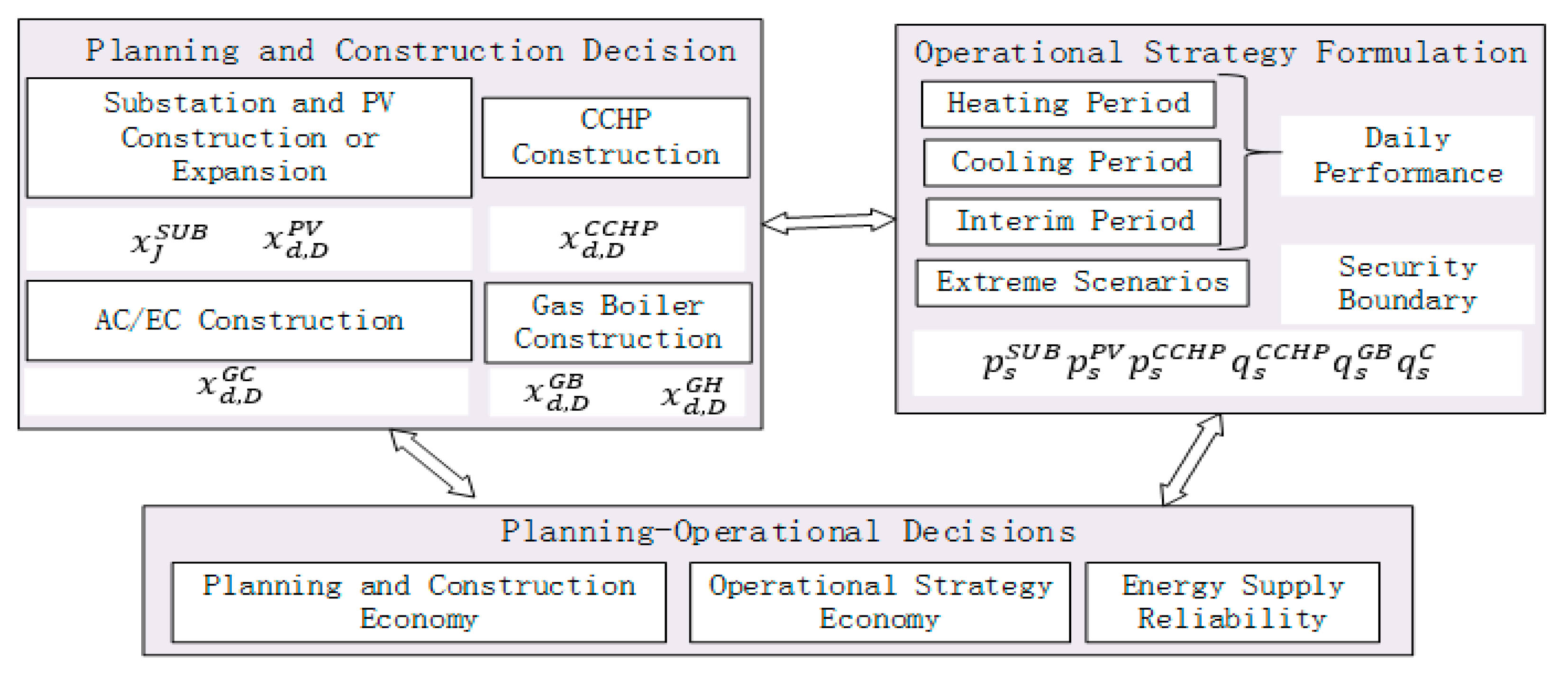
3. The IEMG Planning Optimization Model
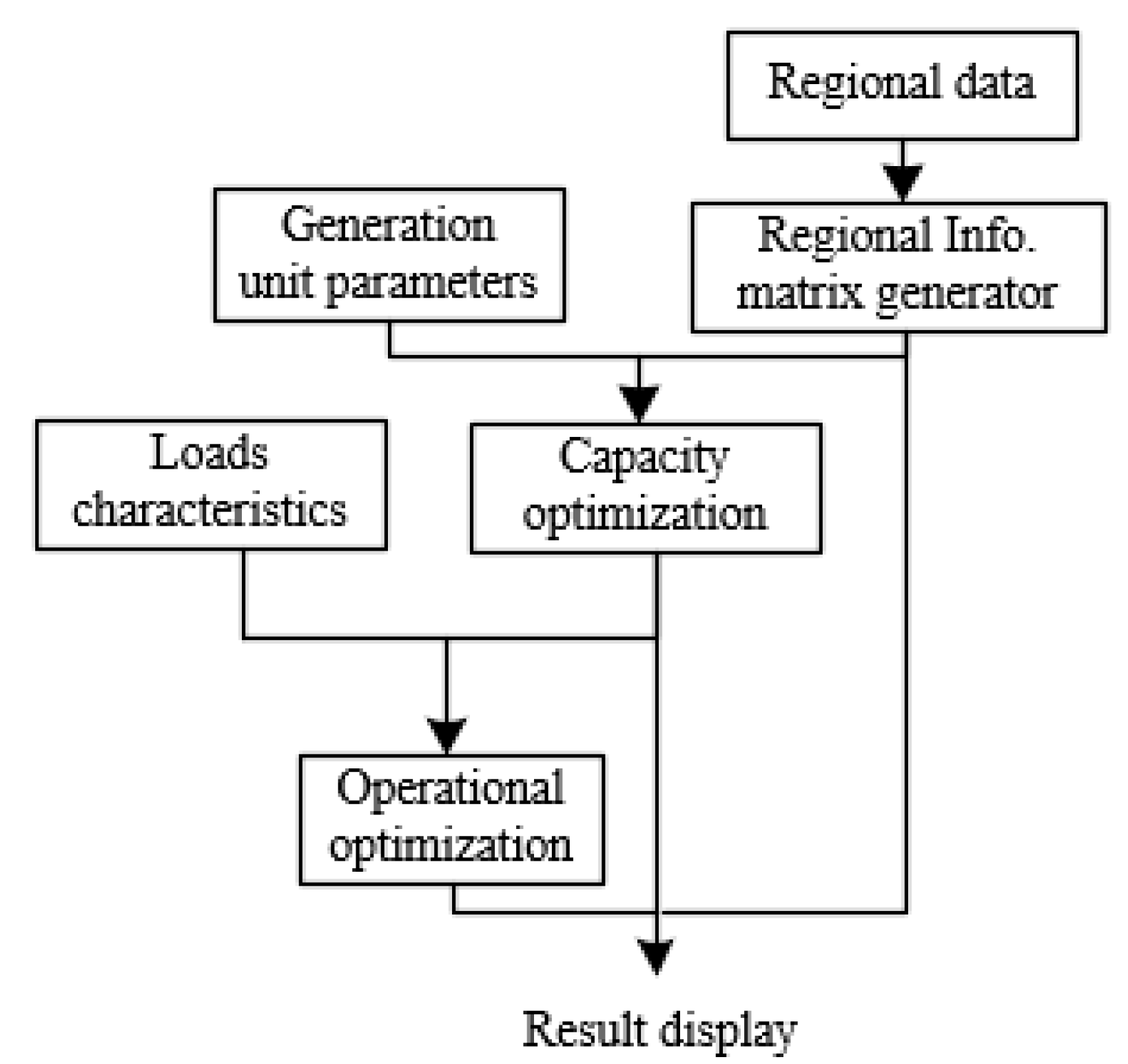
3.1. Planning Process and Framework
- (1)
- Extract the regional division, loads, and other planning-related data and information, and carry out the overall regional energy supply equipment configuration (for electricity, heating, and cooling).
- (2)
- Obtain the overall configuration capacity of the energy supply equipment from step 1, combined with the load characteristics of each region, and do the regional equipment type selection and capacity optimization.
- (3)
- According to the equipment selection and capacity optimizing results, deduce the electricity, heating and the cooling load balance operation simulation of each region, and output the results.
- (4)
- Deduce the load balance operation simulation on the basis of quarterly and extreme scenarios, and output the results.
- (5)
- Test and determine whether the regional and quarterly simulation results conform to the energy flow and all other constraints.
- (6)
- If the result does not satisfy all the constraints, adjust the selection and capacity results until all constraints are met, then output the corresponding configuration.
3.2. The Objective Function
3.3. Constraint Conditions
3.4. Calculation Method
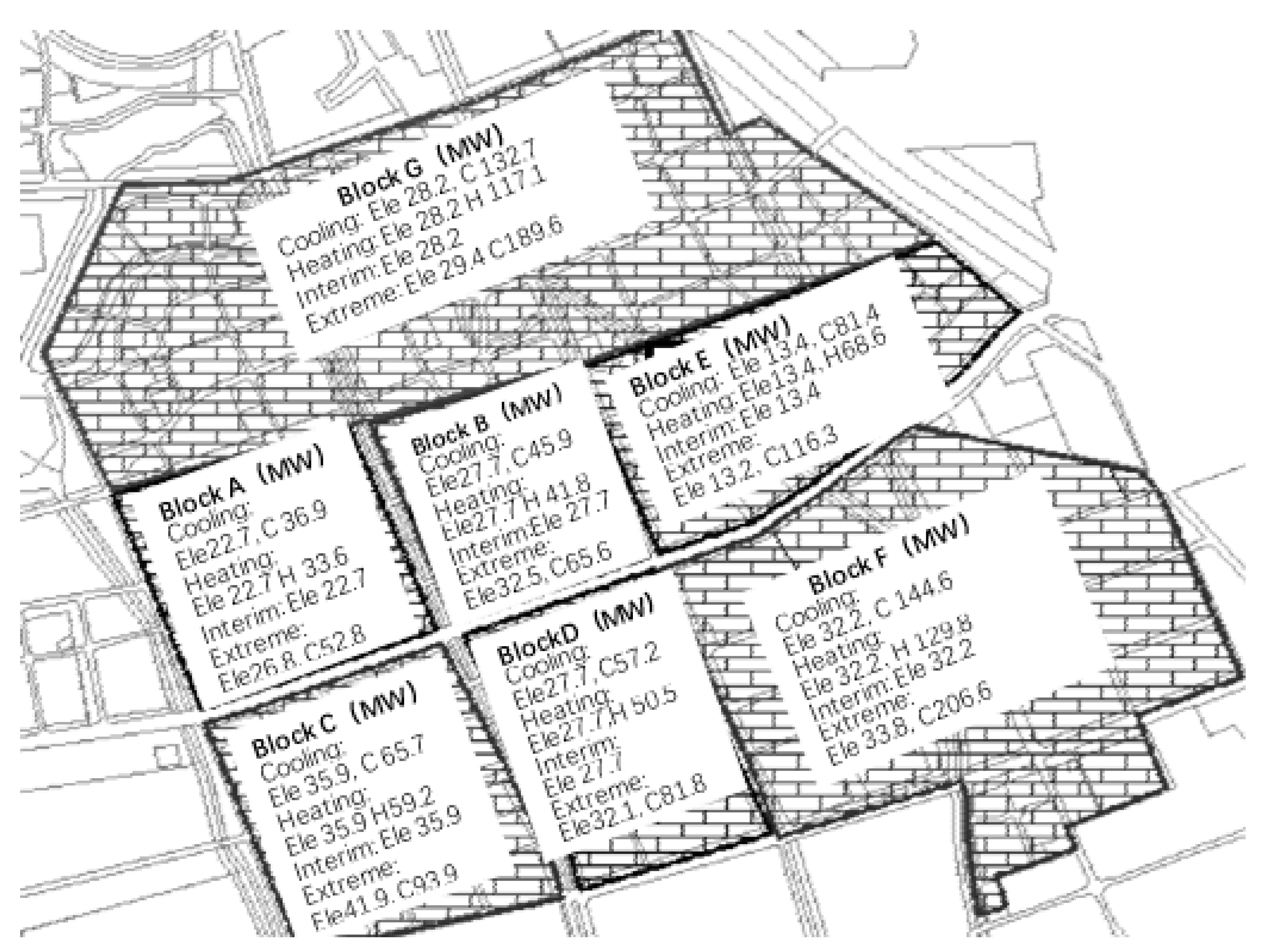
4. Case Study
4.1. Case Description
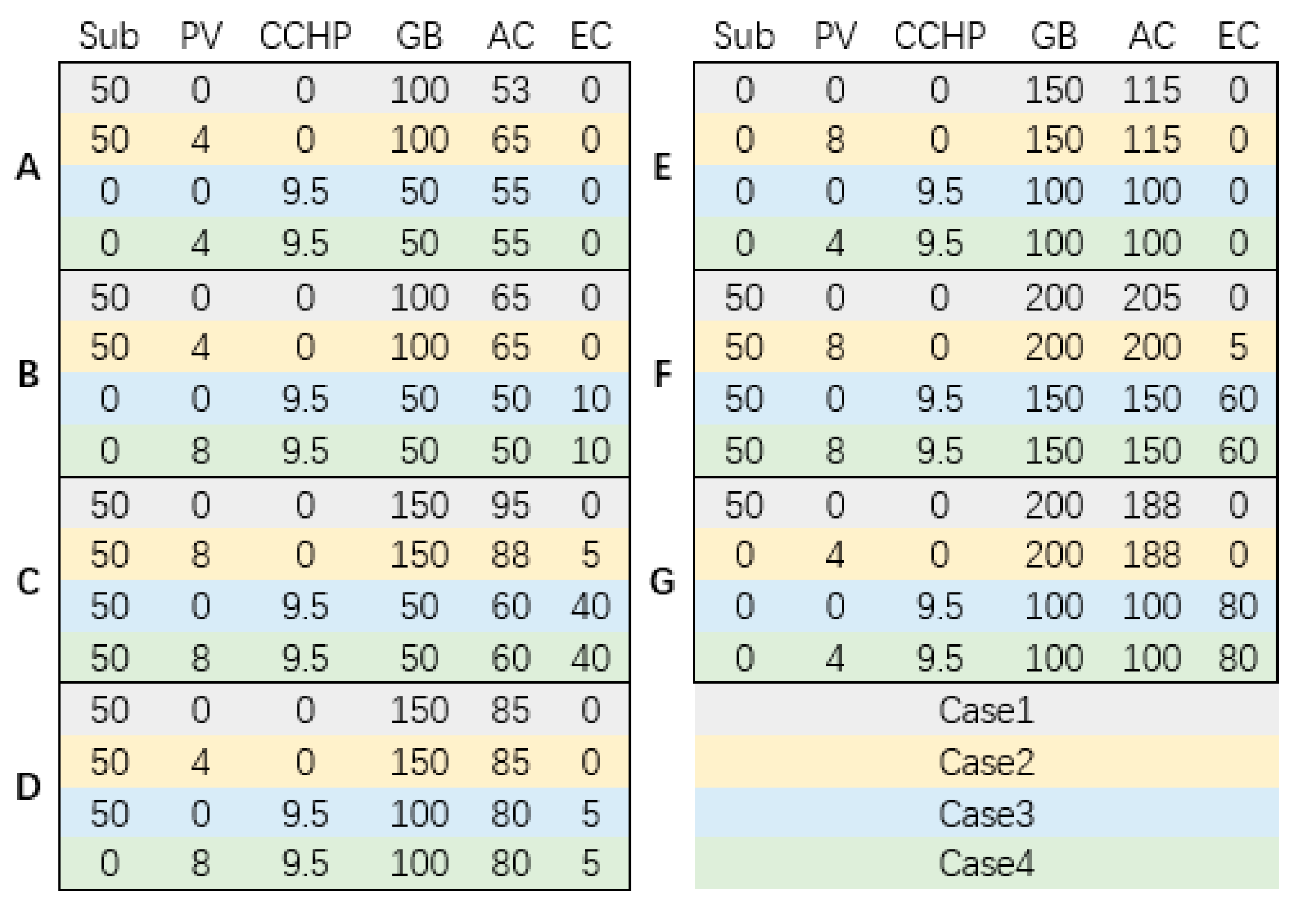
- CASE 1
- Electricity is only purchased from the external power grid, without consideration of PV and CCHP;
- CASE 2
- A 4 MW PV system at least is built in each district and electricity can be purchased from the external power grid, without consideration of the CCHP;
- CASE 3
- CCHP construction is considered and electricity can be purchased from the external power grid when the output of the CCHP is insufficient, without consideration of PV;
- CASE 4
- A 4 MW PV generation system at least is built in each district, a CCHP is considered, and electricity can be purchased from the external power grid when the outputs of the CCHP and the PV are insufficient.
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mei, S.; Li, R.; Xue, X.; Chen, Y.; Lu, Q.; Chen, X.; Carsten, D.A.; Li, R.; Chen, L. Paving the Way to Smart Micro Energy Grid: Concepts, Design Principles, and Engineering Practices. CSEE J. Power Energy Syst. 2017, 3, 440–449. [Google Scholar] [CrossRef]
- Lund, H.; Münster, E. Integrated energy systems and local energy markets. Energy Policy 2006, 34, 1152–1160. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Wang, Y.; Yu, H.; Li, R.; Song, S. Energy Management for Smart Multi-Energy Complementary Micro-Grid in the Presence of Demand Response. Energies 2018, 11, 974. [Google Scholar] [CrossRef]
- Ming, N.; Wei, H.; Guo, J.; Su, L. Research on Economic Operation of Grid-Connected Micro-grid. Power Syst. Technol. 2010, 34, 38–42. [Google Scholar]
- Han, L.; Wang, F.; Tian, C. Economic Evaluation of Actively Consuming Wind Power for an Integrated Energy System Based on Game Theory. Energies 2018, 11, 1476. [Google Scholar] [CrossRef]
- Chicco, G.; Mancarella, P. Distributed Multi-generation: A Comprehensive View. Renew. Sustain. Energy Rev. 2009, 13, 535–551. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Sun, J. Energy Management for Community Energy Network with CHP Based on Cooperative Game. Energies 2018, 11, 1066. [Google Scholar] [CrossRef]
- Liu, X.Z.; Wu, J.Z.; Jenkins, N.; Bagdanavicius, A. Combined Analysis of Electricity and Heat Networks. Appl. Energy 2016, 162, 1238–1250. [Google Scholar] [CrossRef]
- Pan, Z.G.; Guo, Q.L.; Sun, H.B. Interactions of District Electricity and Heating Systems Considering Time-scale Characteristics Based on Quasi-Steady Multi-Energy Flow. Appl. Energy 2016, 167, 230–243. [Google Scholar] [CrossRef]
- Zeng, Q.; Fang, J.K.; Li, J.H.; Chen, Z. Steady-state Analysis of the Integrated Natural Gas and Electric Power System with Bi-directional Energy Conversion. Appl. Energy 2016, 184, 1483–1492. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, D.; Jia, H.J.; Chen, Z.Y.; Guo, B.Q.; Zhou, H.M.; Fang, M.W. Steady State Analysis of Electricity-gas Regional Integrated Energy System with Consideration of NGS Networks Status. Proc. CSEE 2017, 37, 1293–1304. [Google Scholar]
- Shabanpour-Haghighi, A.; Seifi, A.R. An Integrated Steady-state Operation Assessment of Electrical, Natural Gas and District Heating Networks. IEEE Trans. Power Syst. 2016, 31, 3636–3647. [Google Scholar] [CrossRef]
- Wang, Y.R.; Zeng, B.; Guo, J.; Shi, J.Q.; Zhang, J.H. Multi-energy Flow Calculation Method for Integrated Energy System Containing Electricity, Heat and Gas. Power Syst. Technol. 2016, 40, 2942–2950. [Google Scholar]
- Wang, R.; Gu, W.; Wu, Z. Economic and Optimal Operation of Combined Heat and Power Microgrid with Renewable Energy Resources. Autom. Electr. Power Syst. 2011, 35, 22–27. [Google Scholar]
- Liu, X.; Wu, H. A Control Strategy Operation Optimization of Combine Cooling Heating and Power System Considering Solar Comprehensive Utilization. Autom. Electr. Power Syst. 2015, 39, 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, H.; Yong, M.; Huang, Y.; Zhang, F.; Wang, X. Optimal Scheduling of Integrated Energy Systems with Combined Heat and Power Generation, Photovoltaic and Energy Storage Considering Battery Lifetime Loss. Energies 2018, 11, 1676. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, C.; Wang, Y.; Li, W. Optimal Expansion Co-planning of Reconfigurable Electricity and Natural Gas Distribution Systems Incorporating Energy Hubs. Energies 2017, 10, 124. [Google Scholar] [CrossRef]
- Unsihuay-Vila, C.; Marangon-Lima, J.W.; de Souza, A.Z.; Perez-Arriaga, I.J.; Balestrassi, P.P. A Model to Long-term, Multiarea, Multistage, and Integrated Expansion Planning of Electricity and Natural Gas Systems. IEEE Trans. Power Syst. 2010, 25, 1154–1168. [Google Scholar] [CrossRef]
- Saldarriaga, C.A.; Hincapié, R.A.; Salazar, H. A Holistic Approach for Planning Natural Gas and Electricity Distribution Networks. IEEE Trans. Power Syst. 2013, 28, 4052–4063. [Google Scholar] [CrossRef]
- Qiu, J.; Dong, Z.Y.; Zhao, J.H.; Xu, Y.; Zheng, Y.; Li, C.; Wong, K.P. Multi-stage Flexible Expansion Co-planning Under Uncertainties in a Combined Electricity and Gas Market. IEEE Trans. Power Syst. 2015, 30, 2119–2129. [Google Scholar] [CrossRef]
- Barati, F.; Seifi, H.; Sepasian, M.S.; Nateghi, A.; Shafie-khah, M.; Catalao, J.P.S. Multi-period Integrated Framework of Generation, Transmission, and Natural Gas Grid Expansion Planning for Large-scale Systems. IEEE Trans. Power Syst. 2015, 30, 2527–2537. [Google Scholar] [CrossRef]
- Qiu, J.; Dong, Z.Y.; Zhao, J.H.; Meng, K.; Zheng, Y.; Hill, D.J. Low Carbon Oriented Expansion Planning of Integrated Gas and Power Systems. IEEE Trans. Power Syst. 2015, 30, 1035–1046. [Google Scholar] [CrossRef]
- Shao, C.; Shahidehpour, M.; Wang, X.; Wang, X.; Wang, B. Integrated Planning of Electricity and Natural Gas Transportation Systems for Enhancing the Power Grid Resilience. IEEE Trans. Power Syst. 2017, 32, 4418–4429. [Google Scholar] [CrossRef]
- Zhao, B.; Conejo, A.J.; Sioshansi, R. Coordinated Expansion Planning of Natural Gas and Electric Power Systems. IEEE Trans. Power Syst. 2017, 33, 3064–3075. [Google Scholar] [CrossRef]
- Odetayo, B.; MacCormack, J.; Rosehart, W.D.; Zareipour, H. A Sequential Planning Approach for Distributed Generation and Natural Gas Networks. Energy 2017, 127, 428–437. [Google Scholar] [CrossRef]
- Khaligh, V.; Buygi, M.; Anvari-Moghaddam, A.; Guerrero, M. A Multi-Attribute Expansion Planning Model for Integrated Gas–Electricity System. Energies 2018, 11, 2573. [Google Scholar] [CrossRef]
- Li, G.; Wang, R.; Zhang, T.; Ming, M.; Sciubba, E. Multi-Objective Optimal Design of Renewable Energy Integrated CCHP System Using PICEA-g. Energies 2018, 11, 743. [Google Scholar] [CrossRef]
- Wu, D.; Wang, R. Combined Cooling, Heating and Power: A Review. Prog. Energy Combust. Sci. 2006, 32, 459–495. [Google Scholar] [CrossRef]
- Jradi, M.; Riffat, S. Tri-generation systems: Energy policies, prime movers, cooling technologies, configurations and operation strategies. Renew. Sustain. Energy Rev. 2014, 32, 396–415. [Google Scholar] [CrossRef]
- Bao, Z.; Zhou, Q.; Yang, Z.; Yang, Q.; Xu, L.; Wu, T. A Multi Time-scale and Multi Energy-type Coordinated Microgrid Scheduling Solution-Part I: Model and Methodology. IEEE Trans. Power Syst. 2015, 30, 2257–2266. [Google Scholar] [CrossRef]
- Li, Z.; Jenkins, N.; Wu, W.; Shahidehpour, M.; Wang, J.; Zhang, B. Combined Heat and Power Dispatch Considering Pipeline Energy Storage of District Heating Network. IEEE Trans. Sustain. Energy 2016, 71, 12–22. [Google Scholar] [CrossRef]
- Li, J.; Fang, J.; Zeng, Q.; Chen, Z. Optimal Operation of the Integrated Electrical and Heating Systems to Accommodate the Intermittent Renewable Sources. Appl. Energy 2016, 167, 244–254. [Google Scholar] [CrossRef]
- Bloess, A.; Schill, W.; Zerrahn, A. Power-to-heat for renewable energy integration: A review of technologies, modeling approaches, and flexibility potentials. Appl. Energy 2017, 212, 1611–1626. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Magistrati, G.; Marchegiani, G. Optimization Models for Islanded Micro-Grids: A Comparative Analysis between Linear Programming and Mixed Integer Programming. Energies 2017, 10, 241. [Google Scholar] [CrossRef]
- Gu, W.; Wang, Z.; Wu, Z.; Luo, Z.; Tang, Y.; Wang, J. An online optimal dispatch schedule for CCHP microgrids based on model predictive control. IEEE Trans. Smart Grid 2017, 8, 2332–2342. [Google Scholar] [CrossRef]



| Substation Expansion | CCHP | ||||
| Scheme No. | Capacity (MVA) | Construction Cost | Scheme No. | Capacity (MW) | Construction Cost |
| 1 | 1 × 50 | 125 | 1 | 1 | 185 |
| 2 | 2 × 50 | 250 | 2 | 2 | 375 |
| 3 | 3 × 50 | 375 | 3 | 3 | 550 |
| 4 | 4 × 50 | 500 | 4 | 5 | 850 |
| 5 | 5 × 50 | 625 | 5 | 9.5 | 1600 |
| 6 | 6 × 50 | 750 | |||
| Gas Boiler | Others | ||||
| Scheme No. | Alternative Options (MW) | Construction Cost | Equipment | Construction Cost | Unit |
| 1 | 50 | 440 | PV | 130 | USD/MW |
| 2 | 100 | 900 | AC | 10 | USD/MW |
| 3 | 150 | 1350 | EC | 15 | USD/MW |
| 4 | 200 | 1750 | HRB | 2.5 | USD/MW |
| Full Capacity (MW) | Characteristic Function Coefficient | |||||
|---|---|---|---|---|---|---|
| 1 | 0.421 | −222.411 | 0.211 | 3.624 | 0.149 | 81.731 |
| 2 | 0.466 | −657.422 | 0.219 | 13.644 | 0.151 | 90.737 |
| 3 | 0.479 | −758.940 | 0.208 | 94.383 | 0.153 | 173.562 |
| 5 | 0.472 | −896.264 | 0.207 | 125.832 | 0.149 | 204.828 |
| 9.5 | 0.470 | −915.262 | 0.204 | 130.261 | 0.146 | 220.152 |
| Comparative Case | CASE 1 | CASE 2 | CASE 3 | CASE 4 | |
|---|---|---|---|---|---|
| Selected | No PV | With PV | No PV | PV | |
| Scheme | No CCHP | No CCHP | With CCHP | And CCHP | |
| Construction Cost | PV | 0 | 3718.75 | 0 | 3718.75 |
| CCHP | 0 | 0 | 11,221.875 | 11,221.875 | |
| GB&HRB | 11,161.72 | 11,161.72 | 6696.40625 | 6696.40625 | |
| Substation | 750 | 625 | 375 | 250 | |
| AC/EC | 7496.41 | 7496.41 | 6591.40625 | 6591.40625 | |
| In Total | 19,408.13 | 23,001.88 | 24,884.6875 | 28,478.4375 | |
| Operational Cost | PV | 0 | 42,276.42 | 0 | 42,276.42 |
| CCHP | 0 | 0 | 74,857.50 | 65,116.65 | |
| Purchased electricity | 322,498.77 | 257,164.66 | 206,985.31 | 160,298.32 | |
| GB&HRB | 53,500.78 | 53,500.78 | 44,561.415 | 44,561.41 | |
| In Total | 375,999.53 | 352,941.86 | 351,288.91 | 340,731.23 | |
| Total Cost | 395,407.66 | 395,407.66 | 375,943.73 | 376,173.59 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Liang, D.; Tong, Z. Integrated Energy Micro-Grid Planning Using Electricity, Heating and Cooling Demands. Energies 2018, 11, 2810. https://doi.org/10.3390/en11102810
Huang H, Liang D, Tong Z. Integrated Energy Micro-Grid Planning Using Electricity, Heating and Cooling Demands. Energies. 2018; 11(10):2810. https://doi.org/10.3390/en11102810
Chicago/Turabian StyleHuang, He, DaPeng Liang, and Zhen Tong. 2018. "Integrated Energy Micro-Grid Planning Using Electricity, Heating and Cooling Demands" Energies 11, no. 10: 2810. https://doi.org/10.3390/en11102810
APA StyleHuang, H., Liang, D., & Tong, Z. (2018). Integrated Energy Micro-Grid Planning Using Electricity, Heating and Cooling Demands. Energies, 11(10), 2810. https://doi.org/10.3390/en11102810




