Weak Localization and Antilocalization in Topological Materials with Impurity Spin-Orbit Interactions
Abstract
:1. Introduction
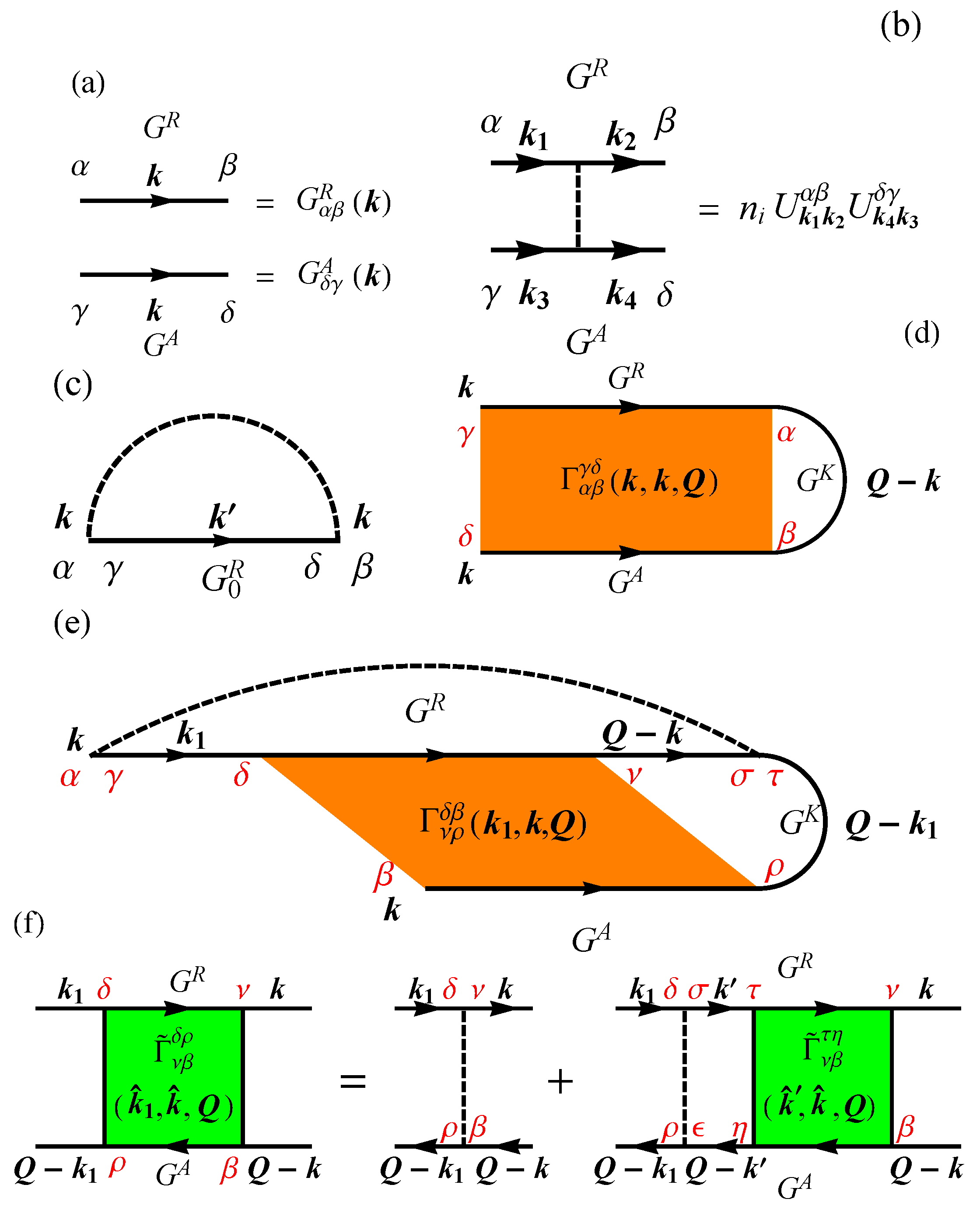
2. General Model
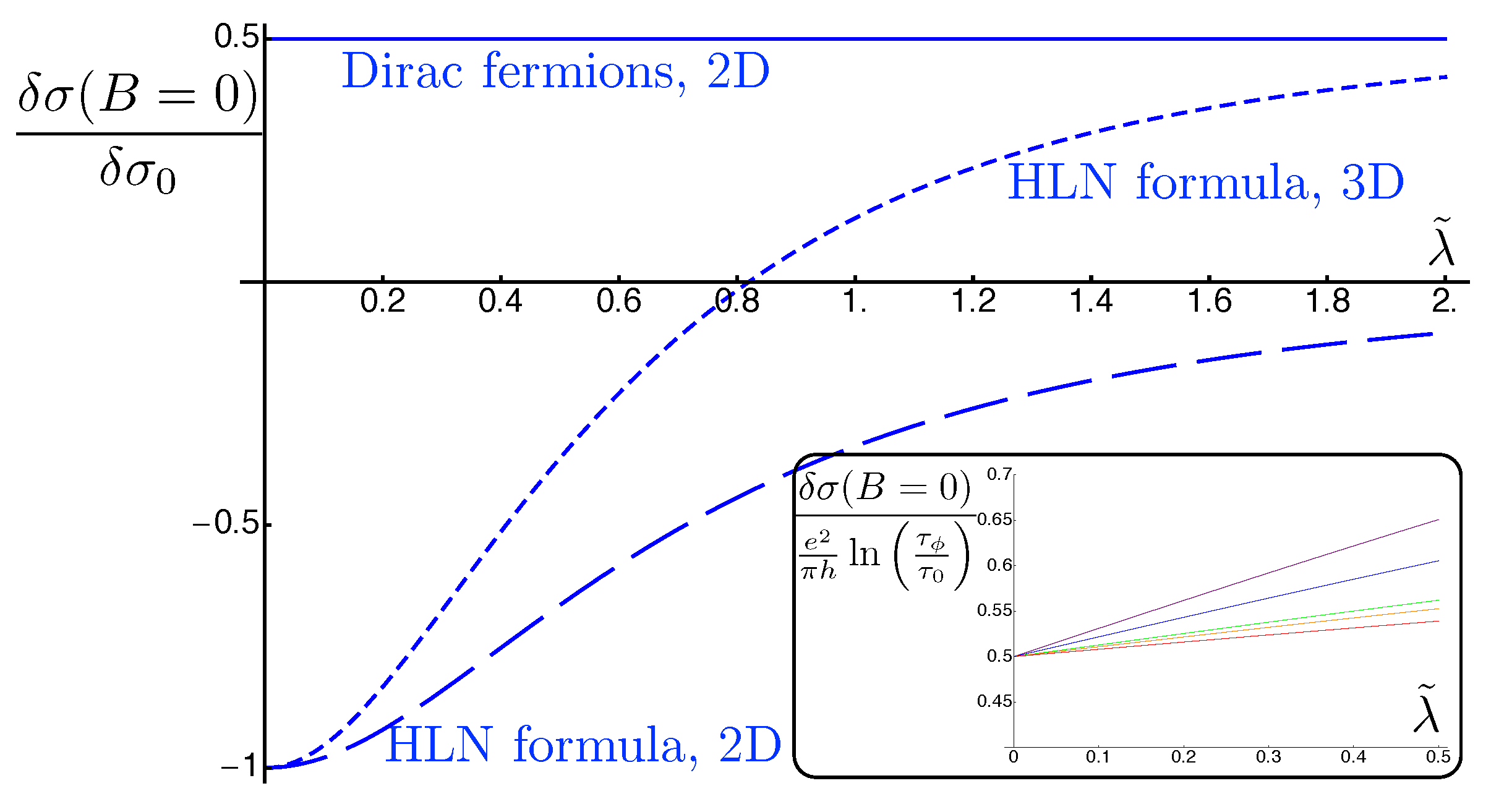
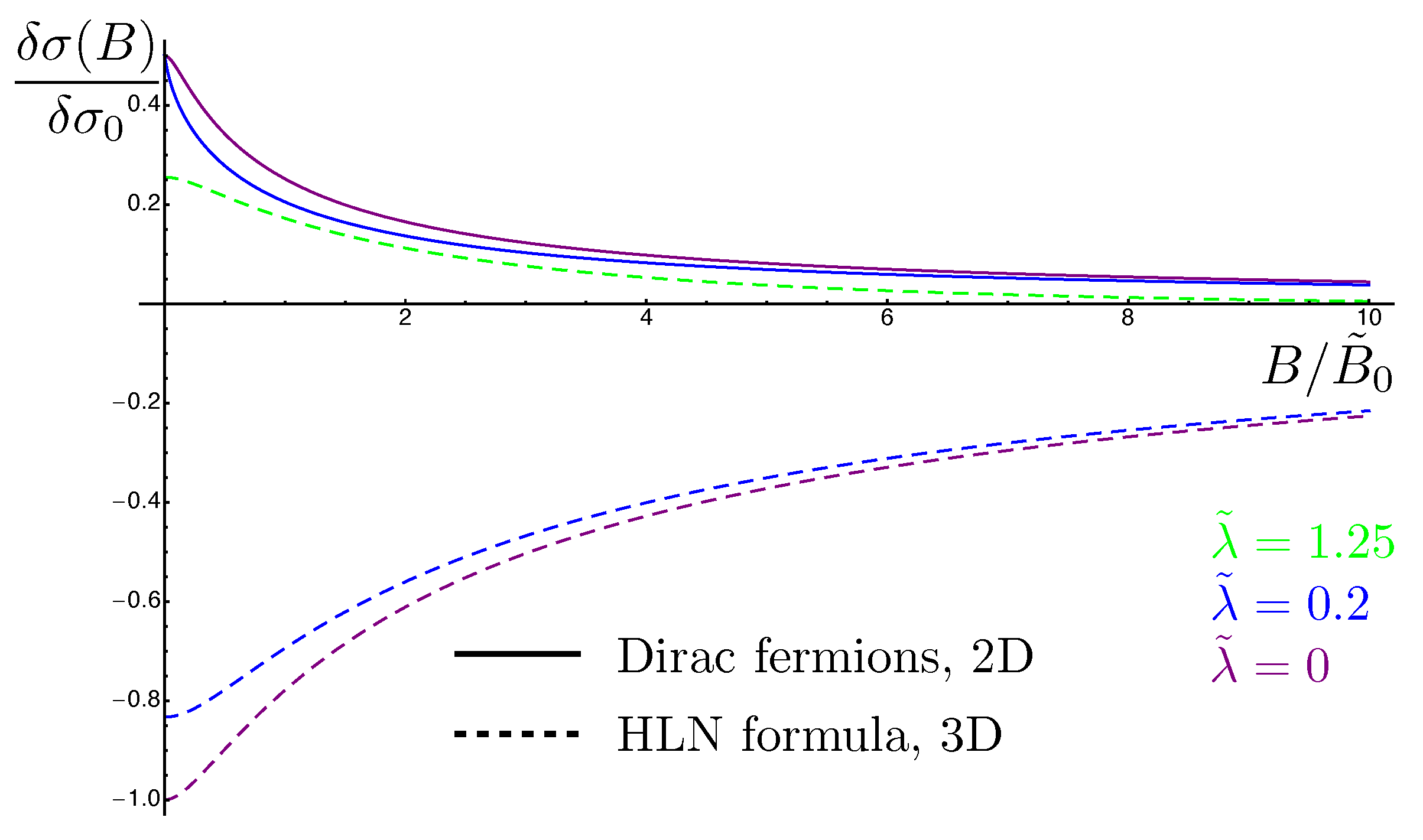
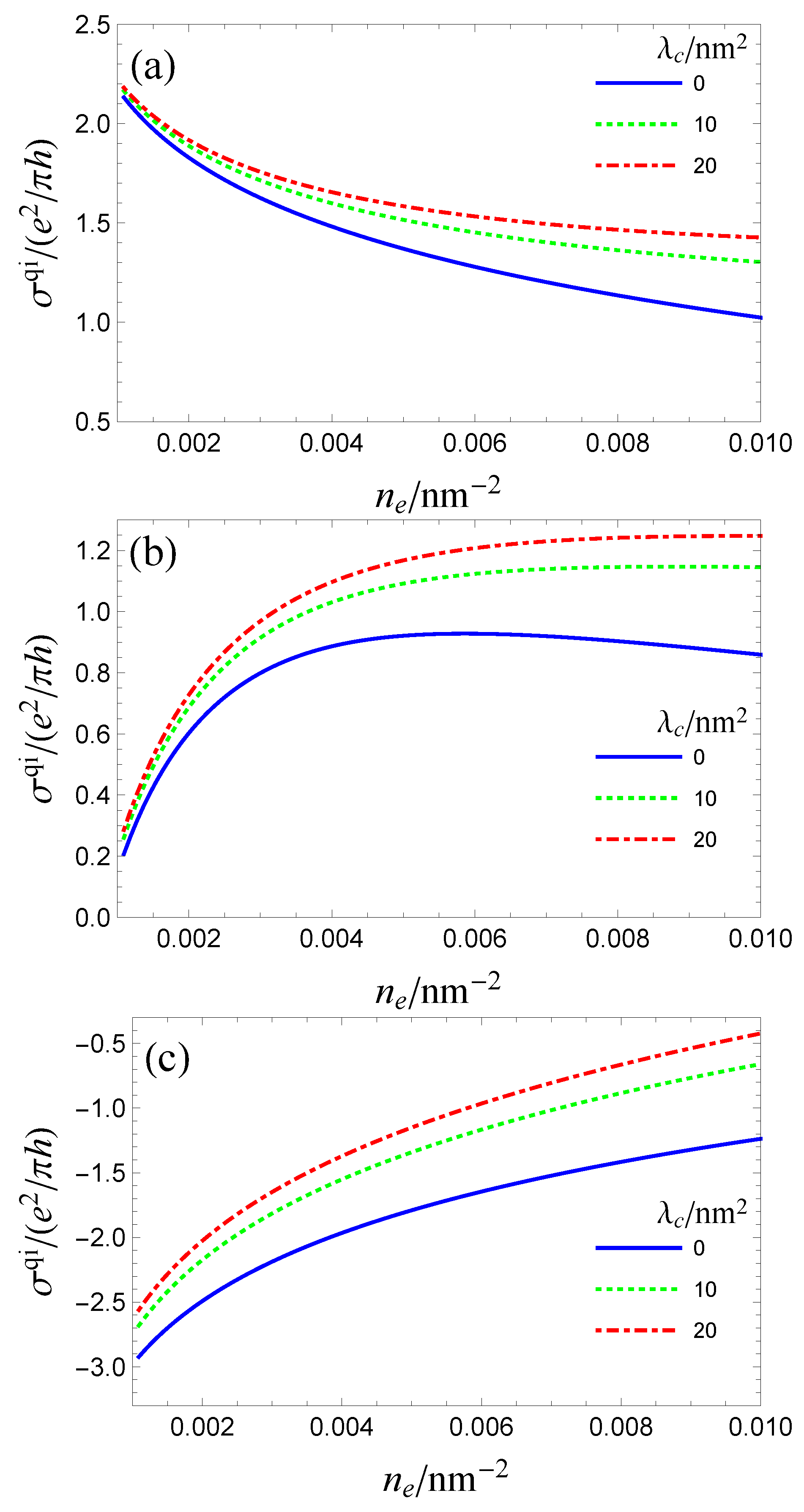
3. Topological Insulators
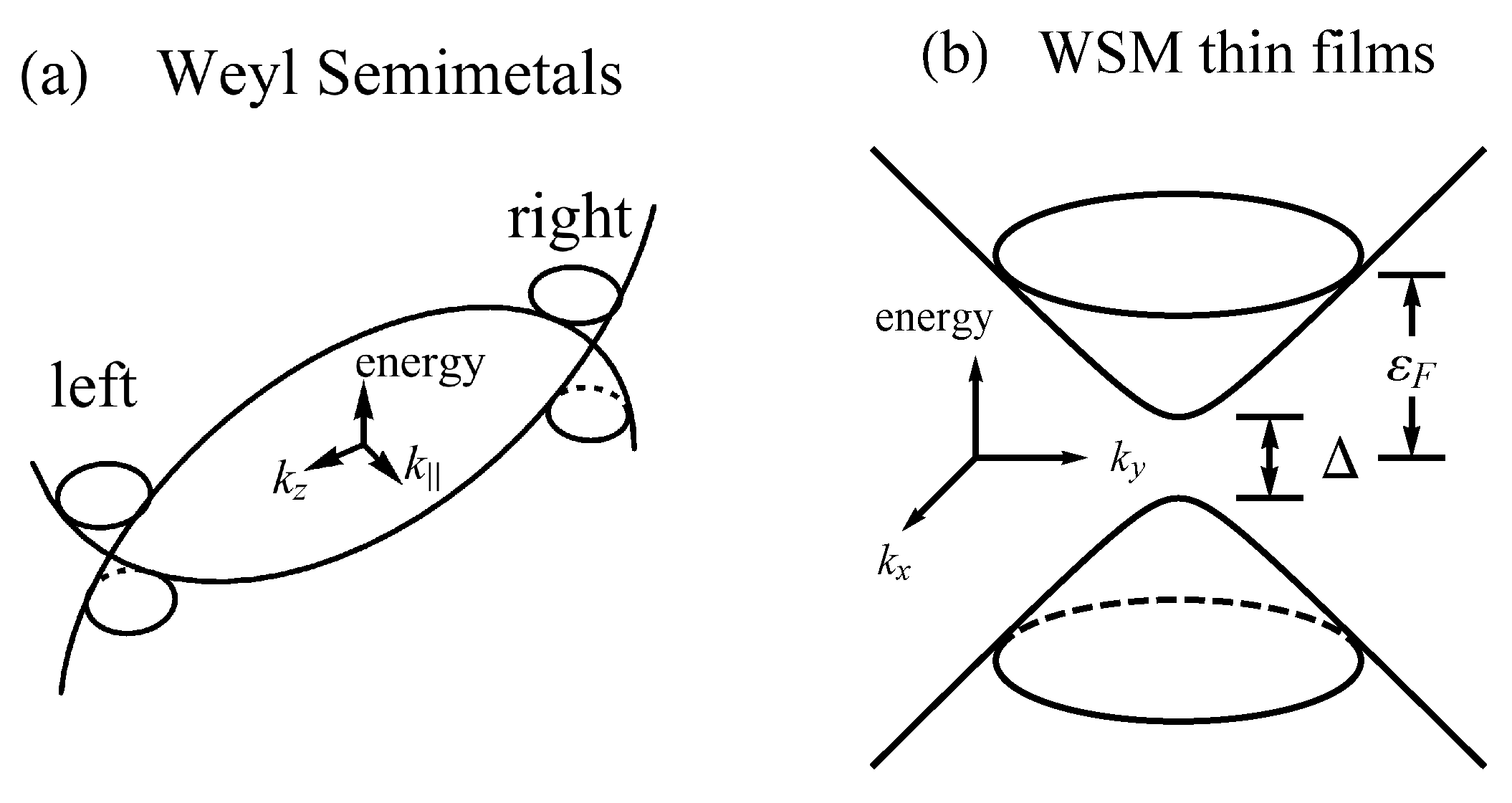
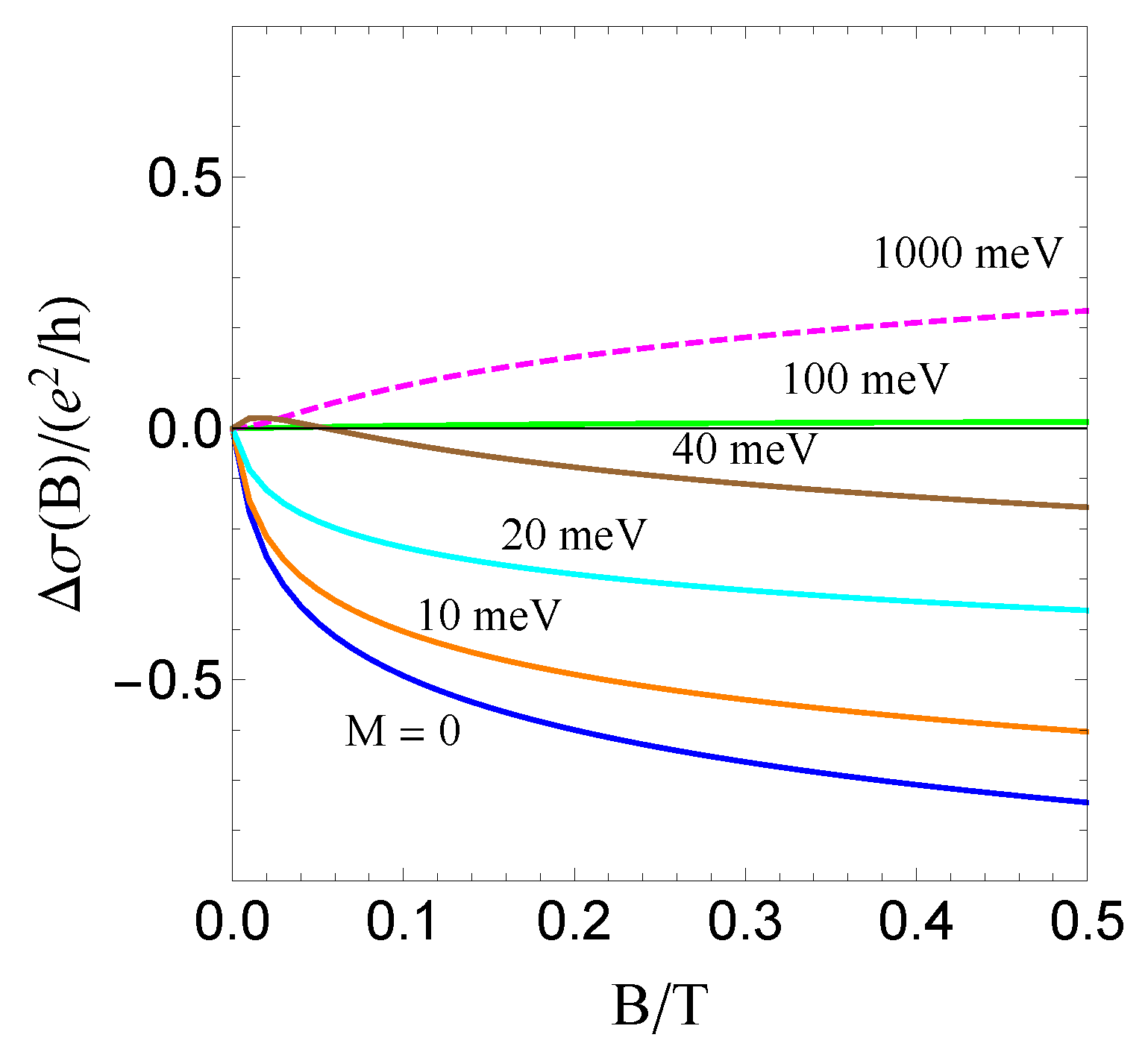
4. Weyl Semimetal Thin Films
5. Other Topological Materials
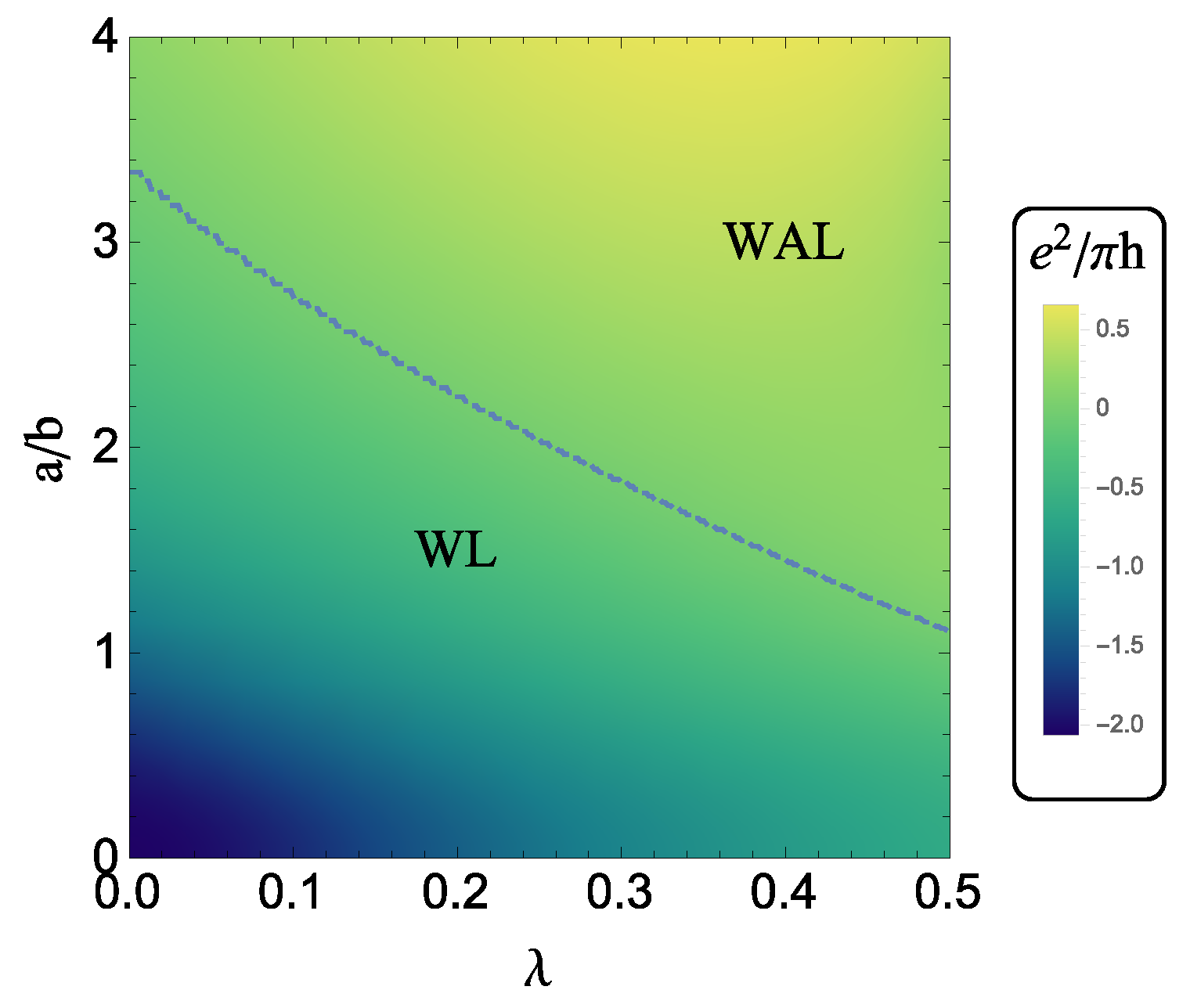
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Topological Insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef] [PubMed]
- Burkov, A.A.; Balents, L. Weyl Semimetal in a Topological Insulator Multilayer. Phys. Rev. Lett. 2011, 107, 127205. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, M.T.; Hellerstedt, J.; O’Donnell, K.M.; Tadich, A.; Fuhrer, M.S. Molecular Doping the Topological Dirac Semimetal Na3Bi across the Charge Neutrality Point with F4-TCNQ. ACS Appl. Mater. Interfaces 2016, 8, 16412. [Google Scholar] [CrossRef] [PubMed]
- Hellerstedt, J.; Edmonds, M.T.; Ramakrishnan, N.; Liu, C.; Weber, B.; Tadich, A.; O’Donnell, K.M.; Adam, S.; Fuhrer, M.S. Electronic Properties of High-Quality Epitaxial Topological Dirac Semimetal Thin Films. Nano Lett. 2016, 16, 3210. [Google Scholar] [CrossRef] [PubMed]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, X.G.; Sun, Y.Y.; Li, Y.Y.; Zhang, T.; Wen, J.; Chen, X.; He, K.; Wang, L.L.; Ma, X.C.; et al. Topological Insulator Thin Films of Bi2Te3 with Controlled Electronic Structure. Adv. Mater. 2011, 23, 2929. [Google Scholar] [CrossRef] [PubMed]
- Sacépé, B.; Oostinga, J.B.; Li, J.; Ubaldini, A.; Couto, N.J.G.; Giannini, E.; Morpurgo, A.F. Gate-tuned normal and superconducting transport at the surface of a topological insulator. Nat. Commun. 2011, 2, 575. [Google Scholar] [CrossRef] [PubMed]
- He, H.T.; Wang, G.; Zhang, T.; Sou, I.K.; Wong, G.K.L.; Wang, J.N.; Lu, H.Z.; Shen, S.Q.; Zhang, F.C. Impurity Effect on Weak Antilocalization in the Topological Insulator Bi2Te3. Phys. Rev. Lett. 2011, 106, 166805. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Taskin, A.A.; Sasaki, S.; Segawa, K.; Ando, Y. Fermi level tuning and a large activation gap achieved in the topological insulator Bi2Te2Se by Sn doping. Phys. Rev. B 2012, 85, 155301. [Google Scholar] [CrossRef]
- Kim, D.; Cho, S.; Butch, N.P.; Syers, P.; Kirshenbaum, K.; Adam, S.; Paglione, J.; Fuhrer, M.S. Surface conduction of topological Dirac electrons in bulk insulating Bi2Se3. Nat. Phys. 2012, 8, 459. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, C.Z.; Tang, P.; Zhang, Z.; Feng, X.; Li, K.; Wang, L.L.; Chen, X.; Liu, C.; Duan, W.; et al. Topology-Driven Magnetic Quantum Phase Transition in Topological Insulators. Science 2013, 339, 1582. [Google Scholar] [CrossRef] [PubMed]
- Barreto, L.; Khnemund, L.; Edler, F.; Tegenkamp, C.; Mi, J.; Bremholm, M.; Iversen, B.B.; Frydendahl, C.; Bianchi, M.; Hofmann, P. Surface-Dominated Transport on a Bulk Topological Insulator. Nano Lett. 2014, 14, 3755. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Chang, L.T.; Kou, X.; Murata, K.; Choi, E.S.; Lang, M.; Fan, Y.; Jiang, Y.; Montazeri, M.; Jiang, W.; et al. Electrical Detection of Spin-Polarized Surface States Conduction in (Bi0.53Sb0.47)2Te3 Topological Insulator. Nano Lett. 2014, 14, 5423. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, D.A.; Kvon, Z.D.; Olshanetsky, E.B.; Mikhailov, N.N.; Dvoretsky, S.A.; Weiss, D. Transport Properties of a 3D Topological Insulator based on a Strained High-Mobility HgTe Film. Phys. Rev. Lett. 2014, 112, 196801. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Syers, P.; Butch, N.P.; Paglione, J.; Fuhrer, M.S. Coherent topological transport on the surface of Bi2Se3. Nat. Commun. 2013, 4, 2040. [Google Scholar] [CrossRef] [PubMed]
- Cacho, C.; Crepaldi, A.; Battiato, M.; Braun, J.; Cilento, F.; Zacchigna, M.; Richter, M.; Heckmann, O.; Springate, E.; Liu, Y.; et al. Momentum-Resolved Spin Dynamics of Bulk and Surface Excited States in the Topological Insulator Bi2Se3. Phys. Rev. Lett. 2015, 114, 097401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Feng, X.; Xu, Y.; Guo, M.; Zhang, Z.; Ou, Y.; Feng, Y.; Li, K.; Zhang, H.; Wang, L.; et al. Disentangling the magnetoelectric and thermoelectric transport in topological insulator thin films. Phys. Rev. B 2015, 91, 075431. [Google Scholar] [CrossRef]
- Hellerstedt, J.; Edmonds, M.T.; Chen, J.H.; Cullen, W.G.; Zheng, C.X.; Fuhrer, M.S. Thickness and growth-condition dependence of in-situ mobility and carrier density of epitaxial thin-film Bi2Se3. Appl. Phys. Lett. 2014, 105, 173506. [Google Scholar] [CrossRef]
- Kastl, C.; Karnetzky, C.; Karl, H.; Holleitner, A.W. Ultrafast helicity control of surface currents in topological insulators with near-unity fidelity. Nat. Commun. 2015, 6, 6617. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Kou, X.; Upadhyaya, P.; Shao, Q.; Pan, L.; Lang, M.; Che, X.; Tang, J.; Montazeri, M.; Murata, K.; et al. Electric-field control of spin-orbit torque in a magnetically doped topological insulator. Nat. Nano. 2016, 11, 352. [Google Scholar] [CrossRef] [PubMed]
- Yoshimi, R.; Tsukazaki, A.; Kozuka, Y.; Falson, J.; Takahashi, K.S.; Checkelsky, J.G.; Nagaosa, N.; Kawasaki, M.; Tokura, Y. Quantum Hall effect on top and bottom surface states of topological insulator (Bi1−xSbx)2Te3 films. Nat. Commun. 2015, 6, 6627. [Google Scholar] [CrossRef] [PubMed]
- Hwang, E.H.; Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 2007, 75, 205418. [Google Scholar] [CrossRef]
- Jung, J.; MacDonald, A.H. Enhancement of nonlocal exchange near isolated band crossings in graphene. Phys. Rev. B 2011, 84, 085446. [Google Scholar] [CrossRef]
- Durst, A.C. Low-temperature thermal transport at the interface of a topological insulator and a d-wave superconductor. Phys. Rev. B 2015, 91, 094519. [Google Scholar] [CrossRef]
- Lu, H.Z.; Shen, S.Q. Weak localization and weak anti-localization in topological insulators. Proc. SPIE 2014, 9167, 91672E. [Google Scholar]
- Zhang, W.; Yu, R.; Zhang, H.J.; Dai, X.; Fang, Z. First Principles Studies on 3-DimenSional Strong Topological Insulators: Bi2Te3, Bi2Se3 and Sb2Te3. New J. Phys. 2010, 12, 065013. [Google Scholar] [CrossRef]
- Liu, S.; Kim, Y.; Tan, L.Z.; Rappe, A.M. Strain-Induced Ferroelectric Topological Insulator. Nano Lett. 2016, 16, 1663. [Google Scholar] [CrossRef] [PubMed]
- Culcer, D.; Das Sarma, S. Anomalous Hall response of topological insulators. Phys. Rev. B 2011, 83, 245441. [Google Scholar] [CrossRef]
- Adam, S.; Hwang, E.H.; Das Sarma, S. Two-dimensional transport and screening in topological insulator surface states. Phys. Rev. B 2012, 85, 235413. [Google Scholar] [CrossRef]
- Yoshida, T.; Fujimoto, S.; Kawakami, N. Correlation effects on a topological insulator at finite temperatures. Phys. Rev. B 2012, 85, 125113. [Google Scholar] [CrossRef]
- Das Sarma, S.; Li, Q. Many-body effects and possible superconductivity in the two-dimensional metallic surface states of three-dimensional topological insulators. Phys. Rev. B 2013, 88, 081404. [Google Scholar] [CrossRef]
- Liu, W.E.; Liu, H.; Culcer, D. Screening, Friedel oscillations, and low-temperature conductivity in topological insulator thin films. Phys. Rev. B 2014, 89, 195417. [Google Scholar] [CrossRef]
- Lu, H.Z.; Shen, S.Q. Finite-Temperature Conductivity and Magnetoconductivity of Topological Insulators. Phys. Rev. Lett. 2014, 112, 146601. [Google Scholar] [CrossRef] [PubMed]
- Das Sarma, S.; Hwang, E.H.; Min, H. Carrier screening, transport, and relaxation in three-dimensional Dirac semimetals. Phys. Rev. B 2015, 91, 035201. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Moore, J.E.; Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 2007, 75, 121306. [Google Scholar] [CrossRef]
- Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef]
- Culcer, D. Linear response theory of interacting topological insulators. Phys. Rev. B 2011, 84, 235411. [Google Scholar] [CrossRef]
- Culcer, D. Transport in three-dimensional topological insulators: theory and experiment. Physica E 2012, 44, 860. [Google Scholar] [CrossRef]
- Tkachov, G.; Hankiewicz, E.M. Spin-helical transport in normal and superconducting topological insulators. Phys. Status Solidi B 2013, 250, 215. [Google Scholar] [CrossRef]
- Li, Y.Q.; Wu, K.H.; Shi, J.R.; Xie, X.C. Electron transport properties of three-dimensional topological insulators. Front. Phys. 2012, 7, 165. [Google Scholar] [CrossRef]
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological Insulators in Three Dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.L.; Analytis, J.G.; Chu, J.H.; Liu, Z.K.; Mo, S.K.; Qi, X.L.; Zhang, H.J.; Lu, D.H.; Dai, X.; Fang, Z.; et al. Experimental Realization of a Three-Dimensional Topological Insulator, Bi2Te3. Science 2009, 325, 178. [Google Scholar] [CrossRef] [PubMed]
- Hor, Y.S.; Roushan, P.; Beidenkopf, H.; Seo, J.; Qu, D.; Checkelsky, J.G.; Wray, L.A.; Xia, Y.; Xu, S.Y.; Qian, D.; et al. The development of ferromagnetism in the doped topological insulator Bi2−xMnxTe3. Phys. Rev. B 2010, 81, 195203. [Google Scholar] [CrossRef]
- Collins-McIntyre, L.J.; Harrison, S.E.; Schönherr, P.; Steinke, N.J.; Kinane, C.J.; Charlton, T.R.; Alba-Veneroa, D.; Pushp, A.; Kellock, A.J.; Parkin, S.S.P.; et al. Magnetic ordering in Cr-doped Bi2Se3 thin films. EPL Europhys. Lett. 2014, 107, 57009. [Google Scholar] [CrossRef]
- Wang, J.; Lian, B.; Zhang, S.C. Electrically Tunable Magnetism in Magnetic Topological Insulators. Phys. Rev. Lett. 2015, 115, 036805. [Google Scholar] [CrossRef] [PubMed]
- Yoshimi, R.; Yasuda, K.; Tsukazaki, A.; Takahashi, K.S.; Nagaosa, N.; Kawasaki, M.; Tokura, Y. Quantum Hall states stabilized in semi-magnetic bilayers of topological insulators. Nat. Commun. 2015, 6, 8530. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Chang, C.Z.; Wu, L.; Tao, J.; Zhao, W.; Chan, M.H.W.; Moodera, J.S.; Li, J.; Zhu, Y. Experimental Verification of the Van Vleck Nature of Long-Range Ferromagnetic Order in the Vanadium-Doped Three-Dimensional Topological Insulator Sb2Te3. Phys. Rev. Lett. 2015, 114, 146802. [Google Scholar] [CrossRef] [PubMed]
- Kou, X.; Pan, L.; Wang, J.; Fan, Y.; Choi, E.S.; Lee, W.L.; Nie, T.; Murata, K.; Shao, Q.; Zhang, S.C.; et al. Metal-to-insulator switching in quantum anomalous Hall states. Nat. Commun. 2015, 6, 8474. [Google Scholar] [CrossRef] [PubMed]
- Katmis, F.; Lauter, V.; Nogueira, F.S.; Assaf, B.A.; Jamer, M.E.; Wei, P.; Satpati, B.; Freeland, J.W.; Eremin, I.; Heiman, D.; et al. A high-temperature ferromagnetic topological insulating phase by proximity coupling. Nature 2016, 533, 513–516. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Chang, C.Z.; Tang, C.; Zheng, J.G.; Moodera, J.S.; Shi, J. Structural and proximity-induced ferromagnetic properties of topological insulator-magnetic insulator heterostructures. AIP Adv. 2016, 6, 055809. [Google Scholar] [CrossRef]
- Fan, Y.; Kou, X.; Upadhyaya, P.; Shao, Q.; Pan, L.; Lang, M.; Che, X.; Tang, J.; Montazeri, M.; Murata, K.; et al. Electric-field control of spin-orbit torque in a magnetically doped topological insulator. Nat. Nanotechnol. 2016, 11, 352–359. [Google Scholar] [CrossRef] [PubMed]
- He, Q.L.; Kou, X.; Grutter, A.J.; Yin, G.; Pan, L.; Che, X.; Liu, Y.; Nie, T.; Zhang, B.; Disseler, S.M.; et al. Tailoring exchange couplings in magnetic topological-insulator/antiferromagnet heterostructures. Nat. Mater. 2017, 16, 94–100. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.Z.; Zhao, A.; Shen, S.Q. Quantum Transport in Magnetic Topological Insulator Thin Films. Phys. Rev. Lett. 2013, 111, 146802. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Yao, W.; Niu, Q. Valley-Contrasting Physics in Graphene: Magnetic Moment and Topological Transport. Phys. Rev. Lett. 2007, 99, 236809. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.; Xiao, D.; Niu, Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys. Rev. B 2008, 77, 235406. [Google Scholar] [CrossRef]
- Ulstrup, S.; Johannsen, J.C.; Cilento, F.; Miwa, J.A.; Crepaldi, A.; Zacchigna, M.; Cacho, C.; Chapman, R.; Springate, E.; Mammadov, S.; et al. Ultrafast Dynamics of Massive Dirac Fermions in Bilayer Graphene. Phys. Rev. Lett. 2014, 112, 257401. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Zhang, W.; Zhang, H.J.; Zhang, S.C.; Dai, X.; Fang, Z. Quantized Anomalous Hall Effect in Magnetic Topological Insulators. Science 2010, 329, 61. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Qiao, Z.; Liu, H.; Niu, Q. Quantum anomalous Hall effect with tunable Chern number in magnetic topological insulator film. Phys. Rev. B 2012, 85, 045445. [Google Scholar] [CrossRef]
- Chang, C.Z.; Zhang, J.; Liu, M.; Zhang, Z.; Feng, X.; Li, K.; Wang, L.L.; Chen, X.; Dai, X.; Fang, Z.; et al. Thin Films of Magnetically Doped Topological Insulator with Carrier-Independent Long-Range Ferromagnetic Order. Adv. Mater. 2013, 25, 1065. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167. [Google Scholar] [CrossRef] [PubMed]
- Weng, H.; Yu, R.; Hu, X.; Dai, X.; Fang, Z. Quantum anomalous Hall effect and related topological electronic states. Adv. Phys. 2015, 64, 227. [Google Scholar] [CrossRef]
- Liu, C.X.; Zhang, S.C.; Qi, X.L. The Quantum Anomalous Hall Effect: Theory and Experiment. Annu. Rev. Condens. Matter Phys. 2016, 7, 301. [Google Scholar] [CrossRef]
- Chang, C.Z.; Zhao, W.; Kim, D.Y.; Zhang, H.; Assaf, B.A.; Heiman, D.; Zhang, S.C.; Liu, C.; Chan, M.H.W.; Moodera, J.S. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 2015, 14, 473477. [Google Scholar] [CrossRef] [PubMed]
- Mahoney, A.C.; Colless, J.I.; Pauka, S.J.; Hornibrook, J.M.; Watson, J.D.; Gardner, G.C.; Manfra, M.J.; Doherty, A.C.; Reilly, D.J. On-Chip Microwave Quantum Hall Circulator. Phys. Rev. X 2017, 7, 011007. [Google Scholar] [CrossRef]
- Kandala, A.; Richardella, A.; Kempinger, S.; Liu, C.X.; Samarth, N. Giant anisotropic magnetoresistance in a quantum anomalous Hall insulator. Nat. Commun. 2015, 6, 7434. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.Z.; Zhao, W.; Kim, D.Y.; Wei, P.; Jain, J.K.; Liu, C.; Chan, M.H.W.; Moodera, J.S. Zero-Field Dissipationless Chiral Edge Transport and the Nature of Dissipation in the Quantum Anomalous Hall State. Phys. Rev. Lett. 2015, 115, 057206. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.Z.; Li, M. Quantum anomalous Hall effect in time-reversal-symmetry breaking topological insulators. J. Phys. Condens. Matter 2016, 28, 123002. [Google Scholar] [CrossRef] [PubMed]
- Sochnikov, I.; Bestwick, A.J.; Williams, J.R.; Lippman, T.M.; Fisher, I.R.; Goldhaber-Gordon, D.; Kirtley, J.R.; Moler, K.A. Direct Measurement of Current-Phase Relations in Superconductor/Topological Insulator/Superconductor Junctions. Nano Lett. 2013, 13, 3086. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.X.; Li, P.; Xu, J.P.; Liu, Z.L.; Ge, J.F.; Wang, G.Y.; Yang, X.; Xu, Z.A.; Ji, S.H.; Gao, C.L.; et al. Interface structure of a topological insulator/superconductor heterostructure. New J. Phys. 2014, 16, 123043. [Google Scholar] [CrossRef]
- Li, Z.Z.; Zhang, F.C.; Wang, Q.H. Majorana modes in a topological insulator/s-wave superconductor heterostructure. Sci. Rep. 2014, 4, 6363. [Google Scholar] [CrossRef] [PubMed]
- Potter, A.C.; Kimchi, I.; Vishwanath, A. Quantum oscillations from surface Fermi arcs in Weyl and Dirac semimetals. Nat. Commun. 2014, 5, 5161. [Google Scholar] [CrossRef] [PubMed]
- Burkov, A.A. Topological semimetals. Nat. Mater. 2016, 15, 1145. [Google Scholar] [CrossRef] [PubMed]
- Pixley, J.H.; Huse, D.A.; Das Sarma, S. Rare-Region-Induced Avoided Quantum Criticality in Disordered Three-Dimensional Dirac and Weyl Semimetals. Phys. Rev. X 2016, 6, 021042. [Google Scholar] [CrossRef]
- Yang, S.A. Dirac and Weyl Materials: Fundamental Aspects and Some Spintronics Applications. SPIN 2016, 6, 1640003. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, X.; Guo, M.; Li, K.; Zhang, J.; Ou, Y.; Feng, Y.; Wang, L.; Chen, X.; He, K.; et al. Electrically tuned magnetic order and magnetoresistance in a topological insulator. Nat. Commun. 2014, 5, 4915. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Yang, Y.; Singh, R.R.P.; Savrasov, S.Y.; Yu, D. Spin generation via bulk spin current in three-dimensional topological insulators. Nat. Commun. 2016, 7, 10878. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, G.; Wu, G.; Chen, H.; Culcer, D.; Zhang, Z. Proximity effects in topological insulator heterostructures. Chin. Phys. B 2013, 22, 097306. [Google Scholar] [CrossRef]
- Culcer, D.; Winkler, R. External gates and transport in biased bilayer graphene. Phys. Rev. B 2009, 79, 165422. [Google Scholar] [CrossRef]
- Liu, H.; Liu, W.E.; Culcer, D. Coulomb drag in topological insulator films. Physica E 2016, 79, 72. [Google Scholar] [CrossRef]
- Liu, H.; Liu, W.E.; Culcer, D. Anomalous Hall Coulomb drag of massive Dirac fermions. Phys. Rev. B 2017, 95, 205435. [Google Scholar] [CrossRef]
- Culcer, D.; Hwang, E.H.; Stanescu, T.D.; Das Sarma, S. Two-dimensional surface charge transport in topological insulators. Phys. Rev. B 2010, 82, 155457. [Google Scholar] [CrossRef]
- Oh, S. The Complete Quantum Hall Trio. Science 2013, 340, 153–154. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Y.; Liu, C.; Kushwaha, S.K.; Sankar, R.; Krizan, J.W.; Belopolski, I.; Neupane, M.; Bian, G.; Alidoust, N.; Chang, T.R.; et al. Observation of Fermi arc surface states in a topological metal. Science 2015, 347, 294–298. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.B.; Lu, H.Z.; Shen, S.Q. Linear magnetoconductivity in an intrinsic topological Weyl semimetal. New J. Phys. 2016, 18, 053039. [Google Scholar] [CrossRef]
- Lau, A.; van den Brink, J.; Ortix, C. Generic coexistence of Fermi arcs and Dirac cones on the surface of time-reversal invariant Weyl semimetals. arXiv, 2017; arXiv:arXiv:1701.01660. [Google Scholar]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Chen, X.Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Wang, Z.; Weng, H.; Wu, Q.; Dai, X.; Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 2013, 88, 125427. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Kushwaha, S.K.; Liang, T.; Krizan, J.W.; Hirschberger, M.; Wang, W.; Cava, R.J.; Ong, N.P. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 2015, 350, 413–416. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Peng, H.; Dudin, P.; et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 2014, 13, 677–681. [Google Scholar] [CrossRef] [PubMed]
- Neupane, M.; Xu, S.Y.; Sankar, R.; Alidoust, N.; Bian, G.; Liu, C.; Belopolski, I.; Chang, T.R.; Jeng, H.T.; Lin, H.; et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 2014, 5, 3786. [Google Scholar] [CrossRef] [PubMed]
- Yi, H.; Wang, Z.; Chen, C.; Shi, Y.; Feng, Y.; Liang, A.; Xie, Z.; He, S.; He, J.; Peng, Y.; et al. Evidence of Topological Surface State in Three-Dimensional Dirac Semimetal Cd3As2. Sci. Rep. 2014, 4, 6106. [Google Scholar] [CrossRef] [PubMed]
- Borisenko, S.; Gibson, Q.; Evtushinsky, D.; Zabolotnyy, V.; Büchner, B.; Cava, R.J. Experimental Realization of a Three-Dimensional Dirac Semimetal. Phys. Rev. Lett. 2014, 113, 027603. [Google Scholar] [CrossRef] [PubMed]
- Burkov, A.A.; Kim, Y.B. 2 and Chiral Anomalies in Topological Dirac Semimetals. Phys. Rev. Lett. 2016, 117, 136602. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, S.K.; Krizan, J.W.; Feldman, B.E.; Gyenis, A.; Randeria, M.T.; Xiong, J.; Xu, S.Y.; Alidoust, N.; Belopolski, I.; Liang, T.; et al. Bulk crystal growth and electronic characterization of the 3D Dirac semimetal Na3Bi. APL Mater. 2015, 3, 041504. [Google Scholar] [CrossRef]
- Xiong, J.; Kushwaha, S.; Krizan, J.; Liang, T.; Cava, R.J.; Ong, N.P. Anomalous conductivity tensor in the Dirac semimetal Na3Bi. EPL 2016, 114, 27002. [Google Scholar] [CrossRef]
- Li, H.; He, H.; Lu, H.Z.; Zhang, H.; Liu, H.; Ma, R.; Fan, Z.; Shen, S.Q.; Wang, J. Negative magnetoresistance in Dirac semimetal Cd3As2. Nat. Commun. 2016, 7, 10301. [Google Scholar] [CrossRef] [PubMed]
- Pixley, J.H.; Goswami, P.; Das Sarma, S. Anderson Localization and the Quantum Phase Diagram of Three Dimensional Disordered Dirac Semimetals. Phys. Rev. Lett. 2015, 115, 076601. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Yang, S.A.; Liu, Z.; Li, H.; Zhou, G. Anisotropic Quantum Confinement Effect and Electric Control of Surface States in Dirac Semimetal Nanostructures. Sci. Rep. 2015, 5, 7898. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Cheng, P.; Pan, H.; Zhang, S.; Wang, B.; Wang, G.; Xiu, F.; Song, F. Weak antilocalization in Cd(3)As(2) thin films. Sci. Rep. 2016, 6, 22377. [Google Scholar] [CrossRef] [PubMed]
- Weng, H.; Fang, C.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Huang, S.M.; Xu, S.Y.; Belopolski, I.; Lee, C.C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 2015, 6, 7373. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Lv, B.Q.; Weng, H.M.; Fu, B.B.; Wang, X.P.; Miao, H.; Ma, J.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031013. [Google Scholar] [CrossRef]
- Wu, D.; Liao, J.; Yi, W.; Wang, X.; Li, P.; Weng, H.; Shi, Y.; Li, Y.; Luo, J.; Dai, X.; Fang, Z. Giant semiclassical magnetoresistance in high mobility TaAs2 semimetal. Appl. Phys. Lett. 2016, 108, 042105. [Google Scholar] [CrossRef]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Borisenko, S.; Evtushinsky, D.; Gibson, Q.; Yaresko, A.; Kim, T.; Ali, M.N.; Buechner, B.; Hoesch, M.; Cava, R.J. Time-Reversal Symmetry Breaking Type-II Weyl State in YbMnBi2. arXiv, 2015; arXiv:arXiv:1507.04847. [Google Scholar]
- Wang, Y.; Liu, E.; Liu, H.; Pan, Y.; Zhang, L.; Zeng, J.; Fu, Y.; Wang, M.; Xu, K.; Huang, Z.; et al. Gate-tunable negative longitudinal magnetoresistance in the predicted type-II Weyl semimetal WTe2. Nat. Commun. 2016, 7, 13142. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, K.; Reutt-Robey, J.; Paglione, J.; Fuhrer, M.S. Breakdown of compensation and persistence of nonsaturating magnetoresistance in gated WTe2 thin flakes. Phys. Rev. B 2016, 93, 121108. [Google Scholar] [CrossRef]
- Shan, W.Y.; Lu, H.Z.; Shen, S.Q. Effective continuous model for surface states and thin films of three-dimensional topological insulators. New J. Phys. 2010, 12, 043048. [Google Scholar]
- Abanin, D.A.; Pesin, D.A. Ordering of Magnetic Impurities and Tunable Electronic Properties of Topological Insulators. Phys. Rev. Lett. 2011, 106, 136802. [Google Scholar] [CrossRef] [PubMed]
- Burkov, A.A. Chiral Anomaly and Diffusive Magnetotransport in Weyl Metals. Phys. Rev. Lett. 2014, 113, 247203. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.Z.; Zhang, S.B.; Shen, S.Q. High-field magnetoconductivity of topological semimetals with short-range potential. Phys. Rev. B 2015, 92, 045203. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, L.; Long, Y.; Wang, P.; Chen, D.; Yang, Z.; Liang, H.; Xue, M.; Weng, H.; Fang, Z.; et al. Observation of the Chiral-Anomaly-Induced Negative Magnetoresistance in 3D Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031023. [Google Scholar] [CrossRef]
- Liu, M.; Chang, C.Z.; Zhang, Z.; Zhang, Y.; Ruan, W.; He, K.; Wang, L.l.; Chen, X.; Jia, J.F.; Zhang, S.C.; et al. Electron interaction-driven insulating ground state in Bi2Se3 topological insulators in the two-dimensional limit. Phys. Rev. B 2011, 83, 165440. [Google Scholar] [CrossRef]
- Yang, Q.I.; Dolev, M.; Zhang, L.; Zhao, J.; Fried, A.D.; Schemm, E.; Liu, M.; Palevski, A.; Marshall, A.F.; Risbud, S.H.; et al. Emerging weak localization effects on a topological insulator-insulating ferromagnet (Bi2Se3-EuS) interface. Phys. Rev. B 2013, 88, 081407. [Google Scholar] [CrossRef]
- Burkov, A.A. Negative longitudinal magnetoresistance in Dirac and Weyl metals. Phys. Rev. B 2015, 91, 245157. [Google Scholar] [CrossRef]
- Goswami, P.; Pixley, J.H.; Das Sarma, S. Axial anomaly and longitudinal magnetoresistance of a generic three-dimensional metal. Phys. Rev. B 2015, 92, 075205. [Google Scholar] [CrossRef]
- Lu, H.Z.; Shen, S.Q. Weak antilocalization and interaction-induced localization of Dirac and Weyl Fermions in topological insulators and semimetals. Chin. Phys. B 2016, 25, 117202. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Li, P.; Yang, X.; Shen, Z.; Sheng, F.; Li, X.; Lu, Y.; Zheng, Y.; Xu, Z.A. Negative magnetoresistance in Weyl semimetals NbAs and NbP: Intrinsic chiral anomaly and extrinsic effects. Front. Phys. 2017, 12, 127205. [Google Scholar] [CrossRef]
- Niemann, A.C.; Gooth, J.; Wu, S.C.; Bäbler, S.; Sergelius, P.; Hühne, R.; Rellinghaus, B.; Shekhar, C.; Süb, V.; Schmidt, M.; et al. Chiral magnetoresistance in the Weyl semimetal NbP. arXiv, 2016; arXiv:1610.01413. [Google Scholar]
- Evers, F.; Mirlin, A.D. Anderson transitions. Rev. Mod. Phys. 2008, 80, 1355–1417. [Google Scholar] [CrossRef]
- Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287–337. [Google Scholar] [CrossRef]
- Mühlbauer, M.; Budewitz, A.; Büttner, B.; Tkachov, G.; Hankiewicz, E.M.; Brüne, C.; Buhmann, H.; Molenkamp, L.W. One-Dimensional Weak Antilocalization Due to the Berry Phase in HgTe Wires. Phys. Rev. Lett. 2014, 112, 146803. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.Z.; Shi, J.; Shen, S.Q. Competition between Weak Localization and Antilocalization in Topological Surface States. Phys. Rev. Lett. 2011, 107, 076801. [Google Scholar] [CrossRef] [PubMed]
- Imura, K.I.; Kuramoto, Y.; Nomura, K. Weak localization properties of the doped Z2 topological insulator. Phys. Rev. B 2009, 80, 085119. [Google Scholar] [CrossRef]
- Tkachov, G.; Hankiewicz, E.M. Weak antilocalization in HgTe quantum wells and topological surface states: Massive versus massless Dirac fermions. Phys. Rev. B 2011, 84, 035444. [Google Scholar] [CrossRef]
- Kammermeier, M.; Wenk, P.; Schliemann, J.; Heedt, S.; Schäpers, T. Weak (anti)localization in tubular semiconductor nanowires with spin-orbit coupling. Phys. Rev. B 2016, 93, 205306. [Google Scholar] [CrossRef]
- Koga, T.; Nitta, J.; Akazaki, T.; Takayanagi, H. Rashba spin-orbit Coupling Probed by the Weak Antilocalization Analysis in InAlAs/InGaAs/InAlAs Quantum Wells as a Function of Quantum Well Asymmetry. Phys. Rev. Lett. 2002, 89, 046801. [Google Scholar] [CrossRef] [PubMed]
- Shan, W.Y.; Lu, H.Z.; Shen, S.Q. spin-orbit scattering in quantum diffusion of massive Dirac fermions. Phys. Rev. B 2012, 86, 125303. [Google Scholar] [CrossRef]
- Hikami, S.; Larkin, A.I.; Nagaoka, Y. spin-orbit Interaction and Magnetoresistance in the Two Dimensional Random System. Progr. Theor. Phys. 1980, 63, 707–710. [Google Scholar] [CrossRef]
- McCann, E.; Kechedzhi, K.; Fal’ko, V.I.; Suzuura, H.; Ando, T.; Altshuler, B.L. Weak-Localization Magnetoresistance and Valley Symmetry in Graphene. Phys. Rev. Lett. 2006, 97, 146805. [Google Scholar] [CrossRef] [PubMed]
- Adroguer, P.; Carpentier, D.; Cayssol, J.; Orignac, E. Diffusion at the surface of topological insulators. New J. Phys. 2012, 14, 103027. [Google Scholar] [CrossRef]
- Garate, I.; Glazman, L. Weak localization and antilocalization in topological insulator thin films with coherent bulk-surface coupling. Phys. Rev. B 2012, 86, 035422. [Google Scholar] [CrossRef]
- König, E.J.; Ostrovsky, P.M.; Protopopov, I.V.; Gornyi, I.V.; Burmistrov, I.S.; Mirlin, A.D. Interaction and disorder effects in three-dimensional topological insulator thin films. Phys. Rev. B 2013, 88, 035106. [Google Scholar] [CrossRef]
- Checkelsky, J.G.; Hor, Y.S.; Cava, R.J.; Ong, N.P. Bulk Band Gap and Surface State Conduction Observed in Voltage-Tuned Crystals of the Topological Insulator Bi2Se3. Phys. Rev. Lett. 2011, 106, 196801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Dolev, M.; Yang, Q.I.; Hammond, R.H.; Zhou, B.; Palevski, A.; Chen, Y.; Kapitulnik, A. Weak localization effects as evidence for bulk quantization in Bi2Se3 thin films. Phys. Rev. B 2013, 88, 121103. [Google Scholar] [CrossRef]
- Lang, M.; He, L.; Kou, X.; Upadhyaya, P.; Fan, Y.; Chu, H.; Jiang, Y.; Bardarson, J.H.; Jiang, W.; Choi, E.S.; et al. Competing Weak Localization and Weak Antilocalization in Ultrathin Topological Insulators. Nano Lett. 2013, 13, 48–53. [Google Scholar] [CrossRef] [PubMed]
- Bao, L.; Wang, W.; Meyer, N.; Liu, Y.; Zhang, C.; Wang, K.; Ai, P.; Xiu, F. Quantum Corrections Crossover and Ferromagnetism in Magnetic Topological Insulators. Sci. Rep. 2013, 3, 2391. [Google Scholar] [CrossRef] [PubMed]
- Bardarson, J.H.; Moore, J.E. Quantum interference and Aharonov–Bohm oscillations in topological insulators. Rep. Prog. Phys 2013, 76, 056501. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, R.; Fujisawa, K.; Sakurai, R.; Kuroda, S. Weak antilocalization in (111) thin films of a topologial crystalline insulator SnTe. J. Phys. Conf. Ser. 2014, 568, 052001. [Google Scholar] [CrossRef]
- Shekhar, C.; Nayak, A.K.; Sun, Y.; Schmidt, M.; Nicklas, M.; Leermakers, I.; Zeitler, U.; Skourski, Y.; Wosnitza, J.; Liu, Z.; et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 2015, 11, 645–649. [Google Scholar] [CrossRef]
- Louvet, T.; Carpentier, D.; Fedorenko, A.A. New quantum transition in Weyl semimetals with correlated disorder. Phys. Rev. B 2017, 95, 014204. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram Technique for Nonequilibrium Processes. Sov. Phys. JETP 1965, 20, 1018. [Google Scholar]
- Vasko, F.T.; Raichev, O.E. Quantum Kinetic Theory and Applications; Springer Science+Business Media, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Rammer, J.; Smith, H. Quantum field-theoretical methods in transport theory of metals. Rev. Mod. Phys. 1986, 58, 323. [Google Scholar] [CrossRef]
- Schwab, P.; Raimondi, R.; Gorini, C. Spin-Charge Locking and Tunneling into a Helical Metal. Eur. Phys. Lett. 2011, 93, 67004. [Google Scholar] [CrossRef]
- Adroguer, P.; Liu, W.E.; Culcer, D.; Hankiewicz, E.M. Conductivity corrections for topological insulators with spin-orbit impurities: Hikami-Larkin-Nagaoka formula revisited. Phys. Rev. B 2015, 92, 241402. [Google Scholar] [CrossRef]
- Lu, H.Z.; Shen, S.Q. Quantum transport in topological semimetals under magnetic fields. Front. Phys. 2016, 12, 127201. [Google Scholar] [CrossRef]
- Ngabonziza, P.; Stehno, M.P.; Myoren, H.; Neumann, V.A.; Koster, G.; Brinkman, A. Gate-tunable transport properties of in-situ capped Bi2Te3 topological insulator thin films. Adv. Electron. Mater. 2016. [Google Scholar] [CrossRef]
- Linder, J.; Yokoyama, T.; Sudbø, A. Anomalous finite size effects on surface states in the topological insulator Bi2Se3. Phys. Rev. B 2009, 80, 205401. [Google Scholar] [CrossRef]
- Liu, C.X.; Zhang, H.; Yan, B.; Qi, X.L.; Frauenheim, T.; Dai, X.; Fang, Z.; Zhang, S.C. Oscillatory crossover from two-dimensional to three-dimensional topological insulators. Phys. Rev. B 2010, 81, 041307. [Google Scholar] [CrossRef]
- Lu, H.Z.; Shan, W.Y.; Yao, W.; Niu, Q.; Shen, S.Q. Massive Dirac fermions and spin physics in an ultrathin film of topological insulator. Phys. Rev. B 2010, 81, 115407. [Google Scholar] [CrossRef]
- Park, K.; Heremans, J.J.; Scarola, V.W.; Minic, D. Robustness of Topologically Protected Surface States in Layering of Bi2Te3 Thin Films. Phys. Rev. Lett. 2010, 105, 186801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; He, K.; Chang, C.Z.; Song, C.L.; Wang, L.; Chen, X.; Jia, J.; Fang, Z.; Dai, X.; Shan, W.Y.; et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 2010, 6, 584. [Google Scholar] [CrossRef]
- Hirahara, T.; Sakamoto, Y.; Saisyu, Y.; Miyazaki, H.; Kimura, S.; Okuda, T.; Matsuda, I.; Murakami, S.; Hasegawa, S. Topological metal at the surface of an ultrathin Bi1−x Sbx alloy film. Phys. Rev. B 2010, 81, 165422. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Hirahara, T.; Miyazaki, H.; Kimura, S.i.; Hasegawa, S. Spectroscopic evidence of a topological quantum phase transition in ultrathin Bi2Se3 films. Phys. Rev. B 2010, 81, 165432. [Google Scholar] [CrossRef]
- Taskin, A.A.; Sasaki, S.; Segawa, K.; Ando, Y. Manifestation of Topological Protection in Transport Properties of Epitaxial Bi2Se3 Thin Films. Phys. Rev. Lett. 2012, 109, 066803. [Google Scholar] [CrossRef] [PubMed]
- Seradjeh, B.; Moore, J.E.; Franz, M. Exciton Condensation and Charge Fractionalization in a Topological Insulator Film. Phys. Rev. Lett. 2009, 103, 066402. [Google Scholar] [CrossRef] [PubMed]
- Seradjeh, B. Topological exciton condensate of imbalanced electrons and holes. Phys. Rev. B 2012, 85, 235146. [Google Scholar] [CrossRef]
- Efimkin, D.K.; Lozovik, Y.E.; Sokolik, A.A. Electron-hole pairing in a topological insulator thin film. Phys. Rev. B 2012, 86, 115436. [Google Scholar] [CrossRef]
- Kim, Y.; Hankiewicz, E.M.; Gilbert, M.J. Topological excitonic superfluids in three dimensions. Phys. Rev. B 2012, 86, 184504. [Google Scholar] [CrossRef]
- Tilahun, D.; Lee, B.; Hankiewicz, E.M.; MacDonald, A.H. Quantum Hall Superfluids in Topological Insulator Thin Films. Phys. Rev. Lett. 2011, 107, 246401. [Google Scholar] [CrossRef] [PubMed]
- Ando, T.; Fowler, A.B.; Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 1982, 54, 437–672. [Google Scholar] [CrossRef]
- Chiu, S.P.; Lin, J.J. Weak antilocalization in topological insulator Bi2Te3 microflakes. Phys. Rev. B 2013, 87, 035122. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, C.Z.; Jiang, Y.; DaSilva, A.; Sun, Y.; Wang, H.; Xing, Y.; Wang, Y.; He, K.; Ma, X.; et al. Demonstration of surface transport in a hybrid Bi2Se3/Bi2Te3 heterostructure. Sci. Rep. 2013, 3, 3060. [Google Scholar] [CrossRef] [PubMed]
- Culcer, D.; Yao, Y.; MacDonald, A.H.; Niu, Q. Electrical generation of spin in crystals with reduced symmetry. Phys. Rev. B 2005, 72, 045215. [Google Scholar] [CrossRef]
- Rossi, E.; Bardarson, J.H.; Fuhrer, M.S.; Das Sarma, S. Universal Conductance Fluctuations in Dirac Materials in the Presence of Long-range Disorder. Phys. Rev. Lett. 2012, 109, 096801. [Google Scholar] [CrossRef] [PubMed]
- Culcer, D.; Winkler, R. Weak momentum scattering and the conductivity of graphene. Phys. Rev. B 2008, 78, 235417. [Google Scholar] [CrossRef]
- Kechedzhi, K.; McCann, E.; Fal’ko, V.I.; Suzuura, H.; Ando, T.; Altshuler, B.L. Weak localization in monolayer and bilayer graphene. Eur. Phys. J. Spec. Top. 2007, 148, 39–54. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.E.; Hankiewicz, E.M.; Culcer, D. Weak Localization and Antilocalization in Topological Materials with Impurity Spin-Orbit Interactions. Materials 2017, 10, 807. https://doi.org/10.3390/ma10070807
Liu WE, Hankiewicz EM, Culcer D. Weak Localization and Antilocalization in Topological Materials with Impurity Spin-Orbit Interactions. Materials. 2017; 10(7):807. https://doi.org/10.3390/ma10070807
Chicago/Turabian StyleLiu, Weizhe Edward, Ewelina M. Hankiewicz, and Dimitrie Culcer. 2017. "Weak Localization and Antilocalization in Topological Materials with Impurity Spin-Orbit Interactions" Materials 10, no. 7: 807. https://doi.org/10.3390/ma10070807




