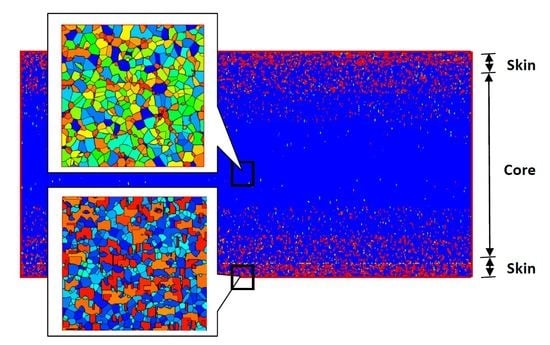
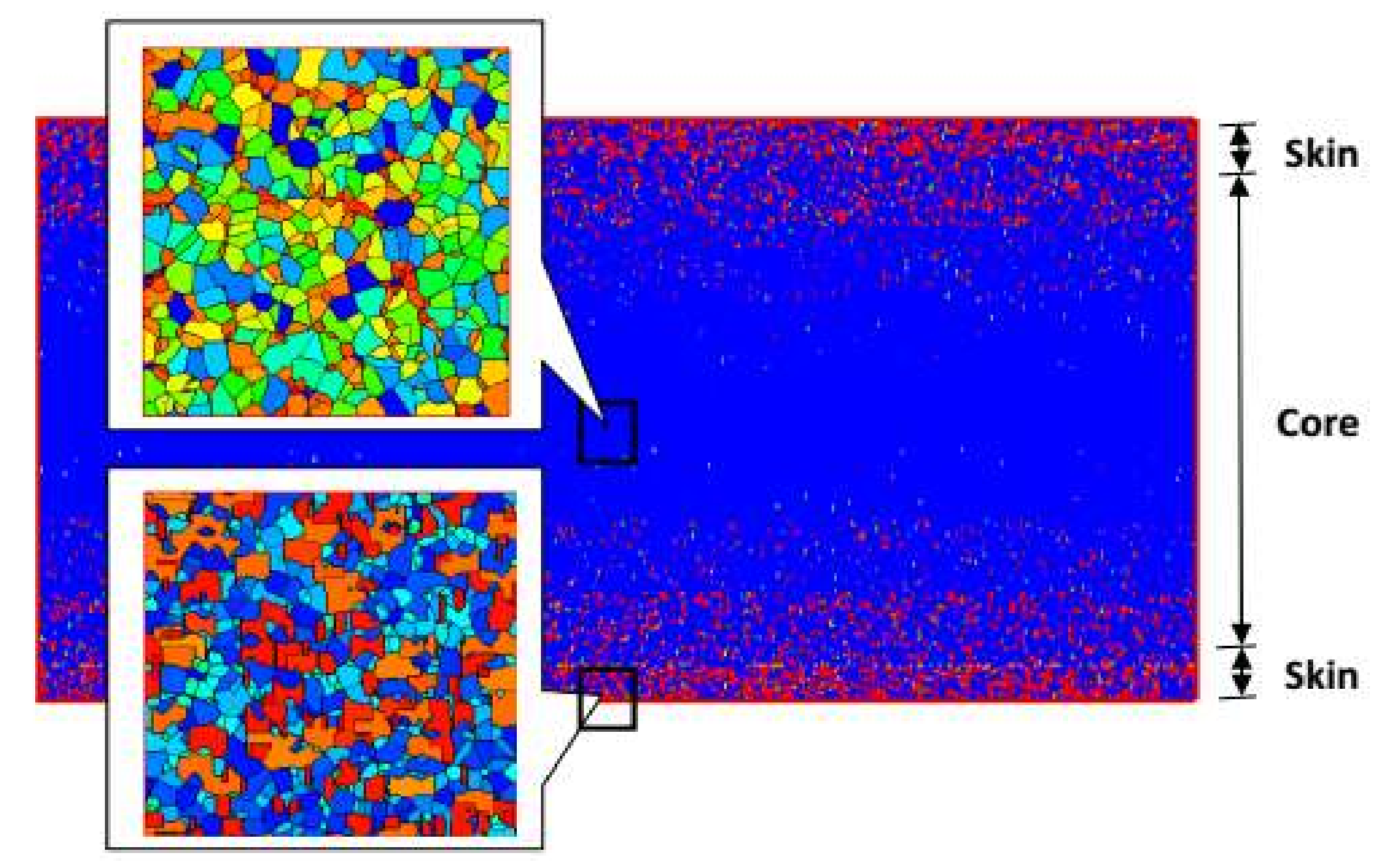
“Skin-Core-Skin” Structure of Polymer Crystallization Investigated by Multiscale Simulation
Abstract
1. Introduction
2. Mathematical Model
2.1. Conservation Equations at the Macroscopic Level
2.2. Crystal Evolution Model at the Microscopic Level
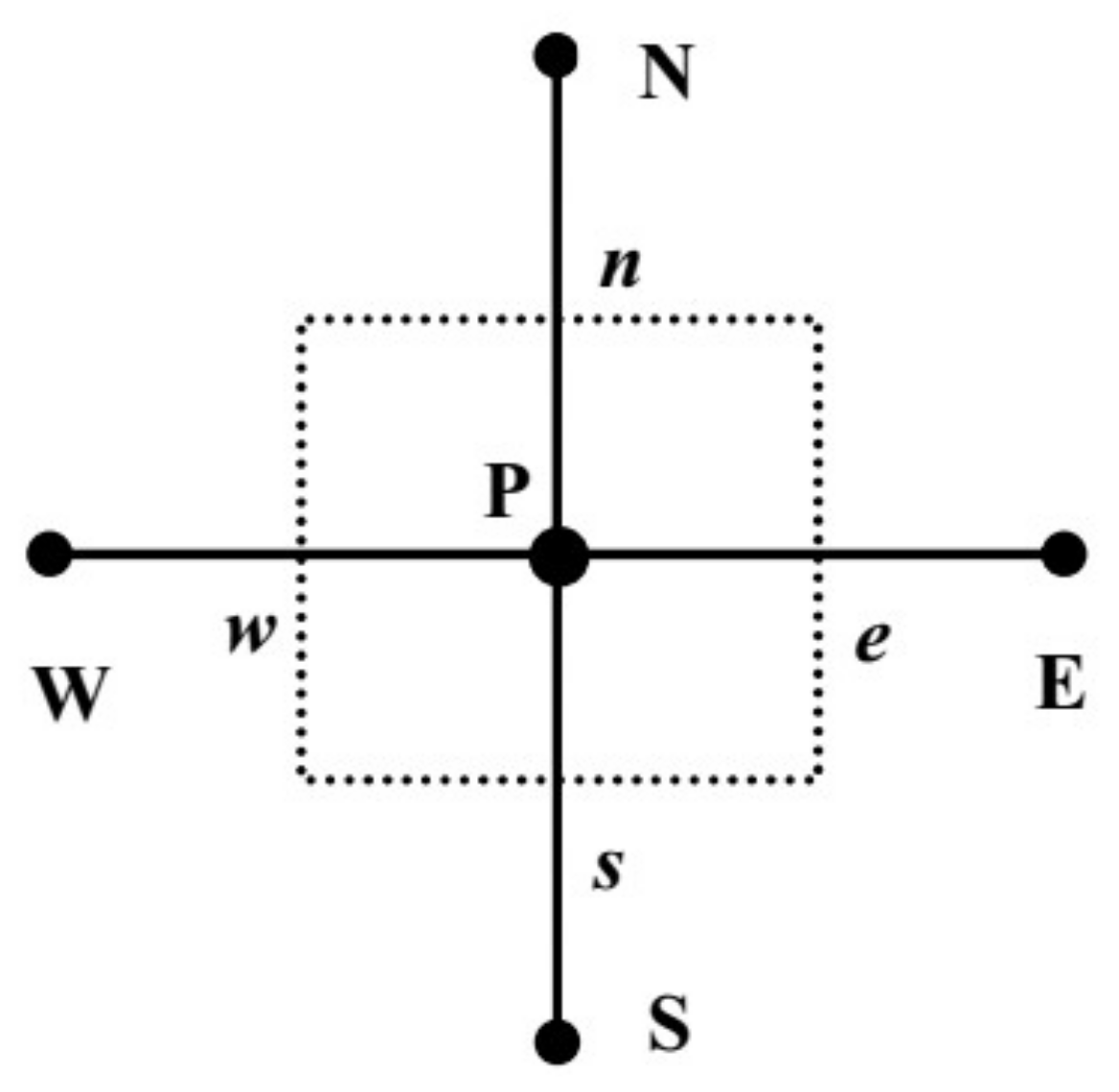
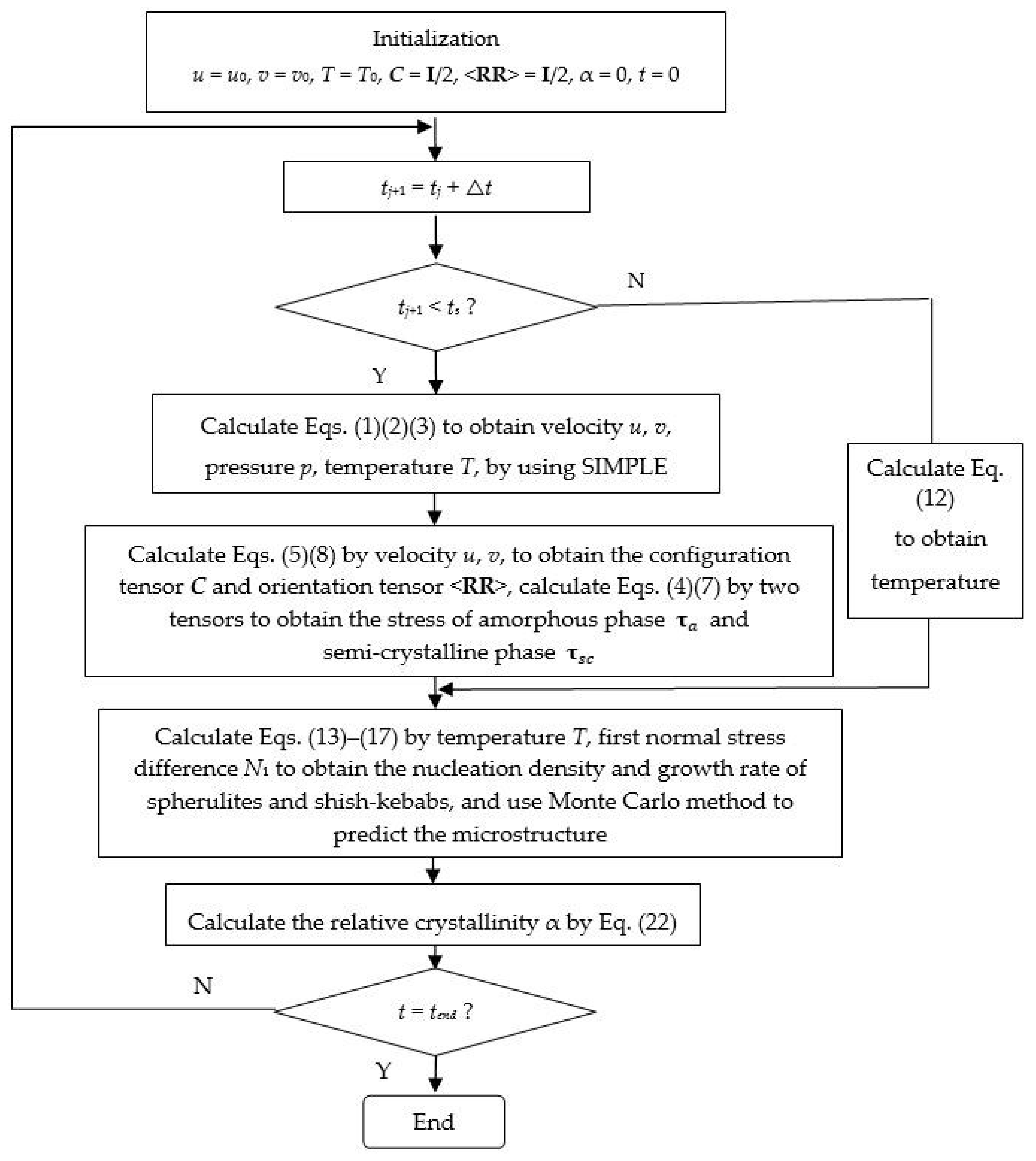
3. Multiscale Method
4. Results and Discussion
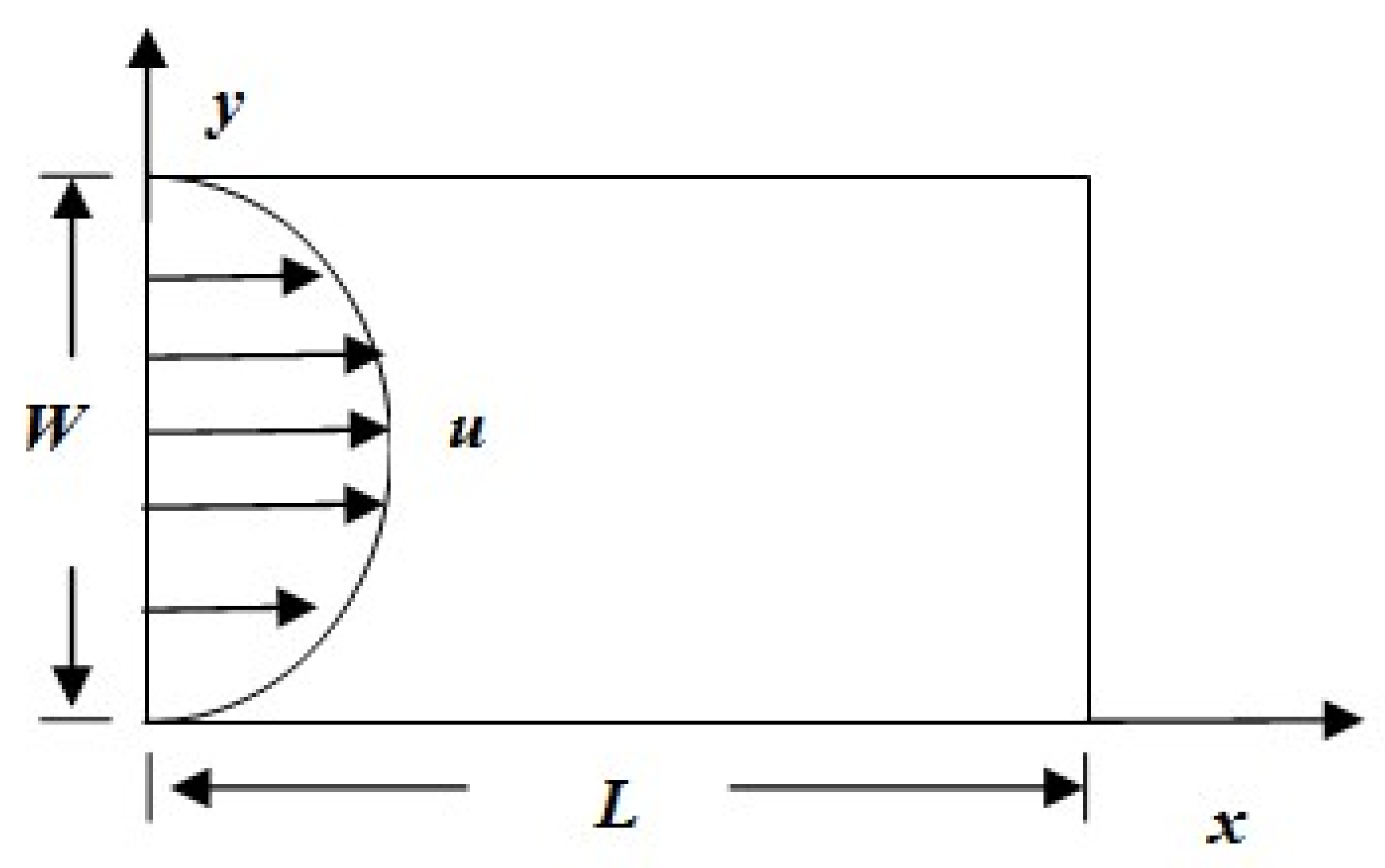
4.1. Problem Definition
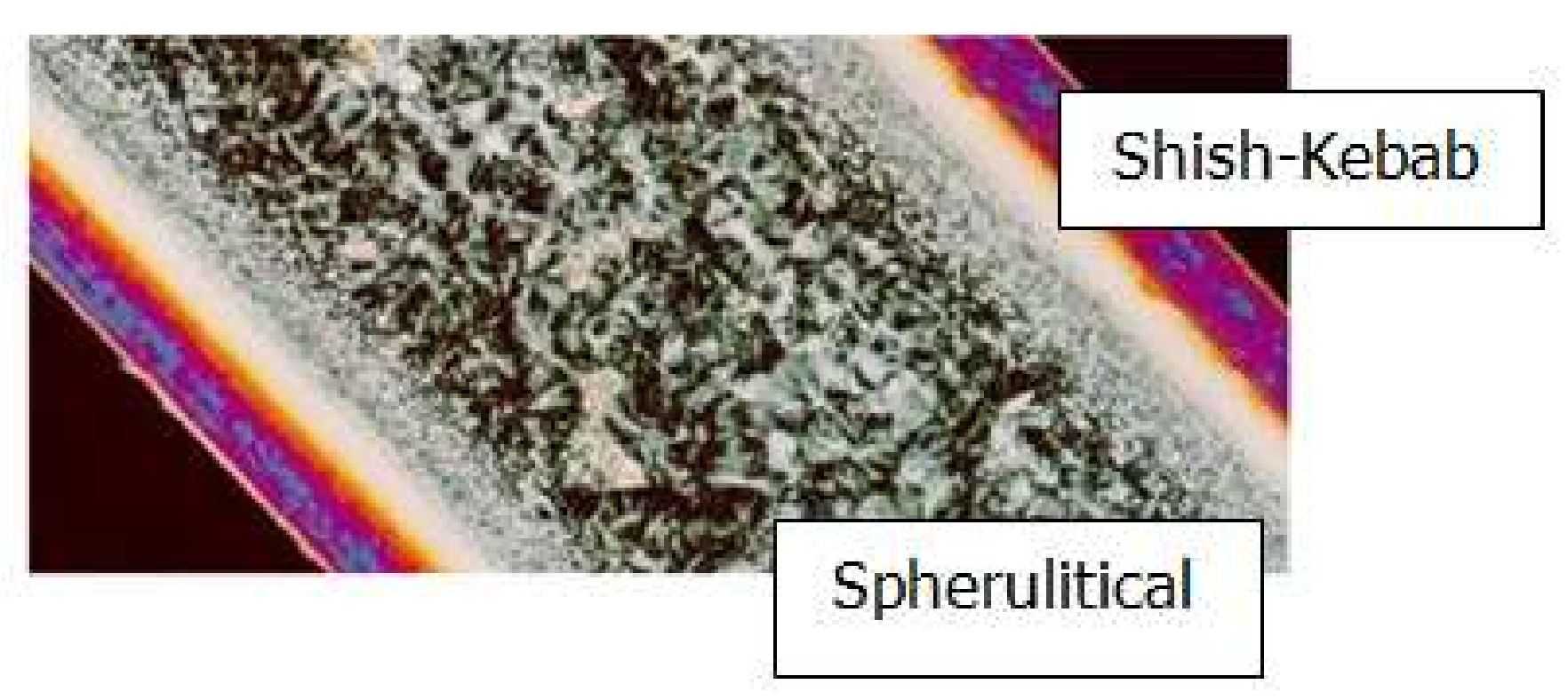
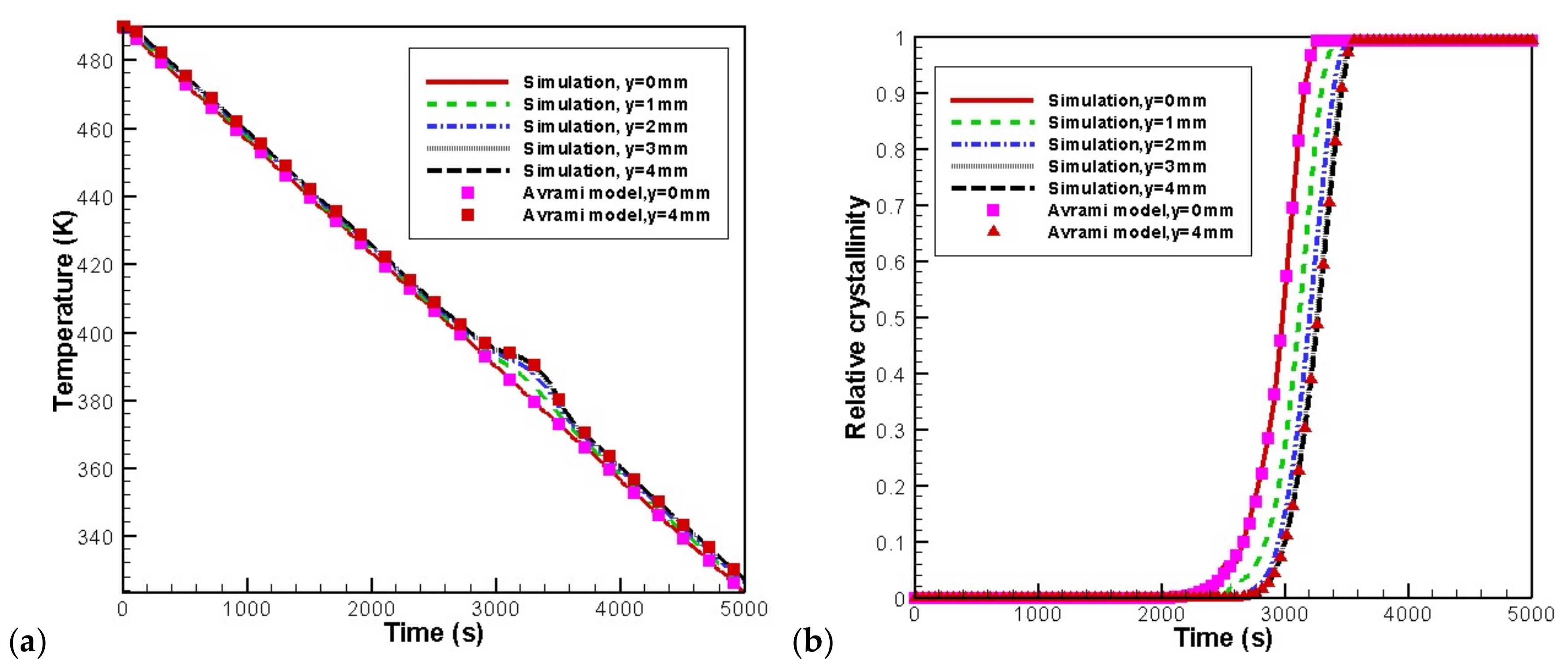
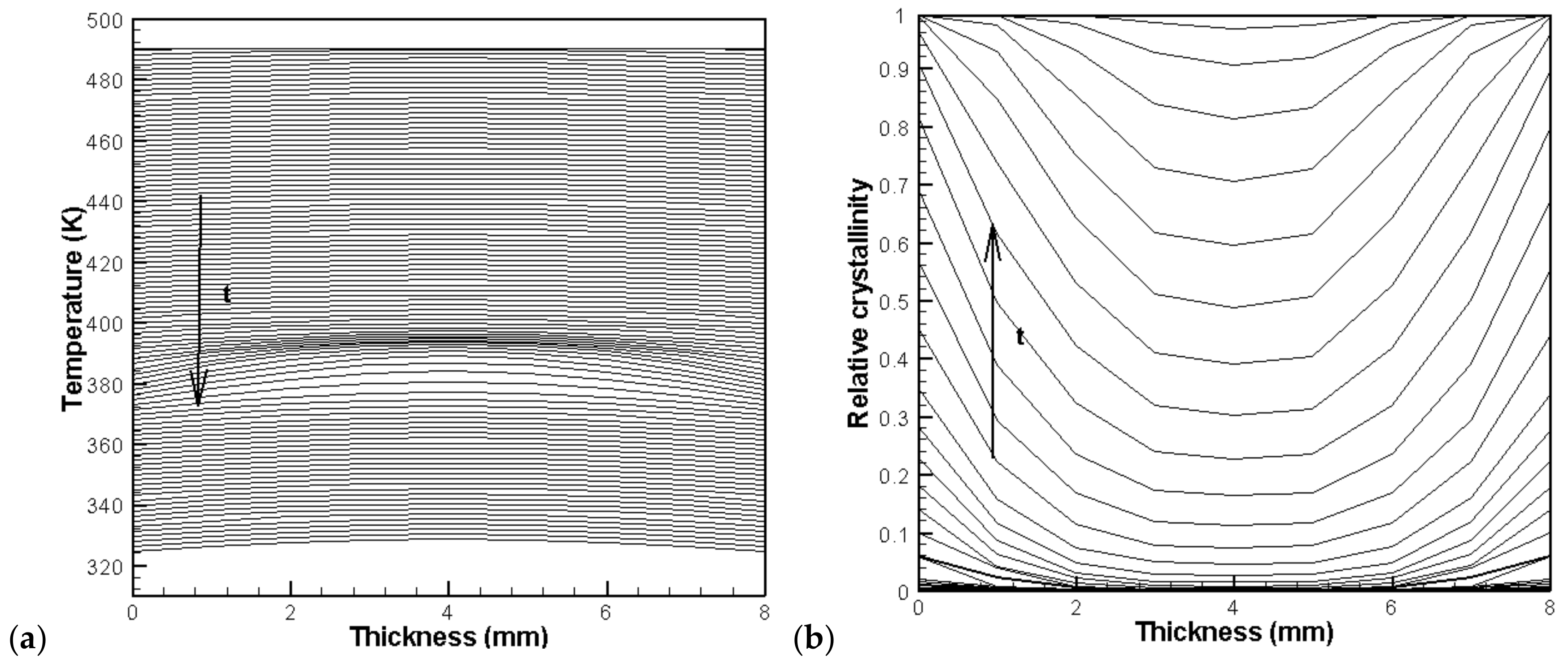
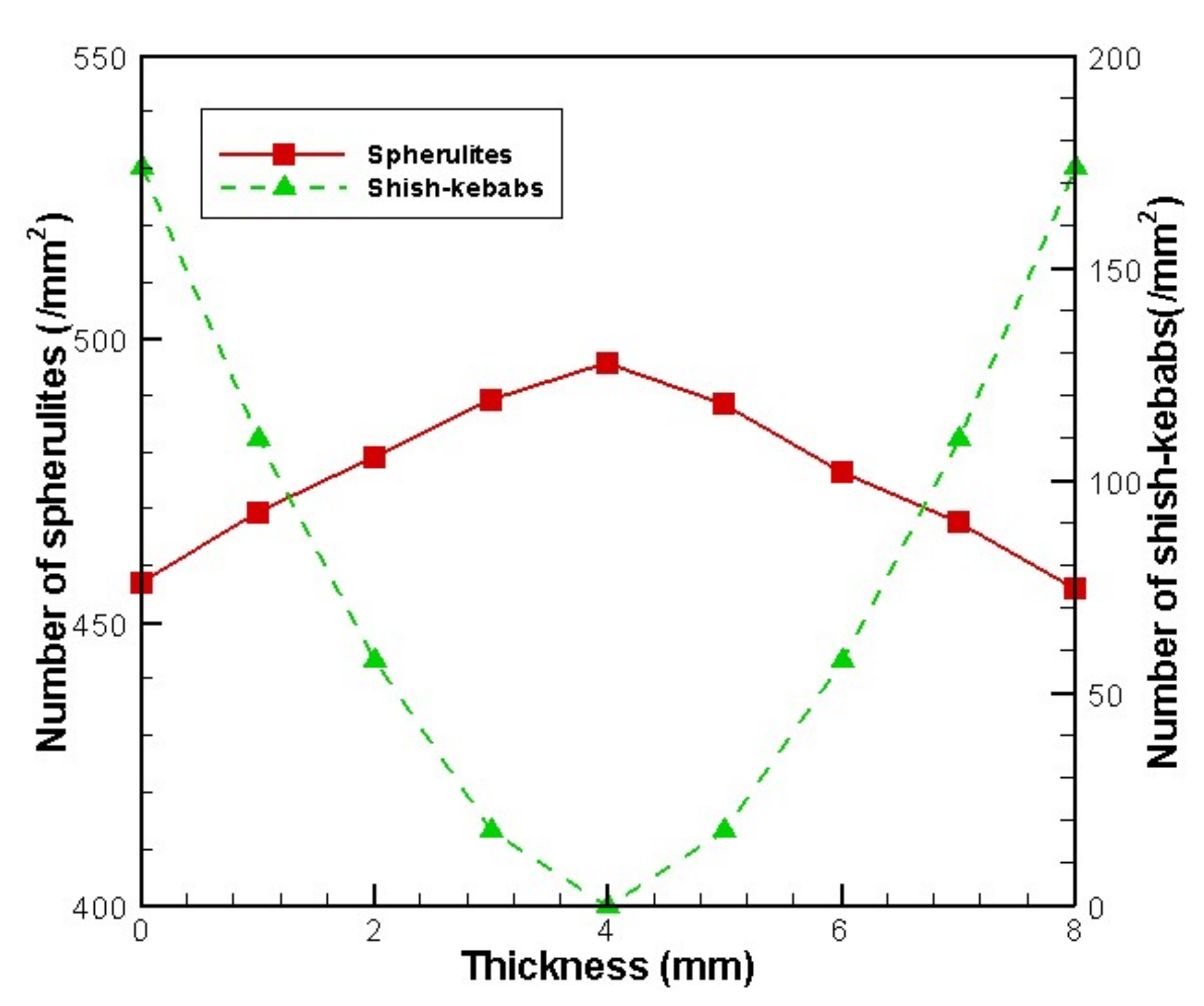
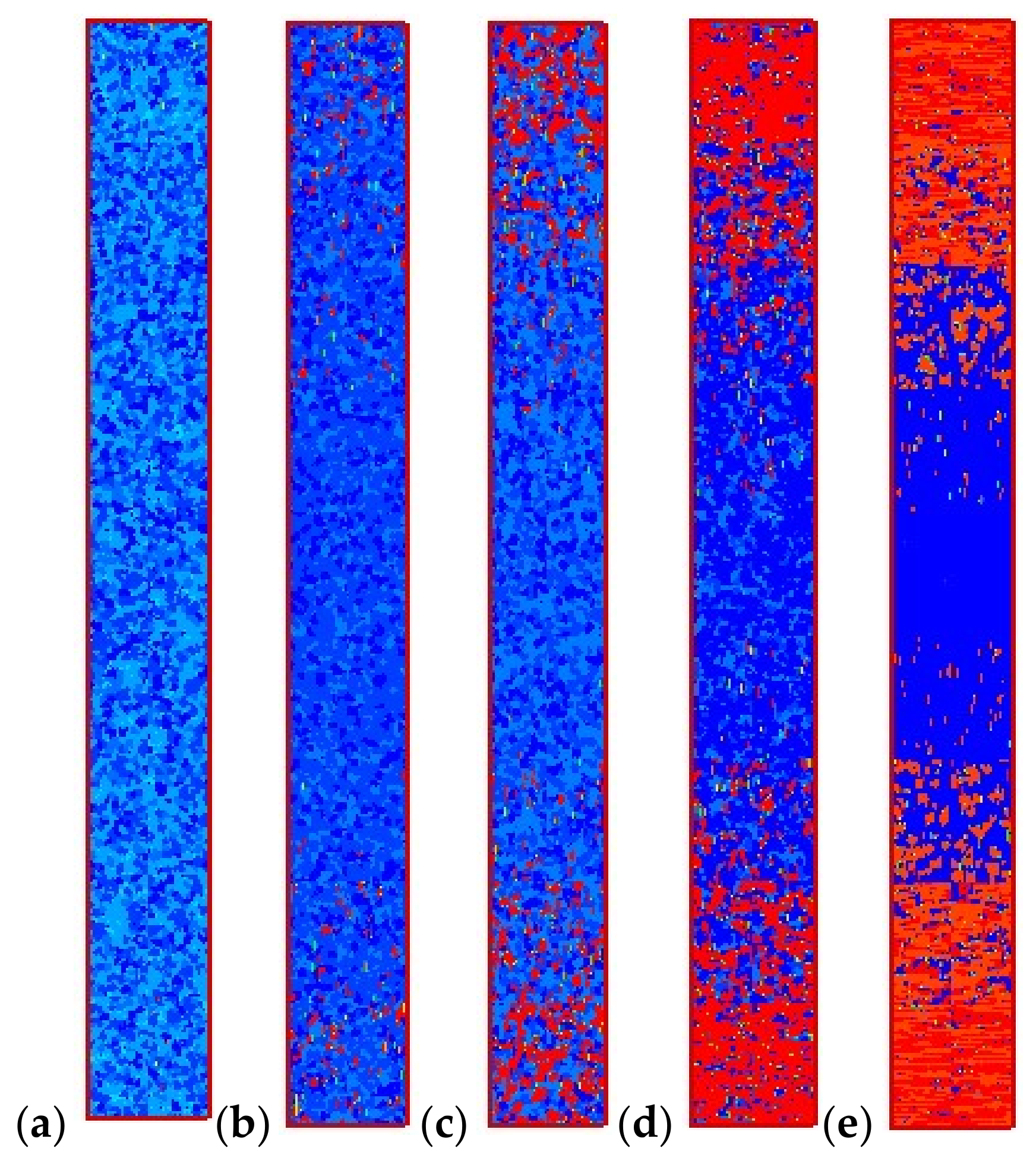
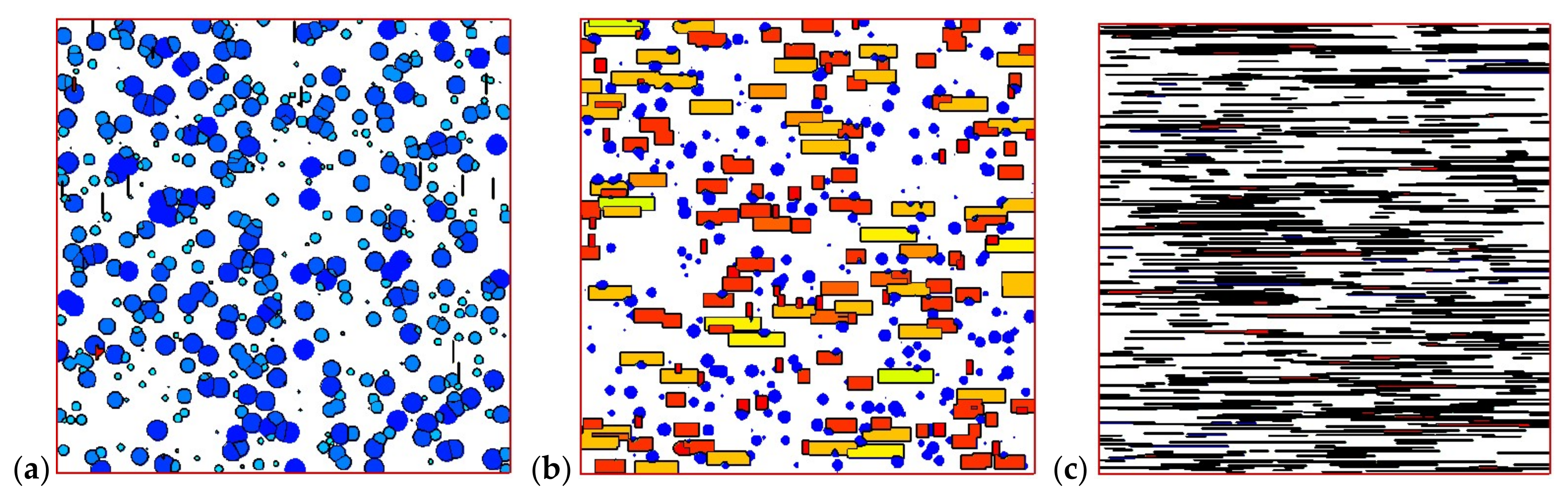
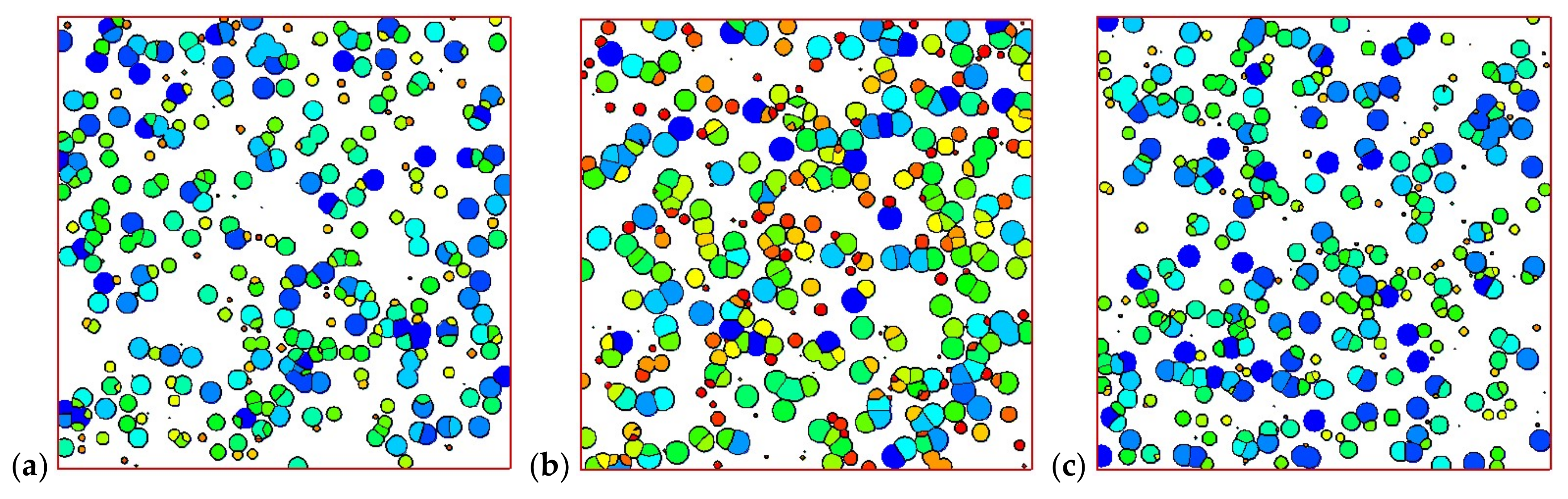
4.2. Temperature, Relative Crystallinity Distribution, and “Skin-Core-Skin” Structure
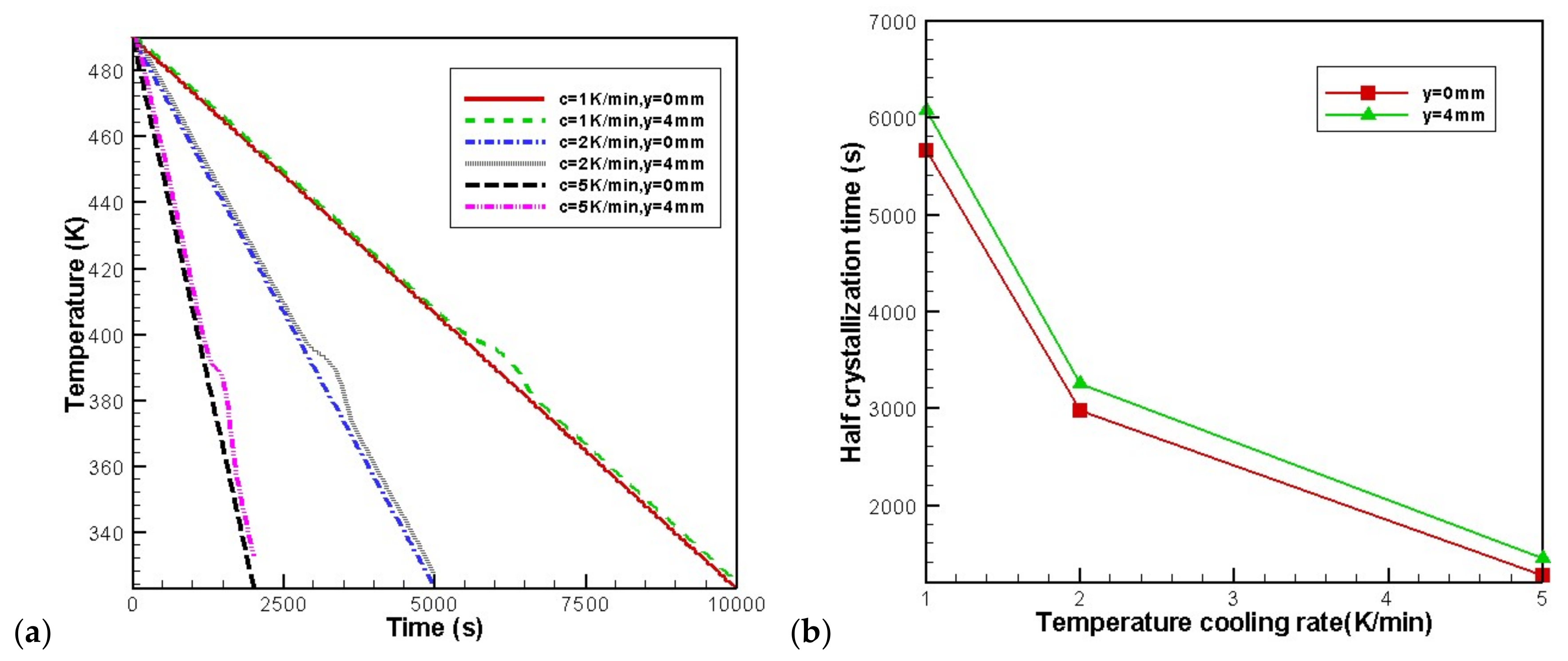
4.3. Effects of Temperature Cooling Rate of the Mold Wall
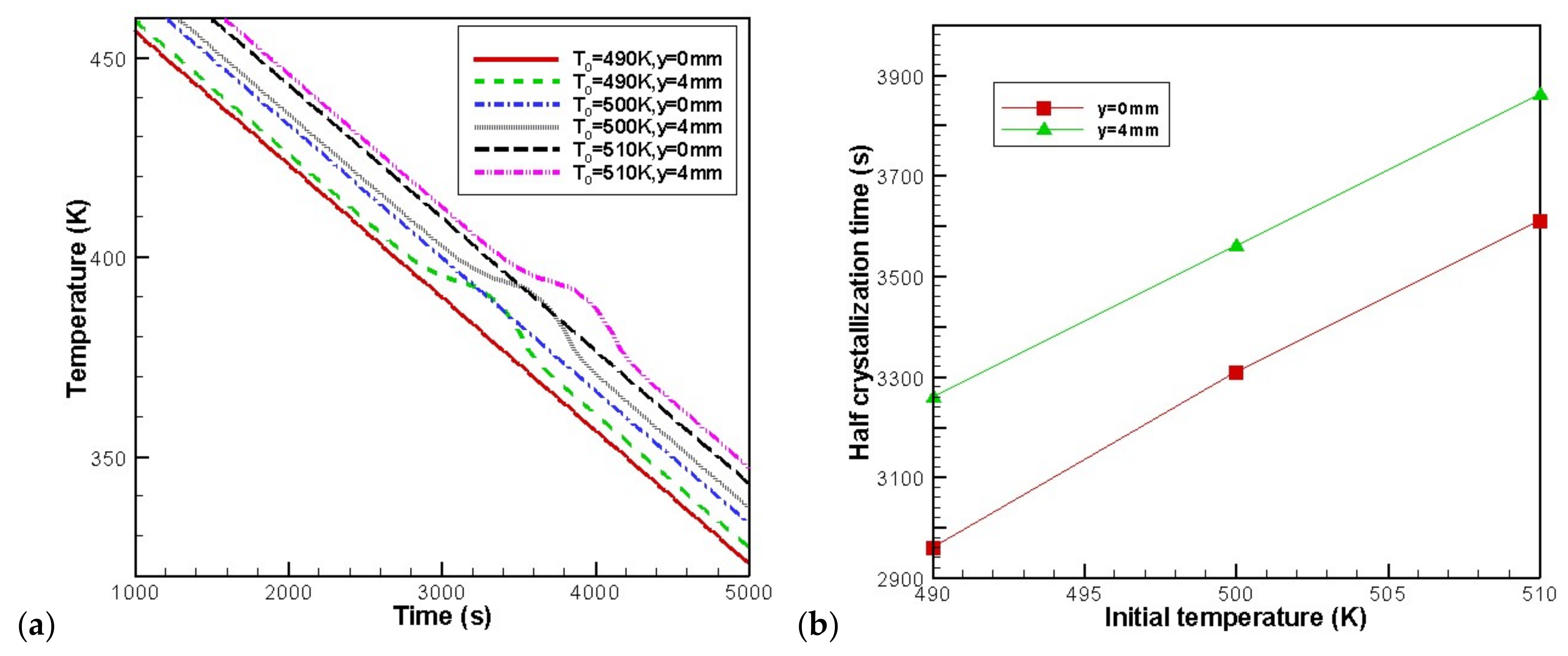
4.4. Effects of Initial Melt Temperature
4.5. Effects of the Maximum Velocity of Melt at the Inlet
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kennedy, P.K.; Zheng, R. Flow Analysis of Injection Molds; Hanser Publishers: Munich, Germany, 2013. [Google Scholar]
- Zuidema, H. Flow Induced Crystallization of Polymers; Eindhoven Technische University: Eindhoven, The Netherlands, 2001. [Google Scholar]
- Boutaous, M.; Bourgin, P.; Zinet, M. Thermally and flow induced crystallization of polymers at low shear rate. J. Non-Newton. Fluid Mech. 2010, 165, 227–237. [Google Scholar] [CrossRef]
- Zinet, M.; EI Otmani, R.; Boutaous, M.; Chantrenne, P. Numerical modeling of nonisothermal polymer crystallization kinetics: flow and thermal effects. Polym. Eng. Sci. 2010, 50, 2044–2059. [Google Scholar] [CrossRef]
- Pantanin, R.; Coccorullo, I.; Speranza, V.; Titomanlio, G. Modeling of morphology evolution in the injection molding process of thermoplastic polymers. Prog. Polym. Sci. 2005, 30, 1185–1222. [Google Scholar] [CrossRef]
- Raabe, D.; Godara, A. Mesoscale simulation of the kinetics and topology of spherulite growth during crystallization of isotactic polypropylene (iPP) by using a cellular automaton. Model. Simul. Mater. Sci. Eng. 2005, 13, 733–751. [Google Scholar] [CrossRef]
- Spina, R.; Spekowius, M.; Hopmann, C. Multiphysics simulation of thermoplatic polymer crystallization. Mater. Des. 2016, 95, 455–469. [Google Scholar] [CrossRef]
- Ketdee, S.; Anantawaraskul, S. Simulation of crystallization kinetics and morphological development during isothermal crystallization of polymers: Effect of number of nuclei and growth rate. Chem. Eng. Commun. 2008, 195, 1315–1327. [Google Scholar] [CrossRef]
- Ruan, C.; Guo, L.; Liang, K.; Li, W. Computer modeling and simulation for 3D crystallization of polymers. II. Non-isothermal case. Polym.-Plast. Technol. Eng. 2012, 51, 816–822. [Google Scholar] [CrossRef]
- Ruan, C.; Guo, L.; Liang, K.; Li, W. Computer modeling and simulation for 3D crystallization of polymers. I. Isothermal case. Polym.-Plast. Technol. Eng. 2012, 51, 810–815. [Google Scholar] [CrossRef]
- Liu, Z.J.; Ouyang, J.; Ruan, C.L.; Liu, Q. Simulation of polymer crystallization under isothermal and temperature gradient conditions using praticle level set method. Crystals 2016, 6, 90. [Google Scholar] [CrossRef]
- Liu, Z.J.; Ouyang, J.; Zhou, W.; Wang, X.D. Numerical simulation of the polymer crystallization during cooling stage by using level set method. Comput. Mater. Sci. 2015, 97, 245–253. [Google Scholar] [CrossRef]
- Eder, G.; Janeschitz-Kriegl, H. Materials Science and Technology; Wiley-VCH: Weinheim, Germany, 1997. [Google Scholar]
- Schneider, W.; Koppl, A.; Berger, J. Non-isothermal crystallization of polymers: System of rate equations. Int. Polym. Process. 1988, 2, 151–154. [Google Scholar] [CrossRef]
- Zuidema, H.; Peters, G.W.M.; Meijer, H.E.H. Development and validation of a recoverable strain-based model for flow induced crystallization of polymers. Macromol. Theory Simul. 2001, 10, 447–460. [Google Scholar] [CrossRef]
- Boutaous, K.; Carror, C.; Guillet, J. Polypropylene during crystallization from the melt as a model for the rheology of molten-filled polymers. J. Appl. Polym. Sci. 1996, 60, 103–117. [Google Scholar]
- Mu, Y.; Zhao, G.; Chen, A.; Wu, X. Numerical investigation of the thermally and flow induced crystallization behavior of semi-crystalline polymers by using finite element-finite difference method. Comput. Chem. Eng. 2012, 46, 190–204. [Google Scholar] [CrossRef]
- Guo, X.; Isayev, A.I.; Demiray, M. Crystallinity and microstructure in injection modelings of Isotactic Polypropylenes. Part II: Simulation and experiment. Polym. Eng. Sci. 1999, 39, 2132–2149. [Google Scholar] [CrossRef]
- Guo, X.; Isayev, A.I.; Guo, L. Crystallinity and microstructure in injection modelings of Isotactic Polypropylenes. Part I: A new approach to modeling and model parameters. Polym. Eng. Sci. 1999, 39, 2096–2114. [Google Scholar] [CrossRef]
- Wang, X.D.; Ouyang, J.; Zhou, W.; Liu, Z.J. A phase field technique for modeling and predicting flow induced crystallization morphology of semi-crystalline polymers. Polymers 2016, 8, 230. [Google Scholar] [CrossRef]
- Ruan, C.; Liu, C.; Zheng, G. Monte carlo simulation for the morphology and kinetics of spherulites and shish-kebabs in isothermal polymer crystallization. Math. Probl. Eng. 2015, 506204. [Google Scholar] [CrossRef]
- Ruan, C.; Liang, K.F.; Liu, E.L. Macro-micro simulation for polymer crystallization in Couette flow. Polymers 2017, 9, 699. [Google Scholar] [CrossRef]
- Ruan, C. Kinetics and morphology of flow induced polymer crystallization in 3D shear flow investigated by Monte Carlo simulation. Crystals 2017, 7, 51. [Google Scholar] [CrossRef]
- Zheng, R.; Kennedy, P.K. A model for post-flow induced crystallization: General equations and predictions. J. Rheol. 2004, 48, 823–842. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L., III. The use of tensors to describe and predict fiber orientation in short fiber composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Chung, D.H.; Kwon, T.H. Improved model of orthotropic closure approximation for flow induced fiber orientation. Polym. Compos. 2001, 22, 636–649. [Google Scholar] [CrossRef]
- Cintra, J.S.; Tucker, C.L., III. Orthotropic closure approximations for flow-induced fiber orientation. J. Rheol. 1995, 39, 1095–1122. [Google Scholar] [CrossRef]
- Chung, D.H.; Kwon, T.H. Invariant-based optimal fitting closure approximation for the numerical prediction of flow-induced fiber orientation. J. Rheol. 2002, 46, 169–194. [Google Scholar] [CrossRef]
- Koscher, E.; Fulchiron, R. Influence of shear on polypropylene crystallization: Morphology development and kinetics. Polymer 2002, 43, 6931–6942. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Miller, R.L. Kinetics of crystallization from the melt and chain folding in polyethylene fractions revisited: Theory and experiment. Polymer 1997, 38, 3151–3212. [Google Scholar] [CrossRef]
- Tanner, R.I. A suspension model for low shear rate polymer solidification. J. Non-Newton. Fluid Mech. 2002, 102, 397–408. [Google Scholar] [CrossRef]
- Rong, Y.; He, H.; Cao, W.; Shen, C.; Chen, J. Multi-scale molding and numerical simulation of the flow-induced crystallization. Comput. Mater. Sci. 2013, 67, 35–39. [Google Scholar] [CrossRef]
- Owens, R.G.; Phillips, T.N. Computational Rheology; Imperial College Press: London, UK, 2002. [Google Scholar]
- Ruan, C.; Ouyang, J.; Liu, S. Multi-scale modeling and simulation of crystallization during cooling in short fiber reinforced composites. Int. J. Heat Mass Transf. 2012, 55, 1911–1921. [Google Scholar] [CrossRef]
- Tao, W.Q. Numerical Heat Transfer; Xi’an Jiao Tong University Press: Xi’an, China, 2001. [Google Scholar]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Oliveira, P.J.; Miranda, A.I.P. A numerical study of steady and unsteady viscoelastic flow past bounded cylinders. J. Non-Newton. Fluid Mech. 2005, 127, 51–66. [Google Scholar] [CrossRef][Green Version]
- Ruan, C.; Ouyang, J. Microstructures of polymer solutions of flow past a confined cylinder. Polym.-Plast. Technol. Eng. 2010, 49, 510–518. [Google Scholar] [CrossRef]
- Ruan, C. Multiscale numerical study of 3D polymer crystallization during cooling stage. Math. Probl. Eng. 2012, 2012, 802420. [Google Scholar] [CrossRef]
- Chang, B.B.; Wang, B.; Zheng, G.Q.; Dai, K.; Liu, C.T.; Shen, C.Y. Tailoring microstructure and mechanical properties of injection molded isotactic-polypropylene via high temperature preshear. Polym. Eng. Sci. 2015, 55, 2714–2721. [Google Scholar] [CrossRef]
- Jan-Willem, H.; Markus, G.; Gerrit, W.M.P. Structure-property relations in molded, nucleated isotactic polypropylene. Polymer 2009, 50, 2304–2319. [Google Scholar]
- Zheng, G.Q.; Yang, W.; Yang, M.B.; Chen, J.B.; Li, Q.; Shen, C.Y. Gas-assisted injection molded polypropylene: the skin-core structure. Polym. Eng. Sci. 2008, 45, 976–986. [Google Scholar] [CrossRef]


| Equation | Γ | ||||
|---|---|---|---|---|---|
| Continuity | 0 | 1 | 1 | 0 | 0 |
| Momentum | |||||
| Energy | T | ||||
| FENE-P model | 1 | 1 | C | 0 | |
| Rigid dumbbell model | 1 | 1 | 0 |
| Thickness, Cooling Rate | Average Diameter of Spherulites (µm) | Relative Crystallinity Contributed by Spherulites | Number of Shish-Kebabs (/mm2) | Relative Crystallinity Contributed by Shish-Kebabs |
|---|---|---|---|---|
| y = 0 mm, c = 1 K/min | 48.63 | 52.93% | 174 | 47.07% |
| y = 0 mm, c = 2 K/min | 40.58 | 57.82% | 174 | 42.18% |
| y = 0 mm, c = 5 K/min | 29.39 | 65.53% | 176 | 34.47% |
| y = 4 mm, c = 1 K/min | 63.06 | 100% | 0 | 0% |
| y = 4 mm, c = 2 K/min | 50.66 | 100% | 0 | 0% |
| y = 4 mm, c = 5 K/min | 37.63 | 100% | 0 | 0% |
| Thickness, Initial Melt Temperature | Average Diameter of Spherulites (µm) | Relative Crystallinity Contributed by Spherulites | NUMBER of Shish-Kebabs (/mm2) | Relative Crystallinity Contributed by Shish-Kebabs |
|---|---|---|---|---|
| y = 0 mm, T0 = 490 K | 40.58 | 57.82% | 174 | 42.18% |
| y = 0 mm, T0 = 500 K | 39.83 | 60.77% | 140 | 39.23% |
| y = 0 mm, T0 = 510 K | 40.32 | 68.15% | 112 | 31.85% |
| y = 4 mm, T0 = 490 K | 50.66 | 100% | 0 | 0% |
| y = 4 mm, T0 = 500 K | 51.77 | 100% | 0 | 0% |
| y = 4 mm, T0 = 510 K | 50.53 | 100% | 0 | 0% |
| Thickness, Shear Rate | Average Diameter of Spherulites (µm) | Relative Crystallinity Contributed by Spherulites | Number of Shish-Kebabs (/mm2) | Relative Crystallinity Contributed by Shish-Kebabs |
|---|---|---|---|---|
| y = 0 mm, = 1 s−1 | 45.05 | 98.64% | 16 | 1.36% |
| y = 0 mm, = 5 s−1 | 40.58 | 57.82% | 174 | 42.18% |
| y = 0 mm, = 10 s−1 | 16.63 | 3.09% | 722 | 96.91% |
| y = 4 mm, = 1 s−1 | 49.98 | 100% | 0 | 0% |
| y = 4 mm, = 5 s−1 | 50.66 | 100% | 0 | 0% |
| y = 4 mm, = 10 s−1 | 49.66 | 100% | 0 | 0% |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, C. “Skin-Core-Skin” Structure of Polymer Crystallization Investigated by Multiscale Simulation. Materials 2018, 11, 610. https://doi.org/10.3390/ma11040610
Ruan C. “Skin-Core-Skin” Structure of Polymer Crystallization Investigated by Multiscale Simulation. Materials. 2018; 11(4):610. https://doi.org/10.3390/ma11040610
Chicago/Turabian StyleRuan, Chunlei. 2018. "“Skin-Core-Skin” Structure of Polymer Crystallization Investigated by Multiscale Simulation" Materials 11, no. 4: 610. https://doi.org/10.3390/ma11040610
APA StyleRuan, C. (2018). “Skin-Core-Skin” Structure of Polymer Crystallization Investigated by Multiscale Simulation. Materials, 11(4), 610. https://doi.org/10.3390/ma11040610