Optimal Design of Shape Memory Alloy Composite under Deflection Constraint
Abstract
:1. Introduction
2. Governing Equations
2.1. Constitutive Model of SMA Wires
2.2. The Constitutive Model of SMAC
2.2.1. Mathematical Modelling for Composite Laminate
2.2.2. Integration of SMA Wire in Composite Laminate
2.3. Optimization of SMAC
- Square edge length ;
- Each ply thickness about the laminate midplane, , , …, ;
- Each ply is made of the same material.
2.3.1. Constrained Optimization Problem
2.3.2. Objective Function
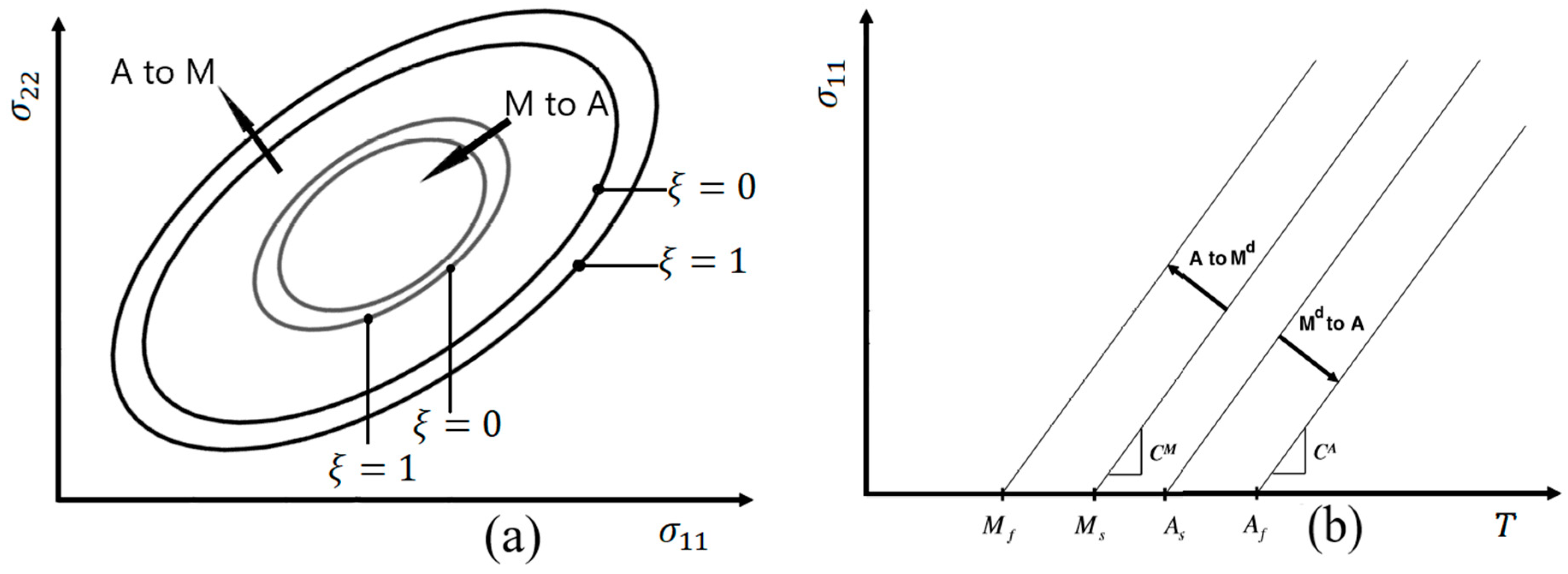
2.3.3. Deflection and Bistability Constraint
3. Results and Discussion
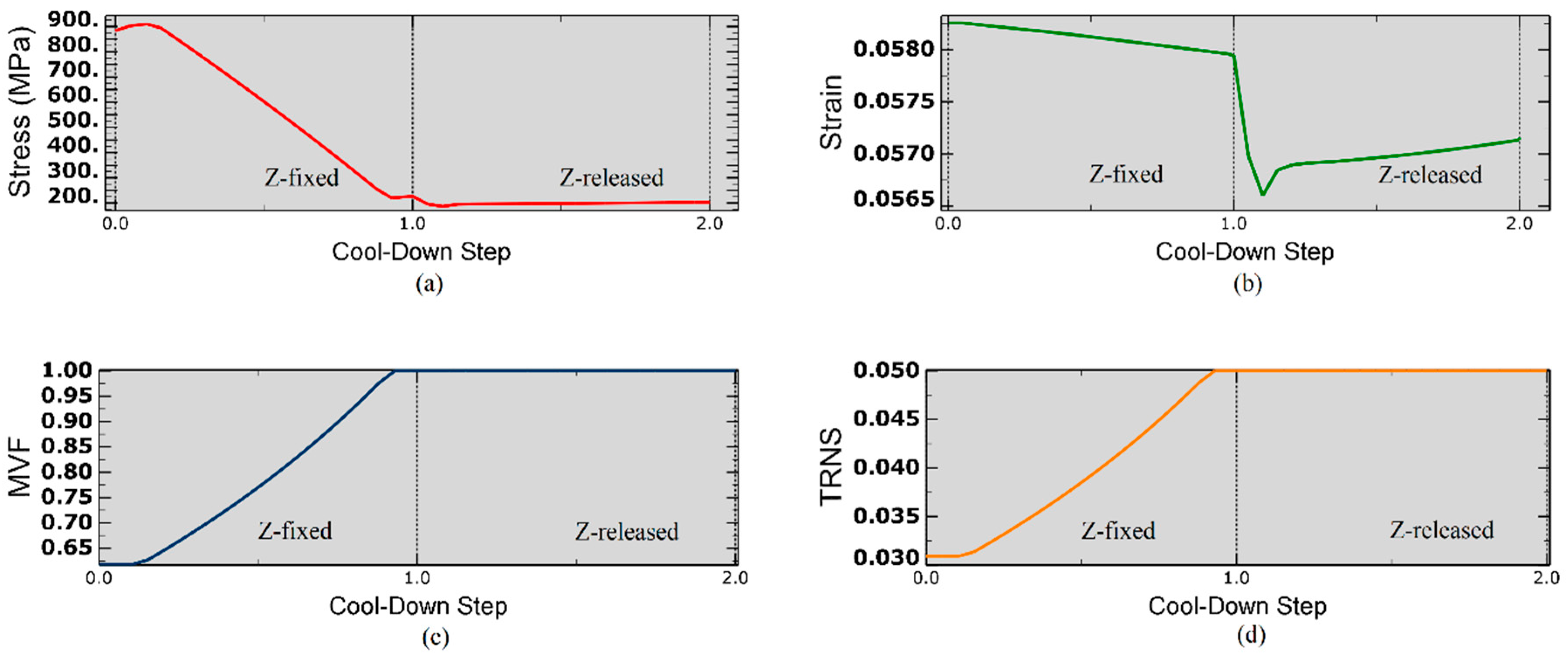
3.1. Simulation of Uniaxial Behavior of an SMA Wire
3.2. SMAC Numerical Optimization
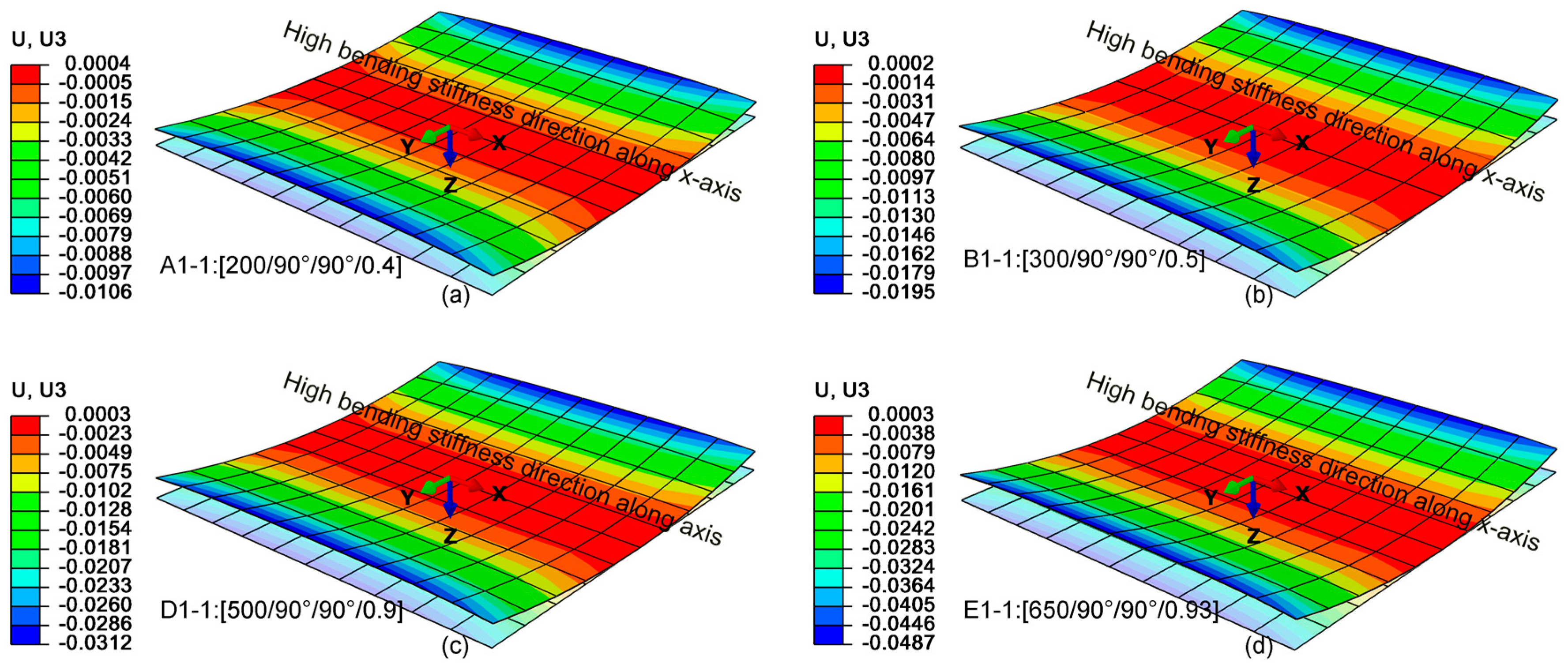
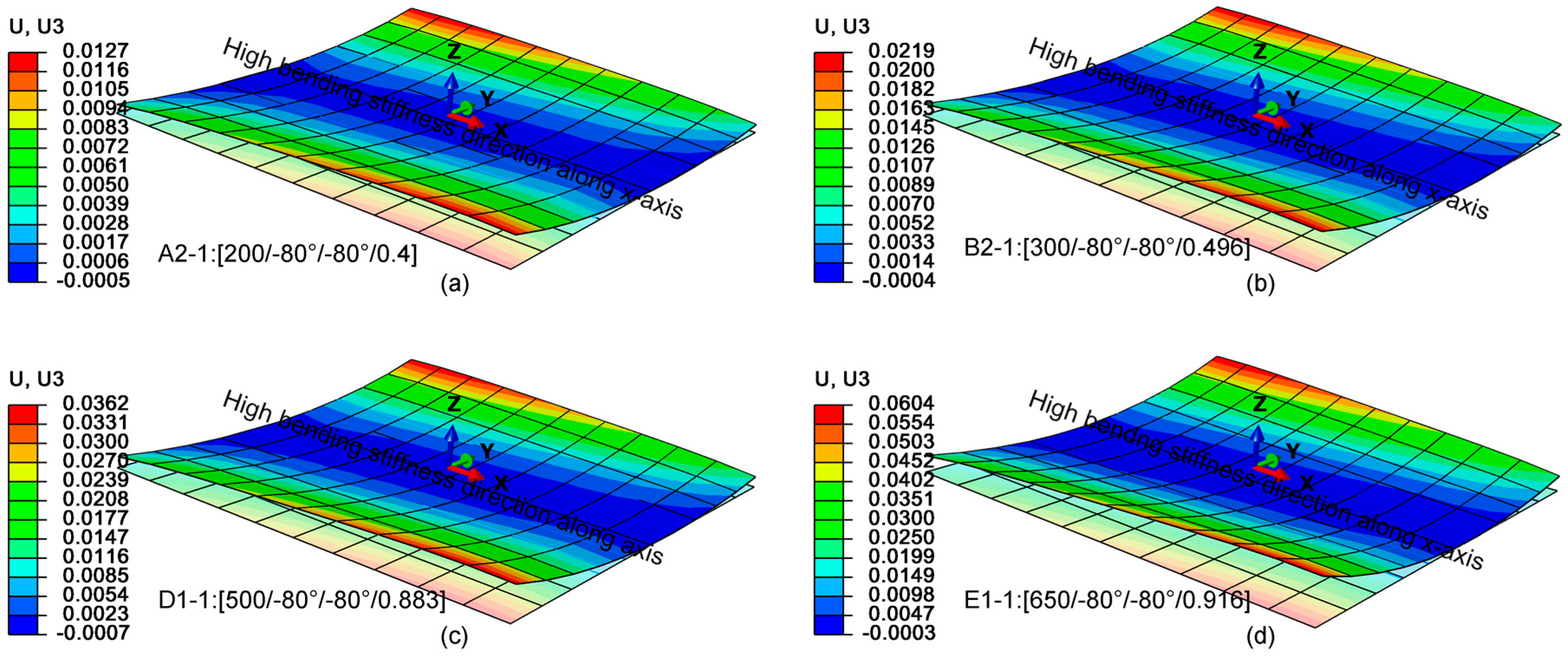
3.3. FE Simulation of SMAC
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix B.1. Karush-Kuhn-Tucker (KKT) Conditions and the Lagrangian Function
Appendix B.2. The SQP Algorithm
Appendix C
References
- Kudva, J.N. Overview of the DARPA smart wing project. JIMSS 2004, 15, 261–267. [Google Scholar] [CrossRef]
- Lachenal, X.; Daynes, S.; Weaver, P.M. Review of morphing concepts and material for wind turbine blade application. Wind Energy 2013, 16, 283–307. [Google Scholar] [CrossRef]
- Hyer, M.W. Calculations of the room-temperature shapes of unsymmetric laminates. J. Comp. Mater. 1981, 15, 296–310. [Google Scholar] [CrossRef]
- Hyer, M.W. Some observations on the cured shape of thin unsymmetric laminates. J. Comp. Mater. 1981, 15, 175–194. [Google Scholar] [CrossRef]
- Jun, W.J.; Hong, C.S. Effect of Residual Shear Strain on the Cured Shape of Unsymmetric Cross-ply Thin Laminates. J. Comp. Mater. 1990, 38, 55–67. [Google Scholar] [CrossRef]
- Schlecht, M.; Schulte, K. Advanced Calculations of the Room-temperature Shapes of Unsymmetric Laminates. J. Comp. Mater. 1999, 33, 627–633. [Google Scholar] [CrossRef]
- Tawfik, S.; Tan, X.; Ozbay, S.; Armanios, E. Anticlastic Stability Modeling for Cross-ply Composites. J. Comp. Mater. 1999, 41, 1325–1338. [Google Scholar] [CrossRef]
- Bo, Z.; Lagoudas, D. Thermomechanical modelling of polycrystalline SMAs under cyclic loading, Part III: Evolution of plastic strains and two-way shape memory effect. IJES 1999, 37, 1175–1203. [Google Scholar]
- Boyd, J.; Lagoudas, D. A thermodynamical constitutive model for shape memory materials. Part I: The monolithic shape memory alloy. Int. J. Plast. 1996, 12, 805–842. [Google Scholar] [CrossRef]
- Brinson, L. One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material functions and redefined martensite internal variable. JIMSS 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Liang, C.; Rogers, C. One-dimensional thermomechanical constitutive relations for shape memory materials. JIMSS 1990, 1, 207–234. [Google Scholar]
- Qidwai, M.; Lagoudas, D. On thermomechanics and transformation surfaces of polycrystalline NiTi shape memory alloy material. Int. J. Plast. 2000, 16, 1309–1343. [Google Scholar] [CrossRef]
- Qidwai, M.; Lagoudas, D. Numerical implementation of a shape memory alloy thermomechanical constitutive model using return mapping algorithms. IJNME 2000, 47, 1123–1168. [Google Scholar] [CrossRef]
- Tanaka, K.; Kobayashi, S.; Sato, Y. Thermomechanics of transformation pseudoelasticity and shape memory effect in alloys. Int. J. Plast. 1986, 2, 59–72. [Google Scholar] [CrossRef]
- Duerig, T.W.; Melton, K.N.; Stoeckel, D.; Wayman, C.M. Engineering Aspects of Shape Memory Alloys; Butterworth-Heinemann: New York, NY, USA, 1990; pp. 283–366. [Google Scholar]
- Stachiv, I.; Sittner, P.; Olejnicek, J.; Landa, M.; Heller, L. Exploiting NiTi shape memory alloy films in design of tunable high frequency microcantilever resonators. Appl. Phys. Lett. 2017, 111, 213105. [Google Scholar] [CrossRef]
- Stachiv, I.; Sittner, P. Nanocantilevers with Adjustable Static Deflection and Significantly Tunable Spectrum Resonant Frequencies for Applications in Nanomechanical Mass Sensors. Nanomaterials 2018, 8, 116. [Google Scholar] [CrossRef]
- Ryu, J.; Lee, J.; Cho, M.; Kim, S.-W.; Koh, J.-S.; Cho, K.-J. Snap-through behavior of bi-stable composite structure using SMA spring actuator. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Material Conference, Denver, CO, USA, 4–7 April 2011. [Google Scholar]
- Dano, M.-L.; Hyer, M.W. SMA-induced snap-through of unsymmetric fiber-reinforced composite laminates. Int. J. Solids Struct. 2003, 40, 5949–5972. [Google Scholar] [CrossRef]
- Hassanli, S.; Samali, B. Buckling analysis of laminated composite curved panels reinforced with linear and non-linear distribution of Shape Memory Alloys. Thin-Walled Struct. 2016, 106, 9–17. [Google Scholar] [CrossRef]
- Tawfik, M.; Ro, J.J.; Mei, C. Thermal post-buckling and aeroelastic behaviour of shape memory alloy reinforced plates. Smart Mater. Struct. 2002, 11, 297–307. [Google Scholar] [CrossRef]
- Turner, T.L. A new thermoelastic model for analysis of shape memory alloy hybrid composites. J. Intell. Mater. Syst. Struct. 2000, 11, 382–394. [Google Scholar] [CrossRef]
- Niknami, A.; Shariyat, M. Influence of the heat generation on the phase transformations and impact responses of composite plates with embedded SMA wires. J. Comput. Appl. Res. Mech. Eng. 2017, 6, 13–26. [Google Scholar]
- Birman, V.; Chandrashekhara, K.; Sain, S. An approach to optimization of shape memory alloy hybrid composite plates subjected to low-velocity impact. Composites Part B Eng. 1996, 27, 439–446. [Google Scholar] [CrossRef]
- Gandhi, Y.; Pirondi, A.; Collini, L. Analysis of bistable composite laminate with embedded SMA actuators. In Proceedings of the 47th AIAS International Conference on Stress Analysis, Reggio Calabria, Italy, 5–8 September 2018. [Google Scholar]
- Betts, D.N. Modelling and Optimization of Bistable Composite Laminates. Ph.D. Thesis, University of Bath, Bath, UK, January 2012. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 1999; pp. 526–569. [Google Scholar]
- Sequential Quadratic Programming. Available online: https://optimization.mccormick.northwestern.edu/ index.php/Sequential_quadratic_programming (accessed on 13 May 2019).
- Lagoudas, D.; Bo, Z.; Qidwai, M.; Entchev, P. SMA_UM: User Material Subroutine for Thermomechanical Constitutive Model of Shape Memory Alloys; Texas A&M University: College Station, TX, USA, 2003. [Google Scholar]
- Hexcel. Available online: https://www.hexcel.com/Resources/DataSheets/ (accessed on 28 May 2019).
- Simmons. Available online: http://www.epoxyworktops.com/epoxy-resin/mech-properties.html (accessed on 27 March 2019).
- Hartl, D.J.; Lagoudas, D.C. Thermomechanical Characterization of Shape Memory Alloy Materials. In Shape Memory Alloy: Modeling and Engineering Applications, 2nd ed.; Lagoudas, D.C., Ed.; Springer: New York, NY, USA, 2008; pp. 53–117. [Google Scholar]
- Liu, Y.; McCormick, P.G. Thermodynamic analysis of the martensitic transformation in NiTi-II. Effect of transformation cycling. Acta Metall. Mater. 1994, 42, 2407–2413. [Google Scholar] [CrossRef]
- Dano, M.L.; Hyer, M.W. Thermally-induced deformation behaviour of unsymmetric laminates. Int. J. Solids Struct. 1988, 35, 2101–2120. [Google Scholar] [CrossRef]




| Material Properties | Value |
|---|---|
| Material Parameter | Value |
|---|---|
| Elastic stiffness of the austenite | |
| Elastic stiffness of the martensite | |
| Poisson’s ratio (equal for both phases) | |
| Coefficient of thermal expansion for the austenite | |
| Coefficient of thermal expansion for the martensite | |
| Martensitic start temperature | |
| Martensitic final temperature | |
| Austenitic start temperature | |
| Austenitic final temperature | |
| Maximum transformation strain | |
| Stress influence coefficient for austenite | |
| Stress influence coefficient for martensite |
| Mechanical Properties | Value |
|---|---|
| Tensile Modulus | |
| Flexural Modulus | |
| Poisson ratio | |
| Coefficient of linear thermal expansion |
| Optimization Set | Deflection Constraint (mm) | The Range of Geometric Design Variables | Optimal Design Parameters | Objective Function |
|---|---|---|---|---|
| A1 | 1 2 | |||
| B1 | 3 4 5 | |||
| C1 | 1 2 3 | |||
| D1 | 1 2 3 4 | |||
| E1 | 1 2 3 4 5 |
| Optimization Set | Deflection Constraint (mm) | The Range of Geometric Design Variables | Optimal Design Parameters | Objective Function |
|---|---|---|---|---|
| A2 | 1 2 | |||
| B2 | 1 2 3 | |||
| C2 | 1 2 3 4 | |||
| D2 | 1 2 3 4 | |||
| E2 | 1 2 3 4 5 |
| Axial Stress | Total Strain | MVF | TRNS |
|---|---|---|---|
| 884 MPa | 0.0583 | 0.631 | 0.0314 |
| Optimization Set | in ABAQUS (mm) | in MATLAB (mm) | Percentage Difference (%) |
|---|---|---|---|
| A1-1 | 21.19 | 18.9 | 10.8 |
| B1-1 | 39.05 | 37.748 | 3.33 |
| C1-1 | 59.57 | 58.722 | 1.42 |
| D1-1 | 59.08 | 58.6 | 0.813 |
| E1-1 | 97.31 | 98.15 | 0.863 |
| Optimization Set | in ABAQUS (mm) | in MATLAB (mm) | Percentage Difference (%) |
|---|---|---|---|
| A2-1 | 20.53 | 18.5 | 9.88 |
| B2-1 | 37.86 | 35.6 | 5.79 |
| C2-1 | 61.58 | 59.14 | 3.96 |
| D2-2 | 62.6 | 63.5 | 1.44 |
| E2-2 | 102.76 | 101.91 | 0.827 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gandhi, Y.; Pirondi, A.; Collini, L. Optimal Design of Shape Memory Alloy Composite under Deflection Constraint. Materials 2019, 12, 1733. https://doi.org/10.3390/ma12111733
Gandhi Y, Pirondi A, Collini L. Optimal Design of Shape Memory Alloy Composite under Deflection Constraint. Materials. 2019; 12(11):1733. https://doi.org/10.3390/ma12111733
Chicago/Turabian StyleGandhi, Yogesh, Alessandro Pirondi, and Luca Collini. 2019. "Optimal Design of Shape Memory Alloy Composite under Deflection Constraint" Materials 12, no. 11: 1733. https://doi.org/10.3390/ma12111733






