Opposition-Based Adaptive Fireworks Algorithm

Abstract

A fireworks algorithm (FWA) is a recent swarm intelligence algorithm that is inspired by observing fireworks explosions. An adaptive fireworks algorithm (AFWA) proposes additional adaptive amplitudes to improve the performance of the enhanced fireworks algorithm (EFWA). The purpose of this paper is to add opposition-based learning (OBL) to AFWA with the goal of further boosting performance and achieving global optimization. Twelve benchmark functions are tested in use of an opposition-based adaptive fireworks algorithm (OAFWA). The final results conclude that OAFWA significantly outperformed EFWA and AFWA in terms of solution accuracy. Additionally, OAFWA was compared with a bat algorithm (BA), differential evolution (DE), self-adapting control parameters in differential evolution (jDE), a firefly algorithm (FA), and a standard particle swarm optimization 2011 (SPSO2011) algorithm. The research results indicate that OAFWA ranks the highest of the six algorithms for both solution accuracy and runtime cost.

1. Introduction

In the past twenty years several swarm intelligence algorithms, inspired by natural phenomena or social behavior, have been proposed to solve various real-world and complex global optimization problems. Observation of the behavior of ants searching for food lead to an ant colony optimization (ACO) [1] algorithm, proposed in 1992. Particle swarm optimization (PSO) [2], announced in 1995, is an algorithm that simulates the behavior of a flock of birds flying to their destination. PSO can be employed in the economic statistical design of $\overline{X}$ control charts, a class of mixed discrete-continuous nonlinear problems [3] and used in solving multidimensional knapsack problems [4,5], etc. Mimicking the natural adaptations of the biological species, differential evolution (DE) [6] was published in 1997. Inspired by the behavior of the flashing characteristics of fireflies, a firefly algorithm (FA) [7] was presented in 2009, and a bat algorithm (BA) [8] was proposed in 2010 which is based on the echolocation of microbats.

The fireworks algorithm (FWA) [9] is considered a novel swarm intelligence algorithm. It was introduced in 2010 and mimics the fireworks explosion process. The FWA provides an optimized solution for searching a fireworks location. In the event of a firework randomly exploding, there are explosive and Gaussian sparks produced in addition to the initial explosion. To determine the firework’s local space, a calculation of explosive amplitude and number of explosive sparks is made based on other fireworks and fitness functions. Fireworks and sparks are then filtered based on fitness and diversity. Using repetition, FWA focuses on smaller areas for optimized solutions.

Various types of real-world optimization problems have been solved by applying FWA, such as factorization of a non-negative matrix [10], the design of digital filters [11], parameter optimization for the detection of spam [12], reconfiguration of networks [13], mass minimization of trusses [14], parameter estimation of chaotic systems [15], and scheduling of multi-satellite control resources [16].

However, there are disadvantages to the FWA approach. Although the original algorithm worked well on functions in which the optimum is located at the origin of the search space, when the optimum of origin is more distant it becomes more challenging to locate the correct solution. Thus, the quality of the results of the original FWA deteriorates severely with the increasing distance between the function optimum and the origin. Additionally, the computational cost per iteration is high for FWA compared to other optimization algorithms. For these reasons, the enhanced fireworks algorithm (EFWA) [17] was introduced to enhance FWA.

The explosion amplitude is a significant variable and affects the performance of both the FWA and EFWA. In EFWA, the amplitude is near zero with the best fireworks, thus employing an amplitude check with a minimum. An amplitude like this is calculated according to the maximum number of evaluations, which leads to a local search without adaption around the best fireworks. Thus, the adaptive fireworks algorithm (AFWA) introduced an adaptive amplitude [18] to improve the performance of EFWA. In AFWA, the adaptive amplitude is calculated from a distance between filtered sparks and the best fireworks.

AFWA improved the performance of EFWA on 25 of the 28 CEC13’s benchmark functions [18], but our in-depth experiments indicate that the solution accuracy of AFWA is lower than that of EFWA. To improve the performance of AFWA, opposition-based learning was added and used to accelerate the convergence speed and increase the solution accuracy.

Opposition-based learning (OBL) was first proposed in 2005 [19]. OBL simultaneously considers a solution and its opposite solution; the fitter one is then chosen as a candidate solution in order to accelerate convergence and improve solution accuracy. It has been used to enhance various optimization algorithms, such as differential evolution [20,21], particle swarm optimization [22], the ant colony system [23], the firefly algorithm [24], the artificial bee colony [25], and the shuffled frog leaping algorithm [26]. Inspired by these studies, OBL was added to AFWA and used to boost the performance of AFWA.

The remainder of this paper is organized in the following manner. Both AFWA and OAFWA are summarized in Section 2. In the third section, twelve benchmark functions and implementations are listed. Section 4 covers simulations that have been conducted, while Section 5 presents our conclusion.

2. Opposition-Based Adaptive Fireworks Algorithm

2.1. Adaptive Fireworks Algorithm

Suppose that N denotes the quantity of fireworks, while $d$ stands for the number of dimensions, and $x_i$ stands for each firework in AFWA. The explosive amplitude $A_i$ and the number of explosion sparks $S_i$ can be defined according to the following expressions:

$$A_i=\widehat{\mathrm{A}}·\frac{f\left(x_i\right)-y_{\text{min}}+ϵ}{{\sum }_{i=1}^N\left(f\left(x_i\right)-y_{\text{min}}\right)+ϵ}$$

(1)

$$S_i={\mathrm{M}}_{\mathrm{e}}·\frac{y_{\text{max}}-f\left(x_i\right)+ϵ}{{\sum }_{i=1}^N\left(y_{\text{max}}-f\left(x_i\right)\right)+ϵ}$$

(2)

where $y_{\text{max}}$ = max($f\left(x_i\right)$), $y_{\text{min}}$ = min($f\left(x_i\right)$), and $\widehat{\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{e}}$ are two constants. $ϵ$ denotes the machine epsilon, $i=(1, 2,\dots ,d$).

In addition, the number of sparks $S_i$ is defined by:

$$S_i=\{\begin{array}{ll}{S}_{\text{min}}& if S_i<S_{\text{min}}\\ S_{\text{max}}& if S_i>S_{\text{max}}\\ S_i& otherwise\end{array}$$

(3)

where $S_{\text{min}}$ and $S_{\text{max}}$ are the lower bound and upper bound of the $S_i$.

Based on the above $A_i$ and $S_i$, Algorithm 1 is performed by generating explosion sparks for $x_i$ as follows:

Algorithm 1 Generating Explosion Sparks

1: for j = 1 to Si do

2: for each dimension k = 1, 2, …, d do

3: obtain r1 from U(0, 1)

4: if r1 < 0.5 then

5: obtain r from U(−1, 1)

6: $s_{ij}^{\left(k\right)}\leftarrow x_i^{\left(k\right)}+r·A_i$

7: if $s_{ij}^{\left(k\right)}\langle LB \vee s_{ij}^{\left(k\right)}\rangle UB$ then

8: obtain r again from U(0, 1)

9: $s_{ij}^{\left(k\right)}\leftarrow LB+r·\left(UB-LB\right)$

10: end if

11: end if

12: end for

13: end for

14: return $s_{ij}$

where x $\in \left[LB, UB\right]$. U(a, b) denotes a uniform distribution between a and b.

After generating explosion sparks, Algorithm 2 is performed for generating Gaussian sparks as follows:

Algorithm 2 Generating Gaussian Sparks

1: for j = 1 to NG do

2: Randomly choose i from 1, 2, ..., m

3: obtain r from N(0, 1)

4: for each dimension k = 1, 2, …, d do

5: $G_j^{\left(k\right)}\leftarrow x_i^{\left(k\right)}+r·\left(x^{*\left(k\right)}-x_i^{\left(k\right)}\right)$

6: if ${\mathrm{G}}_{\mathrm{j}}^{\left(\mathrm{k}\right)}\langle LB \vee {\mathrm{G}}_{\mathrm{j}}^{\left(\mathrm{k}\right)}\rangle UB$ then

7: obtain r from U(0, 1)

8: $G_j^{\left(k\right)}\leftarrow LB+r·\left(UB-LB\right)$

9: end if

10: end for

11: end for

12: return $G_j$

where NG is the quantity of Gaussian sparks, m stands for the quantity of fireworks, $x^{*}$ denotes the best firework, and N(0, 1) denotes normal distribution with an average of 0 and standard deviation of 1.

For the best sparks among the above explosion sparks and Gaussian sparks, the adaptive amplitude of fireworks $A^{*}$ in generation $g$+ 1 is defined as follows [18]:

$$A^{*}\left(g+1\right)=\{\begin{array}{cc}UB-LB,\hfill & \hfill g=0 or f\left(s_i\right)<f\left(x\right)\\ 0.5·\left(\lambda ·|\left|s_i-s^{*}\right|{|}_{\infty }+A^{*}\left(g\right)\right),\hfill & \hfill otherwise\end{array}$$

(4)

where $s_{1\dots }{s}_n$ denotes all sparks generated in generation $g$, ${\mathrm{s}}^{*}$ denotes the best spark and x stands for fireworks in generation $g$.

The above parameter $\lambda$ is suggested to be a fixed value of 1.3, empirically.

Algorithm 3 demonstrates the complete version of the AFWA.

Algorithm 3 Pseudo-Code of AFWA

1: randomly choosing m fireworks

2: assess their fitness

3: repeat

4: obtain Ai (except for A*) based on Equation (1)

5: obtain Si based on Equations (2) and (3)

6: produce explosion sparks based on Algorithm 1

7: produce Gaussian sparks based on Algorithm 2

8: assess all sparks’ fitness

9: obtain A* based on Equation (4)

10: retain the best spark as a firework

11: randomly select other m − 1 fireworks

12: until termination condition is satisfied

13: return the best fitness and a firework location

2.2. Opposition-Based Learning

Definition 1. 

Assume P = (x₁, x₂, ..., x_n) is a solution in n-dimensional space, where x₁, x₂, …, x_n $\in$ R and x_i $\in$ [$a_i$, $b_i$], $\forall$i $\in$ {1, 2, …, n}. The opposite solution OP = (${\breve{x}}_1$, ${\breve{x}}_2$, …, ${\breve{x}}_n$) is defined as follows [19]:

$${\breve{x}}_i=a_i+b_i-x_i$$

(5)

In fact, according to probability theory, 50% of the time an opposite solution is better. Therefore, based on a solution and an opposite solution, OBL has the potential to accelerate convergence and improve solution accuracy.

Definition 2. 

The quasi-opposite solution QOP = (${\breve{x}}_1^q, {\breve{x}}_2^q,\dots , {\breve{x}}_n^q$) is defined as follows [21]:

$${\breve{x}}_i^q=\mathrm{rand}\left(\frac{a_i+b_i}{2},{\breve{x}}_i\right)$$

(6)

It is proved that the quasi-opposite solution QOP is more likely than the opposite solution OP to be closer to the solution.

Figure 1 illustrates the quasi-opposite solution QOP in the one-dimensional case.

2.3. Opposition-Based Adaptive Fireworks Algorithm

The OBL is added to AFWA in two stages: opposition-based population initialization and opposition-based generation jumping [20].

2.3.1. Opposition-Based Population Initialization

In the initialization stage, both a random solution and a quasi-opposite solution QOP are considered in order to obtain fitter starting candidate solutions.

Algorithm 4 is performed for opposition-based population initialization as follows:

Algorithm 4 Opposition-Based Population Initialization

1: randomly initialize fireworks pop with a size of m

2: calculate a quasi opposite fireworks Qpop based on Equation (6)

3: assess 2 × m fireworks’ fitness

4: return the fittest individuals from {pop ∪ Opop} as initial fireworks

2.3.2. Opposition-Based Generation Jumping

In the second stage, the current population of AFWA is forced to jump into some new candidate solutions based on a jumping rate, J_r.

Algorithm 5 Opposition-Based Generation Jumping

1: if (rand(0, 1) < Jr)

2: dynamically calculate boundaries of current m fireworks

3: calculate a quasi opposite fireworks Qpop based on Equation (6)

4: assess 2 × m fireworks’ fitness

5: end if

6: return the fittest individuals from {pop ∪ Opop} as current fireworks

2.3.3. Opposition-Based Adaptive Fireworks Algorithm

Algorithm 6 demonstrates the complete version of the OAFWA.

Algorithm 6 Pseudo-Code of OAFWA

1: opposition-based population initialization based on Algorithm 4

2: repeat

3: obtain Ai (except for A*) based on Equation (1)

4: obtain Si based on Equations (2) and (3)

5: produce explosion sparks based on Algorithm 1

6: produce Gaussian sparks based on Algorithm 2

7: assess all sparks’ fitness

8: obtain A* based on Equation (4)

9: retain the best spark as a firework

10: randomly select other m – 1 fireworks

11: opposition-based generation jumping based on Algorithm 5

12: until termination condition is satisfied

13: return the best fitness and a firework location

3. Benchmark Functions and Implementation

3.1. Benchmark Functions

In order to assess the performances of OAFWA, twelve standardized benchmark functions [27] are employed. The functions are uni-modal and multi-modal. The global minimum is zero.

Table 1. Twelve benchmark functions.

Function	Dimension	Range
$\mathrm{F}1\left(x\right)={{\displaystyle \sum }}_{i=1}^n{x}_i^2$	40	[−10, 10]
$\mathrm{F}2\left(x\right)={{\displaystyle \sum }}_{i=1}^n|x_i|+{{\displaystyle \prod }}_{i=1}^n|x_i|$	40	[−10, 10]
$\mathrm{F}3\left(x\right)={{\displaystyle \sum }}_{i=1}^n{\left({{\displaystyle \sum }}_{j=1}^i{x}_j\right)}^2$	40	[−10, 10]
$\mathrm{F}4\left(x\right)={{\displaystyle \sum }}_{i=1}^{n}i{x}_i^2$	40	[−30, 30]
$\mathrm{F}5\left(x\right)=\text{max}\{\left|x_i\right|,1\le x_i\le n\}$	40	[−100, 100]
$\mathrm{F}6\left(x\right)={10}^6{x}_1^2+{{\displaystyle \sum }}_{i=2}^n{x}_i^2$	40	[−100, 100]
$\mathrm{F}7\left(x\right)={{\displaystyle \sum }}_{i=1}^n\left(x_i^2-10 \text{cos}\left(2\pi x_i\right)+10\right)$	40	[−1, 1]
$\mathrm{F}8\left(x\right)=\frac{1}{4000}{{\displaystyle \sum }}_{i=1}^n{x}_i^2-{{\displaystyle \prod }}_{i=1}^{n}cos\left(\frac{x_i}{\sqrt{i}}\right)+1$	40	[−100, 100]
$\mathrm{F}9\left(x\right)=-20\text{exp}\left(-0.2\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{x}_i^2}\right)- \text{exp}\left(\frac{1}{n}{{\displaystyle \sum }}_{i=1}^{n}cos\left(2\pi x_i\right)\right)+20+e$	40	[−10, 10]
$\mathrm{F}10\left(x\right)={{\displaystyle \sum }}_{i=1}^{n/4}\left({\left(x_{4i-3}+10x_{4i-2}\right)}^2+5{\left(x_{4i-1}-x_{4i}\right)}^2 +{\left(x_{4i-2}-2x_{4i-1}\right)}^4+10{\left(x_{4i-3}-x_{4i}\right)}^4\right)$	40	[−10, 10]
$\mathrm{F}11\left(x\right)={{\displaystyle \sum }}_{i=1}^n\left|x_i\text{sin}\left(x_i\right)+0.1x_i \right|$	40	[−10, 10]
$\mathrm{F}12\left(x\right)=1-cos\left(2\pi \sqrt{{{\displaystyle \sum }}_{i=1}^n{x}_i^2}\right)+0.1\sqrt{{{\displaystyle \sum }}_{i=1}^n{x}_i^2}$	40	[−10, 10]

presents a list of uni-modal (F1~F6) and multi-modal (F7~F12) functions and their features.

3.2. Success Criterion

We utilize the success rates $S_r$ to compare performances of different FWA based algorithms including EFWA, AFWA, and OAFWA.

$S_r$ can be defined as follows:

$$S_r=100·\frac{N_{\text{successful}}}{N_{\text{all}}}$$

(7)

where $N_{\text{successful}}$ is the number of trials that were successful, and $N_{\text{all}}$ stands for the total number of trials. When an experiment locates a solution that is close in range to the global optimum, it is found to be a success. A successful trial is defined by:

$${{\displaystyle \sum }}_{i=1}^D\left(X_i^{gb}-X_i^{*}\right)\le \left(UB-LB\right)\times {10}^{-4}$$

(8)

where D denotes the dimensions of the test function, and $X_i^{gb}$ denotes the dimension of the best result by the algorithm.

3.3. Initialization

We tested the benchmark functions using 100 independent algorithms based on various FWA based algorithms. In order to fully evaluate the performance of OAFWA, statistical measures were used including the worst, best, median, and mean objective values. Standard deviations were also determined.

In FWA based algorithms, m = 4, $\widehat{\mathrm{A}}$ = 100, M_e = 20, $S_{\text{min}}$ = 8, $S_{\text{max}}$ = 13, NG = 2 (population size is equivalent to 40), and J_r = 0.4. Evaluation times from 65,000 to 200,000 were used for different functions.

Finally, we used Matlab 7.0 (The MathWorks Inc., Natick, MA, USA) software on a notebook PC with a 2.3 GHZ CPU (Intel Core i3-2350, Intel Corporation, Santa Clara, CA, USA) and 4GB RAM, and Windows 7 (64 bit, Microsoft Corporation, Redmond, WA, USA).

4. Simulation Studies and Discussions

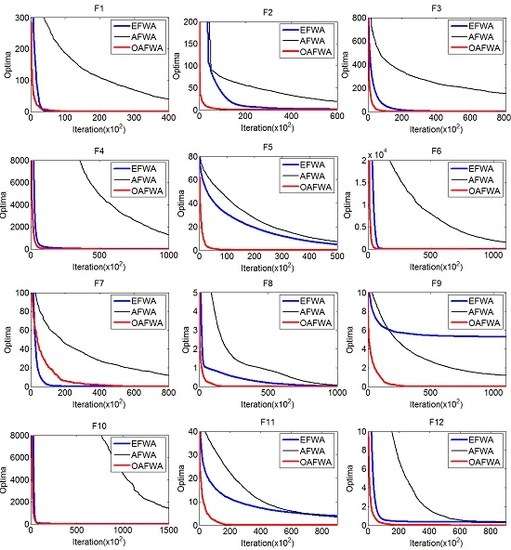
4.1. Comparison with FWA-Based Algorithms

To assess the performance of OAFWA, OAFWA is compared with AFWA, and then with FWA-based algorithms including EFWA and AFWA.

4.1.1. Comparison with AFWA

To compare the performances of OAFWA and AFWA, both algorithms were tested on twelve benchmark functions.

Table 2. Statistical results for OAFWA.

Func.	Best	Mean	Median	Worst	Std. Dev.	Time (s)
F1	<1 × 10−315	2.46 × 10−34	1.91 × 10−34	1.15 × 10−33	2.14 × 10−34	3.23
F2	<1 × 10−315	8.21 × 10−17	3.26 × 10−23	5.31 × 10−16	1.22 × 10−16	5.91
F3	<1 × 10−315	3.56 × 10−38	1.95 × 10−38	2.74 × 10−37	5.32 × 10−38	30.56
F4	<1 × 10−315	3.28 × 10−38	2.52 × 10−42	1.94 × 10−37	4.66 × 10−38	7.63
F5	<1 × 10−315	7.39 × 10−17	8.07 × 10−17	1.75 × 10−16	4.24 × 10−17	5.88
F6	<1 × 10−315	7.17 × 10−46	8.21 × 10−47	3.18 × 10−44	3.24 × 10−45	5.54
F7	<1 × 10−315	1.03 × 10−12	<1 × 10−315	1.02 × 10−10	1.02 × 10−11	4.62
F8	<1 × 10−315	<1 × 10−315	<1 × 10−315	<1 × 10−315	<1 × 10−315	8.73
F9	8.88 × 10−16	9.59 × 10−16	8.88 × 10−16	4.44 × 10−15	5.00 × 10−16	9.61
F10	<1 × 10−315	2.00 × 10−40	<1 × 10−315	2.15 × 10−39	4.11 × 10−40	23.63
F11	<1 × 10−315	5.27 × 10−17	5.32 × 10−17	1.06 × 10−16	2.71 × 10−17	5.84
F12	<1 × 10−315	1.32 × 10−33	1.15 × 10−33	5.11 × 10−33	1.00 × 10−33	7.40

shows the statistical results for OAFWA.

Table 3. Statistical results for AFWA.

Func.	Best	Mean	Median	Worst	Std. Dev.	Time (s)
F1	1.36 × 10−7	64.4	63.4	1.57 × 102	36.6	3.23
F2	1.25 × 10−3	1.07	2.43 × 10−1	38.9	3.95	5.59
F3	6.45 × 10	2.45 × 102	2.49 × 102	4.11 × 102	88.2	30.20
F4	4.42 × 103	1.48 × 104	1.42 × 104	2.54 × 104	4.84 × 103	7.50
F5	31.0	43.7	44.2	52.2	4.86	5.69
F6	1.06 × 104	2.19 × 104	2.19 × 104	3.18 × 104	3.69 × 103	5.38
F7	1.51 × 10−5	7.66	5.32	31.8	7.37	4.54
F8	2.20 × 10−10	3.88 × 10−1	9.86 × 10−3	4.68	7.42 × 10−1	8.28
F9	5.51 × 10−7	2.11	2.17	3.57	6.35 × 10−1	9.39
F10	7.40 × 102	6.75 × 103	6.28 × 103	2.29 × 104	4.43 × 103	23.35
F11	2.11 × 10−1	2.39	1.98	6.69	1.56	5.64
F12	2.00 × 10−1	5.58 × 10−1	5.00 × 10−1	1.10	1.85 × 10−1	7.17

shows the statistical results for AFWA.

Table 4. Comparison of OAFWA and AFWA for solution accuracy.

Func.	Best		Accuracy Improved	Mean		Accuracy Improved
	AFWA	OAFWA		AFWA	OAFWA
F1	1.36 × 10−7	<1 × 10−315	−308	64.4	2.46 × 10−34	−35
F2	1.25 × 10−3	<1 × 10−315	−312	1.07	8.21 × 10−17	−17
F3	64.5	<1 × 10−315	−316	2.45 × 102	3.56 × 10−38	−40
F4	4.42 × 103	<1 × 10−315	−318	1.48 × 104	3.28 × 10−38	−42
F5	31.0	<1 × 10−315	−316	43.7	7.39 × 10−17	−18
F6	1.06 × 104	<1 × 10−315	−319	2.19 × 104	7.17 × 10−46	−50
F7	1.51 × 10−5	<1 × 10−315	−310	7.66	1.03 × 10−12	−12
F8	2.20 × 10−10	<1 × 10−315	−305	3.88 × 10−1	<1 × 10−315	−314
F9	5.51 × 10−7	8.88 × 10−16	−9	2.11	9.59 × 10−16	−16
F10	7.40 × 102	<1 × 10−315	−317	6.75 × 103	2.00 × 10−40	−43
F11	2.11 × 10−1	<1 × 10−315	−314	2.39	5.27 × 10−17	−17
F12	2.00 × 10−1	<1 × 10−315	−314	5.58 × 10−1	1.32 × 10−33	−32
Average			−288			−53

shows the comparison of OAFWA and AFWA for solution accuracy from Table 2 and Table 3.

The statistical results from Table 2, Table 3 and Table 4 indicate that the accuracy of the best solution and the mean solution for OAFWA were improved by average values of 10⁻²⁸⁸ and 10⁻⁵³, respectively, as compared to AFWA. Thus, OAFWA can increase the performance of AFWA and achieve a significantly more accurate solution.

To evaluate whether the OAFWA results were significantly different from those of the AFWA, the OAFWA mean results during iteration for each benchmark function were compared with those of the AFWA. The Wilcoxon signed-rank test, which is a safe and robust, non-parametric test for pairwise statistical comparisons [28], was utilized at the 5% level to detect significant differences between these pairwise samples for each benchmark function.

The signrank function in Matlab 7.0 was used to run the Wilcoxon signed-rank test, as shown in

Table 5. Wilcoxon signed-rank test results for OAFWA and AFWA.

	F1	F2	F3	F4	F5	F6
H	1	1	1	1	1	1
P	4.14 × 10−108	3.33 × 10−165	<1 × 10−315	2.01 × 10−230	1.63 × 10−181	1.63 × 10−181
	F7	F8	F9	F10	F11	F12
H	1	1	1	1	1	1
P	1.39 × 10−132	8.13 × 10−198	1.01 × 10−246	<1 × 10−315	3.33 × 10−165	2.01 × 10−230

.

Here P is the p-value under test and H is the result of the hypothesis test. A value of H = 1 indicates the rejection of the null hypothesis at the 5% significance level.

Table 5 indicates that OAFWA showed a large improvement over AFWA.

4.1.2. Comparison with FWA-Based Algorithms

To compare performances of OAFWA, AFWA, and EFWA, EFWA was tested for twelve benchmark functions. Success rates and mean error ranks for three FWA based algorithms were obtained.

Table 6. Statistical results for EFWA.

Func.	Best	Mean	Median	Worst	Std. dev.	Time (s)
F1	1.66 × 10−3	2.63 × 10−3	2.63 × 10−3	3.44 × 10−3	3.83 × 10−4	4.34
F2	2.07 × 10−1	5.67 × 10−1	2.75 × 10−1	2.84	5.89 × 10−1	8.88
F3	7.52 × 10−3	1.44 × 10−2	1.40 × 10−2	2.77 × 10−2	3.67 × 10−3	42.54
F4	3.31 × 10−1	5.22 × 10−1	4.92 × 10−1	8.91 × 10−1	1.23 × 10−1	13.55
F5	1.62 × 10−1	7.01 × 10−1	2.18 × 10−1	9.26	1.47	9.22
F6	2.01 × 10−1	3.28 × 10−1	3.12 × 10−1	4.75 × 10−1	6.67 × 10−2	9.11
F7	3.22 × 10−3	5.04 × 10−3	5.07 × 10−3	6.87 × 10−3	6.73 × 10−4	6.46
F8	6.01 × 10−3	1.63 × 10−2	1.48 × 10−2	4.91 × 10−2	8.80 × 10−3	12.90
F9	2.39	5.05	5.08	8.51	1.20	16.82
F10	1.68 × 10−1	2.69 × 10−1	2.64 × 10−1	4.57 × 10−1	5.86 × 10−2	37.31
F11	9.73 × 10−1	4.14	3.80	13.6	2.16	8.98
F12	2.00 × 10−1	3.15 × 10−1	3.00 × 10−1	4.00 × 10−1	5.39 × 10−2	13.46

shows the statistical results for EFWA.

Table 7. Success rates and mean error ranks for three FWA-based algorithms.

Func.	EFWA			AFWA			OAFWA
	Mean Error	Sr	Rank	Mean Error	Sr	Rank	Mean Error	Sr	Rank
F1	2.63 × 10−3	2	2	64.4	1	3	2.46 × 10−34	100	1
F2	5.67 × 10−1	2	2	1.07	31	3	8.21 × 10−17	100	1
F3	1.44 × 10−2	0	2	2.45 × 102	6	3	3.56 × 10−38	100	1
F4	5.22 × 10−1	0	2	1.48 × 104	0	3	3.28 × 10−38	100	1
F5	7.01 × 10−1	0	2	43.7	0	3	7.39 × 10−17	100	1
F6	3.28 × 10−1	0	2	2.19 × 104	0	3	7.17 × 10−46	100	1
F7	5.04 × 10−3	100	2	7.66	0	3	1.03 × 10−12	100	1
F8	1.63 × 10−2	0	2	3.88 × 10−1	0	3	<1 × 10−315	100	1
F9	5.05	0	3	2.11	0	2	9.59 × 10−16	100	1
F10	2.69 × 10−1	0	2	6.75 × 103	0	3	2.00 × 10−40	100	1
F11	4.14	0	3	2.39	0	2	5.27 × 10−17	100	1
F12	3.15 × 10−1	0	2	5.58 × 10−1	0	3	1.32 × 10−33	100	1
Average		8.7	2.17		3.2	2.83		100	1

compares three FWA-based algorithms.

The results from Table 6 and Table 7 indicate that the mean error of AFWA is larger than that of EFWA. The Sr of AFWA is lower that of EFWA. Thus, AFWA is not better than EFWA; The Sr of OAFWA is the highest and OAFWA ranks the highest among three FWA algorithms. Thus, OAFWA greatly improved the performance of AFWA.

For the runtimes of EFWA, AFWA and OAFWA, Table 2 and Table 3 indicate that the time cost of OAFWA is not much different from that of AFWA. But Table 2 and Table 6 indicate the time cost of OAFWA drops significantly as compared with that of EFWA.

Figure 2 shows searching curves for EFWA, AFWA, and OAFWA.

Figure 2 shows that OAFWA results in a global optimum for all twelve functions and with fast convergence. However, the alternative EFWA methods do not always locate the global optimum solutions. These include EFWA for F9 and F11. AFWA is the worst among the three algorithms. It is bad for a majority of functions. Thus, OAFWA is the best one in terms of solution accuracy.

4.2. Comparison with Other Swarm Intelligence Algorithms

Additionally, OAFWA was compared with alternative swarm intelligent algorithms, including BA, DE, self-adapting control parameters in differential evolution (jDE) [29], FA, and SPSO2011 [30]. The resulting evaluation times (iteration) and population size are the same for each function. Two cases of population size are tested, 20 and 40, respectively. The parameters are shown in

Table 8. Parameters of the algorithms.

Algorithms	Parameters
BA	A = 0.95, r = 0.8, fmin = 0, f = 1.0
DE	F = 0.5, CR = 0.9
jDE	${\tau }_1 = {\tau }_2$ = 0.1, F $\in$ [0.1, 1.0], CR $\in$ [0, 1]
FA	$\mathsf{\alpha }$ = 0.9, $\beta$ = 0.25, $\gamma$ = 1.0
SPSO2011	w = 0.7213, c1 = 1.1931, c2 = 1.1931

.

How to tune the parameters of the above algorithms is a challenging issue. These parameters are obtained from the literature [31] for BA, [29] for DE and jDE, and [30] for SPSO2011. For FA, reducing randomness increases the convergence. ${\mathsf{\alpha }}^{\mathrm{t}+1}=\left(1-\mathsf{\delta }\right)a^{\mathrm{t}}$ [32] is employed to gradually decrease $\mathsf{\alpha }$. $\mathsf{\delta }$ is a small constant related to iteration.

For OAFWA, m = 2, $\widehat{\mathrm{A}}$ = 100, M_e = 20, $S_{\text{min}}$ = 3, $S_{\text{max}}$ = 6, NG = 1 (population size is equivalent to 20), and J_r = 0.4.

Table 9. Mean errors for the six algorithms when popSize = 20.

Func.	BA	DE	jDE	FA	SPSO2011	OAFWA	Iteration
F1	3.27 × 10−3	11.7	3.67 × 10−35	6.45 × 10−7	8.15 × 10−23	6.75 × 10−23	65,000
F2	30.4	3.37	3.49 × 10−35	4.37 × 10−2	6.27	2.02 × 10−16	100,000
F3	2.10 × 10−2	7.70	5.42 × 10−4	34.8	3.70 × 10−6	1.19 × 10−38	190,000
F4	1.53 × 10−1	2.27 × 103	5.48 × 10−76	1.19 × 10−3	8.57 × 10−4	2.26 × 10−38	140,000
F5	32.3	40.5	27.1	2.28 × 10−2	12.8	2.22 × 10−17	110,000
F6	1.23 × 105	3.80 × 103	2.54 × 10−58	7.37 × 10−5	9.85 × 103	3.56 × 10−42	110,000
F7	18.9	34.3	12.8	19.8	48.5	<1 × 10−315	80,000
F8	1.22	1.07	9.30 × 10−3	1.78 × 10−3	8.13 × 10−3	2.41 × 10−16	120,000
F9	6.64	4.48	5.29 × 10−2	3.82 × 10−4	2.71	3.40 × 10−12	150,000
F10	4.82 × 10−1	5.21 × 103	2.06 × 10−45	1.69 × 10−2	3.23 × 10−3	1.17 × 10−40	200,000
F11	4.85	6.58 × 10−1	5.66 × 10−16	8.21 × 10−1	3.45	3.03 × 10−17	100,000
F12	16.7	2.41	1.92 × 10−1	2.58 × 10−1	1.92 × 10−1	6.38 × 10−34	140,000

and

Table 10. Mean errors for the six algorithms when popSize = 40.

Func.	BA	DE	jDE	FA	SPSO2011	OAFWA	Iteration
F1	3.22 × 10−3	7.77 × 10−10	3.27 × 10−17	2.02 × 10−5	4.16 × 10−31	2.46 × 10−34	65,000
F2	7.15	1.28 × 10−15	1.60 × 10−15	1.51 × 10−1	3.06	8.21 × 10−17	100,000
F3	2.03 × 10−2	3.83 × 10−5	7.91 × 10−2	40.2	3.25 × 10−8	3.56 × 10−38	190,000
F4	1.23 × 10−1	5.12 × 10−22	1.38 × 10−37	1.29 × 10−1	5.77 × 10−6	3.28 × 10−38	140,000
F5	25.1	23.9	7.27	9.04 × 10−2	5.99	7.39E × 10−17	110,000
F6	8.05 × 104	2.21 × 10−6	2.07 × 10−28	2.26 × 10−3	3.56 × 103	7.17E × 10−46	110,000
F7	19.2	26.9	8.08	18.4	49.1	1.03 × 10−12	80,000
F8	5.25 × 10−1	8.39 × 10−3	2.46 × 10−4	1.52 × 10−3	5.22 × 10−3	<1 × 10−315	120,000
F9	5.53	5.39 × 10−1	7.99 × 10−15	3.16 × 10−2	1.54	9.59 × 10−16	150,000
F10	4.62 × 10−1	2.85 × 10−6	1.20 × 10−30	8.71 × 10−2	1.41 × 10−3	2.00 × 10−40	200,000
F11	3.78	2.56 × 10−15	1.01 × 10−3	9.77 × 10−1	2.17 × 10−1	5.27 × 10−17	100,000
F12	11.1	1.59 × 10−1	9.99 × 10−2	2.28 × 10−1	1.11 × 10−1	1.32 × 10−33	140,000

present the mean errors for the six algorithms when population sizes are 20 and 40, respectively.

Table 9 and Table 10 indicate that certain algorithms perform well for some functions, but less well for others. Overall, OAFWA performance was shown to have more stability than the other algorithms.

Figure 3 and Figure 4 present the runtime cost of the six algorithms for twelve functions when population sizes are 20 and 40, respectively.

Figure 3 shows that the runtime cost of DE is the most expensive among the six algorithms, except for F7, F8, F10, and F12. Figure 4 shows that the runtime cost of SPSO2011 is the most expensive among the six algorithms. The time cost of OAFWA is the least.

Table 11. Ranks for the six algorithms when popSize = 20.

Func.	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	Rank
BA	5	6	4	5	5	6	3	6	6	5	6	5	5.17
DE	6	4	5	6	6	4	5	5	5	6	3	4	4.92
jDE	1	1	3	1	4	1	2	4	3	1	2	2	2.08
FA	4	3	6	4	2	3	4	2	2	4	4	3	3.41
SPSO2011	3	5	2	3	3	5	6	3	4	3	5	2	3.67
OAFWA	2	2	1	2	1	2	1	1	1	2	1	1	1.42

and

Table 12. Ranks for the six algorithms when popSize = 40.

Func.	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	Rank
BA	6	6	4	5	5	6	4	6	6	6	6	6	5.50
DE	4	2	3	3	6	3	5	5	4	3	2	4	3.67
jDE	3	3	5	2	4	2	2	2	2	2	3	2	2.67
FA	5	4	6	6	2	4	3	3	3	5	5	5	4.25
SPSO2011	2	5	2	4	3	5	6	4	5	4	4	3	3.91
OAFWA	1	1	1	1	1	1	1	1	1	1	1	1	1.00

present the ranks of the six algorithms for twelve benchmark functions when population sizes are 20 and 40, respectively.

Table 11 and Table 12 indicate that the OAFWA ranks the best (1.42 and 1.00) out of the six algorithms.

5. Conclusions

OAFWA was developed by applying OBL to AFWA. Twelve benchmark functions were investigated for OAFWA. Results indicated a large boost in performance in OAFWA over AFWA when using OBL. The accuracy of the best solution and the mean solution for OAFWA were improved significantly when compared to AFWA.

The experiments clearly indicate that OAFWA can perform significantly better than EFWA and AFWA in terms of solution accuracy. Additionally, OAFWA is compared with BA, DE, jDE, FA and SPSO2011. Overall, the research demonstrates that OAFWA performed the best for both solution accuracy and runtime cost.