Development of Nonlinear Parsimonious Forest Models Using Efficient Expansion of the Taylor Series: Applications to Site Productivity and Taper
Abstract
:1. Introduction
2. Methods
2.1. Foundation
- Sine, , for which and
- Cosine, for which α = −(1 + ξ)/σ and β = (1 − ξ)/σ
- Tangent, . for which α = −ξ/σ and β = (1 − ξ)/σ
- Arcsine or inverse of sine, . for which α = −(π/2 + ξ)/σ and β = (π/2 − ξ)/σ
- Arccosine or inverse of cosine, , for which α = −ξ/σ and β = (π − ξ)/σ
- Arctangent or inverse of tangent, . for which Bn is the nth Bernoulli number that is computed with the recurrence formula and B0 = 1.
- hyperbolic sine, , for which α = −ξ/σ and β = (1 − ξ)/σ
- hyperbolic tangent, , for which α = −ξ/σ and β = (1 − ξ)/σ
- n, k are natural numbers;
- is the combination of n taken k;
- and is the products of the even, or uneven, respectively, numbers less than, including, , or , respectively;
2.2. Modeling Site Productivity for Norway Spruce (Picea abies L) in Carpathian Mountains
- height dominant is the height of dominant trees;
- t Lorey height is transformed Lorey’s height modeled with the expression ;
- SI is site index; and,
- a0, a1, a2, b0, b1, b2 are parameters determined by species.
2.3. Taper Equations for Loblolly Pine (Pinus taeda L.) in East Louisiana
2.4. Models Assessment
- is the predicted value at age/diameter/time i,
- is the measured value at age/height/time i, and
- n is the number of observations.
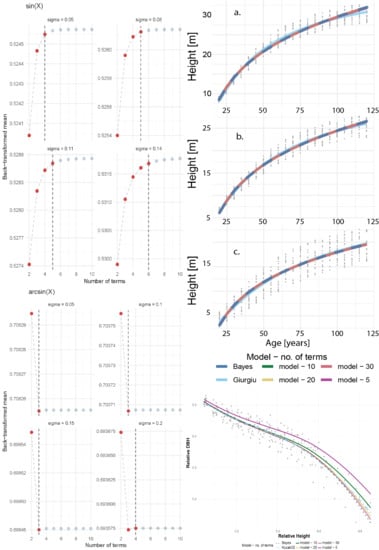
3. Results
3.1. Foundation
3.2. Site Index Models for Norway Spruce
3.3. Taper Models for Loblolly Pine
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tajiki, M.; Schoups, G.; Hendricks Franssen, H.J.; Najafinejad, A.; Bahremand, A. Recursive Bayesian Estimation of Conceptual Rainfall-Runoff Model Errors in Real-Time Prediction of Streamflow. Water Resour. Res. 2020, 56, e2019WR025237. [Google Scholar] [CrossRef]
- Kansanen, K.; Vauhkonen, J.; Lähivaara, T.; Seppänen, A.; Maltamo, M.; Mehtätalo, L. Estimating forest stand density and structure using Bayesian individual tree detection, stochastic geometry, and distribution matching. ISPRS J. Photogramm. Remote. Sens. 2019, 152, 66–78. [Google Scholar] [CrossRef]
- Monnahan, C.C.; Thorson, J.T.; Branch, T.A. Faster estimation of Bayesian models in ecology using Hamiltonian Monte Carlo. Methods Ecol. Evol. 2017, 8, 339–348. [Google Scholar] [CrossRef]
- van Oijen, M. Bayesian Methods for Quantifying and Reducing Uncertainty and Error in Forest Models. Curr. For. Rep. 2017, 3, 269–280. [Google Scholar] [CrossRef] [Green Version]
- Vieilledent, G.; Courbaud, B.; Kunstler, G.; Dhôte, J.-F.; Clark, J. Individual variability in tree allometry determines light resource allocation in forest ecosystems: A hierarchical Bayesian approach. Oecologia 2010, 163, 759–773. [Google Scholar] [CrossRef] [PubMed]
- Balcombe, K.; Rapsomanikis, G. Bayesian Estimation and Selection of Nonlinear Vector Error Correction Models: The Case of the Sugar-Ethanol-Oil Nexus in Brazil. Am. J. Agric. Econ. 2008, 90, 658–668. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, S.; Zhao, F.; Tian, L.; Zhao, Z. Comparison of machine learning algorithms for forest parameter estimations and application for forest quality assessments. For. Ecol. Manag. 2019, 434, 224–234. [Google Scholar] [CrossRef]
- Diamantopoulou, M.J.; Özçelik, R.; Yavuz, H. Tree-bark volume prediction via machine learning: A case study based on black alder’s tree-bark production. Comput. Electron. Agric. 2018, 151, 431–440. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [Green Version]
- Carreiras, J.M.B.; Pereira, J.M.C.; Shimabukuro, Y.E. Land-cover mapping in the Brazilian Amazon using SPOT-4 vegetation data and machine learning classification methods. Photogramm. Eng. Remote. Sens. 2006, 72, 897–910. [Google Scholar] [CrossRef] [Green Version]
- Guan, B.T.; Gertner, G. Machine Learning and Its Possible Roles in Forest Science. Ai Appl. 1991, 5, 27–36. [Google Scholar]
- Marchi, M. Nonlinear versus linearised model on stand density model fitting and stand density index calculation: Analysis of coefficients estimation via simulation. J. For. Res. 2019, 30, 1595–1602. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.E.; Bartling, P.N.S. Comparison of linear and nonlinear overstory-understory models for ponderosa pine. For. Ecol. Manag. 1991, 42, 195–204. [Google Scholar] [CrossRef]
- Warton, D.I.; Hui, F.K.C. The arcsine is asinine: The analysis of proportions in ecology. Ecology 2011, 92, 3–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Williams, C.B. The use of logarithms in the interpretation of certain entomological problems. Ann. Appl. Boil. 1937, 24, 404–414. [Google Scholar] [CrossRef]
- Cochran, W.G. Some difficulties in the statistical analysis of replicated experiments. Emp. J. Exp. Agric. 1938, 157, 157–175. [Google Scholar]
- Finney, D.J. On the distribution of a variate whose logarithm is normally distributed. Suppl. J. R. Stat. Soc. 1941, 7, 155–161. [Google Scholar] [CrossRef]
- Giurgiu, V. Dendrometrie si Auxologie Forestiera; Ceres: Bucharest, Romania, 1979; pp. 1–853. [Google Scholar]
- Neyman, J.; Scott, E.L. Correction for Bias Introduced by a Transformation of Variables. Ann. Math. Stat. 1960, 643–655. [Google Scholar] [CrossRef]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. J. R. Stat. Soc. Ser. A (General) 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; p. 624. [Google Scholar]
- Hoos, H.; Stutzle, T. Stochastic Local Search; Morgan Kaufmann Publishers: New York, NY, USA, 2005; pp. 1–658. [Google Scholar]
- Pujol, J. The solution of nonlinear inverse problems and the Levenberg-Marquardt method. Geophysics 2007, 72, W1–W16. [Google Scholar] [CrossRef]
- Chen, J.; Kemna, A.; Hubbard, S.S. A comparison between Gauss-Newton and Markov-chain Monte Carlo–based methods for inverting spectral induced-polarization data for Cole-Cole parameters. GEOPHYSICS 2008, 73, F247–F259. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.-X. Recent advances in trust region algorithms. Math. Program. 2015, 151, 249–281. [Google Scholar] [CrossRef]
- Bettinger, P.; Graetz, D.; Boston, K.; Sessions, J.; Chung, W.D. Eight heuristic planning techniques applied to three increasingly difficult wildlife planning problems. Silva Fenn. 2002, 36, 561–584. [Google Scholar] [CrossRef] [Green Version]
- Korzukhin, M.D.; TerMikaelian, M.T.; Wagner, R.G. Process versus empirical models: Which approach for forest ecosystem management? Can. J. For. Res. 1996, 26, 879–887. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, 2nd ed.; Chapman and Hall: Boca Raton, FL, USA, 2003; p. 690. [Google Scholar]
- Strimbu, B.M.; Amarioarei, A.; Paun, M. A parsimonious approach for modeling uncertainty within complex nonlinear relationships. Ecosphere 2017, 8, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Shanks, M.E.; Gambill, R. Calculus; Holt, Rinehart and Winston, Inc.: New York, NY, USA, 1973; pp. 1–748. [Google Scholar]
- Nourani, Y.; Andresen, B. A comparison of simulated annealing cooling strategies. J. Phys. A: Math. Gen. 1998, 31, 8373–8385. [Google Scholar] [CrossRef]
- Wah, B.W.; Wang, T.; Jaffar, J. Simulated Annealing with Asymptotic Convergence for Nonlinear Constrained Global Optimization. In Principles and Practice of Constraint Programming; Springer: Heidelberg, Germany, 1999; pp. 461–475. [Google Scholar]
- Zomaya, A.Y.; Kazman, R.; Atallah, M.J. Simulated Annealing Techniques. In Handbook on Algorithms and Theory of Computation; CRC Press: Boca Raton, FL, USA, 1999; pp. 37-19–37-31. [Google Scholar]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems; SIAM: Philadelphia, PA, USA, 2007; p. 328. [Google Scholar]
- Zhu, M.; Ghodsi, A. Automatic dimensionality selection from the scree plot via the use of profile likelihood. Comput. Stat. Data Anal. 2006, 51, 918–930. [Google Scholar] [CrossRef]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics; Allyn and Bacon: Boston, MA, USA, 2001; pp. 1–966. [Google Scholar]
- Cattell, R.B. Scree Test for Number of Factors. Multivar. Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef]
- Rencher, A.C. Methods of Multivariate Analysis; John Wiley and Sons: New York, NY, USA, 2002; p. 708. [Google Scholar]
- Popescu-Zeletin, I. Tabele Dendrometrice; Editura Agrosilvica de Stat: Bucharest, Romania, 1957; p. 1320. [Google Scholar]
- Giurgiu, V.; Draghiciu, D. Modele Matematico-Auxologice şi Tabele de Producţie Pentru Arborete; Ceres: Bucharest, Romania, 2004; p. 607. [Google Scholar]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models; WCB McGraw-Hill: Boston, MA, USA, 1996; pp. 1–1408. [Google Scholar]
- Alder, A. Forest Volume Estimation and Yield Prediction; Food and Agriculture Organization: Rome, IT, USA, 1980; p. 196. [Google Scholar]
- Golivets, M.; Woodall, C.W.; Wallin, K.F. Functional form and interactions of the drivers of understory non-native plant invasions in northern US forests. J. Appl. Ecol. 2019, 56, 2596–2608. [Google Scholar] [CrossRef]
- Stow, C.A.; Reckhow, K.H.; Qian, S.S. A Bayesian approach to retransformation bias in transformed regression. Ecology 2006, 87, 1472–1477. [Google Scholar] [CrossRef]
- The Stan Development Team. Stan Modeling Language: User’s Guide and Reference Manual, 2.22. 2016. Available online: https://mc-stan.org/docs/2_22/stan-users-guide/index.html (accessed on 10 March 2018).
- Gentleman, R.; Ihaka, R. R-project, 3.5.1; Comprehensive R Archive Network: Aukland, NZ, USA, 2018. [Google Scholar]
- Stan Development Team. Rstan: The R interface to Stan, R package version 2.14.1; 2016. Available online: https://mc-stan.org/users/interfaces/ (accessed on 10 March 2018).
- McClure, J.P.; Czaplewski, R.L. Compatible taper equation for loblolly pine. Can. J. For. Res. 1986, 16, 1272–1277. [Google Scholar] [CrossRef]
- Cao, Q.V.; Burkhart, H.E.; Max, T.A. Evaluation of 2 Methods for Cubic-Volume Prediction of Loblolly-Pine to Any Merchantable Limit. For. Sci. 1980, 26, 71–80. [Google Scholar]
- Max, T.A.; Burkhart, H.E. Segmented polynomial regression applied to taper equations. For. Sci. 1976, 22, 283–289. [Google Scholar]
- Lenhart, J.D.; Hackett, T.L.; Laman, C.J.; Wiswell, T.J.; Blackard, J.A. Tree Content and Taper Functions for Loblolly and Slash Pine Trees Planted on Non-Old-Fields in East Texas. South. J. Appl. For. 1987, 11, 147–151. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Strimbu, B. Stem Measurements and Taper Modeling Using Photogrammetric Point Clouds. Remote Sen. 2017, 9, 716. [Google Scholar] [CrossRef] [Green Version]
- Kozak, A. My last words on taper equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Stängle, S.M.; Sauter, U.H.; Dormann, C.F. Comparison of models for estimating bark thickness of Picea abies in southwest Germany: The role of tree, stand, and environmental factors. Ann. For. Sci. 2017, 74, 16. [Google Scholar] [CrossRef] [Green Version]
- Montealegre, A.; Lamelas, M.; Riva, J. Interpolation Routines Assessment in ALS-Derived Digital Elevation Models for Forestry Applications. Remote. Sens. 2015, 7, 8631–8654. [Google Scholar] [CrossRef] [Green Version]
- Bilskie, M.V.; Hagen, S.C. Topographic accuracy assessment of bare earth lidar-derived unstructured meshes. Adv. Water Resour. 2013, 52, 165–177. [Google Scholar] [CrossRef]
- SAS Institute SAS, 9.4; SAS Institute: Cary, NC, USA, 2017.
- Fox, J. Applied Regression Analysis and Generalized Linear Models, 2nd ed.; SAGE Publications: Thousand Oaks, CA, USA, 2008; p. 688. [Google Scholar]
- LeMay, V. Comments on "Modeling in the Age of Big-Data and AI: The Loss of Beauty". In Proceedings of the 2018 Western Mensurationist Annual Meeting, Flagstaff, AZ, USA, 18 June 2017. [Google Scholar]
- Ministerul Silviculturii. Norme 5 Pentru Amenajarea Padurilor; ICAS Lithography: Bucharest, Romania, 1986; pp. 1–197. [Google Scholar]
- Robertson, F.D. Timber Cruising Handbook; USDA Forest Service: Washington, DC, USA, 2000; p. 268. [Google Scholar]
- Wallace, T.; Chandler, R.; Curtis, D.; Foster, A.; de Brauwere, J.; King, C.; Drakes, K.J.; Korn, B. Timber Cruise-Timber Appraisal Standards; Department of Agriculture and Department of Environmental Protection: Tallahassee, FL, USA, 2004; p. 47.
- Brewer, J.; Talbot, B.; Belbo, H.; Ackerman, P.; Ackerman, S. A comparison of two methods of data collection for modelling productivity of harvesters: Manual time study and follow-up study using on-board-computer stem records. Ann. For. Res. 2018, 61, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Narine, L.L.; Popescu, S.; Zhou, T.; Srinivasan, S.; Harbeck, K. Mapping forest aboveground biomass with a simulated ICESat-2 vegetation canopy product and Landsat data. Ann. For. Res. 2019, 62, 69–86. [Google Scholar] [CrossRef]
- Marinello, F.; Rosario Proto, A.; Zimbalatti, G.; Pezzuolo, A.; Cavalli, R.; Grigolato, S. Determination of forest road surface roughness by Kinect depth imaging. Ann. For. Res. 2017, 60, 217–226. [Google Scholar] [CrossRef]










| Transformation | Mean | Variance | Expectation | Number of Terms | |
|---|---|---|---|---|---|
| Scree Plot | Preset Value | ||||
| Sine | 0.5 | 0.05 | 0.525 | 4 | 4 |
| 0.08 | 0.526 | 4 | 4 | ||
| 0.11 | 0.528 | 4 | 5 | ||
| 0.14 | 0.532 | 4 | 6 | ||
| Cosine | 0.5 | 0.05 | 1.045 | 4 | 4 |
| 0.08 | 1.042 | 4 | 4 | ||
| 0.11 | 1.042 | 4 | 5 | ||
| 0.14 | 1.039 | 5 | 6 | ||
| Tangent | 0.5 | 0.05 | 0.463 | 3 | 5 |
| 0.08 | 0.462 | 3 | 6 | ||
| 0.11 | 0.460 | 3 | 7 | ||
| 0.14 | 0.457 | 3 | 9 | ||
| Arcsine | π/4 | π/64 | 0.706 | 3 | 3 |
| π/32 | 0.704 | 3 | 3 | ||
| 3π/64 | 0.699 | 3 | 3 | ||
| π/16 | 0.694 | 3 | 4 | ||
| Arccosine | π/4 | π/64 | 0.706 | 3 | 3 |
| π/32 | 0.704 | 3 | 3 | ||
| 3π/64 | 0.699 | 3 | 3 | ||
| π/16 | 0.694 | 3 | 4 | ||
| Arctangent | π/8 | π/128 | 0.414 | 3 | 4 |
| π/64 | 0.415 | 3 | 5 | ||
| 3π/128 | 0.417 | 3 | 5 | ||
| π/32 | 0.419 | 3 | 5 | ||
| Hyperbolic sine | 0.5 | 0.05 | 0.481 | 3 | 4 |
| 0.08 | 0.480 | 3 | 5 | ||
| 0.11 | 0.479 | 3 | 5 | ||
| 0.14 | 0.478 | 3 | 6 | ||
| Hyperbolic tangent | 0.5 | 0.05 | 0.552 | 4 | 5 |
| 0.08 | 0.555 | 4 | 6 | ||
| 0.11 | 0.561 | 5 | 7 | ||
| 0.14 | 0.569 | 6 | 9 | ||
| Site Index Class | Model | Bias (%) | MAE (%) | RMSE (%) | Correlation Coefficient |
|---|---|---|---|---|---|
| IV (21.9 m) | Giurgiu-Draghiciu | −2.2 | 13.1 | 15.8 | 0.923 |
| Bayesian | −2.2 | 14.4 | 18.1 | 0.917 | |
| Parsimonious 10 terms | −2.2 | 14.4 | 18.1 | 0.917 | |
| Parsimonious 30 terms | −2.2 | 14.4 | 18.1 | 0.917 | |
| III (26.9 m) | Giurgiu-Draghiciu | −0.4 | 5.7 | 6.8 | 0.976 |
| Bayesian | −0.4 | 6.0 | 7.3 | 0.975 | |
| Parsimonious 10 terms | −0.4 | 6.0 | 7.3 | 0.975 | |
| Parsimonious 30 terms | −0.4 | 6.0 | 7.3 | 0.975 | |
| II (31.8 m) | Giurgiu-Draghiciu | −0.3 | 4.8 | 5.9 | 0.981 |
| Bayesian | −4.5 | 5.0 | 6.0 | 0.977 | |
| Parsimonious 10 terms | −4.5 | 5.0 | 6.0 | 0.978 | |
| Parsimonious 30 terms | −4.5 | 5.0 | 6.0 | 0.978 |
| Measure | Parsimonious Model | Kozak– Model 02 | Bayesian Model | |
|---|---|---|---|---|
| 10-Terms | 30-Terms | |||
| Correlation coefficient | 0.961 | 0.964 | 0.980 | 0.960 |
| Bias (%) | −1.9 | −0.05 | −0.18 | 0.16 |
| MAE (%) | 5.0 | 4.4 | 3.2 | 4.5 |
| RMSE (%) | 8.4 | 7.8 | 3.8 | 8.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amarioarei, A.; Paun, M.; Strimbu, B. Development of Nonlinear Parsimonious Forest Models Using Efficient Expansion of the Taylor Series: Applications to Site Productivity and Taper. Forests 2020, 11, 458. https://doi.org/10.3390/f11040458
Amarioarei A, Paun M, Strimbu B. Development of Nonlinear Parsimonious Forest Models Using Efficient Expansion of the Taylor Series: Applications to Site Productivity and Taper. Forests. 2020; 11(4):458. https://doi.org/10.3390/f11040458
Chicago/Turabian StyleAmarioarei, Alexandru, Mihaela Paun, and Bogdan Strimbu. 2020. "Development of Nonlinear Parsimonious Forest Models Using Efficient Expansion of the Taylor Series: Applications to Site Productivity and Taper" Forests 11, no. 4: 458. https://doi.org/10.3390/f11040458