Interconnections Accelerate Collapse in a Socio-Ecological Metapopulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Two-Patch Model
2.2. Ten-Patch Model
2.3. Baseline Parameter Values
3. Results
3.1. Baseline Scenario
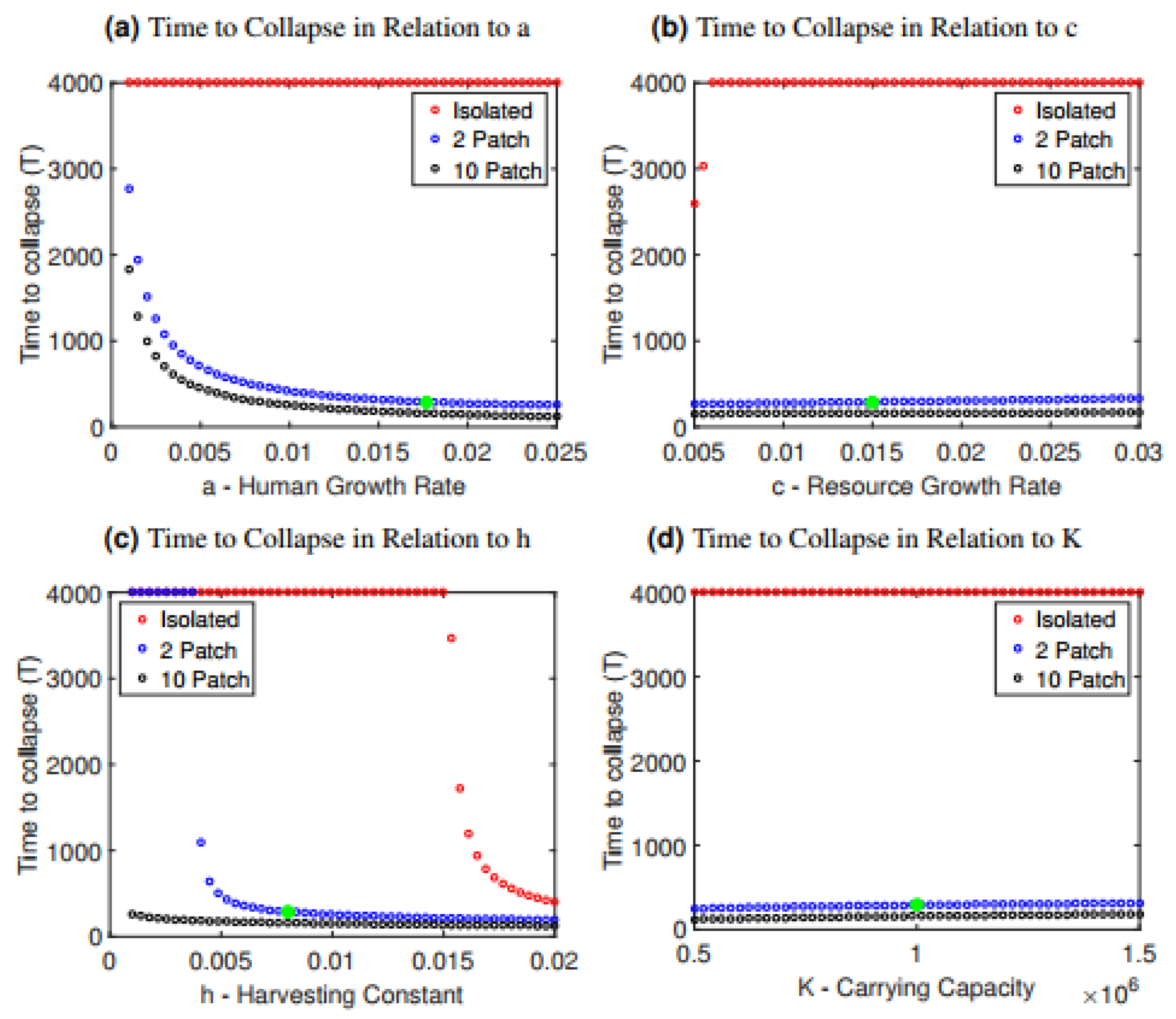
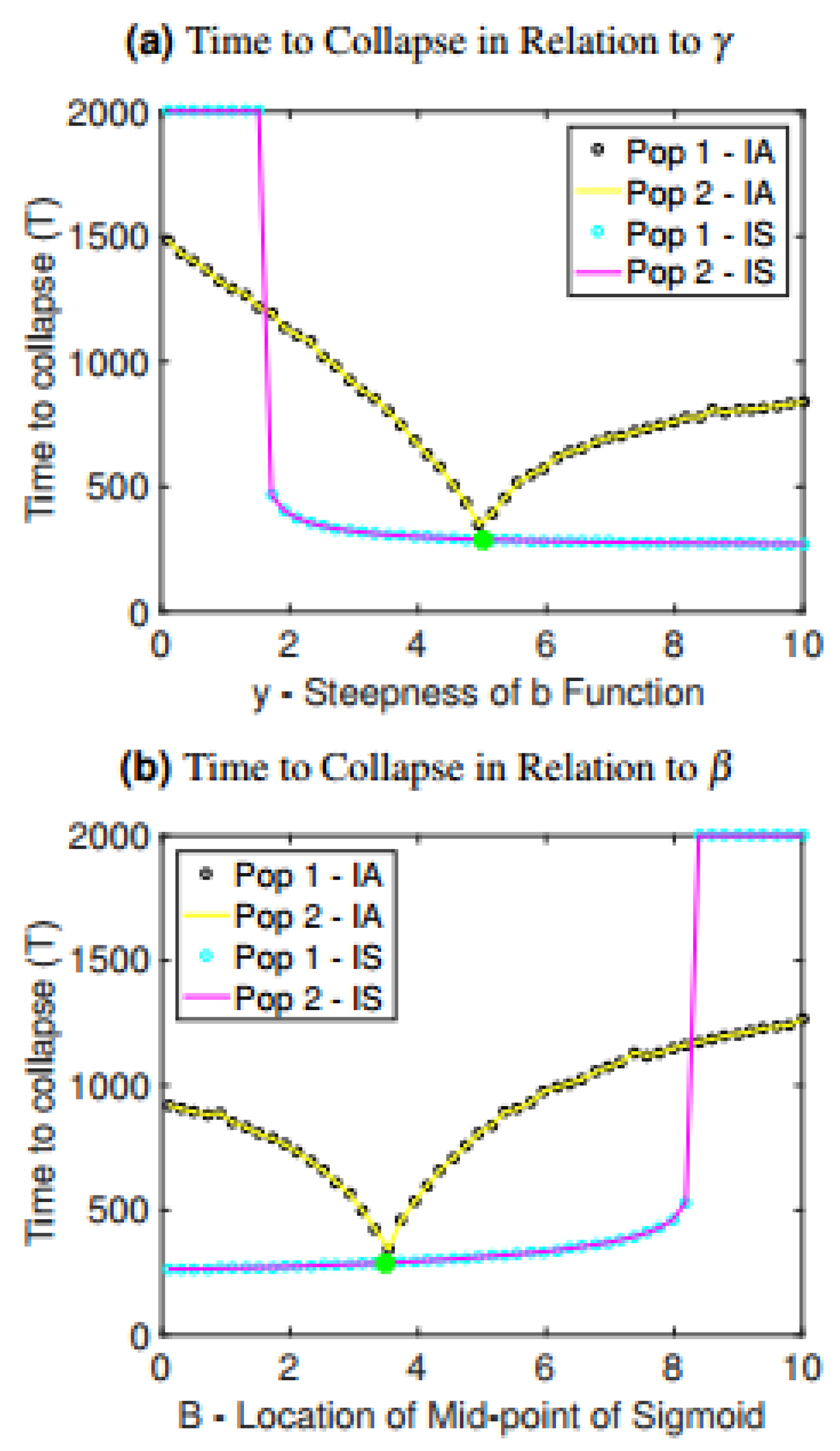
3.2. Time to Collapse
3.3. Parameter Planes
3.4. Impact of Inequality
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Verhulst, P.F. Notice sur la loi que la population suit dans son accroissement. correspondance mathématique et physique publiée par a. Quetelet 1838, 10, 113–121. [Google Scholar]
- Pearl, R.; Slobodkin, L. The Growth of Populations. Q. Rev. Biol. 1976, 51, 6–24. [Google Scholar] [CrossRef]
- Gamito, S. Growth models and their use in ecological modelling: An application to a fish population. Ecol. Model. 1998, 113, 83–94. [Google Scholar] [CrossRef]
- Hanson, F.B.; Tuckwell, H.C. Logistic growth with random density independent disasters. Theor. Popul. Biol. 1981, 19, 1–18. [Google Scholar] [CrossRef]
- Noy-Meir, I. Stability of grazing systems: An application of predator-prey graphs. J. Ecol. 1975, 63, 459–481. [Google Scholar] [CrossRef]
- Rosenzweig, M.L.; MacArthur, R.H. Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 1963, 97, 209–223. [Google Scholar]
- Holt, R.D. Food webs in space: On the interplay of dynamic instability and spatial processes. Ecol. Res. 2002, 17, 261–273. [Google Scholar]
- Hanski, I. Metapopulation dynamics. Nature 1998, 396, 41. [Google Scholar] [CrossRef]
- Nee, S.; Hassell, M.P.; May, R.M. Two-species metapopulation models. In Metapopulation Biology; Elsevier: Amsterdam, The Netherlands, 1997; pp. 123–147. [Google Scholar]
- Hanski, I. Metapopulation ecology; Oxford University Press Inc.: Oxford, UK, 1999; pp. 2–3. [Google Scholar]
- Hanski, I. Spatially realistic theory of metapopulation ecology. Naturwissenschaften 2001, 88, 372–381. [Google Scholar] [CrossRef]
- Tilman, D.; May, R.M.; Lehman, C.L.; Nowak, M.A. Habitat destruction and the extinction debt. Nature 1994, 371, 65–66. [Google Scholar] [CrossRef]
- Brown, J.H.; Kodric-Brown, A. Turnover rates in insular biogeography: Effect of immigration on extinction. Ecology 1977, 58, 445–449. [Google Scholar] [CrossRef]
- Earn, D.J.; Rohani, P.; Grenfell, B.T. Persistence, chaos and synchrony in ecology and epidemiology. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 7–10. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, A.; Elías-Wolff, F.; Mehlig, B.; Manica, A. The emergence of the rescue effect from explicit within-and between-patch dynamics in a metapopulation. Proc. R. Soc. B 2014, 281, 20133127. [Google Scholar] [CrossRef] [PubMed]
- Metcalf, C.; Munayco, C.; Chowell, G.; Grenfell, B.; Bjørnstad, O. Rubella metapopulation dynamics and importance of spatial coupling to the risk of congenital rubella syndrome in Peru. J. R. Soc. Interface 2010, 8, 369–876. [Google Scholar] [CrossRef] [PubMed]
- Gilarranz, L.J.; Bascompte, J. Spatial network structure and metapopulation persistence. J. Theor. Biol. 2012, 297, 11–16. [Google Scholar] [CrossRef] [PubMed]
- Dolrenry, S.; Stenglein, J.; Hazzah, L.; Lutz, R.S.; Frank, L. A metapopulation approach to African lion (Panthera leo) conservation. PLoS ONE 2014, 9, e88081. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, A.L.; May, R.M. Spatial heterogeneity in epidemic models. J. Theor. Biol. 1996, 179, 1–11. [Google Scholar] [CrossRef]
- Moses, M.E.; Brown, J.H. Allometry of human fertility and energy use. Ecol. Lett. 2003, 6, 295–300. [Google Scholar] [CrossRef]
- Bauch, C.T. Wealth as a source of density dependence in human population growth. Oikos 2008, 117, 1824–1832. [Google Scholar] [CrossRef]
- Burger, O.; DeLong, J.P.; Hamilton, M.J. Industrial energy use and the human life history. Sci. Rep. 2011, 1, 56. [Google Scholar] [CrossRef]
- Malthus, T.R. An Essay on the Principle of Population: Or, a View of Its Past and Present Effects on Human Happiness; Reeves & Turner: London, UK, 1888. [Google Scholar]
- Rockström, J.; Steffen, W.; Noone, K.; Persson, Å.; Chapin, F.S., III; Lambin, E.; Lenton, T.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; et al. Planetary boundaries: Exploring the safe operating space for humanity. Ecol. Soc. 2009, 14, 32. [Google Scholar] [CrossRef]
- Lindkvist, E.; Ekeberg, Ö.; Norberg, J. Strategies for sustainable management of renewable resources during environmental change. Proc. R. Soc. B R. Soc. 2017, 284, 20162762. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Innes, C.; Anand, M.; Bauch, C.T. The impact of human-environment interactions on the stability of forest-grassland mosaic ecosystems. Sci. Rep. 2013, 3, 2689. [Google Scholar]
- Barlow, L.; Cecile, J.; Bauch, C.T.; Anand, M. Modelling interactions between forest pest invasions and human decisions regarding firewood transport restrictions. PLoS ONE 2014, 9, e90511. [Google Scholar]
- Henderson, K.; Bauch, C.T.; Anand, M. Alternative stable states and the sustainability of forests, grasslands, and agriculture. Proc. Natl. Acad. Sci. USA 2016, 113, 14552–14559. [Google Scholar] [Green Version]
- Bauch, C.T.; Sigdel, R.; Pharaon, J.; Anand, M. Early warning signals of regime shifts in coupled human—Environment systems. Proc. Natl. Acad. Sci. USA 2016, 113, 14560–14567. [Google Scholar]
- Motesharrei, S.; Rivas, J.; Kalnay, E. Human and nature dynamics (HANDY): Modeling inequality and use of resources in the collapse or sustainability of societies. Ecol. Econ. 2014, 101, 90–102. [Google Scholar] [CrossRef] [Green Version]
- De la Croix, D.; Dottori, D. Easter Island’s collapse: A tale of a population race. J. Econ. Growth 2008, 13, 27–55. [Google Scholar] [CrossRef]
- Reuveny, R.; Maxwell, J.W. Conflict and renewable resources. J. Confl. Resolut. 2001, 45, 719–742. [Google Scholar] [CrossRef]
- Bologna, M.; Flores, J. Mathematical model of Easter Island society collapse. arXiv, 2010; arXiv:1002.0068. [Google Scholar]
- Basener, B.; Ross, D.S. Booming and crashing populations and Easter Island. SIAM J. Appl. Math. 2004, 65, 684–701. [Google Scholar] [CrossRef]
- Nelson, S. Population Modeling with Delay Differential Equations; Rochester Institute of Technology: Rochester, NY, USA, 2013. [Google Scholar]
- Brander, J.A.; Taylor, M.S. The simple economics of Easter Island: A Ricardo-Malthus model of renewable resource use. Am. Econ. Rev. 1998, 88, 119–138. [Google Scholar]
- Dalton, T.R.; Coats, R.M. Could institutional reform have saved Easter Island? J. Evol. Econ. 2000, 10, 489–505. [Google Scholar] [CrossRef]
- D’Alessandro, S. Non-linear dynamics of population and natural resources: The emergence of different patterns of development. Ecol. Econ. 2007, 62, 473–481. [Google Scholar] [CrossRef] [Green Version]
- Dalton, T.R.; Coats, R.M.; Asrabadi, B.R. Renewable resources, property-rights regimes and endogenous growth. Ecol. Econ. 2005, 52, 31–41. [Google Scholar] [CrossRef]
- Pezzey, J.C.; Anderies, J.M. The effect of subsistence on collapse and institutional adaptation in population–resource societies. J. Dev. Econ. 2003, 72, 299–320. [Google Scholar] [CrossRef]
- Reuveny, R.; Decker, C.S. Easter Island: Historical anecdote or warning for the future? Ecol. Econ. 2000, 35, 271–287. [Google Scholar] [CrossRef]
- Anderies, J.M. On modeling human behavior and institutions in simple ecological economic systems. Ecol. Econ. 2000, 35, 393–412. [Google Scholar] [CrossRef]
- Roman, S.; Bullock, S.; Brede, M. Coupled Societies are More Robust Against Collapse: A Hypothetical Look at Easter Island. Ecol. Econ. 2017, 132, 264–278. [Google Scholar] [CrossRef] [Green Version]
- Axtell, R.L.; Epstein, J.M.; Dean, J.S.; Gumerman, G.J.; Swedlund, A.C.; Harburger, J.; Chakravarty, S.; Hammond, R.; Parker, J.; Parker, M. Population growth and collapse in a multiagent model of the Kayenta Anasazi in Long House Valley. Proc. Natl. Acad. Sci. USA 2002, 99, 7275–7279. [Google Scholar] [CrossRef] [Green Version]
- Flores, J.; Bologna, M.; Urzagasti, D. A mathematical model for the Andean Tiwanaku civilization collapse: Climate variations. J. Theor. Biol. 2011, 291, 29–32. [Google Scholar] [CrossRef]
- Meadows, D.; Randers, J.; Meadows, D. Limits to Growth: The 30-Year Update; Chelsea Green Publishing: White River Junction, VT, USA, 2004. [Google Scholar]
- Pearce, D.; Meadows, D.H.; Meadows, D.L.; Randers, J. Beyond the Limits: Global Collapse or a Sustainable Future; Earthscan Publications Ltd.: London, UK, 1992. [Google Scholar]
- Meadows, D.H.; Meadows, D.L.; Randers, J.; Behrens, W.W., III. The Limits to Growth: A Report to the Club of Rome. 1972. Available online: http://www.ask-force.org/web/Global-Warming/Meadows-Limits-to-Growth-Short-1972.pdf (accessed on 26 March 2019).
- Turner, G.M. A comparison of The Limits to Growth with 30 years of reality. Glob. Environ. Chang. 2008, 18, 397–411. [Google Scholar] [CrossRef]
- Maxwell, J.W.; Reuveny, R. Resource scarcity and conflict in developing countries. J. Peace Res. 2000, 37, 301–322. [Google Scholar] [CrossRef]
- Pagnutti, C.; Bauch, C.T.; Anand, M. Outlook on a worldwide forest transition. PLoS ONE 2013, 8, e75890. [Google Scholar] [CrossRef]
- Eberhardt, L. Is wolf predation ratio-dependent? Can. J. Zool. 1997, 75, 1940–1944. [Google Scholar] [CrossRef]
- May, R.M. Uses and abuses of mathematics in biology. Science 2004, 303, 790–793. [Google Scholar] [CrossRef]
- DeSA, U. World Population Prospects: The 2015 Revision, Volume I: Comprehensive Tables; Population Division of the Department of Economic and Social Affairs of the United Nations Secretariat: New York, NY, USA, 2015. [Google Scholar]
- Aizen, M.A.; Garibaldi, L.A.; Cunningham, S.A.; Klein, A.M. Long-Term global trends in crop yield and production reveal no current pollination shortage but increasing pollinator dependency. Curr. Biol. 2008, 18, 1572–1575. [Google Scholar] [CrossRef]
- Dockstader, Z. Population Model. 2016. Available online: https://github.com/zgmdocks/PopulationModel (accessed on 27 March 2019).
- Cumming, G.S.; Buerkert, A.; Hoffmann, E.M.; Schlecht, E.; von Cramon-Taubadel, S.; Tscharntke, T. Implications of agricultural transitions and urbanization for ecosystem services. Nature 2014, 515, 50–57. [Google Scholar] [CrossRef]
- DeFries, R.S.; Rudel, T.; Uriarte, M.; Hansen, M. Deforestation driven by urban population growth and agricultural trade in the twenty-first century. Nat. Geosci. 2010, 3, 178–181. [Google Scholar] [CrossRef]
- Swartz, W.; Sumaila, U.R.; Watson, R.; Pauly, D. Sourcing seafood for the three major markets: The EU, Japan and the USA. Mar. Policy 2010, 34, 1366–1373. [Google Scholar] [CrossRef]
- Novak, M.; Wolf, C.; Coblentz, K.; Shepard, I.D. Quantifying predator dependence in the functional response of generalist predators. Ecol. Lett. 2017, 20, 761–769. [Google Scholar]
- Fair, K.; Bauch, C.T.; Madhur, A. Dynamics of the global wheat trade network and resilience to shocks. Sci. Rep. 2017, 7, 7177. [Google Scholar]


| Symbol | Definition | Value | Source |
|---|---|---|---|
| Population 1,2 net growth rate | 0.0177/year | [54] | |
| Resource growth rate in patch 1, 2 | 0.015/year | [55] | |
| Harvesting efficiency of population 1, 2 | 0.008/year | calibrated | |
| Carrying capacity of resources in patch 1, 2 | 1,000,000 | calibrated | |
| Controls location of the mid-point of the sigmoid for population 1, 2 | 3.5 | calibrated | |
| Controls steepness of the sigmoid for population 1, 2 | 5 | calibrated |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dockstader, Z.; Bauch, C.T.; Anand, M. Interconnections Accelerate Collapse in a Socio-Ecological Metapopulation. Sustainability 2019, 11, 1852. https://doi.org/10.3390/su11071852
Dockstader Z, Bauch CT, Anand M. Interconnections Accelerate Collapse in a Socio-Ecological Metapopulation. Sustainability. 2019; 11(7):1852. https://doi.org/10.3390/su11071852
Chicago/Turabian StyleDockstader, Zachary, Chris T. Bauch, and Madhur Anand. 2019. "Interconnections Accelerate Collapse in a Socio-Ecological Metapopulation" Sustainability 11, no. 7: 1852. https://doi.org/10.3390/su11071852




