Anti-Symmetric Mode Vibration of Electrostatically Actuated Clamped–Clamped Microbeams for Mass Sensing
Abstract
:1. Introduction
2. Problem Formulation
3. Perturbation Analysis
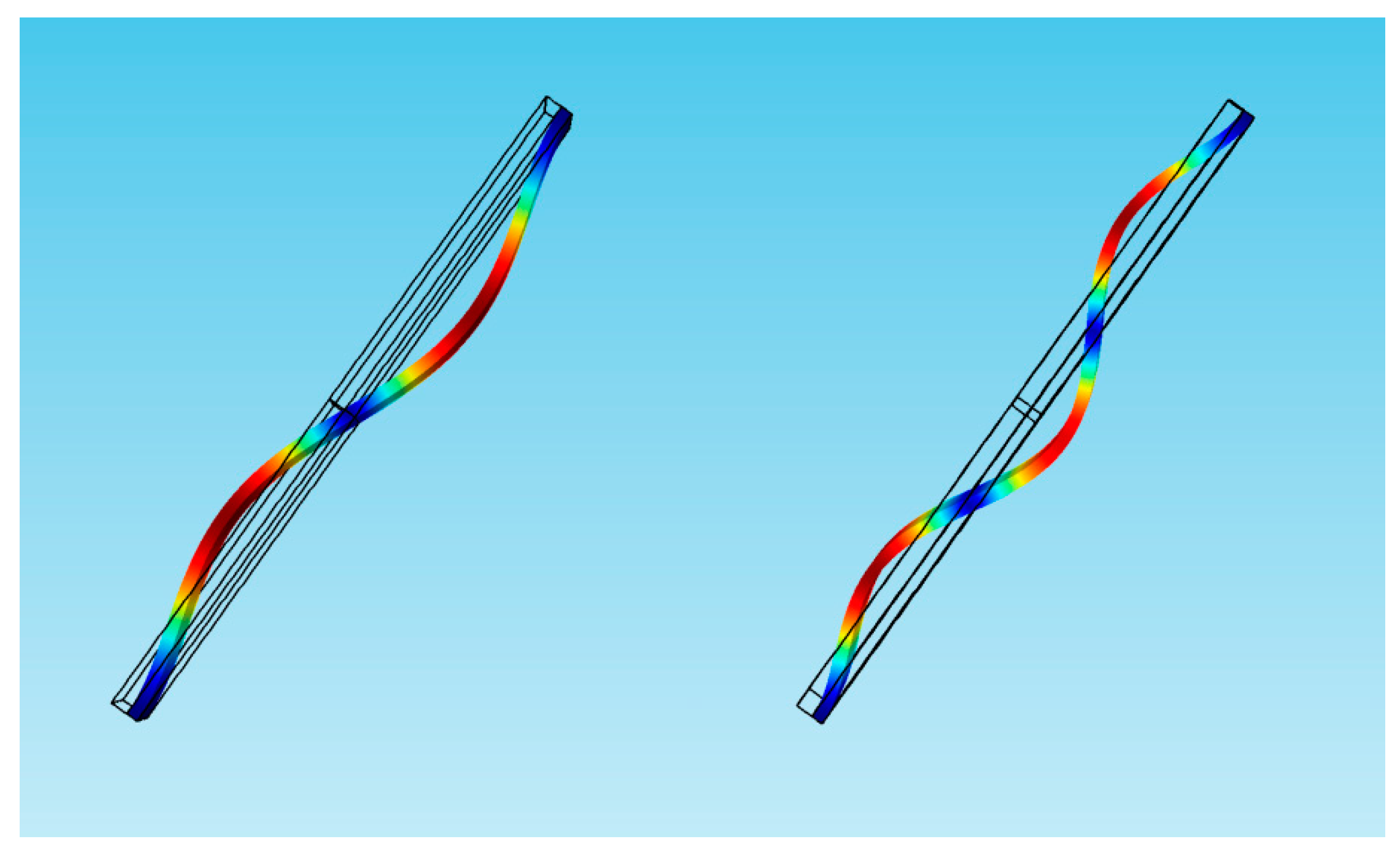
4. The Anti-Symmetric Mode Vibration
4.1. Physical Conditions for Mode Transition
4.2. Stability of the Nontrivial Solution
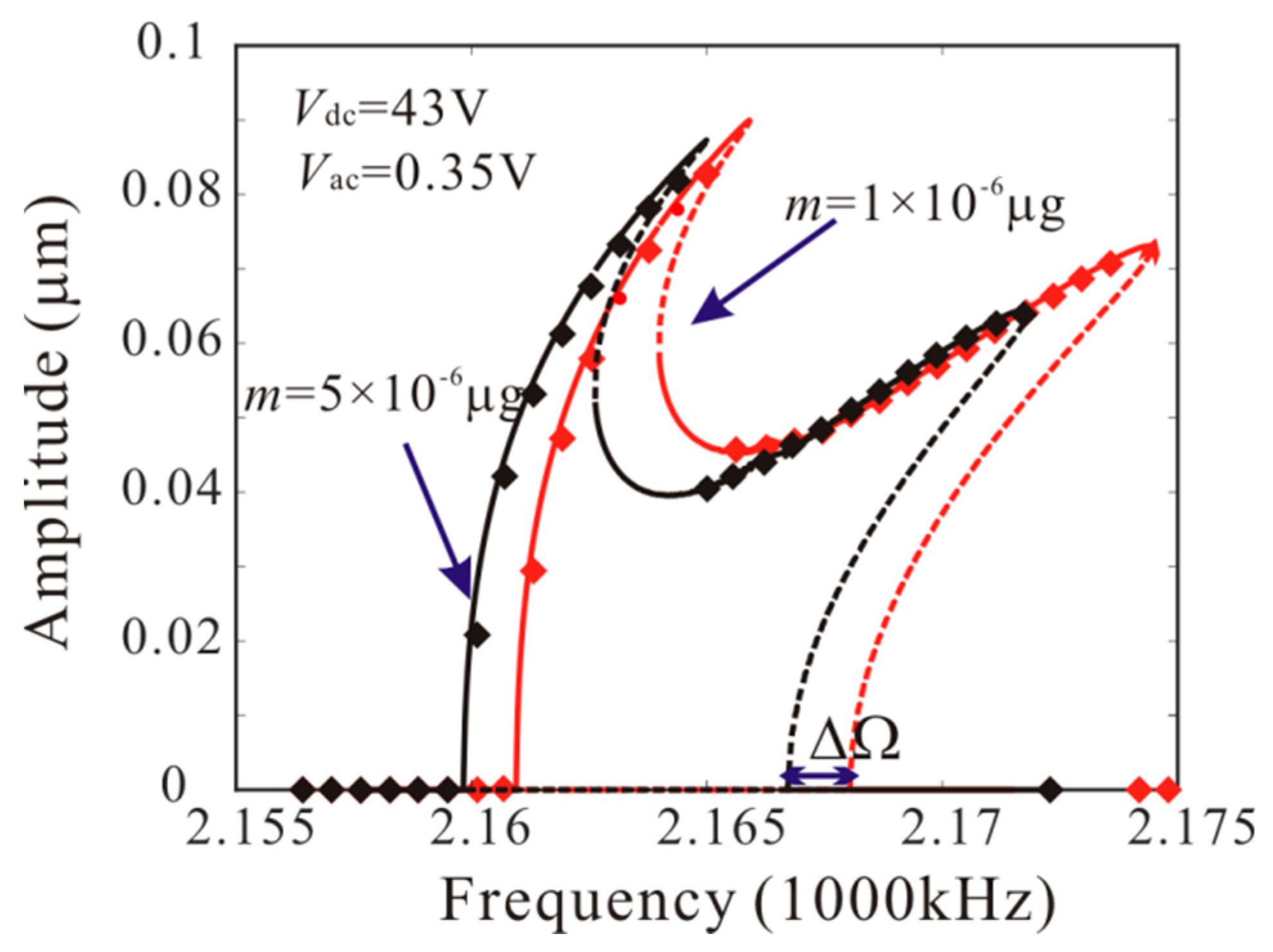
4.3. Dynamic Analysis
- ◆
- L1 = 50 µm
- ◆
- L1 = 75 µm
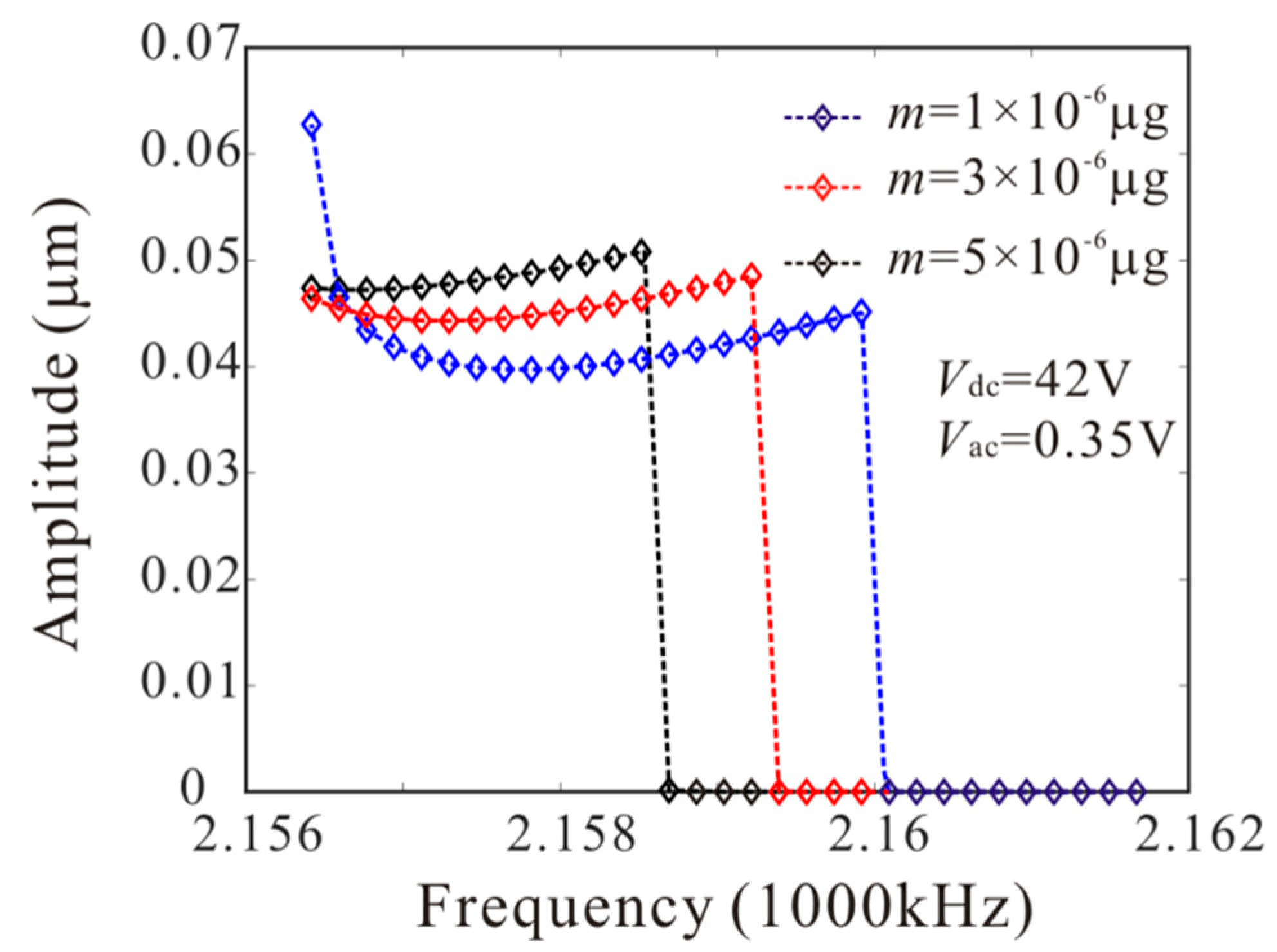
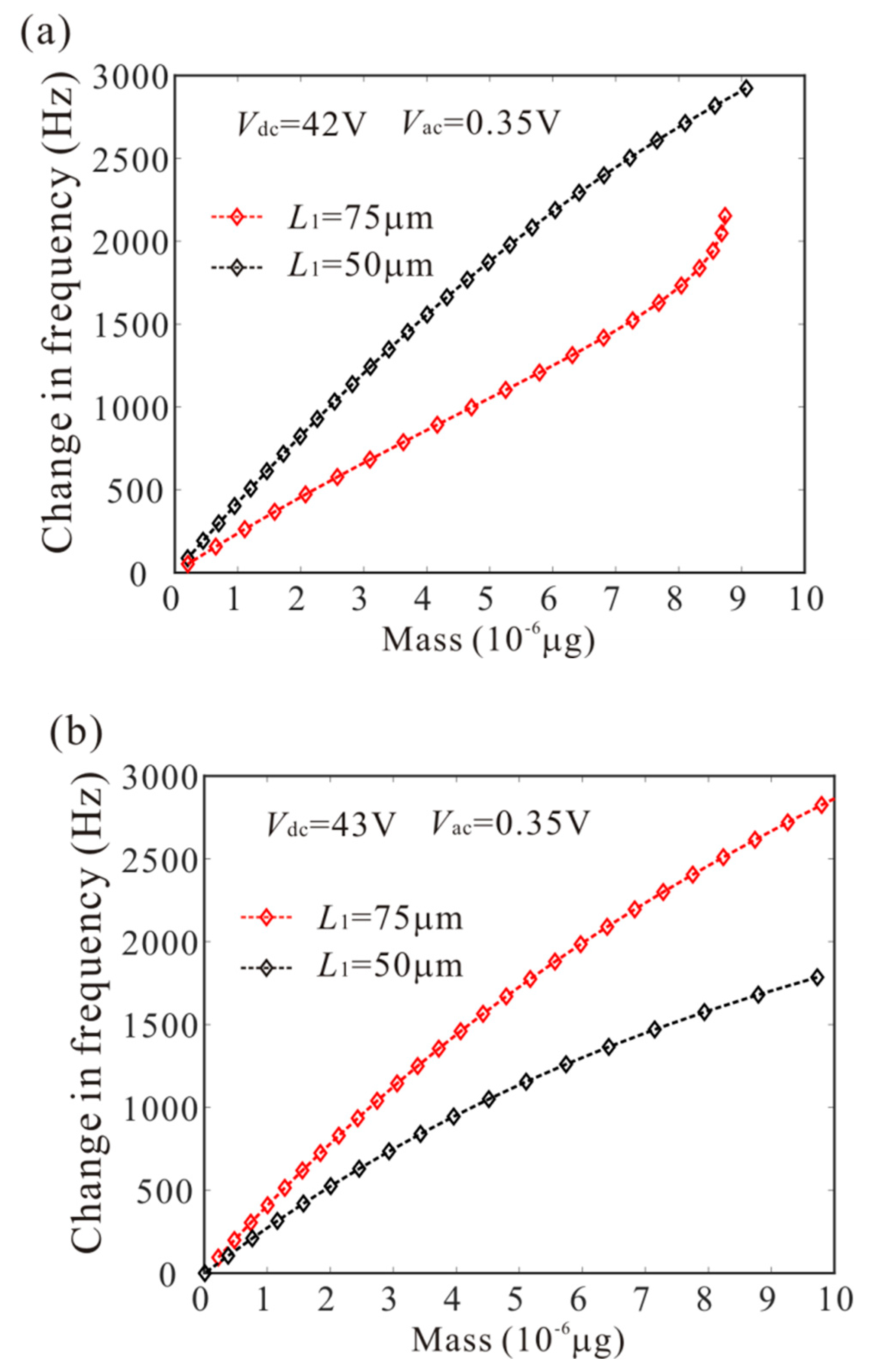
5. Mass Detection Method
- ◆
- L1 = 50 µm
- ◆
- L1 = 75 µm
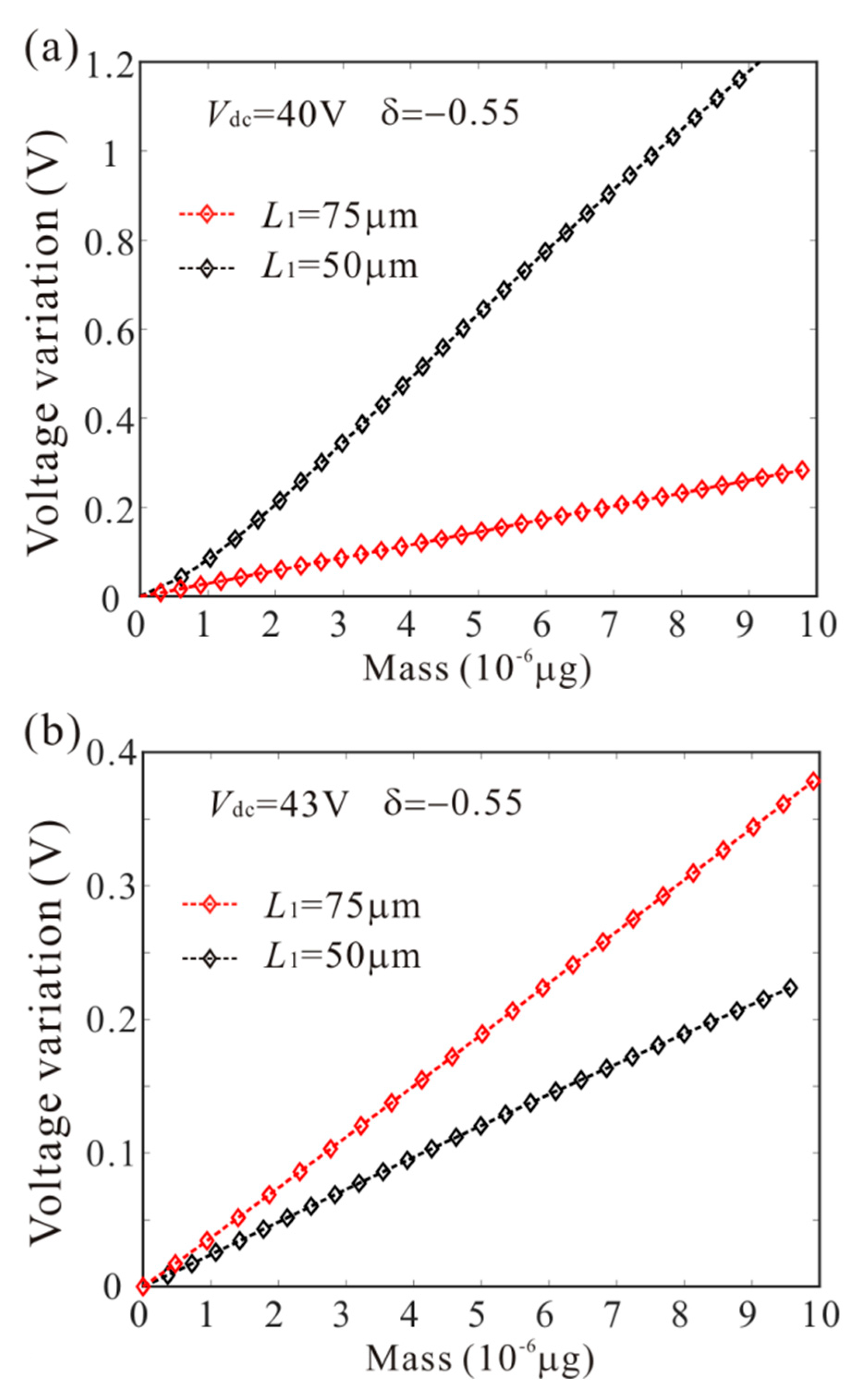
6. Sensor Sensitivity
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Jung, J.; Kim, P.; Lee, J.-I.; Seok, J. Nonlinear dynamic and energetic characteristics of piezoelectric energy harvester with two rotatable external magnets. Int. J. Mech. Sci. 2015, 92, 206–222. [Google Scholar] [CrossRef]
- Mestrom, R.M.C.; Fey, R.H.B.; van Beek, J.T.M.; Phan, K.L.; Nijmeijer, H. Modelling the dynamics of a MEMS resonator: Simulations and experiments. Sens. Actuators A Phys. 2008, 142, 306–315. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, W.; Shi, X.; Yan, H.; Peng, Z.; Meng, G. Adsorption-induced surface effects on the dynamical characteristics of micromechanical resonant sensors for in sit real-time detection. J. Appl. Mech. 2016, 83, 081009. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Shaw, S.W.; Turner, K.L. Nonlinear dynamics and its applications in micro-and nanoresonators. J. Dyn. Syst. Meas. Control. 2010, 132, 034001. [Google Scholar] [CrossRef]
- Li, H.; Preidikman, S.; Balachandran, B.; Mote, C.D. Nonlinear free and forced oscillations of piezoelectric microresonators. J. Micromech. Microeng. 2006, 16, 356–367. [Google Scholar] [CrossRef]
- Burugupally, S.P.; Perera, W.R. Dynamics of a parallel-plate electrostatic actuator in viscousdielectric media. Sens. Actuators A Phys. 2019, 295, 366–373. [Google Scholar] [CrossRef]
- Stachiv, I.; Gan, L. Hybrid Shape Memory Alloy-Based Nanomechanical Resonators for Ultrathin Film Elastic Properties Determination and Heavy Mass Spectrometry. Materials 2019, 12, 3593. [Google Scholar] [CrossRef] [Green Version]
- Nayfeh, A.H.; Younis, M.I.; Abdel-Rahman, E.M. Dynamic pull-in phenomenon in MEMS resonators. Nonlinear Dyn. 2006, 48, 153–163. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q. Nonlinear dynamic analysis of electrically actuated viscoelastic bistable microbeam system. Nonlinear Dyn. 2017, 87, 587–604. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Wang, W.; Han, J. Dynamic analysis and design of electrically actuated viscoelastic microbeams considering the scale effect. Int. J. Non-linear Mech. 2017, 90, 21–31. [Google Scholar] [CrossRef]
- Daichi, E.; Hiroshi, Y.; Yasuyuki, Y.; Sohei, M. Mass sensing in a liquid environment using nonlinear self-excited coupled-microcantilevers. J. Microelectromech. Syst. 2018, 27, 774–779. [Google Scholar]
- Li, L.; Han, J.; Zhang, Q.; Liu, C.; Guo, Z. Nonlinear dynamics and parameter identification of electrostatically coupled resonators. Int. J Non-linear Mech. 2019, 110, 104–114. [Google Scholar] [CrossRef]
- Antonio, D.; Zanette, D.H.; López, D. Frequency stabilization in nonlinear micromechanical oscillators. Nat. Commun. 2012, 3, 806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agrawal, D.K.; Woodhouse, J.; Seshia, A.A. Synchronization in a coupled architecture of microelectromechanical oscillators. J. Appl. Phys. 2014, 115, 164904. [Google Scholar] [CrossRef]
- Kambali, P.N.; Pandey, A.K. Nonlinear coupling of transverse modes of a fixed–fixed microbeam under direct and parametric excitation. Nonlinear Dyn. 2017, 87, 1271–1294. [Google Scholar] [CrossRef]
- Kambali, P.N.; Swain, G.; Pandey, A.K.; Buks, E.; Gottlieb, O. Coupling and tuning of modal frequencies in direct current biased microelectromechanical systems arrays. Appl. Phys. Lett. 2015, 107, 63104. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zhang, Q.; Wang, W.; Han, J. Nonlinear coupled vibration of electrostatically actuated clamped–clamped microbeams under higher-order modes excitation. Nonlinear Dyn. 2017, 90, 1593–1606. [Google Scholar] [CrossRef]
- Baguet, S.; Nguyen, V.N.; Grenat, C.; Lamarque, C.-H.; Dufour, R. Nonlinear dynamics of micromechanical resonator arrays for mass sensing. Nonlinear Dyn. 2019, 95, 1203–1220. [Google Scholar] [CrossRef] [Green Version]
- Kirkendall, C.R.; Kwon, J.W. Multistable internal resonance in electroelastic crystals with nonlinearly coupled modes. Sci. Rep. 2016, 6, 22897. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.F.; Itoh, T.; Ikehara, T.; Maeda, R. Doubling flexural frequency response using synchronised oscillation in a micromechanically coupled oscillator system. Micro Nano Lett. 2012, 7, 717–720. [Google Scholar]
- Okamoto, H.; Kitajima, N.; Onomitsu, K.; Kometani, R.; Warisawa, S.; Ishihara, S. High-sensitivity charge detection using antisymmetric vibration in coupled micromechanical oscillators. Appl. Phys. Lett. 2011, 98, 014103. [Google Scholar] [CrossRef]
- Hammad, B.K.; Abdel-Rahman, E.M.; Nayfeh, A.H. Modeling and analysis of electrostatic MEMS filters. Nonlinear Dyn. 2010, 60, 385–401. [Google Scholar] [CrossRef]
- Hammad, B.K. Natural Frequencies and Mode Shapes of Mechanically Coupled Microbeam Resonators with an Application to Micromechanical Filters. Shock Vib. 2014, 2014, 1–15. [Google Scholar] [CrossRef]
- Younis, M.I.; Nayfeh, A.H. A study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dyn. 2002, 31, 91–117. [Google Scholar] [CrossRef]
- Du, X.; Wang, D.F.; Xia, C.; Isao, S.; Maeda, R. Internal resonance phenomena in coupled ductile cantilevers with triple frequency ratio—part I: Experimental observations. IEEE Sens. J. 2019, 19, 5475–5483. [Google Scholar] [CrossRef]
- Hajjaj, A.; Hafiz, M.A.; Younis, M.I. Mode Coupling and Nonlinear Resonances of MEMS Arch Resonators for Bandpass Filters. Sci. Rep. 2017, 7, 41820. [Google Scholar] [CrossRef] [Green Version]
- Hajhashemi, M.S.; Rasouli, A.; Bahreyni, B. Improving Sensitivity of Resonant Sensor Systems Through Strong Mechanical Coupling. J. Microelectromech. Syst. 2016, 25, 52–59. [Google Scholar] [CrossRef]
- Yi, Z.; Stanciulescu, I. Nonlinear normal modes of a shallow arch with elastic constraints for two-to-one internal resonances. Nonlinear Dyn. 2016, 83, 1577–1600. [Google Scholar] [CrossRef]
- Sidhant, T.; Candler, R. Using flexural MEMS to study and exploit nonlinearities: A review. J. Micromech. Microeng. 2019, 29, 083002. [Google Scholar]
- Bouchaala, A.; Nayfeh, A.H.; Younis, M.I. Analytical study of the frequency shifts of micro and nano clamped-clamped beam resonators due to an added mass. Meccanica 2017, 52, 333–348. [Google Scholar] [CrossRef]
- Kasai, Y.; Yabuno, H.; Ishine, T.; Yamamoto, Y.; Matsumoto, S. Mass sensing using a virtual cantilever virtually coupled with a real cantilever. App. Phys. Lett. 2019, 115, 063103. [Google Scholar] [CrossRef]
- Younis, M.I.; Alsaleem, F. Exploration of new concepts for mass detection in electrostatically-actuated structures based on nonlinear phenomena. J. Comput. Nonlinear Dyn. 2009, 4, 021010. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A bifurcation-based coupled linear-bistable system for microscale mass sensing. J. Sound Vib. 2014, 333, 2241–2252. [Google Scholar] [CrossRef]
- Kumar, V.; Boley, J.W.; Yang, Y.; Ekowaluyo, H.; Miller, J.K.; Chiu, G.T.-C.; Rhoads, J.F. Bifurcation-based mass sensing using piezoelectrically-actuated microcantilevers. Appl. Phys. Lett. 2011, 98, 153510. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.H.; Alsaleem, F.M.; Ouakad, H.M. Novel threshold pressure sensors based on nonlinear dynamics of MEMS resonators. J. Micromech. Microeng. 2018, 28, 065007. [Google Scholar] [CrossRef]
- Alghamdi, M.; Khater, M.; Stewart, K.; Alneamy, A.; Abdel-Rahman, E.M.; Penlidis, A. Dynamic bifurcation mems gas sensors. J. Micromech. Microeng. 2019, 29, 015005. [Google Scholar] [CrossRef]
- Tchakui, M.V.; Fondjo, V.Y.T.; Woafo, P. Bifurcation structures in three unidirectionally coupled electromechanical systems with no external signal and with regenerative process. Nonlinear Dyn. 2016, 84, 1961–1972. [Google Scholar] [CrossRef]
- Zhou, S. Fully Coupled Model for Frequency Response Simulation of Miniaturized Cantilever-Based Photoacoustic Gas Sensors. Sensors 2019, 19, 4772. [Google Scholar] [CrossRef] [Green Version]
- COMSOL. Available online: http://www.comsol.com/ (accessed on 18 December 2019).












| Physical Parameter (units). | Value |
|---|---|
| Length of the beam electrode, L (µm) | 150 |
| Thickness of the beam electrode, h (µm) | 1 |
| Width of the beam electrode, b (µm) | 10 |
| Gap between the electrodes, d (µm) | 1.5 |
| Density of the electrode material, ρ (kg/m3) | 2300 |
| Young’s Modulus, E (GPa) | 169 |
| Dielectric constant of the medium, | 8.85 × 10−12 |
| Quality factor, Q | 12.5 |
| Number | The True Mass m (10−6 µg) | Bifurcation Voltage (V) | Identification Results m (10−6 µg) | Error (10−6 µg) |
|---|---|---|---|---|
| 1 | 1 | 0.537 | 0.995 | 0.005 |
| 2 | 3 | 0.774 | 2.833 | 0.167 |
| 3 | 5 | 1.032 | 4.624 | 0.376 |
| Number | The True Mass m (10−6 µg) | Bifurcation Frequency (100 kHz) | Identification Results m (10−6 µg) | Error (10−6 µg) |
|---|---|---|---|---|
| 1 | 1 | 21.598 | 0.949 | 0.051 |
| 2 | 3 | 21.591 | 2.772 | 0.228 |
| 3 | 5 | 21.585 | 4.542 | 0.458 |
| Number | The True Mass m (10−6 µg) | Bifurcation Voltage (V) | Identification Results m (10−6 µg) | Error (10−6 µg) |
|---|---|---|---|---|
| 1 | 1 | 0.482 | 1.191 | 0.191 |
| 2 | 3 | 0.538 | 3.219 | 0.219 |
| 3 | 5 | 0.602 | 5.342 | 0.342 |
| Number | The True Mass m (10−6 µg) | Bifurcation Frequency (100 kHz) | Identification Results m (10−6 µg) | Error (10−6 µg) |
|---|---|---|---|---|
| 1 | 1 | 21.601 | 0.955 | 0.045 |
| 2 | 3 | 21.597 | 3.112 | 0.112 |
| 3 | 5 | 21.592 | 4.273 | 0.727 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhang, Y.-p.; Ma, C.-c.; Liu, C.-c.; Peng, B. Anti-Symmetric Mode Vibration of Electrostatically Actuated Clamped–Clamped Microbeams for Mass Sensing. Micromachines 2020, 11, 12. https://doi.org/10.3390/mi11010012
Li L, Zhang Y-p, Ma C-c, Liu C-c, Peng B. Anti-Symmetric Mode Vibration of Electrostatically Actuated Clamped–Clamped Microbeams for Mass Sensing. Micromachines. 2020; 11(1):12. https://doi.org/10.3390/mi11010012
Chicago/Turabian StyleLi, Lei, Yin-ping Zhang, Chi-cheng Ma, Can-chang Liu, and Bo Peng. 2020. "Anti-Symmetric Mode Vibration of Electrostatically Actuated Clamped–Clamped Microbeams for Mass Sensing" Micromachines 11, no. 1: 12. https://doi.org/10.3390/mi11010012





