A Noise Reduction Method for Four-Mass Vibration MEMS Gyroscope Based on ILMD and PTTFPF
Abstract
:1. Introduction
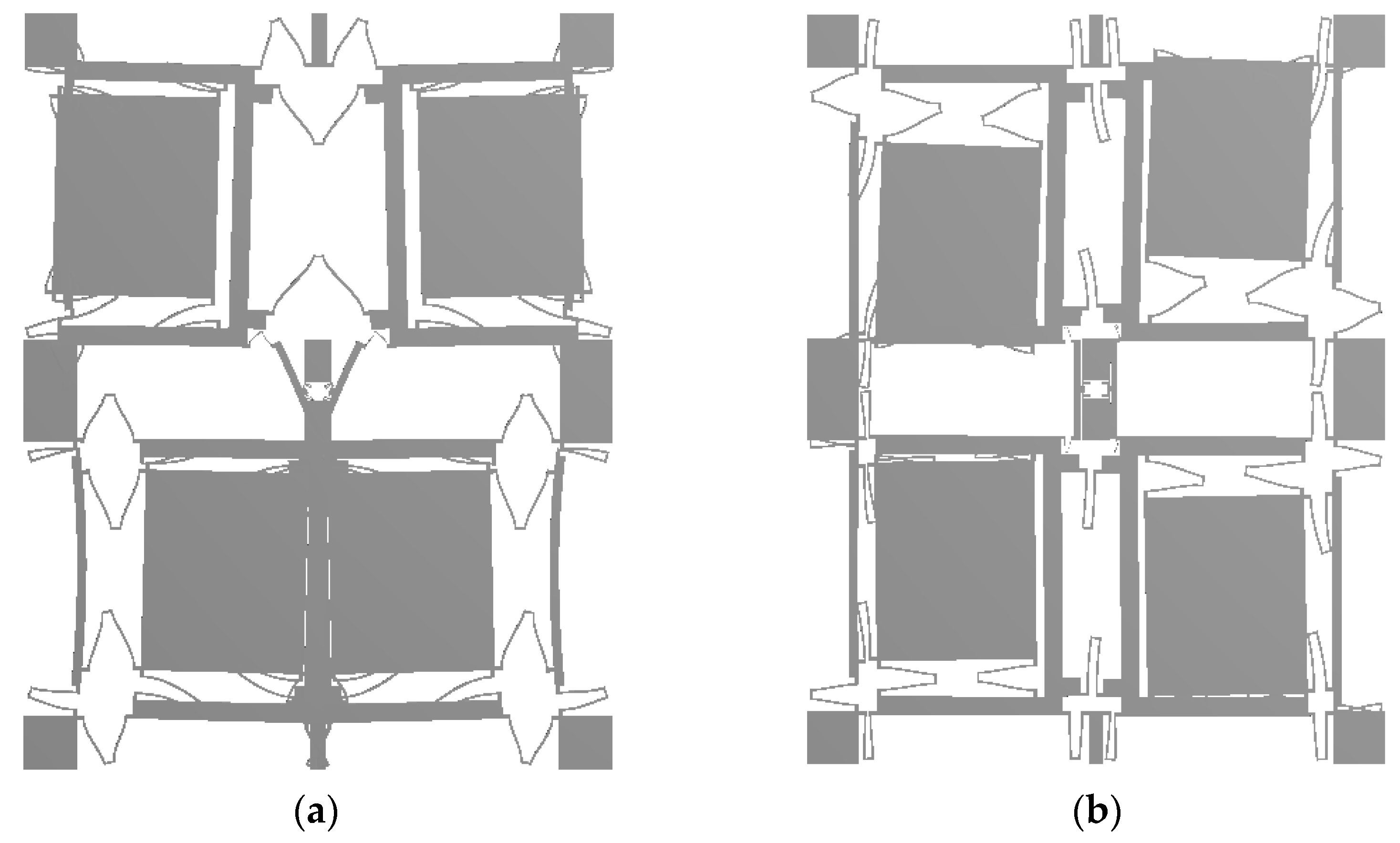
2. Four-Mass Vibration MEMS Gyroscope
2.1. Structure and Workong Principle of FMVMG
2.2. Modal Analysis of FMVMG
3. Denoising Methods
3.1. Interval Local Mean Decomposition
- Step 1: determine all local extreme points ni of the original signal x(t), and calculate the mean value mi of two adjacent extreme points ni and ni+1:
- Step 2: envelope estimates ai are calculated from local mean points ni:
- Step 3: the local mean function m11(t) is separated from the original signal x(t):
- Step 4: divide h11(t) by a11(t) to demodulate h11(t):
- Step 5: the envelope signal is obtained by multiplying all the envelope estimation functions generated in the iteration process:
- Step 6: the first PF component PF1(t) of the original signal is obtained by multiplying the envelope signal a1(t) and the pure frequency-modulated signal s1n(t):
- Step 7: the first PF component PF1(t) is separated from the original signal to obtain a new signal u1(t), using u1(t) as the original data, repeat the above steps for k times until u1(t) is a monotone function.
- Step 1: construct a sequence of m-dimensional vectors by ordinal number, Xm(1), Xm(2), ⋯, Xm(N-m + 1), among them, Xm(i) = { x(i), x(i + 1), …, x(i + m − 1)}, 1≤ i ≤N-m+1.
- Step 2: the distance d[Xm(i), Xm(j)] between vectors Xm(i) and Xm(j) is defined as the absolute value of the maximum difference between the two corresponding elements:
- Step 3: count the number of j (1≤ j ≤N-m, j≠i) whose distance between Xm(i) and Xm(j) is less than r, and define it as Bi:
- Step 4: definition B(m)(r) is:
- Step 5: increase the dimension to m+1, count the number of j (1 ≤ j ≤ N-m, j≠i) whose distance between Xm+1(i) and Xm+1(j) is less than r, and define it as Ai:
- Step 6: definition A(m)(r) is:
3.2. Parabolic Tracking Time Frequency Peak Filtering
3.3. Step of ILMD-PTTFPF
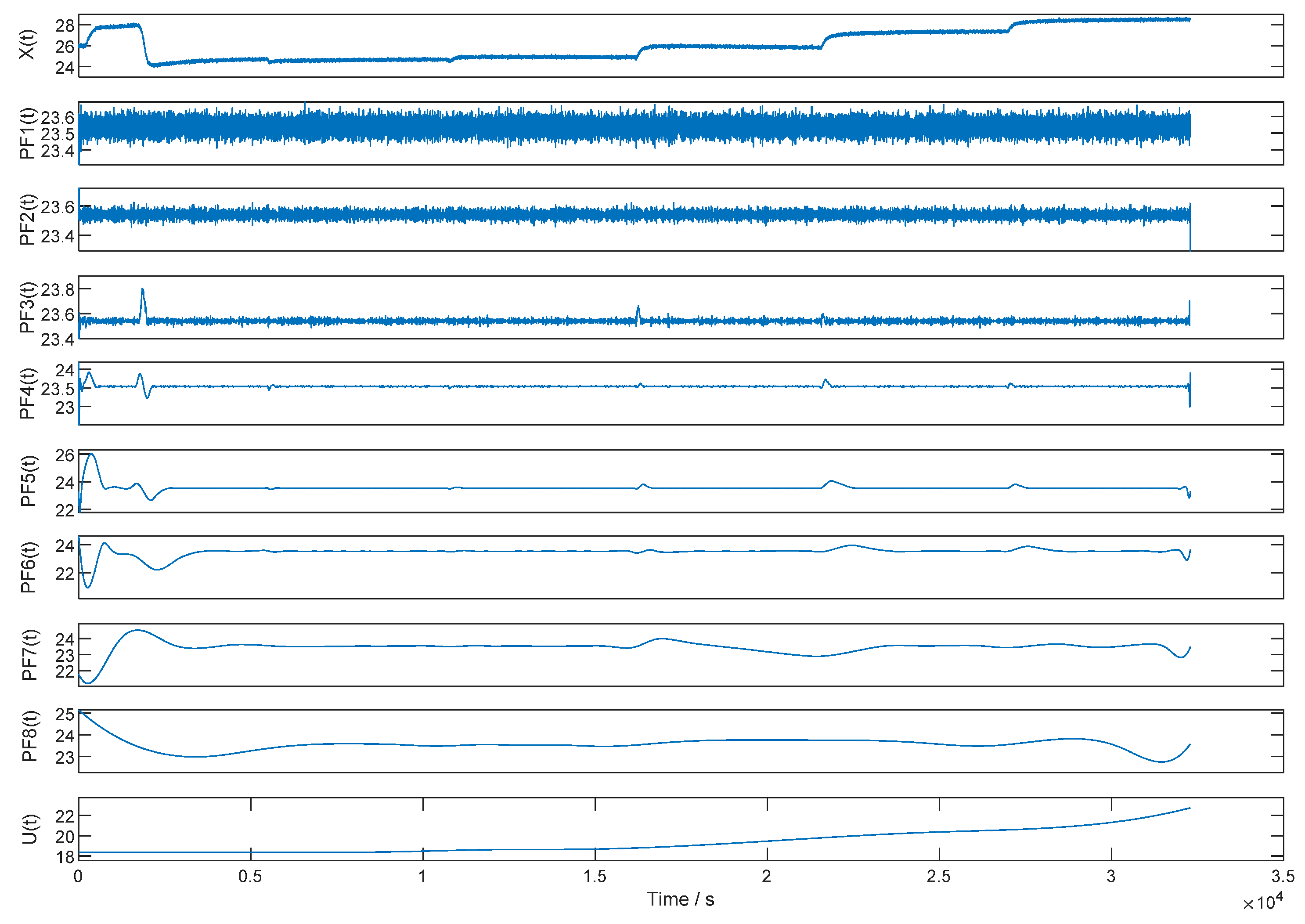
- Step 1: Local mean decomposition
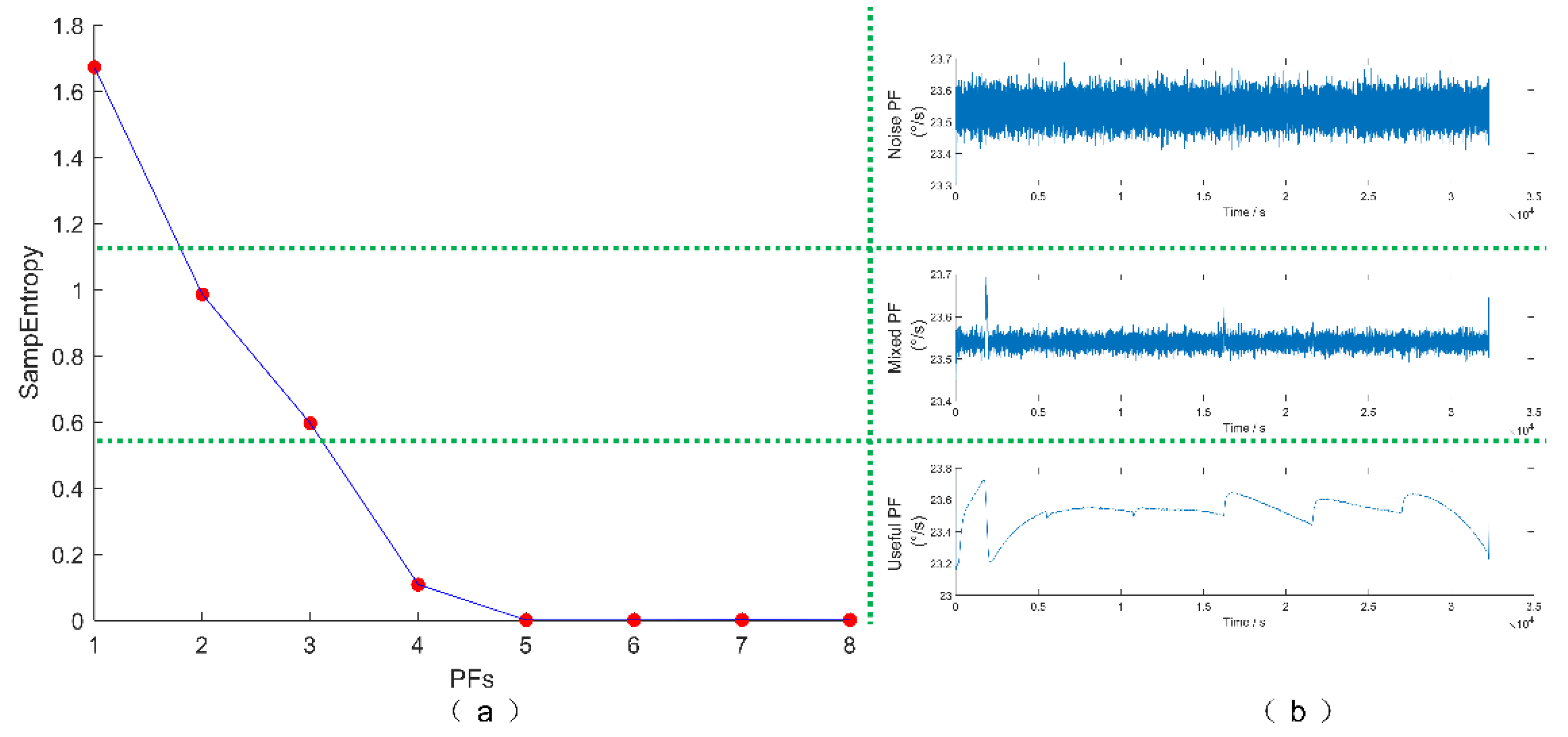
- Step 2: Classify the PF by SE value
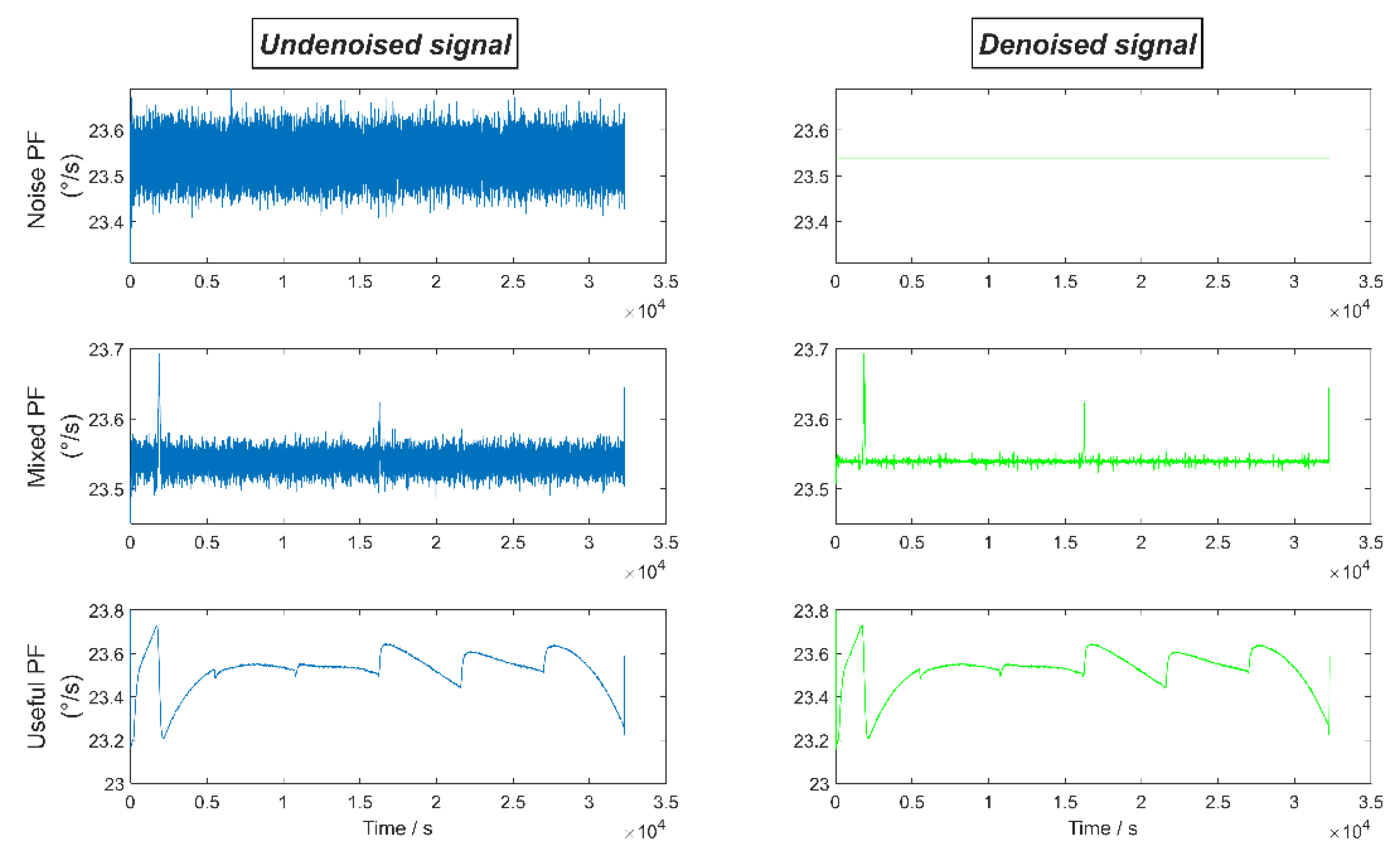
- Step 3: Denoise for different PF
- Step 4: Signal reconstruction
4. Experiment
4.1. Experiment Platform and Equipment
4.2. Denoising Processing
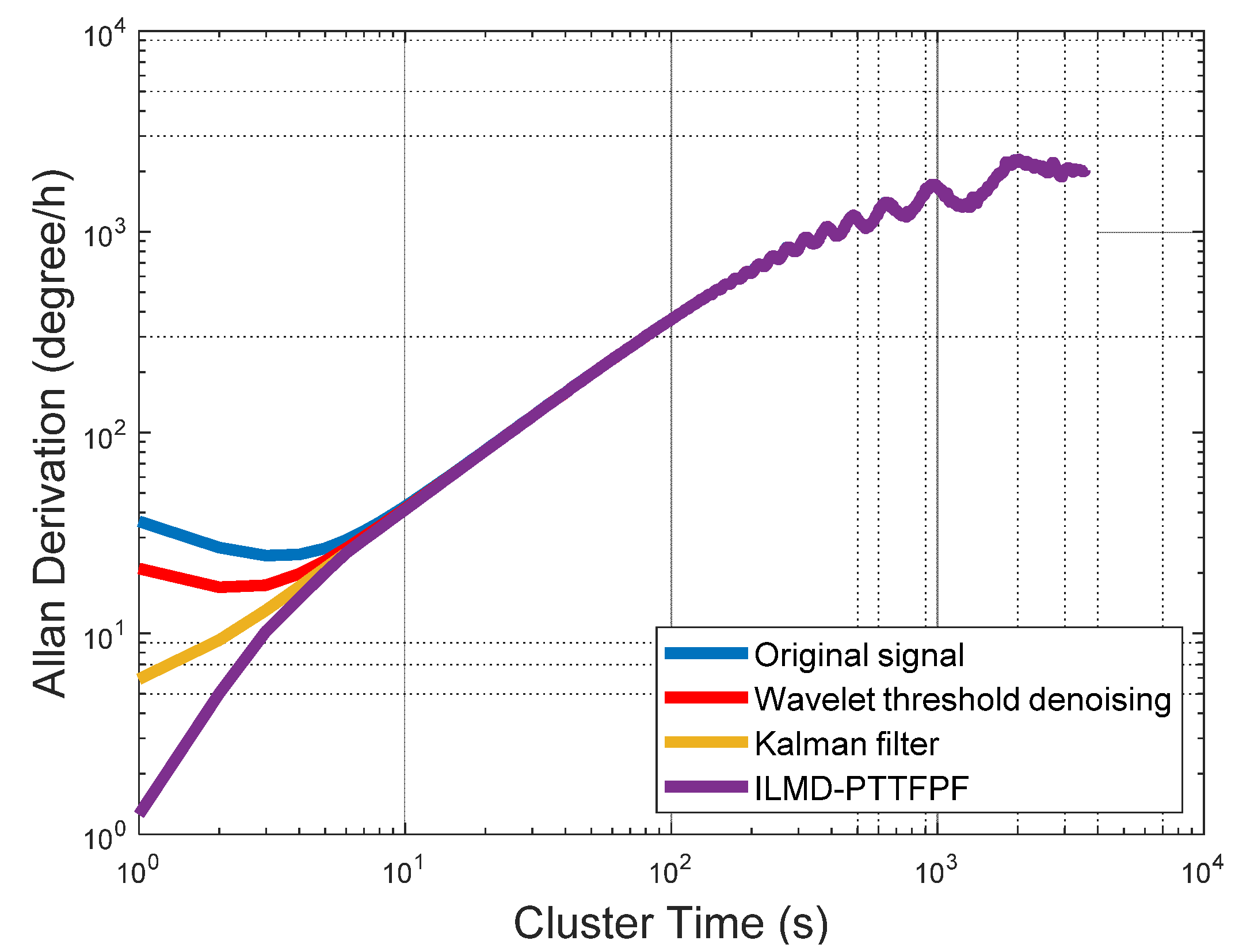
4.3. Discussion of the Denoising Results
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, D.; Yu, C.; Kong, L. The Development of Micromachined Gyroscope Structure and Circuitry Technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, H.; Li, H.; Kou, Z.; Shi, Y.; Tang, J.; Ma, Z.; Shen, C.; Liu, J. Optimization and Experimentation of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods. Sensors 2016, 16, 71. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Li, H.; Shao, X.; Liu, Z.; Kou, Z.; Shan, Y.; Shi, Y.; Shen, C.; Liu, J. Sensing mode coupling analysis for dual-mass MEMS gyroscope and bandwidth expansion within wide-temperature range. Mech. Syst. Signal Process. 2018, 98, 448–464. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Liu, J.; Shi, Y.; Tang, J.; Shen, C. An improved interface and noise analysis of a turning fork microgyroscope structure. Mech. Syst. Signal Process. 2016, 70–71, 1209–1220. [Google Scholar] [CrossRef]
- Yuan, J.; Yuan, Y.; Liu, F.; Pang, Y.; Lin, J. An improved noise reduction algorithm based on wavelet transformation for MEMS gyroscope. Front. Optoelectron. 2015, 8, 413–418. [Google Scholar] [CrossRef]
- Liu, D.; He, C.; Zhao, Q.; Yang, Z.; Hao, Y.; Yan, G. Digital signal processing for a micromachined vibratory gyroscope based on a three dimensional adaptive filter demodulator. Measurement 2014, 50, 198–202. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Y.; Shen, C.; Liu, Y.; Wang, X. Temperature Energy Influence Compensation for MEMS Vibration Gyroscope Based on RBF NN-GA-KF Method. Shock Vib. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Song, J.; Shi, Z.; Du, B.; Han, L.; Wang, H.; Wang, Z. MEMS gyroscope wavelet de-noising method based on redundancy and sparse representation. Microelectron. Eng. 2019, 217, 111112. [Google Scholar] [CrossRef]
- Shen, C.; Cao, H.; Li, J.; Tang, J.; Zhang, X.; Shi, Y.; Yang, W.; Liu, J. Hybrid de-noising approach for fiber optic gyroscopes combining improved empirical mode decomposition and forward linear prediction algorithms. Rev. Sci. Instrum. 2016, 87, 033305. [Google Scholar] [CrossRef]
- Shen, C.; Li, J.; Zhang, X.; Shi, Y.; Tang, J.; Cao, H.; Liu, J. A Noise Reduction Method for Dual-Mass Micro-Electromechanical Gyroscopes Based on Sample Entropy Empirical Mode Decomposition and Time-Frequency Peak Filtering. Sensors 2016, 16, 796. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, G.; Wei, Z.; Yang, J.; Xing, D. Denoising Method of MEMS Gyroscope Based on Interval Empirical Mode Decomposition. Math. Probl. Eng. 2020, 2020, 3019152. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, P.; Feng, L.; Xing, C.; Wu, J. A Filtering Algorithm of MEMS Gyroscope to Resist Acoustic Interference. Sensors 2020, 20, 7352. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Xu, X.; Liu, Y.; Zhang, T.; Li, Y. FOG Random Drift Signal Denoising Based on the Improved AR Model and Modified Sage-Husa Adaptive Kalman Filter. Sensors 2016, 16, 1073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Narasimhappa, M.; Sabat, S.L.; Nayak, J. Adaptive sampling strong tracking scaled unscented Kalman filter for denoising the fibre optic gyroscope drift signal. IET Sci. Meas. Technol. 2015, 9, 241–249. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, S.; Chen, Y.; Bo, Y.; Han, L.; Guo, J.; Feng, Z.; Zhou, H. Performance Analysis of a Deep Simple Recurrent Unit Recurrent Neural Network (SRU-RNN) in MEMS Gyroscope De-Noising. Sensors 2018, 18, 4471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, Y.; Li, Y. Parabolic-Trace Time-Frequency Peak Filtering for Seismic Random Noise Attenuation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 158–162. [Google Scholar] [CrossRef]
- Cao, H.; Cui, R.; Liu, W.; Ma, T.; Zhang, Z.; Shen, C.; Shi, Y. Dual mass MEMS gyroscope temperature drift compensation based on TFPF-MEA-BP algorithm. Sens. Rev. 2021, 41, 162–175. [Google Scholar] [CrossRef]
- Li, J.; Meng, K.; Li, Y.; Li, Y. Adaptive linear TFPF for seismic random noise attenuation. J. Pet. Explor. Prod. Technol. 2018, 8, 1443–1453. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; He, Z.; Zi, Y. A Comparative Study on the Local Mean Decomposition and Empirical Mode Decomposition and Their Applications to Rotating Machinery Health Diagnosis. J. Vib. Acoust. 2010, 132, 021010. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q.; Zhang, X. Time–frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2018, 103, 60–75. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, J.; Du, W.; Lei, Y.; Wang, J. Bearing fault diagnosis method based on adaptive maximum cyclostationarity blind deconvolution. Mech. Syst. Signal Process. 2021, 162, 108018. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Z.; Zheng, Y.; Guo, H.; Zhao, R.; Shi, Y.; Chou, X. A New Joint Denoising Algorithm for High-G Calibration of MEMS Accelerometer Based on VMD-PE-Wavelet Threshold. Shock Vib. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Zhao, L.; Wei, S.; Zhang, C.; Zhang, Y.; Jiang, X.; Liu, F.; Liu, C. Determination of Sample Entropy and Fuzzy Measure Entropy Parameters for Distinguishing Congestive Heart Failure from Normal Sinus Rhythm Subjects. Entropy 2015, 17, 6270–6288. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Shang, P.; Li, Y. Modified generalized multiscale sample entropy and surrogate data analysis for financial time series. Nonlinear Dyn. 2018, 92, 1335–1350. [Google Scholar] [CrossRef]
- Yu, K.; Lin, T.R.; Ma, H.; Li, H.; Zeng, J. A Combined Polynomial Chirplet Transform and Synchroextracting Technique for Analyzing Nonstationary Signals of Rotating Machinery. IEEE Trans. Instrum. Meas. 2019, 69, 1505–1518. [Google Scholar] [CrossRef]
- Riaz, F.; Hassan, A.; Rehman, S.; Niazi, I.K.; Dremstrup, K. EMD-Based Temporal and Spectral Features for the Classification of EEG Signals Using Supervised Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, N.; Li, N.; Du, W.; Wang, J. A new fault diagnosis method based on adaptive spectrum mode extraction. Struct. Health Monit. 2021, 20, 3354–3370. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, W.; Du, W.; Li, N.; Wang, J. Data-driven fault diagnosis method based on the conversion of erosion operation signals into images and convolutional neural network. Process Saf. Environ. Prot. 2021, 149, 591–601. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Lin, T.; Li, X.; Wang, T. Characterization of a fiber optic gyroscope in a measurement while drilling system with the dynamic Allan variance. Measurement 2015, 75, 263–272. [Google Scholar] [CrossRef]








| Modal Order Number | Resonant Frequencies |
|---|---|
| 1 | 25,644 Hz |
| 2 | 25,999 Hz |
| 3 | 26,476 Hz |
| 4 | 26,550 Hz |
| 5 | 29,636 Hz |
| 6 | 30,740 Hz |
| 7 | 30,886 Hz |
| 8 | 37,230 Hz |
| 9 | 38,543 Hz |
| 10 | 40,070 Hz |
| 11 | 41,445 Hz |
| 12 | 41,955 Hz |
| Methods | Bias Stability (°/h) | Standard Deviation | Signal to Noise Ratio (dB) | References |
|---|---|---|---|---|
| Original signal | 24.44 | 0.0108 | 22.5 | - |
| Wavelet threshold denoising | 16.99 | 0.00567 | 35.45 | Cao et al. [22] |
| Kalman filter | 5.93 | 0.00734 | 39.91 | Cao et al. [7] |
| ILMD-PTTFPF | 1.26 | 0.00455 | 46.16 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Gu, Y.; Yang, J.; Cao, H.; Wang, G. A Noise Reduction Method for Four-Mass Vibration MEMS Gyroscope Based on ILMD and PTTFPF. Micromachines 2022, 13, 1807. https://doi.org/10.3390/mi13111807
Li Z, Gu Y, Yang J, Cao H, Wang G. A Noise Reduction Method for Four-Mass Vibration MEMS Gyroscope Based on ILMD and PTTFPF. Micromachines. 2022; 13(11):1807. https://doi.org/10.3390/mi13111807
Chicago/Turabian StyleLi, Zhong, Yikuan Gu, Jian Yang, Huiliang Cao, and Guodong Wang. 2022. "A Noise Reduction Method for Four-Mass Vibration MEMS Gyroscope Based on ILMD and PTTFPF" Micromachines 13, no. 11: 1807. https://doi.org/10.3390/mi13111807




