Next Article in Journal
Lysis of a Single Cyanobacterium for Whole Genome Amplification
Next Article in Special Issue
Monodisperse Water-in-Oil-in-Water (W/O/W) Double Emulsion Droplets as Uniform Compartments for High-Throughput Analysis via Flow Cytometry
Previous Article in Journal
Approaches for a Fair Comparison and Benchmarking of Electromagnetic Vibration Energy Harvesters
Previous Article in Special Issue
FISHprep: A Novel Integrated Device for Metaphase FISH Sample Preparation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Micromachines
Volume 4
Issue 3
10.3390/mi4030306
micromachines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Formation of Tunable, Emulsion Micro-Droplets Utilizing Flow-Focusing Channels and a Normally-Closed Micro-Valve

by
Jung-Hao Wang
and
Gwo-Bin Lee
*
Department of Power Mechanical Engineering, National Tsing Hua University, Hsinchu 300, Taiwan
*
Author to whom correspondence should be addressed.
Micromachines 2013, 4(3), 306-320; https://doi.org/10.3390/mi4030306
Submission received: 13 June 2013 / Revised: 7 July 2013 / Accepted: 8 July 2013 / Published: 17 July 2013
(This article belongs to the Collection Lab-on-a-Chip)
Browse Figures
Versions Notes

Abstract

:
A mono-dispersed emulsion is of great significance in many chemical, biomedical and industrial applications. The current study reports a new microfluidic chip capable of forming tunable micro-droplets in liquids for emulsification applications. It can precisely generate size-tunable, uniform droplets using flow-focusing channels and a normally-closed valve, which is opened by a pneumatic suction force. Experimental data showed that micro-droplets with a diameter ranging from several to tens of micrometers could be precisely generated with a high uniformity. The droplet size is experimentally found to be dependent on the velocity of the dispersed-phase liquid, which is controlled by the deflection of the suction membrane. Emulsions with droplet sizes ranging from 5.5 to 55 μm are successfully observed. The variation in droplet sizes is from 3.8% to 2.5%. The micro-droplets have a uniform size and droplets smaller than those reported in previous studies are possible with this approach. This new microfluidic device can be promising for emulsification and other related applications.

Graphical Abstract

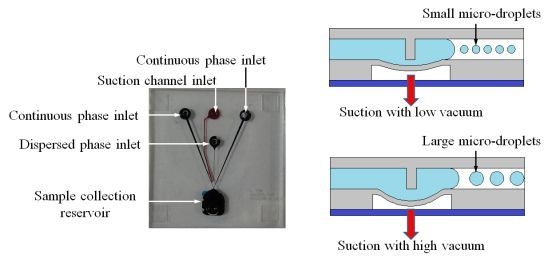
1. Introduction

Formation of liquid droplets in another immiscible fluid is important in emulsion, particularly when the droplet size and size distribution can be controlled on a micro- or nano-scale [1]. This technique for the emulsification process has been widely applied in several industries, including cosmetics, foods, paints and drugs [2]. The benefit of small-droplet emulsions in the oral administration of drugs has been also reported [3] and the absorption of the emulsion in the gastrointestinal tract has been correlated to their droplet size. Small-droplet emulsions are also used as ocular delivery systems to sustain the pharmacological effect of drugs in comparison with their respective solutions [4]. Cationic small-droplet emulsions were evaluated as DNA vaccine carriers to be administered by the pulmonary route [5]. They are also interesting candidates for the delivery of drugs or DNA plasmids through the skin after topical administration [6]. It is known that the quality of the emulsification process is determined by the formation of homogeneous emulsions. Compared to a large-scale stirring process, microfluidic devices improve the quality of emulsion since they generate more uniform droplets. For example, the formation of micro-droplets from membrane emulsification has been reported [7,8]. Microporous membranes with a mean pore size ranging from 0.4 to 6.6 μm were used to generate an oil-in-water (o/w) emulsion. This method generated droplets three times larger than the pore size. Another “microchannel array” method also generated monodispersed emulsion droplets [9]. When the dispersed-phase liquid passed through the terrace/microchannel, the emulsification exploits the interfacial tension, which is the dominating force on a micrometer scale, as the driving force for droplet formation. The model based on the droplet formation mechanism and experimental observation in the microchannel array system was also reported for predicting droplet diameters [10]. These microchannel devices could generate micro-droplets successfully. However, it remains a difficulty of fine-tuning the size of micro-droplets. Consequently, a flow-focusing technique capable of controlling the size of micro-droplets in emulsion was reported [11]. It enabled the break-up of the pre-focused flow forming droplets in immiscible liquids [11,12,13]. Moreover, through the tuning of velocity ratio between the center and the sheath flows, the size of the micro-droplets could be well controlled. Alternatively, an axisymmetric flow-focusing device with co-axial tubing was also proposed [14,15,16,17]. It prevented droplets from adhering or wetting onto the wall in microchannels. The typical diameter of the droplets at the exit orifice ranges from 20 to 200 μm, which allows a wide range adjustment of the droplet size. Note that the variation of the droplet size in these emulsions ranges from 3% to 10%.
Other techniques, such as T-junction channels [18,19,20,21] and tunable micro-choppers [22,23,24], have also been demonstrated for single or even double emulsions. For instance, T-shaped channels force two flows of immiscible liquids to merge in such a way that one liquid forms droplets dispersed in another liquid [18]. Furthermore, double T-junction channel layouts can successfully generate both water-in-oil-in-water (w/o/w) and oil-in-water-in-oil (o/w/o) double emulsion droplets in one chip [25]. Typical diameters of the droplets generated by using the T-shaped channel range from 10 to 250 μm, and droplets produced at each junction could have narrow size distributions with the coefficients of variation (CVs) less than 3%.
In order to fine-tune the size of the emulsion droplets, several types of active emulsion chips were proposed in the literature. For instance, by using the combination of flow focusing or T-junction structures and a controllable chopper, the emulsion droplets can be formed by either a horizontal [22] or a vertical chopping device [24,26]. Furthermore, a microfluidic device with a T-channel equipped with a normally-open valve has been demonstrated to generate emulsion droplets with tunable sizes [21]. For the droplets formed by the flow focusing method, the width of the sample stream can also be fine-turned by using syringe pumps [26] or moving-wall structures [24] such that the size of the droplets can be adjusted accordingly. However, the minimum diameter of the droplets utilizing the tunable choppers was just 10 μm. Therefore, there still remains a great need to fabricate a microfluidic device for the generation of size-tunable micro-droplets with a smaller diameter. In addition, many formations of emulsion performed by thermal [27], magnetic [28], electrostatic [29], optic [30] and many other control methods have also been presented. Briefly, the control schemes of these methods may be relatively complicated. Furthermore, the power consumption of these devices may be relatively high and they also required the peripheral apparatus. In this study, a new technique using flow-focusing channels and a normally-closed (NC) micro-valve with a suction membrane to generate uniform micro-droplets with tunable sizes is demonstrated. Briefly, NC valve restricted volumetric flow to decrease the droplet size. It is well documented that a flow-focusing configuration can be used to provide a stable and continuous stream for generating the emulsion droplets [31]. It has been reported that the diameter of the pre-focused stream depends on the dimensions of the center channel [23,26]. Accordingly, the size of the micro-droplets depends on the dimensions of the center channel. Recently, flow focusing techniques were adopted to generate smaller droplets by fabricating an extremely small center channel for a dispersed-phase liquid [32]. However, this usually involves a delicate fabrication process. The NC micro-valve acting as a nano-channel for sample concentration has been demonstrated in our previous study [33]. In this study, it is used as a center channel with extremely small opening dimensions such that smaller droplets can be generated. To the best of our knowledge, it is the first time that the combination of the flow-focusing channel and a NC mico-valve can be used for generating size-tunable, uniform micro-droplets in liquids. With this approach, a flow-focusing configuration is first used to form a stable and continuous stream for generating the emulsion droplets. Then, without changing the setup of the syringe pumps, the local velocity of the dispersed-phase liquids could be fine-tuned in the central microchannel using the deflection of the suction membrane located on the NC micro-valve, and therefore, changing the size of the emulsion micro-droplets. It is demonstrated that the developed chip is capable of generating the size-tunable droplets by using a NC valve to locally vary the velocity of the dispersed-phase liquid. The droplet size was dependent on the varied velocity of the dispersed-phase liquid caused by the deflection of the suction membrane. Compared to the previous studies using the active choppers [22] or the moving walls [24,26], the NC micro-valve could also precisely control the velocity of the dispersed-phase liquid without leakage to generate droplets with a smaller size. Furthermore, the size of the micro-droplets could be precisely controlled by the pneumatic deflection of the suction membrane. Experimental data show that this microfluidic device could successfully generate micro-droplets in liquids with controllable droplet sizes. The development of this microfluidic device may provide a promising approach for the generation of smaller micro-droplets for a variety of industrial applications.

2. Experimental Section

2.1. Chip Design

The current study uses a NC micro-valve capable of locally changing the velocities of the dispersed-phase liquid by using the deflection of the suction membrane to generate uniform emulsion droplets with variable sizes. Figure 1a shows a schematic illustration of the microfluidic chip with flow-focusing channels and a NC micro-valve. The dimensions of the microchannels and the NC micro-valve are shown in Figure 1b. Continuous-phase liquids in the sheath-flow channels and dispersed-phase liquid in the sample flow channel are first hydrodynamically driven into the microfluidic chip. The velocities of the dispersed-phase liquids can be well controlled by the deflection of the suction membrane of the NC micro-valves (Figure 1c), which determines the opening of the center channel. Then, the center sample flow can be focused into a narrow stream by the surrounding sheath flows to generate droplets with smaller sizes.
Micromachines 04 00306 g001 1024
Figure 1. (a) Schematic illustration of the microfluidic chip. (b) Close-up view of the microchannels and the NC micro-valve. (c) Cross-sectional view of the microfluidic chip. (d) Schematic illustrations of the operation of the NC micro-valve to control the size of the emulsion micro-droplets.
Figure 1. (a) Schematic illustration of the microfluidic chip. (b) Close-up view of the microchannels and the NC micro-valve. (c) Cross-sectional view of the microfluidic chip. (d) Schematic illustrations of the operation of the NC micro-valve to control the size of the emulsion micro-droplets.
Micromachines 04 00306 g001
Figure 1d is a schematic illustration of the working principle of the NC micro-valve. Liquids are pumped into the microchannels by using syringe pumps. When the suction chamber is activated by applying a pneumatic suction force, the polydimethylsiloxane (PDMS) membrane is deflected and the velocity of the dispersed-phase liquid is varied. Then, the dispersed-phase liquid is focused into a narrow stream to generate the emulsion micro-droplets. The deflection of the suction membrane is used to determine the diameters of the droplets. Alternatively, the size of the droplet can be also controlled by changing the velocities of the sheath flows. However, this may cause instability in the flow and non-uniform droplets could be generated during operation [22,23,24,26,31,34]. With this current approach, tunable droplets with smaller sizes can be generated. The micro-droplets with well-controlled sizes are generated by using the flow-focusing technique and the NC micro-valve. Finally, the emulsion droplets are collected at the outlet. Hence, there is no need to change the setup of the syringe pumps, which may cause instability in the flow velocities and lead to non-uniform droplets during the operation.

2.2. Fabrication Process

A microfluidic chip with flow-focusing channels and a NC micro-valve has been fabricated using micro-electro-mechanical-systems (MEMS) fabrication process. Figure 2a shows an exploded view of the microfluidic device consisting of two PDMS layers and one glass plate. A simplified fabrication process is shown in Figure 2b. As shown in Figure 2b-1, a layer of SU-8 negative thick photoresist (PR, MicroChem Corp., Newton, MA, USA) with a thickness of 50 and 250 μm, respectively, were first spun onto a silicon substrate and followed by a soft bake process. A standard lithography process with an exposure dose equal to 750 mJ/cm2 was then performed and followed by a post exposure bake process. In Figure 2b-2, the SU-8 development process was finished by immersing the exposed substrates into a developer solution (MicroChem Corp., Newton, MA, USA) and using ultrasonic agitation to obtain well-defined SU-8 structures. The two SU-8 templates were then replicated by using a PDMS casting process to form microfluidic structures with inverse images, as shown in Figure 2b-3,4. Then the double-layer PDMS and the glass substrate were surface-treated with oxygen plasma and bonded together to form the PDMS membranes and NC micro-valve, as shown in Figure 2b-5. Notably, a cover mask has been employed to cover the surface of the floating-block structures of the normally closed micro-valves during the oxygen plasma treatment, such that surface of the normally closed micro-valves would not be bound with the pneumatic layer. The flexible property of PDMS membranes allows a pneumatic suction force to deflect the membrane such that the NC micro-valve can be opened to generate smaller droplets. Furthermore, the opening can be controlled by the applied suction force (see Figure 1d) for the generation of the micro-droplets with different diameters. Furthermore, the velocity of the dispersed-phase liquids can be adjusted accordingly without changing the setup of the syringe pumps. A photograph of the microfluidic chip after assembly is shown in Figure 3a. The dimensions of the chip are measured to be 35 mm × 35 mm. Figure 3b is a photograph of the NC micro-valve.
Micromachines 04 00306 g002 1024
Figure 2. (a) Exploded view of the microfluidic chip. (b) Simplified fabrication process of the chip.
Figure 2. (a) Exploded view of the microfluidic chip. (b) Simplified fabrication process of the chip.
Micromachines 04 00306 g002
Micromachines 04 00306 g003 1024
Figure 3. Photographs of (a) the microfluidic chip and (b) the NC valve after assembly.
Figure 3. Photographs of (a) the microfluidic chip and (b) the NC valve after assembly.
Micromachines 04 00306 g003

2.3. Experimental Setup

In order to demonstrate the capability of the developed microfluidic chip, water-in-oil emulsions are performed. Most emulsions are not thermodynamically stable. However, quite stable emulsions can occur that resist demulsification treatments and may be stable for weeks/months/years without depending on the emulsion size. Most meta-stable emulsions that will be encountered in practice contain oil, water and an emulsifying agent (or stabilizer), which is usually a surfactant, a macromolecule, or finely divided solids. Emulsions also tend to be more stable when there is tighter packing of hydrophobic groups at the oil/water interface. Deionized (DI) water solution with Triton X-100 (surfactant, concentration = 3 wt%, hydrophilic-lipophilic balance (HLB) = 13.5, Sigma Chemical, St. Louis, MO, USA) was used as the dispersed-phase liquid. Purified olive oil (No. 800-1, Sigma Chemical, St. Louis, MO, USA) was used as the continuous-phase liquid. All liquids were filtered through a 0.45-μm pore-size filter (Millipore Corp., Billerica, MA, USA) prior to use.
The experimental setup was comprised of a vacuum pump (Model No: 50815, Gamela Enterprise Co., Ltd., Taiwan), a control circuit, electromagnetic valves (EMVs, S070M-5BG-32, SMC Inc., Tokyo, Japan), two syringe pumps (KDS 200, Macro Fortunate Co., Ltd., Taiwan), an optical microscope (ECLIPSE L200, Nikon, Melville, NY, USA), a high-speed charge-couple device (CCD, TE/CCD512TKM, Roper Scientific, Princeton, NJ, USA), and a personal computer. Syringe pumps were used to drive two immiscible liquids into the microfluidic chip at well-controlled flow velocities. The formation of the micro-droplets was observed under the microscope and was recorded by the computer equipped with a high-speed CCD. The size and uniformity of the major droplets, the divided droplets, and the double-emulsion droplets were measured and counted from the recorded images.

3. Results and Discussion

The microfluidic device was used to generate micro-droplets with sizes ranging from 5.5 to 55 μm. The membrane deflection of the NC micro-valve was first characterized. The deflection of the membrane was measured via a side-view image by using a camera (FinePix S5 Pro, Fujifilm, Tokyo, Japan) with a high magnification lens, as shown in Figure 4a. Figure 4b shows the relationship between the membrane deflections and the applied absolute pressure. In addition, the theoretical deflection of the suction membrane can be calculated using the following formula [35]:
Micromachines 04 00306 i001
where P is the applied “absolute” pressure, a is the equivalent diaphragm radius of 500 μm, E is the Young’s modulus (about 0.8 MPa for PDMS), h is the diaphragm thickness of 100 μm, ν is the Poisson’s ratio (0.5 for PDMS), and y is the center deflection of the diaphragm. In the Formula (1), the applied “absolute” pressure with a unit of Pa, P, was defined as the total of the atmospheric pressure and the gauge pressure. Note that the gauge with the vacuum pressure was used in this approach, and the applied absolute pressure was used with a unit of psi in this study. The dimensions of the suction membrane are 50, 100, and 100 μm in width, length and thickness, respectively. The dotted line in Figure 4b is the theoretical deflection of the membrane, which is calculated from Formula (1). As expected, a larger membrane deflection is generated at lower applied absolute pressures (a larger suction force). In addition, the measured deflection of the membrane is in agreement with the calculations. In this study, a maximum measured deflection of 11 μm is generated at an applied absolute pressure of 4.5 psi. Therefore, droplets with smaller diameters can be generated since the velocity of the dispersed-phase liquid is varied by tuning the deflection of the suction membrane. Note that an initial membrane defection of 0.8 μm exists when the syringe pumps are activated.
As described above, the downstream velocity of the dispersed-phase liquid can be varied by fine-tuning the deflection of the suction membrane to generate droplets with smaller diameters. Figure 4c shows the regions of the microfluidic chip where the upstream and downstream flow velocities were measured. Note that the motion of 10-μm polystyrene beads flowing through a 100-μm distance was recorded by a high-speed CCD camera with an image acquisition rate of 1000 Hz to measure the downstream velocity of the dispersed-phase liquid (V1’) before the micro-droplets were produced. The flow velocities 200-μm upstream and downstream of the NC micro-valve, respectively, were measured. The time that the beads flowed through a 100-μm distance would be measured and averaged. Then, the upstream and downstream velocities were calculated accordingly. Here, the downstream flow velocity was measured before the micro-droplets were produced. Figure 4d shows that the downstream velocity of the dispersed-phase liquid (V1’) after flowing through the NC micro-valve when operated at different applied absolute pressures. In this approach, the flow cross-section region would be reduced since the fluid flowed through the sub-micro or nano-channel. Based on the continuity equation of fluid, the velocity of the fluid would be increased with the decreasing of the flow region. Therefore, the velocity of the flow in the vicinity of the flow focusing would be higher than that far upstream of the valve. The velocity of the continuous-phase liquid (V2) was set at 50 μm/s in this case. Note that two experiments were performed with syringe pump flow rates for the dispersed-phase liquid set at 3.75 and 4.50 μL/min. respectively. Therefore, the upstream (initial) velocities of the dispersed-phase liquid (V1) were kept at 25 and 30 μm/s, respectively. With a constant volume flow rate provided by the syringe pump, the downstream velocity of the dispersed-phase liquid can be varied by changing the depth of the channel which can be adjusted by fine-tuning the deflection of the suction membrane. As expected, the downstream velocity decreases with the increasing suction force (i.e., a decrease in the absolute pressure). In this study, the maximum V1’ was found to be 1850 μm/s when the deflection of the membrane was 0.8 μm with an applied absolute pressure of 14.7 psi (without any applied suction force).
Micromachines 04 00306 g004 1024
Figure 4. (a) The maximum deflection of membrane were measured as (1) 11 μm (for 4.5 psi) and (2) 0.8 μm (for 14.7 psi), respectively. (b) The membrane deflection of the NC micro-valve at different applied absolute pressures. Note that the initial membrane defection is 0.8 μm when the syringe pumps are activated. (c) The upstream and downstream flow velocities were measured in the (1) upstream and (2) downstream regions which were distant form the NC valve with 200 μm, respectively. (d) The downstream velocity of the dispersed-phase liquid (V1’) after flowing through the NC micro-valve when operated at different suction pressures. The velocity of the continuous-phase liquid (V2) is set at 50 μm/s. Two experiments with two different upstream (initial) velocities of the dispersed-phase liquid (V1) of 25 and 30 μm/s, respectively, are performed.
Figure 4. (a) The maximum deflection of membrane were measured as (1) 11 μm (for 4.5 psi) and (2) 0.8 μm (for 14.7 psi), respectively. (b) The membrane deflection of the NC micro-valve at different applied absolute pressures. Note that the initial membrane defection is 0.8 μm when the syringe pumps are activated. (c) The upstream and downstream flow velocities were measured in the (1) upstream and (2) downstream regions which were distant form the NC valve with 200 μm, respectively. (d) The downstream velocity of the dispersed-phase liquid (V1’) after flowing through the NC micro-valve when operated at different suction pressures. The velocity of the continuous-phase liquid (V2) is set at 50 μm/s. Two experiments with two different upstream (initial) velocities of the dispersed-phase liquid (V1) of 25 and 30 μm/s, respectively, are performed.
Micromachines 04 00306 g004
Figure 5 shows successful formation of emulsion micro-droplets at different applied absolute pressures by deforming the suction membrane of the NC micro-valve. In order to better understand the relationship between the droplet size and the applied absolute pressure, this study only shows the distributions and uniformity of the droplets at the maximum, a selected sub-maximum, the minimum, and the mean applied absolute pressure. Therefore, the applied absolute pressures are 4.5 psi, 10.4 psi, 14.2 psi, and 14.7 psi, respectively. In this case, V2 is kept constant (50 μm/s), and V1 of the dispersed-phase liquid is set at 30 μm/s. It can be clearly seen that the size of emulsion droplets with a low CV value can be well controlled by changing the deflection of the suction membrane. The deflections of the suction membrane were measured to be 10.9 μm for 4.5 psi, 4.2 μm for 10.4 psi, 0.9 μm for 14.2 psi, and 0.8 μm for 14.7 psi, respectively. The average droplet diameters were measured to be 58 μm, 34 μm, 10 μm, and 5.5 μm, respectively, for these four cases. The CVs in droplet size were measured to be 3.8%, 3.3%, 2.9%, and 2.5%, respectively. It was difficult for the formation of droplet by using the T-junction microchannel since the high velocity of the dispersed-phase liquid would break the continuance-phase flow to spot the droplet formation. Compared to the previous study using the flow focusing method [12,36,37], which reported emulsion droplets with a smallest diameter of 20 μm and a CV of more than 3%, the current device has a superior performance because it generates droplets with a smaller diameter (5.5 μm) with a CV of only 2.5%. In addition, it also has a better performance when compared with other devices that use tunable structures (with a smallest diameter of 10 μm for these other devices) [38,39,40]. Smaller droplets with a diameter of several micrometers could be also generated using a similar approach. In this study, the smallest droplet diameter was observed to be 5.5 μm when applying an absolute pressure of 14.7 psi.
Micromachines 04 00306 g005 1024
Figure 5. Formation of micro-droplets using the NC micro-valve with different applied absolute pressures. The size of the emulsion droplets can be precisely controlled using the micro-valve operated at different applied absolute pressures. Average droplet diameters are measured to be (a) 58 μm (for 4.5 psi), (b) 34 μm (for 10.4 psi), (c) 10 μm (for 14.2 psi), and (d) 5.5 μm (for 14.7 psi), respectively. The histograms of size distributions with a total number of 100 micro-droplets for applied absolute pressures of (e) 4.5 psi, (f) 10.4 psi, (g) 14.2 psi, and (h) 14.7 psi, respectively. The CVs in droplet sizes were measured to be 3.8%, 3.3%, 2.9%, and 2.5%, respectively. The V1 and V2 are set at 30 and 50 μm/s, respectively. The droplet diameter without applying any suction force is 5.5 μm.
Figure 5. Formation of micro-droplets using the NC micro-valve with different applied absolute pressures. The size of the emulsion droplets can be precisely controlled using the micro-valve operated at different applied absolute pressures. Average droplet diameters are measured to be (a) 58 μm (for 4.5 psi), (b) 34 μm (for 10.4 psi), (c) 10 μm (for 14.2 psi), and (d) 5.5 μm (for 14.7 psi), respectively. The histograms of size distributions with a total number of 100 micro-droplets for applied absolute pressures of (e) 4.5 psi, (f) 10.4 psi, (g) 14.2 psi, and (h) 14.7 psi, respectively. The CVs in droplet sizes were measured to be 3.8%, 3.3%, 2.9%, and 2.5%, respectively. The V1 and V2 are set at 30 and 50 μm/s, respectively. The droplet diameter without applying any suction force is 5.5 μm.
Micromachines 04 00306 g005
Figure 6 shows the relationship between the average diameters of the droplets and the applied absolute pressures. Again, two experiments with V1 of 25 and 30 μm/s, respectively, for the dispersed-phase liquid were conducted. Static applied absolute pressures ranging from 4.5 psi to 14.7 psi were used to form the micro-droplets in this case. It is clearly seen that diameter of the droplets is well controlled by using the deflection of the suction membrane. As expected, as the applied pressure decreases, the size of the droplet increases accordingly. This is because an increase in the suction force causes more deflection of the membrane, thus increasing the cross sectional area of the channel as shown in Figure 4a. Therefore, the size of the micro-droplets increases accordingly. When the applied pressure was higher than 14.7 psi, the micro-valve would block up the microchannel and the dispersed-phase could not flow through. Therefore, no emulsions can be observed. In addition, the average diameter of the micro-droplet also decreases with a decrease in V1. The smallest droplet diameters without opening the micro-valve are 6.5 and 5.5 μm when V1 is 25 and 30 μm/s, respectively. Compared to the droplets generated by using a microchannel with the moving structure, this device can successfully generate droplets with smaller diameters in a simple manner without using delicate fabrication processes to create the extremely small center channel.
Micromachines 04 00306 g006 1024
Figure 6. The relationship between the average diameters of the droplets and the applied absolute pressures. The V2 is kept constant (50 μm/s). The smallest droplet diameters without opening the micro-valve are 6.5 and 5.5 μm when the V1 are 25 and 30 μm/s, respectively.
Figure 6. The relationship between the average diameters of the droplets and the applied absolute pressures. The V2 is kept constant (50 μm/s). The smallest droplet diameters without opening the micro-valve are 6.5 and 5.5 μm when the V1 are 25 and 30 μm/s, respectively.
Micromachines 04 00306 g006
The droplet formation frequency, which is defined by the number of droplets generated within a set period of time, is also explored. Figure 7 shows the relationship between the droplet formation frequency and the applied absolute pressures on the suction membrane. V2 is kept constant at 50 μm/s. The droplet formation frequency clearly increases with the increase in the applied absolute pressure when the V1’ increases with the decreasing deflection of the suction membrane. When no suction force (at an applied absolute pressure of 14.7 psi) is applied to the membrane structure, the external syringe pump still delivers a discrete volume of fluid to overcome the NC valve mechanism. Therefore, the pressure of the discrete flowing fluid build behind the NC valve to flow pass downstream, and the droplet formation frequency is as high as 96 and 94 Hz, respectively, for corresponding V1’ of 1850 and 1575 μm/s. Note that when the smallest absolute pressure of 4.5 psi is applied, the droplet formation frequency is only around 13 and 7 Hz for corresponding V1’ of 135 and 115 μm/s. Actually, the less pressure of the flowing fluid is required to overcome the NC valve mechanism since the NC valve is always driven with the applied pressure. For this season, the size and formation frequency of droplet were determined by the flow ratios of the dispersed-phase liquid to the continuous-phase liquid.
Micromachines 04 00306 g007 1024
Figure 7. The relationship between the droplet formation frequency and the applied absolute pressures on the suction membrane. The V2 is constant at 50 μm/s.
Figure 7. The relationship between the droplet formation frequency and the applied absolute pressures on the suction membrane. The V2 is constant at 50 μm/s.
Micromachines 04 00306 g007
In addition to use the NC micro-valve to control the gap statically, it is a membrane structure allowing vertical movement and therefore the suction membrane can be also used as an active chopper to partition the liquid streams during the droplet formation process. Previous works reported that the diameter of the droplets decreased with an increase in the chopping frequency [22,23,24,26,31,34]. However, those active choppers were used to break a “pre-focused” stream into micro-droplets. In this study, the effect of the chopping frequency of the suction membrane is explored, which partitions the stream before the flow focusing process. For the minimum membrane deflection of 0.8 μm without any suction force (the applied absolute pressure is 14.7 psi), the suction membrane driven at different frequencies from 0 Hz to 60 Hz could not break the continuity of the liquid stream since V1’ is too high. Besides, the maximum deflection of 11 μm (at an applied absolute pressure of 4.5 psi) could not be achieved at high driving frequencies ranging from 35 Hz to 60 Hz, also to break the continuity of the stream. Therefore, an absolute pressure of 10.4 psi was chosen to explore the relationship between the driving frequency of the EMV and the resulting droplet sizes. Note that the deflection of the suction membrane when driven at an applied absolute pressure of 10.4 psi is 4.2 μm. Figure 8 shows the relationship between the droplet diameters and the driving frequencies of the EMVs at a mean applied absolute pressure of 11.8 psi. It can be clearly seen that the diameters of the droplets vary significantly when the driving frequency of the EMV is changed from 30 Hz to 50 Hz. It is seen in Figure 8 that droplets with the smallest diameter of 7.0 and 6.5 μm for corresponding V1 of 25 and 30 μm/s, respectively, can be successfully generated. However, the droplet size does not change significant at lower driving frequencies (less than 30 Hz) or at higher driving frequencies (higher than 50 Hz).
The droplet formation frequency at 10.4 psi was found to be 57 Hz (Figure 7). Therefore, when the chopping frequency is too low, it does not affect the formation of the droplet and the resulting droplet size. If the chopping frequency is close to the droplet formation frequency, then the droplet can be effectively chopped into a smaller size, as shown in Figure 8. However, when the chopping frequency is too high, the release time of the applied pressure limits the complete deflection of the suction membrane; therefore, the chopping is not effective [41,42].
Micromachines 04 00306 g008 1024
Figure 8. The relationship between the average diameter of the droplets and the driving frequency of the EMV at an applied absolute pressure of 10.4 psi. The V2 is 50 μm/s, and the V1 are 30 μm/s and 25 μm/s, respectively.
Figure 8. The relationship between the average diameter of the droplets and the driving frequency of the EMV at an applied absolute pressure of 10.4 psi. The V2 is 50 μm/s, and the V1 are 30 μm/s and 25 μm/s, respectively.
Micromachines 04 00306 g008

4. Conclusions

We have successfully demonstrated a new microfluidic chip capable of formation of micro-droplets in liquids using flow-focusing channels and a NC micro-valve. This chip is capable of generating uniform micro-droplets with smaller sizes when compared to other devices. In this study, the NC micro-valve could act as a nano-channel to regulate the flow rates for generating the micor-droplets with different sizes by controlling the pneumatic pressure provided to the valve. Compared to the previous studies using the active choppers or normally-open valves, the NC micro-valve could precisely control the flow rate without leakage to generate droplets with an even smaller size. Besides, the delicate fabrication process to fabricate an extremely small channel is not required. To the best of author’s knowledge, it is the first time that a normally-closed valve has been used to generate uniform emulsion droplets with smaller sizes. It has been demonstrated that this developed chip is capable of performing water-in-oil emulsions by using the NC micro-valve to locally vary the velocity of the dispersed-phase liquid. The droplet size is experimentally founded to be dependent on the velocity of the dispersed-phase liquid, which is controlled by the deflection of the suction membrane. Emulsions with droplet sizes ranging from 5.5 to 55 μm are successfully observed. The variation in droplet sizes is form 3.8% to 2.5%. The development of this microfluidic chip could have a great impact on various industries by enabling high-quality emulsification processes.

Acknowledgments

The authors gratefully acknowledge the financial support provided to this study by the National Science Council in Taiwan (NSC101-2218-E-007-006). Partial financial support from the “Towards a World-Class University” Project is also greatly appreciated.

Conflict of Interest

The authors declare no conflict of interest.

References

  1. Wibowo, C.; Ng, K.M. Product-oriented process synthesis and development: Creams and pastes. AIChE J. 2001, 47, 2746–2767. [Google Scholar] [CrossRef]
  2. Hamouda, T.; Hayes, M.M.; Cao, Z.; Tonda, R.; Johnson, K.; Wright, D.C.; Brisker, J.; Baker, J.R. A novel surfactant nanoemulsion with broad-spectrum sporicidal activity against bacillus species. J. Infect. Dis. 1999, 180, 1939–1949. [Google Scholar] [CrossRef]
  3. Nicolaos, G.; Crauste-Manciet, S.; Farinotti, R.; Brossard, D. Improvement of cefpodoxime proxetil oral absorption in rats by an oil-in-water submicron emulsion. Int. J. Pharm. 2003, 263, 165–171. [Google Scholar] [CrossRef]
  4. Rabinovich-Guilatt, L.; Couvreur, P.; Lambert, G.; Dubernet, C. Cationic vectors in ocular drug delivery. J. Drug Target. 2004, 12, 623–633. [Google Scholar] [CrossRef]
  5. Bivas-Benita, M.; Oudshoorn, M.; Romeijn, S.; van Meijgaarden, K.; Koerten, H.; van der Meulen, H.; Lambert, G.; Ottenhoff, T.; Benita, S.; Junginger, H.; et al. Cationic submicron emulsions for pulmonary DNA immunization. J. Control. Release 2004, 100, 145–155. [Google Scholar] [CrossRef]
  6. Fang, J.-Y.; Leu, Y.-L.; Chang, C.-C.; Lin, C.-H.; Tsai, Y.-H. Lipid nano/submicron emulsions as vehicles for topical flurbiprofen delivery. Drug Deliv. 2004, 11, 97–105. [Google Scholar] [CrossRef]
  7. Nakashima, T.; Shimizu, M.; Kukizaki, M. Membrane emulsification by microporous glass. Key Eng. Mater. 1992, 61–62, 513–516. [Google Scholar] [CrossRef]
  8. Charcosset, C.; Limayem, I.; Fessi, H. The membrane emulsification process—A review. J. Chem. Technol. Biotechnol. 2004, 79, 209–218. [Google Scholar] [CrossRef]
  9. Sugiura, S.; Nakajima, M.; Kumazawa, N.; Iwamoto, S.; Seki, M. Characterization of spontaneous transformation-based droplet formation during microchannel emulsification. J. Phys. Chem. B 2002, 106, 9405–9409. [Google Scholar] [CrossRef]
  10. Sugiura, S.; Nakajima, M.; Iwamoto, S.; Seki, M. Interfacial tension driven monodispersed droplet formation from microfabricated channel array. Langmuir 2001, 17, 5562–5566. [Google Scholar] [CrossRef]
  11. Anna, S.L.; Bontoux, N.; Stone, H.A. Formation of dispersions using “flow focusing” in microchannels. Appl. Phys. Lett. 2003, 82, 364–366. [Google Scholar] [CrossRef]
  12. Takeuchi, S.; Garstecki, P.; Weibel, D.B.; Whitesides, G.M. An axisymmetric flow-focusing microfluidic device. Adv. Mater. 2005, 17, 1067–1072. [Google Scholar] [CrossRef]
  13. Tan, Y.-C.; Cristini, V.; Lee, A.P. Monodispersed microfluidic droplet generation by shear focusing microfluidic device. Sens. Actuat. B Chem. 2006, 114, 350–356. [Google Scholar] [CrossRef]
  14. Lorenceau, E.; Utada, A.S.; Link, D.R.; Cristobal, G.; Joanicot, M.; Weitz, D.A. Generation of polymerosomes from double-emulsions. Langmuir 2005, 21, 9183–9186. [Google Scholar] [CrossRef]
  15. Utada, A.S.; Lorenceau, E.; Link, D.R.; Kaplan, P.D.; Stone, H.A.; Weitz, D.A. Monodisperse double emulsions generated from a microcapillary device. Science 2005, 308, 537–541. [Google Scholar] [CrossRef]
  16. Xu, S.; Nie, Z.; Seo, M.; Lewis, P.; Kumacheva, E.; Stone, H.A.; Garstecki, P.; Weibel, D.B.; Gitlin, I.; Whitesides, G.M. Generation of monodisperse particles by using microfluidics: control over size, shape, and composition. Angew. Chem. Int. Ed. 2005, 44, 724–728. [Google Scholar] [CrossRef]
  17. Yobas, L.; Martens, S.; Ong, W.-L.; Ranganathan, N. High-performance flow-focusing geometry for spontaneous generation of monodispersed droplets. Lab Chip 2006, 6, 1073–1079. [Google Scholar] [CrossRef]
  18. Link, D.R.; Anna, S.L.; Weitz, D.A.; Stone, H.A. Geometrically mediated breakup of drops in microfluidic devices. Phys. Rev. Lett. 2004, 92, 054503. [Google Scholar] [CrossRef]
  19. Tan, Y.-C.; Fisher, J.S.; Lee, A.I.; Cristini, V.; Lee, A.P. Design of microfluidic channel geometries for the control of droplet volume, chemical concentration, and sorting. Lab Chip 2004, 4, 292–298. [Google Scholar] [CrossRef]
  20. Nisisako, T.; Okushima, S.; Torii, T. Controlled formulation of monodisperse double emulsions in a multiple-phase microfluidic system. Soft Matter 2005, 1, 23–27. [Google Scholar] [CrossRef]
  21. Willaime, H.; Barbier, V.; Kloul, L.; Maine, S.; Tabeling, P. Arnold tongues in a microfluidic drop emitter. Phys. Rev. Lett. 2006, 96, 054501. [Google Scholar] [CrossRef]
  22. Chen, C.-T.; Lee, G.-B. Formation of microdroplets in liquids utilizing active pneumatic choppers on a microfluidic chip. J. Microelectromech. Syst. 2006, 15, 1492–1498. [Google Scholar] [CrossRef]
  23. Hsiung, S.-K.; Chen, C.-T.; Lee, G.-B. Micro-droplet formation utilizing microfluidic flow focusing and controllable moving-wall chopping techniques. J. Micromech. Microeng. 2006, 16, 2403. [Google Scholar] [CrossRef]
  24. Hsiung, S.-K.; Lee, C.-H.; Lin, J.-L.; Lee, G.-B. Active micro-mixers utilizing moving wall structures activated pneumatically by buried side chambers. J. Micromech. Microeng. 2007, 17, 129. [Google Scholar] [CrossRef]
  25. Okushima, S.; Nisisako, T.; Torii, T.; Higuchi, T. Controlled production of monodisperse double emulsions by two-step droplet breakup in microfluidic devices. Langmuir 2004, 20, 9905–9908. [Google Scholar] [CrossRef]
  26. Lee, C.-Y.; Lin, Y.-H.; Lee, G.-B. A droplet-based microfluidic system capable of droplet formation and manipulation. Microfluid. Nanofluid. 2009, 6, 599–610. [Google Scholar] [CrossRef]
  27. Nguyen, N.-T.; Ting, T.-H.; Yap, Y.-F.; Wong, T.-N.; Chai, J.C.-K.; Ong, W.-L.; Zhou, J.; Tan, S.-H.; Yobas, L. Thermally mediated droplet formation in microchannels. Appl. Phys. Lett. 2007, 91, 084102. [Google Scholar] [CrossRef]
  28. Montagne, F.; Mondain-Monval, O.; Pichot, C.; Mozzanega, H.; Elaı̈ssari, A. Preparation and characterization of narrow sized (o/w) magnetic emulsion. J. Magn. Magn. Mater. 2002, 250, 302–312. [Google Scholar] [CrossRef]
  29. Nakano, M.; Nakai, N.; Inoue, M.; Takashima, K.; Katsura, S.; Mizuno, A. Electrostatic Droplet-Formation in Water/Oil Flow in a Microchannel System. In Proceedings of the 39th Industry Applications Conference, Seattle, WA, USA, 3–7 October 2004; Volume 2374, pp. 2373–2376.
  30. Bunyan, H. Optical deformation of emulsion droplets. Master’s Thesis, Durham University, Durham City, UK, 2010. [Google Scholar]
  31. Lai, C.-W.; Lin, Y.-H.; Lee, G.-B. A microfluidic chip for formation and collection of emulsion droplets utilizing active pneumatic micro-choppers and micro-switches. Biomed. Microdevices 2008, 10, 749–756. [Google Scholar] [CrossRef]
  32. Lan, C.H.; Yang, C.; Lin, S.; Lin, C.H. Microfluidic T-Junction With An Undercut Orifice To Generate Ultra-Small Droplets. In Proceedings of the 5th Asia-Pacific Conference on Transducers and Micro-Nano Technology, Perth, Australia, 2010; p. 33.
  33. Kuo, C.-H.; Wang, J.-H.; Lee, G.-B. A microfabricated CE chip for DNA pre-concentration and separation utilizing a normally closed valve. Electrophoresis 2009, 30, 3228–3235. [Google Scholar] [CrossRef]
  34. Lin, Y.-H.; Lee, C.-H.; Lee, G.-B. Droplet formation utilizing controllable moving-wall structures for double-emulsion applications. J. Microelectromech. Syst. 2008, 17, 573–581. [Google Scholar] [CrossRef]
  35. Van Mullem, C.J.; Gabriel, K.J.; Fujita, H. Large Deflection Performance of Surface Micromachined Corrugated Diaphragms. In Proceedings of International Conference on Solid-State Sensors and Actuators, Piscataway, NJ, USA, 1991; pp. 1014–1017.
  36. Huang, S.-H.; Tan, W.-H.; Tseng, F.-G.; Takeuchi, S. A monolithically three-dimensional flow-focusing device for formation of single/double emulsions in closed/open microfluidic systems. J. Micromech. Microeng. 2006, 16, 2336. [Google Scholar] [CrossRef]
  37. Luque, A.; Perdigones, F.A.; Esteve, J.; Montserrat, J.; Ganan-Calvo, A.M.; Quero, J.M. Silicon microdevice for emulsion production using three-dimensional flow focusing. J. Microelectromech. Syst. 2007, 16, 1201–1208. [Google Scholar] [CrossRef]
  38. Abate, A.R.; Romanowsky, M.B.; Agresti, J.J.; Weitz, D.A. Valve-based flow focusing for drop formation. Appl. Phys. Lett. 2009, 94, 023503–023503. [Google Scholar]
  39. Guo, F.; Liu, K.; Ji, X.-H.; Ding, H.-J.; Zhang, M.; Zeng, Q.; Liu, W.; Guo, S.-S.; Zhao, X.-Z. Valve-based microfluidic device for droplet on-demand operation and static assay. Appl. Phys. Lett. 2010, 97, 233701–233703. [Google Scholar] [CrossRef]
  40. Romanowsky, M.B.; Heymann, M.; Abate, A.R.; Krummel, A.T.; Fraden, S.; Weitz, D.A. Functional patterning of PDMS microfluidic devices using integrated chemo-masks. Lab Chip 2010, 10, 1521–1524. [Google Scholar] [CrossRef]
  41. Wang, C.-H.; Lee, G.-B. Pneumatically driven peristaltic micropumps utilizing serpentine-shape channels. J. Micromech. Microeng. 2006, 16, 341. [Google Scholar] [CrossRef]
  42. Huang, C.-W.; Hhuang, S.-B.; Lee, G.-B. Pneumatic micropumps with serially connected actuation chambers. J. Micromech. Microeng. 2006, 16, 2265. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Wang, J.-H.; Lee, G.-B. Formation of Tunable, Emulsion Micro-Droplets Utilizing Flow-Focusing Channels and a Normally-Closed Micro-Valve. Micromachines 2013, 4, 306-320. https://doi.org/10.3390/mi4030306

AMA Style

Wang J-H, Lee G-B. Formation of Tunable, Emulsion Micro-Droplets Utilizing Flow-Focusing Channels and a Normally-Closed Micro-Valve. Micromachines. 2013; 4(3):306-320. https://doi.org/10.3390/mi4030306

Chicago/Turabian Style

Wang, Jung-Hao, and Gwo-Bin Lee. 2013. "Formation of Tunable, Emulsion Micro-Droplets Utilizing Flow-Focusing Channels and a Normally-Closed Micro-Valve" Micromachines 4, no. 3: 306-320. https://doi.org/10.3390/mi4030306

Article Metrics

Back to TopTop