Mechanical Response of MEMS Inductor with Auxiliary Pillar under High-g Shock
Abstract
:1. Introduction
2. Mechanical Response of a Suspended Inductor with Auxiliary Pillar under Shock
2.1. Model of the MEMS Suspended Inductor with Auxiliary Pillar and Shock Loads
2.2. Acceleration Response of the Suspended Inductor with Auxiliary Pillar
2.3. Mechanical Response of the Suspended Inductor with Auxiliary Pillar under Mechanical Shock
3. Results and Discussion
4. Extension of the Theory to the Suspended Inductor with Double Auxiliary Pillars
4.1. Mechanical Response of the Suspended Inductor with Double Auxiliary Pillars
- Obtain the natural frequency of the coil part and calculate the acceleration response of the coil part by using a SDOF model.
- Each coil part is a statically indeterminate structure, so its equivalent system can be determined by releasing the constraint of one of its clamped end. Then the canonical equation of the coil part can be established as:where and can be expressed as Equations (82) and (83), respectively, according to Mohr’s integration:where and are the bending moment and torque of the k-th wire segment caused by the impact load, respectively. and are the bending moment and torque of the k-th wire segment caused by the unit load along the direction at the released end, respectively. and are the bending moment and torque of the k-th wire segment caused by the unit load along the direction at the released end, respectively.
- The generalized forces , and can be obtained by solving the canonical equation. Then the bending moment and the torque of the k-th wire segment can be calculated.
- Calculate the critical normal stress and the critical shear stress of the k-th wire segment. Then the Von Mises equivalent stress of the k-th wire segment can be expressed as:
- Apply a unit force to the position wherever the deformation needs to be solved and adopt the Mohr’s integration for calculating the deformation of the coil part. The deformation at any position of the k-th wire segment can be expressed as:where and are the bending moments of the i-th and k-th wire segment, respectively. and are the torques of the i-th and k-th wire segment, respectively. and are the bending moments of the i-th and k-th wire segment caused by the unit force, respectively. and are the torques of the i-th and k-th wire segment caused by the unit force, respectively. is a position indicator variable, .
4.2. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hikmat, O.F.; Ali, M.S.M. RF MEMS Inductors and Their Applications-A Review. J. Microelectromech. Syst. 2017, 26, 17–44. [Google Scholar] [CrossRef]
- Yoon, J.B.; Han, C.H.; Yoon, E.; Kim, C.K. Monolithic high-Q overhang inductors fabricated on silicon and glass substrates. In Proceedings of the IEEE International Electron Devices Meeting, Washington, DC, USA, 5–8 December 1999; pp. 753–756. [Google Scholar]
- Yoon, J.B.; Han, C.H.; Yoon, E.; Kim, C.K. High-performance three-dimensional on-chip inductors fabricated by novel micromachining technology for RF MMIC. In Proceedings of the IEEE International Microwave Symposium Digest, Anaheim, CA, USA, 13–19 June 1999; pp. 1523–1526. [Google Scholar]
- Brown, T.G.; Davis, B.; Hepner, D.; Faust, J. Strap-down microelectromechanical (MEMS) sensors for high-g munition applications. IEEE Trans. Magn. 2017, 37, 336–342. [Google Scholar] [CrossRef]
- Hsieh, M.C.; Jair, D.K.; Lin, C.S. Design and fabrication of the suspended high-Q spiral inductors with X-beams. Microsyst. Technol. 2008, 14, 903–907. [Google Scholar] [CrossRef]
- Lin, J.W.; Chen, C.C.; Cheng, Y.T. A Robust High-Q Micromachined RF Inductor for RFIC Applications. IEEE Trans. Electron Devices 2005, 52, 1489–1496. [Google Scholar] [CrossRef]
- Ribas, R.P.; Lescot, J.; Leclercq, J.L.; Karam, J.M. Micromachined Microwave Planar Spiral Inductors and Transformers. IEEE Trans. Microw. Theory Tech. 2000, 48, 1326–1335. [Google Scholar] [CrossRef]
- Wang, X.N.; Zhao, X.L.; Zhou, Y.; Dai, X.H.; Cai, B.C. Fabrication and performance of a novel suspended RF spiral inductor. IEEE Trans. Electron Devices 2004, 51, 814–816. [Google Scholar] [CrossRef]
- Millet, O.; Collard, D.; Buchaillot, L. Reliability of packaged MEMS in shock environment: Crack and stiction modeling. In Proceedings of the Design, Test, Integration and Packaging of MEMS/MOEMS, Cannes-Mandelieu, France, 19 April 2002; pp. 696–703. [Google Scholar]
- Fang, X.W.; Huang, Q.A.; Tang, J.Y. Modeling of MEMS Reliability in Shock Environment. In Proceedings of the 7th International Conference on Solid-State and Integrated Circuits Technology, Beijing, China, 18–21 October 2004; pp. 860–863. [Google Scholar]
- Fang, X.W.; Tang, J.Y.; Tang, J.Y. Analysis of Micromachined Cantilevers in Transverse Shock. Chin. J. Semicond. 2005, 26, 379–384. [Google Scholar]
- Younis, M.I.; Jordy, D.; Pitarresi, J.M. Computationally Efficient Approaches to Characterize the Dynamic Response of Microstructures under Mechanical Shock. J. Microelectromech. Syst. 2007, 16, 628–638. [Google Scholar] [CrossRef]
- Srikar, V.T.; Senturia, S.D. The Reliability of Microelectromechanical Systems (MEMS) in Shock Environments. J. Microelectromech. Syst. 2002, 11, 206–214. [Google Scholar] [CrossRef]
- Li, G.X.; Shemansky, F.A., Jr. Drop test and analysis on micro-machined structures. Sens. Actuators A Phys. 2000, 85, 280–286. [Google Scholar] [CrossRef]
- Sundaram, S.; Tormen, M.; Timotijevic, B.; Lockhart, R.; Overstolz, T.; Stanley, R.P.; Shea, H.R. Vibration and shock reliability of MEMS: Modeling and experimental validation. J. Micromech. Microeng. 2011, 21, 1–13. [Google Scholar] [CrossRef]
- Lu, C.Y.; Xu, L.X.; Li, J.H.; Fu, B.; Ou, X.L. CMOS-compatible High-Q Micro-electro-mechanical System Suspended on-chip Spiral Inductor. Acta Armamentarii 2014, 35, 634–639. [Google Scholar]
- Shi, Y.B.; Zhu, Z.Q.; Liu, X.P.; Liu, J.; Tan, Q.L. Dynamic Property Test of a Novel High g Microaccelerometer. In Proceedings of the IEEE International Conference on Asic, Changsha, China, 20–23 October 2009; pp. 633–635. [Google Scholar]
- Shi, Y.B.; Zhu, Z.Q.; Liu, X.P.; Du, K.; Liu, J. Design and impact analysis of a high-g accelerometer. Explos. Shock Waves 2010, 30, 329–332. [Google Scholar]
- Harris, C.M.; Piersol, A.G. Harris’s Shock and Vibration Handbook, 5th ed.; McGraw-Hill: New York, NY, USA, 2010; Chapter 8. [Google Scholar]
- Dolbow, J.; Gosz, M. Effect of out-of-plane properties of a polymide film on the stress fields in microelectronic structures. Mech. Mater. 1996, 23, 311–321. [Google Scholar] [CrossRef]








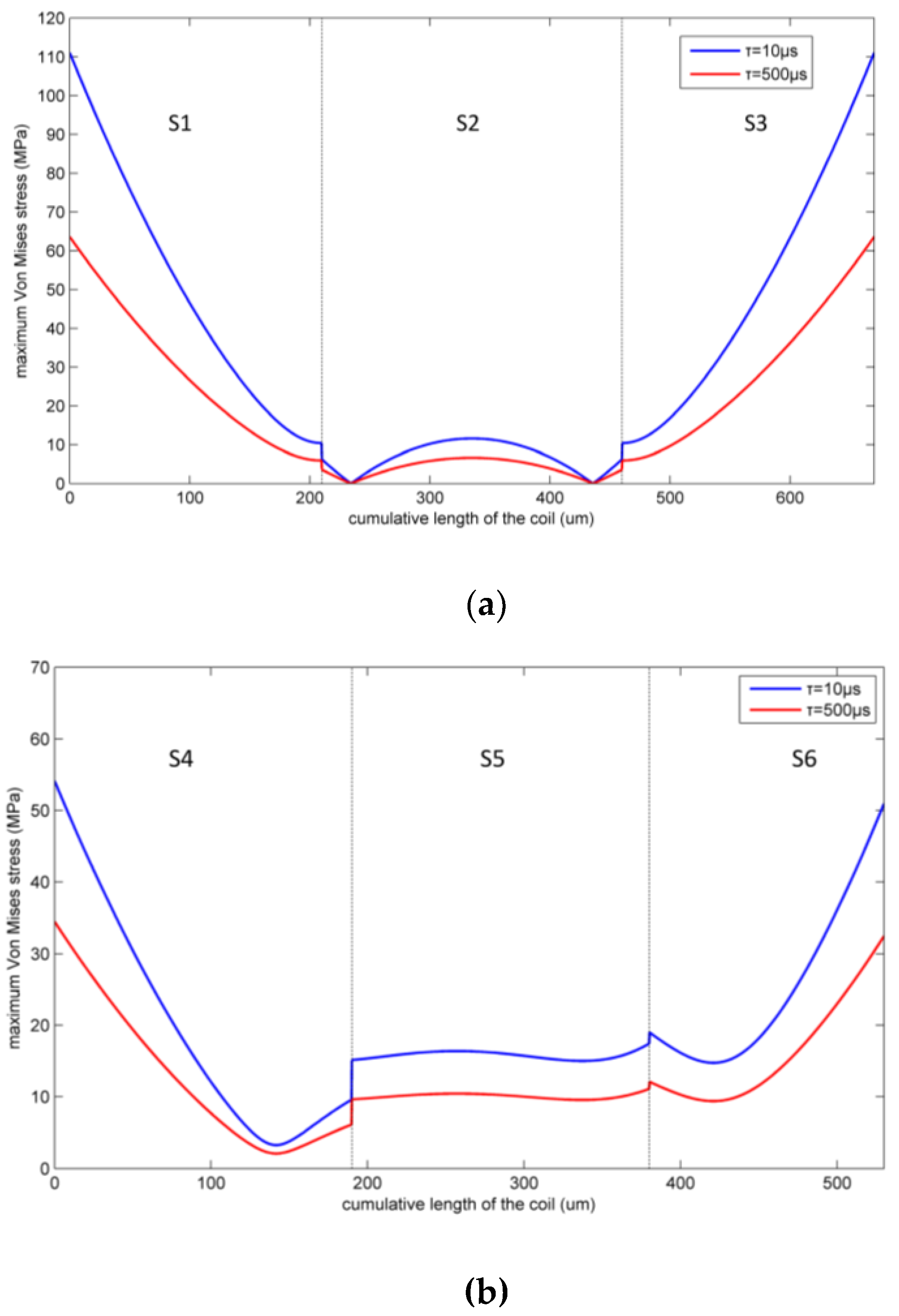



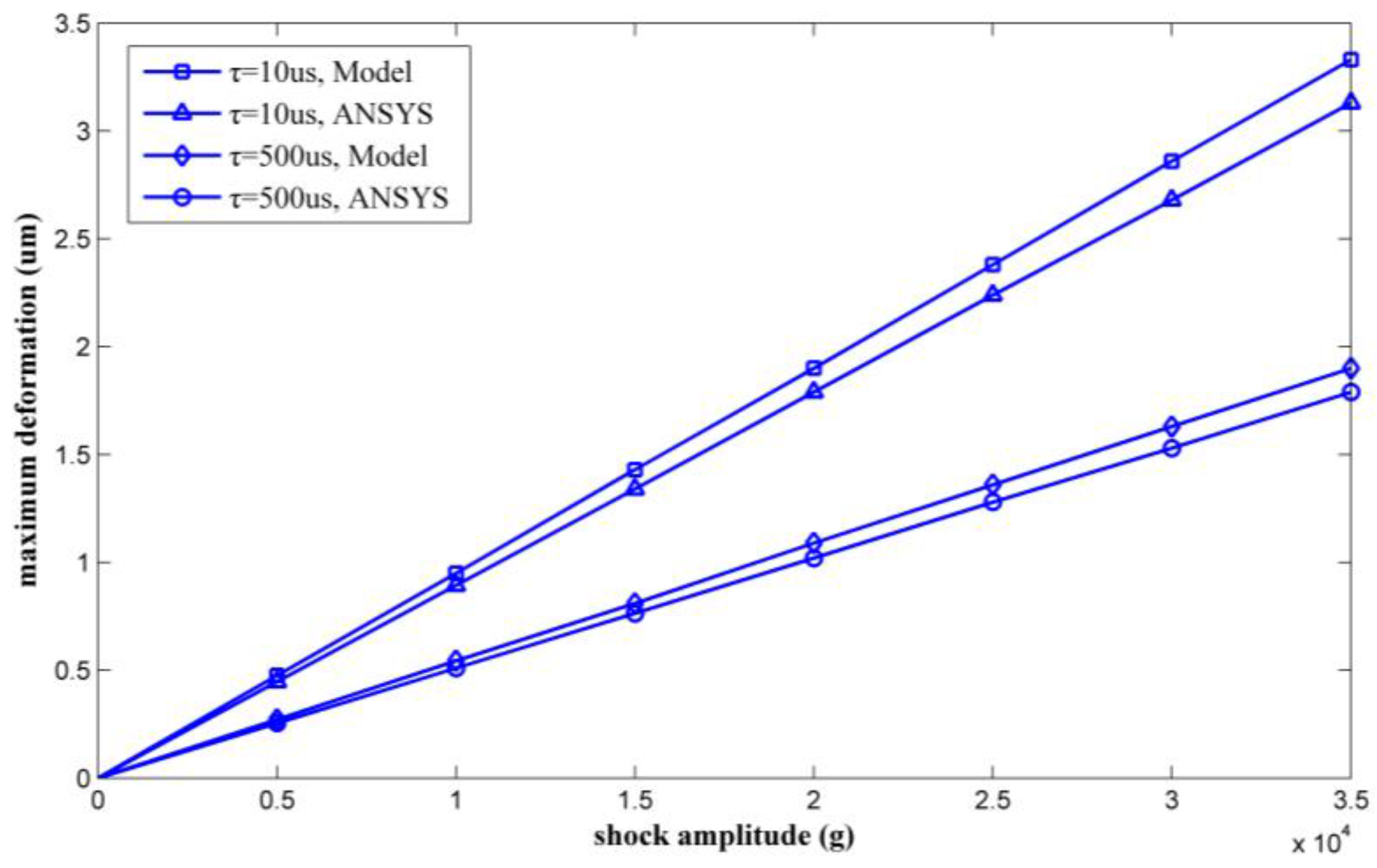
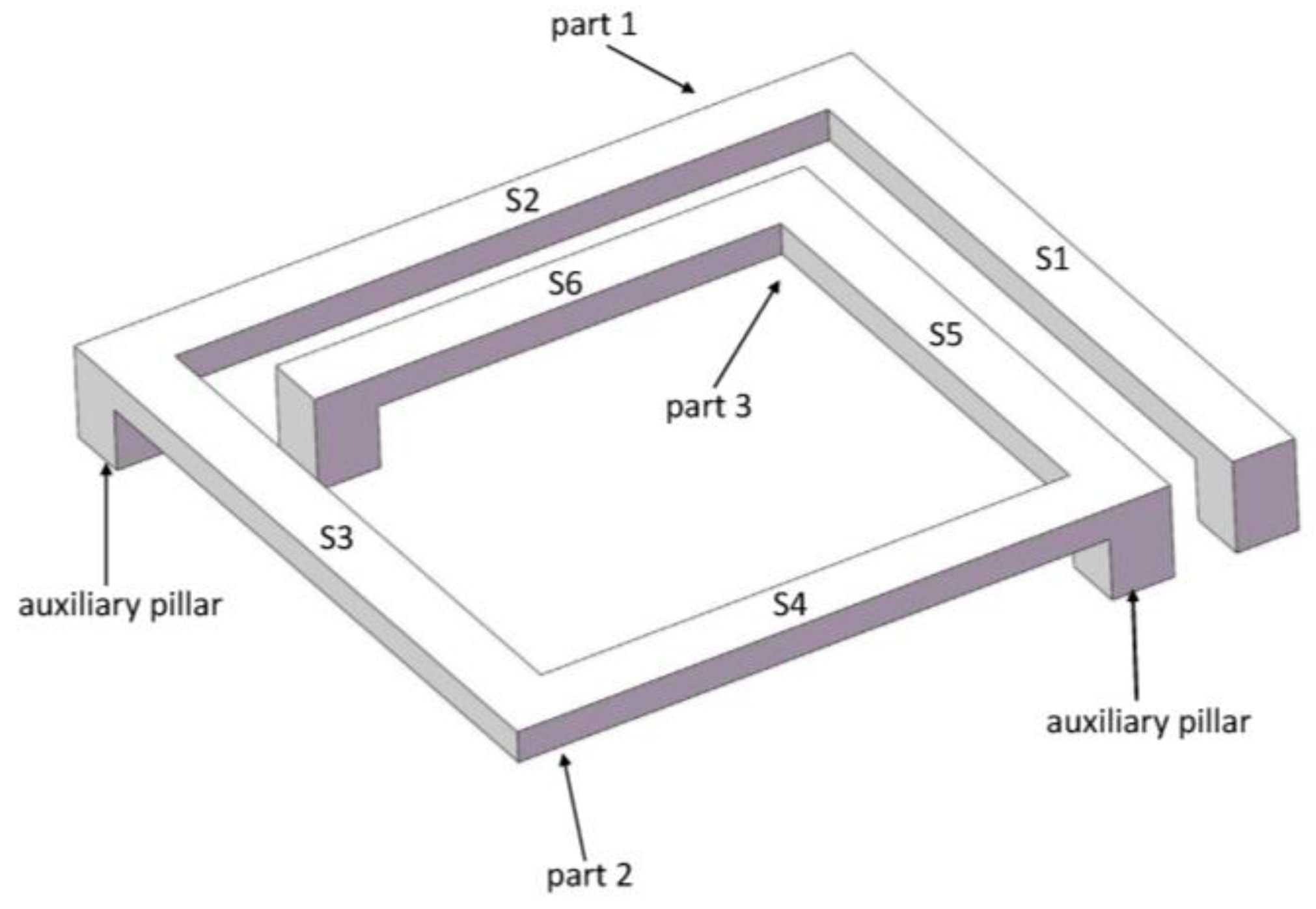





| Part Number | Modal 1 Frequency/MHz | Modal 2 Frequency/MHz | Modal 3 Frequency/MHz |
|---|---|---|---|
| 1 | 0.083042 | 0.18326 | 0.26661 |
| 2 | 0.13383 | 0.31126 | 0.44392 |
| Amplitude of Shock/g | Duration of Shock/μs | Max Von Mises Stress by Model/MPa | Max Von Mises Stress by ANSYS/MPa | Relative Deviation |
|---|---|---|---|---|
| 35,000 | 10 | 111.1 | 115.4 | 3.73% |
| 500 | 63.7 | 68 | 6.32% |
| Amplitude of Shock/g | Duration of Shock/μs | Max Deformation by Model/μm | Max Deformation by ANSYS/μm | Relative Deviation |
|---|---|---|---|---|
| 35,000 | 10 | 3.33 | 3.13 | 6.38% |
| 500 | 1.90 | 1.79 | 6.14% |
| Amplitude of Shock/g | Duration of Shock/μs | Max Von Mises Stress by Model/MPa | Max Von Mises Stress by ANSYS/MPa | Relative Deviation |
|---|---|---|---|---|
| 100,000 | 10 | 109.1 | 108.6 | 0.46% |
| 500 | 78.37 | 77.21 | 1.50% |
| Amplitude of Shock/g | Duration of Shock/μs | Max Deformation by Model/μm | Max Deformation by ANSYS/μm | Relative Deviation |
|---|---|---|---|---|
| 100,000 | 10 | 1.88 | 1.94 | 3.09% |
| 500 | 1.35 | 1.38 | 2.17% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Li, Y.; Li, J.; Lu, C. Mechanical Response of MEMS Inductor with Auxiliary Pillar under High-g Shock. Micromachines 2018, 9, 176. https://doi.org/10.3390/mi9040176
Xu L, Li Y, Li J, Lu C. Mechanical Response of MEMS Inductor with Auxiliary Pillar under High-g Shock. Micromachines. 2018; 9(4):176. https://doi.org/10.3390/mi9040176
Chicago/Turabian StyleXu, Lixin, Yiyuan Li, Jianhua Li, and Chongying Lu. 2018. "Mechanical Response of MEMS Inductor with Auxiliary Pillar under High-g Shock" Micromachines 9, no. 4: 176. https://doi.org/10.3390/mi9040176





