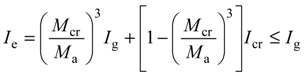Abstract
This study investigates the impact of accelerated aging conditions on the long-term flexural behavior and ductility of reinforced concrete (RC) members with glass fiber-reinforced polymer (GFRP) bars (RC-GFRP specimen) and steel bars (RC-steel specimen). A total of thirty six specimens were designed with different amounts of reinforcement with three types of reinforcing bars (i.e., helically wrapped GFRP, sand-coated surface GFRP and steel). Eighteen specimens were subjected to sustained loads and accelerated aging conditions (i.e., 47 °C and 80% relative humidity) in a chamber. The flexural behavior of specimens under 300-day exposure was compared to that of the companion specimens without experiencing accelerated aging conditions. Results indicate that the accelerated aging conditions reduced flexural capacity in not only RC-steel, but also RC-GFRP specimens, with different rates of reduction. Different types of GFRP reinforcement exhibited different rates of degradation of the flexural capacity when embedded in concrete under the same exposure conditions. Several existing models were compared with experimental results for predicting the deflection and deformability index for specimens. Bischoff and Gross’s model exhibited an excellent prediction of the time-dependent deflections. Except for the deformability index proposed by Jaeger, there was no general trend related to the aging duration. This study recommends the need for further investigation on the prediction of the deformability index.
1. Introduction
The corrosion of steel reinforcement in concrete is a major deterioration mechanism, leading to degradation in the strength and stiffness of reinforced concrete structures. The reduction in the useful service-life of steel-reinforced concrete structures is a cause of concern to the construction industry, mainly due to reinforcement corrosion [1]. However, to reduce costs for repairing significantly corroded structures, in recent years, non-metallic materials of fiber-reinforced polymer (FRP) are increasingly being used as an alternative to steel reinforcement. The growing application of FRP reinforcement is a result of its resistance to corrosion and high strength-to-weight ratio when compared to conventional steel reinforcement [2].
Significant research has been conducted in the past decade to assess the suitability of FRP reinforcement in reinforced concrete beams. Additionally, FRP application is more common in repair or rehabilitation fields, because it is easily attached to the surface of structures [3,4]. There are typically three popular types of fibers, including carbon, glass and aramid fiber. Recently, hybrid carbon-glass FRP sheets have also been used [5]. Among them, this study focuses on glass-FRP (GFRP) reinforcement as a construction material. Particularly, GFRP reinforcement is widely used for flexural reinforcement. The application is not limited to bridge decks, pavements, walls and other systems exposed to harsh environments. GFRP gained momentum when the American Association of State Highway and Transportation Officials (AASTHO) approved the use of GFRP for bridge deck elements [6]. This approval resulted from significant efforts by engineers and researchers to standardize test methods and designs for structural elements using composite reinforcement [7]. Even though GFRP bars exhibit a high strength-to-weight ratio, the modulus of elasticity of GFRP rods is lower than that of steel. Therefore, the design of concrete reinforced with glass fiber (RC-GFRP) beams is often governed by the serviceability limit state (e.g., the maximum allowable deflection and crack widths) rather than the strength limit state (i.e., flexural capacity) [8,9]. Therefore, the prediction of the deflection in a cracked section is considered the important design and analytical procedure. However, various prediction models were formulated based on conventional steel-reinforced concrete. The applicability of existing models to evaluate flexural behavior is still not fully understood. For example, Branson [8] proposed the concept of effective moment of inertia for concrete beams reinforced with steel to predict the deflection of a cracked GFRP beam. Later, Gao et al. [10] proposed a modified expression for the effective moment of inertia in order to account for reduced tension stiffening (i.e., the contribution of concrete for tensile stress after cracking). The modification was adopted in the current American Concrete Institute (ACI) 440.1R-06, “Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars” [7]. However, the information on the applicability of these models for degraded GFRP beam is essentially unknown. Moreover, regarding ductility, due to the linear elastic properties of the GFRP bars up to failure, the conventional definition of ductility cannot be applied to concrete beams reinforced with GFRP reinforcement. Several research papers on GFRP in concrete structures identified the major measure of pseudo-ductility as the deformability index [11,12,13]. Several evaluation methods, such as the energy-based method and the deformation-based method, have been suggested to calculate the ductility index (also called the deformability index) for concrete reinforced with GFRP reinforcement.
Although GFRP reinforcing bars do not exhibit “classical” corrosion, many researchers [14,15,16,17] have reported that there is a significant reduction in the tensile capacity of GFRP reinforcement when exposed to aggressive solutions and exposure conditions (e.g., high pH, salt water, high temperature, freeze-thaw cycles and wet/dry cycles). Therefore, the long-term performance of concrete members reinforced with FRP bars under harsh environmental conditions has been recognized as an emerging concern. To address these concerns, many researchers adopted accelerated aging test methods using the bare GFRP bars to evaluate the tensile strength of GFRP bars. Although much research has reported significant loss in the tensile capacity of GFRP bars exposed to concrete pore solution, a field study conducted by Mufti et al. [18,19] and Benmokrane and Cousin [20] concluded that GFRP reinforcement is durable when embedded in concrete. Recent findings [21] indicate that the interface of fiber and matrix is prone to damage initiation under high temperature (24 °C). Similar debonding was also reported by Benmokrane et al. in 2006 [22]. A significant number of simulated aging tests on GFRP bars have been conducted in the past decades. Long-term performance prediction approaches have also been developed, which provide a good basis for the durability evaluation and design of GFRP bars [23]. Based on these results, the current ACI 440.1R-06 [7] requires using a specific environmental reduction factor, CE, as a design parameter to consider the reduction in the tensile strength of GFRP in actual structures. The value of CE is varied depending on the exposure conditions of GFRP-reinforced concrete: for concrete not exposed to earth and weather, the reduction factor is 0.8, and for concrete exposed to earth and weather, the reduction factor is 0.7.
However, the information on the impact of the degraded GFRP reinforcement on the flexural performance of concrete members is limited. Furthermore, in situ or realistic environmental conditions (i.e., service load level and aggressive temperature and humidity for GFRP reinforcement) were rarely implemented in the experimental program in the literature. Trejo et al. [24] reported experimental tension test data for over one hundred GFRP reinforcement embedded in concrete and exposed to actual environmental conditions (mean annual temperature of 23 °C and average annual precipitation of 1008 mm) for seven years. Based on this study, Gardoni et al. [25] developed the time-variant model. Later, time-dependent reliability analysis on a bridge deck was analyzed [26]. However, this research has the limited data of the GFRP reinforcement subjected to a higher mean temperature, representing a more aggressive temperature. In addition, this test method performed tension testing of bar samples extracted from the beam specimens. Therefore, further data are needed, and a more systematic experimental plan is needed to consider the impact of the degradations of reinforcing systems embedded in concrete under harsh environmental conditions.
This research provides valuable information on the flexural performance of concrete beams reinforced with GFRP bars after accelerated environmental aging. The main aim of the study is to evaluate the long-term flexural behavior of GFRP in comparison with steel reinforcement by varying the reinforcement ratio and the exposure duration.
2. Experimental Program
2.1. Materials
The concrete mix design was: 226 kg/m3 of Type I/II Portland cement, 990 kg/m3 of coarse aggregate with a maximum size of 10 mm, 1010 kg/m3 of sand (fine aggregate), 74 kg/m3 of Class F Fly ash and 198 kg/m3 of water. The average slump of the concrete was 71 mm, and the average compressive strength (f'c) at 28 days was 29.5 MPa. The average modulus of elasticity of concrete was estimated to be 25.6 GPa by the 4700 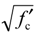 equation of ACI 318-11 [27].
equation of ACI 318-11 [27].
Two types of GFRP bars from two different manufacturers were used for the main flexural reinforcement of the beams. Figure 1 shows the reinforcement types used in this study. As shown in Figure 1a, Type A GFRP reinforcement (GA (Glass fiber bar–Aslan) series in the designation of beam specimens) was made of E-glass fiber (wrapped/partial sand coating surface, E-glass fiber impregnated in a vinyl-ester resin). As shown in Figure 1b, Type B GFRP reinforcement (GH (Glass fiber bar–High modulus) series in the designation of beam specimens) was made of E-glass formulation using the pultrusion-process (sand-coated surface with a high relative modulus of elasticity, vinyl ester-based resin with E-glass formulation). The Type B bar has a much higher glass fiber content at approximately 80% by weight, while the Type A bar has 70% minimum fiber content per the ASTM D2584 “Standard Test Method for Ignition Loss of Cured Reinforced Resins” [23]. Plain carbon-steel bars were used with a minimum yield strength (fy) of 415 MPa (Grade 60), as shown in Figure 1c. The mechanical properties of glass fiber-reinforced polymer bars and steel bars, as reported by the manufacturer, are presented in Table 1. As shown in Table 1, a Type B bar exhibits approximately a 47% to 57% higher tensile elastic modulus than a Type A bar.

Figure 1.
Reinforcements of (a) A-type GFRP; (b) B-type GFRP and (c) steel bars.

Table 1.
Mechanical properties of FRP bars.
| FRP Bar Type | Bar Size | Nominal Diameter (mm) | Nominal Area (mm2) | Guaranteed Tensile Strength (ffu *: MPa) | Tensile Modulus of Elasticity (Ef *: GPa) | Tensile Strain (εu *: %) |
|---|---|---|---|---|---|---|
| GA series (Type A) | #4 | 13 | 126.7 | 690 | 40.8 | 1.50 |
| #5 | 16 | 197.9 | 655 | 40.8 | 1.50 | |
| GH series (Type B) | #4 | 13 | 126.7 | 1300 | 60.0 | 2.42 |
| #5 | 16 | 197.9 | 1259 | 64.1 | 2.24 | |
| Steel (Grade 60) | #4 | 12.7 | 129.0 | 620 (415: yield) | 200 | 9.00 |
| #5 | 15.875 | 200.0 | 620 (415: yield) | 200 | 9.00 |
* Test results were obtained in accordance with ACI 440.1R-06 [7]. Grade 60 in the U.S. is equivalent to Grade 420.
2.2. Test Matrix and Design of Specimens for Fabrication
A total of thirty six specimens were fabricated in the structural laboratory at the University of Texas at Arlington. The dimensions of each specimen are 200 mm by 300 mm by 1800 mm (width × height × length). For the tensile reinforcement, the longitudinal reinforcement consisted of two #4 (13-mm diameter) or three #5 (16-mm diameter) bars for each specimen with a single layer of reinforcement. The three variables are: (1) the types of reinforcement (Type A and Type B GFRP bars and steel); (2) the reinforcement areas (two #4 or three #5); and (3) the environmental aging (non-exposure and exposure to the designated temperature and humidity for 300 days). Based on the test variables, the nomenclature of test specimens is as follow. The first character, “GA” or “GH” or “S”, represents the type of reinforcement for glass fiber of Type A, Type B (relatively higher Young’s modulus) and steel, respectively. The second and third characters, “2-4” or “3-5”, are the number and size of the reinforcement for varying the reinforcement ratio. For example, 3-5 represents that the reinforcement consists of three #5 bars. The last character, varying from 0 to 300, represents the exposure duration (days).
Failure modes are varied depending on the GFRP reinforcement ratios. According to ACI 440.1R-06 [7], the concrete crushing failure mode is obtained when the reinforcement ratio (ρf) is greater than the balanced reinforcement ratio (ρfb) in Equations (1) and (2):
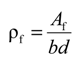
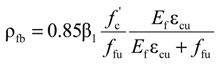
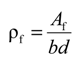
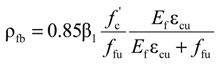
where Af is the area of GFRP reinforcement, b is the width of the section, d is the effective depth, β1 is the ratio of the depth of the equivalent rectangular stress block to the depth of the neutral axis, f'c is the concrete compressive strength, ffu is the rebar tensile strength, Ef is the modulus of elasticity of the FRP rebar and εcu is the maximum concrete strain (0.003 for ACI provisions).
Figure 2 shows that variations in the reinforcement ratio affect the strength reduction factor in accordance with ACI 440.1R-06 [7]. This chart is used to determine the reinforcement ratio of specimens. It can be seen that the values of ρf/ρfb are 0.997 and 4.761 to induce the failure mode of theoretically balanced failure (FRP-rupture and concrete crushing simultaneously: strains of the top fiber in concrete and GFRP bars reach their predefined limiting or useable concrete strain value, εcu, and rupture strain of GFRP reinforcement, εfu, simultaneously) for GA-2-4-300 and concrete crushing for GH-3-5-0, respectively. Unaged specimens with GFRP reinforcement were designed to fail by concrete crushing, which means that failure was expected to occur when the concrete reached its maximum useable compressive strain (εcu). The GA2-4-0 and GA2-4-300 specimens were expected to have a balanced failure, resulting in GFRP rupture and concrete failure. The reinforcement ratios (ρs/ρsb) of steel are less than those (ρf/ρfb) of GFRP specimens with the same amount of reinforcement area (two #4 and three #5). It should be noted that this reinforcement ratio led to yielding of the steel reinforcement (referred to as under-reinforced concrete beam) before concrete crushing failure. No stirrups were used in the testing region to secure the pure bending behavior, while #3 steel stirrups were used with a spacing of 100 mm to prevent shear failure at both ends of the beams. The detailed reinforcement layout is shown in Figure 4.
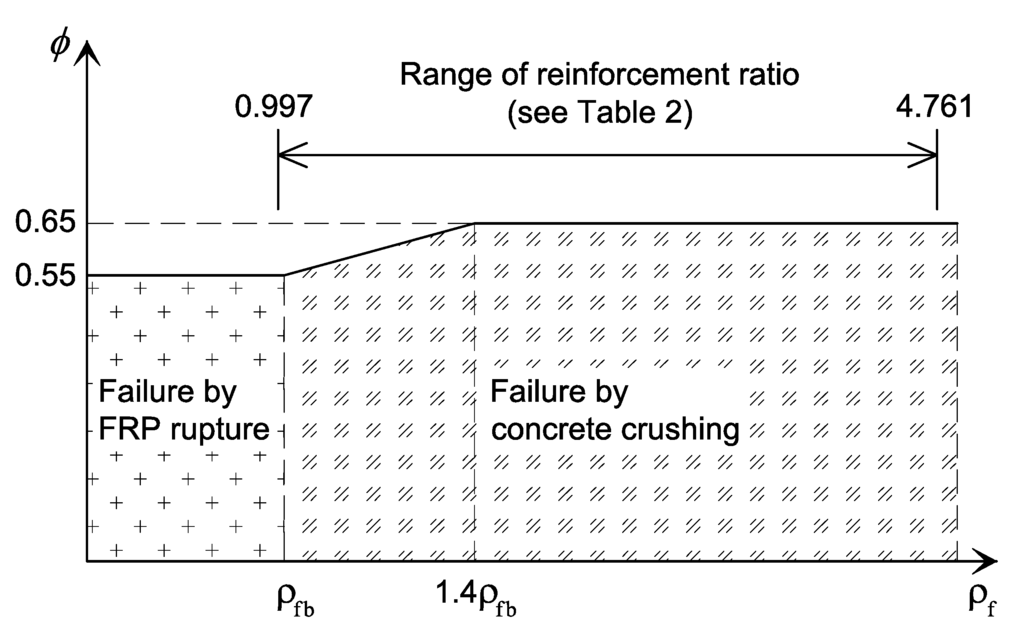
Figure 2.
The strength reduction factor as a function of the reinforcement ratio (adapted from ACI 440.1R-06 [7]).
2.3. Sustained Loading and Accelerated Aging Method in the Chamber
All beams were clamped in pairs using externally transverse steel rods at the beam end to simulate crack damage under service conditions by a maximum mid-span deflection of L/240 (L, the clear span of the beam), as shown in Figure 3a. Two roller supports were placed on the top surface of each beam at the one-third location of the beam length measured from each end. The region between two roller supports is considered as a pure bending zone (zero shear zone). Two main pre-cracks appeared in the pure bending zone and were measured by a portable microscope (×200). As shown in Figure 3b, the widths of pre-cracks ranged from 0.26 to 0.61 mm (Average: 0.43 mm), and the average spacing of the pre-cracks was 120 mm (two #4 series) and 164 mm (three #5 series). These cracks were generated at the same 30% of ultimate moment capacity, Mu (i.e., service load level), as the design requirement. This is more valuable information for structural engineers to design and evaluate the performance of structures. Therefore, the differences of the initial damages (for example, between 0.26 mm and 0.61 mm of the width of the pre-crack) were not focused on in this paper. More information on crack widths is reported in Park [28]. Prior to exposure in the chamber, pre-cracked specimens were initially immersed in a 3.0% saline solution for 72 h, and equal end moments were applied to the test beams using clamping. The sustained load level was selected as 0.3P (30% of P), where P is the ultimate flexural load capacity of the beam reinforced with GFRP bars. A constant deformation was maintained during the test through clamping.
For more aggressive environmental conditions, the test focused on the simulated environmental conditions at an average high temperature of 47 °C and an average relative humidity (RH) of 80% based on records from the last 30 years in North Texas in the United States. Re-clamping to simulate service loading in the chamber after immersion into the 3.0% saline solution and placing the specimens in the chamber are shown in Figure 3c. Cracks resulting from the clamping at both ends to simulate service loading were marked, and the crack width and spacing were measured within the constant moment zone. Cracks induced by sustained loading also accelerate the aging effect in the chamber, as shown in Figure 3e.

Figure 3.
Test procedure: (a) pre-cracking for simulating service loading; (b) crack widths due to service loading; (c) beamimmersed in saline solution; (d) penetration of saline solution; and (e) accelerated aging in the chamber (47°C and a relative humidity (RH) of 80%).
2.4. Four-Point Bending Test
All specimens were subjected to four-point bending after the accelerated environmental conditioning. All tests were displacement-controlled at a rate of 0.15 mm/min. Comparative studies were necessary to investigate the various effects of the conditioning. Figure 4 shows the test set-up and geometry of the beam specimens. The ultimate loads are defined as the maximum loads measured by the load cell used with the data acquisition (DAQ) system. A hydraulic jack applied the load to the reinforced concrete beams with GFRP (single-layered reinforcement) and steel bars through a spreader beam. In order to measure the deflection of the tested beam, two transducers (linear variable differential transducers and strain gauge-based transducers) were used in the mid-span section (pure bending region). An optical magnifier with an accuracy of 0.05 mm was used to measure crack widths at the location of the bottom reinforcement.
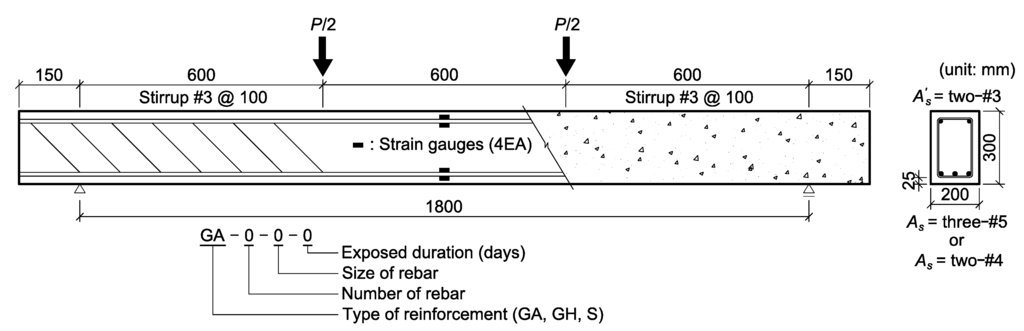
Figure 4.
Test set-up and details of a specimen.
3. Test Results
This section presents the summary of the overall flexural behavior of the control beams (unaged specimens) and the exposed specimens (aged specimens in accelerated aging for 300 days) in terms of moment-deflection response, failure mode and ductility. The experimental results between control specimens and the exposed specimens for 300 days are also compared and discussed. Finally, predicted deflections and deformability indices of unaged/aged specimens are compared and discussed.
3.1. Moment-Deflection Response
Figure 5 shows the experimental moment-deflection curves for concrete beams reinforced with steel reinforcement (RC-steel) and GFRP reinforcement (RC-GFRP) with varied reinforcement ratios in the mid-span section. Corresponding important values are presented in Table 2. RC-GFRP specimens exhibited no sign of yielding due to the linear-elastic behavior of the GFRP bars until failure, whereas RC-steel specimens with under-reinforcement exhibited yielding of steel before the crushing of concrete. As shown in Figure 5, the specimens, S2-4 series and S3-5 series, exhibited the tri-linear moment-curvature relationship. After the moment exceeded the cracking moment (Mcr), regardless of the GFRP bar type and the reinforcement ratio, the flexural stiffness of the beams was significantly reduced, and the curves of RC-GFRP specimens increased almost linearly until the crushing of concrete. The reinforcement ratio, GFRP bar type and the concrete compressive strength all had an influence on the stiffness of the beam specimens. Larger deformations were obtained for lower reinforcement ratios, and vice versa. Moreover, for the same reinforcement ratio, GA series (specimens reinforced with Type A GFRP bars) also showed larger deflections due to less relative stiffness compared with the GH series. Except one specimen, GA2-4-300, all specimens demonstrated a concrete crushing mode of failure in line with the design philosophy. The GA2-4-300 specimen exhibited a balanced failure, which indicates the bar failure and concrete crushing failure occurring simultaneously. The moment-carrying capacity was decreased with the occurrence of concrete crushing or balanced failure.
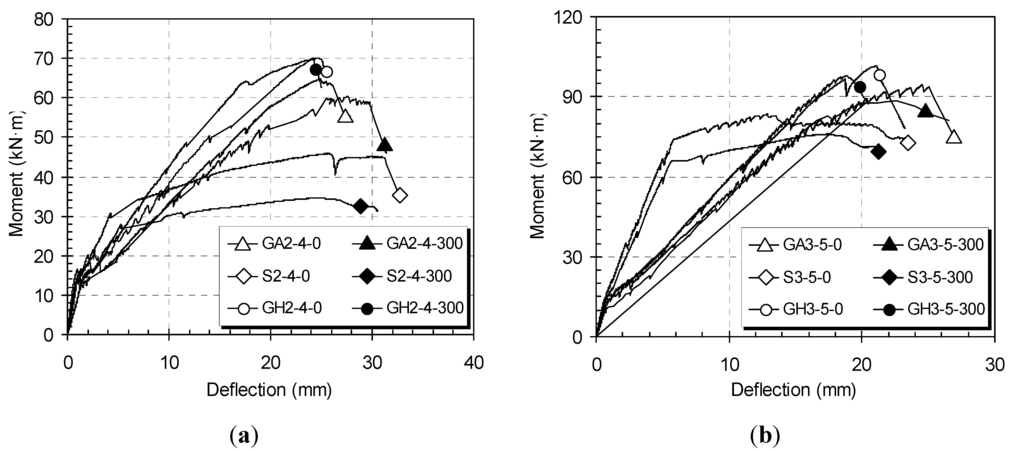
Figure 5.
Moment-deflection curves: (a) the group of two #4 (GA2-4, GH2-4 and S2-4 series) and (b) the group of three #5 (GA3-5, GH3-5 and S3-5 series).

Table 2.
Summary of the test results.
| Specimen I.D. | ρf/ρfb 1 or ρs/ρsb 2 | f'c (MPa) | Mu-th (kN·m) | Mu-exp (kN·m) | Δu-exp (mm) | Failure Mode 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | Avg. | 1 | 2 | 3 | Avg. | |||||
| GA2-4-0 | 1.242 1 | 29.30 | 50.2 | 64.8 | 60.9 | 62.1 | 62.6 | 24.49 | 26.67 | 22.88 | 24.68 | C.C. |
| GA2-4-300 | 0.997 1 | 36.06 | 51.8 | 58.6 | 56.2 | 55.8 | 56.9 | 29.66 | 30.84 | 28.43 | 29.64 | B |
| GA3-5-0 | 2.157 1 | 29.30 | 68.1 | 93.4 | 88.2 | 92.1 | 91.2 | 17.89 | 20.81 | 19.43 | 19.38 | C.C. |
| GA3-5-300 | 1.678 1 | 36.47 | 72.9 | 86.1 | 79.4 | 82.6 | 82.7 | 21.31 | 22.45 | 23.36 | 22.37 | C.C. |
| GH2-4-0 | 2.273 1 | 29.92 | 52.6 | 70.1 | 66.7 | 68.9 | 68.6 | 23.14 | 25.31 | 23.76 | 24.07 | C.C. |
| GH2-4-300 | 1.776 1 | 36.47 | 59.9 | 69.9 | 68.1 | 66.9 | 68.3 | 28.93 | 26.43 | 25.76 | 27.04 | C.C. |
| GH3-5-0 | 4.761 1 | 29.92 | 74.8 | 101.4 | 98.3 | 99.4 | 99.7 | 17.22 | 21.09 | 20.36 | 19.56 | C.C. |
| GH3-5-300 | 3.578 1 | 36.61 | 85.2 | 96.1 | 94.0 | – | 95.1 | 20.75 | 23.41 | – | 22.08 | C.C. |
| S2-4-0 | 0.155 2 | 29.10 | 27.3 | 45.9 | 41.7 | 43.7 | 43.8 | 31.17 | 30.83 | 33.14 | 31.71 | S.Y. + C.C. |
| S2-4-300 | 0.119 2 | 36.06 | 27.8 | 34.6 | 33.9 | – | 34.3 | 35.14 | 35.29 | – | 35.22 | S.Y. + C.C. |
| S3-5-0 | 0.352 2 | 29.92 | 60.1 | 84.6 | 82.1 | 80.6 | 82.4 | 25.29 | 24.80 | 27.16 | 25.75 | S.Y. + C.C. |
| S3-5-300 | 0.267 2 | 36.75 | 61.8 | 75.1 | 72.6 | – | 73.9 | 21.34 | 20.09 | – | 20.72 | S.Y. + C.C. |
Notes: f'c is the average concrete strength at testing day, but those at 28 days were 29.30 MPa in the GA series, 29.92 MPa in the GH series and 29.51 MPa in the S series; Mu-th is the theoretical ultimate moment; and Mu-exp and Δu-exp are the experimental ultimate moment and its corresponding deflection. 1 ρf/ρfb (see Equations (1) and (2)); 2 ρs/ρsb, where ρs = As/bd and ρsb = (0.85β1 f 'c/fy)(0.003/(0.003+εy)); 3 C.C., concrete crushing; B, balanced failure; S.Y. + C.C., steel yielding and concrete crushing; –, no data available; Avg., Average.
In all the cases, except the GA2-4 series, however, the moment-carrying capacity decreased and the deflection increased as a function of time when exposed to accelerated aging conditions. In general, all beams showed a reduction in moment-carrying capacity after 300 days of accelerated aging in the environmental chamber (with 47 °C and relative humidity of 80%). Environmental conditioning had an effect on the structural degradation of not only RC-steel, but also RC-GFRP specimens. In all of the cases, the reductions in moment-carrying capacity were observed under the aggressive aging conditions to which the specimens were exposed. RC-steel specimens had a higher reduction in flexural strength than RC-GFRP specimens in both reinforcement cases, as expected in 21.7% and 10.3% in the S2-4 and S2-5 series, respectively. The GA2-4, GH2-4 and S2-4 series exhibited a reduction in the moment-carrying capacity of approximately 9.1%, 0.5% and 21.7%, respectively. Furthermore, the GA3-5, GH3-5 and S3-5 series exhibited a reduction in the moment-carrying capacity of approximately 9.3%, 4.6% and 10.3%, respectively, after exposure for 300 days in the environmental chamber. The substitution of GFRP reinforcement for steel reinforcement in the flexural members is beneficial for improving the durability of reinforced beams. From the results, the rate of flexural strength degradation of Type A GFRP beams (i.e., GA series) is greater than that of Type B GFRP beams (i.e., GH series). This can be attributed to the coating materials of GFRP reinforcement. The Type B GFRP bars in the GH series with a sand-coated surface exhibited better protection against moisture and temperature as compared to the Type A GFRP bars in the GA series. It should be noted that among the entire specimens, the lowest reduction was observed in the GH2-4-0 and GH2-4-300 specimens. A higher GFRP reinforcement with larger-sized diameter bars led to a decrease in the rate of reduction in the flexural strength (GA2-4 series versus GA3-5 and GH3-5 series). Whereas the observed corrosion of the steel reinforcement led to significant degradation of the flexural strength, the GFRP reinforcement showed no significant changes (below 10%) in the flexural strength. Within this range, only marginal degradation of GFRP reinforcement occurred.
The theoretical ultimate moments (Mu-th) were calculated according to ACI 440.1R-06 [7] with the ultimate concrete strain (εcu) of 0.003. Concrete compressive strengths were considered when calculating reinforcement ratios tabulated in Table 2. All beams exhibited a higher capacity than the theoretically predicted value. Mean ratios of RC-GFRP beams between the experimental and theoretical values calculated by ACI 440.1R-06 [7] are 1.20 and 1.22, respectively, before and after the aging. The ratio above 1.0 represents that the design approach of ACI 440.1R-06 is still conservative and appropriate.
3.2. Deflection
Using various existing models, the calculated deflections at mid-span for a simply-supported beam of total length L subjected to four-point bending are given in Table 3. As mentioned earlier, the low elastic modulus of GFRP reinforcement requires the design of RC-GFRP specimens at the serviceability limit state in accordance with ACI 440.1R-06 [7]. Therefore, an assessment is needed to understand the influence of the low stiffness of GFRP reinforcement coupled with degradation on overall flexural deflection.
The ACI 440.1R-06 model [7] recommends using Equations (3) and (4) to calculate the effective moment of inertia (Ie) (see Table 3). The factor, βd, is a reduction factor related to the reduced tension stiffening exhibited by GFRP-reinforced members [8]. The approach of Toutanji and Saafi [29] of Equation (5) was also compared with experimental data. In Toutanji and Saafi’s model, the exponent of Branson’s model [8] was modified by adopting Es of the steel modulus of elasticity, ρf of the FRP reinforcement ratio and Ef of the FRP modulus of elasticity when using this method. Finally, Bischoff and Gross’s model [30] of Equation (6) was also compared to the experimental data. As seen in Equation (6), an equivalent moment of inertia based on the change in stiffness along the span was adopted in Bischoff and Gross’s expression.

Table 3.
The equivalent moment of inertia (Ie) for the calculation of deflections under the four-point bending.
| Loading and support condition |  | |
| Theoretical deflection | 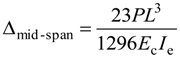 | (3) |
| ACI 440 1.R-06 [7] | 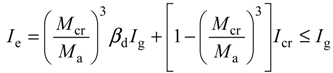 where βd = 0.2(ρf/ρfb) ≤ 1.0 where βd = 0.2(ρf/ρfb) ≤ 1.0 | (4) |
| Toutanji and Saffi [29] | For (Ef/Es) ρf < 0.3, 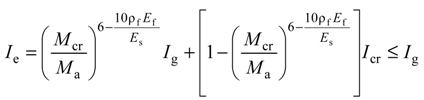 | (5a) |
| Bischoff and Gross [30] | 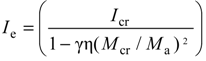 where Ma = PL/6, η = 1−Icr/Ig where Ma = PL/6, η = 1−Icr/IgFor considering tension stiffening, γ = 1.72–0.72Mcr/Ma For considering no tension stiffening in the cracked region, γ = 0.35Mcr/Ma | (6) |
Notes: Ec = concrete modulus of elasticity; Es = steel modulus of elasticity; Ig = moment of inertia of gross section; Ma = applied moment (PL/6); all other parameters are presented in the text.
As compared with theoretical predictions obtained using ACI 440.1R-06 [7] and other existing models, Figure 6 shows the experimental data and predicted values of deflections for 300-day aged and control RC-GFRP specimens subjected to four-point loading (only the GA2-4 series). Note that samples that exhibited the maximum capacities in each case are compared. Similar trends are observed for all other specimens. After 300 days of accelerated aging in the chamber, the deflections of the GA2-4 (or GH2-4) and GA3-5 (or GH3-5) beams reinforced with Type A GFRP bars experienced an average increase of approximately 21% (or 25%) and 19% (or 20%), respectively, when comparing GA2-4-0 (or GH2-4-0) with GA2-4-300 (or GH3-5-300). This indicates that the accelerated aging exaggerated the effect of the smaller amount of reinforcement (or stiffness) on the increase in deflection (e.g., GA2-4 versus GA3-5; GH2-4 versus GH3-5). The larger deflection after aging may be due to the degradation in the cracked stiffness (EcIcr) of specimens. Up to the cracking moment in flexural tests, there were no significant differences between any of the deflections and cracking moments for RC-GFRP beams. However, from approximately 30% of the ultimate moment (corresponding to the service level) up to failure, the theoretical approaches showed different trends in Figure 6.
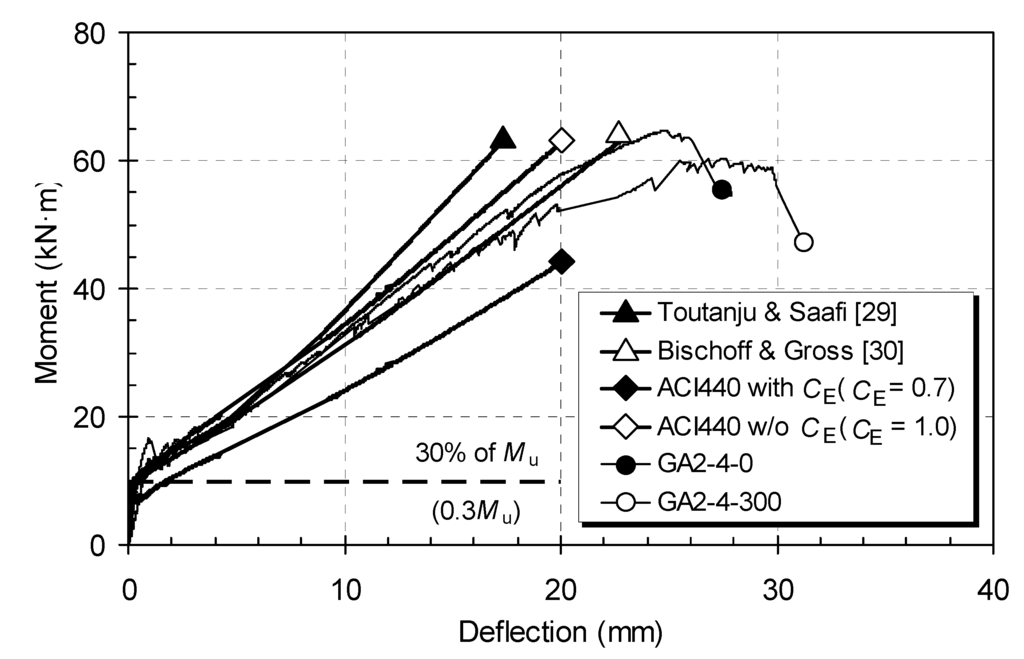
Figure 6.
Comparison of predicted and measured results in the GA2-4 series.
The Bischoff and Gross model [30] overestimated deflection, while ACI 440.1R-06 [7] without CE (i.e., CE = 1.0) and the Toutanji and Saafi model [29] underestimated deflection in all cases at the service (0.3 Mu) and ultimate load level, Mu. Differences between theoretical and experimental data were not significant, as the reinforcing ratio increased, because tension stiffening (simply, defined as tension force carried by the concrete between the two adjacent or multiple cracks) decreased at the higher reinforcing ratios. When an environmental reduction factor of 0.7 (CE: exposed to earth and weather in ACI 440.1R-06 [7]) was used to calculate the deflection of a member with concrete crushing failure, the ACI 440 provision [7] was still conservative for specimens subjected to the 300 days of accelerated aging. Accordingly, the equations underestimated the deflection at the ultimate moment. Similarly, the prediction models for all cases tend to overestimate the value of Ie, resulting in the underestimation of the deflection. The exposure condition exaggerates the overestimation of prediction models on the deflection at the ultimate moment. The actual loss of stiffness over time in this specimen did not occur as much as the predicted values based on CE = 0.7 in ACI 440.1R-06 [7]. Therefore, the accuracy of the predicted deflections gets lower as the load increases.
Table 4 shows the comparisons between experimental and predicted deflections at the ultimate moment. Note that samples that exhibited the maximum moment capacities in each case are compared. Similar trends are observed for all other specimens. The ratio of predicted value to experimental value for the Bischoff and Gross equation [30] exhibited a mean value of 0.99 (0.82) and standard deviations of 0.09 (0.09) for unaged specimens (aged specimens). The Bischoff and Gross equation [30] exhibited the smallest average error for the long-term performance of aged specimens. Thus, it provided the best predictions of load and deflections for the accelerated aged specimens, while the Toutanji and Saafi model [29] exhibited poor performance on predicting the deflection in not only the accelerated aged specimens, but also control specimens. From these results, Toutanji and Saafi model [29] exhibited an inappropriate model for the design, because it underestimated short-term and long-term deflections considerably for GFRP-reinforced concrete beams.

Table 4.
Deflections at the ultimate moment.
| Specimen I.D. | Reinforcement Ratio (Af/bd) | Deflection (mm) | 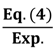 | 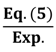 | 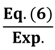 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Exp. * | Eq. (4) (CE = 1.0) | Eq. (5) | Eq. (6) | |||||||
| GA2-4-0 | 0.0045 (0.45%) | 24.488 | 21.699 | 16.969 | 23.404 | 0.886 | 0.693 | 0.956 | ||
| GA2-4-300 | 29.655 | 21.699 | 16.969 | 23.404 | 0.732 | 0.572 | 0.789 | |||
| GA3-5-0 | 0.0109 (1.09%) | 17.882 | 16.318 | 13.257 | 19.870 | 0.913 | 0.741 | 1.111 | ||
| GA3-5-300 | 21.311 | 16.318 | 13.257 | 19.870 | 0.766 | 0.622 | 0.932 | |||
| GH2-4-0 | 0.0045 (0.45%) | 23.146 | 17.672 | 14.552 | 20.359 | 0.764 | 0.629 | 0.880 | ||
| GH2-4-300 | 28.931 | 17.672 | 14.552 | 20.359 | 0.611 | 0.503 | 0.704 | |||
| GH3-5-0 | 0.0109 (1.09%) | 17.223 | 15.160 | 12.866 | 17.509 | 0.880 | 0.747 | 1.017 | ||
| GH3-5-300 | 20.752 | 15.160 | 12.866 | 17.509 | 0.731 | 0.620 | 0.844 | |||
| 0 day | Mean | – | – | – | – | – | 0.86 | 0.71 | 0.99 | |
| Std. | – | – | – | – | – | 0.07 | 0.06 | 0.09 | ||
| 300 days | Mean | – | – | – | – | – | 0.71 | 0.58 | 0.82 | |
| Std. | – | – | – | – | – | 0.07 | 0.06 | 0.09 | ||
Notes: Eq. means Equation; Std. means Standard Deviation; Equation (4) is taken in ACI 440-1R-06 [7]; Equation (5) is taken in Toutanji and Saafi [29]; and Equation (6) is taken in Bischoff and Gross [30]. * Exp., experimental deflection at mid-span at the ultimate stage of one sample in each case.
3.3. Failure Mode and Cracks
When the cracking moment was reached in the pure bending zone, some cracks began to appear, and the existing cracks were propagated and opened. These cracks were predominantly vertical and perpendicular to the direction of the maximum stress induced by the bending moment.
As the load increased, additional cracks developed in the mid-span and new vertical cracks formed in the shear span. The cracks that developed in the tested specimens of RC-GFRP and RC-steel specimens at the ultimate stage are shown in Figure 7. For RC-GFRP beams, cracking initiated in the constant moment region, with the cracks originating from the bottom fibers, as the principal stresses were the greatest at these extreme fibers. These initial cracks traversed quite deeply into the compression zone. The height of the initial cracks was varied from 64 to 99 mm, measured from the bottom fiber. The crack spacing also decreased rapidly with increasing load. This is also observed in the specimens exposed for 300 days. However, the spacing of cracks remained approximately constant after the applied moment of approximately 46 kN·m for all the cases. Beyond this load level, the existing cracks propagate into the compression zone without any newly forming cracks. Similar to RC-GFRP beams, cracking in RC-steel beams also started with vertical flexural cracks in the constant moment region. However, for RC-steel beams, very few cracks outside the pure bending zone turned into inclined cracks, and most of these were relatively vertical, as shown in Figure 7c. These beams showed a classic reinforced concrete crack pattern involving fewer and larger cracks. The spacing of cracks, however, decreased as the load increased.

Figure 7.
Crack pattern at the ultimate stage of the (a) GA2-4-0 and GA2-4-300; (b) GH2-4-0 and GH2-4-300; and (c) S2-4-0 and S2-4-300 specimens.
3.4. Ductility
The conventional concept of ductility is based on the beam’s capacity to absorb energy without critical failure and is generally related to the post-yielding deformational response before bar failure or concrete crushing failure. However, the concept of ductility in its traditional consensus in RC-steel is not applicable for RC-GFRP beams due to non-existent yielding or no post-yielding deformation of GFRP reinforcement. It is for this reason that many researchers and design codes have suggested other ductility models referred to as pseudo-ductility measures. In order to discuss the flexural ductility of RC-GFRP specimens quantitatively, the term deformability has been introduced by researchers as a means of assessment of the displacement, curvature, applied moment and energy that occurs before the rupture of the GFRP and other types of FRP reinforcement [31,32,33,34,35]. Researchers have proposed several different models to evaluate the deformability of concrete beams with FRP bars, including GFRP reinforcement. However, there is still a lack of general agreement as to how the deformability characteristics of such members may be quantified and analyzed, even for unaged specimens.
Table 5 shows the parameters of each specimen for estimating ductility indices. Note that samples that exhibited the maximum moment capacities in each case are compared. Similar trends are observed for all other specimens. They are curvature, deflection and moment, at different stages. The definition of each parameter is presented in Table 5. Naaman and Jeong [33] proposed an energy-based deformability index (referred to as the Naaman Index) to compute the ductility index of µe for beams reinforced or prestressed with GFRP tendons. This index is suitable for beams with steel reinforcement, as well as GFRP reinforcement [31]. Grace et al. [31] proposed the equation as a function of four parameters. The parameters are: the influence of the type of reinforcement (e.g., longitudinal reinforcement and stirrups), α; the failure mode of the beam, β; the ratio of modulus of elasticity of GFRP to steel reinforcement, Ef/Es; and the failure strength of the reinforcement, γ. These parameters are used to determine the slope of the load-deflection as the parameter of S in Equation (8) (referred to as the Grace Index).

Table 5.
Deformability indices.
| Approach Type | Deformability Index | ||
|---|---|---|---|
Energy-based approach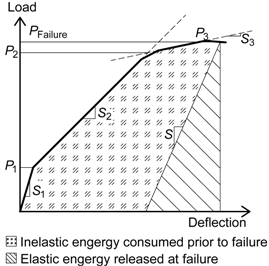 | Naaman and Jeong [33] | | (7a) |
| | (7b) | ||
| Grace et al. [31] | 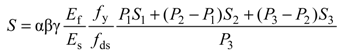 | (8) | |
| α: stirrup factor (GFRP: 0.95) β: failure mode factor (compression and flexure: 1.0) γ: reinforcement factor (GFRP: 4.0) | |||
| Moment and deformation-based approach | Jaeger et al. [32] | | (9) |
| Zou [34] | | (10) | |
Deflection-based approach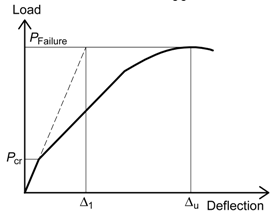 | Abdelrahman et al. [35] | 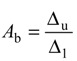 | (11) |
Notes: P1 and P2 = loads as shown in the energy-based approach; S1 and S2 = corresponding slope; ET = the total energy as the area under the load-deflection curve up to the failure load; Eel = elastic energy released at the failure; fds = design strength of FRP; Ef = FRP modulus of elasticity; Δu = deflection corresponding to the ultimate load; and Δcr = deflection at cracking loads.
Jaeger et al. [32] defined the service limit state as the strain state corresponding to a maximum compressive strain in concrete of 0.001 and used the moment and curvature ratios at the ultimate and service limit states (referred to as the Jaeger Index). The Intelligent Sensing for Innovative Structures (ISIS-Canada) [36] adopted the Jaeger model, with deformability index values greater than four and six for rectangular sections and T-sections, respectively. Zou [34] proposed a deformability index (referred to as the Zou Index) defined in terms of both a moment factor and a deflection factor for FRP prestressed concrete beams. The moment part is the ratio of the ultimate moment to the cracking moment, while the deflection part is the ratio of the deflection at failure to that at first crack. Abdelrahman et al. [35] established a deformability model based on deflection for beams prestressed by FRP tendons (referred to as the Abdelrahman Index) [35]. The value of Ab, is the ratio of the maximum deflection, ∆u corresponding to the failure or maximum load to the equivalent deflection, ∆1, of the uncracked section at a load equal to the ultimate load. It should be noted that the Naaman [33], Zou [34] and Abdelrahman indices [35] have been developed for FRP prestressed concrete beams defined in terms of both a deflection factor and a moment factor.
Although there are different ways to calculate the ductility index, there is no doubt that ductility is the ability to absorb inelastic energy without losing load-carrying capacity. From this standpoint, it is necessary to evaluate the change of deformability after accelerated aging for long-term performance.
Table 7 summarizes the variation of deformability indices with different exposure conditions and durations (i.e., control versus 300 days) for the six groups of beams studied based on the test results in Table 6. Note that samples that exhibited the maximum moment capacities in each case are compared. Similar trends are observed for all other specimens. Higher amounts of reinforcement (i.e., GA3-5 and GH3-5 series) reduced the deformation and curvatures, resulting in the reduction of the value of the deformability indices (i.e., GA2-4 and GH2-4 series) (see Table 7). For example, it is obvious that RC-GFRP beams have lower values of ∆u/∆cr than RC-steel beams. Furthermore, compression failure is observed in the specimens containing higher amounts of reinforcement (i.e., GA3-5 and GH3-5 series). This can be attributed to plastic hinge formation and significant concrete cracking in the compression zone, as well as stress redistribution.
All ductility indices showed inconsistent compatibility with the deformability of aged specimens except the Jaeger index [32], which is consistent in all cases. For all cases, the normalized Jaeger index decreased for aged specimens as compared to unaged specimens. It indicates that the Jaeger index is appropriate for comparing the ductility of aged and unaged specimens. However, the other indices do not exhibit the consistent trend in some cases. For example, the Abdelrahman index [35] increased from 6.03 (GA2-4-0) to 6.14 (GA2-4-300) after the aged condition.

Table 6.
Experimental bending moments, displacements and curvatures of specimens at cracking, service and ultimate stages for estimating the ductility indices in Table 7.
| Specimen I.D. | M0.001 (kN·m) | Mcr (kN·m) | Mu (kN·m) | φ0.001 (rad/mm) | φu (rad/mm) | Δcr (mm) | Δu (mm) | Δu/Δcr | Δ1 (mm) |
|---|---|---|---|---|---|---|---|---|---|
| GA2-4-0 | 22.07 | 16.10 | 64.82 | 0.000024 | 0.000048 | 1.245 | 24.488 | 19.67 | 4.064 |
| GA2-4-300 | 24.23 | 15.23 | 58.57 | 0.000031 | 0.000071 | 1.372 | 29.655 | 21.61 | 4.826 |
| GA3-5-0 | 29.65 | 16.03 | 93.40 | 0.000016 | 0.000054 | 0.737 | 17.881 | 24.26 | 3.302 |
| GA3-5-300 | 27.19 | 15.58 | 86.07 | 0.000018 | 0.000059 | 0.991 | 21.311 | 21.51 | 4.572 |
| GH2-4-0 | 25.47 | 14.68 | 70.12 | 0.000016 | 0.000059 | 1.194 | 23.146 | 19.38 | 4.572 |
| GH2-4-300 | 22.24 | 14.26 | 69.85 | 0.000021 | 0.000067 | 1.092 | 28.932 | 26.49 | 5.334 |
| GH3-5-0 | 33.00 | 16.33 | 101.39 | 0.000013 | 0.000044 | 0.533 | 17.223 | 32.31 | 3.302 |
| GH3-5-300 | 27.84 | 15.70 | 96.07 | 0.000016 | 0.000048 | 0.787 | 20.752 | 26.37 | 5.334 |
| S2-4-0 | 31.21 | 15.01 | 45.92 | 0.000010 | 0.000079 | 0.787 | 31.173 | 39.61 | 2.667 |
| S2-4-300 | 28.74 | 12.02 | 34.60 | 0.000012 | 0.000096 | 0.533 | 35.143 | 65.93 | 2.159 |
| S3-5-0 | 34.03 | 15.13 | 84.62 | 0.000008 | 0.000071 | 1.143 | 25.287 | 22.12 | 3.175 |
| S3-5-300 | 32.56 | 12.02 | 75.05 | 0.000009 | 0.000083 | 0.787 | 21.343 | 27.12 | 2.413 |
Notes: M0.001 (φ0.001) = moment (curvature) at a service limit corresponding concrete strain (compression zone) of 0.001; Mcr = cracking moment; Mu = ultimate moment; φu = curvature at ultimate state; Δcr = deflection at cracking loads; and Δ1 = the equivalent deflection of the uncracked section at a load equal to the ultimate load).

Table 7.
Comparison of deformability indices and normalized deformability.
| Specimen I.D. | Deformability Index | Normalized Deformability | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Naaman [33] | Grace [31] | Zou [34] | Jaeger [32] | Abdelrahman [35] | Naaman [33] | Grace [31] | Zou [34] | Jaeger [32] | Abdelrahman [35] | |
| GA2-4-0 | 2.13 | 1.31 | 79.19 | 5.87 | 6.03 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| GA2-4-300 | 1.51 | 0.99 | 83.12 | 5.54 | 6.14 | 0.71 | 0.76 | 1.04 | 0.93 | 1.02 |
| GA3-5-0 | 1.12 | 0.98 | 141.36 | 10.63 | 5.42 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| GA3-5-300 | 0.98 | 1.11 | 118.80 | 10.38 | 4.66 | 0.88 | 1.13 | 0.84 | 0.98 | 0.86 |
| GH2-4-0 | 1.35 | 1.13 | 92.59 | 10.15 | 5.07 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| GH2-4-300 | 1.04 | 1.29 | 129.78 | 10.02 | 5.42 | 0.77 | 1.14 | 1.40 | 0.99 | 1.07 |
| GH3-5-0 | 1.28 | 1.11 | 200.63 | 10.40 | 5.22 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| GH3-5-300 | 1.32 | 1.03 | 161.35 | 10.25 | 3.89 | 1.03 | 0.93 | 0.80 | 0.99 | 0.75 |
| S2-4-0 | 6.22 | 4.16 | 121.18 | 11.62 | 11.63 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| S2-4-300 | 7.51 | 5.69 | 189.78 | 9.63 | 16.28 | 1.21 | 1.37 | 1.57 | 0.83 | 1.40 |
| S3-5-0 | 2.93 | 1.96 | 123.73 | 22.07 | 7.96 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| S3-5-300 | 4.57 | 3.06 | 169.33 | 21.26 | 8.85 | 1.56 | 1.56 | 1.37 | 0.96 | 1.11 |
As mentioned earlier, the inconsistent results may be attributed to the fact that the Naaman [33], Zou [34] and Abdelrahman indices [35] have been developed for FRP prestressed concrete beams. Furthermore, the inelastic slope (S2), the cracking deflection (∆cr) and the equivalent deflection (∆1) are difficult to assess experimentally, due to the linear elastic behavior of GFRP material up to the rupture of the GFRP reinforcement without the sign of yielding that usually exists in RC-steel. Moreover, the deformability indices of the Jaeger index [32] were more than two times higher than the recommended minimum value of four of the ISIS Canada design manual. Comparison of the deformability for RC-GFRP beams and RC-steel beams indicates that the values are not similar, since RC-steel specimens showed a true yielding behavior. RC-steel specimens exhibited an increase of the deformability for aged specimens, except for when the Jaeger index [32] is used.
However, it is clear that there is still no general agreement on the quantification of an appropriate index for aged specimens. Essentially, more data are needed. Further investigation is necessary to determine the requirements for deformability.
4. Conclusions
This study presents the flexural behaviors and ductility of concrete beams reinforced with GFRP bars after accelerated environmental aging. A total of thirty six beams, with different reinforcement amounts of GFRP and different types of reinforcement, were subjected to sustained loads and placed for 300 days in an environmental chamber. The following concluding remarks have been developed:
- The substitution of GFRP reinforcement for steel bars in the concrete beams affected the load-deflection response with higher strength and less deflection at the failure stage due to the non-ductile behavior of FRP reinforcement. Flexural GFRP reinforcement in the concrete led to a significant improvement in the flexural strength.
- Environmental conditioning has an effect on the flexural strength degradation of both RC-steel and RC-GFRP beams. The test results confirm that steel reinforcement had a higher reduction in flexural strength than GFRP reinforcement. It can be concluded that the substitution of GFRP reinforcement for steel reinforcement in the flexural members affected the durability positively.
- The rate of flexural strength degradation of concrete beams reinforced with Type A GFRP reinforcement (i.e., GA series) was greater than those with Type B GFRP reinforcement (i.e., GH series). This can be attributed to the coating materials: the Type B GFRP bars with a sand-coated surface seem to have better protection against moisture and temperature.
- For both unaged and aged specimens, the predictions of flexural deflection by the ACI 440.1R-06 [7], Toutanji and Saafi [15] and Bischoff and Gross [30] models were in close agreement with the experimental data at the service load level. However, as the applied load and aging duration increased, the ACI 440.1R-06 [7] and Toutanji and Saafi [29] models tend to underestimate deflections. The Bischoff and Gross model [30] provided the smallest error and is the best predictor of deflections before and after accelerated aging.
- If an environmental strength reduction factor (CE) of 0.7 was used for the flexure design of a member failing in compression with GFRP reinforcement, the ACI 440.1R-06 model [7] was still conservative under the accelerated environmental aging, with a 47 °C temperature and 80% relative humidity. Therefore, the CE factor is appropriate for estimating the reduced capacity of GFRP reinforcement until 300 days of accelerated environmental aging.
- Except for the Jaeger index [32], there is no general trend related to the aging duration (days). Rationally, the Jaeger index [32] represents the degradation of ductility due to the aging conditions. However, the deformability indices attained from the Jaeger index were higher than the recommended value of four in ISIS-Canada. Finally, there is still no general agreement on how much degradation of deformability is enough for the aged structures. Further investigation is necessary to determine the requirement of deformability.
Acknowledgments
The work described in this paper has been supported by Hughes Brothers Inc. (Seward, NE, USA) and Concrete Protection Product. Inc. (Kernersville, NC, USA).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Almusallam, T.H.; Al-Salloum, Y.A.; Alsayed, S.H.; Mosallam, A.S. Durability and long-term behavior of reinforced concrete beams strengthened with FRP composites. In Proceedings of International Conference on FRP Composites in Civil Engineering (CICE 2001), Hong Kong, China, 12–15 December 2001; pp. 1579–1588.
- Micelli, F.; Nanni, A. Durability of FRP rods for concrete structures. Constr. Build. Mater. 2004, 18, 491–503. [Google Scholar] [CrossRef]
- Böer, P.; Holliday, L.; Kang, T.H.-K. Independent environmental effects on durability of fiber-reinforced polymer wraps in civil applications: A review. Constr. Build. Mater. 2013, 48, 360–370. [Google Scholar] [CrossRef]
- Böer, P.; Holliday, L.; Kang, T.H.-K. Interaction of environmental factors on fiber-reinforced polymer composites and their inspection & maintenance: A review. Constr. Build. Mater. 2014, 50, 209–218. [Google Scholar] [CrossRef]
- Choi, D.-U.; Kang, T.H.-K.; Ha, S.-S.; Kim, K.-H.; Kim, W. Flexural and bond behavior of concrete beams strengthened with hybrid carbon-glass fiber-reinforced polymer sheets. ACI Struct. J. 2011, 108, 90–98. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). AASHTO LRFD Bridge Design Guide Specifications for GFRP-Reinforced Concrete Bridge Decks and Traffic Railings; AASHTO: Washington, DC, USA, 2009; p. 68. [Google Scholar]
- American Concrete Institute (ACI). Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars; ACI 440.1R-06; ACI: Farmington Hills, MI, USA, 2006. [Google Scholar]
- Branson, D.E.; Metz, G.A. Instantaneous and Time-Dependent Deflections of Simple and Continuous Reinforced Concrete Beams; Alabama Highway Department, Bureau of Public Roads: Montgomery, AL, USA, 1965. [Google Scholar]
- Razaqpur, A.G.; Isgor, O.B. Rational method for calculating deflection of continuous FRP R/C beams. ACI Spec. Publ. 2003, 210, 191–208. [Google Scholar]
- Gao, D.; Benmokrane, B.; Masmoudi, R. A Calculating Method of Flexural Properties of FRP-Reinforced Concrete Beam: Part 1–Crack Width and Deflection; Department of Civil Engineering, University of Sherbrooke: Sherbrooke, QC, Canada, 1998. [Google Scholar]
- Au, F.T.K.; Du, J.S. Deformability of concrete beams with unbonded FRP tendons. Eng. Struct. 2008, 30, 3764–3770. [Google Scholar] [CrossRef]
- Jeong, S. Evaluation of Ductility in Prestressed Concrete Beams Using Fiber Reinforced Plastic Tendons. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, January 1994. [Google Scholar]
- Robert, M.; Benmokrane, B. Combined effects of saline solution and moist concrete on long-term durability of gfrp reinforcing bars. Constr. Build. Mater. 2013, 38, 274–284. [Google Scholar] [CrossRef]
- Trejo, D.; Aguiniga, F.; Yuan, R.; James, R.W.; Keating, P.B. Characterization of Design Parameters for Fiber Reinforced Polymer Composite Reinforced Concrete Systems; Texas Transportation Institute Research Report; The Texas A&M University System: College Station, TX, USA, 2005. [Google Scholar]
- Tannous, F.E.; Saadatmanesh, H. Environmental effects on the mechanical properties of E-glass frp rebars. ACI Mater. J. 1998, 95, 87–100. [Google Scholar]
- Mukherjee, A.; Arwikar, S.J. Performance of glass fiber-reinforced polymer reinforcing bars in tropical environments—Part I: Structural scale tests. ACI Struct. J. 2005, 102, 745–753. [Google Scholar]
- Bakis, C.E.; Nanni, A.; Terosky, J.A.; Koehler, S.W. Self-monitoring, pseudo-ductility, hybrid FRP reinforcement rods for concrete applications. Compos. Sci. Technol. 2001, 61, 815–823. [Google Scholar] [CrossRef]
- Mufti, A.; Banthia, N.; Benmokrane, B.; Boulfiza, M.; Newhook, J. Durability of GFRP composite rods. Am. Concr. Inst. Concr. Int. 2007, 37–42. [Google Scholar]
- Mufti, A.; Onofrei, M.; Benmokrane, B.; Banthia, N.; Boulfiza, M.; Newhook, J.P.; Bakht, B.; Tadros, G.S.; Brett, P. Field study of glass-fibre-reinforced polymer durability in concrete. Can. J. Civ. Eng. 2007, 34, 355–366. [Google Scholar] [CrossRef]
- Benmokrane, B.; Cousin, P. University of Sherbrook GFRP Durability Study Report; Intelligent Sensing for Innovative Structures (ISIS): Winnipeg, MB, Canada, 2005. [Google Scholar]
- Kamal, A.S.M.; Boulfiza, M. Durability of GFRP rebars in simulated concrete solutions under accelerated aging conditions. ASCE J. Compos. Constr. 2012, 15, 473–481. [Google Scholar] [CrossRef]
- Benmokrane, B.; Wnag, P.; Pavate, T.; Robert, M. Durability of FRP Composites for Civil Infrastructure Applications; Whittles Publishing: Dunbeath, Scotland, 2006. [Google Scholar]
- American Society for Testing and Materials (ASTM). Standard Test Method for Ignition Loss of Cured Reinforced Resins; ASTM D 2584–13; ASTM: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Trejo, D.; Gardoni, P.; Kim, J.J. Long-term performance of GFRP reinforcement embedded in concrete. ACI Mater. J. 2011, 108, 605–613. [Google Scholar]
- Gardoni, P.; Trejo, D.; Kim, Y.H. Time-variant capacity model for GFRP bars embedded in concrete. ASCE J. Eng. Mech. 2013, 139, 1435–1445. [Google Scholar] [CrossRef]
- Kim, Y.H.; Trejo, D.; Gardoni, P. Time-variant capacity and reliability of GFRP-reinforced bridge decks. ASCE J. Compos. Constr. 2012, 16, 359–370. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI). Building Code Requirements for Structural Concrete and Commentary; ACI 318, 318–11; ACI: Farmington Hills, MI, USA, 2011. [Google Scholar]
- Park, Y. Long-Term Performance of GFRP Reinforced Concrete Beams and Bars Subjected to Aggressive Environments. Ph.D. Thesis, The University of Texas at Arlington, Arlington, TX, USA, May 2012. [Google Scholar]
- Toutanji, H.A.; Saafi, M. Flexural behavior of concrete beams reinforced with glass fiber-reinforced polymer (GFRP) bars. ACI Struct. J. 2000, 97, 712–719. [Google Scholar]
- Bischoff, P.; Gross, S. Equivalent moment of inertia based on integration of curvature. ASCE J. Compos. Constr. 2011, 15, 263–273. [Google Scholar] [CrossRef]
- Grace, N.; Soliman, A.; Abdel-Sayed, G.; Saleh, K. Behavior and ductility of simple and continuous frp reinforced beams. ASCE J. Compos. Constr. 1998, 2, 186–194. [Google Scholar]
- Jaeger, L.G.; Mufti, A.A.; Tadros, G. The concept of the overall performance factor in rectangular-section reinforced concrete members. In Proceedings of the 3rd International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structures, Sapporo, Japan, 14–16 October 1997; pp. 551–559.
- Naaman, A.; Jeong, S.M. Structural ductility of concrete beams prestressed with FRP tendons. In non-metric (FRP) reinforcement for concrete structures. In Proceedings of the 2nd International RILEM Symposium (FRPRCS-2), Ghent, Belgium, 23–25 August 1995; pp. 379–386.
- Zou, P. Flexural behavior and deformability of fiber reinforced polymer prestressed concrete beams. ASCE J. Compos. Constr. 2003, 7, 275–284. [Google Scholar] [CrossRef]
- Abdelrahman, A.; Tadros, G.; Rizkalla, S. Test model for the first canadian smart highway bridge. ACI Struct. J. 1995, 92, 1–9. [Google Scholar]
- Newhook, J.; Svecova, D. Reinforcing Concrete Structures with Fibre Reinforced Polymers; The Canadian Network of Centres of Excellence, ISIS Canada, University of Manitoba: Winnipeg, Canada, 2007. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).