Conformation Change, Tension Propagation and Drift-Diffusion Properties of Polyelectrolyte in Nanopore Translocation
Abstract
:1. Introduction
2. Model and Setup
3. Mapping Simulation Units to Real Units
4. Results and Discussion
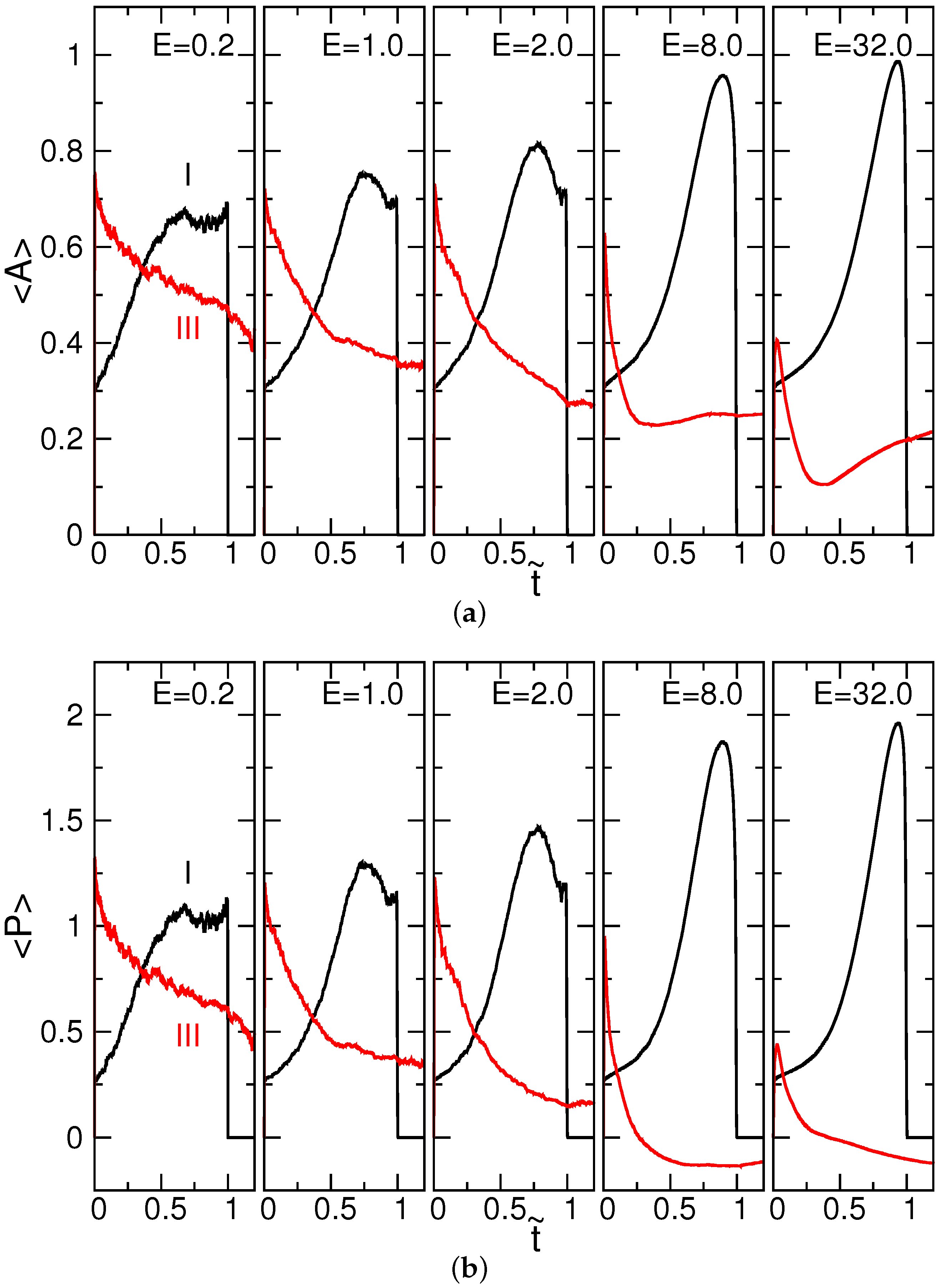
4.1. Chain Conformation and Orientation
4.2. Tension Propagation on a Chain
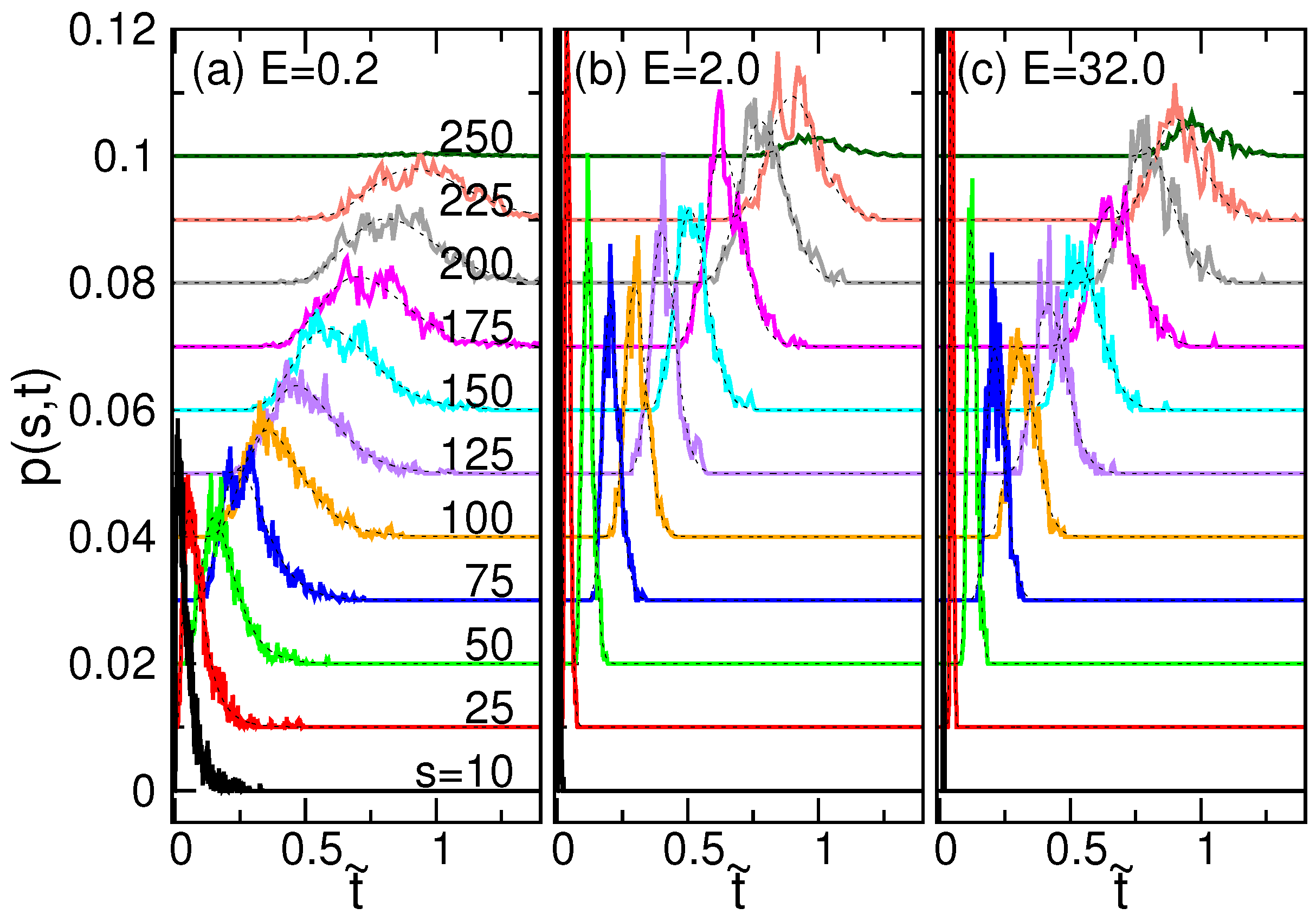
4.3. Waiting Time
4.4. Drift-Diffusion Properties
5. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
List of Symbols:
| Mean value of physical quantity X | |
| , , | Values of physical quantity X in the cis (I), pore (II) and trans (III) regions |
| A | Asphericity |
| α, δ | Exponents for the scaling behavior of |
| Retardation | |
| Salt concentration | |
| Direct distance from the n-th monomer to the pore | |
| Diffusion coefficient | |
| E | Strength of electric field (applied only inside the pore) |
| e | Charge unit |
| (, ), (, ) | Energy and length parameters of WCA potential for bead-bead (bb) and bead-wall (bw) interactions |
| tensile force on the n-th bond | |
| I | Ionic strength |
| Gyration tensor | |
| κ | Inverse Debye length |
| k | Spring constant of bond |
| Boltzmann constant | |
| Equilibrium bond length | |
| Charge distance on the chain backbone | |
| Length of the n-th bond | |
| , , | Persistence length, intrinsic and electrostatic persistence lengths |
| η | Shape factor () |
| Contour distance from the n-th monomer to the pore | |
| Bjerrum length | |
| , , | Eigenvalues of the gyration tensor |
| Mean of the eigenvalues () | |
| m | Mass unit of simulation |
| N | Number of monomers of a chain |
| , | Number of condensed -ions, number of condensed -ions |
| Number of monomers in a region | |
| n, | Monomer ID number, scaled n () |
| ϕ | Azimuthal angle |
| P | Prolateness |
| Probability density distribution | |
| Square of the end-to-end distance | |
| Square of the radius of gyration | |
| σ | Length unit of simulation |
| , | Fitting parameters for Equation (19) |
| s, | Translocation coordinate, scaled s () |
| , | Hump position of the function, scaled () |
| θ | Polar angle |
| T | Temperature |
| t, | Time, scaled time () |
| , | Time needed to reach the translocation coordinate s, |
| τ | Translocation time |
| Time unit of simulation | |
| , | Drift velocity, estimated drift velocity |
| Mean threading velocity () | |
| , | Full width at half maximum of a log-normal distribution, |
| , | Waiting time function, normalized waiting time function |
| ξ | Exponent for the scaling behavior of |
| ζ | Friction coefficient |
References
- Oosawa, F. Polyelectrolytes; Marcel Dekker: New York, NY, USA, 1971. [Google Scholar]
- Bloomfield, V.A. DNA condensation. Curr. Opin. Struct. Biol. 1996, 6, 334–341. [Google Scholar] [CrossRef]
- Radeva, T. Physical Chemistry of Polyelectrolytes; CRC Press: Boca Raton, FL, USA, 2001; Volume 99. [Google Scholar]
- Grosberg, A.Y.; Nguyen, T.; Shklovskii, B. Colloquium: The physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002, 74, 329–345. [Google Scholar] [CrossRef]
- Holm, C.; Joanny, J.; Kremer, K.; Netz, R.; Reineker, P.; Seidel, C.; Vilgis, T.A.; Winkler, R. Polyelectrolyte theory. Adv. Polym. Sci. 2004, 166, 67–111. [Google Scholar]
- Dobrynin, A.V.; Rubinstein, M. Theory of polyelectrolytes in solutions and at surfaces. Prog. Polym. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Dobrynin, A.V. Theory and simulations of charged polymers: From solution properties to polymeric nanomaterials. Curr. Opin. Colloid Interface Sci. 2008, 13, 376–388. [Google Scholar] [CrossRef]
- Visakh, P.M.; Bayraktar, O.; Picó, G. Polyelectrolytes: Thermodynamics and Rheology; Springer: Berlin, Germany, 2014. [Google Scholar]
- Stevens, M.J.; Kremer, K. The nature of flexible linear polyelectrolytes in salt free solution: A molecular dynamics study. J. Chem. Phys. 1995, 103, 1669. [Google Scholar] [CrossRef]
- Sarraguça, J.; Skepö, M.; Pais, A.; Linse, P. Structure of polyelectrolytes in 3:1 salt solutions. J. Chem. Phys. 2003, 119, 12621. [Google Scholar] [CrossRef]
- Hsiao, P.Y.; Luijten, E. Salt-induced collapse and reexpansion of highly charged flexible polyelectrolytes. Phys. Rev. Lett. 2006, 97, 148301. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, P.Y. Linear polyelectrolytes in tetravalent salt solutions. J. Chem. Phys. 2006, 124, 044904. [Google Scholar] [CrossRef] [PubMed]
- Dobrynin, A.V. Effect of counterion condensation on rigidity of semiflexible polyelectrolytes. Macromolecules 2006, 39, 9519–9527. [Google Scholar] [CrossRef]
- Grass, K.; Holm, C. Polyelectrolytes in electric fields: Measuring the dynamical effective charge and effective friction. Soft Matter 2009, 5, 2079–2092. [Google Scholar] [CrossRef]
- Wei, Y.F.; Hsiao, P.Y. Effect of chain stiffness on ion distributions around a polyelectrolyte in multivalent salt solutions. J. Chem. Phys. 2010, 132, 024905. [Google Scholar] [CrossRef] [PubMed]
- Carnal, F.; Stoll, S. Chain stiffness, salt valency, and concentration influences on titration curves of polyelectrolytes: Monte Carlo simulations. J. Chem. Phys. 2011, 134, 044909. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Odijk, T. Polyelectrolytes near the rod limit. J. Polym. Sci. B Polym. Phys. 1977, 15, 477–483. [Google Scholar] [CrossRef]
- Skolnick, J.; Fixman, M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules 1977, 10, 944–948. [Google Scholar] [CrossRef]
- Ha, B.Y.; Thirumalai, D. Electrostatic persistence length of a polyelectrolyte chain. Macromolecules 1995, 28, 577–581. [Google Scholar] [CrossRef]
- Dobrynin, A.V. Electrostatic persistence length of semiflexible and flexible polyelectrolytes. Macromolecules 2005, 38, 9304–9314. [Google Scholar] [CrossRef]
- Manning, G.S. The persistence length of DNA is reached from the persistence length of its null isomer through an internal electrostatic stretching force. Biophys. J. 2006, 91, 3607–3616. [Google Scholar] [CrossRef] [PubMed]
- Savelyev, A.; Papoian, G.A. Chemically accurate coarse graining of double-stranded DNA. Proc. Natl. Acad. Sci. USA 2010, 107, 20340–20345. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Meisburger, S.P.; Pabit, S.A.; Sutton, J.L.; Webb, W.W.; Pollack, L. Ionic strength-dependent persistence lengths of single-stranded RNA and DNA. Proc. Natl. Acad. Sci. USA 2012, 109, 799–804. [Google Scholar] [CrossRef] [PubMed]
- Brunet, A.; Tardin, C.; Salomé, L.; Rousseau, P.; Destainville, N.; Manghi, M. Dependence of DNA persistence length on ionic strength of solutions with monovalent and divalent salts: A joint theory–experiment study. Macromolecules 2015, 48, 3641–3652. [Google Scholar] [CrossRef]
- Hsiao, P.Y. Chain morphology, swelling exponent, persistence length, like-charge attraction, and charge distribution around a chain in polyelectrolyte solutions: Effects of salt concentration and ion size studied by molecular dynamics simulations. Macromolecules 2006, 39, 7125–7137. [Google Scholar] [CrossRef]
- Kasianowicz, J.J.; Brandin, E.; Branton, D.; Deamer, D.W. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. USA 1996, 93, 13770–13773. [Google Scholar] [CrossRef] [PubMed]
- Kasianowicz, J.J.; Robertson, J.W.; Chan, E.R.; Reiner, J.E.; Stanford, V.M. Nanoscopic porous sensors. Annu. Rev. Anal. Chem. 2008, 1, 737–766. [Google Scholar] [CrossRef] [PubMed]
- Venkatesan, B.M.; Bashir, R. Nanopore sensors for nucleic acid analysis. Nat. Nanotechnol. 2011, 6, 615–624. [Google Scholar] [CrossRef] [PubMed]
- Reiner, J.E.; Balijepalli, A.; Robertson, J.W.; Campbell, J.; Suehle, J.; Kasianowicz, J.J. Disease detection and management via single nanopore-based sensors. Chem. Rev. 2012, 112, 6431–6451. [Google Scholar] [CrossRef] [PubMed]
- Fyta, M. Threading DNA through nanopores for biosensing applications. J. Phys. Condens. Matter 2015, 27, 273101. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Polymer Translocation; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Milchev, A. Single-polymer dynamics under constraints: Scaling theory and computer experiment. J. Phys. Condens. Matter 2011, 23, 103101. [Google Scholar] [CrossRef] [PubMed]
- Panja, D.; Barkema, G.T.; Kolomeisky, A.B. Through the eye of the needle: Recent advances in understanding biopolymer translocation. J. Phys. Condens. Matter 2013, 25, 413101. [Google Scholar] [CrossRef] [PubMed]
- Palyulin, V.V.; Ala-Nissila, T.; Metzler, R. Polymer translocation: The first two decades and the recent diversification. Soft Matter 2014, 10, 9016–9037. [Google Scholar] [CrossRef] [PubMed]
- Tian, P.; Smith, G.D. Translocation of a polymer chain across a nanopore: A Brownian dynamics simulation study. J. Chem. Phys. 2003, 119, 11475. [Google Scholar] [CrossRef]
- Huopaniemi, I.; Luo, K.; Ala-Nissila, T.; Ying, S.C. Langevin dynamics simulations of polymer translocation through nanopores. J. Chem. Phys. 2006, 125, 124901. [Google Scholar] [CrossRef] [PubMed]
- Matysiak, S.; Montesi, A.; Pasquali, M.; Kolomeisky, A.B.; Clementi, C. Dynamics of polymer translocation through nanopores: Theory meets experiment. Phys. Rev. Lett. 2006, 96, 118103. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, A.; Morrison, W.H.; Luo, K.; Ala-Nissila, T.; Ying, S.C.; Milchev, A.; Binder, K. Scaling exponents of forced polymer translocation through a nanopore. Eur. Phys. J. E 2009, 29, 423–429. [Google Scholar] [CrossRef] [PubMed]
- Alapati, S.; Fernandes, D.V.; Suh, Y.K. Numerical and theoretical study on the mechanism of biopolymer translocation process through a nano-pore. J. Chem. Phys. 2011, 135, 055103. [Google Scholar] [CrossRef] [PubMed]
- Ikonen, T.; Bhattacharya, A.; Ala-Nissila, T.; Sung, W. Influence of non-universal effects on dynamical scaling in driven polymer translocation. J. Chem. Phys. 2012, 137, 085101. [Google Scholar] [CrossRef] [PubMed]
- Suhonen, P.; Kaski, K.; Linna, R. Criteria for minimal model of driven polymer translocation. Phys. Rev. E 2014, 90, 042702. [Google Scholar] [CrossRef] [PubMed]
- Sean, D.; Haan, H.W.; Slater, G.W. Translocation of a polymer through a nanopore starting from a confining nanotube. Electrophoresis 2015, 36, 682–691. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, P.Y. Polyelectrolyte threading through a nanopore. Polymers 2016, 8, 73. [Google Scholar] [CrossRef]
- Bishop, M.; Saltiel, C.J. Application of the pivot algorithm for investigating the shapes of two-and three-dimensional lattice polymers. J. Chem. Phys. 1988, 88, 6594. [Google Scholar] [CrossRef]
- Jagodzinski, O.; Eisenriegler, E.; Kremer, K. Universal shape properties of open and closed polymer chains: Renormalization group analysis and Monte Carlo experiments. J. Phys. I Fr. 1992, 2, 2243–2279. [Google Scholar] [CrossRef]
- Nakamura, I.; Wang, Z.G. Effects of dielectric inhomogeneity in polyelectrolyte solutions. Soft Matter 2013, 9, 5686–5690. [Google Scholar] [CrossRef]
- Farahpour, F.; Maleknejad, A.; Varnik, F.; Ejtehadi, M.R. Chain deformation in translocation phenomena. Soft Matter 2013, 9, 2750–2759. [Google Scholar] [CrossRef]
- Sakaue, T. Sucking genes into pores: Insight into driven translocation. Phys. Rev. E 2010, 81, 041808. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Sakaue, T. Dynamical diagram and scaling in polymer driven translocation. Eur. Phys. J. E 2011, 34, 135. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Sakaue, T. Process time distribution of driven polymer transport. Phys. Rev. E 2012, 85, 061803. [Google Scholar] [CrossRef] [PubMed]
- Lam, P.M.; Zhen, Y. Dynamic scaling theory of the forced translocation of a semi-flexible polymer through a nanopore. J. Stat. Phys. 2015, 161, 197–209. [Google Scholar] [CrossRef]
- Meller, A.; Nivon, L.; Branton, D. Voltage-driven DNA translocations through a nanopore. Phys. Rev. Lett. 2001, 86, 3435–3438. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Stein, D.; McMullan, C.; Branton, D.; Aziz, M.J.; Golovchenko, J.A. Ion-beam sculpting at nanometre length scales. Nature 2001, 412, 166–169. [Google Scholar] [CrossRef] [PubMed]
- Storm, A.J.; Storm, C.; Chen, J.; Zandbergen, H.; Joanny, J.F.; Dekker, C. Fast DNA translocation through a solid-state nanopore. Nano Lett. 2005, 5, 1193–1197. [Google Scholar] [CrossRef] [PubMed]
- Wanunu, M.; Sutin, J.; McNally, B.; Chow, A.; Meller, A. DNA translocation governed by interactions with solid-state nanopores. Biophys. J. 2008, 95, 4716–4725. [Google Scholar] [CrossRef] [PubMed]
- Schneider, G.F.; Kowalczyk, S.W.; Calado, V.E.; Pandraud, G.; Zandbergen, H.W.; Vandersypen, L.M.; Dekker, C. DNA translocation through graphene nanopores. Nano Lett. 2010, 10, 3163–3167. [Google Scholar] [CrossRef] [PubMed]
- Merchant, C.A.; Healy, K.; Wanunu, M.; Ray, V.; Peterman, N.; Bartel, J.; Fischbein, M.D.; Venta, K.; Luo, Z.; Johnson, A.C.; et al. DNA translocation through graphene nanopores. Nano Lett. 2010, 10, 2915–2921. [Google Scholar] [CrossRef] [PubMed]
- Qian, W.; Doi, K.; Uehara, S.; Morita, K.; Kawano, S. Theoretical Study of the Transpore velocity control of single-stranded DNA. Int. J. Mol. Sci. 2014, 15, 13817–13832. [Google Scholar] [CrossRef] [PubMed]
- Shankla, M.; Aksimentiev, A. Conformational transitions and stop-and-go nanopore transport of single-stranded DNA on charged graphene. Nat. Commun. 2014, 5, 5171. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, Y.; Yang, J.; Bi, K.; Ni, Z.; Li, D.; Chen, Y. Molecular dynamics study of DNA translocation through graphene nanopores. Phys. Rev. E 2013, 87, 062707. [Google Scholar] [CrossRef] [PubMed]
- Piguet, F.; Foster, D. Translocation of short and long polymers through an interacting pore. J. Chem. Phys. 2013, 138, 084902. [Google Scholar] [CrossRef] [PubMed]
- Luo, K.; Ala-Nissila, T.; Ying, S.C. Polymer translocation through a nanopore: A two-dimensional Monte Carlo study. J. Chem. Phys. 2006, 124, 034714. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, R.; Bhattacharya, A. Driven translocation of a semi-flexible chain through a nanopore: A Brownian dynamics simulation study in two dimensions. J. Chem. Phys. 2013, 138, 204909. [Google Scholar] [CrossRef] [PubMed]
- Sarabadani, J.; Ikonen, T.; Ala-Nissila, T. Iso-flux tension propagation theory of driven polymer translocation: The role of initial configurations. J. Chem. Phys. 2014, 141, 214907. [Google Scholar] [CrossRef] [PubMed]
- Sung, W.; Park, P. Polymer translocation through a pore in a membrane. Phys. Rev. Lett. 1996, 77, 783–786. [Google Scholar] [CrossRef] [PubMed]
- Park, P.J.; Sung, W. Polymer translocation induced by adsorption. J. Chem. Phys. 1998, 108, 3013–3018. [Google Scholar] [CrossRef]
- Lubensky, D.K.; Nelson, D.R. Driven polymer translocation through a narrow pore. Biophys. J. 1999, 77, 1824–1838. [Google Scholar] [CrossRef]
- Muthukumar, M. Polymer translocation through a hole. J. Chem. Phys. 1999, 111, 10371. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods, 3rd ed.; Springer: Berlin, Germany, 2004. [Google Scholar]
- Risken, H. Fokker-Planck Equation, 2nd ed.; Springer: Berlin, Germany, 1989. [Google Scholar]
- Slonkina, E.; Kolomeisky, A.B. Polymer translocation through a long nanopore. J. Chem. Phys. 2003, 118, 7112. [Google Scholar] [CrossRef]
- Panja, D.; Barkema, G.T. Passage times for polymer translocation pulled through a narrow pore. Biophys. J. 2008, 94, 1630–1637. [Google Scholar] [CrossRef] [PubMed]
- Vocks, H.; Panja, D.; Barkema, G.T.; Ball, R.C. Pore-blockade times for field-driven polymer translocation. J. Phys. Condens. Matter 2008, 20, 095224. [Google Scholar] [CrossRef]
- Sakaue, T. Memory effect and fluctuating anomalous dynamics of a tagged monomer. Phys. Rev. E 2013, 87, 040601. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Klafter, J. When translocation dynamics becomes anomalous. Biophys. J. 2003, 85, 2776–2779. [Google Scholar] [CrossRef]
- Dubbeldam, J.; Milchev, A.; Rostiashvili, V.; Vilgis, T.A. Polymer translocation through a nanopore: A showcase of anomalous diffusion. Phys. Rev. E 2007, 76, 010801. [Google Scholar] [CrossRef] [PubMed]
- Sakaue, T. Nonequilibrium dynamics of polymer translocation and straightening. Phys. Rev. E 2007, 76, 021803. [Google Scholar] [CrossRef] [PubMed]
- Rowghanian, P.; Grosberg, A.Y. Force-driven polymer translocation through a nanopore: An old problem revisited. J. Phys. Chem. B 2011, 115, 14127–14135. [Google Scholar] [CrossRef] [PubMed]
- Dubbeldam, J.; Rostiashvili, V.; Milchev, A.; Vilgis, T.A. Forced translocation of a polymer: Dynamical scaling versus molecular dynamics simulation. Phys. Rev. E 2012, 85, 041801. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Sakaue, T. Driven anomalous diffusion: An example from polymer stretching. Phys. Rev. E 2015, 92, 012601. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Sakaue, T. Cis-trans dynamical asymmetry in driven polymer translocation. Phys. Rev. E 2013, 88, 042606. [Google Scholar] [CrossRef] [PubMed]
- Dubbeldam, J.L.; Rostiashvili, V.G.; Vilgis, T.A. Driven translocation of a polymer: Role of pore friction and crowding. J. Chem. Phys. 2014, 141, 124112. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.Z.; Luo, M.B. Study on the polymer translocation induced blockade ionic current inside a nanopore by Langevin dynamics simulation. J. Phys. Condens. Matter 2013, 25, 465101. [Google Scholar] [CrossRef] [PubMed]
- Katkar, H.; Muthukumar, M. Effect of charge patterns along a solid-state nanopore on polyelectrolyte translocation. J. Chem. Phys. 2014, 140, 135102. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Chuang, J.; Kantor, Y.; Kardar, M. Anomalous dynamics of translocation. Phys. Rev. E 2001, 65, 011802. [Google Scholar] [CrossRef] [PubMed]
- Eisenriegler, E. Polymers Near Surfaces: Conformation Properties and Relation to Critical Phenomena; World Scientific: Singapore, 1993. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical RecipesThe Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Ariga, K.; Ji, Q.; Hill, J.P.; Vinu, A. Coupling of soft technology (layer-by-layer assembly) with hard materials (mesoporous solids) to give hierarchic functional structures. Soft Matter 2009, 5, 3562–3571. [Google Scholar] [CrossRef]
- Ariga, K.; Yamauchi, Y.; Rydzek, G.; Ji, Q.; Yonamine, Y.; Wu, K.C.W.; Hill, J.P. Layer-by-layer nanoarchitectonics: Invention, innovation, and evolution. Chem. Lett. 2014, 43, 36–68. [Google Scholar] [CrossRef]











© 2016 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, P.-Y. Conformation Change, Tension Propagation and Drift-Diffusion Properties of Polyelectrolyte in Nanopore Translocation. Polymers 2016, 8, 378. https://doi.org/10.3390/polym8100378
Hsiao P-Y. Conformation Change, Tension Propagation and Drift-Diffusion Properties of Polyelectrolyte in Nanopore Translocation. Polymers. 2016; 8(10):378. https://doi.org/10.3390/polym8100378
Chicago/Turabian StyleHsiao, Pai-Yi. 2016. "Conformation Change, Tension Propagation and Drift-Diffusion Properties of Polyelectrolyte in Nanopore Translocation" Polymers 8, no. 10: 378. https://doi.org/10.3390/polym8100378





