Figure 1.
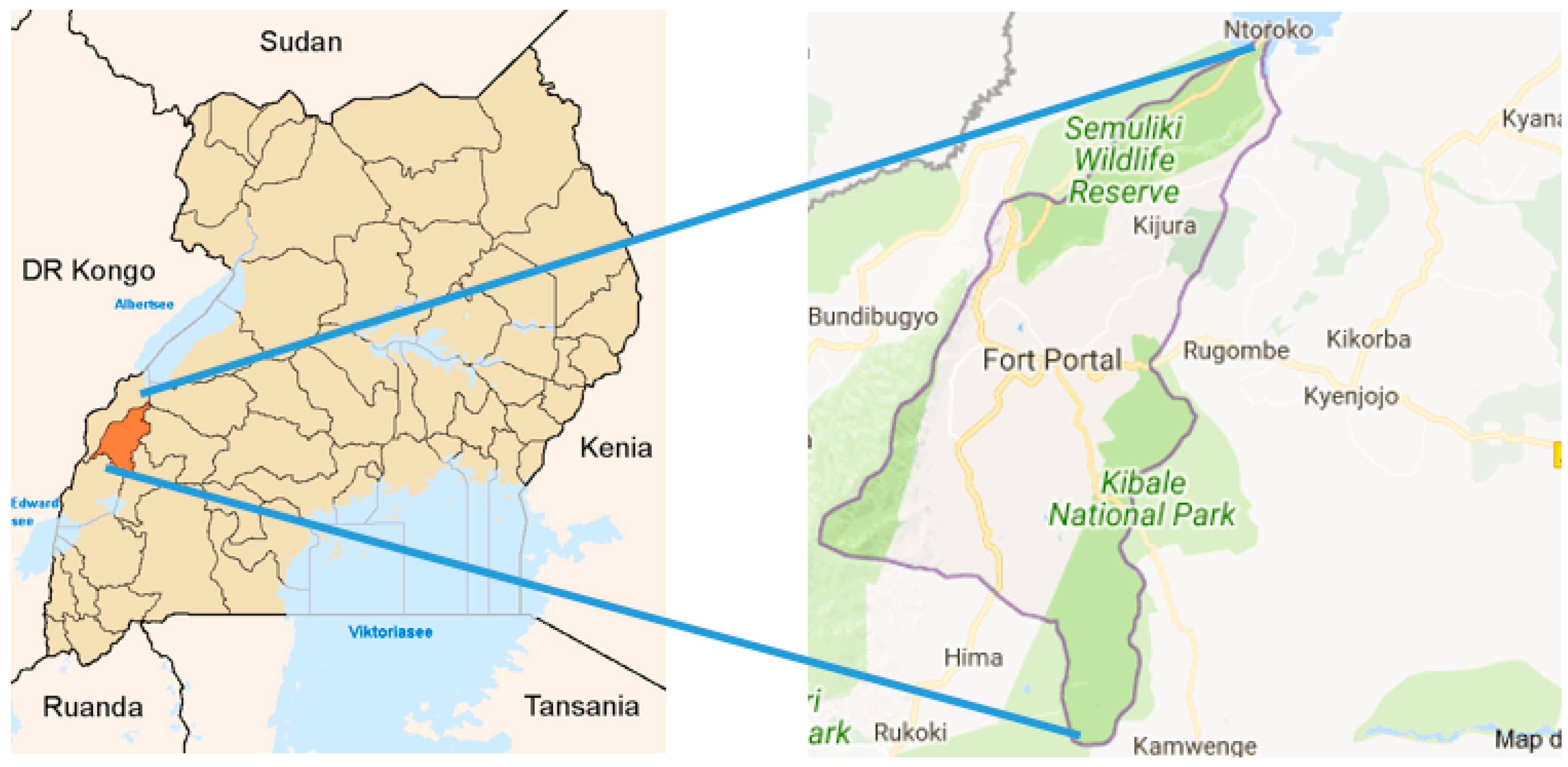
Location of Kabarole district on the Ugandan map (Source: Google maps).
Figure 1.
Location of Kabarole district on the Ugandan map (Source: Google maps).
Figure 2.
Daily observed rainfall for Kyembogo station (1992–2012).
Figure 2.
Daily observed rainfall for Kyembogo station (1992–2012).
Figure 3.
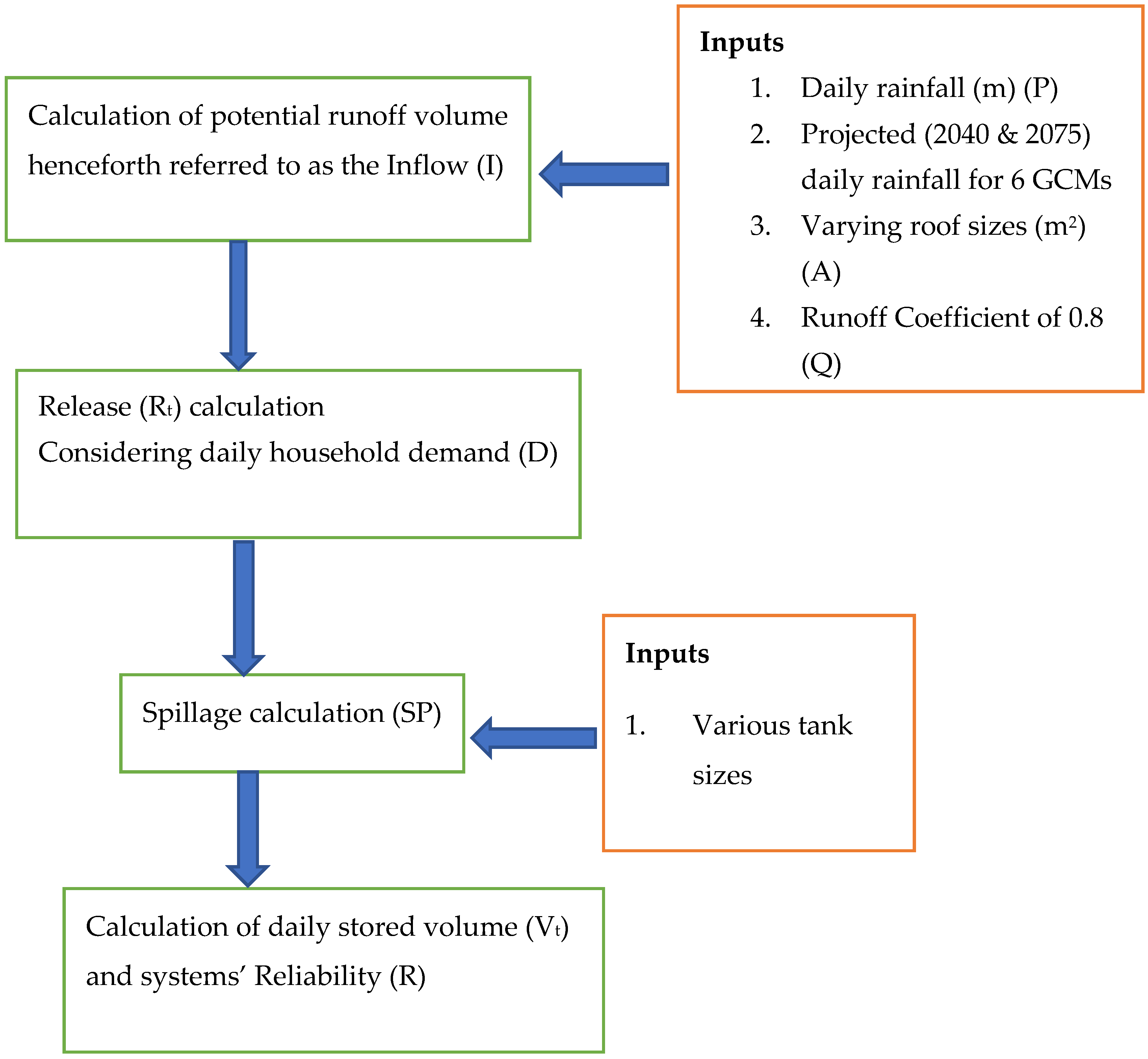
Summary of steps taken in estimation of reliability of rainwater harvesting systems with climate change and varying design combinations.
Figure 3.
Summary of steps taken in estimation of reliability of rainwater harvesting systems with climate change and varying design combinations.
Figure 4.
Illustrates the difference between formal and informal rainwater harvesting systems. (a) Formal harvesting systems; (b) Informal harvesting systems.
Figure 4.
Illustrates the difference between formal and informal rainwater harvesting systems. (a) Formal harvesting systems; (b) Informal harvesting systems.
Figure 5.
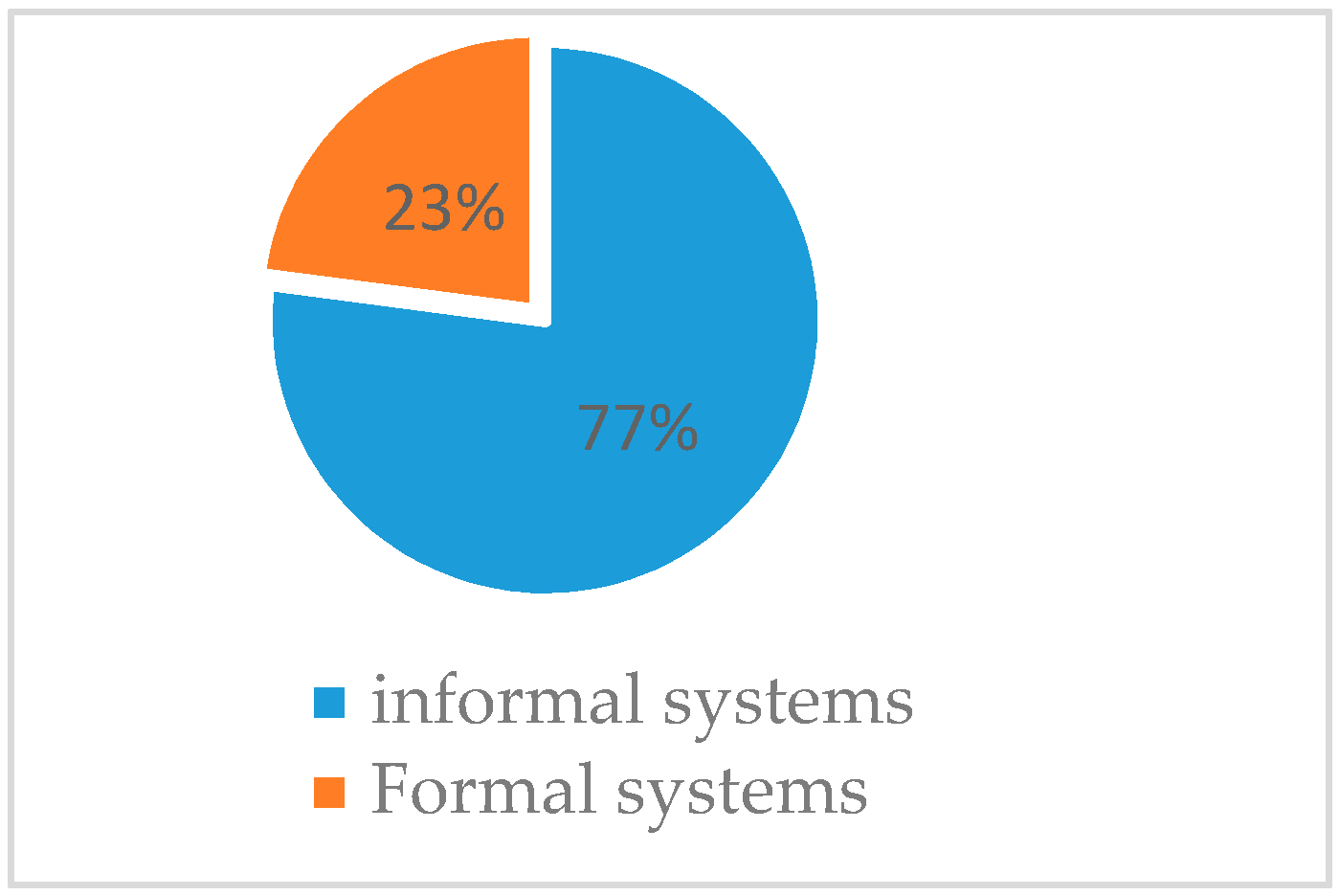
Proportion of households practicing both technologies.
Figure 5.
Proportion of households practicing both technologies.
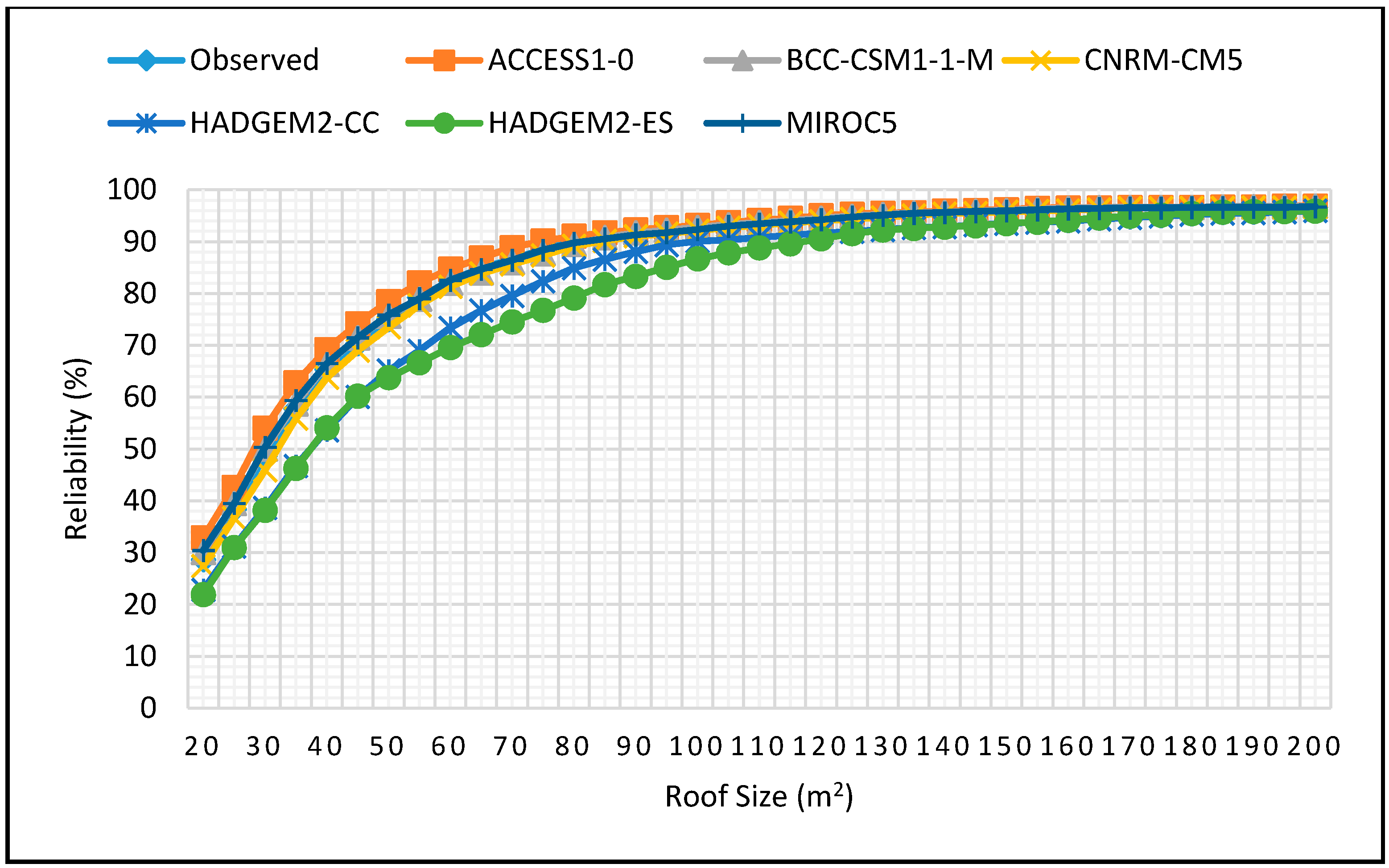
Figure 6.
Climate change prediction of daily average rainfall for 2025–2055.
Figure 6.
Climate change prediction of daily average rainfall for 2025–2055.
Figure 7.
Climate change prediction of daily average rainfall for 2060–2090.
Figure 7.
Climate change prediction of daily average rainfall for 2060–2090.
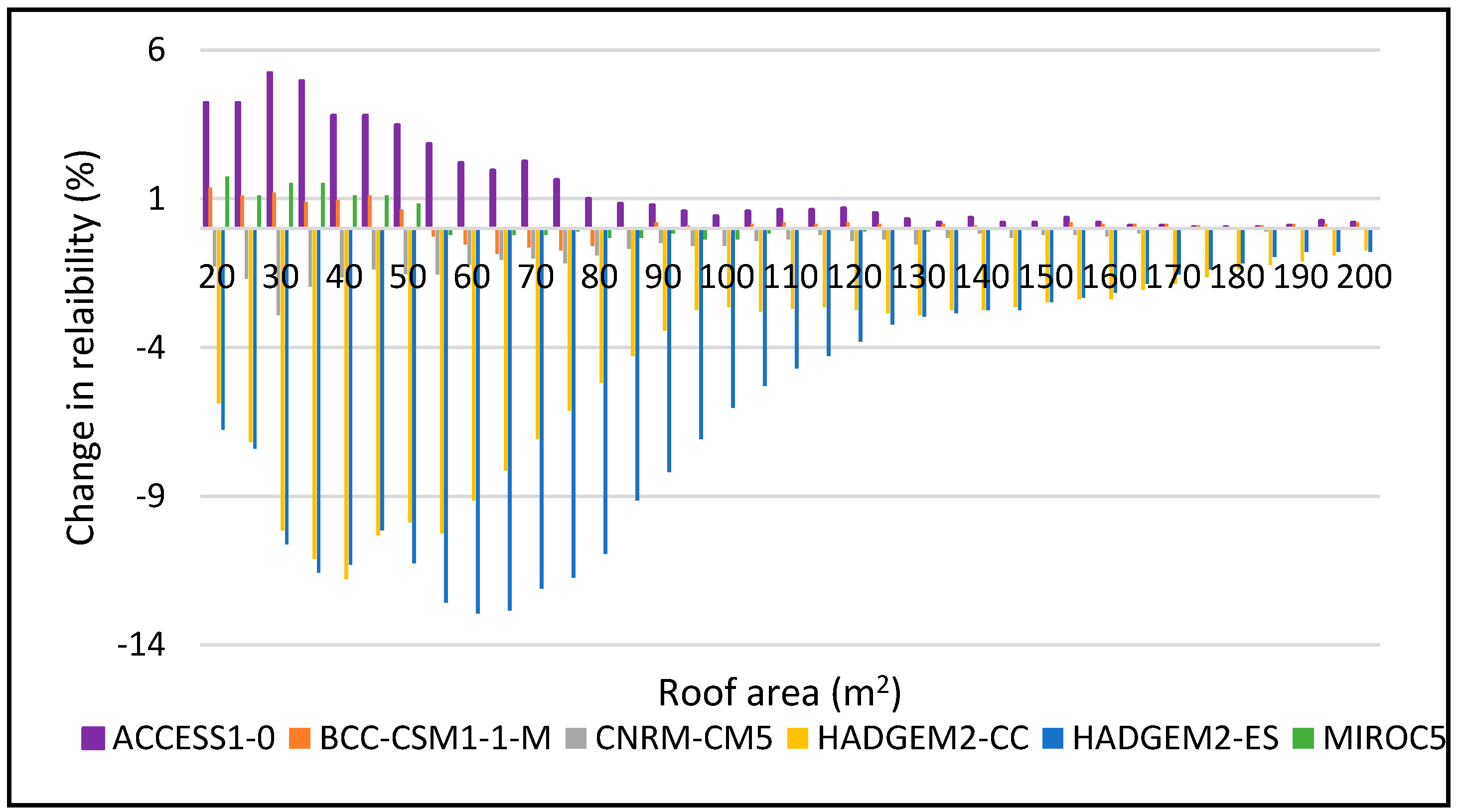
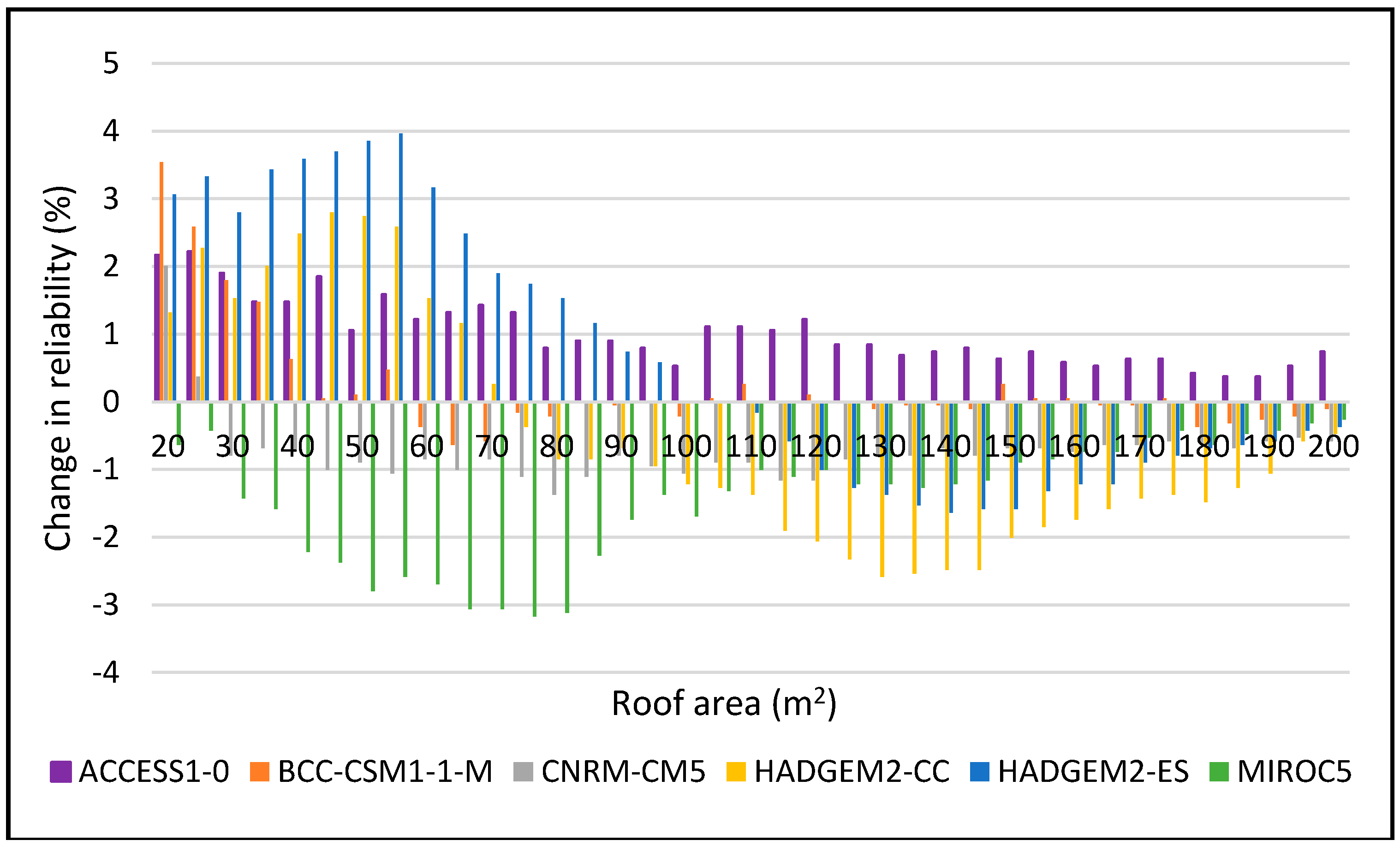
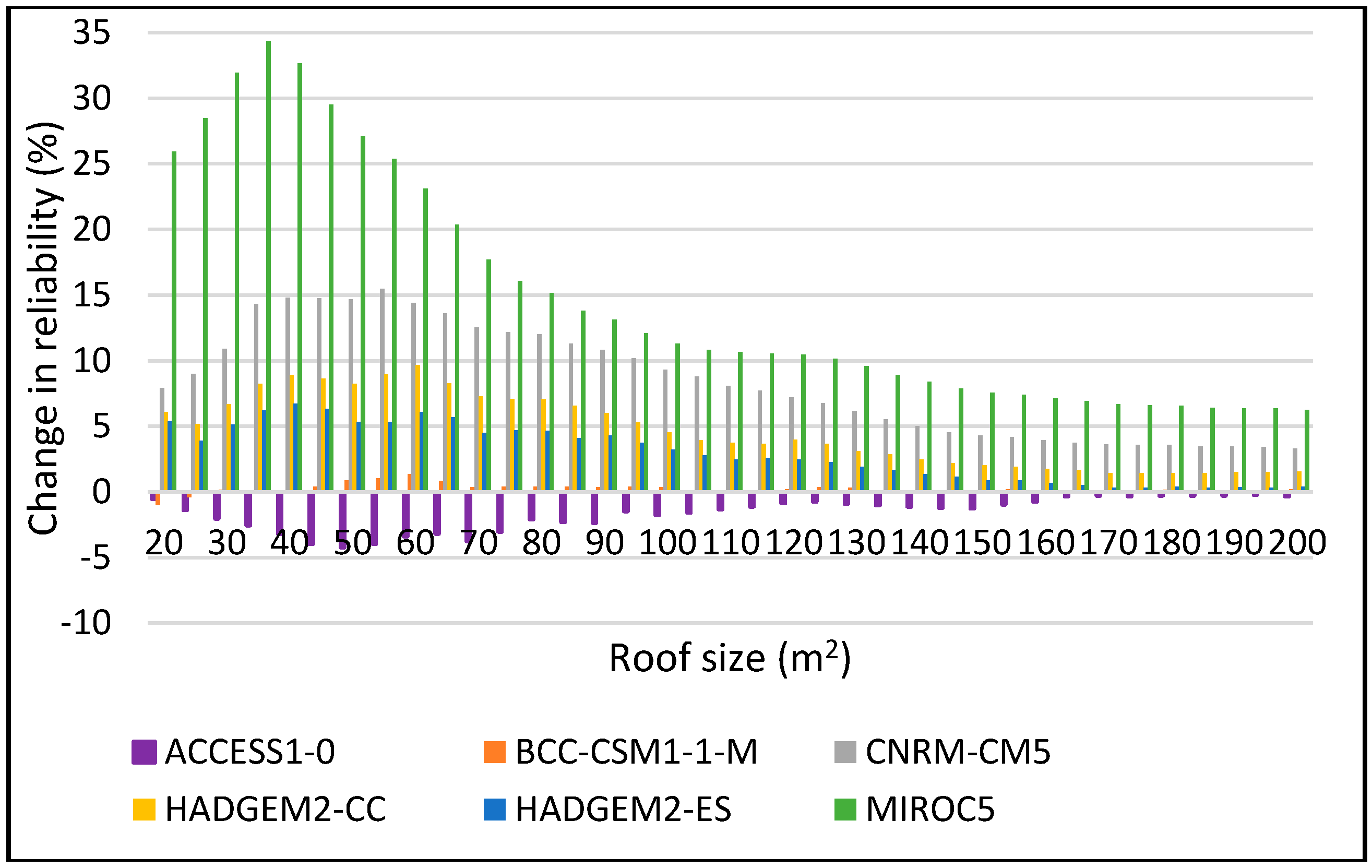
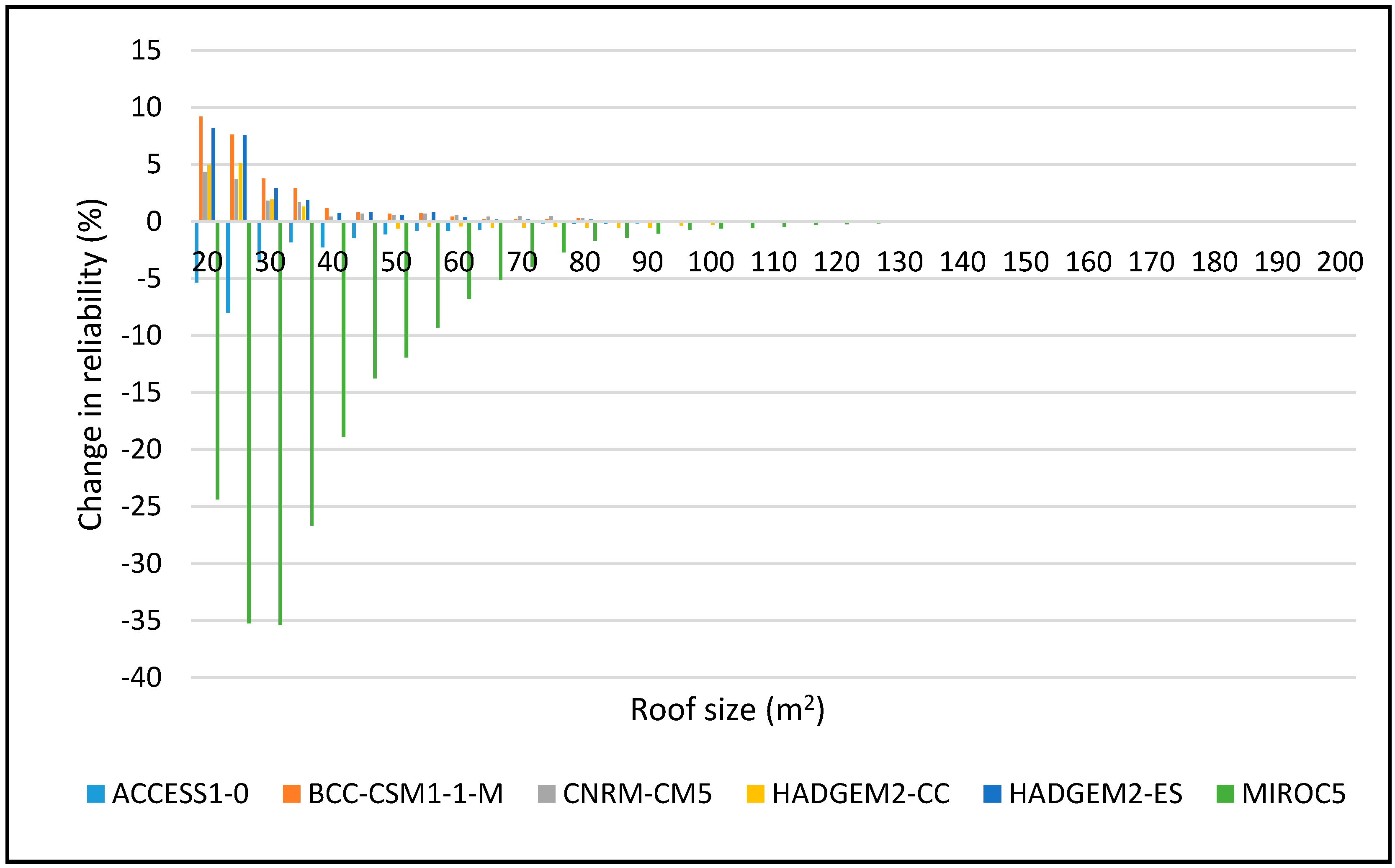
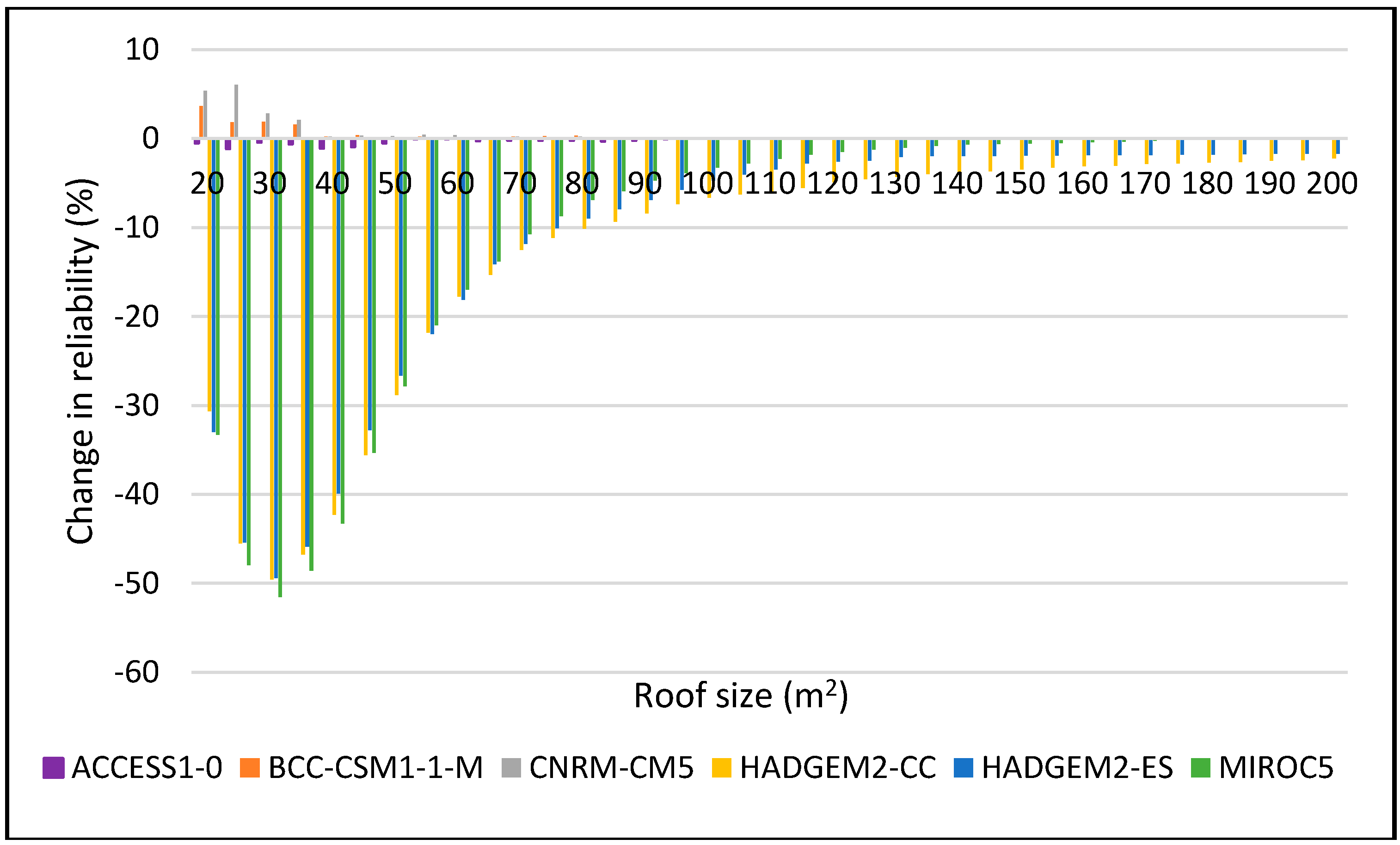
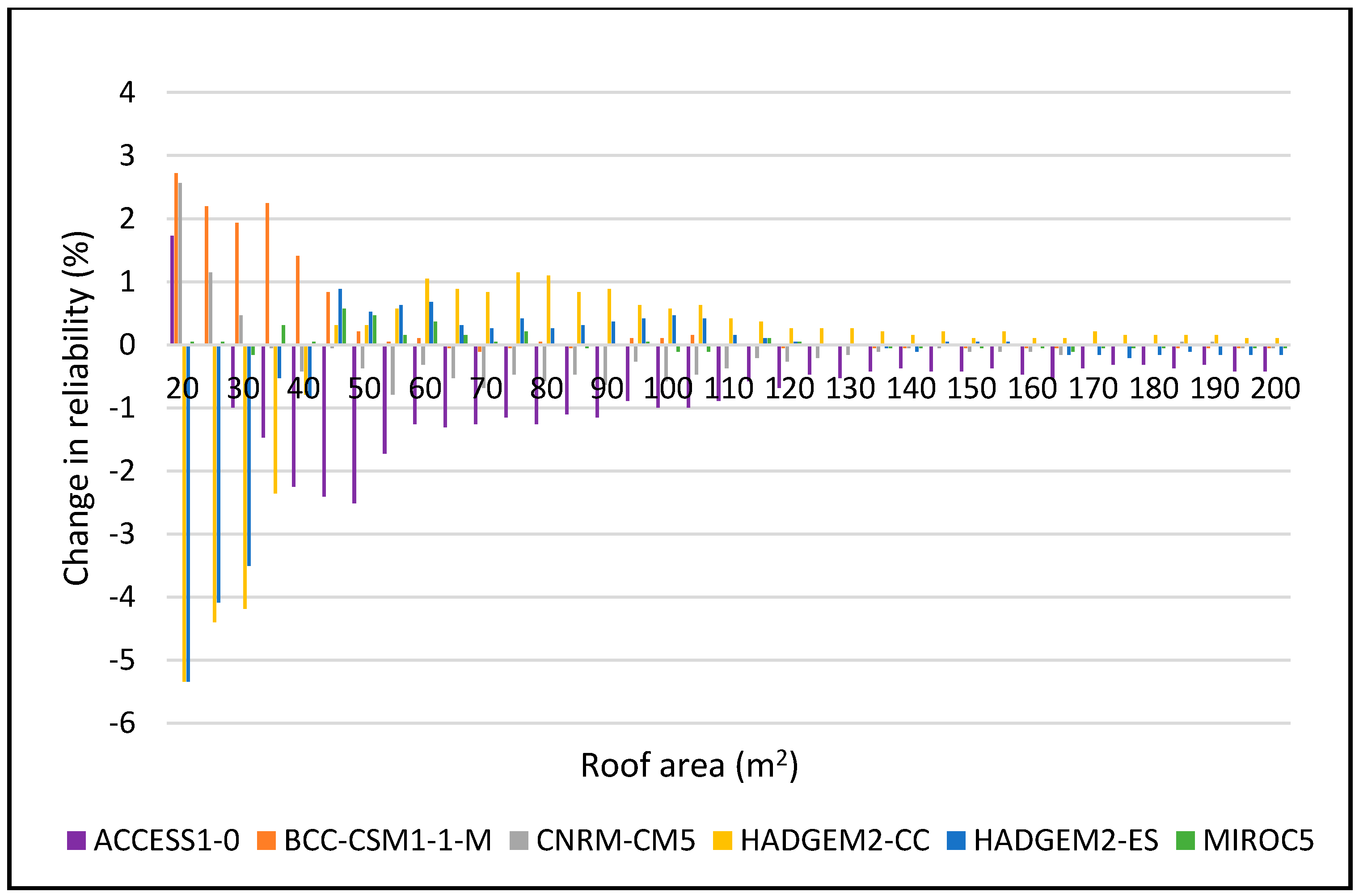
Figure 8.
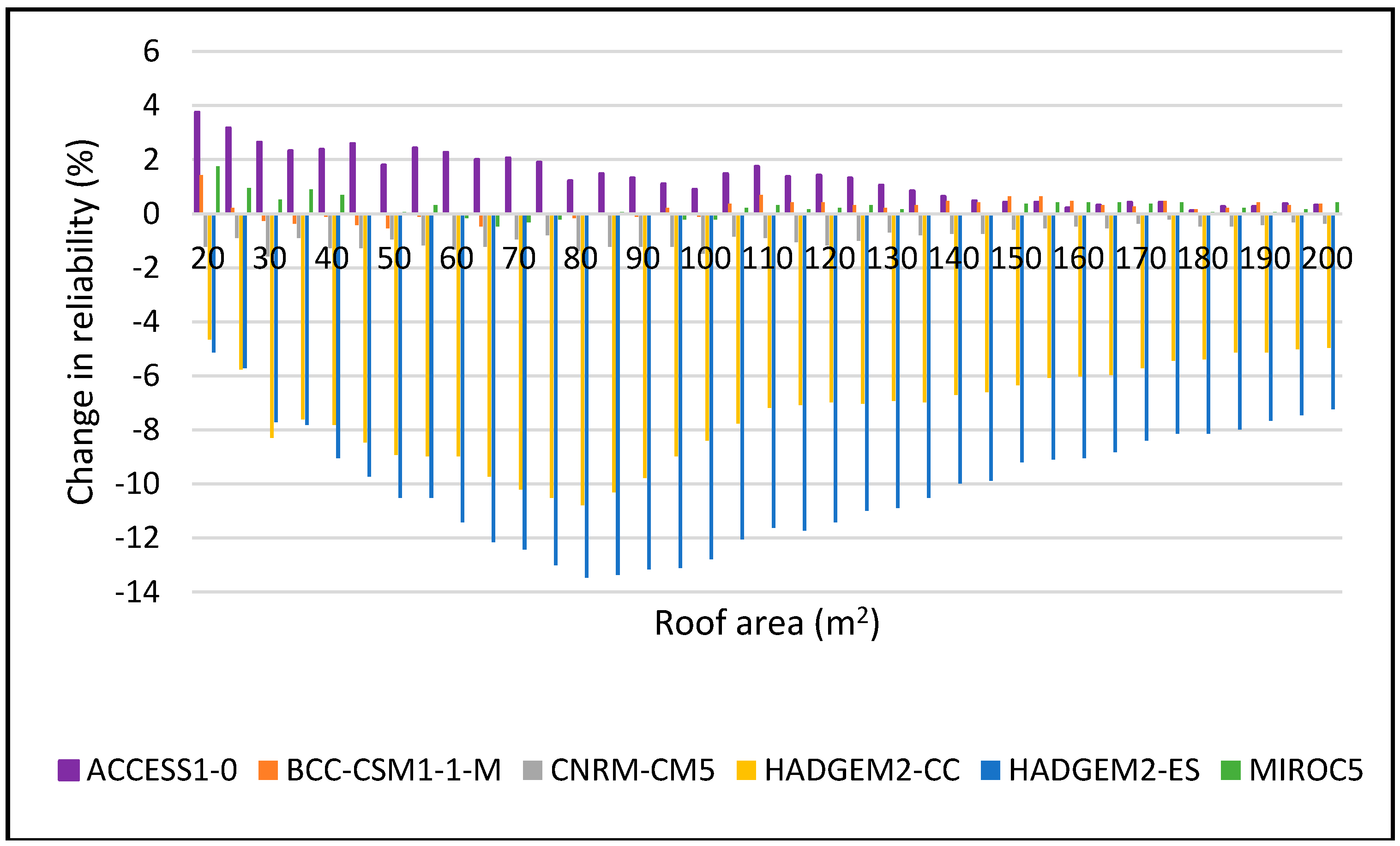
Change in reliability for DJF 2025–2055 period for 2 m3.
Figure 8.
Change in reliability for DJF 2025–2055 period for 2 m3.
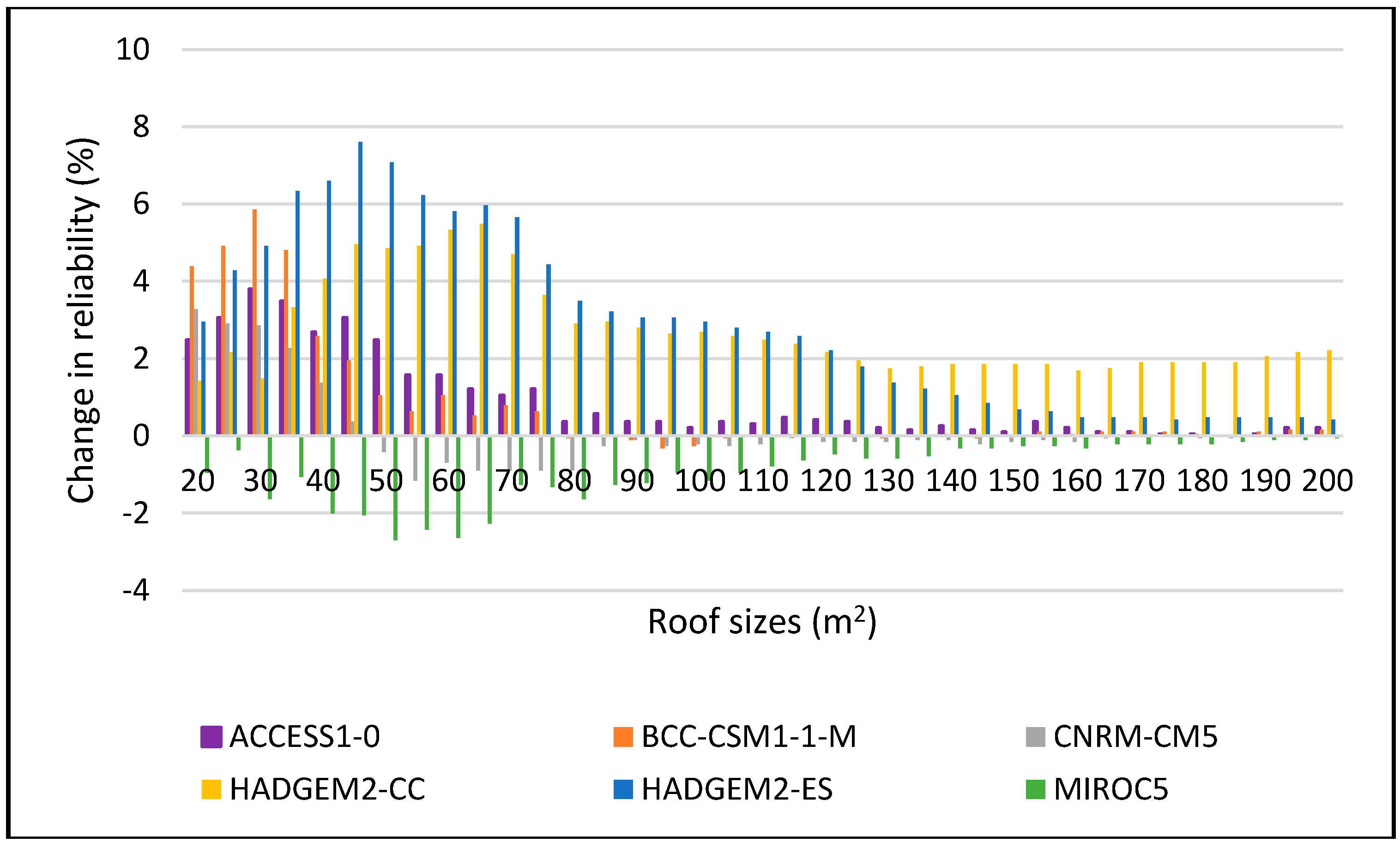
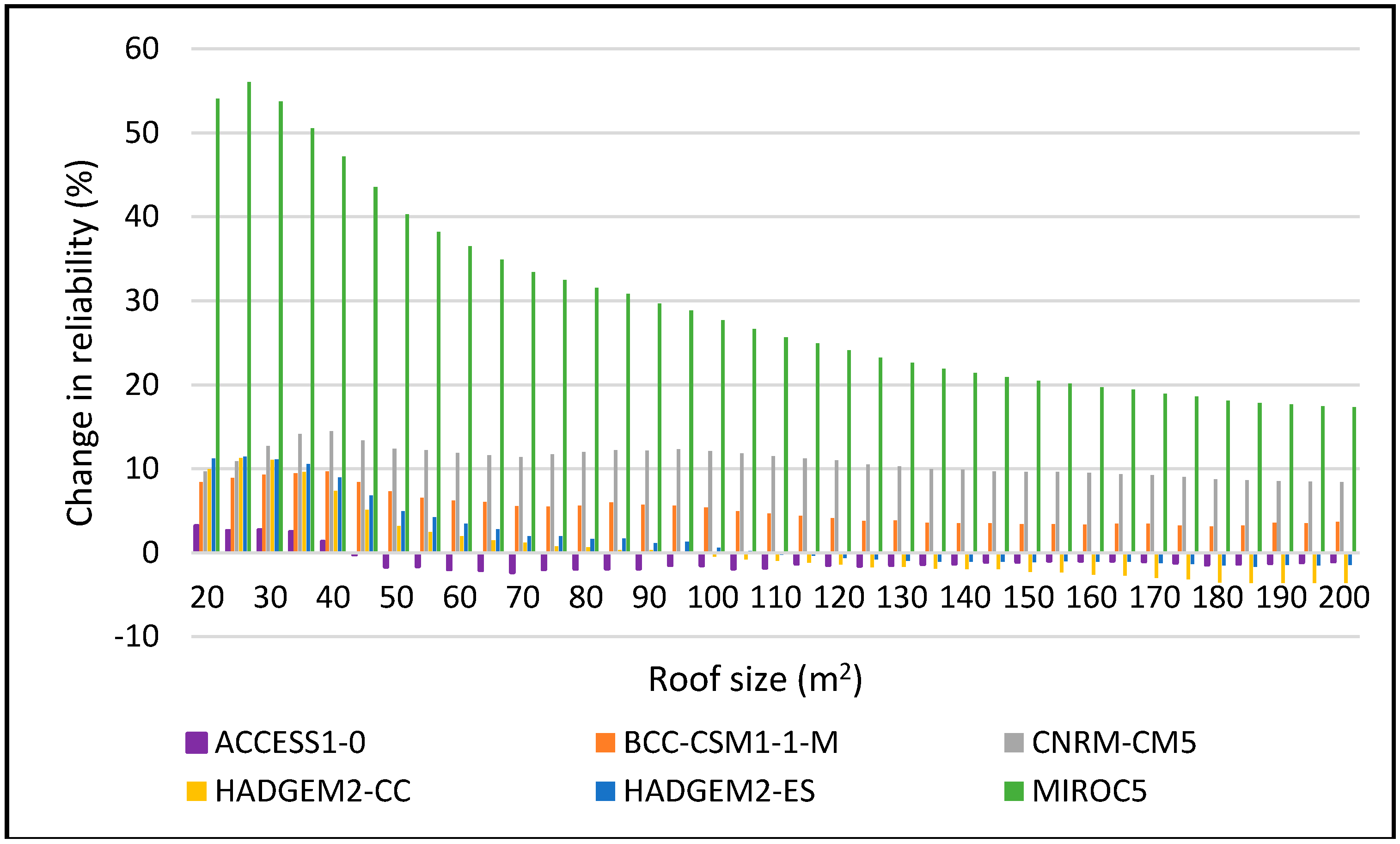
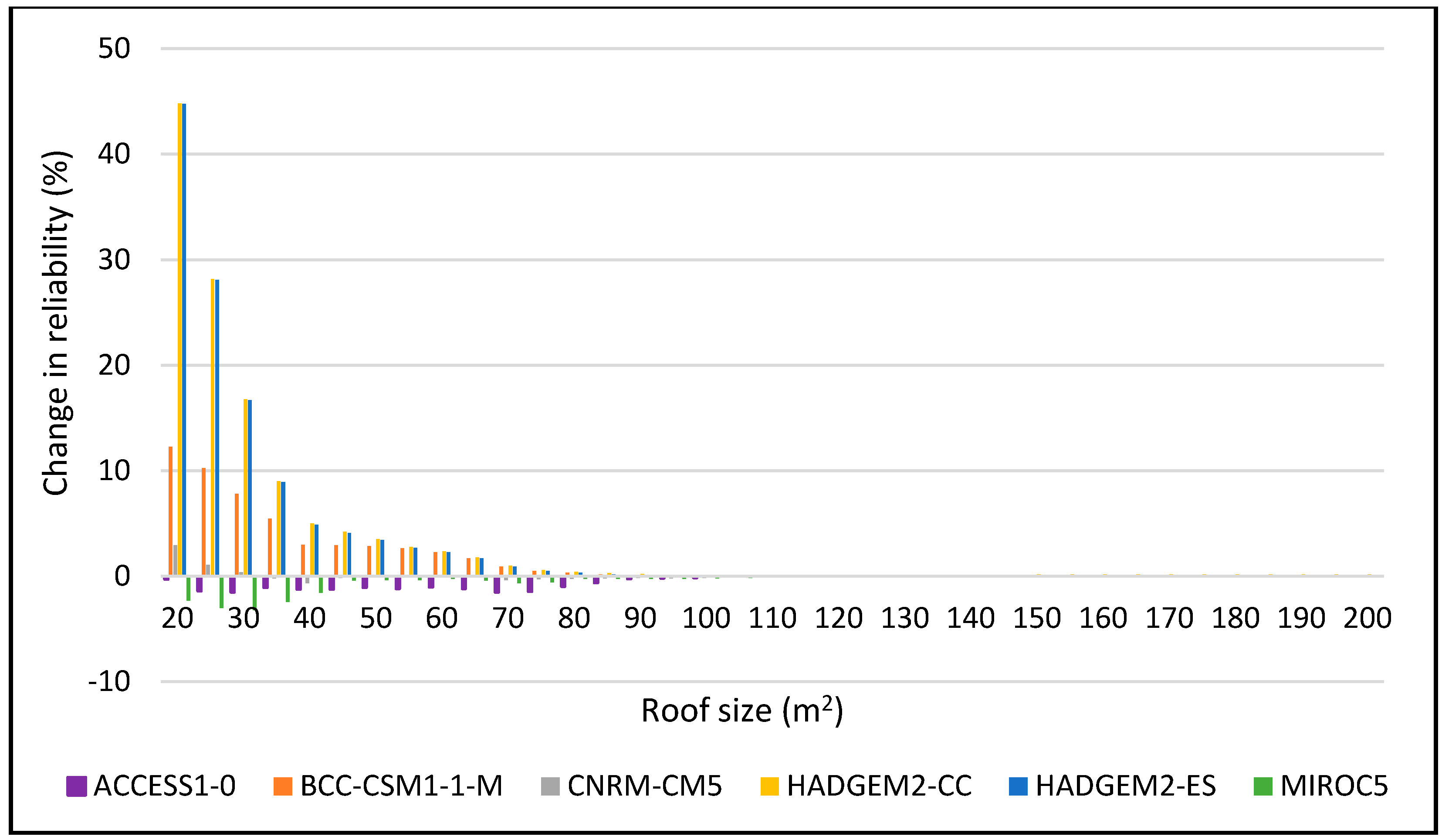
Figure 9.
Change in reliability for DJF 2025–2055 period for 5 m3.
Figure 9.
Change in reliability for DJF 2025–2055 period for 5 m3.
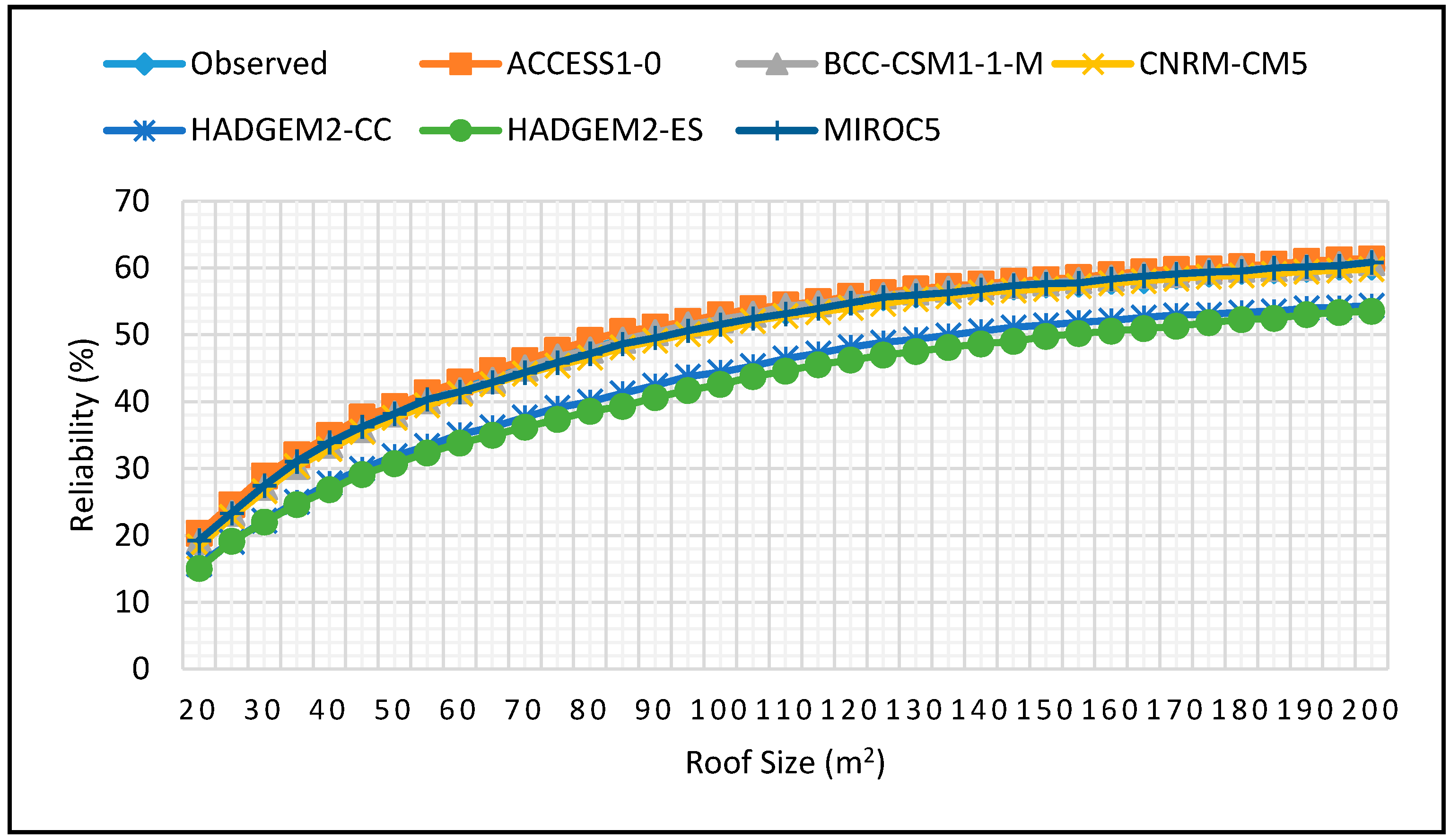
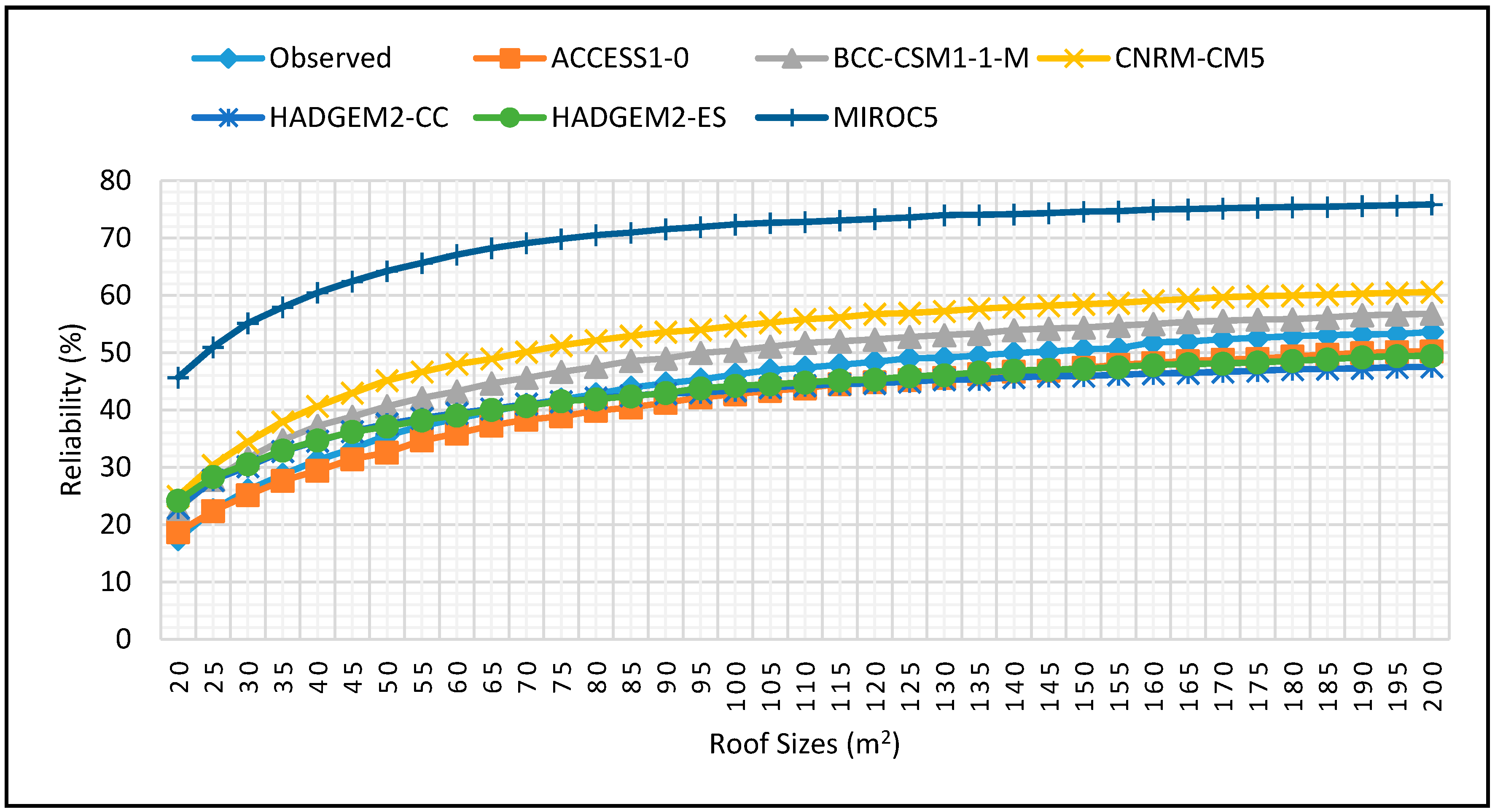
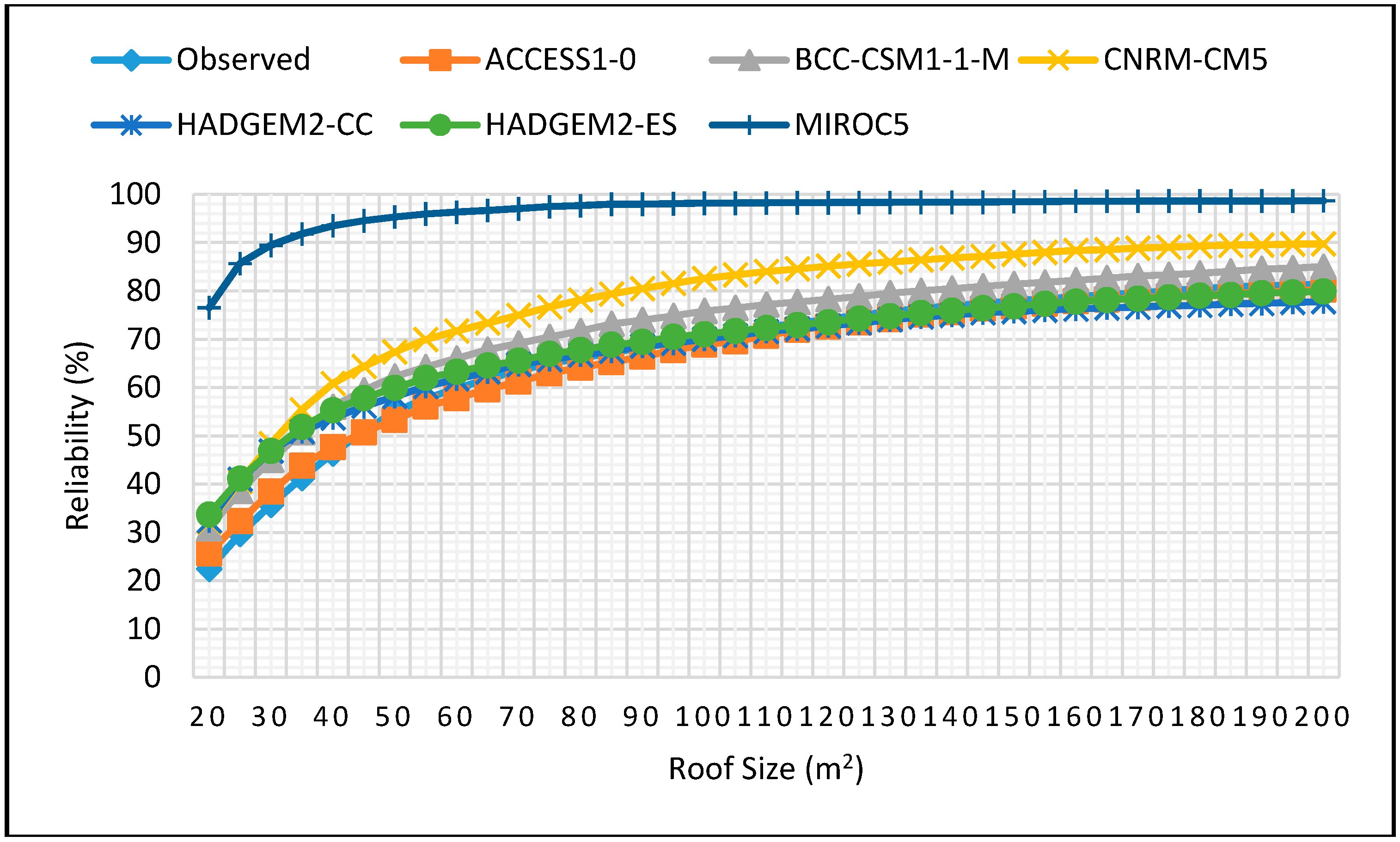
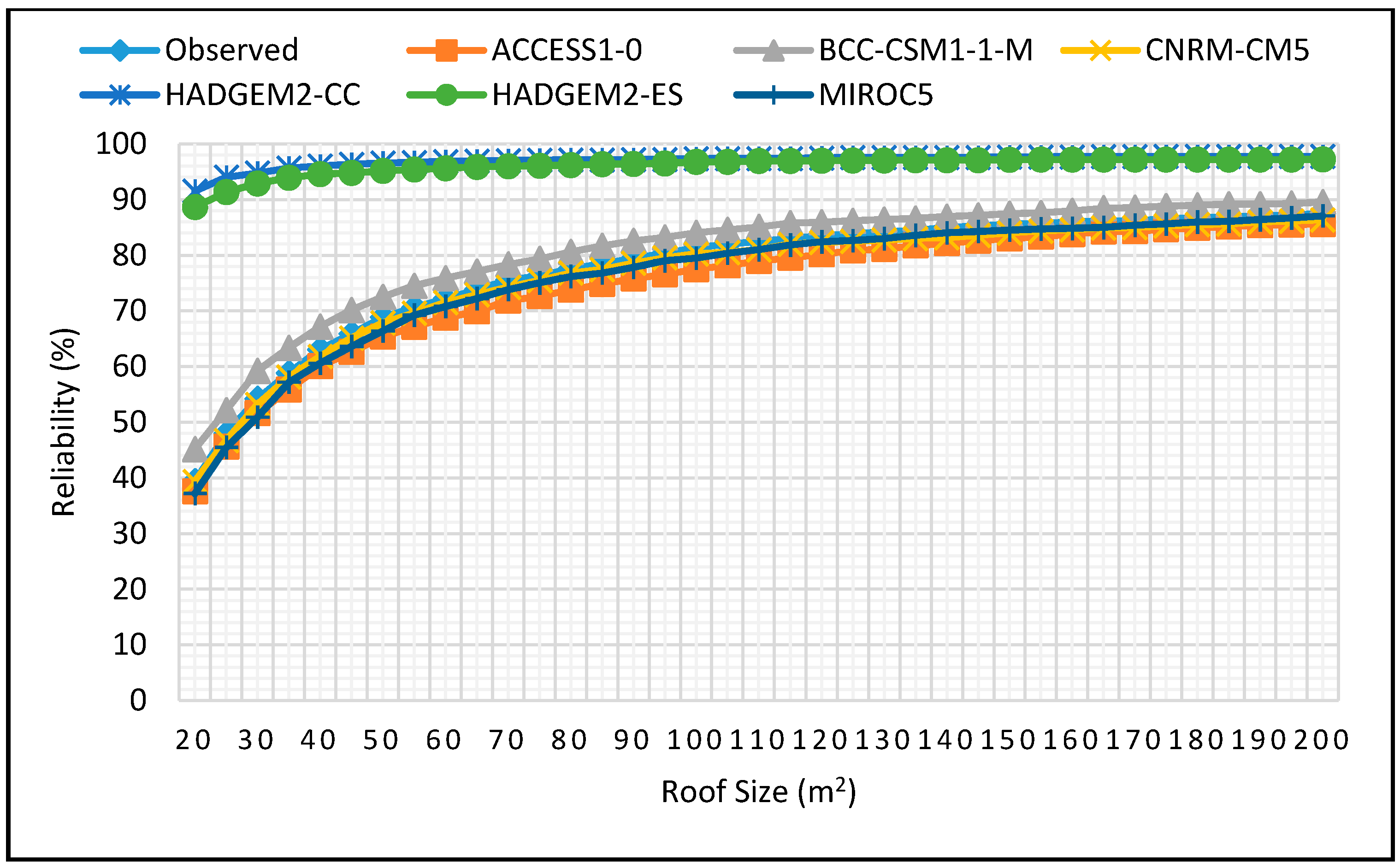
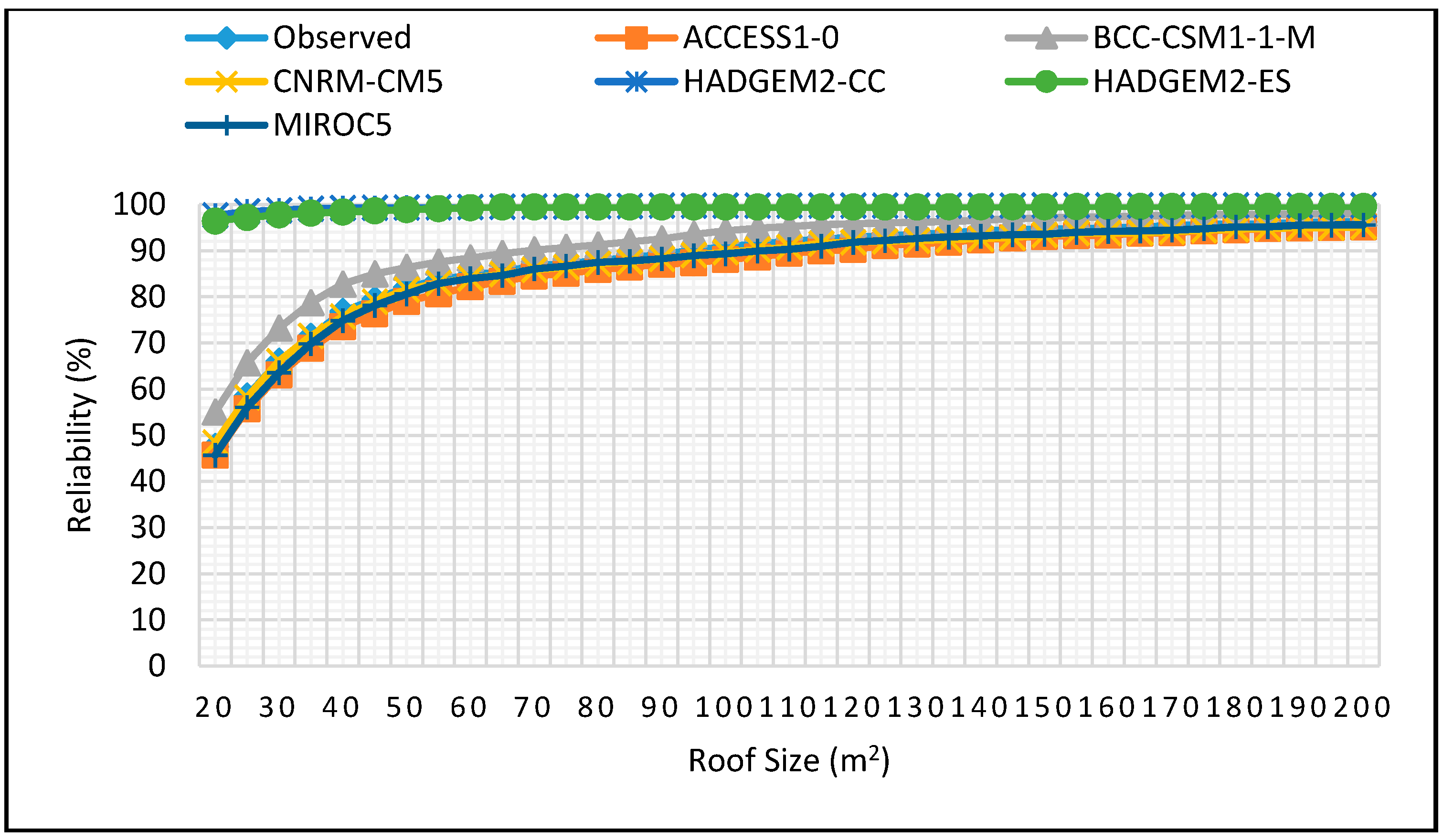
Figure 10.
Reliability projections for DJF season for 0.5 m3 tank size for 2025–2055.
Figure 10.
Reliability projections for DJF season for 0.5 m3 tank size for 2025–2055.
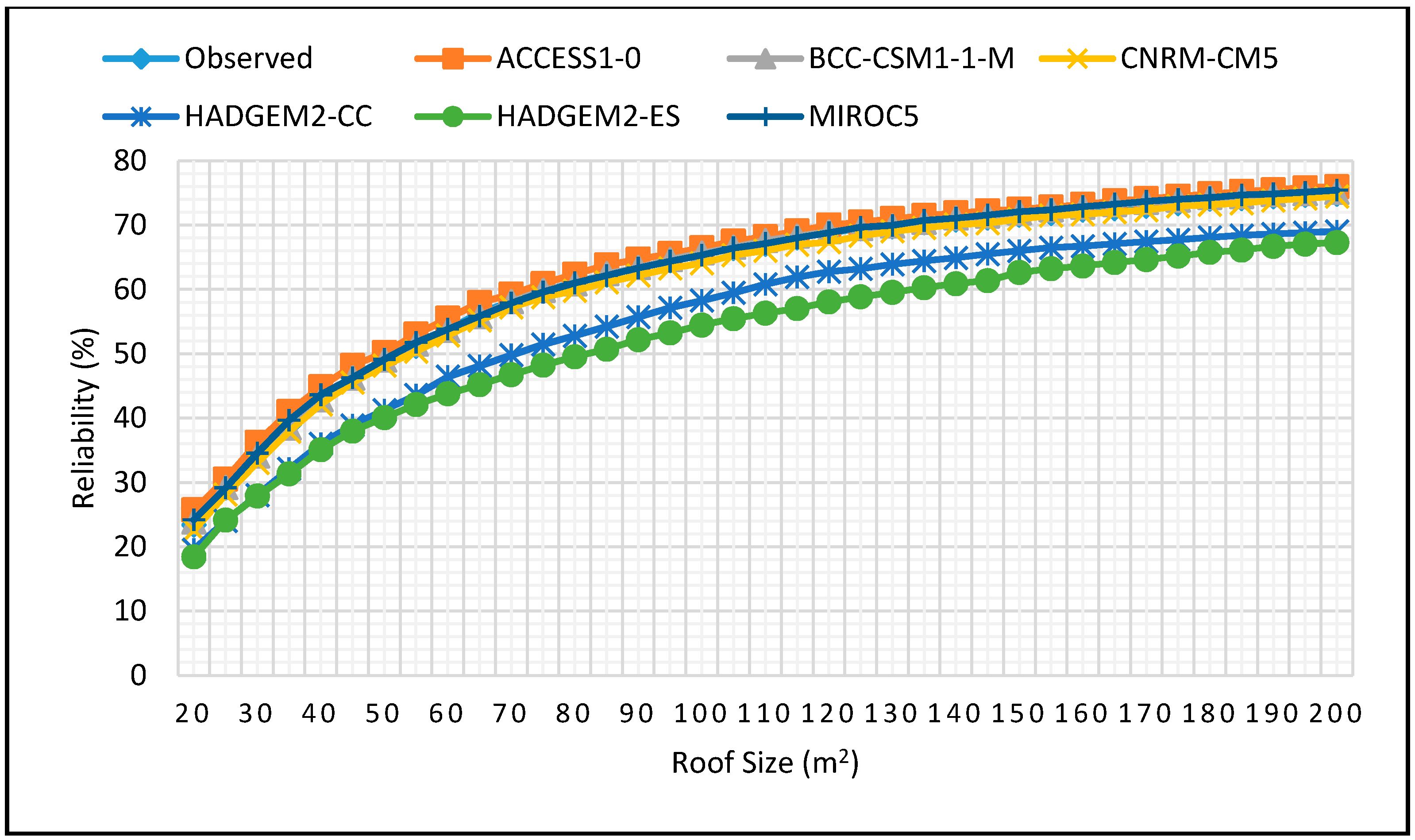
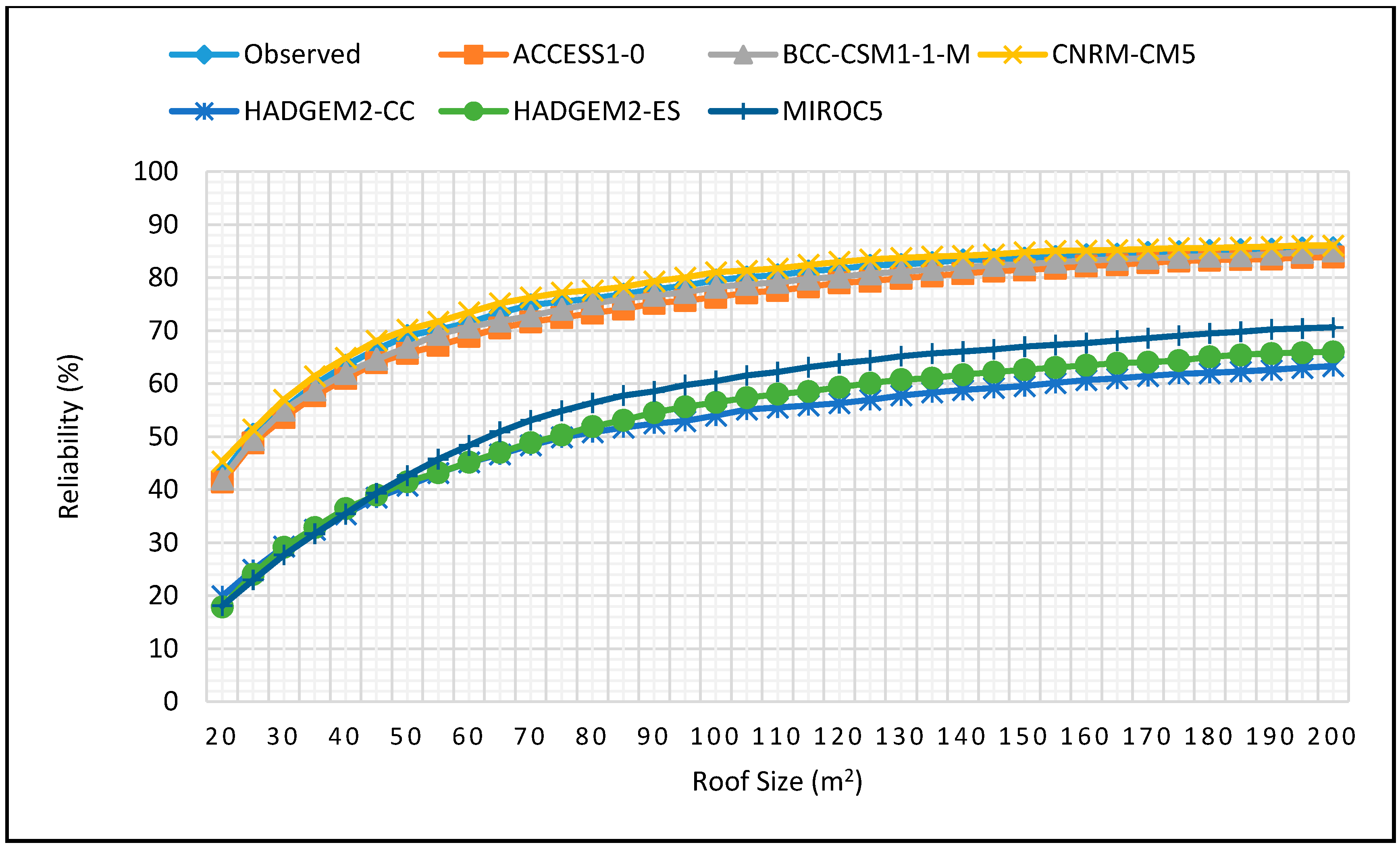
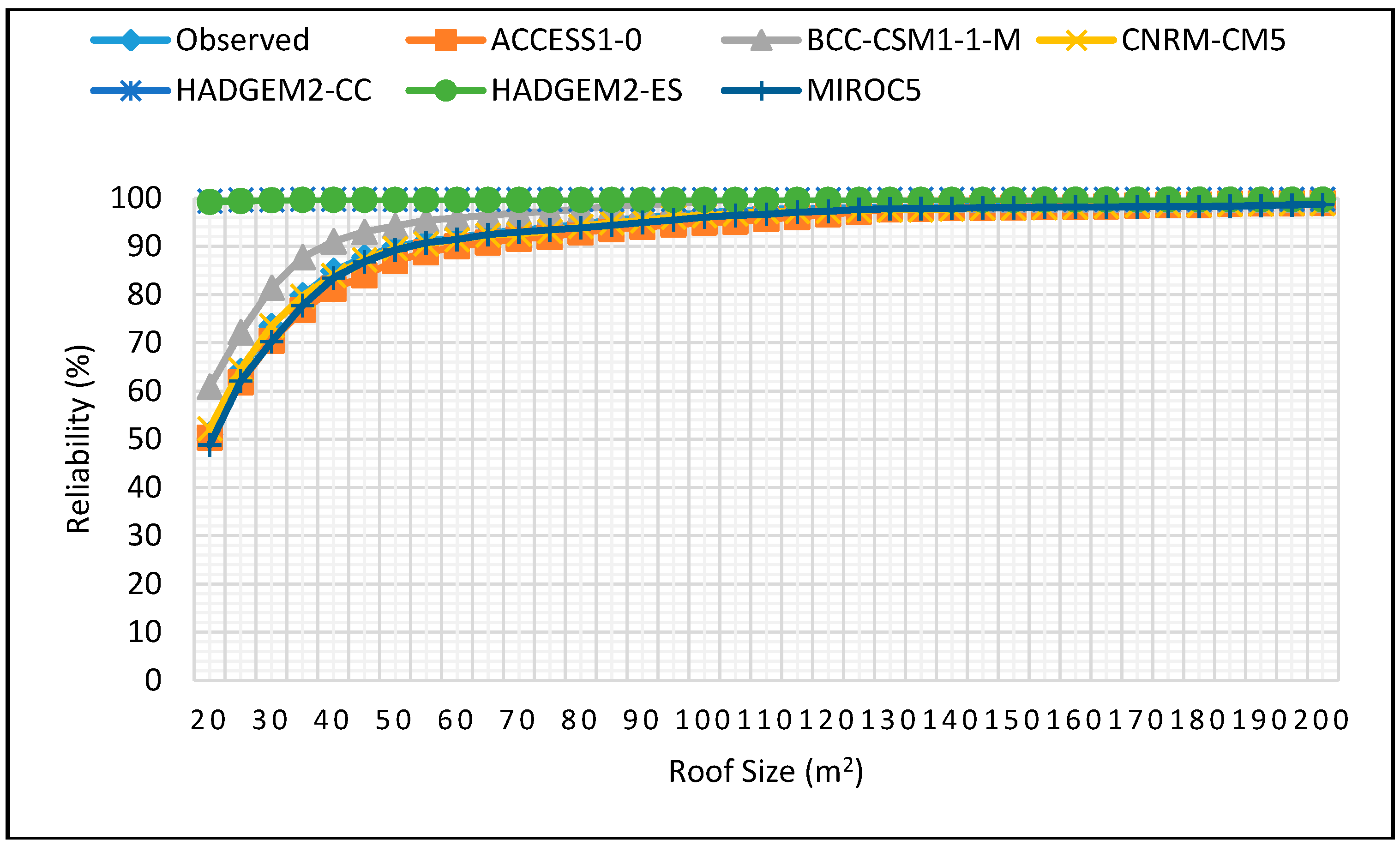
Figure 11.
Reliability projections for DJF season for 1 m3 tank size for 2025–2055.
Figure 11.
Reliability projections for DJF season for 1 m3 tank size for 2025–2055.
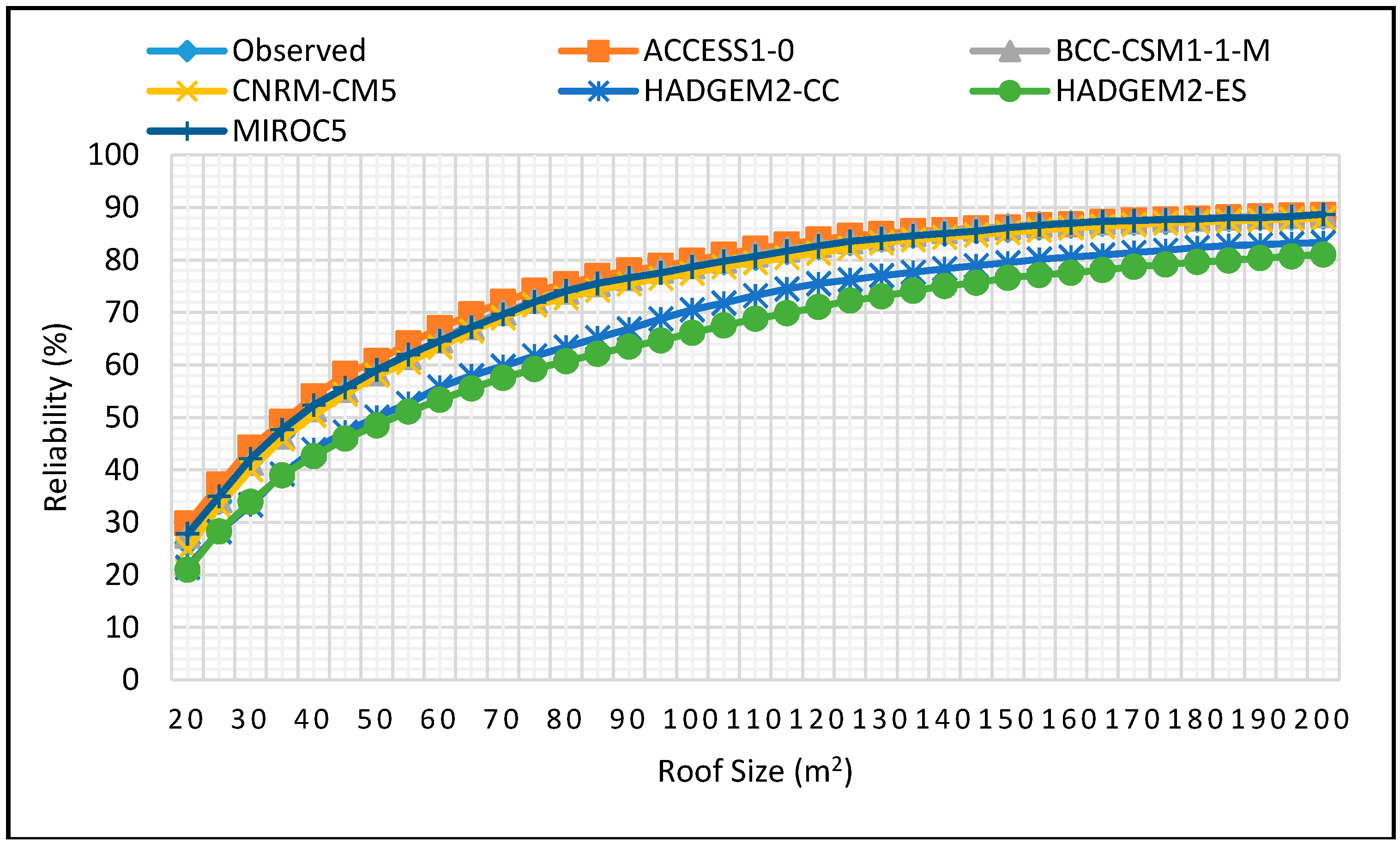
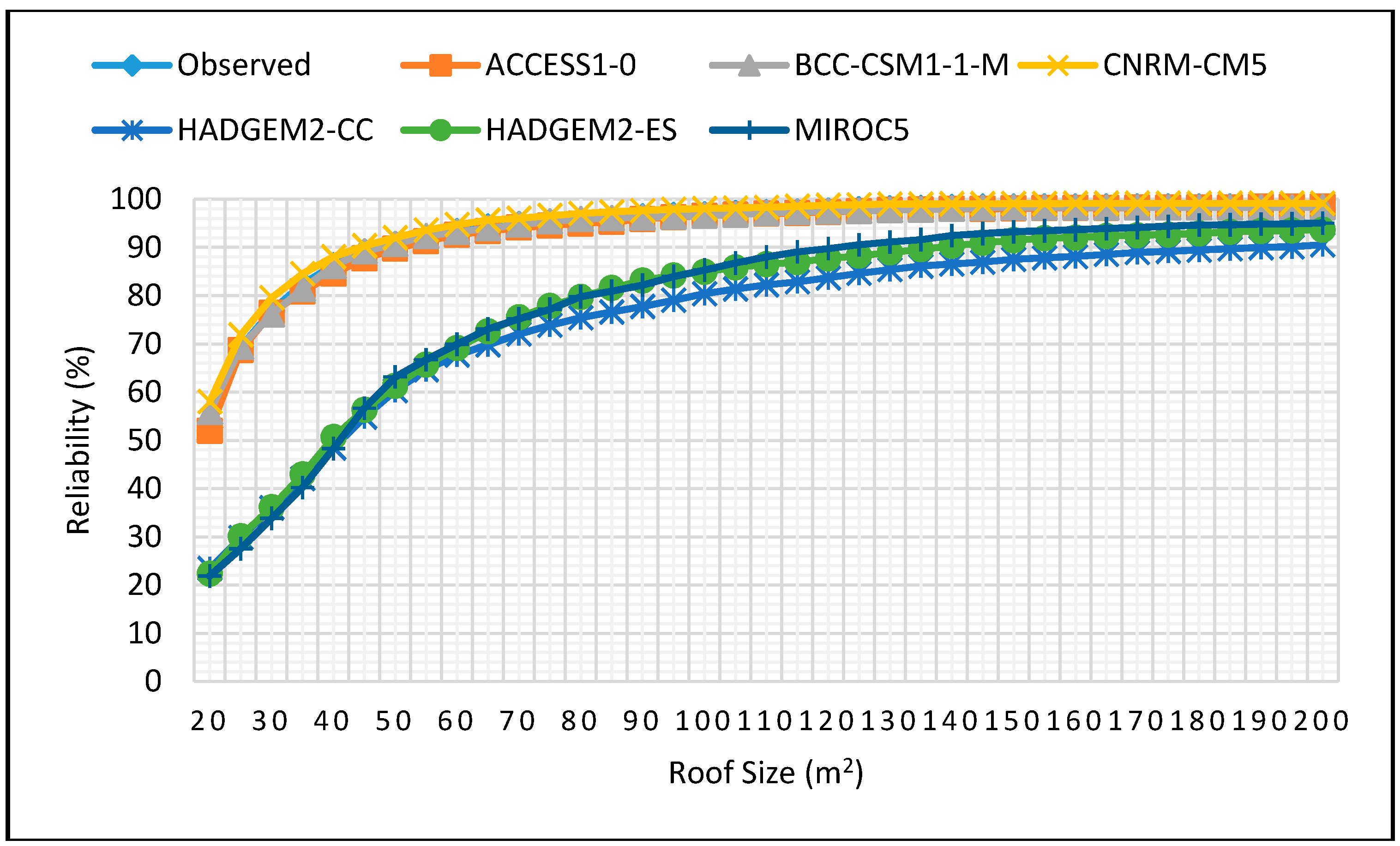
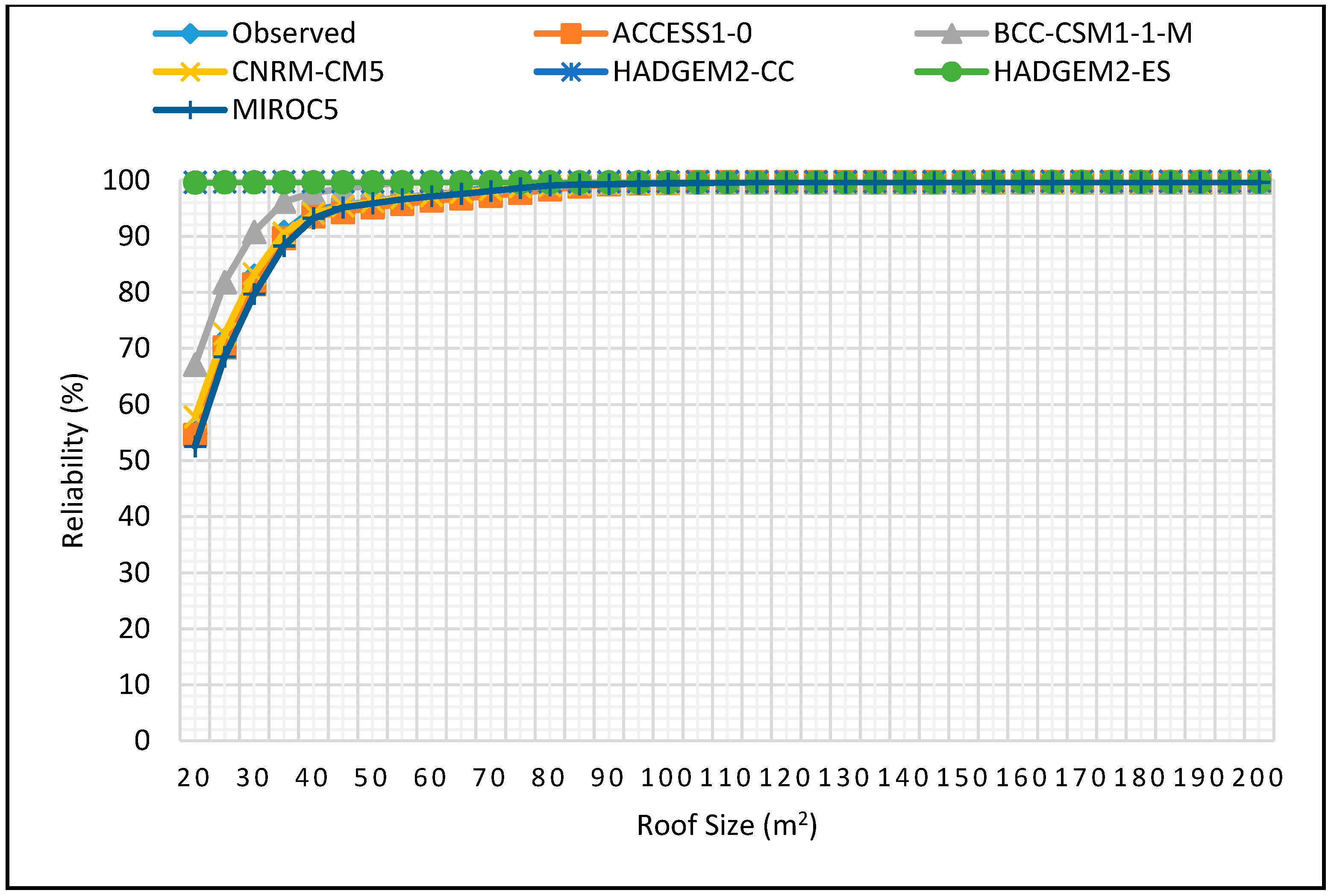
Figure 12.
Reliability projections for DJF season for 2 m3 tank size for 2025–2055.
Figure 12.
Reliability projections for DJF season for 2 m3 tank size for 2025–2055.
Figure 13.
Reliability projections for DJF season for 5 m3 tank size for 2025–2055.
Figure 13.
Reliability projections for DJF season for 5 m3 tank size for 2025–2055.
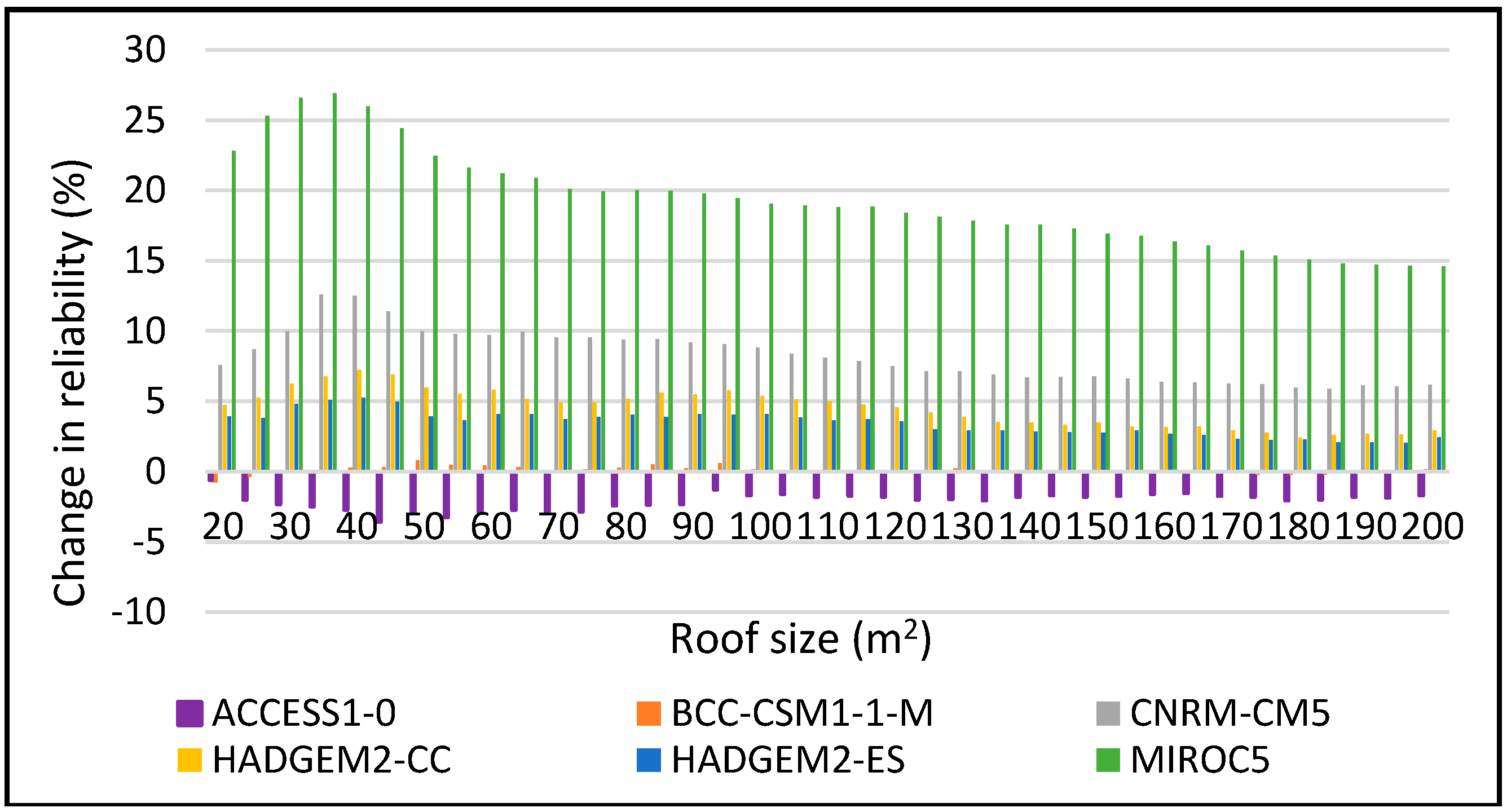
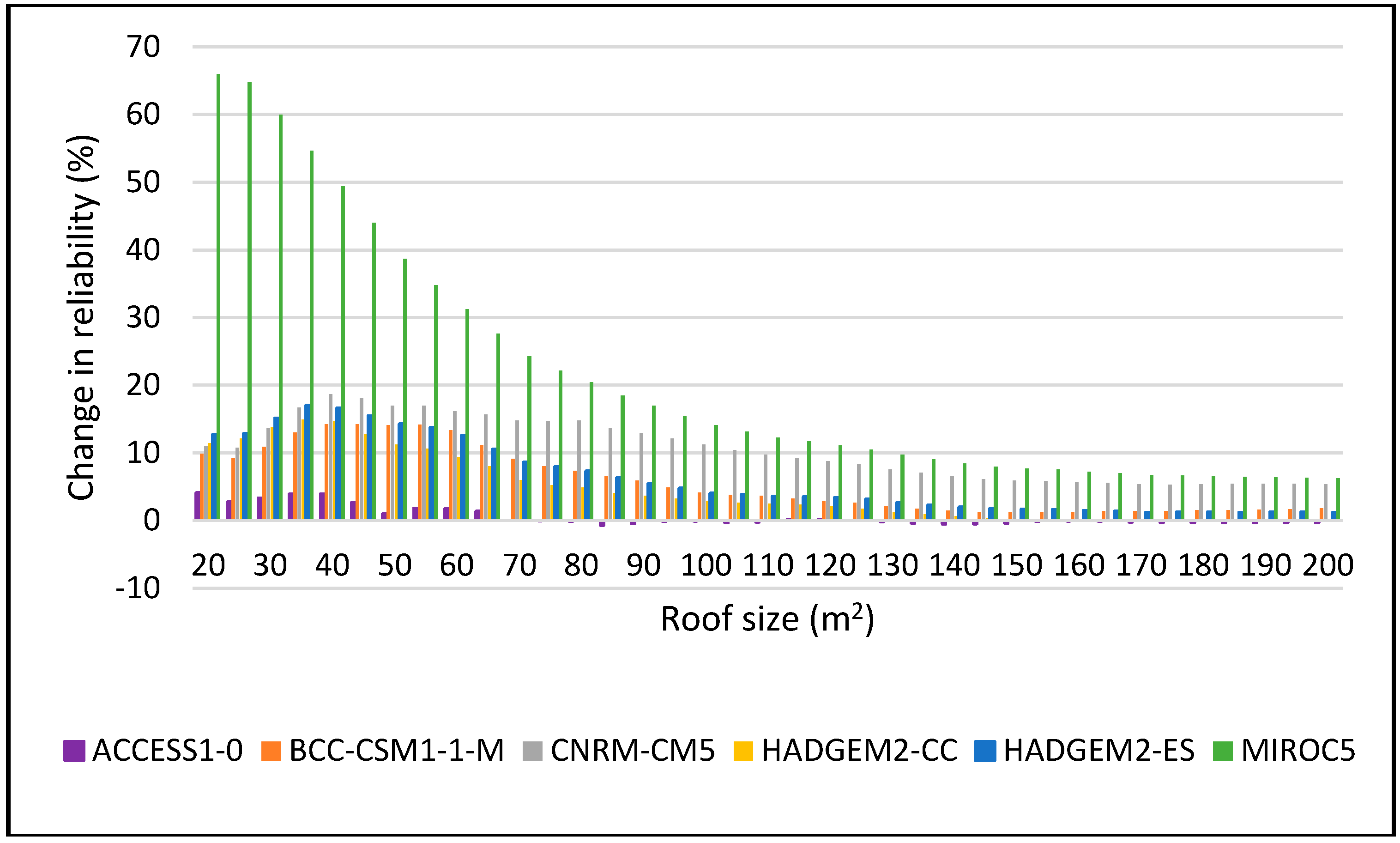
Figure 14.
Change in reliability for DJF 2060–2090 period for 2 m3.
Figure 14.
Change in reliability for DJF 2060–2090 period for 2 m3.
Figure 15.
Change in reliability for DJF 2060–2090 period for 5 m3.
Figure 15.
Change in reliability for DJF 2060–2090 period for 5 m3.
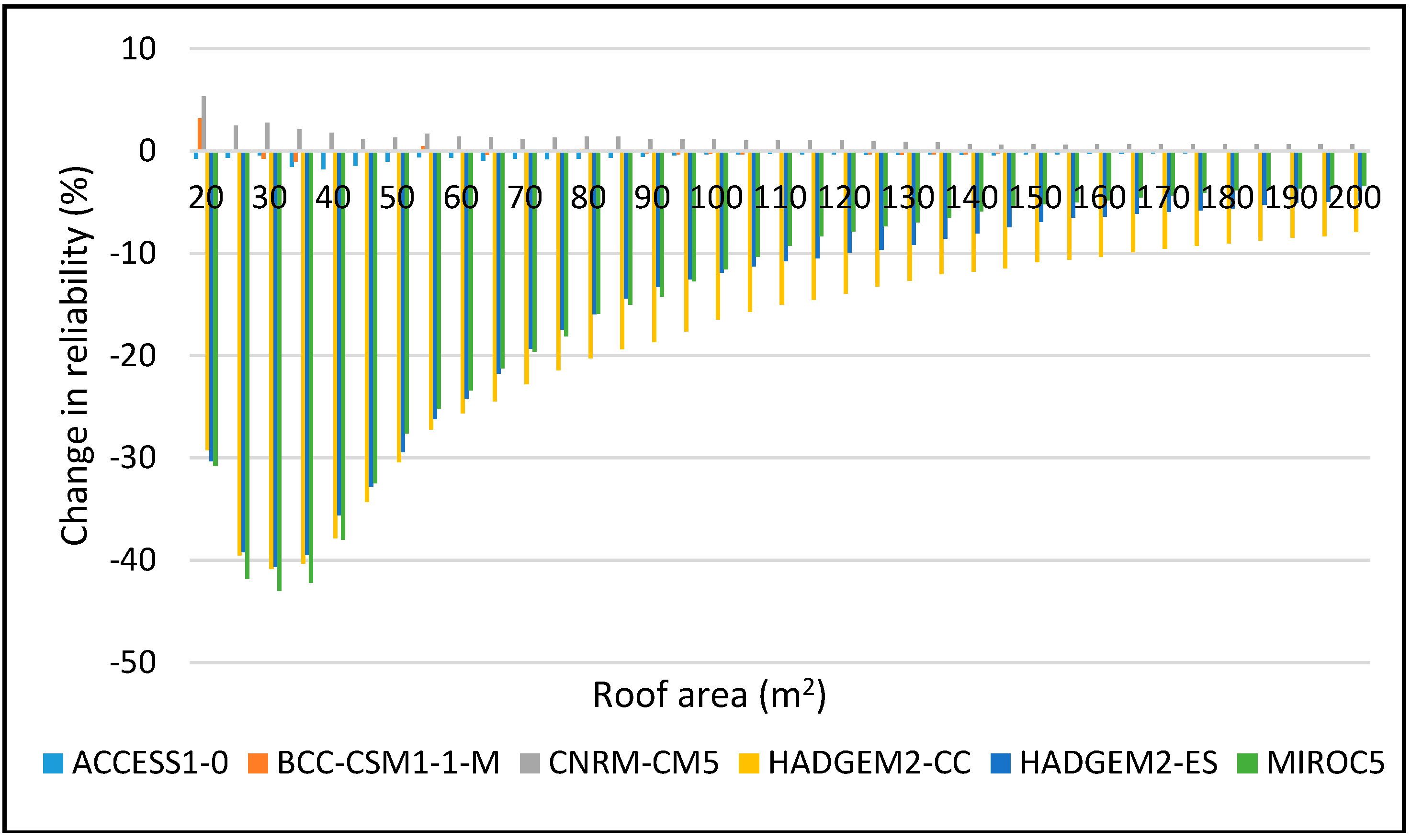
Figure 16.
JJA Change in reliability for 2 m3 during 2025–2055.
Figure 16.
JJA Change in reliability for 2 m3 during 2025–2055.
Figure 17.
JJA Change in reliability for 5 m3 during 2025–2055.
Figure 17.
JJA Change in reliability for 5 m3 during 2025–2055.
Figure 18.
JJA showing change in reliability for 2060–2090 period for 2 m3.
Figure 18.
JJA showing change in reliability for 2060–2090 period for 2 m3.
Figure 19.
JJA showing change in reliability for 2060–2090 period for 5 m3.
Figure 19.
JJA showing change in reliability for 2060–2090 period for 5 m3.
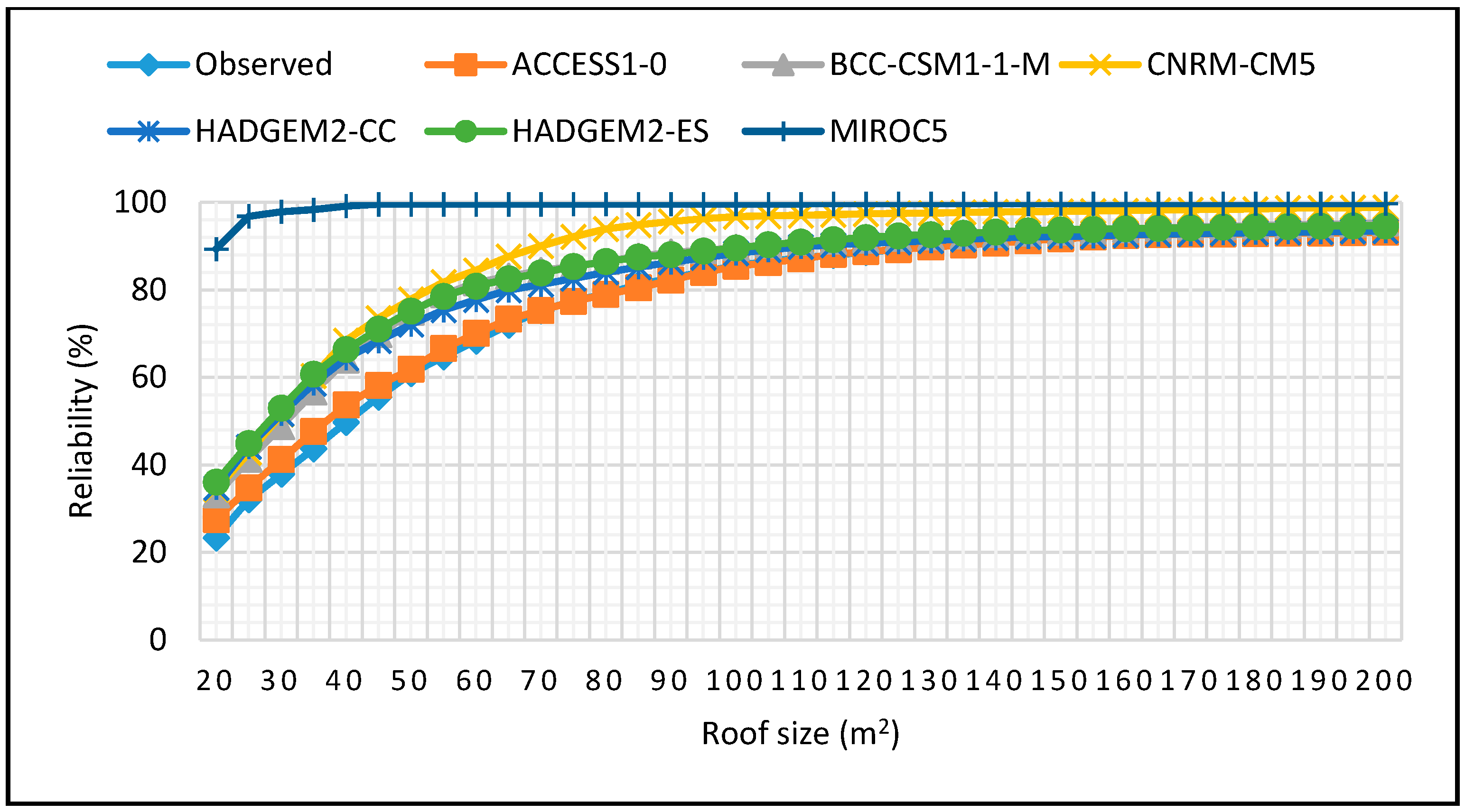
Figure 20.
Reliability projections for JJA season for 0.5 m3 tank size for 2060–2090 period.
Figure 20.
Reliability projections for JJA season for 0.5 m3 tank size for 2060–2090 period.
Figure 21.
Reliability projections for JJA season for 1 m3 tank size for 2060–2090 period.
Figure 21.
Reliability projections for JJA season for 1 m3 tank size for 2060–2090 period.
Figure 22.
Reliability projections for JJA season for 2 m3 tank size for 2060–2090 period.
Figure 22.
Reliability projections for JJA season for 2 m3 tank size for 2060–2090 period.
Figure 23.
Reliability projections for JJA season for 5 m3 tank size for 2060–2090 period.
Figure 23.
Reliability projections for JJA season for 5 m3 tank size for 2060–2090 period.
Figure 24.
Change in reliability for MAM 2025–2055 period for 2 m3 tank size.
Figure 24.
Change in reliability for MAM 2025–2055 period for 2 m3 tank size.
Figure 25.
Change in reliability for MAM 2025–2055 period for 5 m3 tank size.
Figure 25.
Change in reliability for MAM 2025–2055 period for 5 m3 tank size.
Figure 26.
Change in reliability for MAM 2060–2090 period for 2 m3 tank size.
Figure 26.
Change in reliability for MAM 2060–2090 period for 2 m3 tank size.
Figure 27.
Change in reliability for MAM 2060–2090 period for 5 m3 tank size.
Figure 27.
Change in reliability for MAM 2060–2090 period for 5 m3 tank size.
Figure 28.
Reliability projections for MAM season for 0.5 m3 tank size for 2060–2090 period.
Figure 28.
Reliability projections for MAM season for 0.5 m3 tank size for 2060–2090 period.
Figure 29.
Reliability projections for MAM season for 2 m3 tank size for 2060–2090 period.
Figure 29.
Reliability projections for MAM season for 2 m3 tank size for 2060–2090 period.
Figure 30.
Reliability projections for MAM season for 5 m3 tank size for 2060–2090 period.
Figure 30.
Reliability projections for MAM season for 5 m3 tank size for 2060–2090 period.
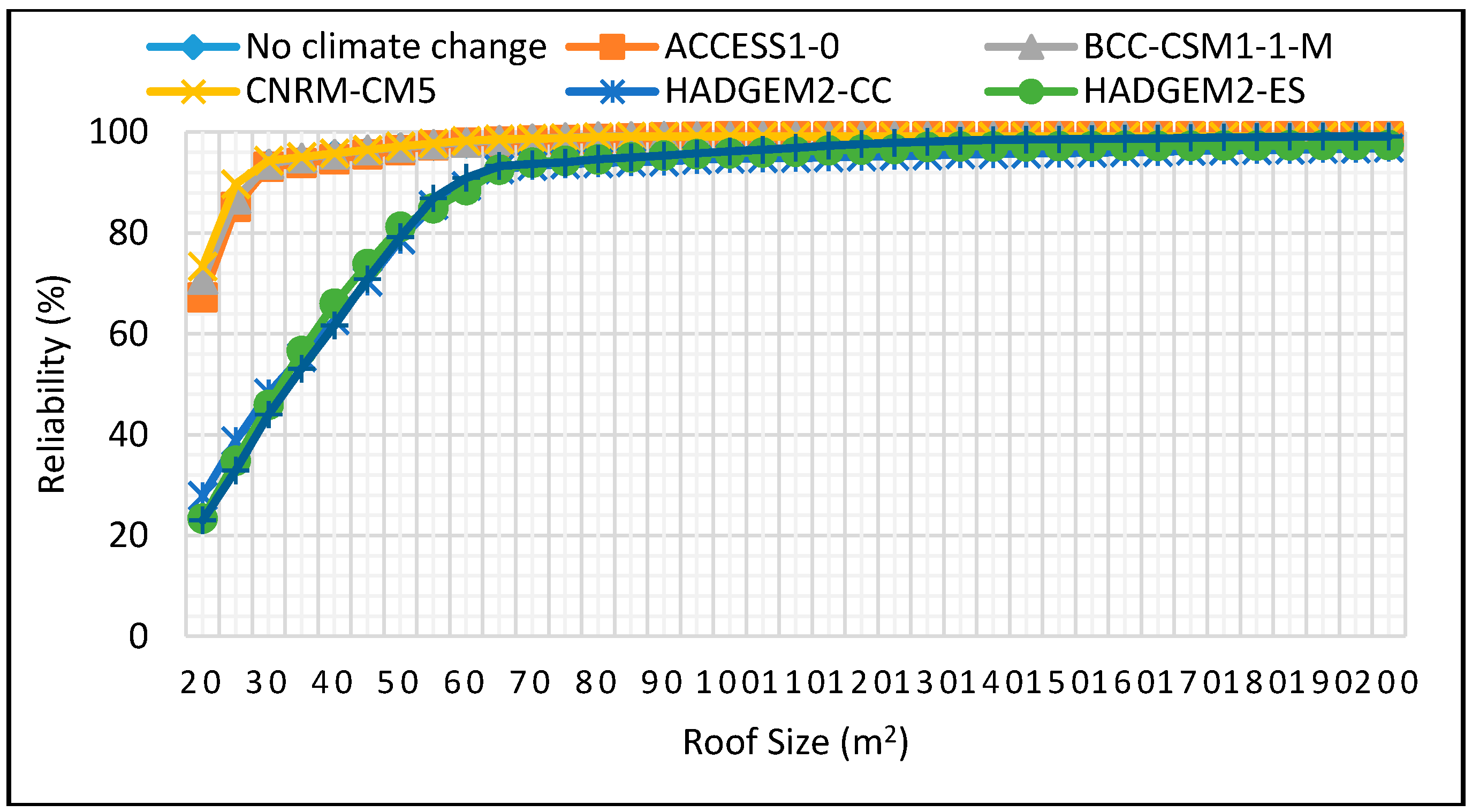
Figure 31.
Reliability projections for MAM season for 20 m3 tank size.
Figure 31.
Reliability projections for MAM season for 20 m3 tank size.
Figure 32.
Change in reliability for SON season for 2025–2055 period for 2 m3 tank size.
Figure 32.
Change in reliability for SON season for 2025–2055 period for 2 m3 tank size.
Figure 33.
Change in reliability for SON season for 2025–2055 period for 5 m3 tank size.
Figure 33.
Change in reliability for SON season for 2025–2055 period for 5 m3 tank size.
Figure 34.
Change in reliability for SON season for 2060–2090 period for 2 m3 tank.
Figure 34.
Change in reliability for SON season for 2060–2090 period for 2 m3 tank.
Figure 35.
Change in reliability for SON season for 2060–2090 period for 5 m3 tank.
Figure 35.
Change in reliability for SON season for 2060–2090 period for 5 m3 tank.
Figure 36.
Reliability projections for SON season for 0.5 m3 tank size for 2060–2090 period.
Figure 36.
Reliability projections for SON season for 0.5 m3 tank size for 2060–2090 period.
Figure 37.
Reliability projections for SON season for 1 m3 tank size for 2060–2090 period.
Figure 37.
Reliability projections for SON season for 1 m3 tank size for 2060–2090 period.
Figure 38.
Reliability projections for SON season for 2 m3 tank size for 2060–2090 period.
Figure 38.
Reliability projections for SON season for 2 m3 tank size for 2060–2090 period.
Figure 39.
Reliability projections for SON season for 5 m3 tank size for the 2060–2090 period.
Figure 39.
Reliability projections for SON season for 5 m3 tank size for the 2060–2090 period.
Table 1.
Characteristics of the 6 General circulation models (GCMs) considered in this study.
Table 1.
Characteristics of the 6 General circulation models (GCMs) considered in this study.
| Model Center | Country | Model | Latitude | Longitude | Resolution |
|---|
| Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology | Japan | MIROC5 | 1.40 | 1.40 | High |
| Beijing Climate Center, China Meteorological Administration | China | BCC-CSM1.1 | 2.81 | 2.79 | Low |
| Commonwealth Scientific and Industrial Research Organization/Bureau of Meteorology (CSIRO-BOM) | Australia | ACCESS1.0 | 1.87 | 1.25 | Medium |
| Centre National de Recherches Meteorologiques/Centre Europeen de Recherche et Formation Avancees en Calcul Scientifique (CNRM/CERFACS) | France | CNRM-CM5 | 1.41 | 1.40 | High |
| Met Office Hadley Centre | UK-Exeter | HadGEM2-CC | 1.87 | 1.25 | Medium |
| HadGEM2-ES | 1.75 | 1.25 | Medium |
Table 2.
Shows roof sizes for 80% reliability for DJF season for 2060–2090.
Table 2.
Shows roof sizes for 80% reliability for DJF season for 2060–2090.
| Climate Change Models | Tank Size (m3) |
|---|
| 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | - | - | 105–110 | 55–60 | 45–50 | 40–45 | 40–45 |
| ACCESS1-0 | - | - | 100–105 | 55 | 40–45 | 40–45 | 35–40 |
| BCC-CSM1-1-M | - | - | 105–110 | 55–60 | 40–45 | 40–45 | 35–40 |
| CNRM-CM5 | - | - | 110–115 | 55–60 | 45–50 | 40–45 | 40–45 |
| HADGEM2-CC | - | - | 115–120 | 50–55 | 40–45 | 40–45 | 35–40 |
| HADGEM2-ES | - | - | 105–110 | 45–50 | 40–45 | 35–40 | 35–40 |
| MIROC5 | - | - | 115–110 | 60–65 | 45–50 | 40–45 | 40–45 |
Table 3.
Roof size requirement during JJA for 80% reliability (2025–2055).
Table 3.
Roof size requirement during JJA for 80% reliability (2025–2055).
| Climate Change Models | Tank Size (m3) |
|---|
| 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | - | - | 170–175 | 80–85 | 75–80 | 75–80 | 75–80 |
| ACCESS1-0 | - | - | >200 | 85–90 | 80–85 | 80–85 | 80–85 |
| BCC-CSM1-1-M | - | - | 175–180 | 80–85 | 75–80 | 75–80 | 75–80 |
| CNRM-CM5 | - | - | 105–110 | 50–55 | 45–50 | 45–50 | 45–50 |
| HADGEM2-CC | - | - | 135–140 | 60–65 | 60–65 | 60–65 | 60–65 |
| HADGEM2-ES | - | - | 140–145 | 70–75 | 65–70 | 65–70 | 65–70 |
| MIROC5 | | 125–130 | 55–60 | 35–40 | 35–40 | 35–40 | 35–40 |
Table 4.
Roof sizes required to achieve 80% reliability during MAM season (2025–2055).
Table 4.
Roof sizes required to achieve 80% reliability during MAM season (2025–2055).
| Climate Change Models | Tank Capacity (m3) |
|---|
| 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | 100–105 | 45–50 | 30–35 | 25–30 | 20–25 | 20–25 | 20–25 |
| ACCESS1-0 | 135–140 | 50–55 | 35–40 | 25–30 | 25–30 | 25–30 | 20–25 |
| BCC-CSM1-1-M | 85–90 | 40–45 | 25–30 | 20–25 | 20–25 | 20–25 | 20–25 |
| CNRM-CM5 | 110–115 | 40–45 | 30–35 | 20–25 | 20–25 | 20–25 | 20–25 |
| HADGEM2-CC | 115–120 | 45–50 | 30–35 | 20–25 | 20–25 | 20–25 | 20–25 |
| HADGEM2-ES | 95–100 | 40–45 | 25–30 | 20–25 | 20–25 | 20–25 | 20–25 |
| MIROC5 | >200 | 90–95 | 60–65 | 40–45 | 35–40 | 35–40 | 35–40 |
Table 5.
SON roof size required for 80% reliability for varying tank sizes (2025–2055).
Table 5.
SON roof size required for 80% reliability for varying tank sizes (2025–2055).
| Climate Change Models | Tank Capacity (m2) |
|---|
| 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | 90–95 | 45–50 | 35–40 | 25–30 | 25–30 | 25–30 | 20–25 |
| ACCESS1-0 | 100–105 | 50–55 | 35–40 | 25–30 | 25–30 | 20–25 | 20–25 |
| BCC-CSM1-1-M | 90–95 | 40–45 | 30–35 | 25–30 | 20–25 | 20–25 | 20–25 |
| CNRM-CM5 | 90–95 | 45–50 | 35–40 | 20–35 | 25–30 | 20–25 | 20–25 |
| HADGEM2-CC | 85–90 | 45–50 | 35–40 | 30–35 | 25–30 | 25–30 | 25–30 |
| HADGEM2-ES | 85–90 | 45–50 | 35–40 | 30–35 | 25–30 | 25–30 | 25–30 |
| MIROC5 | 90–95 | 40–45 | 30–35 | 25–30 | 25–30 | 25–30 | 20–25 |
Table 6.
Observed and projected water security (%) for MAM rain season.
Table 6.
Observed and projected water security (%) for MAM rain season.
| Scenario | Tank Size (m3), 30 m2 Roof Size |
|---|
| Period | 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | a | 35 | 26 | 19 | 10 | 5 | 5 | 5 |
| b | 35 | 26 | 19 | 10 | 5 | 5 | 5 |
| ACCESS1.0 | a | 39 | 29 | 22 | 13 | 8 | 8 | 8 |
| b | 37 | 27 | 19 | 10 | 6 | 6 | 6 |
| BCC-CSM1.1 | a | 33 | 23 | 15 | 6 | 5 | 5 | 5 |
| b | 36 | 27 | 19 | 8 | 5 | 5 | 5 |
| CNRM-CM5 | a | 35 | 25 | 17 | 8 | 5 | 5 | 5 |
| b | 33 | 24 | 17 | 7 | 5 | 5 | 5 |
| HADGEM2-CC | a | 34 | 25 | 17 | 8 | 5 | 5 | 5 |
| b | 62 | 59 | 57 | 55 | 51 | 49 | 46 |
| HADGEM2-ES | a | 33 | 23 | 16 | 8 | 5 | 5 | 5 |
| b | 62 | 58 | 56 | 54 | 51 | 48 | 48 |
| MIROC5 | a | 52 | 46 | 42 | 40 | 37 | 34 | 31 |
| b | 62 | 59 | 57 | 55 | 52 | 49 | 49 |
Table 7.
Observed and projected water security for SON rain season.
Table 7.
Observed and projected water security for SON rain season.
| Scenario | Tank Size (m3) 30 m2 Roof Size |
|---|
| Period | 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | a | 36 | 28 | 22 | 14 | 11 | 9 | 9 |
| b | 36 | 28 | 22 | 14 | 11 | 9 | 9 |
| ACCESS1.0 | a | 37 | 28 | 22 | 14 | 9 | 7 | 7 |
| b | 39 | 30 | 24 | 15 | 10 | 8 | 8 |
| BCC-CSM1.1 | a | 35 | 26 | 19 | 11 | 7 | 7 | 7 |
| b | 31 | 21 | 15 | 7 | 4 | 4 | 4 |
| CNRM-CM5 | a | 36 | 27 | 21 | 13 | 8 | 7 | 7 |
| b | 37 | 28 | 22 | 14 | 8 | 8 | 8 |
| HADGEM2-CC | a | 37 | 29 | 24 | 17 | 13 | 13 | 13 |
| b | 4 | 2 | <1 | <1 | <1 | <1 | <1 |
| HADGEM2-ES | a | 37 | 29 | 24 | 17 | 14 | 13 | 13 |
| b | 5 | 2 | <1 | <1 | <1 | <1 | <1 |
| MIROC5 | a | 36 | 27 | 21 | 14 | 10 | 9 | 9 |
| b | 38 | 29 | 24 | 16 | 13 | 11 | 11 |
Table 8.
Observed and projected water security for JJA dry season.
Table 8.
Observed and projected water security for JJA dry season.
| Scenario | Tank Size (m3) 30 m2 Roof Size |
|---|
| Period | 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | a | 67 | 61 | 59 | 57 | 54 | 52 | 52 |
| b | 67 | 61 | 59 | 57 | 54 | 52 | 52 |
| ACCESS1.0 | a | 70 | 64 | 61 | 59 | 56 | 55 | 55 |
| b | 68 | 62 | 57 | 55 | 52 | 49 | 48 |
| BCC-CSM1.1 | a | 67 | 61 | 59 | 57 | 54 | 52 | 52 |
| b | 61 | 54 | 50 | 46 | 44 | 41 | 39 |
| CNRM-CM5 | a | 59 | 52 | 48 | 46 | 43 | 40 | 39 |
| b | 58 | 51 | 46 | 43 | 41 | 38 | 35 |
| HADGEM2-CC | a | 63 | 56 | 52 | 50 | 48 | 45 | 42 |
| b | 64 | 56 | 50 | 45 | 42 | 40 | 37 |
| HADGEM2-ES | a | 64 | 57 | 54 | 52 | 49 | 46 | 44 |
| b | 63 | 56 | 49 | 44 | 41 | 38 | 35 |
| MIROC5 | a | 53 | 43 | 33 | 26 | 23 | 23 | 23 |
| b | 36 | 22 | 8 | 2 | 2 | 2 | 2 |
Table 9.
Observed and projected water security for DJF dry season.
Table 9.
Observed and projected water security for DJF dry season.
| Scenario | Tank Size (m3) 30 m2 Roof Size |
|---|
| Period | 0.5 | 1 | 2 | 5 | 10 | 15 | 20 |
|---|
| Observed | a | 64 | 59 | 53 | 46 | 43 | 43 | 43 |
| b | 64 | 59 | 53 | 46 | 43 | 43 | 43 |
| ACCESS1.0 | a | 63 | 57 | 50 | 41 | 39 | 36 | 36 |
| b | 63 | 57 | 50 | 41 | 39 | 36 | 36 |
| BCC-CSM1.1 | a | 65 | 59 | 53 | 45 | 42 | 41 | 41 |
| b | 64 | 59 | 53 | 45 | 42 | 41 | 41 |
| CNRM-CM5 | a | 65 | 69 | 54 | 48 | 45 | 45 | 45 |
| b | 65 | 60 | 53 | 48 | 45 | 45 | 45 |
| HADGEM2-CC | a | 71 | 66 | 61 | 56 | 55 | 55 | 55 |
| b | 64 | 66 | 61 | 56 | 55 | 55 | 55 |
| HADGEM2-ES | a | 72 | 66 | 61 | 61 | 56 | 56 | 56 |
| b | 62 | 66 | 61 | 61 | 56 | 56 | 56 |
| MIROC5 | a | 64 | 58 | 52 | 45 | 42 | 41 | 41 |
| b | 66 | 58 | 52 | 45 | 41 | 41 | 41 |