Estimating Time of Concentration for Overland Flow on Pervious Surfaces by Particle Tracking Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Shallow Water Equations (SWEs) and FullSWOF_2D
2.2. Particle Tracking Method (PTM) and FullSWOF-PTM
2.3. Modeling Cases
2.3.1. FullSWOF-PTM Testing Cases
2.3.2. Impervious Modeling Cases
2.3.3. Pervious Modeling Cases
3. Results and Discussion
3.1. FullSWOF-PTM Testing Results
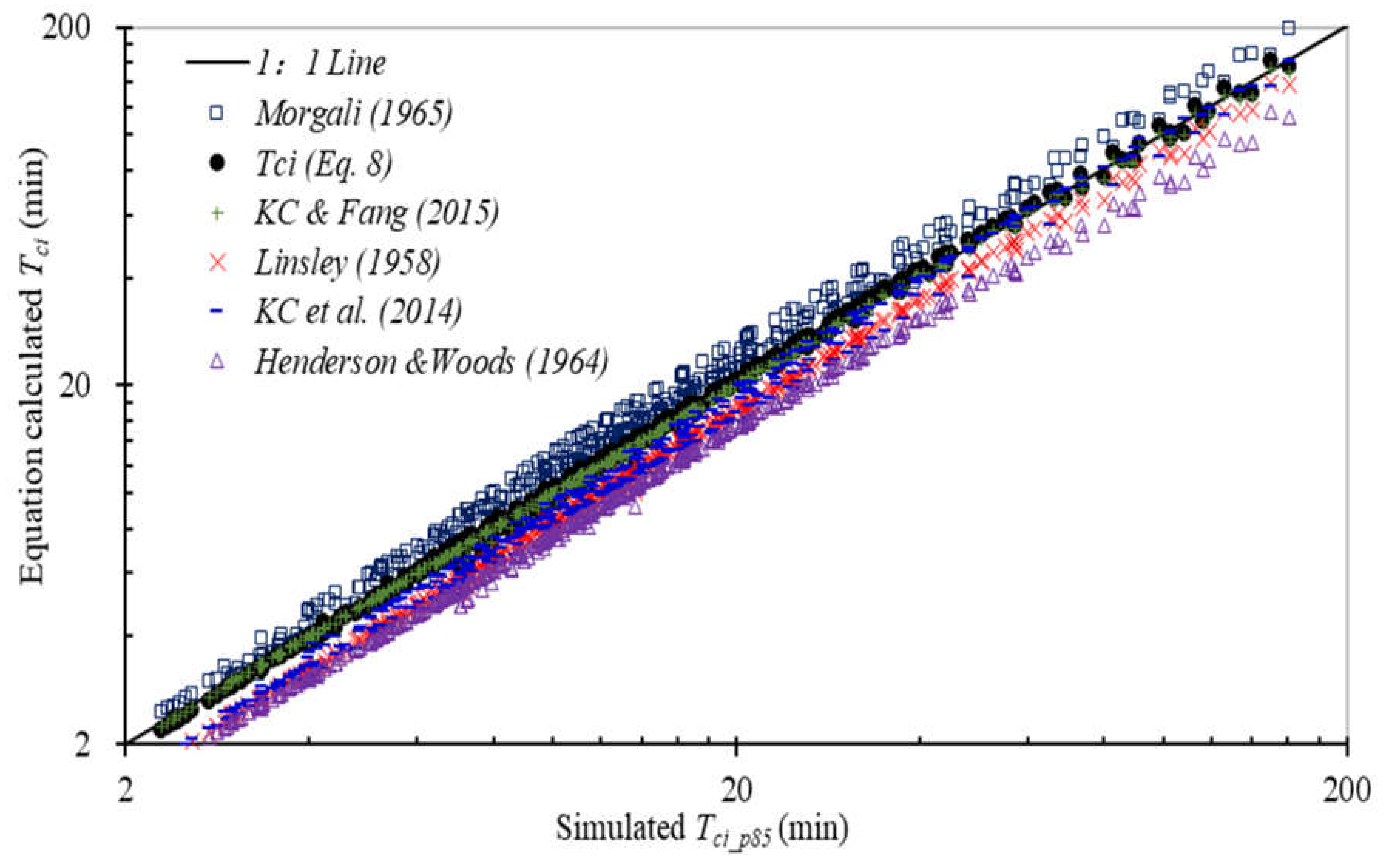
3.2. Time of Concentration (Tci) of Impervious Surfaces
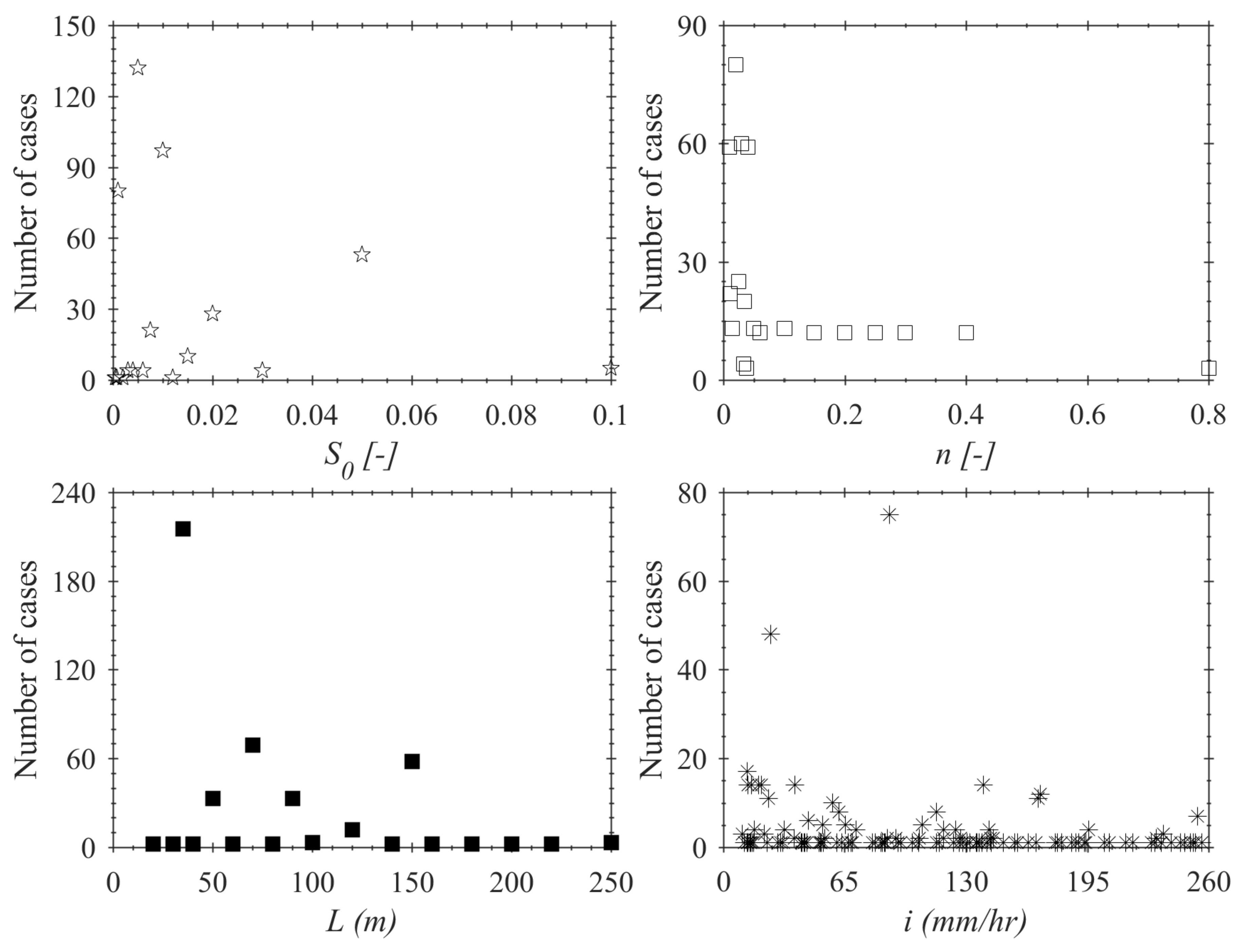
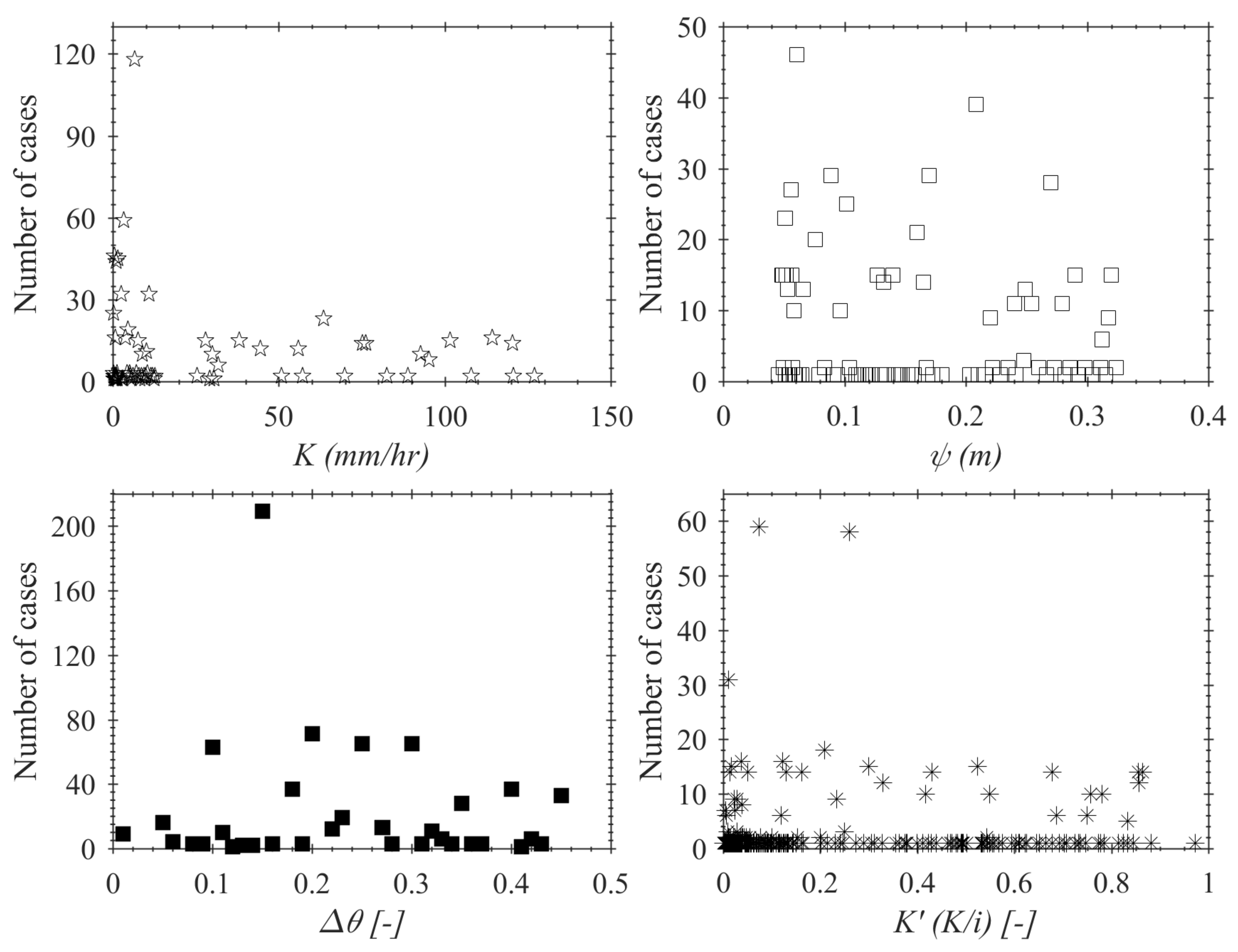
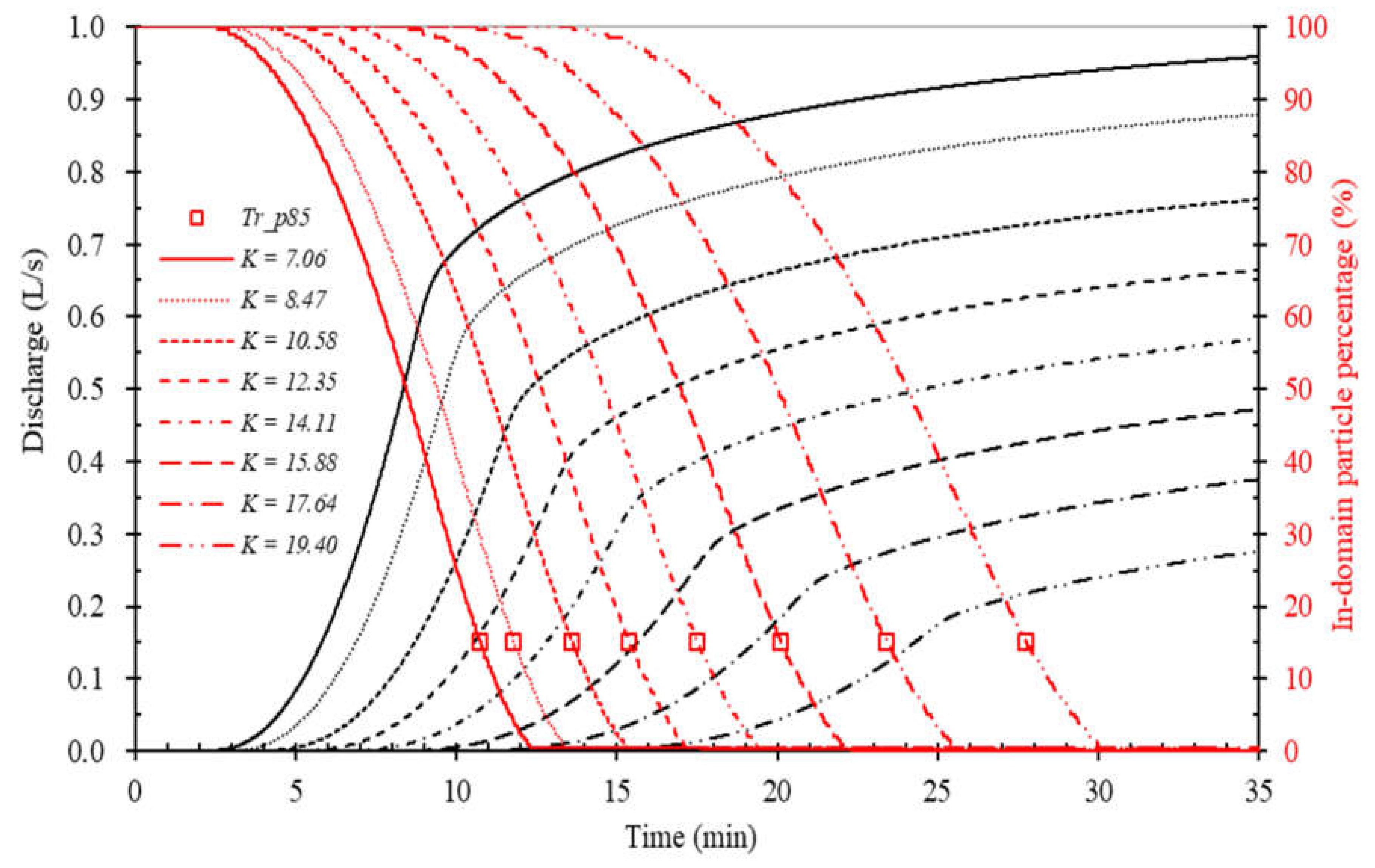
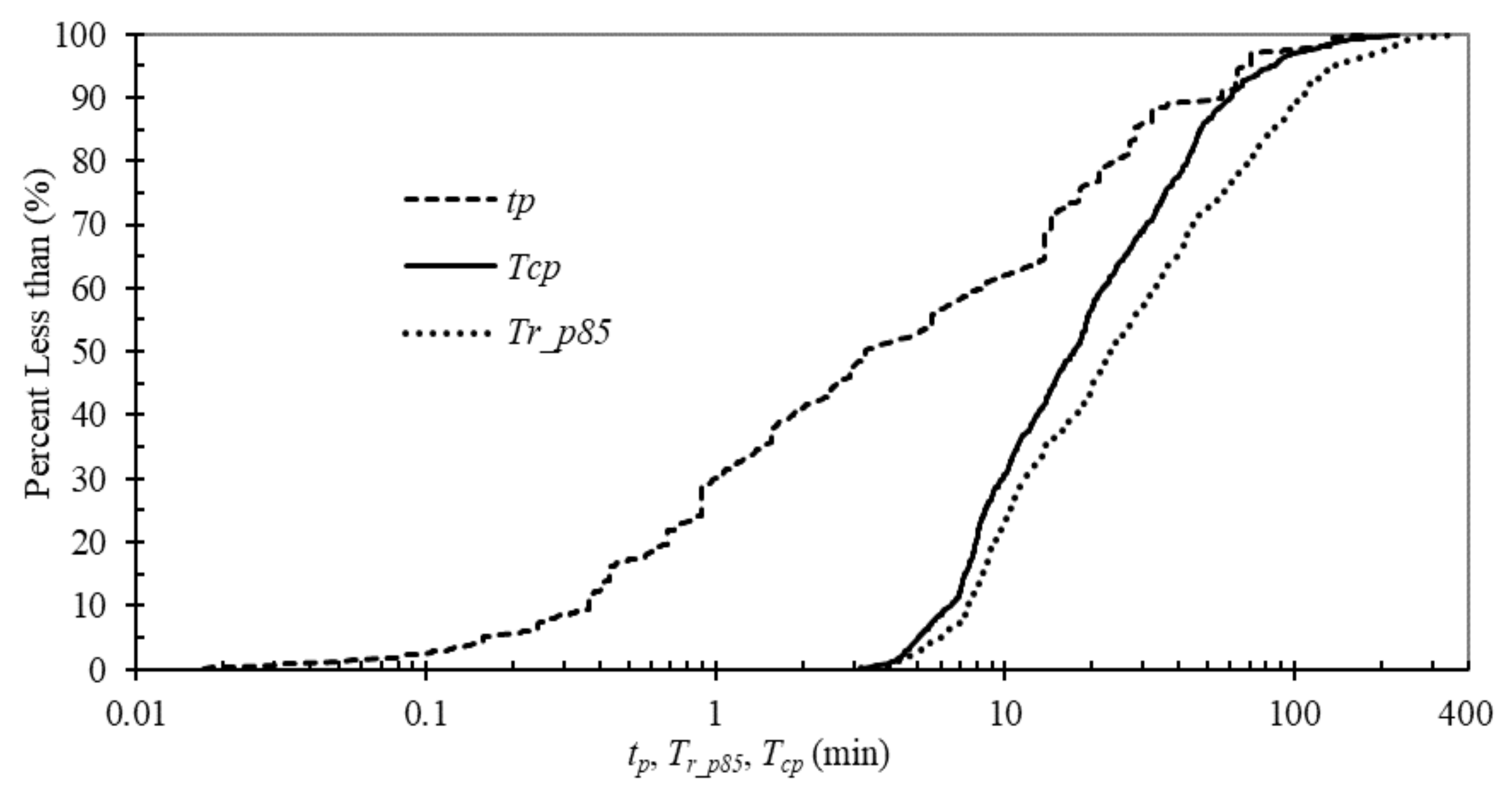
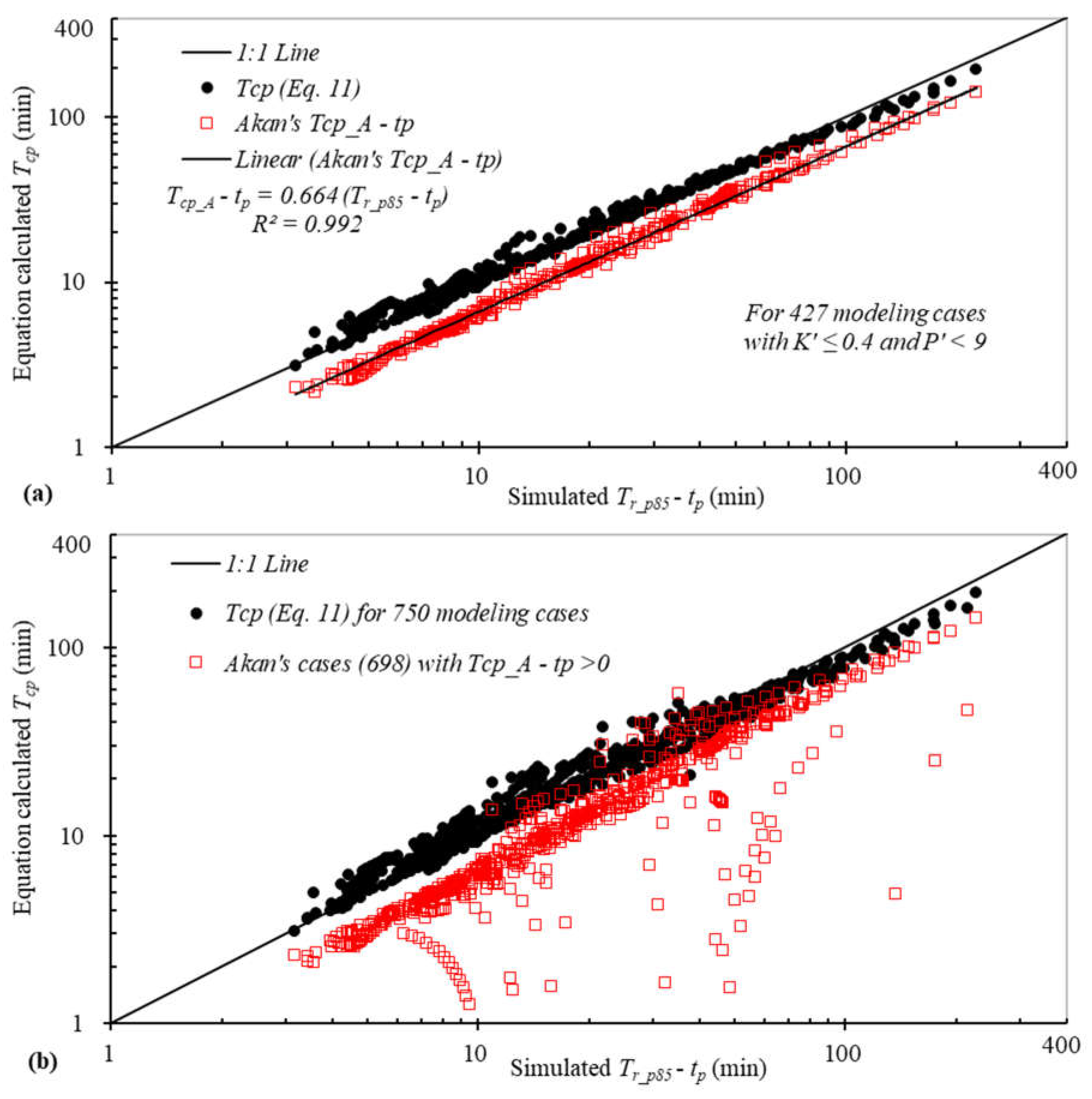
3.3. Time of Concentration (Tcp) of Pervious Surfaces
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mulvany, T.J. On the use of self-registering rain and flood gauges in making observations of the relations of rainfall and flood discharges in a given catchment. Proc. Inst. Civil Eng. Irel. 1851, 4, 18–33. [Google Scholar]
- Kuichling, E. The relation between the rainfall and the discharge of sewers in populous areas. Trans. Am. Soc. Civ. Eng. 1889, 20, 1–56. [Google Scholar]
- Brown, S.; Stein, S.; Warner, J. Urban Drainage Design Manual: Hydraulic Engineering Circular No. 22; FHWA-NHI-10–009 HEC-22; National Highway Institute: Fort Collins, CO, USA, 2009.
- Guo, J.C.Y. Overland flow on a pervious surface. Water Int. 1998, 23, 91–96. [Google Scholar] [CrossRef]
- Kibler, D.F. Desk-top methods for urban stormwater calculation. Urban Stormwater Hydrol. 1982, 87–135. [Google Scholar] [CrossRef]
- McCuen, R.H.; Wong, S.L.; Rawls, W.J. Estimating urban time of concentration. J. Hydraul. Eng. 1984, 110, 887–904. [Google Scholar] [CrossRef]
- Izzard, C.F. Hydraulics of runoff from developed surfaces. In Proceedings of the 26th Annual Meetings of the Highway Research Board, Washington, DC, USA, 5–8 December 1946; Crum, R.W., Burggraf, F., William, N.C., Jr., Eds.; Highway Research Board: Washington, DC, USA, 1946; pp. 129–150. [Google Scholar]
- Muzik, I. Laboratory experiments with surface runoff. J. Hydraul. Div. 1974, 100, 501–516. [Google Scholar]
- Wong, T.S.W. Assessment of time of concentration formulas for overland flow. J. Irrig. Drain. Eng. 2005, 131, 383–387. [Google Scholar] [CrossRef]
- Akan, A.O. Time of concentration of overland flow. J. Irrig. Drain. Eng. 1986, 112, 283–292. [Google Scholar] [CrossRef]
- Wooding, R.A. A hydraulic model for the catchment-stream problem: I. Kinematic-wave theory. J. Hydrol. 1965, 3, 254–267. [Google Scholar] [CrossRef]
- Woolhiser, D.A.; Liggett, J.A. Unsteady, one-dimensional flow over a plane—The rising hydrograph. Water Resour. Res. 1967, 3, 753–771. [Google Scholar] [CrossRef]
- Olivera, F.; Maidment, D.R. Geographic information systems (GIS)-based spatially distributed model for runoff routing. Water Resour. Res. 1999, 35, 1155–1164. [Google Scholar] [CrossRef]
- Hromadka, T.V., II; McCuen, R.H.; Yen, C.C. Comparison of overland flow hydrograph models. ASCE J. Hydraul. Eng. 1987, 113, 1422–1439. [Google Scholar] [CrossRef]
- Su, D.; Fang, X. Estimating traveling time of flat terrain by 2-dimensional overland flow model. In Proceedings of the International Symposium on Shallow Flows, Delft University of Technology, Delft, The Netherlands, 16–18 June 2003. [Google Scholar]
- Niri, M.Z.; Saghafian, B.; Golian, S.; Moramarco, T.; Shamsai, A. Derivation of travel time based on diffusive wave approximation for the time-area hydrograph simulation. J. Hydrol. Eng. 2012, 17, 85–91. [Google Scholar] [CrossRef]
- Gourbesville, P.; Cunge, J.; Caignaert, G. Advances in Hydroinformatics-Simhydro 2014, 1st ed.; Springer: Singapore, 2014; p. 624. [Google Scholar]
- Teng, J.; Jakeman, A.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Akan, A.O. Similarity solution of overland flow on pervious surface. J. Hydraul. Eng. 1985, 111, 1057–1067. [Google Scholar] [CrossRef]
- Deng, Z.Q.; De Lima, J.L.M.P.; Singh, V.P. Transport rate-based model for overland flow and solute transport: Parameter estimation and process simulation. J. Hydrol. 2005, 315, 220–235. [Google Scholar] [CrossRef]
- Hamouda, B.; Lahbassi, O. Integration of pervious area stream flow in urban hydrological model. Energy Procedia 2012, 18, 1573–1582. [Google Scholar] [CrossRef]
- García Serrana, M.; Gulliver, J.S.; Nieber, J.L. Non-uniform overland flow-infiltration model for roadside swales. J. Hydrol. 2017, 552, 586–599. [Google Scholar] [CrossRef]
- Hjelmfelt, A. Influence of infiltration on overland flow. J. Hydrol. 1978, 36, 179–185. [Google Scholar] [CrossRef]
- Akan, A.O. Time of concentration formula for pervious catchments. J. Irrig. Drain. Eng. 1989, 115, 733–735. [Google Scholar] [CrossRef]
- Suk, H.; Yeh, G.T. Development of particle tracking algorithms for various types of finite elements in multi-dimensions. Comput. Geosci. 2010, 36, 564–568. [Google Scholar] [CrossRef]
- Schafer-Perini, A.L.; Wilson, J.L. Efficient and accurate front tracking for two-dimensional groundwater flow models. Water Resour. Res. 1991, 27, 1471–1485. [Google Scholar] [CrossRef]
- Bensabat, J.; Zhou, Q.; Bear, J. An adaptive pathline-based particle tracking algorithm for the eulerian–lagrangian method. Adv. Water Resour. 2000, 23, 383–397. [Google Scholar] [CrossRef]
- Cheng, H.P.; Cheng, J.R.; Yeh, G.T. A particle tracking technique for the lagrangian-eulerian finite element method in multi-dimensions. Int. J. Numer. Methods Eng. 1996, 39, 1115–1136. [Google Scholar] [CrossRef]
- KC, M.; Fang, X. Estimating time parameters of overland flow on impervious surfaces by the particle tracking method. Hydrol. Sci. J. 2015, 60, 294–310. [Google Scholar] [CrossRef]
- Delestre, O.; Darboux, F.; James, F.; Lucas, C.; Laguerre, C.; Cordier, S. FullSWOF: A free software package for the simulation of shallow water flows. arXiv 2014. preprint arXiv:1401.4125. [Google Scholar]
- Barré de Saint-Venant, A.J.C. Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et à l’introduction des marées dans leurs lits. Comptes Rendus des Séances de l’Académie des Sci. 1871, 73, 237–240. [Google Scholar]
- Zhang, W.; Cundy, T.W. Modeling of two-dimensional overland flow. Water Resour. Res. 1989, 25, 2019–2035. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.-O.; Klein, R.; Perthame, B.T. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef]
- Unterweger, K.; Wittmann, R.; Neumann, P.; Weinzierl, T.; Bungartz, H.-J. Integration of FullSWOF_2D and PeanoClaw: Adaptivity and local time-stepping for complex overland flows. In Recent Trends in Computational Engineering-CE2014; Springer: Cham, Switzerland, 2015; pp. 181–195. [Google Scholar]
- Cordier, S.; Coullon, H.; Delestre, O.; Laguerre, C.; Le, M.H.; Pierre, D.; Sadaka, G. FullSWOF paral: Comparison of two parallelization strategies (MPI and SkelGIS) on a software designed for hydrology applications. In ESAIM: Proceedings; EDP Sciences: Les Ulis, France, 2013; pp. 59–79. [Google Scholar]
- Esteves, M.; Faucher, X.; Galle, S.; Vauclin, M. Overland flow and infiltration modelling for small plots during unsteady rain: Numerical results versus observed values. J. Hydrol. 2000, 228, 265–282. [Google Scholar] [CrossRef]
- Bouchut, F. Nonlinear Stability of Finite Volume Methods for Hyperbolic Conservation Laws and Well-Balanced Schemes for Sources; Springer Science & Business Media: Berlin, Germany, 2004. [Google Scholar]
- Delestre, O.; Lucas, C.; Ksinant, P.A.; Darboux, F.; Laguerre, C.; Vo, T.N.; James, F.; Cordier, S. Swashes: A compilation of shallow water analytic solutions for hydraulic and environmental studies. Int. J. Numer. Methods Fluids 2013, 72, 269–300. [Google Scholar] [CrossRef] [Green Version]
- Abily, M.; Delestre, O.; Amossé, L.; Bertrand, N.; Laguerre, C.; Duluc, C.-M.; Gourbesville, P. Use of 3D classified topographic data with FullSWOF for high resolution simulation of a river flood event over a dense urban area. arXiv 2016. arXiv:1603.07463. [Google Scholar]
- Abily, M.; Bertrand, N.; Delestre, O.; Gourbesville, P.; Duluc, C.-M. Spatial global sensitivity analysis of high resolution classified topographic data use in 2D urban flood modelling. Environ. Model. Softw. 2016, 77, 183–195. [Google Scholar] [CrossRef] [Green Version]
- Cordes, C.; Kinzelbach, W. Continuous groundwater velocity fields and path lines in linear, bilinear, and trilinear finite elements. Water Resour. Res. 1992, 28, 2903–2911. [Google Scholar] [CrossRef]
- Pollock, D.W. User’s Guide for MODPATH/MODPATH-PLOT, Version 3: A Particle Tracking Post-Processing Package for MODFLOW, the U.S. Geological Survey Finite-Difference Ground-Water Flow Model; U.S. Geological Survey: Reston, VA, USA, 1994; pp. 4–9.
- Lu, N. A semianalytical method of path line computation for transient finite-difference groundwater flow models. Water Resour. Res. 1994, 30, 2449–2459. [Google Scholar] [CrossRef]
- Matlab and Statistics Toolbox Release 2017a; The MathWorks Inc.: Natick, MA, USA, 2017.
- Peugeot, C.; Esteves, M.; Galle, S.; Rajot, J.-L.; Vandervaere, J. Runoff generation processes: Results and analysis of field data collected at the east central supersite of the hapex-sahel experiment. J. Hydrol. 1997, 188, 179–202. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-Ampt infiltration parameters from soils data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- KC, M.; Fang, X.; Yi, Y.-J.; Li, M.-H.; Thompson, D.B.; Cleveland, T.G. Improved time of concentration estimation on overland flow surfaces including low-sloped planes. J. Hydrol. Eng. 2014, 19, 495–508. [Google Scholar] [CrossRef]
- Viessman, W.; Lewis, G.L. Introduction to Hydrology, 5th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2003; p. 612. [Google Scholar]
- Henderson, F.M.; Wooding, R.A. Overland flow and groundwater flow from a steady rainfall of finite duration. J. Geophys. Res. 1964, 69, 1531–1540. [Google Scholar] [CrossRef]
- Morgali, J.R.; Linsley, R.K. Computer analysis of overland flow. J. Hydraul. Div. 1965, 91, 81–100. [Google Scholar]
- Kirpich, Z.P. Time of concentration of small agricultural watersheds. Civ. Eng. 1940, 10, 362. [Google Scholar]
- Johnstone, D.; Cross, W.P. Elements of Applied Hydrology; Ronald Press: New York, NY, USA, 1949. [Google Scholar]
- Linsley, R.K.; Kohler, M.A.; Paulhus, J.L.H. Hydrology for Engineers; McGraw Hill Publications: New York, NY, USA, 1958. [Google Scholar]
- Diskin, M.; Nazimov, N. Ponding time and infiltration capacity variation during steady rainfall. J. Hydrol. 1996, 178, 369–380. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, 2nd ed.; McGraw Hill: New York, NY, USA, 1988. [Google Scholar]
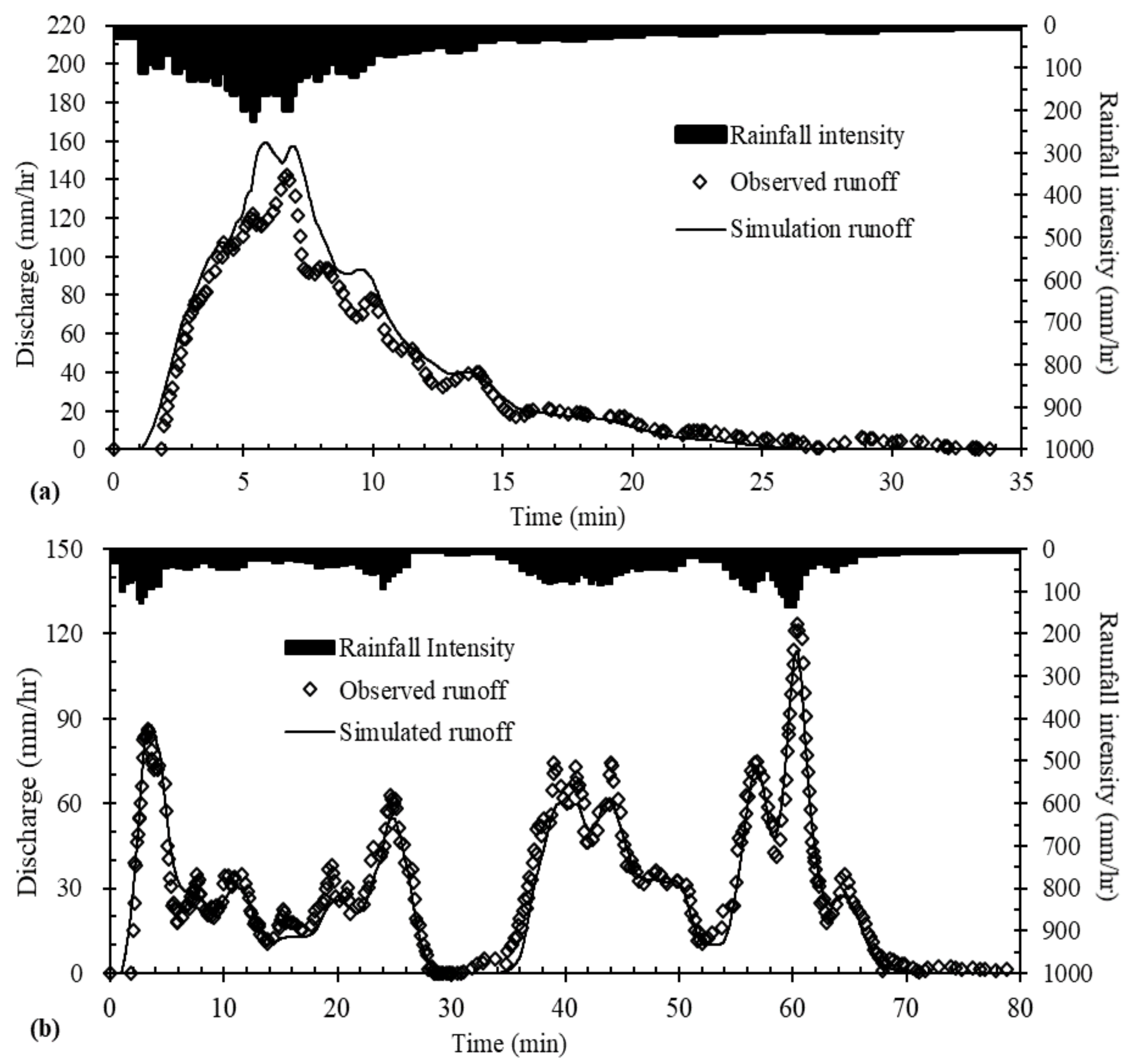

| Events [θi, RD] | NSE 1 | NSE 2 | Dob 2 (mm) | Dsi 1 (mm) | ∆D (%) | Qpo 2 (mm/h) | Qps 1 (mm/h) | ∆Qp (%) |
|---|---|---|---|---|---|---|---|---|
| Jul 20 [0.048, 51.5] | 0.81 | 0.85 | 29.0 | 32.4 | 11.7 | 144.5 | 165.5 | 14.5 |
| Jul 21 [0.103, 59.5] | 0.68 | 0.66 | 26.7 | 30.1 | 12.7 | 77.0 | 85.2 | 10.6 |
| Aug 7 [0.100, 30.0] | 0.71 | 0.90 | 22.0 | 20.8 | −5.5 | 179.4 | 138.3 | −22.9 |
| Aug 10 [0.106, 11.0] | 0.75 | 0.90 | 5.6 | 5.6 | 0.0 | 59.1 | 52.4 | −11.3 |
| Aug 20 (1) [0.067, 22.0] | 0.69 | 0.63 | 9.7 | 7.2 | −25.8 | 42.0 | 33.1 | −21.2 |
| Aug 20 (2) [0.095, 4.0] | 0.70 | 0.90 | 2.2 | 1.7 | −22.7 | 50.5 | 37.0 | −26.7 |
| Aug 24 [0.088, 31.0] | 0.90 | 0.88 | 18.8 | 21.0 | 11.7 | 142.2 | 159.0 | 11.8 |
| Aug 25 [0.085, 24.0] | 0.82 | 0.89 | 14.3 | 14.3 | 0.0 | 91.6 | 86.7 | −5.3 |
| Sep 4 [0.082, 62.0] | 0.95 | 0.93 | 37.8 | 35.1 | −7.1 | 123.5 | 113.7 | −7.9 |
| Sep 8 [0.082, 31.0] | 0.62 | 0.46 | 15.3 | 20.4 | 33.3 | 86.7 | 107.3 | 23.8 |
| Sep 16 [0.061, 9.5] | 0.60 | 0.66 | 2.4 | 2.7 | 12.5 | 48.4 | 41.8 | −13.6 |
| Source | Tci Formula (min) | R2 | RMSE (min) |
|---|---|---|---|
| Tci (Equation (8)) | 0.996 (1.00 × Tci_p85) 1 | 1.45 | |
| Linsley (1958) | 0.998 (0.87 × Tci_p85) | 4.15 | |
| Henderson & Woods (1964) | 0.997 (0.74 × Tci_p85) | 8.04 | |
| Morgali (1965) | 0.995 (1.19 × Tci_p85) | 6.08 | |
| KC et al., (2014) | 0.994 (0.96 × Tci_p85) | 2.33 | |
| KC & Fang (2015) | 0.997 (0.98 × Tci_p85) | 1.38 |
| Parameter | tp (min) | Tr_p85 (min) | Tcp (min) |
|---|---|---|---|
| Minimum | 0.02 | 3.2 | 3.2 |
| 50 percentiles | 3.3 | 23.2 | 17.3 |
| 75 percentiles | 18.0 | 56.6 | 35.8 |
| 90 percentiles | 56.0 | 104.7 | 60.3 |
| 95 percentiles | 69.1 | 136.3 | 82.6 |
| Maximum | 180.1 | 351.6 | 227.8 |
| Parameter | Value | 95% Confidence Interval |
|---|---|---|
| C1 | 2.162 | [0.875, 5.340] |
| C2 | 0.535 | [0.488, 0.582] |
| C3 | 0.161 | [0.030, 0.292] |
| C4 | 0.645 | [0.591, 0.699] |
| C5 | 1.213 | [1.172, 1.255] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Fang, X.; Li, J.; KC, M.; Gong, Y.; Chen, G. Estimating Time of Concentration for Overland Flow on Pervious Surfaces by Particle Tracking Method. Water 2018, 10, 379. https://doi.org/10.3390/w10040379
Li X, Fang X, Li J, KC M, Gong Y, Chen G. Estimating Time of Concentration for Overland Flow on Pervious Surfaces by Particle Tracking Method. Water. 2018; 10(4):379. https://doi.org/10.3390/w10040379
Chicago/Turabian StyleLi, Xiaoning, Xing Fang, Junqi Li, Manoj KC, Yongwei Gong, and Gang Chen. 2018. "Estimating Time of Concentration for Overland Flow on Pervious Surfaces by Particle Tracking Method" Water 10, no. 4: 379. https://doi.org/10.3390/w10040379
APA StyleLi, X., Fang, X., Li, J., KC, M., Gong, Y., & Chen, G. (2018). Estimating Time of Concentration for Overland Flow on Pervious Surfaces by Particle Tracking Method. Water, 10(4), 379. https://doi.org/10.3390/w10040379








