Identification of a Contaminant Source Location in a River System Using Random Forest Models
Abstract
:1. Introduction
2. Background
2.1. Problem Description
2.2. Hydrodynamics Simulation
3. Method
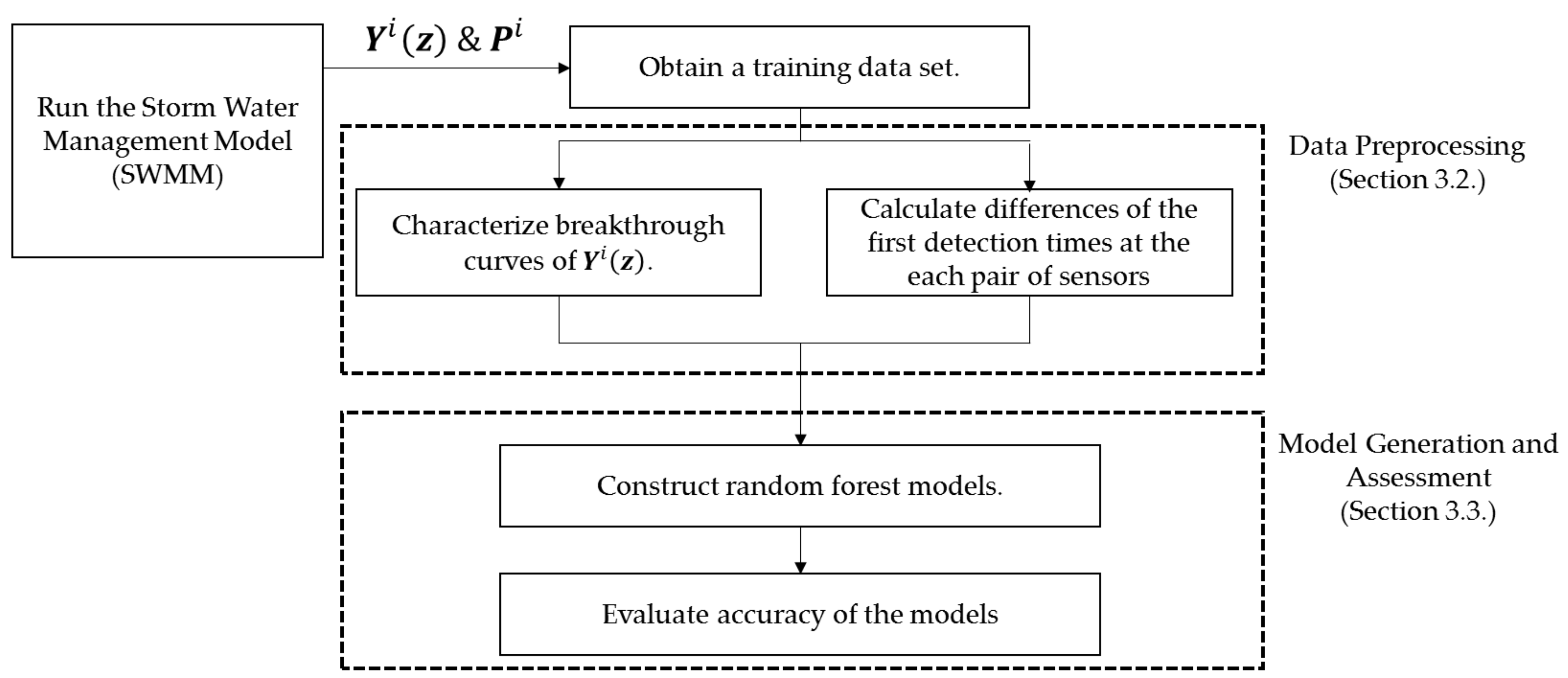
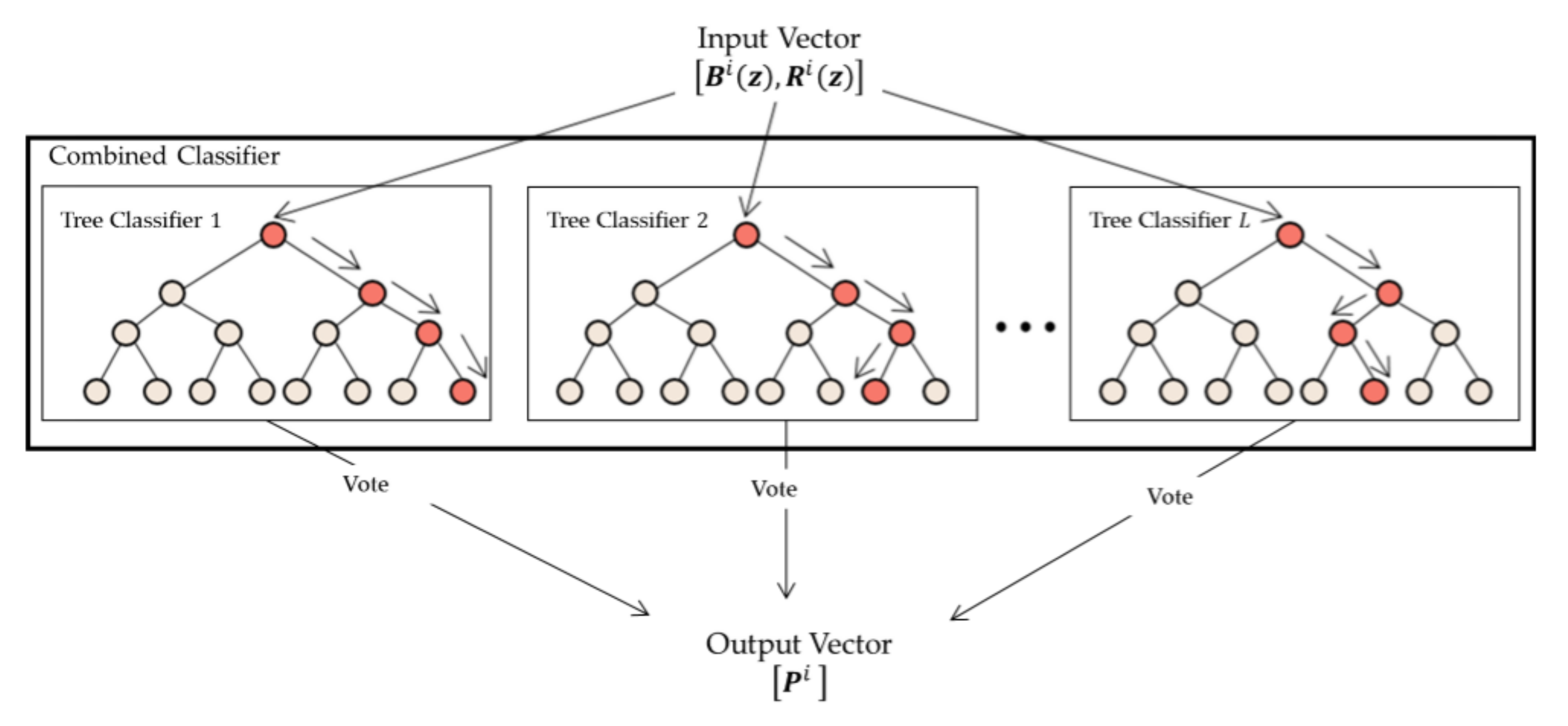
3.1. Overall Workflow
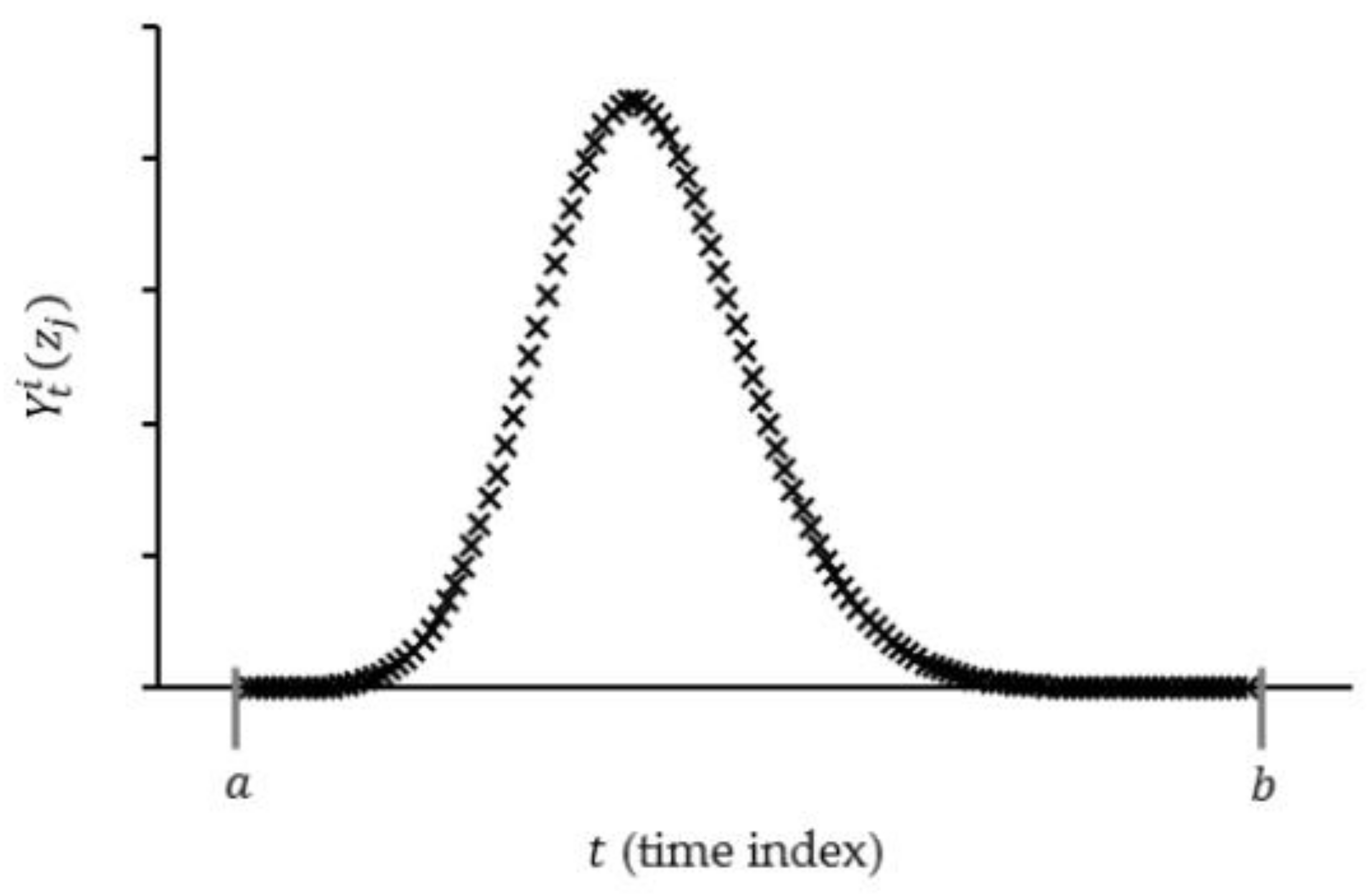
3.2. Data Pre-Processing
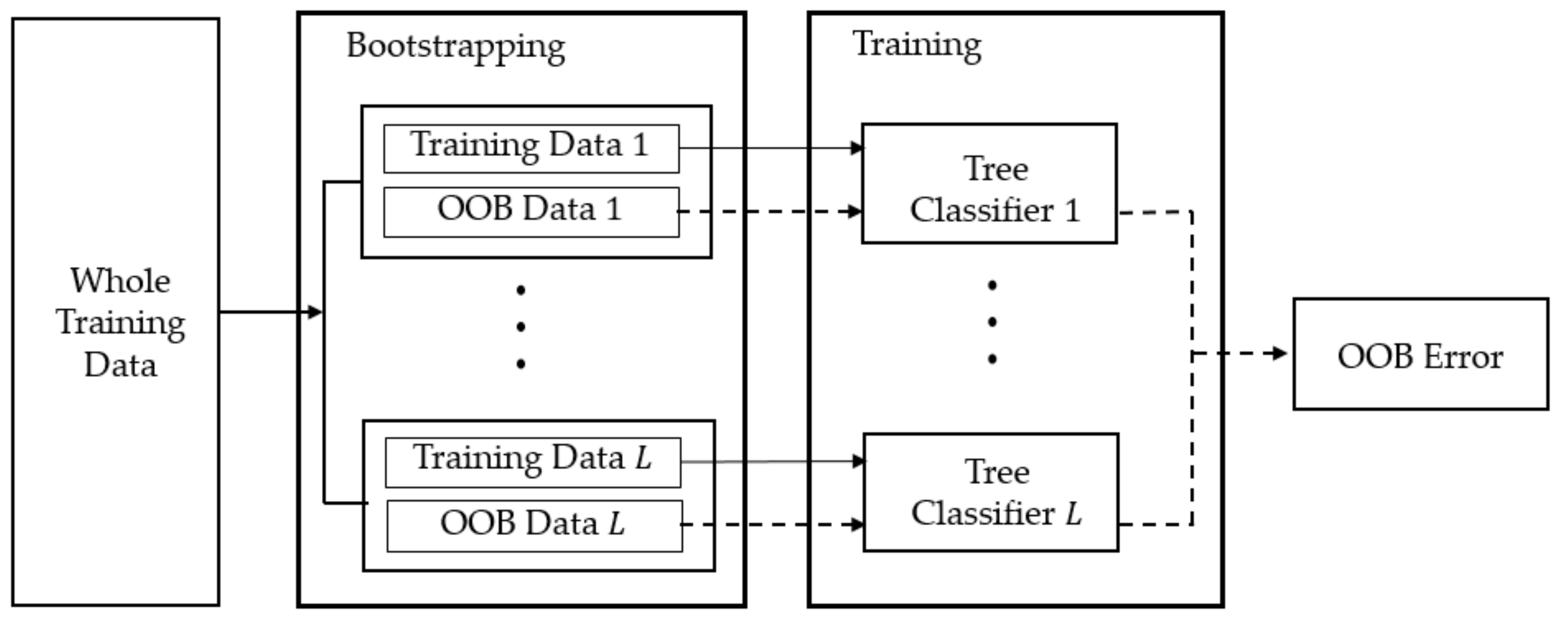
3.3. Model Generation and Assessment
4. Case Study
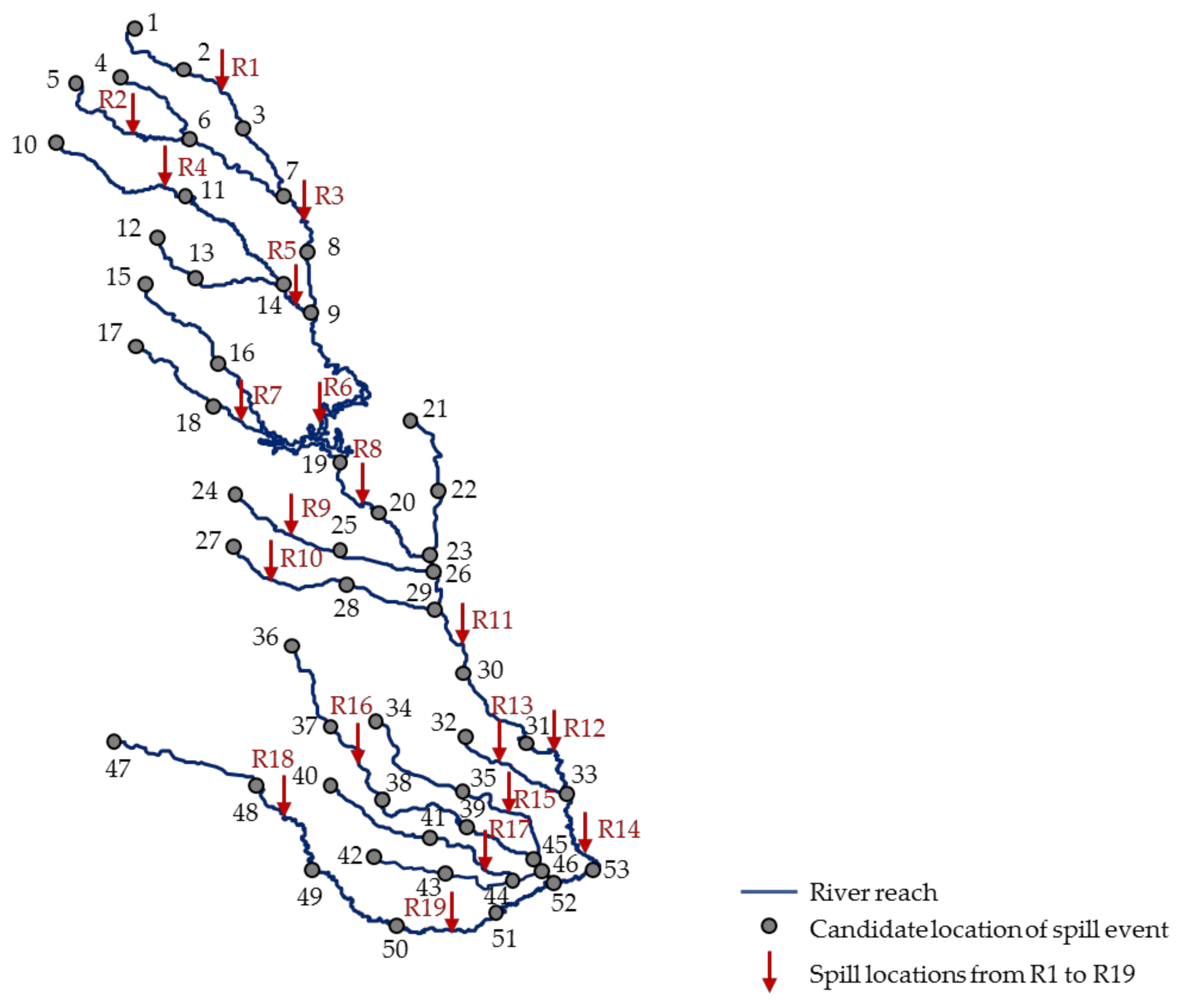
4.1. Study Area and Simulation Setup
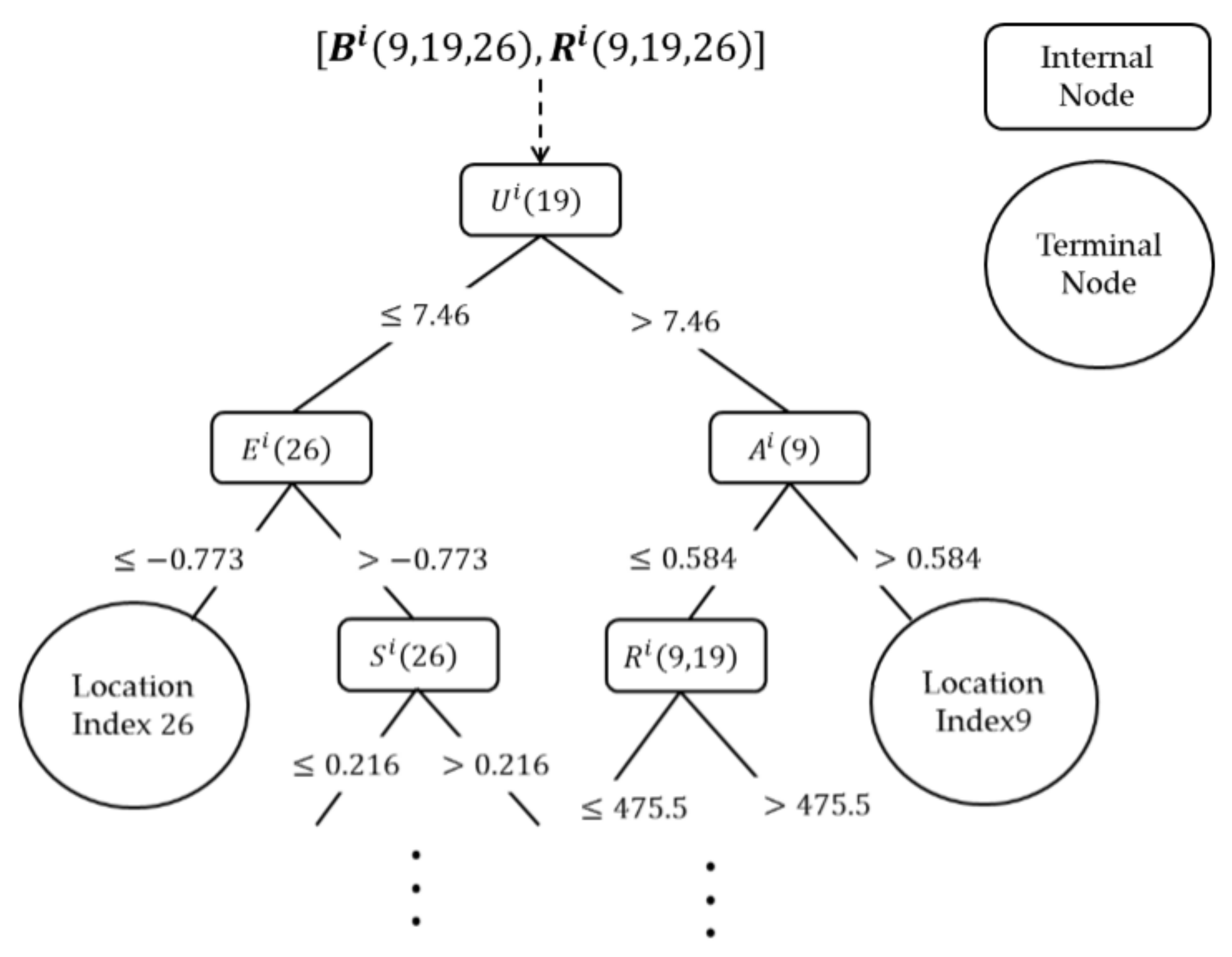
4.2. Random Forest Model Generation
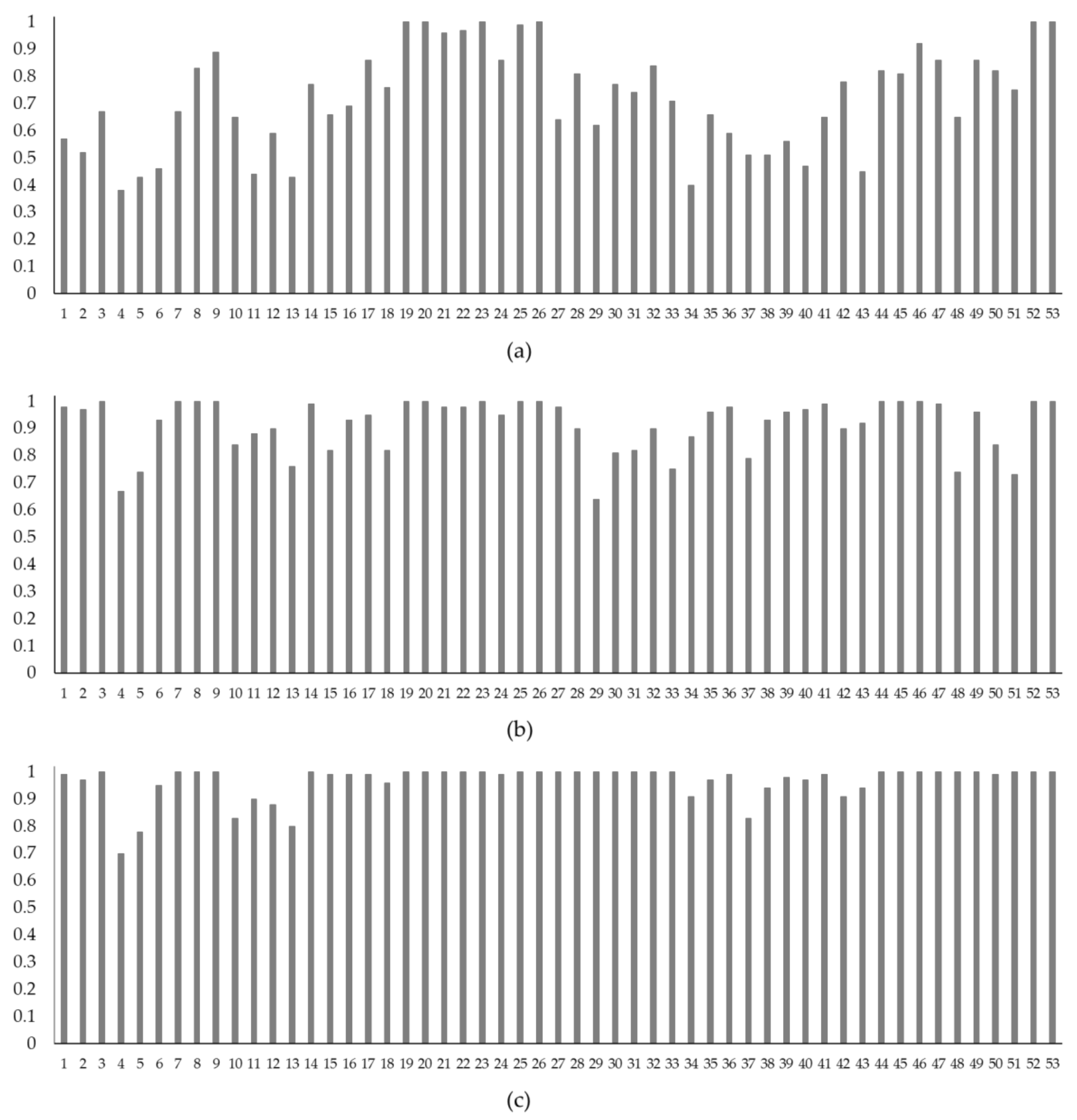
4.3. Model Assessment 1: Spill at a Candidate Location
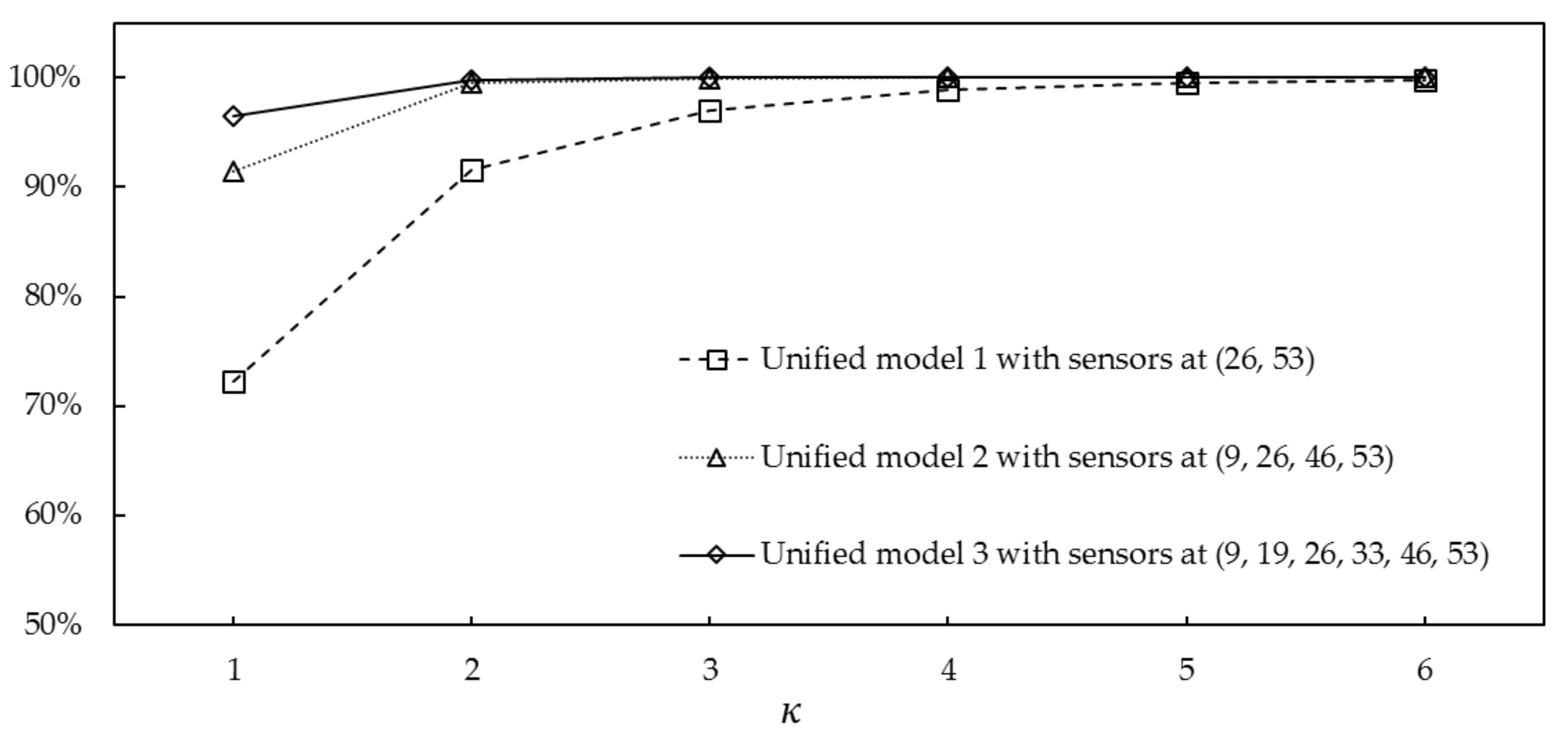
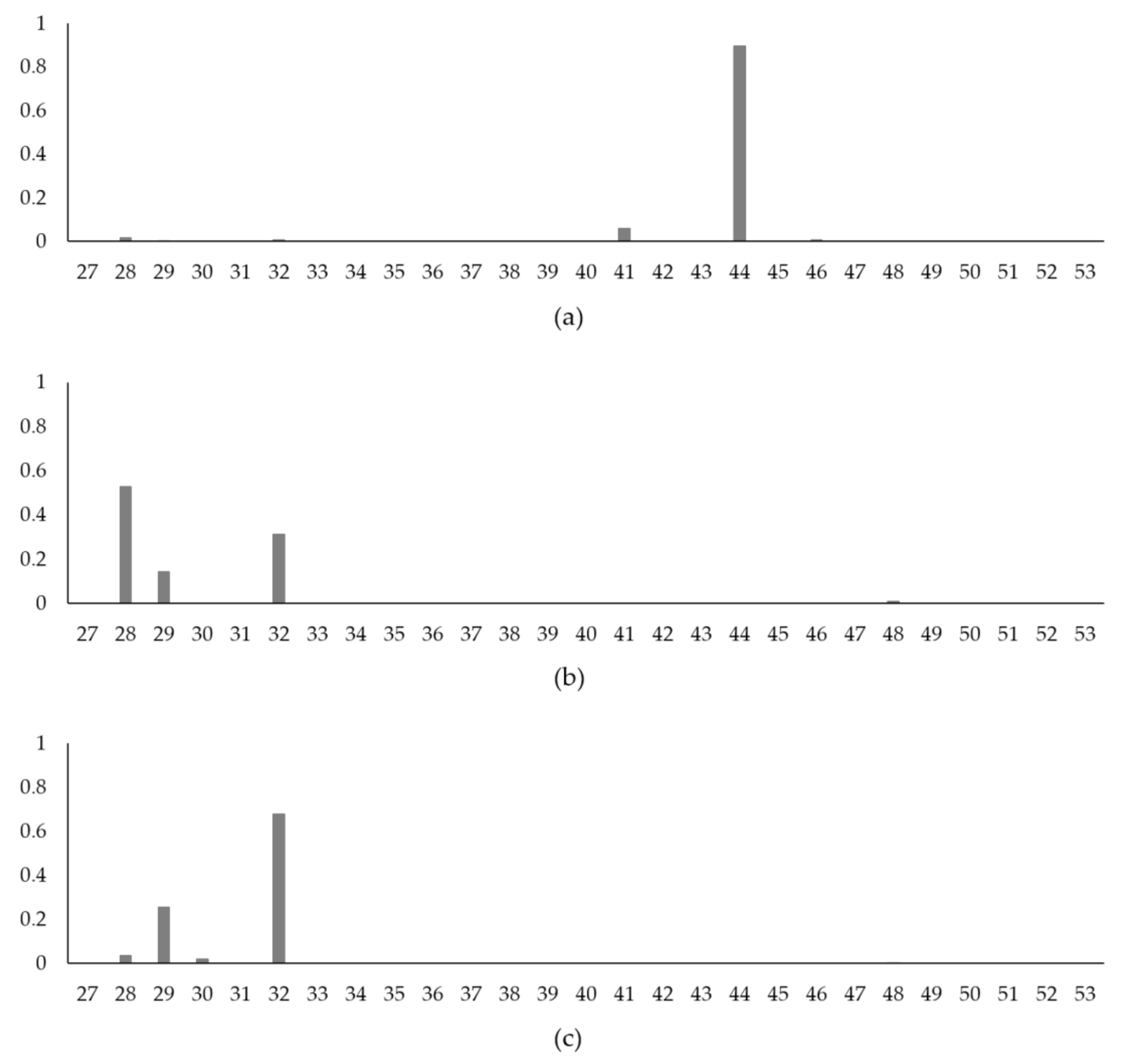
4.4. Model Assessment 2: Spill Near a Candidate Location
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gorelick, S.M.; Evans, B.; Remson, I. Identifying sources of groundwater pollution: An optimization approach. Water Resour. Res. 1983, 19, 779–790. [Google Scholar] [CrossRef]
- Aral, M.M.; Guan, J. Genetic algorithms in search of groundwater pollution sources. In Advances in Groundwater Pollution Control and Remediation; Aral, M.M., Ed.; Springer: Dordrecht, The Netherlands, 1996; pp. 347–369. ISBN 978-94-009-0205-3. [Google Scholar]
- Aral, M.M.; Guan, J.; Maslia, M.L. Identification of contaminant source location and release history in aquifers. J. Hydrol. Eng. 2001, 6, 225–234. [Google Scholar] [CrossRef]
- Sun, A.Y.; Painter, S.L.; Wittmeyer, G.W. A robust approach for iterative contaminant source location and release history recovery. J. Contam. Hydrol. 2006, 88, 181–196. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.M.; Datta, B. Identification of groundwater pollution sources using GA-based linked simulation optimization model. J. Hydrol. Eng. 2006, 11, 101–109. [Google Scholar] [CrossRef]
- Neupauer, R.M.; Lin, R. Identifying sources of a conservative groundwater contaminant using backward probabilities conditioned on measured concentrations. Water Resour. Res. 2006, 42, W03424. [Google Scholar] [CrossRef]
- Neupauer, R.M.; Wilson, J.L. Numerical implementation of a backward probabilistic model of ground water contamination. Groundwater 2004, 42, 175–189. [Google Scholar] [CrossRef]
- Sun, A.Y. A robust geostatistical approach to contaminant source identification. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Singh, R.M.; Datta, B.; Jain, A. Identification of unknown groundwater pollution sources using artificial neural networks. J. Water Resour. Plan. Manag. 2004, 130, 506–514. [Google Scholar] [CrossRef]
- Singh, R.M.; Datta, B. Artificial neural network modeling for identification of unknown pollution sources in groundwater with partially missing concentration observation data. Water Resour. Manag. 2007, 21, 557–572. [Google Scholar] [CrossRef]
- Srivastava, D.; Singh, R.M. Breakthrough curves characterization and identification of an unknown pollution source in groundwater system using an artificial neural network (ANN). Environ. Forensics 2014, 15, 175–189. [Google Scholar] [CrossRef]
- Boano, F.; Revelli, R.; Ridolfi, L. Source identification in river pollution problems: A geostatistical approach. Water Resour. Res. 2005, 41, W07023. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, K.; Wu, Y.; Gao, S.; Cao, W.; Bo, Y.; Shang, Z.; Wu, J.; Zhou, F. Spatio-temporal patterns and source identification of water pollution in Lake Taihu (China). Water 2016, 8, 86. [Google Scholar] [CrossRef]
- Ghane, A.; Mazaheri, M.; Samani, J.M.V. Location and release time identification of pollution point source in river networks based on the backward probability method. J. Environ. Manag. 2016, 180, 164–171. [Google Scholar] [CrossRef] [PubMed]
- Telci, I.T.; Aral, M.M. Contaminant source location identification in river networks using water quality monitoring systems for exposure analysis. Water Qual. Expo. Health 2011, 2, 205–218. [Google Scholar] [CrossRef]
- Grubner, O. Interpretation of asymmetric curves in linear chromatography. Anal. Chem. 1971, 43, 1934–1937. [Google Scholar] [CrossRef]
- Jiang, H. Adaptive Feature Selection in Pattern Recognition and Ultra-Wideband Radar Signal Analysis; California Institute of Technology: Ann Arbor, MI, USA, 2008; ISBN 978-1-2674-8642-4. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2004.
- Telci, I.T.; Nam, K.; Guan, J.; Aral, M.M. Optimal water quality monitoring network design for river systems. J. Environ. Manag. 2009, 90, 2987–2998. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7138-7. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Bernard, S.; Heutte, L.; Adam, S. Influence of hyperparameters on random forest accuracy. In Multiple Classifier Systems; Benediktsson, J.A., Kittler, J., Roli, F., Eds.; Springer: Berlin, Germany, 2009; pp. 171–180. ISBN 978-3-642-02326-2. [Google Scholar]
- Feng, Q.; Liu, J.; Gong, J. Urban flood mapping based on unmanned aerial vehicle remote sensing and random forest classifier—A case of Yuyao, China. Water 2015, 7, 1437–1455. [Google Scholar] [CrossRef]
- Breiman, L. Manual on Setting up, Using, and Understanding Random Forests V3.1; University of California at Berkeley: Berkeley, CA, USA, 2002. [Google Scholar]
- Park, C.; Telci, I.T.; Kim, S.-H.; Aral, M.M. Designing an optimal water quality monitoring network for river systems using constrained discrete optimization via simulation. Eng. Optim. 2014, 46, 107–129. [Google Scholar] [CrossRef]
- Kim, S.-H.; Aral, M.M.; Eun, Y.; Park, J.J.; Park, C. Impact of sensor measurement error on sensor positioning in water quality monitoring networks. Stoch. Environ. Res. Risk Assess. 2017, 31, 743–756. [Google Scholar] [CrossRef]


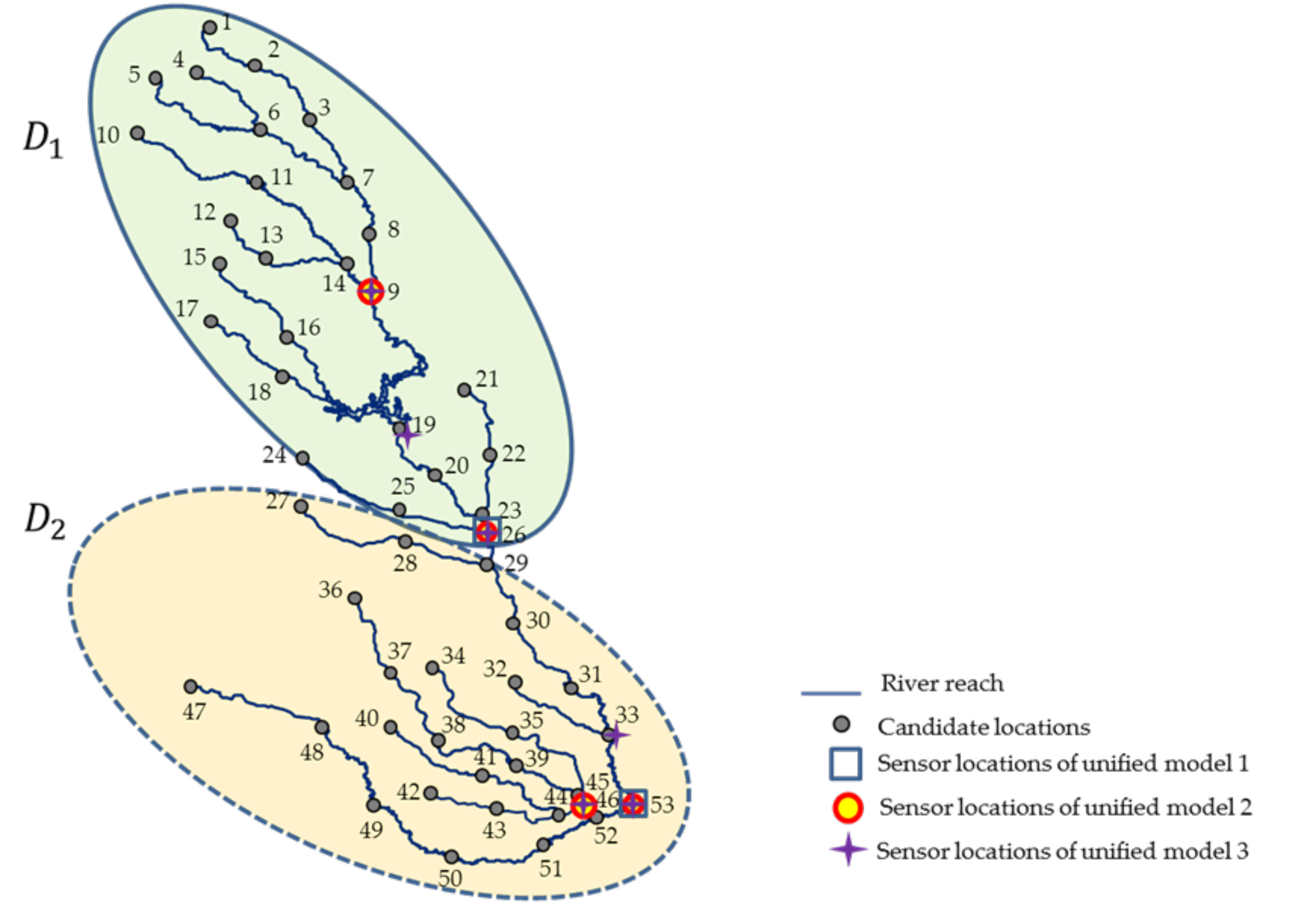

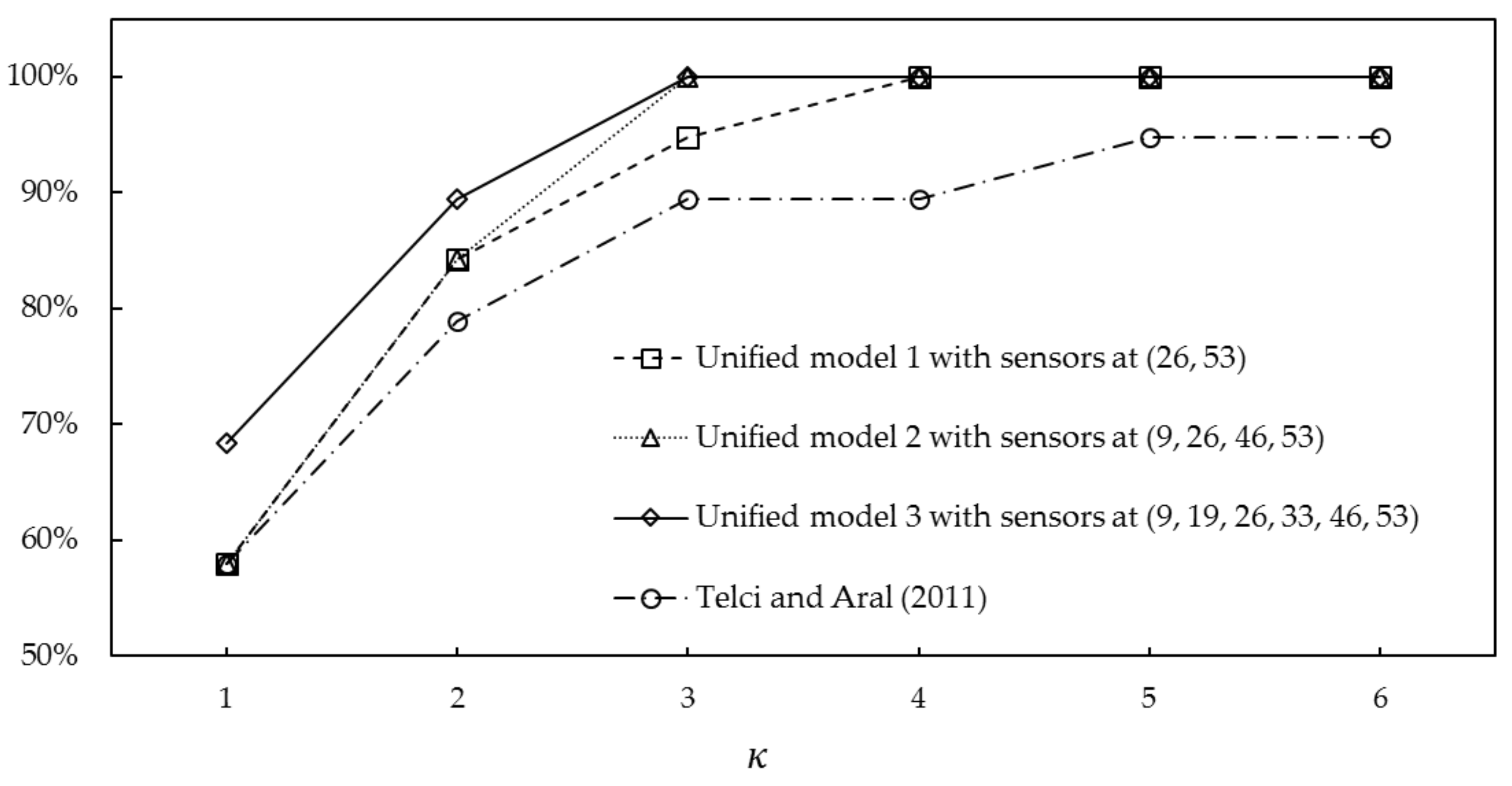
| Unified Model # | Sensor Locations | Set of Candidate Spill Locations | Random Forest Models | OOB Error (%) | |
|---|---|---|---|---|---|
| 1 | (26, 53) | 8 | 26.11 | ||
| 3 | 29.37 | ||||
| 2 | (9, 26, 46, 53) | 9 | 7.09 | ||
| 7 | 10.56 | ||||
| 3 | (9, 19, 26, 33, 46, 53) | 10 | 4.87 | ||
| 9 | 2.43 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.J.; Park, C.; Lee, M.L. Identification of a Contaminant Source Location in a River System Using Random Forest Models. Water 2018, 10, 391. https://doi.org/10.3390/w10040391
Lee YJ, Park C, Lee ML. Identification of a Contaminant Source Location in a River System Using Random Forest Models. Water. 2018; 10(4):391. https://doi.org/10.3390/w10040391
Chicago/Turabian StyleLee, Yoo Jin, Chuljin Park, and Mi Lim Lee. 2018. "Identification of a Contaminant Source Location in a River System Using Random Forest Models" Water 10, no. 4: 391. https://doi.org/10.3390/w10040391
APA StyleLee, Y. J., Park, C., & Lee, M. L. (2018). Identification of a Contaminant Source Location in a River System Using Random Forest Models. Water, 10(4), 391. https://doi.org/10.3390/w10040391




